Abstract
Focal epilepsy is conceived of as activating local areas of the brain as well as engaging regional brain networks. Graph theory represents a powerful quantitative framework for investigation of brain networks. Here we investigate whether functional network changes are present in extratemporal focal epilepsy.
Task-free functional magnetic resonance imaging data from 15 subjects with extratemporal epilepsy and 26 age and gender matched healthy controls were used for analysis. Local network properties were calculated using local efficiency, clustering coefficient and modularity metrics. Global network properties were assessed with global efficiency and betweenness centrality metrics. Cost-efficiency of the networks at both local and global levels was evaluated by estimating the physical distance between functionally connected nodes, in addition to the overall numbers of connections in the network.
Clustering coefficient, local efficiency and modularity were significantly higher in individuals with focal epilepsy than healthy control subjects, while global efficiency and betweenness centrality were not significantly different between the two groups. Local network properties were also highly efficient, at low cost, in focal epilepsy subjects compared to healthy controls.
Our results show that functional networks in focal epilepsy are altered in a way that the nodes of the network are more isolated. We postulate that network regularity, or segregation of the nodes of the networks, may be an adaptation that inhibits the conversion of the interictal state to seizures. It remains possible that this may be part of the epileptogenic process or an effect of medications.
Keywords: Extratemporal, Focal epilepsy, Graph theory, Network, Connectomics, fMRI
Highlights
-
•
Focal epilepsy is a neurological disorder known to affect neural networks.
-
•
We examine fMRI network changes during rest in extratemporal epilepsy patients.
-
•
Extratemporal epilepsy subjects show increased (isolated) local network regularity.
-
•
Network isolation may represent a ‘seizure-protection’ mechanism in focal epilepsy.
1. Introduction
Extratemporal epilepsy is a common form of focal epilepsy that is often treatment resistant (Kutsy, 1999). It has also become increasingly apparent that focal epilepsy is a disorder that affects common neuronal networks beyond the seizure onset zone (Bertram, 2013; Fahoum etal., 2012; Flanagan etal., 2014; Laufs etal., 2011).
Graph theoretic approaches have been widely used for brain connectivity analysis to quantify macroscopic structural and functional properties of brain networks (Bullmore and Sporns, 2009; Sporns, 2011). Networks can be conceptualised within a framework of regular, random and complex networks. Regular networks display high local connectivity and low global connectivity, while random networks show the opposite pattern with low local connectivity and high global connectivity. Complex networks show an optimised balance between local and global connectivity (Latora and Marchiori, 2001; Watts and Strogatz, 1998). The human brain displays a complex network topology with a small-world and scale-free configuration (Oh etal., 2014; van den Heuvel etal., 2008), with many nodes facilitating local functioning and a fewer set of nodes subserving global information processing (Bullmore and Sporns, 2012). Deviates from such a complex network topology towards randomness or regularity in the human brain may serve as a marker of neuropathology (Stam, 2014).
Graph analysis of the large-scale neural network topology is of particular interest in epilepsy research, as it may improve our understanding about epilepsy as a network disorder in which several normal and abnormal brain nodes are interacting with each other dynamically. Several studies have investigated functional brain network changes during focal seizure periods using different modalities such as electroencephalography (EEG; Ponten etal., 2007; Schindler etal., 2008), electrocorticography (Kramer etal., 2010; Vega-Zelaya etal., 2014), and magnetoencephalography (Ibrahim etal., 2014). Findings of these studies suggest that seizure onset and seizure propagation phases are associated with an increase in local network connectivity and a decrease in global connectivity processes, thus resembling regular network activity. It has been suggested that inter-ictal functional networks in focal epilepsy may be more regular than that of healthy controls (see van Diessen etal., 2014 for a meta-analysis), but studies applying graph theoretic analysis in task-free functional MRI data (fMRI) are lacking in specific cohorts such as extratemporal focal epilepsy.
A proper characterisation of the interactions between brain regions is crucial to a contemporary understanding of focal epilepsy. To this end, we use a graph theory-based functional connectivity approach applied to task-free fMRI data to investigate functional network properties in subjects with extratemporal epilepsy.
2. Materials and methods
2.1. Subjects and ethics
In total, 41 adult subjects were included in the study: 15 subjects with extratemporal epilepsy (mean age: 31.1 ± 11.7 years, 8 female) and 26 healthy controls (mean age: 31.4 ± 9.6 years, 14 female). Age and gender were not different between groups (this was tested using a two-samplet-test assuming unequal variance and 5000 random permutations with p-values of 0.92 and 0.98, respectively). Information of age of seizure onset, number of antiepileptic drugs and surgery is provided in Supplementary Table1. Only focal epilepsy patients with a non-temporal neocortical seizure onset were included in this study. Based on structural imaging, 8 patients were MRI-negative while 7 patients were MRI-positive with imaging features of a subtle focal cortical dysplasia on their structural MRI. All MRI-negative patients are also suspected to have a uniform onset likely to be associated with focal cortical dysplasia, despite negative imaging. With regard to the seizure-onset areas, 7 subjects had a frontal lobe onset and 4 subjects had a seizure onset in central cortices, while 4 subjects had seizure onset in posterior brain regions (including temporo-parieto-occipital junction onset). No subjects had structural imaging features of hippocampal sclerosis. The Austin Health Human Research Ethics Committee approved the study, and all subjects gave written consent to participate in the study.
In total, 41 adult subjects were included in the study: 15 subjects with extratemporal epilepsy (mean age: 31.1 ± 11.7 years, 8 female) and 26 healthy controls (mean age: 31.4 ± 9.6 years, 14 female). Age and gender were not different between groups (this was tested using a two-samplet-test assuming unequal variance and 5000 random permutations with p-values of 0.92 and 0.98, respectively). Information of age of seizure onset, number of antiepileptic drugs and surgery is provided in Supplementary Table1. Only focal epilepsy patients with a non-temporal neocortical seizure onset were included in this study. Based on structural imaging, 8 patients were MRI-negative while 7 patients were MRI-positive with imaging features of a subtle focal cortical dysplasia on their structural MRI. All MRI-negative patients are also suspected to have a uniform onset likely to be associated with focal cortical dysplasia, despite negative imaging. With regard to the seizure-onset areas, 7 subjects had a frontal lobe onset and 4 subjects had a seizure onset in central cortices, while 4 subjects had seizure onset in posterior brain regions (including temporo-parieto-occipital junction onset). No subjects had structural imaging features of hippocampal sclerosis. The Austin Health Human Research Ethics Committee approved the study, and all subjects gave written consent to participate in the study.
2.2. Imaging parameters
All subjects were scanned on a Siemens MRI at 3T system (Skyra/Trio, Siemens, Erlanger, Germany). Blood oxygen level dependent (BOLD) functional imaging parameters were as follows: 44 slices with 3 mm thickness; TR = 3000 ms, TE = 30 ms, flip angle = 85°, voxel size of 3 × 3 × 3 mm and an acquisition matrix of 72 × 72. T1 weighted images were also acquired during the same session for coregistration to functional images.
2.3. Data pre-processing
Ten minutes of task-free fMRI data (200 volumes) was used for analysis for all subjects. No EEG was recorded during the scans; hence we cannot exclude the presence of interictal epileptic discharges during the scans. None of the focal epilepsy subjects experienced an ictal event during the scan, based on post-scan interview. SPM8 (Friston etal., 2011; http://www.fil.ion.ucl.ac.uk/spm/) and DPARSF(Chao-Gan and Yu-Feng, 2010; http://rfmri.org/DPARSF) toolboxes, both in MATLAB R2013a (MathWorks Inc., Natick, MA,United States), were used for pre-processing purposes. The functional images were slice-time corrected, realigned and co-registered to the anatomical T1-weighted images before segmentation was conducted using DARTEL(Ashburner, 2007). The fMRI time-series were further detrended and the average signals associated with the cerebrospinal fluid and white matter regions, in addition to 24 motion parameters (Friston etal., 1996), were regressed out from the data. No global signal regression was used. Images from all subjects were normalised to the common Montreal Neurological Institute (MNI) space (3 mm3 voxels). A narrow band-pass filter was used with cutoff frequencies of 0.03 and 0.07 Hz. Task-free fMRI data in this frequency range contain minimal noise and physiological confounds (Glerean etal., 2012), while possessing reliable and biologically meaningful network information (Achard etal., 2006; Liang etal., 2012; Schroter etal., 2012). Average in-scanner head movement was not different between focal epilepsy patients and healthy controls. This was tested using a two-samplet-test assuming unequal variance and 5000 random permutations (p = 0.47). In order to preserve the continuity of the original BOLD signals, and equal number of timepoints for all subjects, volumes with head movement higher than 0.5 mm were omitted and replaced by the average timeseries of their nearest neighbours. Head movement estimates were calculated using a framewise displacement algorithm (Power etal., 2012).
2.4. Graph theory analysis
An in-house network analysis pipeline was used implementing Matlab codes from the Brain Connectivity Toolbox (BCT: Rubinov and Sporns (2010); https://sites.google.com/site/bctnet/Home). The pre-processedtask-free fMRI data (Fig.1A) of each subject was divided into sub-regions using a brain mask consisting of 278 nodes. This mask was derived from a previous study that used functional connectivity data from 78 healthy individuals to form functionally homogenous brain regions (Shen etal., 2013). The parcellation mask was used because of its biological plausibility for task-free fMRI analysis and accurate spatial grey matter boundaries (see Fig.1B). Subsequently, these 278 segregated brain regions were represented as nodes in our network framework. After averaging the time-series within each node (Fig.1C), a Pearson correlation score was calculated between all nodes to determine their pair-wise functional connectivity strength. This step resulted in a symmetric connectivity matrix of size 278 × 278 for each individual where each element was associated with a correlation score between the mean time series of two regions in the functional connectivity mask (Fig.1D). The resulting individual connectivity matrices (Fig.1E) were Fisher's R to Z transformed (Mudholkar, 2004).
Fig. 1.
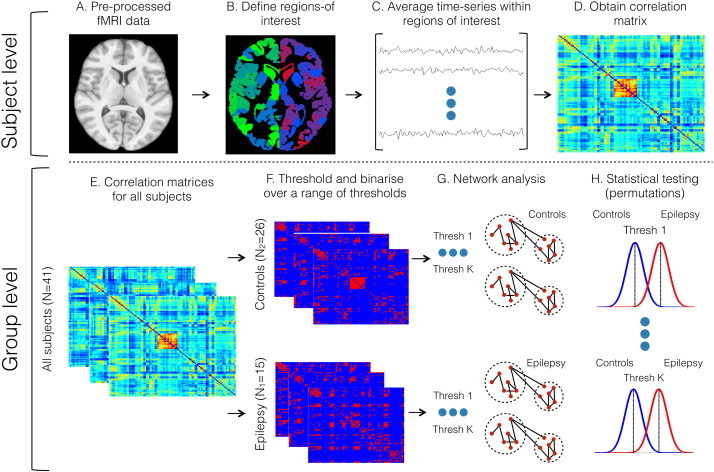
A schematic overview of the functional connectivity steps.
The connectivity matrices were tested on a range of different threshold levels to negate the issue of semi-arbitrary network thresholding (Langer etal., 2013— Fig.1F). Here, changing the density of the networks controlled the threshold levels. The network density denotes the percentage of the pair-wise connections (i.e.,edges) in the network that survive after thresholding. Here, a network density of 5–30% highest correlation coefficients was preserved with a 1% edge increment for each threshold step, resulting in a total of 26 network thresholds for each subject. The chosen network density range has previously been reported to contain biologically plausible information about brain functional networks (Dennis etal., 2012; Fornito etal., 2010). After thresholding, the matrices were binarised such that the pair-wise correlation values above the given threshold were marked as 1 (connection between nodes) and others were set to 0 (no connection between nodes).
2.5. Local network properties (network segregation)
To assess local connectivity properties, i.e.,network segregation, we firstly used the local efficiency(LE) metric (Latora and Marchiori, 2001). LE is defined as the inverse of the shortest path length between connected nodes that are neighbours with the node of interest. The shortest path is defined as number of steps, or links, between network nodes. Clustering coefficient (CCnorm) was also used (Watts and Strogatz, 1998). The clustering coefficient estimates the degree of triangular connected nodes around the node of interest, obtaining an estimate of graph cliquiness. The clustering coefficient was normalised by dividing the original clustering coefficient values with a random clustering coefficient estimate (random clustering coefficient scores were estimated by randomising the original correlation matrices 20 times for every subject), resulting in a normalised clustering coefficient(CCnorm) score. The modularity(MOD) index is estimated based on how greatly sub-communities of nodes (i.e.,modules) in the network are overlapping (Rubinov and Sporns, 2010). The MOD index subsequently gives an estimate of relative isolation of sub-communities in the network.
2.6. Global network properties (network integration)
To estimate global network functioning, or network integration, global efficiency (GE) was calculated. GE takes the inverse of the shortest path length between nodes, giving a value of the relative quality of information travel between all nodes in the network (Latora and Marchiori, 2001). Betweenness centrality(BC) is a metric that measures the relative importance of a node within the network, i.e.,neural hubs. The BC estimates the fraction of the shortest paths that travel through each node. In turn, nodes that relay information in a range of network-wide nodes will have a high BC. See Rubinov and Sporns (2010), for a full overview of the metrics used in this study.
2.7. Network cost-efficiency
Neural networks strive to optimise local and global neural functioning for lowest possible (metabolic) cost (Attwell and Laughlin, 2001; Bullmore and Sporns, 2012). To quantify cost-efficiency tradeoffs of functional brain networks, we used two different estimates of network cost. The first cost parameter denoted the number of functional connections in the network, assuming that an increase in the number of connections will lead to a more cost-expensive network. The second cost parameter was derived from the length of functional connections (Euclidean distance) between nodes that were interconnected in the network (Alexander-Bloch etal., 2013; Fornito etal., 2011). Euclidean distances between all functionally connected nodes were calculated based on the centre-of-mass coordinates for all nodes in the MNI space. In this context, we assume that the average Euclidean distance between functionally connected nodes represents the relative cost of the network, i.e.,longer connections are more costly than short connections. Subsequently, averaged local cost-efficiency(CEloc) over all nodes in the network can be defined as (Fornito etal., 2011):
| (1) |
and average global cost-efficiency(CEglob) over all network nodes is defined as (Fornito etal., 2011):
| (2) |
A high score of CEloc/ CEglob is indicative of highly efficient network functioning at the local/global scale with minimal connection cost. The LE and GE estimates in Eq.(1) and Eq.(2) always take values within the range of 0–1. We also normalised the pair-wiseEuclidean distances by their maximum value over all possible combinations resulting in a numerical range between 0 and 1. Network density estimates also range from 0 to 1, where 0 is a non-connected network and 1 is a fully connected network.
2.8. Statistical analysis
For each of the seven measures used in this study (LE, CCnorm, MOD, GE, BC, CElocand CEglob), a subject-dependentnetwork-wide value was obtained by averaging the measure over all graph nodes. Two-sample permutation t-tests assuming unequal variances between the two groups (epilepsy vs. controls) with 5000 non-parametric permutations were performed to quantify group differences at each of the 26 thresholds (see also Section2.4). For each permutation, group labels were randomly assigned to all subjects and the shuffled population was divided into two random groups. The graph measures were then extracted from each randomised combination leading to a non-parametric distribution under the null hypothesis of no-difference between epilepsy and control groups. To control for multiple comparisons over 26 thresholds (within-measure variability) and 7 network measures (between-measure variability), False Discovery Rate (FDR) correction using a q-value of 0.05 was applied to all p-values derived from our analysis (26 thresholds × 7 measures = 182 p-values). To further estimate the reliability of group effects, standardised effect sizes and the corresponding 95% confidence intervals (CI) were calculated for all metrics.
2.9. Network models
To assess how network metrics behave under different network topologies we simulated a complex, regular and random network. The complex network model was derived from an independent dataset based on group averaged task-free fMRI data from 26 healthy control subjects (Crossley etal., 2013), freely available online (BCT: GroupAverage_rsfMRI.m-https://sites.google.com/site/bctnet/datasets). This network consisted of 638 nodes and a network density of 9.14%. Regular (BCT: makelatticeCIJ.m) and random (BCT; makerandCIJ_und.m) matrices were constructed with the same number of nodes (n = 634) and network density (9.14%) as the complex network model (see Fig.2 for the three network models).
Fig. 2.
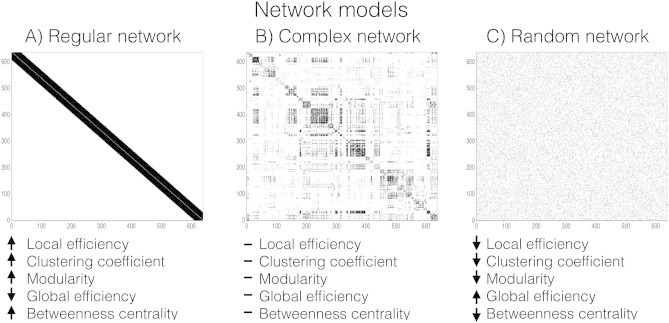
Network models— regular (left), complex (middle) and random (right) networks.
We ran LE, CCnorm,MOD, GE, and BC for the three generated network models (Fig.2). LE, CC, MOD and BC had highest values in the simulated regular network (LEregular = 0.88, CCnorm−regular = 8.15, MODregular = 0.71, BCregular = 4227) over the complex (LEcomplex = 0.75, CCnorm−complex = 5.97,MODcomplex = 0.47, BCcomplex = 1026) and simulated random networks (LErandom = 0.44, CCnorm−random = 1, MODrandom = 0.11, BCrandom = 582). GE was highest in the random network configuration (GErandom = 0.55) compared to regular and complex networks (GEregular = 0.26 and GEcomplex = 0.44). For all the metrics, complex network estimates lie between the random and regular networks highlighting integration/segregation trade-offs in biological networks. These results are consistent with previous work on regular, random, and complex networks (Latora and Marchiori, 2001; Watts and Strogatz, 1998).
3. Results
3.1. Network metrics between focal epilepsy subjects and controls
An increase of LE was seen in the extratemporal focal epilepsy group compared to healthy controls (Fig.3A) with 10 of 26 network densities statistically significant after FDR correction (median effect size = 0.90, CI 95% of 0.16–1.65). CCnorm was significantly higher in focal epilepsy subjects compared to controls for 23 of 26 network density thresholds (FDR-corrected). Median effect size for CCnorm was 1.21 with CI 95% of 0.41–2.01. Focal epilepsy subjects also displayed increased network MOD versus controls (Fig.3B) in 4 of 26 density thresholds (FDR-corrected) with a median effect size of 0.76 and CI 95% of 0.05–1.48. No statistically significant differences were seen between focal epilepsy subjects and healthy controls for GE (median effect size = −0.53, CI 95% of 0.15 to −1.23— Fig.3C) and BC (median effect size = 0.56, CI 95% of −0.12–1.25— Fig.3D).
Fig. 3.
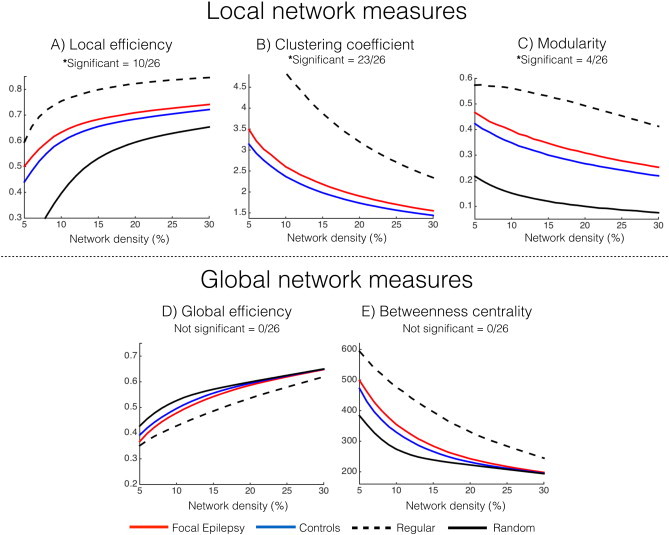
Whole-brain local and global network differences between extratemporal focal epilepsy subjects (red line) and healthy controls (blue line). Regular and random networks are displayed with black dotted and solid line respectively. A)LE. B)CCnorm. Note that the random networks for CCnorm have a value of 1 for all 26 thresholds as CCnorm incorporates random networks (see Section2.5). C)MOD. D)GE. E)BC.
3.2. Network cost-efficiency
CEloc was significantly higher in focal epilepsy compared to controls in 10 of the 26 network density thresholds computed after FDR correction (median effect size = 0.84, CI 95% of 0.12–1.32— Fig.4A). CEglob was not statistically different between groups (median effect size = −0.63, CI 95% of 0.09 to −1.82— Fig.4B).
Fig. 4.
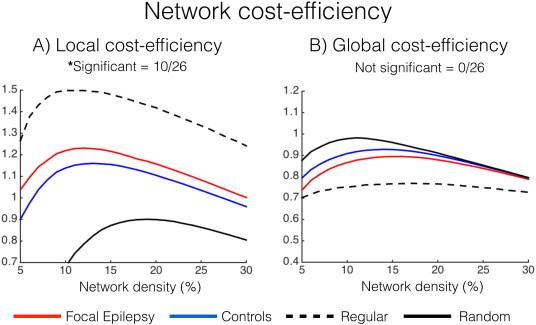
Local and global network cost-efficiency: A)CEloc. B)CEglob.
4. Discussion
4.1. Focal epilepsy and increased network segregation
Since the advent of using graph theory to extract network information from neuroimaging data, attempts have been made to apply graph theory to focal epilepsy (see van Diessen etal. (2014) for an overview), providing evidence that epilepsy is a disorder affecting neural networks (Engel etal., 2013; Richardson, 2012). There is still, however, a gap in the literature when it comes to building reliable network models to specific epilepsy cohorts. We used an fMRI graph theory based approach to delineate whole-brain network effects between subjects with extratemporal focal epilepsy and healthy controls. To this end, we used multiple network density thresholds with permutation testing (Fig.1) and demonstrated increased local network segregation (measured with clustering coefficient, local efficiency and modularity) in patients with focal epilepsy compared to healthy controls (Fig.3A–C). Increased MOD suggests that sub-communities of nodes are isolated, while increased CCnorm together with LE indicates excessive ‘cliquiness’ between neighbour nodes in this particular patient group. Based on our simulation results (Fig.2), we confirm that these network features are characteristic of a brain topology that is shifted towards a regular as compared to a complex network topology (Latora and Marchiori, 2001; Watts and Strogatz, 1998). A regular network consists of nodes that are more isolated and fragmented (Fig.2— left) than a complex or random network (Fig.2— middle and right). Although all biological networks are inherently complex (Sporns, 2011), parameters such as network regularity and randomness may be useful indicators of network alterations in disease states (Stam, 2014; Stam and van Straaten, 2012).
4.2. Focal epilepsy— a fault tolerant network view
To maximise the fault tolerance of the network, i.e.,maintaining overall network functioning despite local network disruption (Dubrova, 2013), an ‘unhealthy’ node in an adaptive network is best to detach itself from the wider network. Simulation data based on our network models outlined in Fig.2 show that a regular network is more robust to local network damage than a complex or random network (see Supplementary Fig.1A). This indicates that regular networks are more fault tolerant. Although the underlying biological mechanisms of our finding of a more regularised network topology in focal epilepsy is unknown, we postulate that a neuromechanistic process of fault tolerance that segregates network nodes may prevent the brain from continuously seizing, and in the event of a seizure, prevent seizure spread. Perilesional cortex contains neurons with aberrant firing patterns, giving them a propensity to seize (Neubauer etal., 2014). Neuronal processes that contain or counteract these abnormal epileptic effects, such as network fault tolerance, may result in ‘isolation’ of perilesional cell structures, thus preventing focal seizure instigation and spread.
Supplementary Fig. 1.
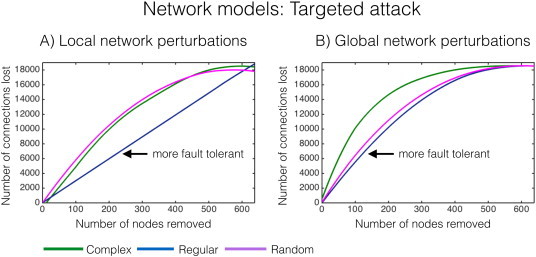
Targeted attack of networks. Network nodes of highest LE (A)and GE (B)were removed iteratively for the complex, regular and random network models in Fig.2, and the subsequent number of surviving connections was counted. A high number of lost connections indicate that the network is fault intolerant, i.e.,the curve in the above graph above is ‘left shifted’, or more in the upper left quadrant. The graphs towards the lower right quadrant are more fault tolerant. A)The regular network is robust to local network perturbations (arrow), whereas in B)both regular and random networks are robust to global network perturbations (arrow).
To maximise the fault tolerance of the network, i.e.,maintaining overall network functioning despite local network disruption (Dubrova, 2013), an ‘unhealthy’ node in an adaptive network is best to detach itself from the wider network. Simulation data based on our network models outlined in Fig.2 show that a regular network is more robust to local network damage than a complex or random network (see Supplementary Fig.1A). This indicates that regular networks are more fault tolerant. Although the underlying biological mechanisms of our finding of a more regularised network topology in focal epilepsy is unknown, we postulate that a neuromechanistic process of fault tolerance that segregates network nodes may prevent the brain from continuously seizing, and in the event of a seizure, prevent seizure spread. Perilesional cortex contains neurons with aberrant firing patterns, giving them a propensity to seize (Neubauer etal., 2014). Neuronal processes that contain or counteract these abnormal epileptic effects, such as network fault tolerance, may result in ‘isolation’ of perilesional cell structures, thus preventing focal seizure instigation and spread.
Support for the idea that elevated network regularity is related to focal epilepsy mostly comes from studies using electrophysiological measures. Network segregation (regularity) is likely to constitute a spatio-temporal signature of onset and propagation stages during focal seizures (Ibrahim etal., 2014; Kramer etal., 2010; Ponten etal., 2007; Schindler etal., 2008; Vega-Zelaya etal., 2014; Warren etal., 2010). Luo etal. (2014) report that fMRI connectivity between the seizure onset area and its immediate neighbour areas is increased in frontal lobe epilepsy patients, while connectivity between the seizure onset area and more distant areas is decreased. This effect did not differ between epochs with and without epileptic activity on simultaneously recorded EEG. Le Van Quyen etal. (2003) also proposed a model where the seizure onset area isolates itself from the wider network preictally. These studies support our finding of increased network segregation in focal epilepsy and suggest that these phenomena may be an important aspect of preventing the conversion of the interictal state to a seizure.
4.3. Focal epilepsy and network cost-efficiency
To obtain physically meaningful information of networks, we explored cost-efficiency of local and global network properties (Achard and Bullmore, 2007; Alexander-Bloch etal., 2013; Bullmore and Sporns, 2012; Fornito etal., 2011). To our knowledge, cost-efficiency of networks has previously not been reported in epilepsy. Our results demonstrate that patients with focal epilepsy display high local network efficiency, at low cost, compared to healthy controls. Increased local cost-efficiency is different from graph theory as it incorporates physical properties of the brain (distance between functionally connected nodes) rather than an abstract model of all nodes. The finding that local network properties are also altered using this parameter in focal epilepsy; and is related to regularised network functioning (Fig.4A— black dotted line) supports the idea that these changes are biologically real and not simply a feature of the graph theory model. In the context of running cost and energy budgeting of the human brain (Attwell and Laughlin, 2001), regular networks are (metabolically) cheaper to run on a day-to-day basis mainly due to inefficient global information travel within this particular network configuration (Bullmore and Sporns, 2012). It is therefore tempting to speculate that high cost-efficiency represents an adaptive neural process that may contribute to high fault tolerance of networks in focal epilepsy. It may be that this is at the price of optimal network capability and function.
Worthy of note is that cost-efficiency measures peaked around a network density of ~10% (Fig.4), which is in contrast to LE, CCnorm, MOD, GE and BC that increased/decreased proportional to the number of connections in the network, i.e.,network density (Fig.3). This finding is similar to Fornito etal. (2011) and suggests that cost-efficiency measures may be used to estimate optimal network functioning in a graph theory framework.
4.4. Spatial resolution of macroscopic functional networks
Network models using fMRI data typically contain between 50 and 200 nodes (Tzourio-Mazoyer etal., 2002), which makes spatial characterisation of network properties challenging compared to voxel-level fMRI (>50,000 nodes). All metrics used in our study are computationally exhaustive rendering this problem non-trivial. Using sparse graphs and increasingly efficient algorithms (Konganti etal., 2013) may help in obtaining a voxel-level interpretation of graph networks (Zuo etal., 2012). Functional networks with high node resolution that are robust enough for single-subject analysis may help in delineating whether network isolation in focal epilepsy is a product of the seizure focus detaching itself from the wider network, or represents a network-wide effect. Whether treatment effects or chronic seizures influence these network findings cannot be examined in this cross sectional study of chronic epilepsy patients.
5. Conclusion
Patients with extratemporal focal epilepsy show more ‘isolated’ network nodes than healthy controls. This finding of increased network segregation is consistent with previous research recorded during focal seizures and is indicative of a potential network marker of focal epilepsy. We postulate that an isolated network configuration may constitute a brain mechanism that prevents instigation or spread of focal seizures.
The following are the supplementary data related to this article.
A clinical overview of all epilepsy patients.
Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.nicl.2015.05.009.
Acknowledgements
We acknowledge Evan Curwood for methodological guidance and Mira Semmelroch for assistance with the patient data. This study was supported by the National Health and Medical Research Council (NHMRC) of Australia (grant no. 628952). The Florey Institute of Neuroscience and Mental Health acknowledges the strong support from the Victorian Government and in particular the funding from the Operational Infrastructure Support Grant. G Jackson is supported by an NHMRC practitioner's fellowship (1060312). G Jackson has received honouraria from UCB, and royalties from Elsevier for Magnetic Resonance in Epilepsy 2nd ed. M Pedersen is supported by the University of Melbourne scholarships (MIRS & MIFRS).
References
- Achard S., Bullmore E. Efficiency and cost of economical brain functional networks. PLOS Comput. Biol. 2007;3(2):e17. doi: 10.1371/journal.pcbi.0030017. 17274684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Achard S., Salvador R., Whitcher B., Suckling J., Bullmore E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 2006;26(1):63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. 16399673 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander-Bloch A.F., Vértes P.E., Stidd R., Lalonde F., Clasen L., Rapoport J., Giedd J., Bullmore E.T., Gogtay N. The anatomical distance of functional connections predicts brain network topology in health and schizophrenia. Cereb. Cortex. 2013;23(1):127–138. doi: 10.1093/cercor/bhr388. 22275481 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner J. A fast diffeomorphic image registration algorithm. NeuroImage. 2007;38(1):95–113. doi: 10.1016/j.neuroimage.2007.07.007. 17761438 [DOI] [PubMed] [Google Scholar]
- Attwell D., Laughlin S.B. An energy budget for signaling in the grey matter of the brain. J. Cereb. Blood Flow Metab. 2001;21(10):1133–1145. doi: 10.1097/00004647-200110000-00001. 11598490 [DOI] [PubMed] [Google Scholar]
- Bertram E.H. Neuronal circuits in epilepsy: do they matter? Exp. Neurol. 2013;244:67–74. doi: 10.1016/j.expneurol.2012.01.028. 22342991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E., Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009;10(3):186–198. doi: 10.1038/nrn2575. 19190637 [DOI] [PubMed] [Google Scholar]
- Bullmore E., Sporns O. The economy of brain network organization. Nat. Rev. Neurosci. 2012;13(5):336–349. doi: 10.1038/nrn3214. 22498897 [DOI] [PubMed] [Google Scholar]
- Chao-Gan Y., Yu-Feng Z. DPARSF: a MATLAB Toolbox for “pipeline” data analysis of resting-state fMRI. Front. Syst. Neurosci. 2010;4:13. doi: 10.3389/fnsys.2010.00013. 20577591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossley N.A., Mechelli A., Vértes P.E., Winton-Brown T.T., Patel A.X., Ginestet C.E., McGuire P., Bullmore E.T. Cognitive relevance of the community structure of the human brain functional coactivation network. Proc. Natl. Acad. Sci. U. S. A. 2013;110(28):11583–11588. doi: 10.1073/pnas.1220826110. 23798414 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dennis E.L., Jahanshad N., Toga A.W., McMahon K.L., de Zubicaray G.I., Martin N.G., Wright M.J., Thompson P.M. Test–retest reliability of graph theory measures of structural brain connectivity. Med Image Comput Comput Assist Interv. 2012;15(3):305–312. doi: 10.1007/978-3-642-33454-2_38. 23286144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubrova E. Fault-Tolerant Design. Springer; New York, New York, NY: 2013. [Google Scholar]
- Engel J., Thompson P.M., Stern J.M., Staba R.J., Bragin A., Mody I. Connectomics and epilepsy. Curr. Opin. Neurol. 2013;26(2):186–194. doi: 10.1097/WCO.0b013e32835ee5b8. 23406911 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahoum F., Lopes R., Pittau F., Dubeau F., Gotman J. Widespread epileptic networks in focal epilepsies: EEG-fMRI study. Epilepsia. 2012;53(9):1618–1627. doi: 10.1111/j.1528-1167.2012.03533.x. 22691174 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flanagan D., Badawy R.A., Jackson G.D. EEG-fMRI in focal epilepsy: local activation and regional networks. Clin. Neurophysiol. 2014;125(1):21–31. doi: 10.1016/j.clinph.2013.06.182. 23871167 [DOI] [PubMed] [Google Scholar]
- Fornito A., Zalesky A., Bassett D.S., Meunier D., Ellison-Wright I., Yücel M., Wood S.J., Shaw K., O'Connor J., Nertney D., Mowry B.J., Pantelis C., Bullmore E.T. Genetic influences on cost-efficient organization of human cortical functional networks. J. Neurosci. 2011;31(9):3261–3270. doi: 10.1523/JNEUROSCI.4858-10.2011. 21368038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fornito A., Zalesky A., Bullmore E.T. Network scaling effects in graph analytic studies of human resting-stateFMRI data. Front. Syst. Neurosci. 2010;4:22. doi: 10.3389/fnsys.2010.00022. 20592949 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K.J., Ashburner J.T., Kiebel S.J., Nichols T.E., Penny W.D. Statistical Parametric Mapping: The Analysis of Functional Brain Images. Academic Press; 2011. [Google Scholar]
- Friston K.J., Williams S., Howard R., Frackowiak R.S., Turner R. Movement-related effects in fMRI time-series. Magn. Reson. Med. 1996;35(3):346–355. doi: 10.1002/mrm.1910350312. 8699946 [DOI] [PubMed] [Google Scholar]
- Glerean E., Salmi J., Lahnakoski J.M., Jääskeläinen I.P., Sams M. Functional magnetic resonance imaging phase synchronization as a measure of dynamic functional connectivity. Brain Connect. 2012;2(2):91–101. doi: 10.1089/brain.2011.0068. 22559794 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibrahim G.M., Morgan B.R., Lee W., Smith M.L., Donner E.J., Wang F., Beers C.A., Federico P., Taylor M.J., Doesburg S.M., Rutka J.T., Snead O.C. Impaired development of intrinsic connectivity networks in children with medically intractable localization-related epilepsy. Hum. Brain Mapp. 2014;35(11):5686–5700. doi: 10.1002/hbm.22580. 24976288 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konganti K., Wang G., Yang E., Cai J.J. SBEToolbox: a Matlab Toolbox for biological network analysis. Evol. Bioinform. Online. 2013;9:355–362. doi: 10.4137/EBO.S12012. 24027418 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer M.A., Eden U.T., Kolaczyk E.D., Zepeda R., Eskandar E.N., Cash S.S. Coalescence and fragmentation of cortical networks during focal seizures. J. Neurosci. 2010;30(30):10076–10085. doi: 10.1523/JNEUROSCI.6309-09.2010. 20668192 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutsy R.L. Focal extratemporal epilepsy: clinical features, EEG patterns, and surgical approach. J. Neurol. Sci. 1999;166(1):1–15. doi: 10.1016/s0022-510x(99)00107-0. 10465493 [DOI] [PubMed] [Google Scholar]
- Langer N., Pedroni A., Jäncke L. The problem of thresholding in small-world network analysis. PLOS One. 2013;8(1):e53199. doi: 10.1371/journal.pone.0053199. 23301043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latora V., Marchiori M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001;87(19):198701. doi: 10.1103/PhysRevLett.87.198701. 11690461 [DOI] [PubMed] [Google Scholar]
- Laufs H., Richardson M.P., Salek-Haddadi A., Vollmar C., Duncan J.S., Gale K., Lemieux L., Löscher W., Koepp M.J. Converging PET and fMRI evidence for a common area involved in human focal epilepsies. Neurol. 2011;77(9):904–910. doi: 10.1212/WNL.0b013e31822c90f2. 21849655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Van Quyen M., Navarro V., Martinerie J., Baulac M., Varela F.J. Toward a neurodynamical understanding of ictogenesis. Epilepsia. 2003;44:30–43. doi: 10.1111/j.0013-9580.2003.12007.x. 14641559 [DOI] [PubMed] [Google Scholar]
- Liang X., Wang J., Yan C., Shu N., Xu K., Gong G., He Y. Effects of different correlation metrics and preprocessing factors on small-world brain functional networks: a resting-state functional MRI study. PLOS One. 2012;7(3):e32766. doi: 10.1371/journal.pone.0032766. 22412922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo C., An D., Yao D., Gotman J. Patient-specific connectivity pattern of epileptic network in frontal lobe epilepsy. Neuroimage Clin. 2014;4:668–675. doi: 10.1016/j.nicl.2014.04.006. 24936418 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mudholkar G.S. Encyclopedia of Statistical Sciences. John Wiley & Sons; 2004. Fisher's Z-transformation. [Google Scholar]
- Neubauer F.B., Sederberg A., MacLean J.N. Local changes in neocortical circuit dynamics coincide with the spread of seizures to thalamus in a model of epilepsy. Front. Neural Circuits. 2014;8:101. doi: 10.3389/fncir.2014.00101. 25232306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh S.W., Harris J.A., Ng L., Winslow B., Cain N., Mihalas S., Wang Q., Lau C., Kuan L., Henry A.M., Mortrud M.T., Ouellette B., Nguyen T.N., Sorensen S.A., Slaughterbeck C.R., Wakeman W., Li Y., Feng D., Ho A., Nicholas E., Hirokawa K.E., Bohn P., Joines K.M., Peng H., Hawrylycz M.J., Phillips J.W., Hohmann J.G., Wohnoutka P., Gerfen C.R., Koch C., Bernard A., Dang C., Jones A.R., Zeng H. A mesoscale connectome of the mouse brain. Nature. 2014;508(7495):207–214. doi: 10.1038/nature13186. 24695228 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponten S.C., Bartolomei F., Stam C.J. Small-world networks and epilepsy: graph theoretical analysis of intracerebrally recorded mesial temporal lobe seizures. Clin. Neurophysiol. 2007;118(4):918–927. doi: 10.1016/j.clinph.2006.12.002. 17314065 [DOI] [PubMed] [Google Scholar]
- Power J.D., Barnes K.A., Snyder A.Z., Schlaggar B.L., Petersen S.E. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. NeuroImage. 2012;59(3):2142–2154. doi: 10.1016/j.neuroimage.2011.10.018. 22019881 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson M.P. Large scale brain models of epilepsy: dynamics meets connectomics. J. Neurol. Neurosurg. Psychiatry. 2012;83(12):1238–1248. doi: 10.1136/jnnp-2011-301944. 22917671 [DOI] [PubMed] [Google Scholar]
- Rubinov M., Sporns O. Complex network measures of brain connectivity: uses and interpretations. NeuroImage. 2010;52(3):1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. 19819337 [DOI] [PubMed] [Google Scholar]
- Schindler K.A., Bialonski S., Horstmann M.-T., Elger C.E., Lehnertz K. Evolving functional network properties and synchronizability during human epileptic seizures. Chaos. 2008;18(3):033119. doi: 10.1063/1.2966112. 19045457 [DOI] [PubMed] [Google Scholar]
- Schröter M.S., Spoormaker V.I., Schorer A., Wohlschläger A., Czisch M., Kochs E.F., Zimmer C., Hemmer B., Schneider G., Jordan D., Ilg R. Spatiotemporal Reconfiguration of large-scale brain functional networks during propofol-induced loss of consciousness. J. Neurosci. 2012;32(37):12832–12840. doi: 10.1523/JNEUROSCI.6046-11.2012. 22973006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X., Tokoglu F., Papademetris X., Constable R.T. Groupwise whole-brain parcellation from resting-state fMRI data for network node identification. NeuroImage. 2013;82:403–415. doi: 10.1016/j.neuroimage.2013.05.081. 23747961 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O. Networks of the Brain. MIT Press; Cambridge: 2011. [Google Scholar]
- Stam C.J. Modern network science of neurological disorders. Nat. Rev. Neurosci. 2014;15(10):683–695. doi: 10.1038/nrn3801. 25186238 [DOI] [PubMed] [Google Scholar]
- Stam C.J., van Straaten E.C.W. The organization of physiological brain networks. Clin. Neurophysiol. 2012;123(6):1067–1087. doi: 10.1016/j.clinph.2012.01.011. 22356937 [DOI] [PubMed] [Google Scholar]
- Tzourio-Mazoyer N., Landeau B., Papathanassiou D., Crivello F., Etard O., Delcroix N., Mazoyer B., Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. NeuroImage. 2002;15(1):273–289. doi: 10.1006/nimg.2001.0978. 11771995 [DOI] [PubMed] [Google Scholar]
- Van den Heuvel M.P., Stam C.J., Boersma M., Hulshoff Pol H.E. Small-world and scale-free organization of voxel-basedresting-state functional connectivity in the human brain. NeuroImage. 2008;43(3):528–539. doi: 10.1016/j.neuroimage.2008.08.010. 18786642 [DOI] [PubMed] [Google Scholar]
- Van Diessen E., Zweiphenning W.J.E.M., Jansen F.E., Stam C.J., Braun K.P.J., Otte W.M. Brain network organization in focal epilepsy: a systematic review and meta-analysis. PLOS One. 2014;9(12) doi: 10.1371/journal.pone.0114606. 25493432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vega-Zelaya L., Pastor J.E., de Sola R.G., Ortega G.J. Inhomogeneous cortical synchronization and partial epileptic seizures. Front. Neurol. 2014;5:187. doi: 10.3389/fneur.2014.00187. 25309507 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren C.P., Hu S., Stead M., Brinkmann B.H., Bower M.R., Worrell G.A. Synchrony In normal and focal epileptic brain: the seizure onset zone is functionally disconnected. J. Neurophysiol. 2010;104(6):3530–3539. doi: 10.1152/jn.00368.2010. 20926610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts D.J., Strogatz S.H. Collective dynamics of “small-world” networks. Nature. 1998;393(6684):440–442. doi: 10.1038/30918. 9623998 [DOI] [PubMed] [Google Scholar]
- Zuo X.-N., Ehmke R., Mennes M., Imperati D., Castellanos F.X., Sporns O., Milham M.P. Network centrality in the human functional connectome. Cereb. Cortex. 2012;22(8):1862–1875. doi: 10.1093/cercor/bhr269. 21968567 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
A clinical overview of all epilepsy patients.


