Conformational Frustration in Calmodulin-Target Recognition

Abstract

Calmodulin (CaM) is a primary calcium (Ca²⁺) signaling protein that specifically recognizes and activates highly diverse target proteins. We explored the molecular basis of target recognition of CaM with peptides representing the CaM-binding domains from two Ca²⁺-CaM dependent kinases, CaMKI and CaMKII, by employing experimentally-constrained molecular simulations. Detailed binding route analysis revealed that the two CaM target peptides, although similar in length and net charge, follow distinct routes that lead to a higher binding frustration in the CaM-CaMKII complex than the CaM-CaMKI complex. We discovered that the molecular origin of the binding frustration is caused by intermolecular contacts formed with the C-domain of CaM that need to be broken before the formation of intermolecular contacts with the N-domain of CaM. We argue that the binding frustration is important for determining the kinetics of the recognition process of proteins involving large structural fluctuations.

Introduction

Protein-protein interactions are crucial for various biological functions, such as signal transduction, metabolism, and regulation of gene expression, among others (Nussinov et al. 2005). Aberrant protein-protein interactions also result in diseases (Ryan et al. 2005). Therefore, understanding the principles controlling the protein-protein recognition process will lead to novel insights into how proteins achieve their biological functions and why these processes go awry leading to pathologies. To achieve a molecular understanding from theoretical perspectives, transition state theory (Alsallaq et al. 2007a; Alsallaq et al. 2007b; Alsallaq et al. 2008) and computational methods based on Brownian dynamics (Camacho et al. 2000; Elcock et al. 1999; Gabdoulline et al. 1997; Gabdoulline et al. 2001; Kang et al. 2011; Northrup et al. 1988; Northrup et al. 1992; Northrup et al. 1984; Spaar et al. 2005; Trylska et al. 2007; Wieczorek et al. 2008; Yap et al. 2013) were developed to study protein-protein and protein-ligand association kinetics. Some of these studies successfully predicted the effect of ionic strength and the cause of mutations on the association rate constant (k_a). However, most of these studies were limited by the use of rigid protein models in which the structural flexibility of proteins is ignored in the computation. One of the examples illustrating this problem is coupled folding and binding of intrinsically disordered proteins (IDP) (Chu et al. 2012; Chu et al. 2013; Dunker et al. 2001; Fink 2005; Huang et al. 2009; Papoian et al. 2003; Sickmeier et al. 2007; Tompa 2002; Uversky 2002; Wright et al. 1999) in which an IDP remains unfolded before interacting with its binding partner (Dyson et al. 2005; Dyson et al. 2002). Recently, several groups have used atomistic simulations (with explicit or implicit solvent molecules) to study coupled folding and binding of IDPs (Chen et al. 2007a; Chen 2009; Ganguly et al. 2009; Higo et al. 2011). However, the computational cost required to calculate the association rate using atomistic simulation of these processes is beyond the reach of current computational power.

Because of a lack of computational capability in an all-atomistic representation for investigating the structural changes upon protein-protein interactions and binding free energies, several other studies (De Sancho et al. 2012; Ganguly et al. 2011; Ganguly et al. 2012; Huang et al. 2009; May et al. 2014; Periole et al. 2012; Ravikumar et al. 2012; Turjanski et al. 2008) developed coarse-grained protein models to probe such a mechanism at a low resolution; however, most rely on a structure-based model that requires a priori knowledge of the structures of the bound protein complexes. To address the multiple bound states (Goh et al. 2004), researchers used a protein model that is unconstrained by a single structure-based framework. For example, Knott and Best (Knott et al. 2014) used a two-state structural based model to address binding with multiple bound conformations. In recent studies (Wang et al. 2013a; Wang et al. 2013b), researchers explored a myriad of bound conformations from intrinsically disordered peptides by mixing in some extent of transferrable potentials into a Hamiltonian. In Wang’s paper (Wang et al. 2013b), most of the long-range interactions on amino acid side chains are still based on the structure of the bound complex. In our previous study (Wang et al. 2013a), we used a Hamiltonian that permits structural flexibility of both partners and that does not require a priori knowledge of the final bound complex. Subsequently, our approach allows both the binding partners to adopt diverse conformations in their search to establish a variety of bound complexes.

In our previous study (Wang et al. 2013a), a coarse-grained side chain C_α model (SCM) (Cheung et al. 2003) was used to study the binding of calmodulin (CaM) and two calmodulin binding targets (CaMBTs): CaMKI and CaMKII from the CaM-binding domain of Ca²⁺-CaM dependent kinase I (Fig. 1(A)) and Ca²⁺-CaM dependent kinase II (Fig. 1(B)), respectively. The ratio of the experimentally measured association rates between the CaM-CaMKI and CaM-CaMKII was used as a guide to develop the criterion for a successful association event in the complementary coarse-grained molecular simulations (Wang et al. 2013a). The association rate of CaM-CaMKI is two times higher than that of CaM-CaMKII. This approach allowed the investigation of CaM-CaMBT association that involves mutually induced and conformational changes of both partners. However, a detailed investigation of the molecular origin of the conformational change of CaM and CaMBT during their association that accounts for their subtle, but statistically significant, differences was not evaluated.

Figure 1.

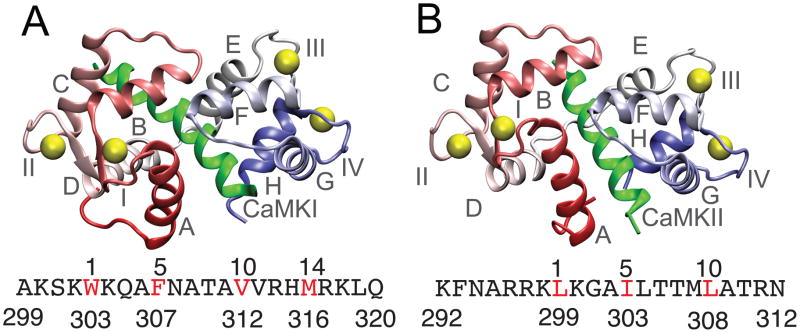
Native structures of the CaM-CaMBT complexes (A) and (B) show the PDB structures of the CaM-CaMKI (PDB ID: 2L7L) (Gifford et al. 2011) and CaM-CaMKII (PDB ID: 1CDM) (Meador et al. 1993) complexes. Helices and the Ca²⁺-binding loops of CaM are denoted by A-H and I-IV, respectively in (A) and (B). CaM is colored red (N-terminal domain) and blue (C-terminal domain) and the Ca²⁺ ions are represented with yellow spheres. The CaMKI and CaMKII peptides are shown in green. The sequence of CaMKI and CaMKII are indicated below (A) and (B), respectively with one letter code. The hydrophobic residues of the CaMBTs from the hydrophobic motifs (1-5-10 and 1-14 for CaMKI and 1-5-10 for CaMKII) in both the sequences are colored in red.

In this study we performed a binding route analysis from the coarse-grained molecular simulations. The results reveal that the CaMKI and CaMKII peptides follow distinct binding routes when each interacts with CaM. In particular, we observed greater “conformational frustration” for CaMKII than CaMKI during their association with CaM. The frustration evolves through a sequence of events from the early to the late stage of association that require both CaM and CaMBT to undergo structural rearrangements before the formation of a “functional complex”.

The analyses in this study further shows that the interactions of the N- and C-terminal CaM domains are distinct during their association with a CaMBT. By dissecting the binding routes of CaM-CaMBT, we found that the interactions of a CaMBT with the helix-linkers (that connect the two EF-hands within each domain of CaM) and the Ca²⁺-binding loops have partly contributed to the frustration during association. Particularly, at the late stage of the association the conformational changes of CaM and CaMBT are mutually induced, where most of these intermolecular interactions are either absent or exhibit significant reorganizations before the formation of a functional CaM-CaMBT complex. This is especially evident for the interactions between CaM and CaMKII and emphasizes the potential role of binding frustration in dictating CaM’s target selectivity. Our work can potentially advance the understanding of the mechanism of protein-protein interactions for other kinds of intrinsically disordered proteins.

Materials and Methods

I. Calmodulin and Calmodulin Binding Targets

CaM is a relatively small (148 amino acids) ubiquitous intracellular Ca²⁺-signaling protein and is highly conserved in its sequence across all vertebrate species. The protein consists of two globular domains: nCaM (the N-terminal domain of CaM) and cCaM (the C-terminal domain of CaM). The two domains are connected by an interdomain linker (or central linker), which is largely flexible in solution (Barbato et al. 1992). Upon binding Ca²⁺, CaM undergoes a conformational change that allows it to specifically bind and activate various cellular targets (Finn et al. 1995; Meador et al. 1993). In past years, several crystal and nuclear magnetic resonance (NMR) structures of CaM in complex with different targets were elucidated and revealed novel ways for CaM to interact with its targets (Tidow et al. 2013; Vetter et al. 2003). It is known that CaM’s plasticity plays a crucial role in enabling its interaction with the diverse partners (Ikura et al. 2006; Yamniuk et al. 2004). In particular, the flexibility of the interdomain linker is essential to the rearrangement of the two domains of CaM in order to accommodate binding of a wide selection of targets (Ikura et al. 2006; Wriggers et al. 1998). Simulation and theoretical studies have suggested that in addition to the conformational flexibility of CaM (Barton et al. 2002; Chen et al. 2007b; Tripathi et al. 2009; Vigil et al. 2001) both the hydrophobic and the electrostatic interactions are important in CaM-target binding (Fiorin et al. 2006; Smith et al. 2012; Yang et al. 2004; Zhang et al. 2009). Nevertheless, the molecular basis of the binding mechanism that enables CaM to recognize highly diverse target proteins remains elusive. CaMKI and CaMKII peptides representing their CaM-binding domains, although similar in length, share little sequence similarity. These CaMBTs have hydrophobic residues with a conserved spacing along their sequence [see Fig. 1(A) and (B)], and these hydrophobic residues play an important role in binding (Yamniuk et al. 2004). These short CaMBTs are naturally unstructured in solution and typically have a propensity to form amphipathic α-helices in the bound complex (Crivici et al. 1995; O’Neil et al. 1990). Here we used the notation of CaMKI and CaMKII for peptides in the CaMKI and CaMKII enzymes that bind to CaM. The bound structures of the CaM-CaMKI and CaM-CaMKII complexes are shown in Fig. 1(A) and (B), respectively.

II. Coarse-grained model for CaM-CaMBT interactions

A side-chain C_α model (SCM) (Cheung et al. 2003) is used to study the association of CaM and CaMBTs at the individual amino acid level. In SCM, each amino acid (except glycine) is represented by two beads: one at the C_α position and the other at the center of mass of the side-chain. A detailed description of the CaM-CaMBT model is given in our previous work (Wang et al. 2013a).

The potential energy of CaM or CaMBT is given by,

$$E^{\mathit{intra}}=E_{\mathit{bond}}+E_{\mathit{angle}}+E_{\mathit{dihedral}}+E_{\mathit{chirality}}+E_{\mathit{elec}}+E_{HB}+E_{LJ}$$ Eqn (1)

A detailed description of bond stretching term E_bond, bond-angle term E_angle, side-chain chirality term E_chirality can be found in our previous work (Homouz et al. 2008). The dihedral angle term E_dihedral is described as,

$$E_{\mathit{dihedral}}^{\mathit{ijkl}}={\mathrm{\sum }}_{n=1,3}{k}_{\phi }^{(n)}[1-cos(n\times ({\phi }_{\mathit{ijkl}}-{\phi }_{\mathit{ijkl}}^0))]$$ Eqn (2)

where φ_ijkl is the dihedral angle defined over four C_α beads of consecutive residues i, j, k and l; ${\phi }_{\mathit{ijkl}}^0$ is the corresponding dihedral angle measured in the referenced structure of CaM (PDB ID: 1CLL) and CaMBTs (PDB ID: 2L7L and 1CDM for CaM-CaMKI and CaM-CaMKII, respectively).

For CaM, $k_{\phi }^{(1)}=40.0\text{kcal}/\text{mol}$ and $k_{\phi }^{(3)}=20.0\text{kcal}/\text{mol}$ were used for parameterization (Wang et al. 2013a) based on the experimental data of unbound CaM (Anthis et al. 2011; Heidorn et al. 1989). CaM retains in an extended, open conformation in solution state. Based on this parameterization the average radius of gyration (R_g) of CaM in an unbound state is ~21.1 Å, close to the experimental value 21.3 Å measured from the x-ray scattering experiments (Heidorn et al. 1989). Additionally, the R_g of CaM shows two peaks corresponding to the extended state and compact state at the ratio of ~ 9:1 in agreement with the paramagnetic relaxation enhancement experiment (for details of the parameterization please see our previous work in reference (Wang et al. 2013a). For CaMBTs, a set of $k_{\phi }^{(1)}=1.2\text{kcal}/\text{mol}$ and $k_{\phi }^{(3)}=0.6\text{kcal}/\text{mol}$ which are typical values for the strength of dihedral angles in the side-chain C_α model (Cheung et al. 2003), render structural flexibility for these CaMBTs in the unbound form than CaM. The equilibration positions of bond, bond angle and pseudo dihedral angle energies were taken from the crystal structure of CaM (PDB ID: 1CLL). Thus, the Hamiltonian of CaM in our coarse-grained model did not depend on the structure of the bound complex, making it possible to study a variety of CaM-CaMBT interactions.

Debye-Hückel potential (Debye et al. 1923) was used to describe the screening effect of ionic solutions on electrostatic interactions between charged units. The Debye-Hückel potential E_elec in Eqn (1) between beads i and j follows the equation given by,

$$E_{\mathit{elec}}^{ij}=\frac{q_i{q}_j}{4\pi {\epsilon }_r{\epsilon }_0{r}_{ij}}{e}^{-r_{ij}/\sqrt{{\epsilon }_r{\epsilon }_0{k}_{B}T/2e^{2}I}}$$ Eqn (3)

q_i or q_j is the partial charges on bead i or j, which can be obtained using a combined method of quantum chemistry calculation, statistical physics, and coarse-grained molecular simulations (Wang et al. 2011). In the above equation r_ij is the distance between beads i and j, ε₀ is the permittivity of free space, ε_r is the relative dielectric constant (80 for aqueous solutions), k_B is the Boltzmann constant, T is the temperature, e is elementary charge and I is the ionic strength of the aqueous solution (that was set to 0.1M). The partial charges assigned to CaM and two CaMBTs are given in our previous work (Wang et al. 2013a).

In Eqn (1) the backbone-backbone interactions for the C_α beads are represented by the hydrogen-bonding interactions term E_HB, as described in our previous work (Homouz et al. 2008). The Lennard-Jones (LJ) potential E_LJ in Eqn (1) was used to represent the sidechain-sidechain and backbone-sidechain interactions between beads i and j.

$$E_{LJ}^{ij}={\epsilon }_{ij}\left[{\left(\frac{{\rho }_{ij}}{r_{ij}}\right)}^{12}-2{\left(\frac{{\rho }_{ij}}{r_{ij}}\right)}^6\right].$$ Eqn (4)

where r_ij is the separation between sidechain beads (or, between backbone and sidechain beads) i and j (|i − j| ≥ 2). For sidechain-sidechain interactions the above equation is used, where ρ_ij = f(ρ_i + ρ_j) and ρ_i and ρ_j are the van der Waals radii of the side chains i and j, calculated from the extended structure of CaM (PDB ID: 1CLL); f is the scaling factor to be 0.9 to avoid the clashes between bulky sidechains. The sidechain-sidechain interaction strength ε_ij in Eqn (4) represent the solvent-mediated interaction defined by the Betancourt-Thirumalai (BT) statistical potential ${\epsilon }_{ij}^{\text{BT}}$ (Betancourt et al. 1999). We applied the BT statistical potential in the protein model to explore the conformations beyond the experimentally determined one (Homouz et al. 2009; Wang et al. 2011). For the backbone-sidechain interactions, hard-core repulsion is considered by taking only the ${\epsilon }_{ij}{\left(\frac{{\rho }_{ij}}{r_{ij}}\right)}^{12}$ term ρ_i for a backbone bead is 0.5σ (σ=3.8Å). For the backbone-sidechain interactions ε_ij = ε = 0.6 kcal/mol in Eqn (4).

For intramolecular interaction strengths the BT potential ${\epsilon }_{ij}^{\text{BT}}$ is rescaled to ${\epsilon }_{ij}^{\text{intra}}$ due to the explicit inclusion of electrostatic interactions in our Hamiltonian in Eqn (1), as follows,

$$-{\epsilon }_{ij}^{int\mathit{ra}}+\frac{1}{4\pi {\epsilon }_0{\epsilon }_r}\frac{Q_i{Q}_j}{r_0}=-{\epsilon }_{ij}^{BT}$$ Eqn (5)

Q_i (Q_j) is the charge summation on the side chain of amino acid i (j) from the united atom force field. r₀ = ρ_i + ρ_j, where ρ_i and ρ_j are the van der Waals radii of amino acid i and j, respectively. The values for both ${\epsilon }_{ij}^{\text{BT}}$ and ${\epsilon }_{ij}^{\text{intra}}$ are given in our previous work (Wang et al. 2013a).

The intermolecular interactions between CaM and a CaMBT are given by,

$$E^{\mathit{inter}}=E_{\mathit{elec}}+E_{HB}+E_{LJ}$$ Eqn (6)

E_elec is a term for electrostatic interactions (same as Eqn (3)), E_HB is a term for backbone hydrogen bond interactions (described in our previous work (Homouz et al. 2008)), and E_LJ is a term for side-chain van der Waals interactions (same as Eqn (4)) between CaM and CaMBT. However, the strengths of the intermolecular hydrogen bond interactions (E_HB in Eqn (6)) and van der Waals interactions (E_LJ in Eqn (6)) between CaM and CaMBTs are twice as large as the strength of the intramolecular interactions in order to make the functional CaM-CaMBT complex stable in which the two domains of CaM wrap around the CaMBT. Based on these parameterization of our model the computationally obtained generalized order parameter of the methyl symmetry axis (O²_axis) for the residues in CaM-CaMKI complexes are positively correlated with the measurements published by the Wand group (Marlow et al. 2010), as stated in the supplement of our previous work (Wang et al. 2013a)

III. Summary of simulation methods

The association process between CaM and CaMBT (CaMKI or CaMKII) was investigated by Brownian Dynamics (BD). The rate of association was computed by an algorithm developed by Northrup, Allison and McCammon (NAM) (Northrup et al. 1984). Further discussion on the NAM algorithm and diffusion coefficient is provided in the Supplement. The viscosity of the system was set to be equal to the aqueous solution 1.0×10⁻³ Pa·s at the temperature k_BT/ε =1.1, where ε =0.6 kcal/mol and k_B is the Boltzmann constant. In the BD simulation of CaM-CaMBT association, an initial configuration of CaM was randomly distributed in a spherical surface at b = 15σ (σ is a reduced unit length in our coarse-grained model, which equals to 3.8 Å) away from a CaMBT. The simulation of a trajectory would be stopped when the distance between center of mass of CaM and the center of mass of the CaMBT exceeded q = 75σ (see Fig. S1 in the Supplement). Otherwise a total time of 240,000τ was carried out for each trajectory where an integration time step is 0.0005 τ. In an overdamped limit (Veitshans et al. 1997), τ is mapped to the real time between 0.01–0.37 ns as described in the Supplement. For each system, 1000 association trajectories were performed. Criteria for a successful association event are discussed in section IV. Analyses.

IV. Analyses

Definition of successful and unsuccessful associations

The definition of a successful association event of a trajectory from the simulations was guided by the experimentally measured association rates (Wang et al. 2013a), shown by our previous study. Here, we summarize the method: In order to determine a successful association process between CaM and a CaMBT we monitored the formation of side-chain contacts between the residue Lys75 (of CaM) and any amino acids from the CaMBT, which we denote as Z₇₅. We used a cut-off distance of 2σ (σ is the reduced unit of length in our coarse-grained model, which equals to 3.8 Å) to define a contact. The choice of Z₇₅ was motivated from the stopped-flow fluorescence study used to determine association rates (Wang et al. 2013a) in which the reporter dye was positioned on residue Lys75 at the N-terminal end of the linker region of CaM after mutating it to Cys75.

In our simulation a successful association event was determined once the threshold of Z₇₅ reached a value of 9 (Wang et al. 2013a). This is a value where the ratio of the association rates between CaM-CaMKI and CaM-CaMKII closely matches with that measured experimentally. We set the maximum time of 240,000 τ to ensure that the portion of the trajectories that fail to reach the b-shell or the q-shell is less than 3% of the total trajectories. We calculated the estimated error in Table S1 of our previous work (Wang et al. 2013a). We conclude that the statistics from our sampling and the justification of the termination of a simulation is sound.

Contact analyses for the N- and C-lobes of CaM: Definition of Z_n and Z_c

First, we defined a parameter Z to calculate the number of intermolecular side chain contacts between the CaM and the CaMBTs. We used a cut-off distance of 2σ to define a contact when we calculated Z. For binding route analysis we simply divided the total number of intermolecular contacts Z in two components: Z_n and Z_c. Z_n is defined as the number of intermolecular contacts between nCaM (counted from residue 1 to residue 75 of CaM) and CaMBT. Similarly, Z_c is defined as the number of contacts between cCaM (counted from residue 76 to residue 148 of CaM) and CaMBT. For successful trajectories Z, Z_n and Z_c were normalized by their corresponding maximum values observed from our simulation, labeled as Z̄, $\overline{Z_n}$ and $\overline{Z_c}$, respectively.

Calculation of the EF-hand angles (of CaM)

Each domain of CaM contains two helix-loop-helix Ca²⁺-binding motifs (also known as the EF-hands). Helices A/B and C/D in nCaM constitute EF-hand I and II, respectively and helices E/F and G/H in cCaM constitute EF-hand III and IV, respectively. The helix-linker BC connects EF-hand I and II. Similarly, helix-linker FG connects EF-hand III and IV. We first defined a direction for each helix by considering the unit vector pointing from an average position of the first four residues (from the N-terminus) to the average position of the last four residues (from the C-terminus). The EF-hand angles for the helix-binding loop-helix motif were then calculated as the arccosine of the inner product of the two vectors from the corresponding helices within each EF-hand (Wang et al. 2011). This permitted a quantitative assessment of how individual helices reoriented relative to each other during the association process.

Results

I. Interactions of the CaMBTs with the N- and C-domains of CaM

For CaM-CaMKI and CaM-CaMKII, there were 45 and 18 successful associations, respectively, out of one thousand trajectories from simulations performed in our prior work (Wang et al. 2013a). The computed association rates, k_a for CaM-CaMKI and CaM-CaMKII are 56.14±0.26×10⁷ and 22.61±0.17×10⁷ M⁻¹ s⁻¹, respectively, from Eqn S1. The standard error was estimated assuming the number of successful trajectories follows Poisson distribution; a bootstrap resampling method also gave similar standard error is similar as shown in Table S1 in the supplementary information in Ref. (Wang et al. 2013a). The difference in the association rates between CaM-CaMKI and CaM-CaMKII is statistically meaningful.

To understand the binding mechanism of the CaMBTs with the N- and C-domains of CaM, we show three distinct trajectories (out of 45 successful associations) for CaM-CaMKI (Fig 2 A–C) and three (out of 18 successful associations) for CaM-CaMKII projected on the corresponding 2D distribution –ln P (Z_n, Z_c) (Fig. 2 D–F). The 2D distribution for both systems is obtained by combining all the trajectories from both successful and unsuccessful association. The intermolecular contacts Z_n and Z_c between CaM-CaMBTs are described in the Materials and Method section.

Figure 2.

Interactions between the CaM domains and the CaMBTs during association. (A), (B) and (C) represent three successful trajectories for the association of CaM-CaMKI projected on the 2D distribution (in log-scale) –ln P(Z_n, Z_c) of all the trajectories. Similarly, (D), (E) and (F) are for CaM-CaMKII. The trajectories are colored by a normalized time from blue to red. The 2D distribution is colored from black to white proportional to the population (from high to low). See the Models and Method section for the definition of Z_n and Z_c. The basins (I and II in A–C for CaM-CaMKI, and I′ and II′ in D–F for CaM-CaMKII) are indicated by the black arrows.

The profiles of 2D distribution in Fig. 2(A)–(C) show that for CaM-CaMKI there are two basins that are mostly populated: basin I (Z_n< Z_c; Z_n~40, Z_c~70) and basin II (Z_n>Z_c; Z_n~60, Z_c~30). Note that there is a third basin (Z_n~80, Z_c~20); however, for the successful trajectories from our simulation this basin is rarely populated (data not shown). In Fig. 2(A)–(C) we showed three representative binding trajectories of CaM-CaMKI. The trajectory in Fig. 2(A) shows that initially CaMKI binds to cCaM at Z_n~0 and Z_c~60 before it ends up in basin I. The trajectory in Fig. 2(B) indicates that there are interactions of CaMKI with both domains of CaM. Z_c becomes greater than Z_n and finally it reaches to basin II. For the trajectory in Fig. 2(C) we found that CaMKI interacts with both domains of CaM and it spends significant time around basin II before reaching basin I. For CaM-CaMKI we found that ~85% of the successful trajectories end in basin I.

Similarly, the distribution –ln P (Z_n, Z_c) in Fig. 2(D)–(F) indicates that for CaM-CaMKII there are two major basins that are mainly populated: basin I′ (Z_n<Z_c; Z_n~40, Z_c~70) and basin II′ (Z_n>Z_c; Z_n~60, Z_c~40). The trajectory in Fig. 2(D) shows that initially CaMKII interacts only with the cCaM at Z_n~0 and Z_c~70. Then it enters basin I′, where Z_n increases to ~40 but Z_c remains similar. The trajectory in Fig. 2(E) shows CaMKII interacts with both domains of CaM when it reaches to basin II′ (Z_n~60, Z_c~40). For the trajectory in Fig. 2(F) we noticed that at first Z_c is ~60 and Z_n is ~0, and then Z_c reduces to ~50 and Z_n increases to ~40. Finally, when reaching to basin I′ Z_c again increases to ~70 and Z_n decreases to ~20, as indicated by the white arrows. This trajectory in Fig 2(F) is particularly interesting because it clearly demonstrates that some contacts between CaMKII and cCaM or between CaMKII and nCaM need to be broken before it proceeds and reaches basin I′. We found that ~70% of the successful trajectories end in basin I′ for CaM-CaMKII. This phenomenon is analogous to “backtracking” (Gosavi et al. 2006) (or local unfolding) due to incorrect ordering of two subsets of (native) contacts of a protein competing with each other along the folding route (Capraro et al. 2008; Gosavi et al. 2008; Hills et al. 2008; Wang et al. 2013a).

II. Binding route analysis

In order to gain a deeper understanding of the underlying mechanism of target recognition of CaM, we performed a detailed binding route analysis on the trajectories from the successful associations, using the idea from the folding route analysis (Gosavi et al. 2006; Plotkin et al. 2000). Specifically, we analyzed the binding mechanism of CaM-CaMKI as well as CaM-CaMKII by plotting the (normalized) intermolecular contact formation between nCaM and CaMBT that is $\overline{Z_n}$ (or between cCaM and CaMBT that is $\overline{Z_c}$) against Z̄ ( $\overline{Z}=\overline{Z_n+Z_c}$, the normalized total contacts between CaM and CaMBT) in Fig. 3. If $\overline{Z_n}$ or $\overline{Z_c}$ grows linearly with Z̄, then this profile should collapse on a diagonal (solid black) line showing a “mean field” result. The rise and fall of profiles crossing a diagonal line indictate frustrations in the “binding routes” similar to backtracking (Gosavi et al. 2006) during the folding of a protein, explained below.

Figure 3.

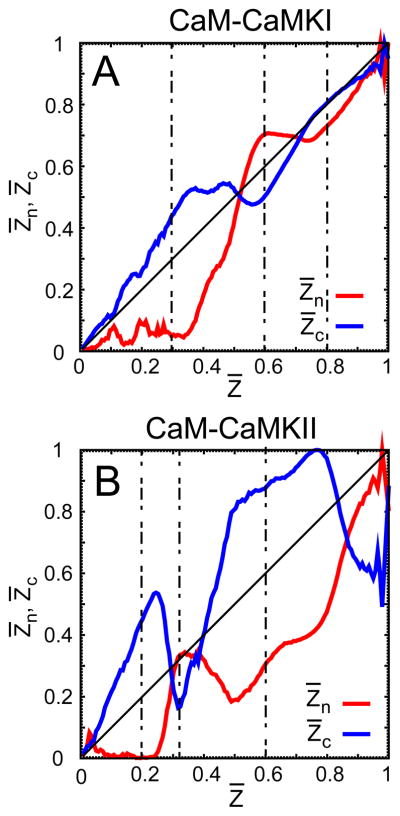
The binding route analysis on the trajectories from the successful associations between CaM and the CaMBTs. (A) and (B) illustrate the formation of the normalized intermolecular contacts $\overline{Z_n}$ and $\overline{Z_c}$ from the N- and C-terminal domain of CaM compared to the average Z̄ (normalized) and the targets CaMKI and CaMKII, respectively. For both systems Z̄ is defined as the total number of intermolecular contacts between CaM and the target, such that $\overline{Z}=\overline{Z_n+Z_c}$. See the Models and Method section for a detailed discussion on Z̄, $\overline{Z_n}$ and $\overline{Z_c}$. In each plot, the diagonal line is drawn as a reference for the intermolecular contacts $\overline{Z_n}$ or $\overline{Z_c}$ that ideally follow the average Z̄. The vertical dashed lines in the plots indicate the values of Z̄ for which the corresponding values of $\overline{Z_n}$ and $\overline{Z_c}$ differ significantly during the association for both systems.

Fig. 3 shows that both CaMBTs initially bind to cCaM ( $\overline{Z_c}>\overline{Z}$). For CaM-CaMKI (Fig 3A) it happens at Z̄ < 0.5 and for CaM-CaMKII it happens at Z̄ < 0.3. Afterward, for CaM-CaMKI there is a transient decrease in $\overline{Z_c}$ and then an increase at 0.5 < Z̄ < 0.9, while $\overline{Z_n}$ increases and then decreases. For CaM-CaMKII (Fig 3B) this happens at 0.3 < Z̄ < 0.85, while $\overline{Z_n}$ increases and then decreases. This suggests that in order to initiate the association between nCaM and CaMBT, there are some contacts between cCaM and CaMBT that must first be broken, which reveals a significant level of frustration in these two systems. Interestingly, the comparison of Fig. 3(A) and (B) further shows that along the binding routes the difference between $\overline{Z_n}$ and $\overline{Z_c}$ is more prominent in CaM-CaMKII compared to CaM-CaMKI, indicating an increased degree of frustration.

To further explore whether the backtracking is common to the successful trajectories of CaM-CaMBT association, we performed binding route analysis for each successful trajectory of CaM-CaMKI (Fig. S2) and CaM-CaMKII (Fig. S3). Our results show that the characteristics of backtracking are evident for all the successful trajectories of CaM-CaMKI and CaM-CaMKII; however, the extent of backtracking differs among the trajectories.

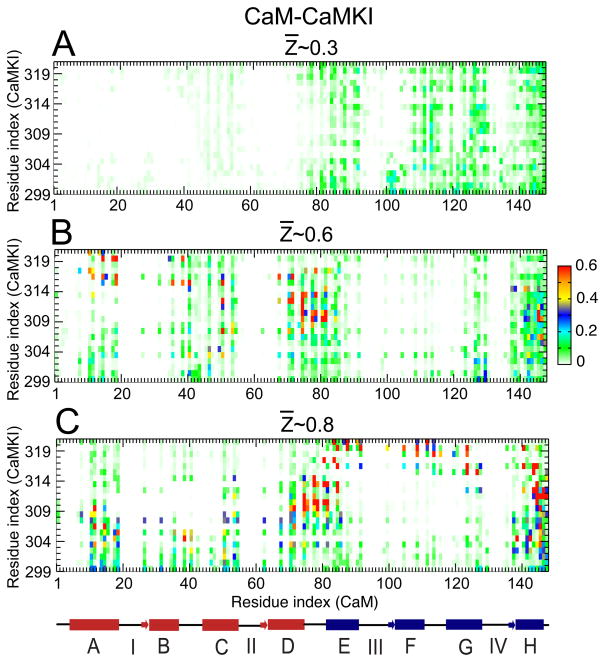
In order to understand the molecular basis for the frustration, we plotted the probability of contact formation at several values of Z̄ for CaM-CaMKI and CaM-CaMKII, (Fig. 4 and 5, respectively). For both systems the contact maps are plotted at Z̄ values for which the difference between $\overline{Z_n}$ and $\overline{Z_c}$ is significant during binding (the vertical dash lines in Fig. 3 indicate the corresponding Z̄ values for the contact maps shown in Fig. 4 and 5). For CaM-CaMKI, we found that at Z̄ ~0.3, intermolecular contacts are broadly formed with cCaM (see Fig. 4(A)). However, the contact probability, P_i is low (P_i < 0.2). At Z̄ ~0.6, intermolecular contacts around residues 110 to 125 (part of the F and G helices and the FG helix-linker) of cCaM are lost while the contacts of CaMKI with nCaM (part of the A, B, C helices and BC helix-linker) start to form (see Fig. 4(B)). This further indicates that the contacts between cCaM and CaMKI must be broken in order to permit contacts between nCaM and CaMKI to form. At Z̄ ~0.8, Fig. 4(C) shows that although the pattern of the intermolecular contacts are very similar to those at Z̄ ~0.6 (in Fig 4(B)) along the residue index of CaM, there is a significant change in the P_i values for the contacts along the residue index of CaMKI.

Figure 4.

Probability of contact formation between CaM and CaMKI along the binding route. (A), (B) and (C) represent the contact maps calculated between the amino acids from the side-chain of CaM and CaMKI, at the different values of Z̄ ~0.3, 0.6 and 0.8 (as indicated in Fig. 3 (A)), respectively. A linearized model of CaM is shown below the plots with the individual helices displayed as cylinders, the linkers connecting the helices shown as lines, and the N-terminal and C-terminal helices are shown in red and blue, respectively.

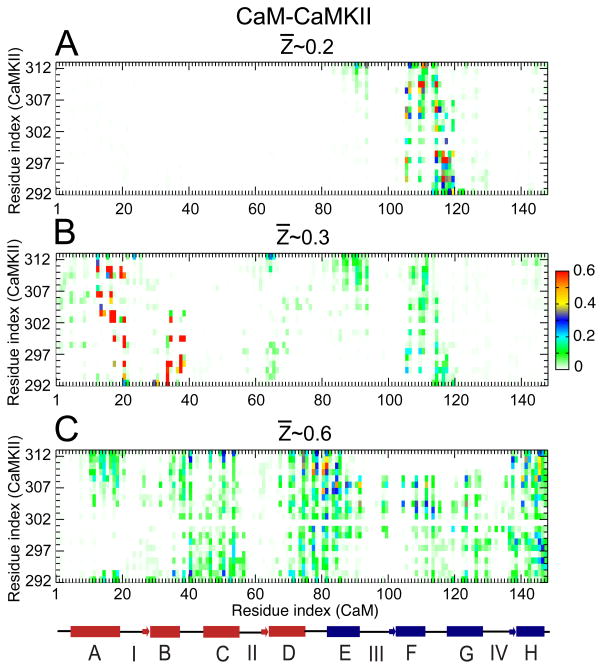
Figure 5.

Probability of contact formation between CaM and CaMKII along the binding route. (A), (B) and (C) represent the contact maps calculated between the amino acids from the side-chain of CaM and CaMKII, at the different values of Z̄ ~0.2, 0.3 and 0.6 (as indicated in Fig. 3(B)), respectively. A linearized model of CaM is shown below the plots with the individual helices displayed as cylinders, the linkers connecting the helices shown as lines, and the N-terminal and C-terminal helices are shown in red and blue, respectively.

Compared to CaM-CaMKI, the contact maps are quite different for CaM-CaMKII, as shown in Fig. 5. First, we noted that at Z̄ ~0.2, a narrow selection of contacts with high probabilities is formed between cCaM (part of helix F and the FG helix-linker) and CaMKII (Fig. 5(A)). At Z̄ ~0.3, these intermolecular contacts in cCaM weaken and most of the contacts are then formed with nCaM (part of helices A and B) with a high P_i~0.6, as shown in Fig. 5(B). At Z̄ ~0.6, we observed an overall increase in the intermolecular contacts particularly in the cCaM and the central linker region of CaM (Fig. 5(C)), although most of these contacts have low P_i values (~0.2). As a result, the intermolecular contacts from helix-A and helix-B show significant decrease from P_i~0.6 at Z̄ ~0.3 to P_i~0.2 at Z̄ ~0.6. This indicates that some contacts from nCaM (helix-A and helix-B) need to be broken to form the contacts in cCaM and the central-linker.

To further investigate the origin of the binding frustration that impacts the mechanism of recognition of CaMBTs, we calculated the distribution of the distance between the Ca²⁺ ions (at the center of each of the Ca²⁺-binding loops) and the center of mass of the CaMBTs. Additionally, we calculated the distance between the helix-linker of CaM (that connects two EF-hands in each CaM domain, i.e. BC-linker and FG-linker) and the center of mass of CaMBTs at the same values of Z̄ from the binding route analyses (see Fig. S4 and S5 in the Supplement). These regions have played a significant role in the binding route analysis other than the helices. In Fig. 6 we summarized that during the transition from Z̄ ~0.3 to Z̄ ~0.6 for CaM-CaMKI and the transition from Z̄ ~0.2 to Z̄ ~0.3 for CaM-CaMKII the CaMBTs make intermolecular contacts with the helix-linkers and the binding loops of CaM (Fig 6A to 6B). Next for the transition from Z̄ ~0.6 to Z̄ ~0.8 for CaM-CaMKI and the transition from Z̄ ~0.3 to Z̄ ~0.6 for CaM-CaMKII (Fig 6B to Fig 6C), either most of these intermolecular contacts are broken (from the Ca²⁺ binding loops of CaM) or there are new intermolecular contacts formed between CaMBTs and the helix-linkers of CaM. This so called backtracking is particularly evident for the intermolecular interactions between CaM and CaMKII. A detailed discussion on these interactions is included in the Supplement.

Figure 6.

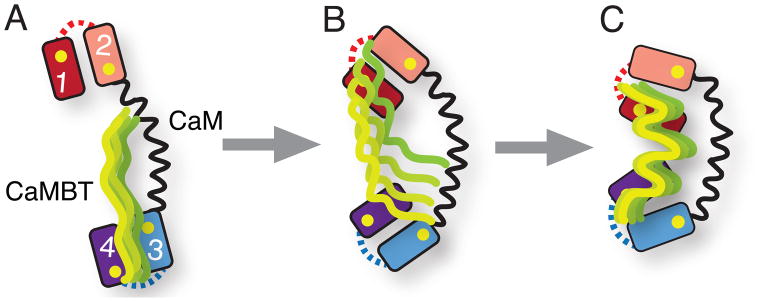
Conformational frustration in CaM-CaMBT recognition. (A), (B) and (C) represent the schematic diagram of CaM-CaMBT association process along the binding route (see Fig. 3). The unstructured CaMBT (CaMKI or CaMKII) initially interacts with one of the domain of CaM (predominantly the cCaM). At the early stage of association (from A to B) the conformational frustration comes into play as the CaMBT starts to interact with the other domain of CaM (predominantly the nCaM). The conformational frustration at the late stage (from B to C) occurs, as the CaMBT approaches towards the binding pocket of CaM. As a result, intermolecular contacts between CaM and CaMBT are either broken or new intermolecular contacts are formed. In the schematic diagram of CaM the number 1-4 denotes the four EF-hands. The BC and FG helix-linkers of CaM are represented by the dotted lines in red and blue, respectively. Yellow spheres denote positions of four Ca²⁺ ions. The binding loops of CaM are not shown. The ensemble of CaMBT structures is shown in green.

III. Conformational changes of CaM during back tracking

In the non target-bound CaM, the orientation of the helices within each EF-hand remains nearly perpendicular (see Table 1 and 2), which corresponds to an open conformation in each domain. To explore how the target binding changes these angles during back tracking, we calculated the average EF-hand angles of CaM (θ) at selected values of Z̄ from the binding route analysis for CaM-CaMKI and CaM-CaMKII (Table 1 and 2, respectively). Specifically, we are interested in knowing the parts of CaM that are involved in the conformational change during backtracking along the binding route of CaM-CaMKI and CaM-CaMKII.

Table 1.

Change in the EF-hand angles (θ in °) of CaM during the association with CaMKI along the binding route at different values of Z̄ (normalized intermolecular contacts between CaM and CaMBT). θ calculated for the unbound holoCaM (PDB ID: 1CLL) and the CaM from native bound complex (PDB ID: 2L7L) are also presented (see the Model and Methods section for the calculation of θ). EF-hand of CaM is defined as helix-loop-helix Ca²⁺-binding motif (helices A/B and C/D in nCaM constitute EF hand I and II, respectively; helices E/F and G/H in cCaM constitute EF hand III and IV, respectively; see Fig. 1(A) and (B)).

Intermolecular contacts	EF I (θI)	EF II (θII)	EF III (θIII)	EF IV (θIV)
Unbound (holo)	95.52	97.29	80.67	89.17
Z̄~0.3	93.68 (±0.11)	87.91 (±0.16)	79.07 (±0.14)	87.15 (±0.17)
Z̄~0.6	92.49 (±0.03)	88.33 (±0.03)	75.50 (±0.04)	91.16 (±0.04)
Z̄~0.8	95.36 (±0.05)	99.75 (±0.05)	73.19 (±0.06)	97.76 (±0.07)
Native complex	92.81	81.78	84.02	85.09

Table 2.

Change in the EF-hand angles (θ in °) of CaM during the association with CaMKII along the binding route at different values of Z̄. The EF-hand angles calculated for the unbound holoCaM (PDB ID: 1CLL) and the CaM from native bound complex (PDB ID: 1CDM) are also presented.

Intermolecular contacts	EF I (θI)	EF II (θII)	EF III (θIII)	EF IV (θIV)
Unbound (holo)	95.52	97.29	80.67	89.17
Z̄~0.2	93.33 (±0.14)	86.72 (±0.18)	81.39 (±0.15)	83.79 (±0.21)
Z̄~0.3	92.79 (±0.11)	89.77 (±0.15)	79.37 (±0.13)	83.29 (±0.18)
Z̄~0.6	91.15 (±0.10)	81.99 (±0.14)	71.03 (±0.16)	86.39 (±0.15)
Native complex	93.43	90.77	87.82	99.02

For the CaM-CaMKI complex, we found that at Z̄ ~0.3 the most significant change in θ occurs to the EF-hand II (θ_II) from the nCaM (see Table 1) and that θ_II decreased by ~10% compared to that of the unbound CaM. This is interesting because the contact map of CaM-CaMKI in Fig. 4(A) indicates that, although at Z̄ ~0.3 CaMKI mostly interacts with cCaM, it can still significantly induce conformational changes within EF-hand II from nCaM. This is most probably due to the long-range charge-charge interactions between the two domains of CaM as shown by our previous study (Wang et al. 2011). Along the binding route from Z̄ ~0.3 to Z̄ ~0.6, most of the changes in the angles occur in EF-hands III (θ_III) and IV (θ_IV) in cCaM where θ_III decreases by 4.5% and θ_IV increases by 4.6%. Between Z̄ ~0.6 and Z̄ ~0.8 we noted that θ_II and θ_IV increases by ~13% and ~7%, respectively, while θ_I and θ_III remain the same.

For CaM-CaMKII complex (Table 2), we observed that similar to CaM-CaMKI the initial interactions of CaMKII to cCaM (see Fig. 5(A)) cause a noticeable change in conformations within the EF-hand II in the nCaM (~11% decrease in θ_II) at Z̄ ~0.2. Along the binding route from Z̄ ~0.2 to Z̄ ~0.3, other than a small increase (3.5%) in θ_II the angles of the rest of the EF-hands decrease by a lesser amount (see Table 2). As Z̄ increases to ~0.6, we noted that other than θ_IV, the angles of the rest of the EF-hands decrease. Specifically, for θ_II (θ_III) there is a ~9% (12%) decrease compared to that at Z̄ ~0.3.

To explore how the conformational change within CaM impacts the interdomain interactions along the binding route, we also plotted the intramolecular contact maps of CaM (Fig. S6) during the back tracking. At high Z̄ values (indicated by an arrow in Fig. S6(B) and S6(C) for CaM-CaMKI at Z̄ ~0.6 and Z̄ ~0.8, respectively; Fig. S6(F) for CaM-CaMKII at Z̄ ~0.6), interdomain contacts of CaM start to increase. These interdomain contacts are between the BC-linker of nCaM and the segment from helix G to H, including the Ca²⁺ binding loop IV of cCaM. Based on our calculation on the EF-hand angles we found that at Z̄ ~0.6 in CaM-CaMKII, θ_II (between helices C and D, 81.99°±0.14°) and θ_IV (between helices G and H, 86.39°±0.15°) (see Table 2) remained significantly smaller than those in CaM-CaMKI at Z̄ ~0.8 (99.75°±0.05° and 97.76°±0.07°, respectively) (see Table 1). As a result, the EF-hands II and IV remained in a more closed conformation in CaM (of CaM-CaMKII) compared to these EF-hands of CaM in the CaM-CaMKI complex and facilitate the formation of interdomain contacts in CaM.

The results show that differences in the EF-hand angles of CaM along the binding route are small, as discussed above. However, these differences are statistically significant because they are still greater than the estimated errors in Table 1 and 2. In addition, compared to the native complex the EF-hand angles θ_I, θ_II, θ_IV of CaM are higher by 3%, 22%, and 15%, respectively, and θ_III is lower by 13% for CaM-CaMKI at Z̄ ~0.8. For the EF-hand angles of CaM for CaM-CaMKII we found that θ_I, θ_II, θ_III and θ_IV all are lower by 2%, 10%, 19%, and 13%, respectively, at Z̄ ~0.6, compared to the native complex. In addition, the EF-hand angles of CaM in CaM-CaMKI (at Z̄ ~0.8) are larger than the corresponding angles of CaM-CaMKII (at Z̄ ~0.6) by 4%, 18%, 3%, and 12%, respectively. The binding of CaMKI vs. CaMKII induces a differential response in both the interdomain contacts (Fig. S6 in the Supplement) and the orientation of helices within each of the domains of CaM.

Discussion

Binding frustration is important for target recognition

The results based on the binding route analysis reveals the presence of binding frustration between CaM and CaMKI (or CaMKII) during the recognition process. In our model, the Hamiltonian for CaM in a CaM-CaMBT complex is based on the unbound CaM structure that resembles a dumbbell shape (Fig. S1). For this reason, CaM has no bias from the structure of the bound complexes; hence, the same Hamiltonian of CaM can be used to study association of any CaMBT.

Our study elucidated that the difference in the frustration of CaM-CaMKI and CaM-CaMKII association depends on the sequence of the CaMBTs that play a key role in the recognition process. Ca²⁺-binding loops and the helix-linkers in the N- and C-domains of CaM partly contributed to the binding frustration. Our results suggested that for both CaM-CaMKI and CaM-CaMKII the binding frustration is partly caused by the inability of the helix-linker BC and FG (of CaM) to form contacts with the CaMBT simultaneously. Such frustrations in the CaM-CaMBT association might have a role in higher association rate of CaM-CaMKI (Wang et al. 2013a), which exhibits lower frustration compared to CaM-CaMKII.

In addition, according to our binding route analysis we suggest that the transient interactions of the Ca²⁺ binding loops and CaMBT before the formation of the final stable complexes partly cause the frustration in binding. This is particularly interesting because target binding is well known experimentally to affect the affinity of CaM for Ca²⁺ (Byrne et al. 2009; Forest et al. 2008). Although in our simulations the positions of the four Ca²⁺ ions were fixed in the binding loops of CaM, the present results suggest that developing a more dynamic model for the Ca²⁺-binding loops of CaM is warranted.

From a clustering analysis of the targets in the bound structures from the association simulations (please see Supplementary Information), the CaMKI peptide mostly forms a helical structure in the bound complex with CaM, whereas for CaMKII there is a similar probability to form either a helical, or a bent helical structure in the bound complex with CaM (Fig. S7). Our results further unveiled that the binding energies CaM-CaMBT complex are lowest when the relative contact order (CO) of CaMBT is ~ 0.25 (helical like structure) for the CaM-CaMKI complex (Fig. S8(A)) and CO ~ 0.3 (bent helical like structure) for the CaM-CaMKII complex (Fig. S8(B)). Interestingly, a bent-helical conformation of a target was similarly observed in the x-ray crystal structure of CaM-CaMKK (Ca²⁺-CaM dependent kinase kinase peptide), indicating this conformation is experimentally viable (Kurokawa et al. 2001; Osawa et al. 1999). While not identical, the CaM-CaMKK structure bears the resemblance to the structure of CaMKII in CaM-CaMKII complex from our current study and we speculate that this structure is represented in the conformational ensemble of the complex. It is important to note that in the available crystal structure of the CaM-CaMKII complex CaMKII is helical; however, the structure may represent only one of the conformations populated in solution.

It is important to note that we determined the structures from the kinetic trajectories. These structures are not necessarily at the global minimum or an energetically trapped state (Schreiber et al. 2009). We did not choose them based on their binding stability. However, we were interested in comparing these conformations with the experimentally determined ones. We reconstructed these coarse-grained complexes into all-atomistic protein models (Homouz et al. 2008; Samiotakis et al. 2010). We ran all-atomistic molecular dynamics simulations with explicit solvents on these structures using both CHARMM and AMBER forces fields (please see methods in the Supplementary Information). We averaged over the mean-square fluctuation (MSF) for all of these complexes and compared them to the experimental B-factor values. We also ran all-atomistic molecular dynamics simulations on the experimentally determined structures as an initial condition. We computed that MSF as a control. We analyzed these values for both CaMKI (PDB: 1MXE from x-ray as an alternative because the native complex 2L7L was determined from NMR) and CaMKII (PDB: 1CDM) in Fig S9 and Fig S10, respectively. We computed the correlation coefficients between the MSFs and the B-factors. The correlation coefficients (CC) were provided in the supplementary materials (Fig S9 and S10). CC values are greater than or close to 0.3 for both the reconstructed protein models and the controls. They both represent the experimental B-values qualitatively well. The amplitude of the $\overline{\mathit{MSF}}$ values of the reconstructed proteins are overall greater than the controls, meaning that the structural distribution in the ensemble of reconstructed proteins is broader than those in the global minimum of a binding energy landscape. Given that both profiles on the MSF plots are qualitatively similar to the experimental B-values, we speculate that the ensemble of the reconstructed proteins is not so far away from the global minimum of the binding energy landscape.

Binding frustration contributes to the conformational and mutually induced fit

The binding frustration is caused by the sequence of conformational changes required in both binding partners before the formation of a stable complex. The extent of conformational changes in CaM is induced by the specific and unique amino acid sequence and composition of the CaMBT and was termed “conformational and mutually induced fit” in our previous study (Wang et al. 2013a). There are two main stages, the early stage and the late stage, of the association when trajectories were diagnosed with Z₇₅ as a function of normalized time (the parameters Z̄ and Z₇₅ are defined in the Materials and Methods section of the Main text). We can identify when the binding frustration occurs along the association process by computing Z₇₅ at several Z̄ for CaM-CaMKI and for CaM-CaMKII in Table S1. At low Z̄ (early stage), Z₇₅ is less than 1 for both systems. It means that the binding frustration starts during the early stage, when the two partners initiate contacts. At median Z̄ when contacts with cCaM need to be broken for allowing contacts with nCaM, Z₇₅ is ~5 (transition from the early stage to the late stage) for CaMKI, while Z₇₅ is still less than 1 for CaMKII. This means that such binding frustration evolves closer to the binding pocket of CaM for CaMKI than for CaMKII. At high Z̄, for CaMKI, Z₇₅ is ~5 and for CaMKII, Z₇₅ is ~ 3. As a result, most of the binding frustration is resolved before the late stage when the CaM-CaMBT forms a functional complex.

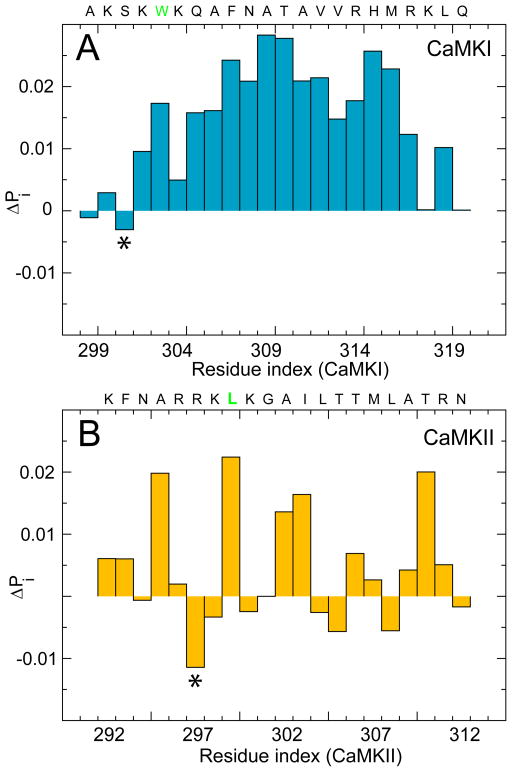
We speculate that the association rate for CaMKII with CaM can increase by a simple mutation that lessens its binding frustration. We focused on the contact formation between CaM and CaMKII, as well as CaM and CaMKI, at the onset of association because it dictates the subsequent frustration in the binding route. We computed the intermolecular contact probability of the residues from the CaMBTs before and after backtracking at low Z. We evaluated their differences (ΔP_i) on each residue i in Fig 7. A residue from CaMBT with a negative ΔP must first form and then break contacts with the residues from CaM. For CaMKI, S301 is the most frustrated residue. For CaMKII, R297 is the most frustrated residue. They share the same analogous position (labeled with an asterisk) counting towards the N-terminus from the first hydrophobic residues that form the anchors of the binding motifs (colored in green). We speculate that by mutating the arginine 297 in CaMKII to a serine (like in CaMKI), we might be able to lessen its binding frustration and increase its rate of association. This will be an interesting hypothesis to verify experimentally in future studies.

Figure 7.

Difference in the intermolecular contact probability of the residues from the CaMBTs along the binding route at the early stage of association. (A) Difference in the contact probability (ΔP_i) for each residue of CaMKI, at Z̄ ~0.3 and Z̄ ~0.6 (see Fig. 3A in the Main text). (B) ΔP_i for each residue of CaMKII, at Z̄ ~0.2 and Z̄ ~0.3 (see Fig. 3B in the Main text). The sequences of CaMBTs are shown on top of each plot. The first hydrophobic residues from the binding motif of the CaMBTs are shown in green (W303 from CaMKI and L299 from CaMKII).

Conclusions

Molecular recognition is important in all biomolecular association (Wodak et al. 2002). For proteins, the association rates can be accurately modeled when conformational changes are not rate limiting (Frembgen-Kesner et al. 2010; Schreiber 2002; Zhou et al. 2013). Nonetheless, protein recognition requires flexibility to facilitate structural rearrangement during association, especially for the IDPs (Mittag et al. 2010). The role of protein flexibility has been also addressed in other recent studies of protein-protein association (Rogers et al. 2013; Wang et al. 2013a). Here, we showed that the subtle difference in the binding route of CaMKI and CaMKII with CaM depends on the sequence of the target peptides and that conformational frustration appears to be a likely explanation for the slower association rate constant for CaMKII measured experimentally. This further highlights the importance of conformational flexibility in both the binding partners during the recognition process of the CaM-CaMBT association (O’Neil et al. 1990; Yamniuk et al. 2004).