A comparison of two worlds: How does Bayes hold up to the status quo for the analysis of clinical trials?

Abstract

Background

There is a paucity of literature comparing Bayesian analytic techniques with traditional approaches for analyzing clinical trials using real trial data.

Methods

We compared Bayesian and frequentist group sequential methods using data from two published clinical trials. We chose two widely accepted frequentist rules, O'Brien–Fleming and Lan–DeMets, and conjugate Bayesian priors. Using the nonparametric bootstrap, we estimated a sampling distribution of stopping times for each method. Because current practice dictates the preservation of an experiment-wise false positive rate (Type I error), we approximated these error rates for our Bayesian and frequentist analyses with the posterior probability of detecting an effect in a simulated null sample. Thus for the data-generated distribution represented by these trials, we were able to compare the relative performance of these techniques.

Results

No final outcomes differed from those of the original trials. However, the timing of trial termination differed substantially by method and varied by trial. For one trial, group sequential designs of either type dictated early stopping of the study. In the other, stopping times were dependent upon the choice of spending function and prior distribution.

Conclusions

Results indicate that trialists ought to consider Bayesian methods in addition to traditional approaches for analysis of clinical trials. Though findings from this small sample did not demonstrate either method to consistently outperform the other, they did suggest the need to replicate these comparisons using data from varied clinical trials in order to determine the conditions under which the different methods would be most efficient.

1. Introduction

The high price tag associated with clinical trials has motivated researchers to find more cost-effective ways to conduct research. In addition, research ethics mandate that we do not continue clinical studies beyond the point at which sufficient information is available to answer the research question, so that the smallest number of patients receive the inferior therapy [1,2]. Finally, it is important to complete clinical trials as quickly as possible to assure that superior treatments are incorporated into regular practice in a timely fashion.

Bayesian analysis is a widely promoted response to these mandates. With Bayesian methods, prior knowledge is formally organized to direct the course of the study, and participants are randomized only as necessary [3,4]. Though these methods are increasingly accepted in the field of cancer treatment and device trials [5–11], they are seldom implemented in other types of trials.

Traditional (“frequentist”) statistical methods have evolved to include group sequential analysis (in which a series of interim analyses is performed over the collection of the sample) [12]. This technique allows for the early termination of a trial, and thus can save funds, participant time, and provide knowledge about therapeutic efficacy more quickly. Frequentist conclusions rely on the preservation of an experiment-wise error rate (alpha level), and the size of this error relies heavily on the fact that the data be processed only once. Because this issue of multiple testing is tantamount, frequentist statisticians have developed alpha spending functions which penalize the alpha level at each look based on the number of interim analyses and the amount of accumulated data [13–18].

While frequentist methodology is the widely accepted paradigm, Bayesian methodology has not, until recently, been easily accessible because of its need for enormous computer resources. This reliance on high-level computer programming combined with the perceived subjective nature of the priors has resulted in skepticism from clinical investigators.

Statisticians have demonstrated the efficiency of Bayesian methods with simulated data under various scenarios [4,6,19,20], but many clinical researchers remain unconvinced for several reasons. First, simulations can be constructed to favor one's preferred methods, and though many articles in the literature demonstrate Bayesian advantages in real observational data, we have found only three such demonstrations of the comparison between Bayesian and frequentist methods for the analysis of clinical trials using real data [21–23]. Thus, these clinical-trial methods need to be investigated using real data where one can examine their performance with regards to criteria researchers and policy makers care about. Second, simulations are inevitably based on assumptions which may not be realistic. Finally, the status quo demands meeting certain operating criteria, such as Type I error rates and power, which are frequentist concepts not inherent in Bayesian methods.

We compared these two approaches with data from completed clinical trials in order to test their performance in the real world. Our goal was to use a simple methodology to compare the results under Bayesian and frequentist analyses on the same data. To that end, we performed post hoc analyses of the data from two completed clinical trials.

2. Analytical methods

2.1. Bayesian

In the context of clinical trials, Bayesian analysis is an iterative process in which investigators use all available data (external evidence) and prior knowledge to construct a prior distribution of the parameter of interest (e.g., the between-group difference in treatment outcomes). Next, part of an experiment is conducted and the results (called the likelihood) are applied to the prior distribution to obtain an updated “posterior” distribution. This posterior distribution is then used to calculate the probability that the treatment is superior to the control. If these posterior probabilities dictate the continuation of the data collection process, the posterior distribution serves as the prior distribution for the next iteration [4] (see Appendix).

2.2. Frequentist

Frequentist statistical methodology depends on the assumption that sampled data come from a population with a specific distribution and set parameters. Further, the frequentist concept of probability is based on long-run expected frequencies of occurrence. Data are collected and used to test hypotheses about the value of the fixed parameter. The goal is to use estimates of variation in repeated experiments to determine whether the observed data are consistent with a specified null distribution [24].

Clinicians apply Bayesian principles to the science of diagnostic testing by incorporating likelihood and prior probability into recommendations they present to patients [25]. However, few clinical trials use Bayesian methods, primarily because the techniques are difficult to understand, and depend largely on the investigator's specific assumptions. In addition, the performance of these techniques, evaluated within the frequentist world of gold standards (e.g., type I and II error rates) has not been adequately addressed [8,11,26].

Bayesian and frequentist methods differ in their goals. Bayesian methods seek to determine the probability that the population has a certain characteristic, given the observed data and the prior information, whereas frequentist methods seek to determine the probability that we would see the observed data if the null hypothesis were true. Put another way, both deal with conditional probabilities, but frequentist inference centers around P(data|parameter) while Bayesian is concerned with P(parameter|data) [23]. The frequentist approach to an effectiveness trial is to choose a natural null (usually no effect), and examine whether the data can provide evidence against it, whereas the Bayesian approach is to choose a hypothesis about the presence of an effect and assess evidence in its favor.

Our primary goal was to compare frequentist group sequential and Bayesian clinical trial analyses to determine how sensitive Bayesian methodology is to starting assumptions, as measured by trial outcome under different prior distributions, as practically applied to actual trial data. We considered both informative (i.e. distributions in which we used prior knowledge to inform the initial parameter estimates) and non-informative priors (i.e. flat prior distributions that assume no prior knowledge regarding the superiority of either treatment arm). A secondary aim was to examine how frequentist group sequential analysis differs by method of conservation of Type I error as measured by the outcome in each trial under two commonly used frequentist group sequential methods: Obrien–Fleming, and Lan–DeMets power function. Finally, we combined the results to determine what proportion of Bayesian sequential analysis methods would yield different outcomes from their frequentist counterparts in a series of comparative simulations.

3. Study methods

3.1. The data

We considered a variety of trial characteristics including sample size, number of events, type of outcome, availability of datasets and relative impact in their fields. We present the re-analysis of two such trials to represent two distinct types of outcomes (continuous and time-to-event).

The Studies of Left Ventricular Dysfunction–Treatment Trial (SOLVD-TT) was a double-blind, placebo-controlled trial of enalapril in patients with symptomatic heart failure with a primary endpoint of all-cause mortality [27]. The study followed 2569 participants for a mean of 41 months; final results showed a 16% reduction in total mortality among the enalapril-allocated participants (HR=0.84, 95% CI: 0.74, 0.95) [27,28]. Data for these analyses were obtained from the National Heart, Lung, and Blood Institute Data Repository of Epidemiology and Clinical Trials of the National Institutes of Health [29].

The Stimulation of Points to Investigate Needling Efficacy (SPINE) study was a four-arm single-blind randomized controlled trial to assess the effect of acupuncture on mechanical low back pain. Eligible participants (N=611) were randomized equally to one of four treatments: individualized acupuncture point stimulation, standardized acupuncture point stimulation, non-insertive simulated acupuncture point stimulation, or usual care[30,31]. At eight weeks, investigators found a 2.47 (95% CI: 1.40, 3.53) point larger improvement on the Roland–Morris disability scale score for the individualized acupuncture arm than the standard care arm (P<0.05) [31,32]. We focus on just two of the groups in this trial: individualized acupuncture, and standard care. Roland–Morris post intervention average scores for these two arms were 6.41 (SD:5.35) and 8.87 (SD:5.93), respectively. Data for this trial were obtained from the Principal Investigator at the Group Health Cooperative Center for Health Studies, Seattle, Washington.

3.2. Re-analysis

We re-analyzed the data for each trial in chronological order as if we had turned back the clock to restart the study. We compared two different frequentist alpha spending rules with one another and with results from two different Bayesian prior distributions, with the decision to terminate the trial based on a predetermined posterior probability of success of ≥85%. For all four analyses, we performed three equally-spaced interim analyses of the data, the spacing determined by accumulation of the data over time with the fourth and final analysis after all data had accumulated. There is no guarantee that the data we observed from this particular sample were the truth, however we were able to mimic repeated sampling using bootstrap analyses (creating “new” trial data by randomly re-sampling the subjects with replacement) to determine a distribution of all possible trial outcomes under the two frequentist group sequential analyses and the two Bayesian approaches. Once we had determined the timing of our interim analyses, we arranged each dataset in order of randomization, and “began each trial”. We repeated all analyses on each of these 10,000 samples.

3.3. Bayesian analysis

Emerson et al. [23] suggests using a ‘spectrum of normal prior distributions’, so we chose two. We used a Normal prior with both informative and non-informative parameters because the outcomes in our trials were continuous or, in the case of the Cox models, the coefficients were assumed to be normally distributed. To keep our informative-prior comparisons consistent, we used the same information used by the trial team when calculating the power and sample size estimates for their frequentist analyses. In this manner, we assumed the priors to be normally distributed with mean, μ and standard deviation, σ as offered by the frequentist power calculations and relevant effect sizes as specified by the original investigators prior to the start of each trial.

For the non-informative prior distributions, we simply assumed a between-group mean difference of 0 and an infinite variance, which is essentially a flat prior distribution. Programmatically, when we set μ=0 and σ=1,000,000, the resulting posterior mean and standard deviations approach those derived from straightforward maximum likelihood inference (see Appendix).

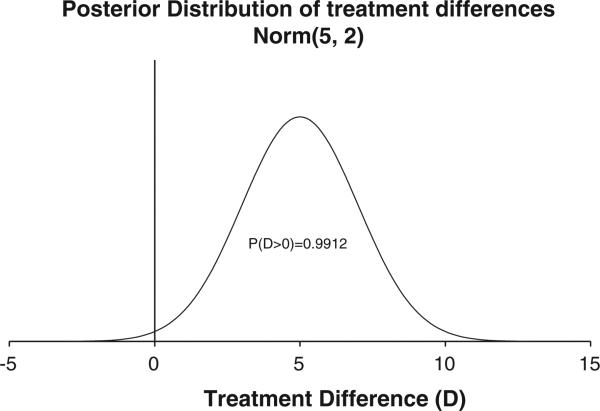
We used an arbitrary cut-point of ≥85% posterior probability of success for a stopping rule. That is, we recommended stopping for effectiveness if the posterior probability that the treatment was superior to the placebo was ≥85% at any specific iteration. The example in Fig. 1 shows a Normal posterior distribution (μ=5 and σ=2). The area under the curve to the right of the null (i.e., treatment difference of 0) is approximately 99%. From this posterior distribution, the Bayesian conclusion is that there is a 99% probability that the treatment is superior to the placebo.

Fig. 1.

Posterior distribution of treatment differences (D) from a hypothetical Bayesian analysis of a clinical trial comparing blood levels in the treatment versus placebo.

3.4. Frequentist group sequential analysis

Frequentist sequential analyses include the specification of a distribution that the sample estimate is assumed to follow were there to be repeated experiments. In the case of the SPINE trial, we use the standard normal distribution for the continuous outcome of change in disability score. For SOLVD, in order to use Cox proportional hazards modeling for the time-to-event we assumed that the hazard functions from the two treatment groups were proportional over time. Review of the hazard plots at each look showed a relatively stable picture of this relationship over time. In addition, log (–log(survival) plots provided further evidence of this assumption of proportional hazards. For the Cox proportional hazards models, the estimates of the coefficients also are assumed to be normally distributed [33,34].

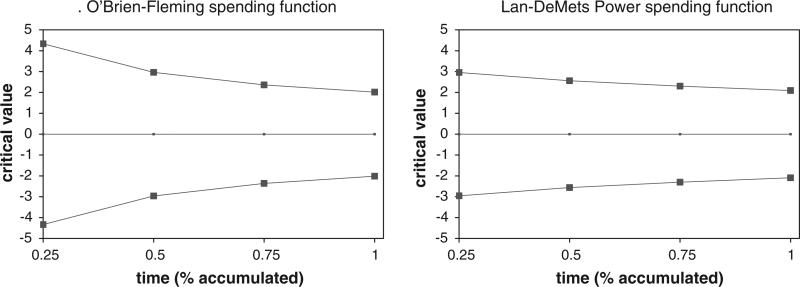
Frequentist group sequential designs generally parse out the alpha in such a way as to save most until the last look when most statistical power is needed to detect differences in the treatment. For our analyses, we used O'Brien–Fleming and Lan–DeMets Power alpha spending functions [17,18,35]. The boundaries for these spending functions as used in our analyses for the SPINE trial are plotted in Fig. 2 [12].

Fig. 2.

Boundaries for frequentist alpha spending functions for SPINE study.

3.5. Bootstrap sampling

For all analyses, we used bootstrap sampling, stratified on treatment, to create 10,000 samples to determine distributions of all possible trial outcomes under the conditions in each design. With this tool, we were able to calculate point estimates for the average outcomes and confidence intervals under each scenario.

3.6. False positive rate

Frequentist spending function boundaries are calculated to preserve the experiment-wise Type I error rate in the face of multiple testing. However, there is no simple Type I error rate calculation inherent in the Bayesian methods because they are not based on the concept of long-run repeated sampling. Because Type I error rate is the probability of finding an effect when the null hypothesis is true, we created a null situation, and tested our Bayesian procedures to measure this probability. For consistency, we also estimated the experiment-wise error rate for the frequentist analyses in the same manner.

Analyses were conducted with SAS9.1, [36] and R [37].

4. Results

4.1. SOLVD-TT trial

Frequentist group sequential methods with three interim analyses could have had a marked effect on the length of this trial as these data were actually collected. When we applied the Lan-DeMets stopping rule to the trial data as they accrued, we reached significance after only 75% of the expected deaths had accumulated. This corresponded to less than half the total study time (Table 1a). However, with O'Brien–Fleming bounds, the test statistic did not cross the critical boundaries until the final analysis. Compared with the published results from the trial, these results indicate a stronger relationship of treatment with total mortality when the trial was stopped early, but arrive at the same hazard ratio (HR) and confidence interval (in the case of O'Brien-Fleming) when the analysis did not indicate an early stop, as expected.

Table 1a.

SOLVD-TT trial comparison of results.

Actual trial data			Bootstrap (10,000 samples)
Analysis	Time (days)	HR (95% CI)	Average time (days)	Average hazard ratio (95% CI)	Type I errora
Published results	1688	0.84 (0.74, 0.95)
Frequentist
OBF	1688	0.84 (0.74, 0.86)	1254	0.79 (0.57, 0.95)	5.4%
LD	771	0.76 (0.56, 1.00)	1062	0.74 (0.51, 0.95)	5.4%
Bayesian
Non-Inform	1688	0.83 (0.73, 0.94)	1165	0.78 (0.61, 0.95)	1.0%
Informative	519	0.71 (0.56. 0.90)	944	0.72 (0.51, 0.95)	1.5%

^aType I error is estimated from bootstrap of null distribution.

From the bootstrap analyses, the average HRs (for the different analyses) ranged from 0.72–0.79, with average stopping times of 1062 days (Lan–DeMets) and 1254 days (O'Brien–Fleming) corresponding to collection of 63% (1062/1688), and 74% (1254/1688) of the data as measured by number of days, respectively. For both stopping rules, approximately one fifth of all the samples resulted in a non-significant trial after completing all four analyses (data not shown), and in both cases, calculated Type I errors were 5.4% (Table 1a).

For the Bayesian analysis only the informative prior reached significance with our cutoff of 85%, and it did so after a single look, 519 days (31% of total time) into the trial after collecting only 25% of the expected deaths. This corresponded to an HR (credible interval) of 0.71 (0.56, 0.90). Estimated type I error rates were low for these analyses (1.0%, and 1.5% for non-informative and informative, respectively; Table 1a).

The results from the Bayesian bootstrap samples were similar to those of the frequentist analyses (Table 1a). However, 42% of the non-informative prior trials and 34% of the informative prior trials never reached significance at any of the analysis points (data not shown).

4.2. SPINE trial

In the case of both frequentist alpha spending functions, stopping for effectiveness would have been recommended after the third interim look at the data, corresponding to 628 days from randomization of the first participant (210 (25%) fewer days than the original trial). The trial team reported a clinically and statistically significant 2.47-point between-group difference in change of the disability scale score from baseline (95%CI:1.40, 3.53), while we found that, under both frequentist stopping rules, the difference at the recommended stopping times was 2.85, with slightly wider confidence intervals for both (Table 1b).

Table 1b.

SPINE trial comparison of results.

Actual trial data			Bootstrap (10,000 samples)
Analysis	Time (days)	Diff (95% CI)	Average time (days)	Average difference (95% CI)	Type I errora
Published Results	838	2.47 (1.40, 3.53)
Frequentist
OBF	628	2.85 (1.08, 2.63)	608	2.68 (1.36, 3.99)	5.1%
LD	628	2.85 (1.12, 4.58)	565	2.68 (1.33, 4.37)	5.3%
Bayesian
Non-Inform	628	2.97 (1.52, 4.42)	703	3.32 (0.16, 6.67)	0.2%
Informative	628	2.85 (1.52, 4.18)	691	3.35 (0.20, 6.69)	0.3%

^aType I Error is estimated from Bootstrap of Null distribution.

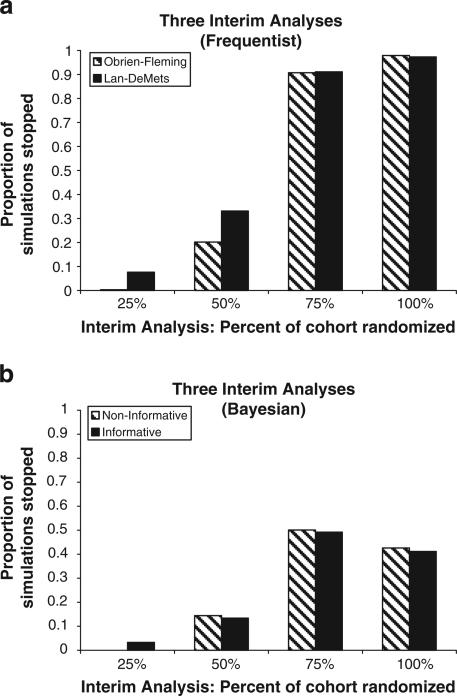
For the bootstrap samples, the average difference in Roland Morris disability score between the two groups was 2.68 (95% CI:1.36,3.99) for Obrien-Fleming, and 2.68 (95%CI:1.33,4.37) for Lan-DeMets (Table 1b), The average stopping time ranged from 565–608 days, corresponding to average proportions of 67%–72% of the accumulated data. Only 2% of the 10,000 bootstrap samples failed to reach significance for both O'Brien–Fleming, and Lan–DeMets methods. Fig. 3a demonstrates that the majority of the 3rd and 4th analyses resulted in significant results strong enough to recommend stopping the trial. Frequentist-estimated Type I error rates were 5.1%, and 5.3% for O'Brien–Fleming, and Lan–DeMets respectively.

Fig. 3.

a. SPINE study frequentist stopping times with 3 interim analyses. b. SPINE study Bayesian stopping times with 3 interim analyses.

For the actual sample, Bayesian analysis with a non-informative prior resulted in a 91% probability that the treatment was more effective than the control at the third interim analysis (data not shown). Using an informative prior, the posterior probability of effectiveness was 89% at the third interim analysis. In this case, use of a non-informative prior would have resulted in the same early decision to stop the trial as the informative prior.

The average difference at the time of stopping (credible interval) was 3.32 (0.16,6.67) for the non-informative, and 3.35 (0.20,6.69) for the informative prior distributions with the bootstrapping, both higher estimates than in the actual trial, and both credible intervals were wider than the confidence intervals of the original and the frequentist group sequential analyses. Had the actual trial been performed using Bayesian techniques with these parameters, both the informative and the non-informative priors would have indicated stopping at the third look, corresponding to 703 and 691 days, respectively. Fig. 3b shows the proportion of the bootstrapped samples which indicated stopping at each of the 4 time points. As with the frequentist analysis, more trials are stopped as more data are collected, however, the proportion of trials stopped never approaches unity; in fact, no more than about 50% of trials are stopped at any one point in time. Forty-three percent of the non-informative prior samples, and 44% of the informative prior samples never reached significance even after the fourth and final look at the data (data not shown). Overall estimated type I error rates were small, <1% in both cases.

5. Discussion

Given the great ethical and practical need to find more efficient ways to conduct clinical trials [1,38], we sought to compare the performance of Bayesian analytic approaches to the more common frequentist methods, using frequentist criteria. Whereas Bayesian methods have been widely promoted, they have seldom been compared to the traditional analysis methods using real clinical trial data.

Through our re-analysis of these previously reported trials, we found that the outcomes from neither frequentist nor Bayesian sequential methods differed appreciably from those of the standard analyses performed by the original trialists. However, in the case of the SPINE trial, both the frequentist and Bayesian sequential methods consistently came to the same conclusions faster than the original analysis, and suggested a reduction of recruitment by approximately 25%. In contrast, in the SOLVD-TT trial, the frequentist sequential methods’ outcomes were dependent upon the choice of alpha spending function. O'Brien–Fleming did not alter the timeline, but Lan–DeMets reduced the follow-up time by 50%. Similarly, Bayesian methods were dependent upon the choice of prior distribution, with early stopping dictated after only 30% accumulation of the events for the informative prior and complete study time for the non-informative. Hazard ratio and credible intervals appeared to be independent of prior distribution.

Our results indicate that, in these two trials, the newer Bayesian sequential methods did not appear markedly different from existing sequential and non-sequential methods in terms of decision-making outcomes. However, the speed with which we obtained these conclusions varied with the choice of method. As we consider the relative merits of Bayesian and frequentist methods, it is imperative that we consider the differences in the interpretations of the outcomes arising from the different methodologies. For both of our trials, the frequentist analyses tell us that it is unlikely that the two treatment arms come from the same distribution and therefore it is logical for us to draw the conclusion that the arms are different. In contrast, the Bayesian results indicate that, given our data, there is a greater than 85% probability that the treatment is superior to the placebo. While these statements may sound similar, they are in fact quite different. The frequentist “answer” is based on long-run repeated-analysis expected frequencies, while the Bayesian “answer” is based on posterior probability distributions which are constructed from all the accumulating data in each sample. For some, it may be easier to think about the probability that a treatment is superior to a placebo (Bayesian), than to think about the probability that an observed effect came from a specific distribution (frequentist).

It is important to remember that in the course of the frequentist analysis we don't exclusively consider distributions. We also estimate effects; the difference in average effect size in the two SPINE trial arms is a positive number, and the estimate of the ratio of effects in the SOLVD-TT trial is less than 1.0. With these estimates, we can draw away from the concept of the distribution and arrive at a practical answer. In fact, we conclude under both methodologies that the treatment is superior to the control group.

Our comparison of the proportion of significant results using Bayesian methods with that proportion arising from frequentist methods suggested that the frequentist methods were more consistent in their trial outcomes. For the SPINE trial, which published a significant result, the Bayesian methods determined significance less than half the time while the frequentist concluded significance about 98% of the time. The different analysis types agreed about half the time. Similarly for the SOLVD-TT trial, 80% of the frequentist trials reached significance, while approximately only half of the Bayesian trials did so. In general, for these particular trials, the frequentist group sequential methods reported significance more often and did so faster than the Bayesian methods. This implies that if, in fact, an effect is present, then the power of the frequentist analysis is greater than that of the Bayesian analysis when non-informative prior distributions are used. Despite the fact that all these methods are available and in use today, the real-life applications presented here indicate substantial differences in their performance. Since therapeutic decisions are based on the results of these types of clinical trials, the variation in the performance of these methods in real-world comparisons suggests that much more work is needed to better understand when and how we can have confidence in the statistical analyses.

5.1. Limitations

This study has several limitations. First, we did not evaluate these trials for futility. The analytic techniques used to detect futility are distinct from those we employed in the present comparison [12,39,40]. For a frequentist analysis, this can be determined by another set of boundaries sometimes referred to as the inner wedge [12]. In this instance, if the test statistic falls outside the critical bounds for the given stopping rule, the trial is stopped for effectiveness, but if it falls within the inner wedge of values, the trial is stopped for futility. If the statistic falls in any other region, the trial continues. For the Bayesian analyses, futility is measured by a cut-point on the posterior probability corresponding to a very low probability of superiority. This limit is usually set to a very small probability, generally ranging from 0.01%–1.0% [41,42].

Second, we present here only two types of outcomes; continuous (SPINE trial), and hazard ratio (SOLVD-TT). In reality, there are many types of outcomes, and each type would require different family of prior distributions, likelihoods, and general analysis techniques.

Third, our choice of posterior probability cut-points was subjective. In a trial designed to be analyzed with Bayesian techniques, a series of simulations would likely be performed with a null distribution in order to determine the cut-point which would yield a 5% error rate.

Fourth, this comparison was carried out with only two trials. Many more such comparisons are needed before firm conclusions regarding the relative real-world performance of the two approaches can be made.

Fifth, because the effect sizes are larger for the cases when the trials would have stopped earlier, there is evidence for some attenuation in the effect size over time in these two sets of analyses. Of course, the pre-specified end-of-trial time point is as arbitrary as any pre-specified interim analysis point and the true nature of the association, if a function of time, would require longer trials to better elucidate this time dependency.

Finally, we have chosen only the most basic family of prior distributions for our examples. There are many types of priors, some of which can be described with closed mathematical formulae, and others which must be generated from complicated computer simulations. In order to make these techniques more convincing, they must be demonstrated using other types of priors.

6. Conclusions

These examples, in which different methodologies appeared to lead to similar conclusions, do not prove a rule, but rather they begin to help us understand the mechanisms and outcomes from these different methodologies. With our comparative methodology and computer programs, we are now able to plan further comparative analyses with a variety of clinical trials in order to determine the conditions under which each specific method would be most effective. Future plans also include sensitivity analysis to compare these results with those from re-analyses with a greater number of interim looks at the data, different types of prior distributions, different posterior probability cut-points, and other alpha spending functions. Specifically, we plan to expand these analyses to include Bayesian methods with non-conjugate prior distributions such as non-closed form distributions and robust priors. In addition, future analyses are planned for studying early stopping for futility and harm as well as studies which have non-normally distributed outcomes such as counts and disease status. Finally, we plan to validate these methods prospectively with Bayesian-frequentist parallel analyses of future clinical trials. The analyses presented here help us to gain greater insight into the performance and value of newer clinical-trial analytic methods as we gradually make progress towards more efficient and ethical trials that accelerate the process of discovery.

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Appendix A

Formulae for posterior mean (μ_post) and standard deviation (σ_post) from Normal conjugate prior with Normal likelihood function.

$${\mu }_{post}=\frac{\left({\mu }_{prior}∕{\sigma }_{prior}^2\right)+\left({\mu }_{likelihood}∕{\sigma }_{likelihood}^2\right)}{\frac{1}{{\sigma }_{prior}^2}+\frac{1}{{\sigma }_{likelihood}^2}}$$

$${\sigma }_{post}=\frac{1}{\sqrt{\frac{1}{{\sigma }_{prior}^2}+\frac{1}{{\sigma }_{likelihood}^1}}}$$