Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2015 May 12;2(5):572–577. doi: 10.1021/acsphotonics.5b00053

Five-Photon Absorption and Selective Enhancement of Multiphoton Absorption Processes

Daniel H Friese †,*, Radovan Bast ‡,§,✉, Kenneth Ruud †,*
PMCID: PMC4477907  PMID: 26120588

Abstract

graphic file with name ph-2015-00053t_0003.jpg

We study one-, two-, three-, four-, and five-photon absorption of three centrosymmetric molecules using density functional theory. These calculations are the first ab initio calculations of five-photon absorption. Even- and odd-order absorption processes show different trends in the absorption cross sections. The behavior of all even- and odd-photon absorption properties shows a semiquantitative similarity, which can be explained using few-state models. This analysis shows that odd-photon absorption processes are largely determined by the one-photon absorption strength, whereas all even-photon absorption strengths are largely dominated by the two-photon absorption strength, in both cases modulated by powers of the polarizability of the final excited state. We demonstrate how to selectively enhance a specific multiphoton absorption process.

Keywords: UV/vis spectroscopy, response theory, quantum chemistry, ab initio calculations, molecular modeling, nonlinear optical properties, structure−activity relations

The concept of multiphoton absorption (MPA) dates back to 1931, when it was predicted theoretically by Maria Göppert-Mayer.1 After the introduction of high-intensity laser light sources, multiphoton absorption has gained a lot of attention during the past five decades, with the first experimental proof for two-photon absorption as the starting point in 1961.2

Two-photon absorption has by now found a wide range of applications.3−6 Simultaneously, electronic excitations involving absorption of up to five photons have been observed experimentally.7 The theoretical treatment of multiphoton absorption has also been pushed forward during the last decades, and computational methods for the calculation of two-photon transition strengths are available for SCF-based8,9 as well as for correlated wave-function-based methods.10−13 Implementations of three-photon absorption have been realized only for SCF-based methods,14−16 but SCF-based density-functional theory studies give good agreement with experiment for TPA and 3PA processes for small and medium-sized molecules.17,18 In our group, a recursive open-ended response theory19 has been expanded to the treatment of single residues of response functions, enabling the calculation of multiphoton absorption cross sections to infinite order using SCF-based methods, with results having been reported for four-photon absorption.20

In order to design molecules with high multiphoton absorption cross sections, general and qualitative structure–property relations are important. However, very few general structure–property relations exist for higher-order multiphoton absorption properties, although some interesting observations have been made in the case of three-photon absorption.21,22 The major scope of this work is both to present the first computational treatment of five-photon absorption and to study the relations between different multiphoton absorption processes. As experimental data for four- and five-photon absorption are very limited, in particular when it comes to complete spectra, we have to rely on a computational treatment of these properties to compare their behavior. In order to amplify the general observations presented here, we will focus on centrosymmetric molecules.

The multiphoton absorption cross sections calculated for the molecules in Figure 1 are shown in Table 1 for the p-dinitrobenzene (PDNB) molecule, which has D2h symmetry, and in Figure 2 for the diaminoazobenzene (Ci symmetry) and indigo molecules (C2h symmetry). Note that the units for the absorption cross sections differ and that the cross sections differ by orders of magnitude. The results reported have been calculated using the CAM-B3LYP functional23 and the augmented correlation-consistent polarized valence double-ζ basis sets (aug-cc-pVDZ) of Dunning and Woon.24,25 A recent study has shown that this level of theory is a good compromise between accuracy and computational cost.20 The calculations have been performed using a recursive response theory code19,20 interfaced to a development version of the Dalton program.26

Figure 1.

Figure 1

Open in a new tab

Three centrosymmetric molecules that have been studied in this work: para-dinitrobenzene (1), diaminoazobenzene (2), and indigo (3).

Table 1. Calculated MPA Cross Sections for PDNB and Their Ratios.

        jPA cross sections [cm2j sj–1/photonj–1]
   cross section ratios
no. energy [eV]   irrep OPA (10–19) TPA (10–54) 3PA (10–86) 4PA (10–118) 5PA (10–150)   OPA/3PA (1062) TPA/4PA (1061) 3PA/5PA (1062) OPA/5PA (10128)
1 3.90 1 b3g   3.44   0.08       43 860    
2 3.95 1 au     0.04   0.02       269  
3 4.39 1 b2g   9.26   0.96       9689    
4 4.42 1 b1u 2.46   1.78   0.13   138 013   1338 18 466
5 4.62 1 b2u 89.4   803   65.5   11 132   1226 1365
6 5.03 1 b3u 1240   52 557   13 226   2359   397 94
7 6.06 2 b2u 278   1695   1911   16 390   89 145
8 6.06 1 b1g   29 100   263 357       110    
9 6.15 1 ag   801 169   3 041 400       263    
10 6.20 2 b1g   21 602   4 893 130       4    
11 6.68 2 b2u 607   7395   42 997   8220   17 14
12 6.79 2 b3u 1626   60 375   412 524   2693   15 4
13 6.82 2 au     2.93   1.27       231  
14 6.85 2 b3g   1.90   2.57       740    
15 6.92 3 au     25.1   1.48       1694  
Open in a new tab

Figure 2.

Figure 2

Open in a new tab

Multiphoton absorption behavior of the two molecules under investigation. TPA cross sections have been scaled with 1032. 3PA cross sections are scaled with 1065, 4PA cross sections are scaled with 1094, and 5PA cross sections are scaled with 10126.

There are remarkable parallels in the absorption behavior of the different states depending on whether an even or an odd number of photons is absorbed; see Table 1. The PDNB molecule deviates from this observation with its Au states, which cannot be reached by one-photon processes for symmetry reasons.

Investigating the results, we note that the qualitative agreement between the absorption cross sections is not as obvious for the even-order processes as for odd-photon absorption processes. The best correlation between the different even-photon absorption processes has been found in the diaminoazobenzene molecule.

The similarity in the multiphoton absorption cross sections observed in Figure 2 can be explained by considering the sum-over-states expressions for the multiphoton absorption cross sections. For a complete discussion of the basic theory of multiphoton absorption we refer to the literature,20,27−30 and we restrict ourselves here only to provide the general expression for the multiphoton absorption cross sections that we will use in the analysis and to show the approximation we do in order to explain our observations.

The general j-photon absorption cross section σjPA is proportional to the square of the j-photon transition matrix element MjPA for j ≥ 2.20,27

graphic file with name ph-2015-00053t_m001.jpg 1

with MjPA being defined as (atomic units)29

graphic file with name ph-2015-00053t_m002.jpg 2

where ωi is the frequency of perturbation Xi and where we have already used the fact that the ground-state dipole moment vanishes for centrosymmetric molecules.30 μXi is the dipole operator with respect to perturbation Xi, and ωli is the excitation energy between the ground state 0 and the excited state li. f is the final state of the excitation, and the operator 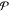Inline graphicX1, X2, ..., Xj generates all permutations of the perturbations. j is the number of photons absorbed in the described process. The calculations we present in this Letter have been performed using this equation in a slightly different formulation. To interpret them, we now simplify this expression using symmetry considerations.

For centrosymmetric molecules we can easily identify the symmetry of the accessible final states f as well as the intermediate states li in eq 2. Because all electric dipole perturbations are ungerade and the ground state always gerade, the excited state li that appears in the numerator of eq 2 must be ungerade. All final states for odd-photon absorption processes must be ungerade. In contrast, TPA and all higher-order even-photon absorption processes are allowed only for excitations with gerade final states.

However, from Figure 2 and Table 1, we note that there is even a semiquantitative agreement between the absorption cross sections of different excited states. The orders of magnitude that are covered by the different cross section values are very similar in all cases, and the order of the states with respect to their MPA behavior is similar within the even- and odd-photon absorption groups. This is illustrated in particular by the ratios between the cross sections that have been calculated for the PDNB molecule. Apart from the one for the 1B1u state, which shows a rather small cross section, we find that all ratios between OPA and 3PA are within the range of about an order of magnitude. The behavior of the TPA/4PA ratios is rather similar with the exception of the one for the 1B1g state. We will return to this anomaly.

In order to explain these observations, we first give the explicit expressions for the one- and two-photon absorption matrix elements:

graphic file with name ph-2015-00053t_m004.jpg 3
graphic file with name ph-2015-00053t_m005.jpg 4

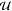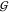where the individual perturbations are marked by lowercase letters. Inline graphic and Inline graphic represent ungerade and gerade states, respectively, and the index f marks the final state. 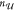Inline graphic is the number of ungerade excited states that are symmetry allowed. The operator 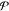Inline graphic generates all permutations of the perturbations and their individual frequencies.

Let us now consider the 3PA transition matrix element

graphic file with name ph-2015-00053t_m010.jpg 5

For a molecule with a strong, isolated OPA state, the dominating intermediate state of ungerade symmetry is the final state of interest; in the spirit of few-state models for multiphoton absorption cross sections, the 3PA matrix element then reduces to

graphic file with name ph-2015-00053t_m011.jpg 6

Note that in this expression the summation over the ungerade states has been dropped, but the summation over gerade states is not affected. The validity of this approach has been shown, for example, in work by Vivas and co-workers, where a three-level model for TPA yielded impressive results compared to experiment.31 Using this expression, we can write the 3PA matrix element as

graphic file with name ph-2015-00053t_m012.jpg 7

This quasi-few-state model now explains the similarity of the OPA and 3PA absorption cross sections, the 3PA cross section being proportional to the OPA cross section, and the proportionality factor being the excited-state polarizability divided by an energy denominator. The permutation operator that is still present in the approximated equation takes into account that several spatial components of MaOPA can contribute to the transition dipole moment.

This is also an explanation for the low 3PA and 5PA cross sections of the Au states in PDNB since these states cannot be dominated by an OPA excitation according to eq 6. We can therefore separate 3PA excitations into OPA-dominated and pure-3PA absorptions.

We can extend this analysis to 4PA. The matrix element for four-photon absorption is

graphic file with name ph-2015-00053t_m013.jpg 8

where both the summations over k and m cover the same manifold of ungerade states. In the same manner, we can now assume a dominant contribution from 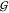Inline graphicf as the intermediate gerade state and write eq 8 as

graphic file with name ph-2015-00053t_m015.jpg

Analogous to the results for 3PA, we find that the 4PA cross sections are proportional to the TPA cross section, the proportionality factor being the excited-state polarizability divided by an energy term.

For five-photon absorption, we can in a similar manner write

graphic file with name ph-2015-00053t_m016.jpg 11

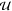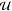noting that we now have two ungerade intermediate states that can be substituted by the Inline graphicf state. If we only introduce the final state for the second ungerade state (Inline graphicm in the equation) we obtain

graphic file with name ph-2015-00053t_m019.jpg 12

which is an expression for 3PA-dominated 5PA, which is representative for the Au states of the PDNB molecule. (In principle there should also be a term arising from introducing the final state for the first ungerade intermediate state. However, this would lead to a term that would correspond to the OPA transition moment scaled by the excited-state second hyperpolarizability and thus can be expected to be smaller.) In most cases, we can simplify eq 12 further by substituting all ungerade intermediate states by the final state, giving

graphic file with name ph-2015-00053t_m020.jpg

which shows that the 5PA absorption cross section can be expected to be proportional to the OPA transition moment scaled by the excited-state polarizability squared.

These expressions explain why we observe the orthogonality of the odd- and even-order multiphoton absorption cross sections. Furthermore, they also explain the strong parallelism of the odd- and even-order multiphoton absorption cross sections, as they are in all cases related to the lowest-order one- or two-photon absorption cross section, scaled by the energy difference between the excitation energy to the final state and the incoming laser frequencies, and scaled by (products of) excited-state polarizabilities. It is important to point out that this model does not allow quantitative predictions of higher-order MPA from OPA or TPA data, but it gives a qualitative to semiquantitative description of the behavior of the different properties.

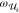Multiphoton absorption cross sections can be enhanced through resonances, occurring when the frequency (or sums of frequencies) of the incoming laser light matches that of intermediate excited states (e.g., when ωa =Inline graphic/2 ≈ Inline graphic in the case of TPA). We note from the equations above that the frequency prefactor in the few-state models has the same poles as that of the TPA or 3PA processes, respectively. Thus, boosting TPA and 3PA processes through near-resonance conditions will also boost the higher-order multiphoton absorption cross sections.

Boosting a higher-order multiphoton absorption cross section selectively without a simultaneous increase in the lower-order multiphoton absorption cross section will thus be possible only if we can make the excited-state polarizability approach a pole for one of the frequency combinations of the incoming laser light. Consider for example the 4PA transition moment in eq 10. 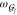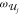Whereas the TPA cross section, and thus also the 4PA cross section, will have a pole if there are intermediate states at half the energy of the excited state, the 4PA will be selectively enhanced if there is an excited state of ungerade symmetry at 3 Inline graphic/4. Similar considerations can be made for the 5PA process, and we can selectively enhance the 5PA process if there are intermediate states of gerade symmetry with energy 2 Inline graphic/5 and 4 Inline graphic/5.

If we now return to the unexpected enhancement of the 4PA cross section of the 2B1g (and the close-lying 1B1g and 1Ag states) in PDNB, we note that there exists an intermediate B2u state of ungerade symmetry at approximately 3/4 of the energy of these final states, thus creating a resonance in the excited-state polarizability and enhancement of the 4PA process relative to the TPA process.

To summarize our findings, we have presented the first 5PA cross section calculations at the density-functional level of theory using the CAM-B3LYP exchange–correlation functional for three centrosymmetric molecules. These calculations have shown that for molecules with an inversion center the selection rules for dipole-allowed transitions make the relative magnitude of all the even (odd) multiphoton absorption cross sections similar for different excited states. Assuming the validity of a few-state model for the states with the same symmetry as the final state of the multiphoton absorption process, we have shown that higher-order multiphoton absorption cross sections are proportional to the TPA (even-order absorption processes) or OPA (odd-order absorption processes) cross sections, scaled by an energy denominator and powers of the polarizability of the final excited state.

Our analysis shows that for centrosymmetric molecules excited states that display strong one- or two-photon absorption cross sections will also display strong multiphoton absorption cross sections. We have also shown how to selectively enhance the higher-order multiphoton absorption cross section by designing molecules with intermediate states that match selected frequency combinations for the frequency of the incoming light. We predict, for instance, a strong enhancement of 5PA processes by designing molecules with intermediate states of energy 2 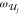Inline graphic/5 and 4 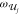Inline graphic/5, as well as for 4PA, as illustrated by our results calculated for the PDNB molecule. These results will be valuable guidelines for designing molecules with strong higher-order multiphoton absorption cross sections.

Computational Details

All multiphoton absorption calculations have been performed using a recursive open-ended response theory code,19 which has recently been expanded to the treatment of single residues of response functions.20 The response code has been interfaced with a development version of the Dalton program.26 All calculations have been performed using the aug-cc-pVDZ basis set from the Dunning family of basis sets24 and the CAM-B3LYP density functional.23 In all calculations of n-photon absorption the energy of the involved photons was the excitation energy divided by n.

The geometry of the para-dinitrobenzene molecule has been optimized using the cc-pVQZ basis set and the B3LYP functional32,33 in Gaussian.34 The geometries of the diaminoazobenzene and indigo molecules have been optimized using TURBOMOLE35 with the B3LYP functional and the TZVP basis set.36

The rotational averaging of the calculated results has been performed following available literature,37−39 and the calculation of the cross sections was done using an approach that has recently been generalized by two of us20 based on work by Peticolas.27 The detailed equations for this are given in the Supporting Information.

Acknowledgments

This work has received support from the Research Council of Norway through a Centre of Excellence Grant (Grant No. 179568/V30), from the European Research Council through a Starting Grant (Grant No. 279619), and from from the Norwegian Supercomputing Program (Grant No. NN4654K).

Supporting Information Available

Some more information about the rotational averaging of the multiphoton absorption tensors and the conversion from atomic units to cgs units can be found in the Supporting Information. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Supplementary Material

ph5b00053_si_001.pdf (166.7KB, pdf)

References

  1. Göppert-Mayer M. Über elementarakte mit zwei quantensprüngen. Ann. Phys. 1931, 401, 273–294. [Google Scholar]
  2. Kaiser W.; Garrett C. G. B. Two-photon excitation in CaF2:Eu2+. Phys. Rev. Lett. 1961, 7, 229–231. [Google Scholar]
  3. Parthenopoulos D. A.; Rentzepis P. M. Three-dimensional optical storage memory. Science 1989, 245, 843–845. [DOI] [PubMed] [Google Scholar]
  4. Zipfel W. R.; Williams R. M.; Webb W. W. Nonlinear magic: multiphoton microscopy in the biosciences. Nat. Biotechnol. 2003, 21, 1369–1377. [DOI] [PubMed] [Google Scholar]
  5. Helmchen F.; Denk W. Deep tissue two-photon microscopy. Nat. Methods 2005, 2, 932–940. [DOI] [PubMed] [Google Scholar]
  6. Pawlicki M.; Collins H. A.; Denning R. G.; Anderson H. L. Two-photon absorption and the design of two-photon dyes. Angew. Chem., Int. Ed. 2009, 48, 3244–3266. [DOI] [PubMed] [Google Scholar]
  7. Zheng Q.; Zhu H.; Chen S.-C.; Tang C.; Ma E.; Chen X. Frequency-upconverted stimulated emission by simultaneous five-photon absorption. Nat. Photonics 2013, 7, 234–239. [Google Scholar]
  8. Hettema H.; Jensen H. J. Aa.; Jørgensen P.; Olsen J. Quadratic response functions for a multiconfigurational self-consistent field wave function. J. Chem. Phys. 1992, 97, 1174–1190. [Google Scholar]
  9. Sałek P.; Vahtras O.; Helgaker T.; Ågren H. Density-functional theory of linear and nonlinear time-dependent molecular properties. J. Chem. Phys. 2002, 117, 9630–9645. [Google Scholar]
  10. Koch H.; Jørgensen P. Coupled cluster response functions. J. Chem. Phys. 1990, 93, 3333–3344. [Google Scholar]
  11. Paterson M. J.; Christiansen O.; Pawłowski F.; Jørgensen P.; Hättig C.; Helgaker T.; Sałek P. Benchmarking two-photon absorption with CC3 quadratic response theory, and comparison with density-functional response theory. J. Chem. Phys. 2006, 124, 054322. [DOI] [PubMed] [Google Scholar]
  12. Hättig C.; Christiansen O.; Jørgensen P. Coupled cluster response calculations of two-photon transition probability rate constants for helium, neon and argon. J. Chem. Phys. 1998, 108, 8355–8359. [Google Scholar]
  13. Friese D. H.; Hättig C.; Ruud K. Calculation of two-photon absorption strengths with the approximate coupled cluster singles and doubles model CC2 using the resolution-of-identity approximation. Phys. Chem. Chem. Phys. 2012, 14, 1175–1184. [DOI] [PubMed] [Google Scholar]
  14. Jonsson D.; Norman P.; Ågren H. Cubic response functions in the multiconfiguration self-consistent field approximation. J. Chem. Phys. 1996, 105, 6401–6419. [Google Scholar]
  15. Cronstrand P.; Luo Y.; Norman P.; Ågren H. Ab initio calculations of three-photon absorption. Chem. Phys. Lett. 2003, 375, 233–239. [Google Scholar]
  16. Cronstrand P.; Jansik B.; Jonsson D.; Luo Y.; Ågren H. Density functional response theory calculations of three-photon absorption. J. Chem. Phys. 2004, 121, 9239–9246. [DOI] [PubMed] [Google Scholar]
  17. Zheng Q.; He G. S.; Baev A.; Prasad P. N. Experimental and quantum chemical studies of cooperative enhancement of three-photon absorption, optical limiting, and stabilization behaviors in multibranched and dendritic structures. J. Phys. Chem. B 2006, 110, 14604–14610PMID:16869561. [DOI] [PubMed] [Google Scholar]
  18. Diaz C.; Vesga Y.; Echevarria L.; Stara I. G.; Starý I.; Anger E.; Shen C.; El Sayed Moussa M.; Vanthuyne N.; Crassous J.; Rizzo A.; Hernández F. E. Two-photon absorption and two-photon circular dichroism of hexahelicene derivatives: a study of the effect of the nature of intramolecular charge transfer. RSC Adv. 2015, 5, 17429–17437. [Google Scholar]
  19. Ringholm M.; Jonsson D.; Ruud K. A general, recursive, and open-ended response code. J. Comput. Chem. 2014, 35, 622–633. [DOI] [PubMed] [Google Scholar]
  20. Friese D. H.; Beerepoot M. T. P.; Ringholm M.; Ruud K. Open-ended recursive approach for the calculation of multiphoton absorption matrix elements. J. Chem. Theory Comput. 2015, 11, 1129–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Alam M. M.; Chattopadhyaya M.; Chakrabarti S.; Ruud K. Effect of donor-acceptor orientation on solvent-dependent three-photon activity in through-space charge-transfer systems - case study of [2,2]-paracyclophane derivatives. Phys. Chem. Chem. Phys. 2013, 15, 17570–17576. [DOI] [PubMed] [Google Scholar]
  22. Alam M. M.; Chattopadhyaya M.; Chakrabarti S.; Ruud K. Chemical control of channel interference in two-photon absorption processes. Acc. Chem. Res. 2014, 47, 1604–1612. [DOI] [PubMed] [Google Scholar]
  23. Yanai T.; Tew D. P.; Handy N. C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar]
  24. Dunning T. H. Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar]
  25. Woon D. E.; Dunning T. H. Gaussian basis sets for use in correlated molecular calculations IV. Calculation of static electrical response properties. J. Chem. Phys. 1994, 100, 2975–2988. [Google Scholar]
  26. Aidas K.; et al. The Dalton quantum chemistry program system. WIREs Comput. Mol. Sci. 2013, 4, 269. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Peticolas W. Multiphoton spectroscopy. Annu. Rev. Phys. Chem. 1967, 18, 233–260. [Google Scholar]
  28. Olsen J.; Jørgensen P. Linear and nonlinear response functions for an exact state and for an MCSCF state. J. Chem. Phys. 1985, 82, 3235–3264. [Google Scholar]
  29. Hättig C.; Christiansen O.; Jørgensen P. Multiphoton transition moments and absorption cross sections in coupled cluster response theory employing variational transition moment functionals. J. Chem. Phys. 1998, 108, 8331–8354. [Google Scholar]
  30. Cronstrand P.; Luo Y.; Ågren H. Generalized few-state models for two-photon absorption of conjugated molecules. Chem. Phys. Lett. 2002, 352, 262–269. [Google Scholar]
  31. Vivas M. G.; Diaz C.; Echevarria L.; Mendonca C. R.; Hernández F. E.; De Boni L. Two-photon circular-linear dichroism of perylene in solution: a theoretical-experimental study. J. Phys. Chem. B 2013, 117, 2742–2747. [DOI] [PubMed] [Google Scholar]
  32. Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar]
  33. Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar]
  34. Frisch M. J.; et al. Gaussian 09 Revision C.01; Gaussian Inc.: Wallingford, CT, 2009.
  35. TURBOMOLE V6.6 2014, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
  36. Schäfer A.; Huber C.; Ahlrichs R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1989, 100, 5829–5835. [Google Scholar]
  37. Andrews D. L.; Thirunamachandran T. On three-dimensional rotational averages. J. Chem. Phys. 1977, 67, 5026–5033. [Google Scholar]
  38. Andrews D. L.; Ghoul W. A. Polarization studies in multiphoton absorption spectroscopy. J. Chem. Phys. 1981, 75, 530–538. [Google Scholar]
  39. Friese D. H.; Beerepoot M. T. P.; Ruud K. Rotational averaging of multiphoton absorption cross sections. J. Chem. Phys. 2014, 141, 204103. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ph5b00053_si_001.pdf (166.7KB, pdf)

Articles from ACS Photonics are provided here courtesy of American Chemical Society

RESOURCES