Handling Missing Values in Longitudinal Panel Data With Multiple Imputation

Abstract

This article offers an applied review of key issues and methods for the analysis of longitudinal panel data in the presence of missing values. The authors consider the unique challenges associated with attrition (survey dropout), incomplete repeated measures, and unknown observations of time. Using simulated data based on 4 waves of the Marital Instability Over the Life Course Study (n = 2,034), they applied a fixed effect regression model and an event-history analysis with time-varying covariates. They then compared results for analyses with nonimputed missing data and with imputed data both in long and in wide structures. Imputation produced improved estimates in the event-history analysis but only modest improvements in the estimates and standard errors of the fixed effects analysis. Factors responsible for differences in the value of imputation are examined, and recommendations for handling missing values in panel data are presented.

The use of longitudinal panel (prospective) survey data is common in the area of family research. From 2010 to 2014, approximately 287 quantitative and qualitative research articles (excluding theory development, research reviews, comments, rejoinders, and methodological innovation articles) were published in the Journal of Marriage and Family (JMF). Of these, 176 (61%) analyzed longitudinal data. Data on the same individuals or families at multiple points in time provide for stronger inferences about change processes and allow for more control of unmeasured differences between individuals that can bias study findings (Johnson, 1995, 2005). What tempers these advantages is the large amount of missing data found in many longitudinal studies. Nearly all of the JMF articles explicitly mentioned the presence of missing values and study dropout—suggestive of the widespread concern with missing data in panel studies.

Few guidelines for the analysis of longitudinal panel data in the presence of missing values are accessible to family researchers. Moreover, no clear appraisals of the consequences of different ways of handling missing data are readily offered. Existing guidelines tend to be directed toward statisticians or focus on types of longitudinal data rarely found in the family literature, such as randomized clinical trials (e.g., Daniels & Hogan, 2008; Enders, 2011; Hedeker & Gibbons, 2006; National Research Council, 2010) or data sets with few cases but many waves, such as cross-national time-series studies (e.g., Honaker & King, 2010). Methods for handling missing values have been addressed in the family literature (e.g., Acock, 2005; Johnson & Young, 2011; Young & Johnson, 2013), but these resources focus primarily on cross-sectional data. Although much of what we know about the approaches to handling missing values in cross-sectional situations applies to longitudinal panel data, panel data have characteristics that complicate the application of techniques such as multiple imputation (MI). Such complications, along with a lack of accessible guides to help address these issues, may be contributing to the limited use of modern methods like maximum likelihood (ML) or MI among the many studies in the area of family that use longitudinal data (Jelicic, Phelps, & Lerner, 2009).

In this article, we review standard approaches to handling missing data in longitudinal panel studies, apply several techniques to a simulations study based on an empirical family research problem using a multiwave panel data set, and assess how different strategies have consequences for the research findings. Our focus is on missing values in panel data sets with large numbers of respondents but small numbers of survey waves administered at fixed intervals—typical conditions for data sets found in much family research. Missing-data MI strategies with fixed effect, pooled time-series models and event-history (Cox proportional hazard) models are examined. Our review of the methods used in 176 JMF articles suggests that the most common models for analyzing longitudinal data were event history (19%), fixed effects(18%, or 19% including change scores), and mixed effect or multilevel (17%, or 22% including growth curve), followed by linear regression (16%), logistic regression (15%), and structural equation models (10%, or 15% including growth curve and latent class analysis). Less common methods for analyzing longitudinal data included multinomial regression (5%) and qualitative analysis (2%). (Note that percentages sum to more than 100% because many articles used more than one method.)

Background

Longitudinal panel studies have several features that complicate the techniques commonly applied when handling missing data. Unlike cross-sectional data sets, longitudinal data sets have both within-wave and whole-wave missingness. Longitudinal data analysis methods require a particular data structure (long vs. wide) that creates issues when handling missing data (Lloyd, Obradovic, Carpiano, & Motti-Stefanidi, 2013). Other complications of missing values in longitudinal data include repeated measures; time-to-event models; nonrandom study dropout; and statistical procedures that routinely handle some, but not all, sources of missing data.

Two Sources of Missing Values

Missing values in panel data can occur in variables within a wave and when a full wave of data are missing for a respondent. Within-wave missing values result from typical item nonresponse that is found in any cross-sectional study. These missing values occur when a valid responses is not recorded for a survey question either because the participant chose not to answer the question or an interviewer failed to record the answer. Item nonresponse occurs most frequently for sensitive questions (e.g., regarding income or sexual behavior) and questions that are difficult to answer (e.g., recalling a date; De Leeuw, Hox, & Huisman, 2003). Within-wave missing data in panel studies can also occur when questions are included in only some study waves.

Whole-wave missingness occurs when respondents do not participate in all data collection time points. In a four-wave panel study, for example, a respondent may participate only in the first two waves before dropping out of the study. This produces missing data on all variables in the two subsequent waves. The result is a substantial amount of missing data for the time period covered by the wave, although time-invariant characteristics (e.g., date of birth) may be carried over from an earlier wave. When respondents are missing entire waves of data, too little information is available in the wave to inform the data analysis, and information on time-varying change is lost because of the missing waves.

Attrition in longitudinal panel studies (or study dropout) has received much attention in the literature, and several strategies for statistically evaluating and adjusting for the consequences of attrition have been developed (Groves, Dillman, Elting, & Little, 2002; Little, 1995). The attrition literature focuses heavily on the potential for biased statistical estimates that could result from overlooking attrition. In medical clinical trials, for instance, the dropouts from the trial may have been persons for whom the treatment was failing or who experienced negative side effects (National Research Council, 2010). In studies of marriages, individuals who divorce between waves may be more likely to leave the study, potentially biasing the effects of variables related to marital instability (VanLaningham, Johnson, & Amato, 2001). Much of the attrition from panel studies, however, may be unrelated (or weakly related) to model variables and thus are unlikely to introduce much bias into model estimates (Fitzgerald, Gottschalk, & Moffitt, 1998).

With panel data, attrition can be modeled using data from prior waves. The primary strategy for modeling whole-wave missingness is to use logistic regression to estimate the extent to which variables in previous waves predict attrition from subsequent ones. If variables in the analysis model are related to attrition, it is unlikely that dropout occurred completely at random (resulting in data that are missing completely at random [MCAR]). For instance, this could occur if people with low marital happiness in the first wave were more likely to drop out of the study than those with initially high levels of marital happiness. In this case, the probability of a value being missing in the second wave would be correlated with the true but unobserved level of marital happiness at follow-up. Knowing that low marital happiness was related to study dropout, a diligent researcher would be concerned about whether the data were missing at random (MAR) or not missing at random (NMAR). If variables that strongly predict attrition are incorporated into the missing data strategy, the plausibility of a MAR assumption would increase.

Data Structure for Longitudinal Models

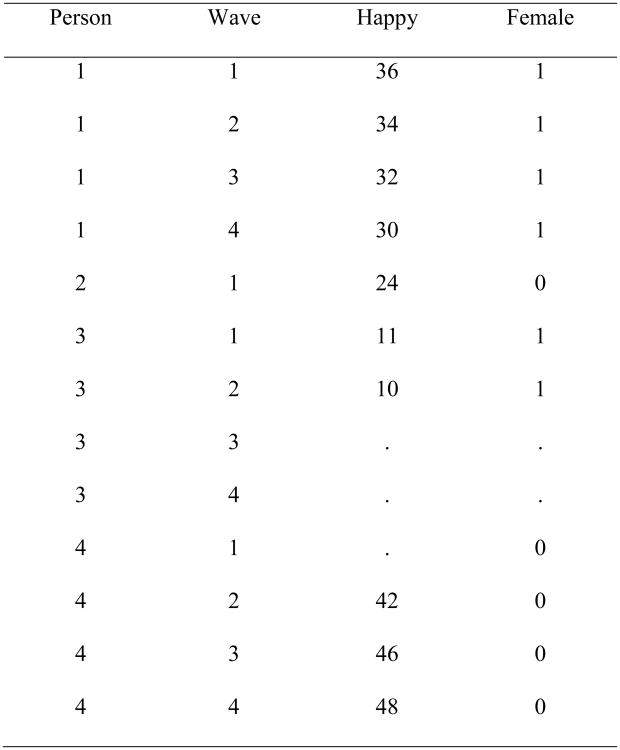
Longitudinal data sets are often organized with as many records as waves per individual—a structure required by many statistical techniques for longitudinal data. Software packages such as SAS, Stata, SPSS, and R refer to this structure as long or stacked (contrasted with a wide data structure, in which there is only record per individual). Most statistical packages have procedures to move back and forth between long and wide structures. Figure 1 and Figure 2 show examples of long and wide data organization. In the long structure, a unique case identifier links the records for the waves to the case. The variables are stacked, with each column containing responses to the same question asked at each wave. Respondents may have records only for the waves to which they responded (e.g., Person 2 in Figure 1), although empty records could also be present for missing waves (e.g., Person 3 in Figure 1). Within-wave missing data are represented in the usual manner by missing value codes.

Figure 1.

Example of Data in the Long Structure.

Note: This is an illustration of longitudinal panel data stored in a long structure. Considered as a multilevel structure, four repeated observations of happiness (Level 1) are nested within individual clusters (Level 2). In a standard Cox model using right censoring, Person 2, for example, may be censored at the time of the first wave and would therefore be excluded from the analysis (contributing 0 person-time).

Figure 2.

Example of Data in the Wide Structure.

Statistical procedures that require the long data structure include pool time-series analysis methods (e.g., xtreg in Stata, PROC POOLED in SAS), multilevel mixed models, and time-to-event models with time-varying variables. The example in Figure 1 is a multilevel structure that differs from classical multilevel models because repeated observations (panels) are nested within individual observations rather than cases being nested within clusters (e.g., students within classrooms).

Data organized in the wide structure, as illustrated in Figure 2, place responses to all waves in the same record, with responses to each wave appearing in separate columns. Each individual has one record that contains repeated observations. When a wave is incomplete, missing data codes are assigned to all the variables for that wave. Within-wave missing values and whole-wave missing values are represented in the same way. Structural equations software usually accepts this data structure, as do many repeated measures and multivariate analysis of variance procedures.

Most MI software was not designed to handle the long data structure. Standard MI treats each record as an independently sampled case with no capability of linking separate wave records to a single respondent. Failure to link the records leads to two problems. First, regression-based techniques assume independent sampling of cases. The assumption is necessary for correct standard errors but has little impact on the estimates of the regression coefficients (Berry, 1993). The more serious problem for MI estimation is that the imputation model cannot be informed by values of variables, including the same variable from other waves, which are often the best predictors of the missing value (Allison, 2001). If the respondent has missing data in one of the waves, his or her responses to the same item in other waves can provide substantial information to estimate the likely missing value, leading to more accurate estimates of the covariance matrix (Little, 1995). Standard MI software, however, cannot directly inform the estimates for the missing values with this information. Consequently, the estimated between-wave item covariance will be attenuated, resulting in downward biased estimates, reducing the advantages of MI.

For a classic multilevel structure in which individuals are nested within a cluster (e.g., students within classrooms) there are two options for imputing data in the long structure that overcome these problems. The first option is to include a set of dichotomous indicator variables for each cluster or Level 2 unit in the imputation model (Eddings & Marchenko, 2011). A second possibility is to use the “cluster” option in software packages with advanced MI programs. In Stata and Mplus, for instance, multilevel data can be imputed if the number of Level 2 groups is reasonably small (Eddings & Marchenko, 2011; Muthén & Muthén, 2012). Imputing some multilevel data with specialized programs such as PAN (Schafer & Yucel, 2001), WinMICE (Jacobusse, 2005), and Amelia II (Honaker, King, & Blackwell, 2007) also is possible. None of the latter programs have gained widespread use and require significant programming effort or have limited use with large panel data sets.

Unfortunately, the ability to impute classic multilevel data does not readily apply when repeated measures are nested within individuals. For example, in a four-wave study of 2,000 participants, treating individuals as clusters would involve adding 1,999 indicator variables to the imputation model, in addition to the main analysis variables. Imputing with the cluster option where individual participants are the second level of analysis is a similarly problematic model specification with such a large number of clusters. Our experience with MI software confirms that estimating models with thousands of clusters produces error messages, identifying the problem as an issue of collinearity or one of too many clusters.

When data are stored in the long structure with repeated measures included on a single record for each case, MI literature recommends rearranging the data to a wide structure for the imputation step (Allison, 2001) and returning it to the long structure for analysis. Sometimes, however, researchers have many waves of data and analysis models that include a large number of variables. In this case, the wide data structure could require adding a large number of variables to the imputation model (though probably still fewer than adding indicators for n – 1 participants), which could impose technical limits on the imputation model and result in a great increase in the time it takes to impute the data. Imputing in the long structure may be statistically flawed, yet it is a practical choice when the wide structure is unwieldy and when the estimates obtained for the missing values yield reasonably accurate results.

Other Special Considerations

Time

For some models, time adds another layer of practical complication. Time-to-event models, for example, explicitly account for amount of time that a person spends at risk of experiencing an outcome. With whole-wave missingness, survey dates and times are unavailable if the respondent did not participate in a wave. If missing outcome variables or missing waves are to be imputed, how missing time information should be handled is a great practical concern. Although guidelines exist for incorporating time-to-event data in an MI model (White & Royston, 2009), other questions remain unanswered by the statistical literature. Should an event be imputed when the outcome has missing values, or should these events be censored at the last observed time point? What should be done if whole waves are imputed and a survey date or time is required by the modeling strategy?

Software considerations

A practical issue with handling missing values in longitudinal panel data is that some of the most widely used statistical software for analyzing models of change in longitudinal data treat within and whole-wave missing data differently. We focus our discussion on the software packages that appear to be most frequently used by family researchers analyzing longitudinal data. Personal communication with all but 10 authors of the 176 JMF articles revealed that Stata was used in 57.4% of these studies, followed by SAS (17.6%), SPSS/AMOS (13.1%), and Mplus (11.4%).

Software tools for analyzing pooled time-series data are designed to estimate models in the presence of a variable numbers of waves for each case(Hedeker & Gibbons, 2006). These procedures (sometimes referred to as mixed regression models) analyze the data in the long structure and can be used to estimate a variety of models such as fixed and random effects models, hybrid models, and variations of multilevel models for longitudinal data (Allison, 2009). Examples are the xt procedures in Stata (e.g., xtlogit, xtmixed), similar procedures in SAS (e.g., PROC MIXED), and other multilevel (mixed model) software routines in packages such as SPSS and R.

Software tools for analyzing event-history data also allow for different amounts of follow-up time, or time at risk of experiencing an event, to be recorded for each case. Examples are the st procedures in Stata and PROC PHREG in SAS. These procedures may analyze data in the long or wide structure depending on the presence of time-varying covariates or spells of time at risk. For longitudinal panel data, where outcome data are collected at each wave, cases with missing waves are right-censored at the time of dropout. For example, a participant who was present for only the first two waves of a four-wave study would contribute two waves of person-time to the model (e.g., Person 3 in Figures 1 and 2).

Although the descriptions available for these commonly used procedures all make it clear that estimation is possible in the presence of missing values in model variables, the documentation is less explicit about pattern of missingness assumptions and whether the same procedures and assumptions are true for both within- and whole-wave missingness. The xt and st procedures in Stata, for example, accommodate data when cases have a variable number of waves, which is viewed by many researchers as “allowing missing data.” An important caveat to this interpretation is that this applies only to whole-wave missingness.

Panel procedures handle whole-wave missing data in a way similar to an ML solution. All nonmissing waves are used in the covariance matrix (as opposed to using no information from cases with missing waves) and the missing-values mechanism is assumed to be MAR (Hedeker & Gibbons, 2006). Within-wave missing values are treated in a different way. Within-wave missing values on variables in the model cause the record from the whole wave to be excluded from analysis. For example, Person 4 in Figures 1 and 2 was present for all study waves but did not answer the “Happy” question at Wave 1; this item nonresponse would cause the entire record to be removed from the analysis.

Thus, panel procedures “allow” missing data in the same way that a linear regression model allows missing values; the records with missing values on any variable in the model are removed. A major limitation of this approach is that complete case analysis assumes that values are MCAR, which is a mechanism of missingness unlikely to occur without intentional design (Graham, 2009). In addition, panel records for a case can be dropped without a researcher's awareness, because the sample size reported for the number of participants could be correct even if the number of records analyzed was fewer than was found in the data set.

Event-history procedures handle whole-wave missing data by censoring cases at the last observed follow-up time. This approach differs from panel procedures in one important way: Cases with no follow-up time will contribute no information to the model and are assumed to be MCAR, whereas cases with incomplete follow-up time are assumed to be MAR and do contribute information to the model. A participant who was present for only the first wave of a four-wave study, such as Person 2 in Figures 1 and 2, would be excluded from the analysis because the case had no follow-up data; this approach is like complete case analysis. A participant who was present for three of four waves would contribute data through the third wave; this is more similar to an ML solution in which all known information is used and study dropout is assumed to be MAR. As in panel procedures, event-history models handle within-wave missing values using complete case analysis that removes records with missing data on any of the variables in the model.

Structural equation models

Another strategy for the analysis of missing data in panel studies is found primarily in structural equation modeling (SEM) software that uses ML methods (often referred to as a full information maximum likelihood) to estimate the covariance structure in the presence of missing values. These methods assumes that the missing data are MAR and yield parameter estimates for similarly structured models that are essentially equivalent to those obtained with MI (Graham, 2009; Young & Johnson, 2013). SEM requires the wide structure for the data, and within-wave and whole-wave missing data are treated in the same way.

Handling Missing Data

The added complications of handling missing data in panel studies raises a number of questions for family researchers about the best course of action, in particular when the analysis model for the study uses data in the long structure. When the data are analyzed with procedures that demand the long data structure, there is ambiguity about how to proceed. Although missing values due to missing waves may be unproblematic, complete case analysis is automatically used for within-wave missingness. This approach is biased unless the data are MCAR and will be inefficient in the sense that known information is discarded from the analysis. If the researcher decided to impute the within-wave missing data, the temptation would be to impute in the long structure because the data in the missed waves would already be removed from the data set. If repeated observations were nested within individuals, imputing in the long structure is believed to be erroneous (Lloyd et al., 2013). This problem could be solved by converting the data to a wide form to impute the variables and then back into the long form for analysis, yielding imputed values for both the within- and whole-wave missing values. Of course, many researchers are hesitant to impute entire waves for which a participant was not actually present, especially when dates or times are required for the missing wave.

Applying MI to panel data raises additional choices for researchers. The data could be imputed in the wide structure. Although some of the waves would contain only imputed values, observed values would be used in situations with time-invariant variables (which would not add more information to the model). An alternative approach would be to delete the missing waves after the imputation step and allow the statistical software to estimate the model with a variable number of waves per respondent, retaining only the within-wave imputed values. If the imputation model included a number of variables that were not in the analysis model (called auxiliary variables), and these variables were related to attrition and to model variables, the MAR assumption would be more plausible when analyzing data from fully imputed waves than when analyzing data from a variable number of waves.

Method

Two of the three most commonly used methods for analyzing longitudinal data in family research, published in the last 4 years of JMF, were fixed effects regression and event-history analysis. These models often require the long data structure and include complications for MI that are not present in cross-sectional analysis. Complete case analysis and long and wide MI methods are tested in a simulation based on the first four waves of the Marital Instability Over the Life Course (MILC) study (www.icpsr.umich.edu/icpsrweb/ICPSR/series/00187). Each method is compared to a “true” or known model and assessed for bias and general performance.

Several reasons motivated the decision to focus on MI. Many family researchers are already comfortable with MI; this technique has been widely adopted in family research. MI programs are available in many statistical software packages, including family researchers' top three packages of choice (Stata, SAS, and SPSS). Maximum likelihood approaches are not widely available for all types of statistical models, with increasing exceptions offered by Mplus (Muthén & Muthén, 2012). Mplus, however, was used by less than 12% of family researchers when analyzing longitudinal data. Finally, because ML in SEM uses the less problematic wide structure to estimate the types of models covered here, we limit our discussion to the best approaches for using MI in longitudinal panel data.

All MI models presented here were produced in Stata 13, using sequential chained regression with models tailored to each variable's level of measurement for the event-history model and using linear regression for the fixed effects analysis. We used 20 imputed data sets. We also evaluated imputing with 50 data sets, and the fraction of missing information (not reported) and stability of the estimates confirmed that 20 data sets were sufficient for the simulations.

Data

To create a realistic simulation, we began with observed data from the first four waves of the MILC study, a panel survey of a national sample of married persons followed over 20 years (Booth, Johnson, Amato, & Rogers, 1999). Respondents were interviewed by telephone in 1980, 1983, 1988, and 1992. During the first wave of the study, random digit dialing was used to select a sample of married individuals age 55 and under. Among eligible households, the interview completion rate for the initial wave of the study was 65%, yielding a sample size of 2,034. The percentage of people remaining in the study was 78% in Wave 2, 66% in Wave 3, and 58% in Wave 4. The study was designed so that once a respondent missed a wave he or she was excluded from the sample for the subsequent waves, resulting in a monotonic dropout pattern.

Attrition from the MILC study was higher than is found in some of the large panel studies used by family researchers (e.g., the National Longitudinal Study of Adolescent Health, the National Longitudinal Survey of Youth), primarily because respondents were recruited and followed up by telephone rather than the personal interview design used in the other large surveys. This mode posed difficulty in locating respondents who changed their telephone number or moved. When considering how our results apply to other studies, we caution researchers that our advice may not apply to studies with higher levels of attrition, or to studies in which dropout is less correlated with data from the first wave than was observed in the MILC study.

To create a simulation that mimicked the observed data, we began with one singly imputed data set (n = 2,034) from the MILC study, and treated this as the “true” model, or the gold standard. The fully imputed data set was informed by the analysis model variables and auxiliary variables. Minor changes were made in the data by rounding and recoding all imputed values to within the range and categories of the observed values. Although rounding and ranging should not be done when MI is used in practice (Horton, Lipsitz, & Parzen, 2003), the purpose of the single imputation here was only to generate a realistic starting point to treat as the true model.

To introduce whole-wave missing data, we used observed data to fit a logistic regression model predicting attrition at each wave. The predicted probability of attrition for each person was used in conjunction with a random number to select cases for attrition. For example, if a respondent's probability of attrition was .30, he or she would be selected for attrition if the random number was also .30 or smaller. Once a respondent left the panel by attrition he or she was set to miss all subsequent waves, mirroring the pattern in the observed data set.

To introduce within-wave missing data, we generated two types of probabilities of a missing value. The first logistic regression model for item nonresponse predicted presence of a missing demographic variable (e.g., age, race/ethnicity, education), which occurred infrequently in the observed data. Missing values were assigned to demographic items using this probability and a random variable. The proportion of missingness assigned to these variables ranged from 3% to 5%for each simulation. The second logistic regression model for item nonresponse predicted the presence of a missing value for questions requiring an attitude or opinion about the participant's marriage. Missing values were more common for marriage-related questions in the observed data and may have been more likely to be related to our outcome variables of marital happiness and divorce. Again, the probability of missingness was used along with a random variable to assign missing values to similar types of items in the simulation. The proportion of missingness assigned to these variables was between 5% and 8%. The variables used to predict the probability of nonresponse had correlations with the missing data ranging from .01 to .18.

One limitation of the observed data was that few of the variables in our analysis models were significant predictors of attrition, and detecting differences between approaches under this condition would be unlikely. To more adequately test the different approaches but still produce a reasonably realistic model, we modified some of the selection probabilities to increase the odds of attrition predicted by our analysis and auxiliary variables. These changes introduced a clear NMAR pattern to the data. For the fixed effects regression simulation we changed the coefficients so that person's with decreased marital interaction (an auxiliary variable) and marital happiness (an outcome variable) from one wave to the next had his or her observed odds of attrition tripled. We also doubled the odds of attrition for persons whose health (an analysis variable) declined from one wave to the next. To do this, we converted the probability of attrition for the case into an odds, altered the observed odds with the above multipliers, and then converted the odds back into probabilities for the random selection. For the event-history simulation, people who had thoughts of divorce (an analysis variable) at Wave 1 and ultimately divorced (an outcome variable) were assigned a probability of dropout three times higher than their original predicted probability of dropout.

Adding purposeful NMAR data to the simulations created a troublesome scenario in which both an important predictor of the outcome and the outcome itself were strongly related to attrition. Our NMAR condition was a dramatic, albeit somewhat unlikely, scenario for the types of data used in most family research. Outside of clinical trial, experimental, or treatment data, study participation seldom has a clear relationship with most outcomes. Testing the NMAR condition, however, offered a rigorous test of how MI performed even when the MAR assumption was known to be violated.

Using the procedures described above, we created 200 simulated data sets that had within- and whole-wave missingness that mirrored the complex patterns observed in the real data yet had enough missing data to be of consequence. The choice of 200 simulated data sets was arbitrary, but comparison to 500 simulations showed little difference, suggesting that 200 simulations was a large enough number for our sampling distributions to have excellent coverage. Most of the variables used in the logistic regression models predicting attrition and item nonresponse were not included in the subsequent MI models or in the analysis models. This step ensured that, as in the real world, the exact predictors of missingness were unknown to the researcher.

Fixed Effects Simulation

The first simulation estimated a fixed effects regression model with an 11-item scale of marital happiness as the outcome and a set of nine time-varying variables as the predictors. The fixed effects model with longitudinal, pooled time series data provides estimates of the effect of change in the predictors on change in the outcome. Variables that were observed to remain constant over time, such as gender, race, and year of birth, were excluded because these cannot be estimated in a fixed effects model that focuses only on within-individual change. Using stepwise logistic regression, we selected six variables for use as auxiliary variables in the imputation models. These variables had significant correlations with analysis variables and were correlated with attrition from the MILC study (Booth et al., 2000). Descriptive information on the analysis and auxiliary variables for each wave is presented in Table 1. Note that by Wave 4, 41.5% of the waves were missing and that wave attrition was the source of most of the missing values.

Table 1. Descriptive Information for Observed Data in Each Wave.

Variable	Wave 1 (n = 2,034)			Wave 2 (21.7% attrition)			Wave 3 (34.1% attrition)			Wave 4 (41.5% attrition)
	M	SD	% Missing	M	SD	% Missing	M	SD	% Missing	M	SD	% Missing
Marital happiness scale	28.50	4.01	3.0	27.89	4.18	28.7	27.78	4.31	42.0	27.80	4.42	50.3
Financial satisfaction	1.63	0.86	0.5	1.69	0.89	22.8	1.74	0.91	35.0	1.93	0.92	42.2
Self-rated health	1.62	0.73	0.1	1.70	0.75	22.9	1.72	0.74	34.5	1.78	0.74	41.7
Children 6–13 years	0.48		0.0	0.45		21.7	0.45		34.1	0.38		41.5
Children < 6 years	0.54		0.0	0.51		21.7	0.34		34.1	0.16		41.5
Nervous problems	1.47	0.50	0.0	1.38	0.49	23.0	1.45	0.50	34.5	1.48	0.50	41.6
Friends (unrelated)	0.89	0.31	0.0	0.89	0.32	27.0	0.90	0.30	34.4	0.92	0.28	41.6
Things as interesting now	1.91	0.59	0.3	2.02	0.56	22.3	1.98	0.56	34.7	1.95	0.60	41.8
Gotten what expected in life	2.03	0.64	1.3	2.11	0.53	22.9	2.10	0.53	35.3	2.11	0.55	42.3
Thoughts of divorce	0.21		0.0	0.21		27.3	0.19		40.4	0.17		49.1
Marital problems scale	2.69	2.58	2.7	2.55	2.53	27.8	2.52	2.51	41.3	2.60	2.51	50.0
Female (ref.: male)	0.60		0.0	0.60		21.7	0.61		34.1	0.63		41.5
White (ref.: non-White)	0.88		0.0	0.91		21.7	0.92		34.1	0.92		41.5
Educational attainment	13.42	2.63	0.0	13.72	2.66	21.7	13.92	2.73	34.1	14.15	2.72	41.5
Age	35.46	9.25	0.1	38.78	9.15	21.8	43.19	9.14	34.1	47.06	9.08	41.6
Marital interaction	15.79	2.88	0.0	15.27	2.94	26.9	14.80	2.97	40.3	14.79	3.00	49.0
Years married in 1980	12.56	9.19	0.2	13.00	9.20	21.7	13.08	9.18	34.1	13.05	9.00	41.6
Second+ marriage	0.15		0.0

Note: ref. = reference category.

Seven fixed effects models were estimated using the xtreg procedure in Stata, each with a different approach to the missing data. The first approach fit the regression model to the observed data with no imputation of missing values. This procedure includes all available waves in the estimation, including respondents with within-wave missing values. This approach accounts for whole-wave missing data but deletes waves that contain any within-wave missing values on the variables in the regression model. Subsequent approaches used MI in the long and the wide structure to estimate models with and without auxiliary variables included, models that retained all waves (including those with all variables imputed), and models that retained the within-wave imputed values but dropped the waves that were not observed. From among these models we report six of them here: three using values imputed wide and three using values imputed long. These include a model with all four waves included for each respondent and a model in which only observed waves were retained. A third model added auxiliary variables to the analysis. Additional models are available on request. These models allow us to compare long and wide, fully imputing the missing wave or only using available waves, and including or excluding auxiliary variables.

Event-History Simulation

The second simulation estimated a proportional hazards Cox regression model that used three time-invariant and three time-varying variables to predict divorce. The outcome variable measured divorce (0 = no divorce or censoring, 1 = divorced). In the observed data, 246 respondents reported that they had divorced, 441 had no follow-up information, and 845 were censored before completing the study. Three time-invariant variables were used as predictors of divorce: (a) age in years at Wave 1, (b) respondent gender (0 = male, 1 = female), and (c) whether the marriage in 1980 was a first marriage or second or higher (0 = first marriage, 1 = second marriage or higher). Three time-varying predictors were also used. Thoughts of divorce came from a question asking each participant whether he or she had seriously considered divorce in the last year (0 = no, 1 = yes). The scale of marital happiness used in the fixed effects model and a scale of marital problems were also included. Descriptive information for these variables is shown in Table 1.

Three strategies for handling missing values were tested in the event-history simulation. The first strategy applied complete case analysis. Respondents who had within-wave missing values were removed from the analysis, and respondents with whole-wave missing values were censored at the time of study dropout. Respondents who were present at Wave 1 only were excluded from the analysis because no follow-up data were obtained for the outcome variable (i.e., divorce). Next, MI was applied to data in the long structure. Values were imputed for all questions in all waves, including waves in which the respondents did not participate. Third, MI was used to impute the missing values in the wide structure. Again, missing values were imputed for all questions in all waves regardless of whether the respondent actually participated in the wave, and outcomes were imputed.

The main difficulty with applying MI to survival data is appropriately performing the imputations. Beyond the general MI recommendations (see Acock, 2005; Johnson & Young, 2011), additional guidelines must be followed because of time-to-event censoring, and time or date variables. In addition to including all variables from the analysis in the imputation model, including the dependent variable, early researchers suggested also including a variable for time-to-event or censoring and the log of this variable (van Buuren, Boshuizen, & Knook, 1999). White and Royston (2009) showed, however, that this approach will bias covariate–outcome associations toward the null. Instead, the most appropriate imputation model for a proportional hazards Cox model should include the dependent variable and the Nelson–Aalen (NA) estimate of the cumulative hazard to the survival time as a covariate (White & Royston, 2009). In Stata, the NA estimate can be obtained with sts generate and specifying NA; in SAS it can be found using PROC LIFETEST statement with the NELSON option.

Results

Results from the simulation models are compared using six measures, shown in Tables 2, 3, 4, and 5. The true model shows the correct or gold standard, by which each of the 200 simulated data sets was compared. For each missing-data technique, the first column shows the bias of the b coefficient, calculated as the average of the difference between each of 200 simulated estimates from the true value. The same method was used to calculate the standard errors' bias. The third column contains the root-mean-squared error (RMSE), which is a combined measure of the bias in the b coefficient and its standard error. A smaller RMSE indicates less bias and more consistency of a method. The bias in the hazard ratio, standard error, and RMSE show, on average across the 200 simulations, how different each number was from the true model, so numbers closer to zero are desirable. The final number in the third column shows the percentage of the time that each coefficient was statistically significant at the p< .05 level. Estimates that were significant in all 200 simulated data sets would have 100% significance; if the coefficient was significant in only half the samples, the % p value would be 50%. Although .05 is an arbitrary cutoff, this practical measure of performance sheds some light on the Type I and Type II error rates that might be expected from a method under these conditions.

Table 2. Simulation of a Fixed Effects Regression Model Predicting Marital Happiness: True Model and No Imputation.

Variable	True model		No imputation (complete case analysis)
			Bias
	b	SE	b	SE	RMSE	%pa
Wave	−0.439*	0.029	0.200	0.020	0.205	100
Financial satisfaction	−0.329*	0.056	0.019	0.038	0.083	95
Self-rated health	−0.122	0.065	0.108	0.050	0.144	3
Children 6–13 years	−0.074	0.058	−0.032	0.039	0.098	20
Children < 6 years	−0.030	0.065	−0.036	0.043	0.099	4
Psychological distress	0.645*	0.084	−0.178	0.051	0.206	98
Friends (unrelated)	0.132	0.139	0.071	0.102	0.216	11
Things as interesting now	−0.533*	0.069	0.175	0.047	0.202	90
Gotten what expected in life	−0.715*	0.072	0.094	0.048	0.136	100

Note:= theThe multiple imputation used m = 20 data sets; data in the table are based on 200 simulated data sets; average bias root-mean-square error (RMSE) = 0.154; bias in b = 0.101; bias in SE = 0.049.

^aPercentage of simulations where the p value of the coefficient was less than .05.

^*p< .05.

Table 3. Simulation of Fixed Effects Regression Model Predicting Marital Happiness: Wide Imputation Strategies.

Variable	MI (wide) All waves				MI (wide) Observed waves				MI (wide) All waves + auxiliary
	Bias			% pa	Bias			% pa	Bias			% pa
	b	SE	RMSE		b	SE	RMSE		b	SE	RMSE
Wave	0.165	0.016	0.169	100	0.190	0.013	0.193	100	0.160	0.016	0.164	100
Financial satisfaction	0.045	0.035	0.078	95	0.034	0.026	0.070	98	0.050	0.035	0.080	92
Self-rated health	0.114	0.036	0.138	1	0.090	0.034	0.118	2	0.101	0.042	0.127	1
Children 6–13 years	−0.051	0.029	0.084	27	−0.042	0.025	0.078	24	−0.047	0.028	0.080	26
Children < 6 years	0.029	−0.010	0.069	0	−0.015	0.028	0.068	2	−0.008	0.027	0.068	2
Psychological distress	0.036	−0.106	0.135	100	−0.115	0.035	0.139	100	−0.093	0.041	0.124	100
Friends (unrelated)	0.038	0.093	0.184	12	0.095	0.065	0.186	15	0.096	0.082	0.188	12
Things as interesting now	0.070	0.159	0.181	97	0.158	0.034	0.179	98	0.154	0.043	0.177	96
Gotten what expected in life	0.037	0.042	0.089	100	0.045	0.035	0.089	100	0.049	0.042	0.096	100
Average (absolute value)	0.087	0.037	0.125		0.087	0.033	0.124		0.084	0.040	0.123

Note: The multiple imputation (MI) used m = 20 data sets; data in the table are based on 200 simulated data sets.RMSE = root-mean-square error.

^aPercentage of simulations where the p value of the coefficient was less than .05.

Table 4. Simulation of Fixed Effects Regression Model Predicting Marital Happiness: Long Imputation Strategies.

Variable	MI (long) All waves				MI (long) Observed waves				MI (long) Observed waves + auxiliary
	Bias			% pa	Bias			% pa	Bias			% pa
	b	SE	RMSE		b	SE	RMSE		b	SE	RMSE
Wave	0.214	0.025	0.218	100	0.204	0.018	0.208	100	0.196	0.016	0.199	100
Financial satisfaction	−0.072	0.035	0.088	100	0.020	0.033	0.066	99	0.030	0.031	0.065	99
Self-rated health	−0.203	0.035	0.210	100	0.044	0.041	0.084	3	0.061	0.039	0.094	3
Children 6–13 years	−0.144	0.032	0.153	83	−0.063	0.034	0.090	24	−0.043	0.031	0.078	19
Children < 6 years	−0.027	0.029	0.048	0	−0.032	0.038	0.076	2	−0.025	0.035	0.074	2
Psychological distress	0.309	0.048	0.317	100	−0.091	0.046	0.121	100	−0.086	0.046	0.114	100
Friends (unrelated)	0.336	0.073	0.353	67	0.147	0.087	0.220	17	0.133	0.081	0.210	16
Things as interesting now	0.003	0.057	0.075	100	0.141	0.044	0.165	98	0.148	0.041	0.169	99
Gotten what expected in life	−0.346	0.051	0.352	100	−0.009	0.045	0.075	100	−0.005	0.042	0.074	100
Average (absolute value)	0.184	0.043	0.202		0.084	0.043	0.123		0.081	0.040	0.120

Note: The multiple imputation (MI) used m = 20 data sets; data in the table are based on 200 simulated data sets. RMSE = root-mean-square error.

^aPercentage of simulations where the p value of the coefficient was less than .05.

Table 5. Simulation of Proportional Hazards Cox Regression Model Predicting Divorce.

Variable	True model		No imputation (complete case analysis)				MI (long) All waves				MI (wide) All waves
			Bias				Bias				Bias
	HR	SE	HR	SE	RMSE	% pa	HR	SE	RMSE	% pa	HR	SE	RMSE	% pa
Non time-varying
Age	0.946*	0.007	−0.012	0.004	0.014	100	−0.010	0.000	0.001	100	0.001	0.001	0.002	100
Female	1.114	0.133	0.022	0.085	0.152	4	0.075	0.029	0.144	19	0.025	0.018	0.041	0
Second+ marriage	1.974*	0.266	0.106	0.200	0.346	96	0.226	0.126	0.327	99	0.279	0.073	0.296	100
Time-varying
Marital happiness	0.907*	0.012	0.002	0.009	0.015	95	−0.011	0.000	0.016	100	0.006	0.002	0.001	100
Marital problems	1.025	0.024	0.027	0.017	0.038	0	0.027	0.003	0.029	18	0.027	0.004	0.014	0
Thoughts of divorce	1.932*	0.027	−0.629	0.031	0.659	10	0.626	0.042	0.648	23	−0.376	0.029	0.385	65

Note: The multiple imputation (MI) used m = 20 data sets; data in the table are based on 200 simulated data sets.HR = hazard ratio; RMSE = root-mean-square error.

^aPercentage of simulations where the p value of the coefficient was less than .05.

^*p< .05.

Fixed Effects Simulation

The estimates for the true model of the b coefficients and their standard errors are found in the first column of Table 2. Five of the predictors have a statistically significant (p < .05) effect on marital happiness. The next model in the table is a fixed effects one with no imputed data but with missing waves excluded from the data set and, as required by the method, input in the long structure. The missing data are accounted for using the ability of the xtreg procedure to analyze data with variable number of waves, treating the whole-wave missing data as MAR but excluding waves that have any within-wave missing values on the variables in the model, assuming MCAR. The substantive findings are similar to the true model with the magnitude, statistical significance, and direction of the effects yielding the same substantive conclusions. There are consistent differences from the true model. The most notable difference is that all the effects that are statistically significant in the true model are underestimated in the simulation model. For example, the effect of wave was substantially smaller in the simulated data.

The results of the analysis models that used MI in the wide structure are presented in Table 3. Overall, all three models are less biased and have smaller standard errors than those obtained in the complete case analysis model in Table 2. On the basis of the average RMSE, the models were very similar, with the smallest value for the wide model with auxiliary variables. The bias in the b coefficients was also similar, with the least bias occurring in the model with auxiliary variables. Although the auxiliary-variable model seems to be preferred, it had the largest average standard errors of the three models. This likely reflects the inability of imputing in the long form to condition the imputed values on the same variables in other waves with which they are usually highly correlated, leading to greater random error in the imputed values. Analyzing only the observed waves performed slightly better than imputing the missing waves, but the difference was not meaningful. Including auxiliary variables in the imputation model produced small reductions in bias, as we expected from the NMAR nature of the missing data. The reduction in bias was not large enough to affect the substantive conclusions drawn from the analysis.

The results of the analysis models that used MI in the long structure are presented in Table 4. Surprisingly, imputing data in the long structure, under certain conditions, appeared to be a viable alternative with little, if any, increase in biased estimation. The most poorly performing model was when the values of the variables in the missing waves were also imputed. This model has substantially poorer fit based on all of the bias indicators. When only the observed waves were included in the analysis, however, data imputed in the long structure produced estimates that were comparable to those imputed in the wide structure. The observed-wave models with and without auxiliary variables had the lowest RMSEs of all models tested, and the auxiliary variable model had the least average bias of any model, although the differences were not large. We do not report the auxiliary-variable model with all waves imputed because of the poor performance of this approach. The higher standard errors observed for the long versus the wide models tempered our enthusiasm for this approach. When we looked more closely at the individual effects we noted that the wide approach more accurately estimated the effect of wave than did the long. No other consistent differences between long and wide models in the individual effects were observed.

Event-History Simulation

Three missing-data approaches were applied to a proportional hazards Cox regression model predicting divorce, shown in Table 5. Complete case analysis excluded people who were missing values for any of the Wave 1 variables being analyzed, excluded people who missed Wave 2 and therefore had no follow-up data (or person-years) to contribute to the time-to-event model, and excluded entire waves if any of the model variables contained item nonresponse within that wave. Right-censoring is the standard approach for Cox models, although whether the assumptions of missingness are met is an important issue that is rarely considered in practice. The alternative to right-censoring is to treat missing waves, including the outcome, as missing data. MI on the long structure data treated each record as an independent observation and did not account for clustering. In the second and third missing-data strategies missing waves were imputed for all covariates and the outcome was treated as missing (rather than censored) for whole-wave missingness.

As shown in Table 5, complete case analysis, using the standard Cox model approach to censoring at the last observed wave, was both a biased and inefficient procedure. No imputation led to misestimated effect sizes and standard errors that were larger than was observed in the true model. The RMSEs, a combined measure of bias and efficiency, were largest for the model with no imputation. The proportion of simulations where complete case analysis correctly identified significance at the p< .05 level showed expected error rates for all variables except thoughts of divorce, which was detected as a significant (p < .05) effect only about 10% of the time in the model with no imputation.

The second simulation model was MI on data in the long structure where accounting for individual-level clusters was not possible. For three of the six variables—age, marital problems, and thoughts of divorce—the average effect size bias was smaller or the same in the MI long model compared to no imputation. For three variables—female, second marriage, and marital happiness—the MI long model was more biased than the model with no imputation. The standard errors in the MI long model were smaller (more efficient) compared to no imputation. The RMSE appeared to be slightly better in the MI long model relative to no imputation, but the differences were quite small. Even if small RMSE gains were achieved by MI using the long structure, this appeared to come at the cost of less accurate significance testing. Two variables that were not significant (p< .05) in the true model, female and marital problems, were detected as significant in the MI long models 18% to 19% of the time. Thoughts of divorce, which was significant in the true model, was detected as significant 23% of the time.

MI on data in the wide structure showed less bias in the hazard ratios and standard errors, in addition to having a lower RMSE and greater proportion of correct significance tests, compared to no imputation or MI in the long structure. For five of the six variables, MI on the wide data structure correctly identified significance of the predictor at the p < .05 level 100% of the time. Thoughts of divorce was detected as significant 65% of the time, and effect size was underestimated by a meaningful amount.

Discussion

We focused on how missing data might be handled in two regression models, fixed effects and event history, because they are typically analyzed using a long data structure whereby repeated observations are nested within individual records. This structure poses additional challenges for applying MI to deal with missing values. In particular, researchers have the option to impute within-wave missingness only or to impute both within-wave and whole-wave missingness. Because many types of panel models have standard or automatic techniques for treating whole-wave missingness (e.g., right-censoring in event history, variable number of waves in fixed effects), whether whole-wave imputation is necessary is sometimes unclear. Researchers were also left with insufficient guidance about whether to apply MI to a long or wide data structure and whether present options for multilevel MI applied to the circumstance where individuals were the Level 2 group (or cluster).

In the analyses of the fixed effect regression models, imputation in either the wide or the long structure had less bias compared to the fixed effects analyses that did not impute either the within-or whole-wave missing values. Most of this improvement reflected the imputation of the within-wave missing data as models that did not include the missing waves generally performed better.

In most cases, imputation in cross-sectional designs increases the amount of information available for analysis, increasing efficiency and reducing standard errors. With few exceptions, fixed effects models imputing data in the missing waves led to the same or even increased standard errors. This likely reflects two factors. First, because in essence all the data in the missed waves were imputed, no additional information was added to the model. In contrast, imputing within-wave data on variables in the analysis model allowed that wave to be included in the estimation, adding information from the variables in that wave that were not missing. Because imputing variables in the missing waves neither added information nor allowed the greater use of known information, no improvement in efficiency was possible.

A second, related explanation is that imputing whole waves also involves imputing the dependent variable, which has been found to do little to improve the efficiency of the analysis (Allison, 2001; Young & Johnson, 2013) and, with a relatively small number of imputed data sets, may even increase the standard error by introducing unnecessary random error into the estimates (von Hippel, 2007).

Because the pooled time-series methods use data in all available waves, and makes the same MAR assumption as MI, imputing whole-wave missing values is probably an unnecessary effort in most cases. An exception to this advice would occur, however, if there were a clear NMAR pattern in the data that could be transformed to MAR by including auxiliary variables in the imputation model. Our auxiliary-variable models showed a small improvement in fit when compared to those using only analysis model variables to inform the imputation. The improvements, however, were quite small. In our simulation, the NMAR we introduced may not have had a strong enough relationship to our auxiliary variables to have much of an effect on the estimates, but this may not always be the case. If an NMAR situation is suspected and there are a sufficient number of variables that are strongly related to both attrition and the variables in the analysis model, then including these to inform the imputation and retaining all waves should be attempted. Comparing results with and without the imputed waves to see whether a difference in the substantive conclusions occurs is a prudent step.

When fitting a fixed effects model we recommend that researchers impute the within-wave missing values because doing so will increase the amount of known information used in the analysis model. According to recommendations in the literature, this should be done in the wide structure, with the researcher converting the data back to long and then dropping the waves that were fully imputed. The wide structure allows the imputation to be informed by observed values in other waves of a missing value, reducing error in the imputed value. When we imputed in the long structure including only the observed waves in the analysis, however, the estimates we obtained would lead to substantive findings similar to those obtained when imputing wide. Our analysis provides some evidence that in conditions similar to those found in many family panel data sets imputing the data in the long structure can yield satisfactory estimates in fixed effects models. Additional research is needed, however, to identify the factors that account for the similarities and differences between the long and wide imputation approaches.

Unlike fixed effects approaches, imputing whole-wave missingness for event-history models allows more of the known information to be incorporated in the analysis model. Event-history analysis assumes that cases with no follow-up data are MCAR, whereas cases with only some whole waves missing are MAR. Right-censoring is an inefficient use of all known information because participants who drop out after the baseline survey contribute no information to the model, given that they are immediately censored and effectively excluded from analysis. In addition, right-censoring requires the strict assumption that the participants who remained in the study had event rates, and relationships between the covariates and the event, similar to those who dropped out. The results of our simulation, in concurrence with literature on this topic, suggest that right-censoring is not robust to violations of this assumption.

Our results confirm the advantages of using MI in the wide structure for event-history models, whereas MI on data in the long structure were nearly as biased and inefficient as no imputation. It is important to note that MI on the long structure appeared to increase both the Type I and Type II error rates when testing whether variables were significant at the p < .05 level. The simulation confirmed with an example what has been argued theoretically: that failing to account for the correlation between within-person measures repeated over time is an incorrect specification of the imputation model. In our event-history example a researcher would have been as well off to ignore the missing values altogether as to apply MI to data in the long structure. The fixed effects model simulation, however, showed that MI in the long structure could be acceptable in circumstances where imputing entire waves is unnecessary.

The event-history model simulations showed that MI on the wide structure performed better than complete case analysis or MI using the long structure, but it was not a perfect method. Recall that the simulation was designed with an extreme NMAR element whereby people who had thought of divorce at Wave 1 and went on to divorce were three times as likely to have dropped out at each of the three remaining waves. Our simulations were a rigorous test of MI under NMAR conditions because not only were within- and whole-wave missing values known to be NMAR, but also the MI model was informed only by the seven variables in the analysis and no auxiliary information. MI nonetheless allowed the use of all known information and appeared to be a fairly robust procedure in the presence of clearly NMAR data.

When fitting an event-history model, we recommend that researchers use MI in circumstances where doing so allows the use of observed information that would be discarded by complete case analysis. In particular when first-wave participants have no follow-up data, right-censoring prevents these cases from contributing information to the estimates. Present statistical research recommends including the NA estimate of the cumulative hazard to the survival time as a covariate in the MI model (White & Royston, 2009). Researchers should omit the actual event date, the time to event, or the natural log transformation of time to event from the imputation model.

Although the MILC data had a monotone dropout pattern, other family data sets, such as the National Longitudinal Study of Adolescent Health, allow continued participation in the study even if one wave or more waves are skipped. We expect that MI would offer additional advantages in this context because the proportion of known information relative to missing information would exceed the levels seen in our simulation here. We do not expect that our results would be applicable to all types of family research data, and our findings should not be generalized to unrelated situations. Clinical trials, randomized experiments, and treatment studies may have study-dropout mechanisms with stronger relationship to the outcome of interest than would be found in national personal or household interview surveys.

There are a number of situations not examined here in which imputing data in the wide structure would not be possible. With a large number of waves or time points, and repeated measures that are highly correlated, a wide imputation model could fail because of collinearity or model overfitting. Our models also did not explore conditional time-varying transitions. For example, a person could not transition from being divorced to being never married. A promising MI approach to these situations is the twofold fully conditional specification algorithm described byWelch, Petersen, et al. (2014) and Welch, Bartlett, and Peterson (2014). This approach uses the waves preceding and following a particular time point to be imputed, essentially allowing a wide imputation without putting too many waves in the model. In addition, this approach can accommodate conditional time-varying transitions. Future research should explore this approach in the context of family research data and where the data are MAR or NMAR. It is also unclear whether nonlinear and interaction terms might be compatible with the fully conditional specification method.

Our results show that whole-wave imputation may be advantageous when doing so allows the researcher to analyze all known information. In the event-history model, for instance, using standard right-censoring techniques may exclude participants who had no follow-up data. Not only does this technique discard known baseline information, but it also requires the assumption that attrition from the second wave was MCAR and that the event rates were similar among individuals who did and did not participate in the second wave. MI, on the other hand, allows researchers to analyze the known baseline values and to assume that attrition was MAR. Even under somewhat extreme NMAR conditions our simulations showed that MI performed well. Although MI was not perfect, it appeared to be a more robust method to NMAR data than right-censoring at the time of dropout. Imputing variables in missing waves may be unnecessary effort, as with our fixed effects regression models, if whole-wave imputation adds no information to the analysis model. Imputing within-wave missing values in these models, however, increases the information available being used, yielding less biased and more stable estimates.