Two-dimensional/three dimensional Hybrid Interstitial Diffuse Optical Tomography of Human Prostate during Photodynamic Therapy: Phantom and Clinical Results

Abstract

We have developed an efficient Levenberg-Marquardt iterative algorithm utilizing a three-dimensional field measurements coupled to a two-dimensional optical property reconstruction scheme. This technique takes advantage of accurate estimation of light distribution in 3D forward calculation and reduced problem size and less computation time in 2D inversion. Important advances in terms of improving algorithm efficiency and accuracy include use of an iterative general minimum residual method (GMRES) for computing the field solutions, application of the dual mesh scheme and adjoint method for Jacobian construction, and implementation of normalization scheme to reduce the absorption-scattering cross talk. The synthetic measurement data were calculated for a cubic phantom containing a single absorption anomaly and a single scattering anomaly. The model had a background of μ_a=0.03mm⁻¹ and μ_s’=1.4mm⁻¹. The absorption and scattering anomalies have the μ_a = 0.06 mm⁻¹ and μ_s’ = 2.0 mm⁻¹. Five sources and 72 detectors are used per slice. A typical human prostate is composed of 6 slices. The reconstruction images successfully recover the both anomalies with good localization. Experiment data from tissue simulated phantom are also presented. The clinical DOT imaging was performed before photodynamic therapy based on the protocol. The preliminary results showed the reconstructed prostate μa varied between 0.025 and 0.07 mm⁻¹ and μ_s’ ranged from 1.1 to 2 mm⁻¹. These results show that this new 2D-3D hybrid algorithm consistently outperform the 2D-2D or 3D-3D counterparts.

INTRODUCTION

Diffuse optical tomography (DOT) is a new imaging modality with potential applications in functional imaging of the brain and breast cancer detection [1-5]. This imaging technique seeks to recover the optical parameters of tissue from boundary measurements of transmitted near-infrared or visible light. Instrumentation for optical tomography system is relatively less expensive and is portable for the clinical settings[1]. It has been proved that DOT system can provide a viable alternative to current available functional imaging systems such as functional magnetic resonance imaging[1].

A typical DOT system often consists of a light source (lasers, white light), illuminating the biological tissue from the surface at different source positions in succession[1]. The photons which propagate through tissue are then collected at multiple detector positions on the tissue surface[1]. Three measurement schemes are used for these measurements: time domain, frequency domain and continuous wave (cw). Of these three measurement types, the cw method is the simplest and least expensive, and can provide fastest data acquisition and greatest signal-to-noise level[6].

One of the applications of cw DOT system is the light dosimetry for interstitial prostate photodynamic therapy (PDT). The effectiveness of PDT treatment largely depends on the number of photons absorbed by the photosensitizers located in the tumor tissue [7]. Thus the light and photosensitizer dosimetry are essential for PDT treatments [8]. In our prostate PDT protocol, optical properties of prostate are first determined before the treatment, so that a real-time modeling and monitoring of photons deposition in the prostate can be achieved. Prostate optical properties are determined via an interstitial DOT system where light sources and detectors are interstitially inserted in the prostate tissue [9].

In this study, we present 2D and 3D inverse models that can recover the heterogeneous optical properties of the prostate tissue. A 2D-3D hybrid model is also presented. These models are built in the COMSOL Multiphysics / MATLab environment, where the partial differential equations are solved in COMSOL Multiphysics and the heterogeneous equation coefficients are updated via Levenberg-Marquardt algorithm written in MATLab. We have validated these proposed models by reconstructing the optical properties of the 2D, 3Dmathematical phantoms with the numerically simulated data. We demonstrated that the 2D-3D hybrid algorithm outperforms the 2D and 3D algorithm in terms of accuracy/computation cost ratio.

MATERIALS AND METHODS

1.1 Problem definition

Assume domain Ω is the prostate tissue under investigation, with surface ∂Ω. We consider source positions $\stackrel{\rightharpoonup }{r}_{s,i}\in \Omega$, i=1… n_source and detector positions $\stackrel{\rightharpoonup }{r}_{d,j}\in \Omega$, j=1… n_detector, for each source i, resulting in a total number of M=n_source×n_detector measurements.

The forward problem is non-linear and is represented by:

$$\overrightarrow{\Phi }=\stackrel{\rightharpoonup }{\mathrm{P}}\left[{\mu }_a\kappa \right]$$ (1)

Following the general-least square approach, we may define the inverse problem as the optimization of an objective function:

$$\Psi =\frac{1}{2}\sum _{i=1}^{n_{\text{source}}}\sum _{j=1}^{n_{\text{detector}}}{({\Phi }_{i,j}^{\left(m\right)}-P_{i,j}[{\mu }_a\kappa \left]\right)}^2$$ (2)

which can be written in a vector form:

$$\Psi =\Vert \stackrel{\rightharpoonup }{\Phi }^{\left(m\right)}-\stackrel{\rightharpoonup }{\Phi }^{\left(c\right)}\Vert =\stackrel{\rightharpoonup }{b}^T\stackrel{\rightharpoonup }{b}$$ (3)

where ${\Phi }_{i,j}^{\left(m\right)}$ is the data for the j-th measurements from i-th source, and $b_{i,j}={\Phi }_{i,j}^{\left(m\right)}-{\Phi }_{i,j}^{\left(c\right)}$ is the residual data for this measurement. Use the subscript i to represent the data for a single source i, $\stackrel{\rightharpoonup }{P}_i\left[{\mu }_a\kappa \right]$ is the projection operator for source i, $\stackrel{\rightharpoonup }{\Phi }_i^{\left(c\right)}$ is the projection data obtained by sampling $\stackrel{\rightharpoonup }{P}_i\left[{\mu }_a\kappa \right]$ at the discrete measurements positions $\{\stackrel{\rightharpoonup }{r}_{i,1},\stackrel{\rightharpoonup }{r}_{i,2},\cdots \stackrel{\rightharpoonup }{r}_{i,n_{\text{detector}}}\}$ and $\stackrel{\rightharpoonup }{b}_i=\stackrel{\rightharpoonup }{\Phi }_i^{\left(m\right)}-\stackrel{\rightharpoonup }{\Phi }_i^{\left(c\right)}$ is the data-model misfit[10].

1.2 Governing Equations

The propagation of near-infrared light through highly scattering media (such as biological tissues) is often modeled as a second order elliptic partial differential equation [10]. For continuous-wave diffuse optical tomography system, steady-state attenuation measurements are made, and the light fluence rate can be calculated using steady-state diffusion approximation to the radiation transfer equation:

$$-\nabla \cdot \kappa \nabla \Phi +{\mu }_a\Phi =q$$ (4)

where Φ is the isotropic photon density and q is an isotropic source distribution. The model is characterized by two spatially varying functions μ_a (absorption coefficient) and κ=1/3(μ_a + μ’_s) (diffusion coefficient)(μ’_s: scattering coefficient), which gives rise to the dual parameter search space nature of the optimization problem as defined in equation (3). We use the modified Robin boundary condition:

$$\Phi +2\kappa ∕\alpha \stackrel{\rightharpoonup }{\widehat{n}}\cdot \nabla \Phi =0,$$

where $\alpha =(1-{\mid \cos {\theta }_{\mathrm{c}}\mid }^2)∕(2∕(1-{\mathrm{R}}_0)-1+{\mid \cos {\theta }_{\mathrm{c}}\mid }^3)$ and R₀ = (n-1)²/(n+1)², n=n_tissue/n_outside is the ratio of refraction index between tissue (n_tissue) and outside medium (n_outside), and θ_c=arcsin(1/n) is the critical angle. In prostate tissue, a matched non-scattering boundary: $\Phi +2\kappa \stackrel{\rightharpoonup }{\widehat{n}}\cdot \nabla \Phi =0$ is used where n_tissue = 1.4, n_outside = 1.4 and α = 1.

1.3 Adjoint sensitivity matrix formulation and image reconstruction algorithm

Several iterative numerical methods can be used to minimize the objective function shown in equation (2) and equation(3), such as Levenberg-Marquardt, Gauss-Newton, conjugate gradient and Algebraic Reconstruction Technique (ART) methods[10-13]. In this study, we chose Levenberg-Marquardt update scheme which incorporates a regularization term λ to steer between Gauss-Newton and gradient method.

Following the L-M scheme, the parameter update can be obtained by:

$$\Delta x^k={({\mathbf{J}}^T\mathbf{J}+\lambda \mathbf{I})}^{-1}{\mathbf{J}}^T(\ln {\Phi }^{\left(m\right)}-\ln {\Phi }^{\left(c\right)}(x^k\left)\right)$$ (5)

where

$$\mathit{J}=\left[\begin{array}{ccccccc}\hfill \frac{\partial \ln {\Phi }_1}{\partial {\kappa }_1}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial \ln {\Phi }_1}{\partial {\kappa }_N}\hfill & \hfill ;\hfill & \hfill \frac{\partial \ln {\Phi }_1}{\partial {\mu }_{a1}}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial \ln {\Phi }_1}{\partial {\mu }_{aN}}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \frac{\partial \ln {\Phi }_M}{\partial {\kappa }_1}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial \ln {\Phi }_M}{\partial {\kappa }_N}\hfill & \hfill ;\hfill & \hfill \frac{\partial \ln {\Phi }_M}{\partial {\mu }_{a1}}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial \ln {\Phi }_M}{\partial {\mu }_{aN}}\hfill \end{array}\right]$$ (6)

is the Jacobian matrix at i-th iteration, representing the sensitivity between the field distribution with respect to the perturbations of optical properties [10].

In order to construct Jacobian matrix, one needs to solve the forward field first, and then solve ∂Φ/∂κ and ∂Φ/∂μ_a for all the parameter nodes and all the source locations. If there is n_nodes in the reconstruction mesh and n_source in the problem, the total number of solutions needed to build the Jacobian matrix is n_source×(n_nodes+1) for each iteration. Experiments showed that with a 2D reconstruction algorithm using direct Jacobian construction, the evaluation of a single iteration requires more than an hour on a PC with a typical problem size of nnodes = 200 and nsource = 5, where 90% of computation time is dedicated to constructing Jacobian matrix. For complex geometry modeling and parameter reconstruction, a more efficient algorithm is needed.

In this paper, we present an algorithm to compute the Jacobian matrix based on reciprocity theory (light transmitted from source A and detected at detector B equals to the light fluence rate transmitted from B and received at A). Jacobian sensitivity matrix can be written as[10]:

$$\frac{\partial {\Phi }_{j,i}}{\partial {\mu }_{a,k}}=-\frac{\langle G(\stackrel{\rightharpoonup }{r}_k,\stackrel{\rightharpoonup }{r}_i)\cdot \Phi (\stackrel{\rightharpoonup }{r}_j,\stackrel{\rightharpoonup }{r}_k)\rangle }{\Phi (\stackrel{\rightharpoonup }{r}_j,\stackrel{\rightharpoonup }{r}_i)}$$ (7)

$$\frac{\partial {\Phi }_{j,i}}{\partial {\kappa }_k}=-\frac{\langle \nabla G(\stackrel{\rightharpoonup }{r}_k,\stackrel{\rightharpoonup }{r}_i)\cdot \nabla \Phi (\stackrel{\rightharpoonup }{r}_j,\stackrel{\rightharpoonup }{r}_k)\rangle }{\Phi (\stackrel{\rightharpoonup }{r}_j,\stackrel{\rightharpoonup }{r}_i)}$$ (8)

where $\Phi (\stackrel{\rightharpoonup }{r}_j,\stackrel{\rightharpoonup }{r}_k)$ is the direct solution at mesh point $\stackrel{\rightharpoonup }{r}_k$ for source position $\stackrel{\rightharpoonup }{r}_j,\Phi (\stackrel{\rightharpoonup }{r}_j,\stackrel{\rightharpoonup }{r}_i)$ is the direct solution at detector position $\stackrel{\rightharpoonup }{r}_i$ and $G(\stackrel{\rightharpoonup }{r}_k,\stackrel{\rightharpoonup }{r}_i)$ is the adjoint solution at mesh point $\stackrel{\rightharpoonup }{r}_k$ for detector position $\stackrel{\rightharpoonup }{r}_i$ [10]. In this adjoint method, evaluating the Jacobian matrix J involves only an inner product of the field distribution multiplied by the weighting coefficients near each mesh vertices in the reconstruction mesh, which is an O(N) operation compared with O(N²) solving the sensitivity equation via direct method for all the perturbation of sources and reconstruction parameters.

1.4 2D-3D hybrid image reconstruction algorithm

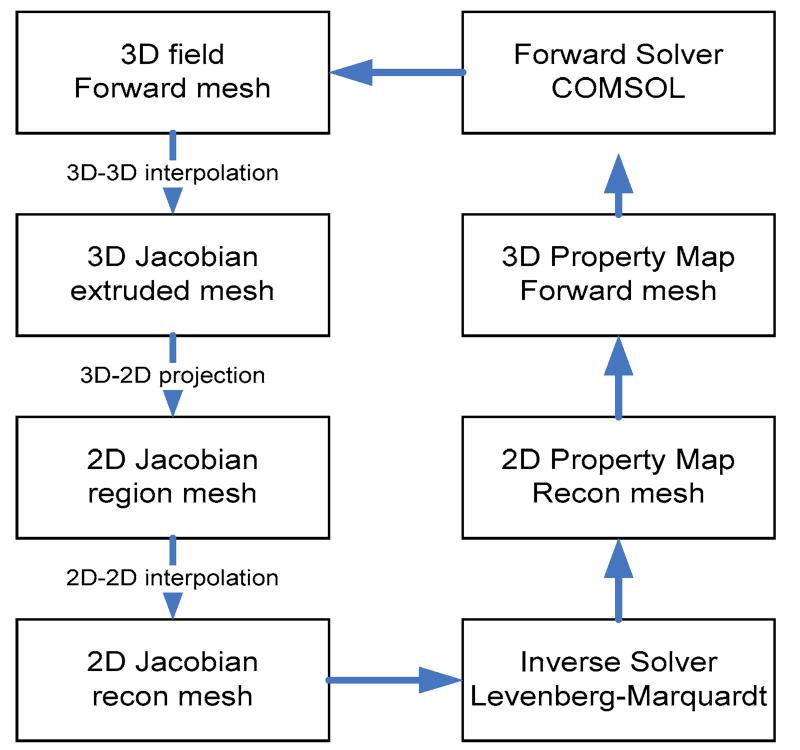
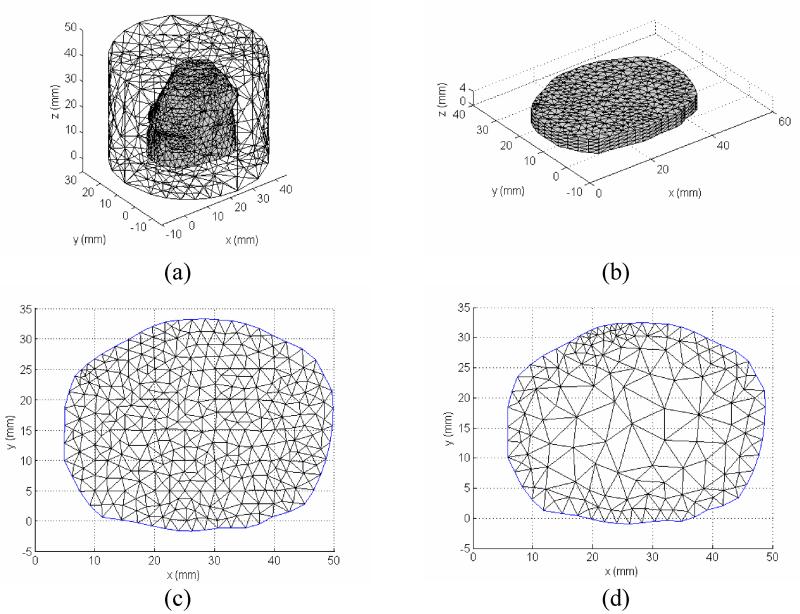
Because the photons are scattered in tissue, both 3D forward and inverse models are theoretically required for accurately reconstruct the tissue optical properties. This full 3D reconstruction scheme leads to a significant memory cost and time consuming algorithm based on a PC environment. For photodynamic therapy light dosimetry, physicians are interested in a fast acquisition of light dose deposition, and/or functional aspects of the prostate being treated, e.g., tissue oxygenation. Thus it would be preferable if some approximation can be assumed and reduce the 3D problem to a 2D problem. Here, we assume a 2D heterogeneous distribution of optical properties in the region under investigation. Specifically, the optical properties are invariable in the axial direction in the image plane. With this 2D-3D hybrid model, we can retain the nature of three-dimensional photon migration, and recover an axially average 2D optical property distribution. Since reconstruction is done in 2D, the number of unknowns in the parameter space is greatly reduced. Figure 2 illustrates the process of the 2D-3D hybrid algorithm. Given a 2D geometry, and an initial guess of 2D heterogeneity, the optical property is mapped to a 3D mesh extruded from the 2D mesh, assuming the optical property at any position (x,y,z) in the extruded 3D mesh is identical to the optical properties at the position (x,y) in the 2D mesh. 3D fluence rate data is calculated in the finer forward 3D mesh (Figure 4 (a)), and then interpolated onto the 3D extruded mesh (Figure 4 (b)), which is a cylinder object extruded from the 2D prostate contour of a specific slice with a limited height (Δz=5 mm). The 3D Jacobian sensitivity matrix is then calculated according to equation (7) and (8) based on this 3D extruded finite element mesh. The 2D Jacobian matrix can be obtained by integrating the 3D extruded Jacobian along the z-axis. For simplicity, we only derive the projection for the first half of the first row of the 3D Jacobian matrix, representing the absorption μ_a sensitivity on measurement where the first source and detector are used.

$$\begin{array}{cc}\hfill \partial {\Phi }_{i,{\mu }_a}& =\sum _{k=1}^{\text{nnode}3D}{J}_{i,k}\cdot \partial {\mu }_{a,k}\hfill \\ \hfill =& \sum _{l=1}^{\text{nnode}2D}(J_{i,l}\partial {\mu }_{a,l})+\cdots +\sum _{l=1}^{\text{nnode}2D}\left(J_{i,l+\text{nnode}2D\times nz}\partial {\mu }_{a,l+\text{nnode}2D\times nz}\right)\hfill \\ \hfill =& \sum _{l=1}^{\text{nnode}2D}\left(\sum _{m=1}^{nz}{J}_{i,(m-1)\times l+1}\right)\partial {\mu }_{a,l}\hfill \end{array}$$ (9)

The resulting 2D Jacobian matrix defined on a finer 2D mesh (Figure 4(c)) can be interpolated onto a coarser reconstruction mesh (Figure 4(d)) to further reduce the number of unknowns. The updated optical properties in the imaging plane are then embedded in the forward 3D mesh (Figure 4(a)) for iteration.

Figure 2.

Diagram of 2D-3D hybrid reconstruction algorithm.

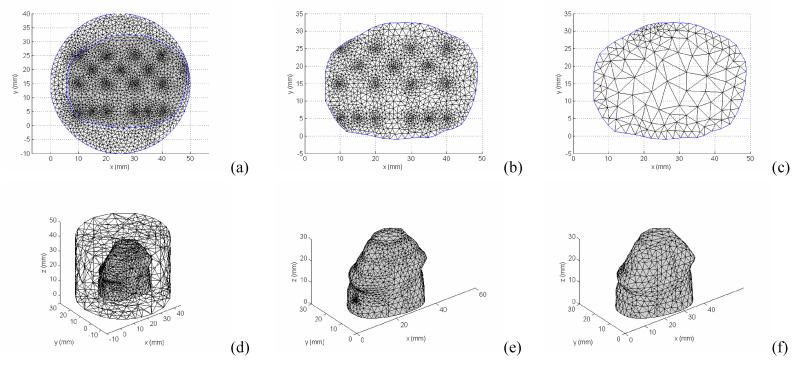
Figure 4.

Mesh used for 2D-3D hybrid reconstruction algorithm. (a) forward calculation mesh; (b) extruded 3D mesh for Jacobian calculation; (c) 2D fine mesh where the projected Jacobian is obtained; and (d) 2D reconstruction mesh.

The 2D-3D hybrid reconstruction is essentially the z-direction Jacobian weighted average of the 3D structure and its quality degrades compared with the full 3D reconstruction, depending on both the height of the heterogeneity to be estimated and the diffusion pattern of the Jacobian matrix. Although this weighting average induces blurring effects in the resulting images, the reconstruction is still on-plane pronounced because of the remarkable difference between the on-plane and off-plane Jacobian magnitudes. In principle, the hybrid reconstruction can attain a comparable quality with the 3D reconstruction when the height of the heterogeneity approaches the true 2D distribution of the optical property.

1.5 Clinical Protocols

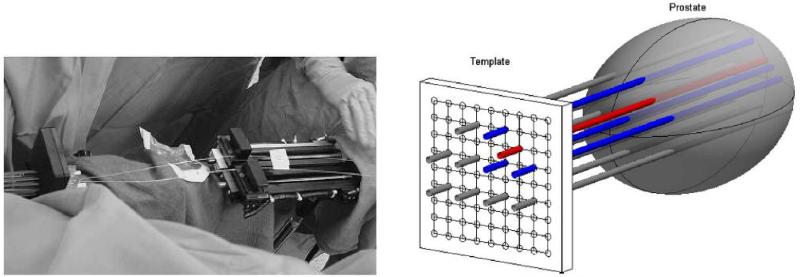
Patients with locally recurrent prostate carcinoma were treated by MLu-medicated photodynamic therapy. This Phase I protocol was approved by the Institutional Review Board of the University of Pennsylvania, the clinical trials and scientific monitoring committee of the university of Pennsylvania cancer center and cancer therapy evaluation program of the national cancer institute. Treatment planning was performed 2 weeks before the treatment based on the transrectal ultrasound (TRUS) performed by the urologist. Locations and length of cylindrical light sources (1, 2, 3, 4, 5 cm long) were then determined. The sources were spaced 1 cm apart and are prepared on a template with 0.5cm grid. The lengths of the optical fibers are selected to cover the full length of the prostate. MLu was intravenously administered at 2mg/Kg dose to patients 3 h prior to the light treatment. Patients were anesthetized in the operating room to minimize the movement during the procedure. The TRUS unit was used to guide the needle insertion, and biopsies for the MLu measurements. Twelve isotropic detectors were inserted in the prostate and kept in place for the entire procedure. Five additional catheters were inserted for the point sources. The diffuse optical tomography was performed before the light delivery using these sources/detectors. The time for the diffuse optical tomography data acquisition is approximately 5 minutes. PDT were then performed one quadrant at a time by inserting the linear light diffusers. A 15W diode laser was used as 732nm light source. After light treatment, another set of data acquisition for diffuse optical tomography was performed. Then the sources and detectors were removed.

RESULTS AND DISCUSSION

We present simultaneous reconstruction of absorption and scattering coefficients using the Levenberg-Marquardt algorithm in conjunction with the adjoint source scheme for two different test cases: a 2D circular object included a 2D prostate with different circular optical inclusions and a 3D cylinder object included 3D prostate geometry with different cylindrical optical inclusions. All the inclusions are embedded in the homogeneous background phantom with optical properties of μ_a=0.03mm⁻¹, μ’_s=1.4 mm⁻¹ [9].

The forward data used in the reconstruction of these test cases were simulated by the steady-state diffusion model, using highly resolved mesh to ensure the good quality of the data. Coarser meshes were used for the inverse solution to speed up the computation times.

3.1 Circle test object

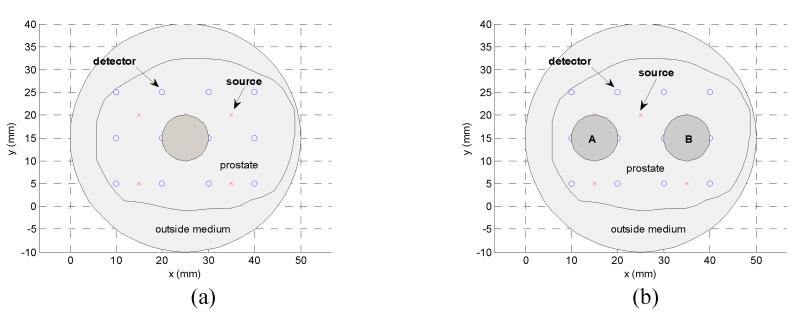
The 2D mathematical phantom is a circle of radius 25mm with: (a) One target, absorption inclusion only: μ_a=0.09 mm⁻¹. (b) One target, scattering inclusion only: μ’_s=2.8 mm⁻¹. (c) Two targets, target A: μ’_s=2.8mm⁻¹ and target B: μ_a = 0.09mm⁻¹. Target A centers at (15mm, 15mm) with radius 5 mm, target B has the same radius and centers at (35mm, 15mm). The geometry configurations for these test cases are depicted in Figure 5.

Figure 5.

2D mathematical synthetic phantom with optical inclusions for case (a) to (d).

Forward data were calculated for 5 sources and 12 detector positions. The mesh for the forward calculation has 2408 nodes and 4719 elements, for the region Jacobian construction has 1497 nodes and 2914 elements, for the optical property reconstruction has 441 elements and 251 nodes. Figure 6 (a)-(f) show the reconstructed absorption and scattering images. All the reconstruction started from a homogeneous optical property the same as the background (μ_a=0.03mm⁻¹, μ’_s=1.4 mm⁻¹), and was terminated after 100 iterations, or the projection error change is less than 2%, whichever occurs first. The 2D algorithm manages to identify the targets with approximate localization. However, large amount of cross talk between the absorption and scattering images are found (Figure 6).

Figure 6.

Reconstructed absorption and scattering images by use of 2D reconstruction algorithm for case 1: (a) and (b), case 2: (c) and (d), and case 3: (e) and (f)

3.2 3D Cylinder test object

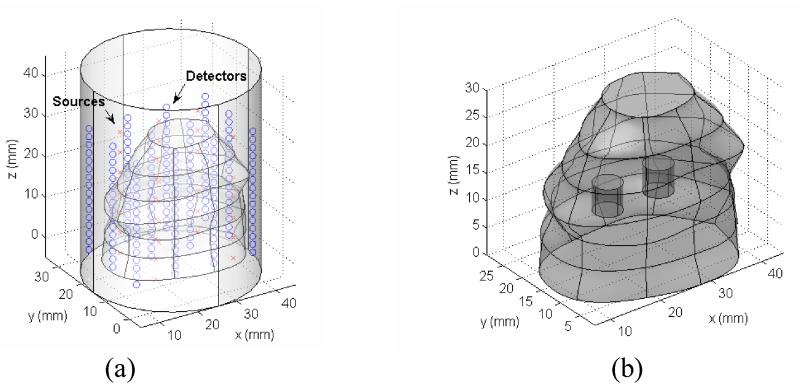
The 3D test objects is a cylinder with a radius R=25mm and a height of z=50mm. The background optical properties are of the same as in 2D phantoms which are chosen to simulate the background optical properties of human prostate. The source-detector positions are depicted in Figure 7, with 25 sources and 192 detectors. The forward calculation mesh contains 10456 tetrahedral elements and 2474 nodes, Jacobian mesh has 7170 tetrahedral elements and 1813 nodes, and the reconstruction mesh has 3692 elements and 1120 nodes. The mesh density is finer around the source/detector positions to ensure the accuracy of calculation of rapidly change field. The reconstruction mesh is uniformly constructed in the prostate subdomain. Two optical targets are embedded in the prostate subdomain: targets, A: μ’_s=2.8 mm⁻¹ and target B: μ_a = 0.09 mm⁻¹. The geometry configurations for these test cases are depicted in Figure 7.

Figure 7.

3D mathematical synthetic phantom with optical inclusions. (a) Prostate geometry with source/detector positions marked. (b) Two optical targets locations.

Figure 8 presents the absorption and scattering images at z=5, 10, 15 and 20mm planes. The initial estimation of optical properties used for reconstruction is homogeneous and is the same as background value. The images reported here were the results of 20 iterations with about 35 minutes per iteration for reconstruction on a dual core Pentium D 3 GHz PC with 1.5G memory. Three-dimensional reconstruction clearly recovers the location and size of the objects. We noticed that the absorption-scattering crosstalk is greatly reduced in this 3D reconstruction results.

Figure 8.

Cross-sections of 3D reconstructed absorption (a,c,e,g) and scattering (b,d,f,h) images. Slice locations are z = 5mm (a,b), z=10mm (c,d), z=15mm (e,f) and z=20 (g,h).

3.3 2D-3D hybrid reconstruction test object

The 2D-3D hybrid model test objects are of the same geometry as those in the 2D cases. The mesh for the forward model contains n_elements= 10456 tetrahedral-shaped elements with 2474 nodes. The Jacobian matrix is calculated on the extruded mesh with 6792 elements and 1538 nodes, which is extruded from a 397 nodes 2D finite element mesh with 733 triangle elements. The extruded mesh contains 6 layers located at Δz = 0, 1, 2, 3, 4 and 5 mm away from the image plane. A customized MATLab function fmeshextrude.m is used to construct the extruded finite element mesh nodes and tetrahedral elements, a fem structure is then constructed using the Comsol Multiphysics function femmesh.m. Another way of constructing the extruded mesh is via Comsol function meshextrude.m. Alternatively, three-dimensional prism elements are created in this method.

The dimension reduction significantly reduced the computation time and cut off the memory requirements. The relative execution time per iteration among 2D, 3D and hybrid reconstructions are 1, 4.6 and 122, where the 2D computation time is set to 1. Five light sources are located on the image plane and 12 detectors are located on each plane Δz = 0, 1, 2, 3, 4, and 5. The source-detector geometry configuration is shown in Figure 9.

Figure 9.

Reconstruction results using 2D-3D hybrid model for case 1: (a) and (b), case 2: (c) and (d) and case 3: (e) and (f).

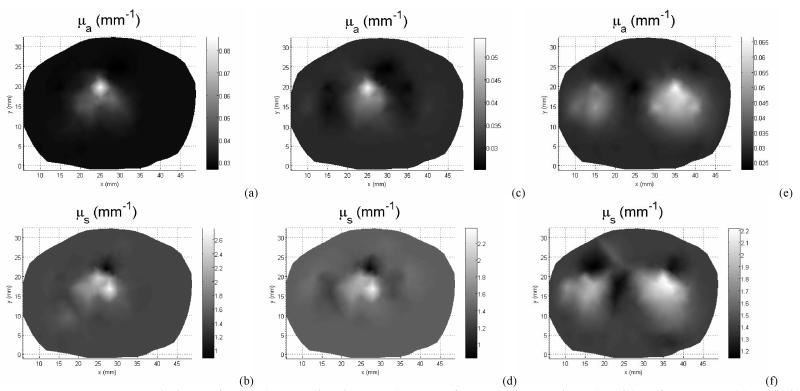
Figure 10 illustrates the reconstructed images of absorption and scattering coefficients from the 2D and 2D-3D hybrid algorithms for the test objects, with a fixed target height h = 5 mm. The 2D-3D hybrid reconstruction algorithm demonstrates a noticeable improvement in image quality and substantial suppression of inter-parameter cross-talks and artifacts.

Figure 10.

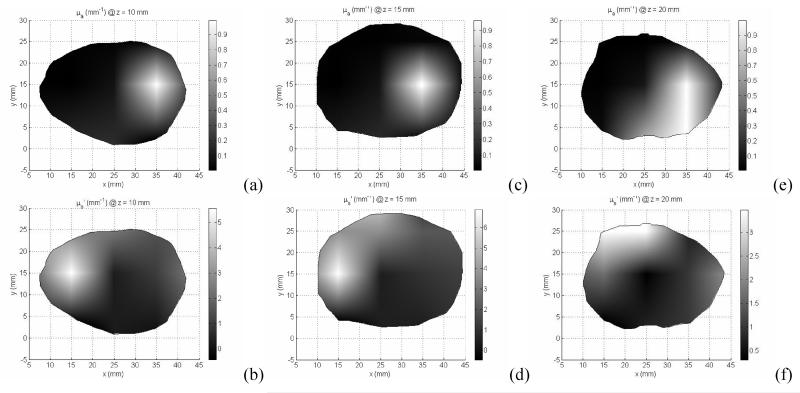
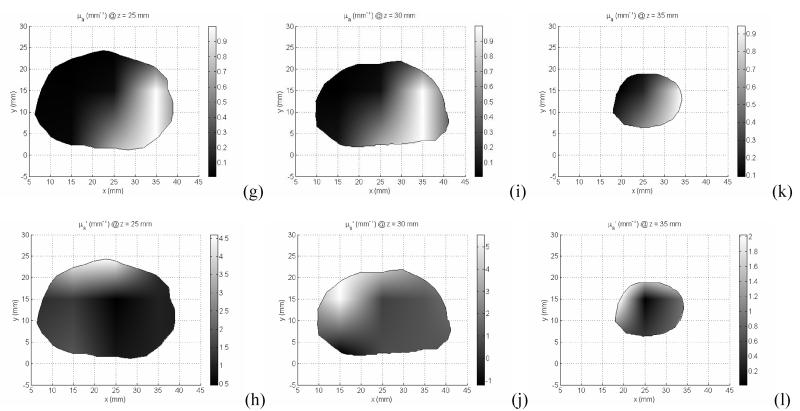
2D/3D hybrid diffuse optical tomography was used to obtained the absorption (a, c, e, g, i, k) and reduced scatter coefficients (b, d, f, h, j, l) of the prostate for different imaging volume: z=10mm (a,b), z=15mm (c,d), z=20mm (e,f), z=25mm (g,h), z=30mm (i,j), and z =35mm (k,l).

1.6 Clinical results

In the clinical study, a total number of measurements used is 360 for one prostate imaging slice, 6 slices for the whole prostate. A finite element meshes with 2408 nodes were used for the forward calculation and 251 nodes were used for the inverse model. Figure 10 illustrates the reconstructed μa and μs’ for one prostate image slice. The imaging volume of each slice is 5 mm. The intra-prostatic heterogeneity of optical properties is demonstrated in Figure 10. The variation in μa and μs’ at different prostate locations leads to up to 3 times difference of the effective attenuation coefficients between different locations of the prostate, and as a results, up to 3 times difference in photon deposition in PDT treatment. This optical property heterogeneity reflects the tumor oxygenation and photosensitizer concentration heterogeneity within the prostate.

CONCLUSION

In this paper, we have presented a method based on Levenberg-Marquardt algorithm to derive the minimization of the objective function for optical tomography in Comsol Multiphysics environment. We have presented simultaneous reconstruction of absorption and scattering from mathematical simulated data for two dimensional and three dimension cases. A 2D-3D hybrid model is presented which uses a 3D diffusion based forward model and a 2D inverse model to reconstruct the optical properties on the imaging plane. We have demonstrated that full 3D reconstruction algorithm can reconstruct multiple planes from multi-plane measurements; however, it requires high computation cost. Two-dimensional reconstruction is fast but exhibits much crosstalk between the absorption and scattering images. The proposed 2D-3D hybrid algorithm outperforms the 2D algorithm in both spatial resolution and fidelity, at considerably less computational expense than a full 3D reconstruction.

Figure 1.

2D and 3D finite element meshes for modeling and optical property reconstruction. Mesh used for calculation of (a) and (d) fluence rate Φ distribution; (b) and (e) Jacobian sensitivity matrix; (c) and (f) coarser reconstruction meshes. The meshes generated in the forward calculation meshes (a),(b),(d) and (e) are finer near the source/detector positions, and grow larger toward the edge of region of interest.

Figure 3.

Setup for clinical diffuse optical tomography. Two step motors were used, one for light sources and one for isotropic detectors. DOT data was acquired by moving point sources and detectors sequentially along the z-axis from the end of catheter.