Graphical Models for Ordinal Data

Abstract

A graphical model for ordinal variables is considered, where it is assumed that the data are generated by discretizing the marginal distributions of a latent multivariate Gaussian distribution. The relationships between these ordinal variables are then described by the underlying Gaussian graphical model and can be inferred by estimating the corresponding concentration matrix. Direct estimation of the model is computationally expensive, but an approximate EM-like algorithm is developed to provide an accurate estimate of the parameters at a fraction of the computational cost. Numerical evidence based on simulation studies shows the strong performance of the algorithm, which is also illustrated on data sets on movie ratings and an educational survey.

1 Introduction

Graphical models have been successful in identifying directed and undirected structures from high dimensional data. In a graphical model, the nodes of the network correspond to random variables and the edges represent their corresponding associations (Lauritzen, 1996). Two canonical classes of graphical models are the Gaussian one, where the dependence structure is fully specified by the inverse covariance matrix and the Markov one, where the dependence structure is captured by the interaction effects in an exponential family model. In the latter model, each interaction effect can be interpreted as the conditional log-odds-ratio of the two associated variables given all other variables. In both models, a zero element in the inverse covariance matrix or a zero interaction effect determines a conditionally independent relationship between the corresponding nodes in the network.

Estimation of such models from high dimensional data under a sparsity assumption has attracted a lot of interest in the statistics and machine learning literature, including regularized likelihood and regression methods, for example, see Yuan and Lin (2007); Banerjee et al. (2008); Friedman et al. (2008); Rothman et al. (2008); Fan et al. (2009); Meinshausen and Buhlmann (2006); Rocha et al. (2008); Peng et al. (2009) and references therein. For a Markov network, direct estimation of a regularized likelihood is infeasible due to the intractable partition function in the likelihood. Instead, existing methods in the literature employ variants of approximation estimation methods. Examples include the surrogate likelihood methods (Banerjee et al., 2008; Kolar and Xing, 2008) and the pseudo-likelihood methods (Höefling and Tibshirani, 2009; Ravikumar et al., 2010; Guo et al., 2010).

In many applications involving categorical data, an ordering of the categories can be safely assumed. For example, in marketing studies consumers rate their preferences for a wide range of products. Similarly, computer recommender systems utilize customer ratings to make purchase recommendations to new customers; this constitutes a key aspect of the business model behind Netflix, Amazon, Tripadvisor, etc (Koren et al., 2009).

Ordinal variables are also an integral part of survey data, where respondents rate items or express level of agreement/disagreement on issues/topics under consideration. Such responses correspond to Likert items and a popular model to analyze such data is the polychotomous Rasch model (von Davier and Carstensen, 2010) that obtains interval level estimates on a continuum, an idea that we explore in this work as well. Ordinal response variables in regression analysis give rise to variants of the classical linear model, including the proportional odds model (Walker and Duncan, 1967; McCullagh, 1980), the partial proportional odds model (Peterson, 1990), the probit model (Bliss, 1935; Albert and Chib, 1993; Chib and Greenberg, 1998), etc. A comprehensive review of ordinal regression is given in McCullagh and Nelder (1989) and O'Connell (2005).

In this paper, we introduce a graphical model for ordinal variables. It is based on the assumption that the ordinal scales are generated by discretizing the marginal distributions of a latent multivariate Gaussian distribution and the dependence relationships of these ordinal variables are induced by the underlying Gaussian graphical model. In this context, an EM-like algorithm is appropriate for estimating the underlying latent network, which presents a number of technical challenges that have to be addressed for successfully pursuing this strategy.

Our work is related to Albert and Chib (1993), Chib and Greenberg (1998) and Stern et al. (2009) in the sense that they are all built on the probit model and/or the EM algorithmic framework. Albert and Chib (1993) proposed an MCMC algorithm for the probit-model-based univariate ordinal regression problem, where an ordinal response is fitted on a number of covariates, while Chib and Greenberg (1998) can be considered an extension to the multivariate case. Stern et al. (2009) aims in building an online recommender system via collaborative filtering and applied the discretization/thresholding idea in the probit model to the ordinal matrix factorization problem. Our model, on the other hand, has a completely different motivation from these works. Our objective is explore associations between a set of ordinal variables, rather than prediction and/or regression problems. Nevertheless, the EM framework employed is related to that in Chib and Greenberg (1998), but due to the different goal, the form of the likelihood function of the proposed model is different from that of the ordinal regression problem. Further, as seen in Section 2, we do not use any MCMC or Gibbs sampling scheme.

The remainder of the paper is organized as follows. Section 2 presents the probit graphical model and discusses algorithmic and model selection issues. Section 3 evaluates the performance of the proposed method on several synthetic examples and Section 4 applies the model to two data examples, one on movie ratings and the other on a national educational longitudinal survey study.

2 Methodology

2.1 The probit graphical model

Suppose we have p ordinal random variables X₁, …, X_p, where X_j ∈ {1, 2, …, K_j} for some integer K_j, which is the number of the ordinal levels in variable j. In the proposed probit graphical model, we assume that there exist p latent random variables Z₁, … , Z_p from a joint Gaussian distribution with mean zero and covariance matrix Σ = (σ_j,j′)_p×p. Without loss of generality, we further assume that Z_j's have unit variances (σ_j,j = 1 for j = 1, … , p), i.e., the Z_j's marginally follow standard Gaussian distributions. Each observed variable X_j is discretized from its latent counterpart Z_j. Specifically, for the j-th variable (j = 1, … , p), we assume that (−∞,+∞) is split into K_j disjointed intervals by a set of thresholds $-\infty ={\theta }_0^{\left(j\right)}\langle {\theta }_1^{\left(j\right)}\langle \dots \langle thet{a}_{K_j-1}^{\left(j\right)}\langle {\theta }_{K_j}^{\left(j\right)}=+\infty$, such that X_j = k if and only if Z_j falls in the interval $[{\theta }_{k-1}^{\left(j\right)},{\theta }_k^{\left(j\right)})$. Thus,

$$\text{Pr}(X_j=k)=\text{Pr}({\theta }_{k-1}^{\left(j\right)}\le Z_j<{\theta }_k^{\left(j\right)})=\Phi \left({\theta }_k^{\left(j\right)}\right)-\Phi \left({\theta }_{k-1}^{\left(j\right)}\right),$$ (1)

where Φ(·) denotes the cumulative density function of the standard normal distribution.

Let $\Omega ={\Sigma }^{-1}={\left({\omega }_{j,j^{\prime }}\right)}_{p\times p}$, $ϴ=\{{\theta }_k^{\left(j\right)}:j=1,\dots ,p;k=1,\dots ,K_j\}$, X = (X₁, …, X_p), Z = (Z₁, … , Z_p). Let C(X,Θ) be the hyper-cube defined by $[{\theta }_{X_1-1}^{\left(1\right)},{\theta }_{X_1}^{\left(1\right)})\times \dots \times [{\theta }_{X_p-1}^{\left(p\right)},{\theta }_{X_p}^{\left(p\right)})$. Then we can write the joint density function of (X,Z) as:

$${\mathrm{f}}_{X,Z}(x,z;\Omega ,ϴ)=\mathrm{f}(\mathit{z};\Omega )\prod _{j=1}^p{\mathrm{f}}_{ϴ}(x_j\mid z_j;ϴ)=\frac{\text{det}\left(\Omega \right)}{{\left(2\pi \right)}^{p∕2}}\text{exp}(-\frac{1}{2}\mathit{z}\Omega {\mathit{z}}^{\mathrm{T}})\mathrm{I}(\mathit{z}\in C(\mathit{x},ϴ\left)\right)$$ (2)

where I(·) is the indicator function. Thus, the marginal probability density function of the observed X is given by

$${\mathrm{f}}_{\mathit{X}}(\mathit{x};\Omega ,ϴ)={\int }_{z\in {\mathbb{R}}^p}{\mathrm{f}}_{X,Z}(x,z;\Omega ,ϴ)\mathit{dz}$$ (3)

We refer to (1)–(3) as the probit graphical model, which is motivated by the probit regression model (Bliss, 1935; Albert and Chib, 1993; Chib and Greenberg, 1998) and the polychotomous Rasch model (von Davier and Carstensen, 2010).

To fit the probit graphical model, we propose maximizing an l₁-regularized log-likelihood of the observed data. Let x_i,j and z_i,j be the i-th realizations of the observed variable X_j and the latent variable Z_j, respectively, with x_i = (x_i,1, … , x_i,p) and z_i = (z_i,1, … , z_i,p). The criterion is given by

$$\sum _{i=1}^n\log {\mathrm{f}}_{\mathit{X}}({\mathit{x}}_i;\Omega ,ϴ)-\lambda \sum _{j\ne j^{\prime }}\mid {\omega }_{j,j^{\prime }}\mid .$$ (4)

The tuning parameter λ in (4) controls the degree of sparsity in the underlying network. When λ is large enough, some ω_j,j′'s can be shrunken to zero, resulting in the removal of the corresponding links in the underlying network. Numerically, it is difficult to maximize criterion (4) directly, because of the integral in (3). Next, we introduce an EM-type algorithm to maximize (4) in an iterative manner.

2.2 An algorithm for fitting the probit graphical model

Criterion (4) depends on the parameters Θ and Ω and the latent variable Z. The former has a closed-form estimator. Specifically, for each j = 1, … , p, we set

$${\widehat{\theta }}_k^{\left(j\right)}=\{\begin{array}{cc}-\infty ,\hfill & \text{if}k=0;\hfill \\ {\Phi }^{-1}\left(n^{-1}{\sum }_{i=1}^n\mathrm{I}\right(x_{i,j}<k\left)\right),\hfill & \text{if}k=1,\dots ,K_j-1;\hfill \\ +\infty ,\hfill & \text{if}k=K_j.\hfill \end{array}\phantom{\}}$$ (5)

where Φ is the cumulative distribution function of the standard normal. One can show that $\widehat{ϴ}$ consistently estimates Θ. The estimation of Ω, on the other hand, is nontrivial due to the multiple integrals in (3). To address this problem, we apply the EM algorithm to optimizing (4), where the latent variables z_i,j's (i = 1, … , n; j = 1, … , p) are treated as “missing data” and are imputed in the E-step, and the parameter Ω is estimated in the M-step.

E-step. Suppose $\widehat{\Omega }$ is the updated estimate of Ω from the M-step. Then the E-step computes the conditional expectation of the joint log-likelihood given the estimates $\widehat{ϴ}$ and $\widehat{\Omega }$, which is usually called the Q-function in the literature:

$$\mathrm{Q}(ϴ,\Omega )=\sum _{i=1}^n{\mathrm{E}}_{\mathit{Z}}\left[\log {\mathrm{f}}_{X,Z}\right({\mathit{x}}_i,\mathit{Z};\widehat{ϴ},\widehat{\Omega }\left)\right]=\frac{n}{2}\left[\log \text{det}\right(\Omega )-\text{trace}(\mathit{S}\Omega )-p\log (2\pi \left)\right]$$ (6)

Here S is a p×p matrix whose (j, j′)-th element is $s_{j,j^{\prime }}=n^{-1}{\sum }_{i=1}^n\mathrm{E}(z_{i,j}{z}_{i,j^{\prime }}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })(1\le j,j^{\prime }\le p)$. The distribution of z_i conditional on x_i is equal to that of z_i conditional on z_i ∈ C(x_i, Θ), which follows a truncated multivariate Gaussian distribution on the hyper-cube C(x_i, Θ). Therefore, $\mathrm{E}(z_{i,j}{z}_{i,j^{\prime }}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })$ is the second moment of a truncated multivariate Gaussian distribution and it can be directly estimated using the algorithms proposed by Tallis (1961), Lee (1979), Leppard and Tallis (1989) and Manjunath and Wilhelm (2012). Nevertheless, the computational cost of these direct estimation algorithms is extremely high and thus not suitable for even moderate size problems. An alternative approach is based on the Markov-chain-Monte-Carlo (MCMC) method. Specifically, we randomly generate a sequence of samples from the conditional distribution $f_{\mathit{Z}\mid \mathit{X}}({\mathit{z}}_i\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })$ using a Gibbs sampler from a multivariate truncated normal distribution (Kotecha and Djuric, 1999) and then $\mathrm{E}(z_{i,j}{z}_{i,j^{\prime }}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })$ is estimated by the empirical conditional second moment from these samples. Although the MCMC approach is faster than the direct estimation method, it is still not efficient for large scale problems. To address this computational issue, we develop an efficient approximate estimation algorithm, discussed in Section 2.3.

M-step. The M-step updates Ω by maximizing the l₁-regularized Q-function (up to a constant and a factor):

$$\tilde{\Omega }=\text{arg}\underset{\Omega }{\text{max}}\log \text{det}\left(\Omega \right)-\text{trace}\left(\mathit{S}\Omega \right)-\lambda \sum _{j\ne j^{\prime }}\mid {\omega }_{j,j^{\prime }}\mid .$$ (7)

The optimization problem (7) can be solved efficiently by existing algorithms such as the graphical lasso (Friedman et al., 2008) and SPICE (Rothman et al., 2008). However, the estimated covariance matrix, $\tilde{\Sigma }={\tilde{\Omega }}^{-1}$, does not necessarily have unit diagonal elements postulated by the probit graphical model. Therefore, we post-process $\tilde{\Sigma }$ by scaling it to a unit-diagonal matrix $\widehat{\Sigma }$ and update $\widehat{\Omega }={\widehat{\Sigma }}^{-1}$, which will be used in the E-step of the next iteration.

2.3 Approximating the conditional expectation

Note that when j = j′, the corresponding conditional expectation is the conditional second moment $\mathrm{E}(z_{i,j}^2\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })$; when j ≠ j′, we use a mean field theory approach (Peterson and Anderson, 1987) to approximate it as $E(z_{i,j}{z}_{i,j^{\prime }}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })\approx E(z_{i,j}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })E(z_{i,j^{\prime }}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })$. Note that the approximation decouples the “interaction” between the two variables z_i,j and z_i,j′. Therefore, one would expect that the approximation performs well when z_j and z_j′ are close to independence given all other random variables, which often holds when Ω or the corresponding graph is sparse. With this approximation, it is sufficient to estimate the first moment $E(z_{i,j}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })$ and the second moment $E(z_{ij}^2\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })$. In general, the latent variable z_i,j not only depends on x_i,j, but also on all other observed variables x_i,−j = (x_i,1, …, x_i,j−1, x_i,j+1, …, x_i,p). We can write the first and second conditional moments as

$$E(z_{i,j}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })=E\left[E\right(z_{i,j}\mid {\mathit{z}}_{i,-j},x_{i,j};\widehat{ϴ},\widehat{\Omega })\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega }],$$ (8)

$$E(z_{i,j}^2\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })=E\left[E\right(z_{i,j}^2\mid {\mathit{z}}_{i,-j},x_{i,j};\widehat{ϴ},\widehat{\Omega })\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega }],$$ (9)

where z_i,−j = (z_i,1, …, z_i,j−1, z_i,j+1, …, z_i,p). The inner expectations in (8) and (9) are relatively straightforward to compute: given the parameter estimate $\widehat{\Omega }$, z_i,1, …, z_i,p jointly follow a multivariate Gaussian distribution with mean zero and covariance matrix $\widehat{\Sigma }={\widehat{\Omega }}^{-1}$. A property of the Gaussian distribution is that the conditional distribution of z_i,j given z_i,−j is also Gaussian, with mean ${\tilde{\mu }}_{i,j}={\widehat{\Sigma }}_{j,-j}{\widehat{\Sigma }}_{-j,-j}^{-1}{{\mathit{z}}_{i,-j}}^{⊺}$ and variance ${\tilde{\sigma }}_{i,j}^2=1-{\widehat{\Sigma }}_{j,-j}{\widehat{\Sigma }}_{-j,-j}^{-1}{\widehat{\Sigma }}_{j,-j}$. Moreover, given the observed data x_i,j, conditioning z_i,j on z_i,−j, x_i,j in (8) is equivalent to conditioning on ${\mathit{z}}_{i,-j},{\theta }_{x_{i,j}-1}^{\left(j\right)}\le z_{i,j}\langle {\theta }_{x_{i,j}}^{\left(j\right)}$, which follows a truncated Gaussian distribution on the interval ${\theta }_{x_{i,j}-1}^{\left(j\right)},{\theta }_{x_{i,j}}^{\left(j\right)}$. The following lemma gives the closed-form expressions for the first and second moments of the truncated Gaussian distribution.

Lemma 1 Suppose that a random variable Y follows the Gaussian distribution with mean μ₀ and variance ${\sigma }_0^2$. For any constants t₁ < t₂, let ξ₁ = (t₁ – μ₀)/σ₀ and ξ₂ = (t₂ – μ₀)/σ₀. Then the first and second moments of Y truncated to the interval (t₁, t₂) are given by

$$E(Y\mid t_1<Y<t_2)={\mu }_0+\frac{\varphi \left({\xi }_1\right)-\varphi \left({\xi }_2\right)}{\Phi \left({\xi }_2\right)-\Phi \left({\xi }_1\right)}{\sigma }_0$$ (10)

$$E(Y^2\mid t_1<Y<t_2)={\mu }_0^2+{\sigma }_0^2+2\frac{\varphi \left({\xi }_1\right)-\varphi \left({\xi }_2\right)}{\Phi \left({\xi }_2\right)-\Phi \left({\xi }_1\right)}{\mu }_0{\sigma }_0+\frac{{\xi }_1\varphi \left({\xi }_1\right)-{\xi }_2\varphi \left({\xi }_2\right)}{\Phi \left({\xi }_2\right)-\Phi \left({\xi }_1\right)}{\sigma }_0^2$$ (11)

where ϕ(·) is the probability density function of the standard normal. For more properties of the truncated Gaussian distribution, see Johnson et al. (1994).

Letting ${\delta }_{i,j,k}=({\theta }_k^{\left(j\right)}-{\tilde{\mu }}_{i,j})∕{\tilde{\sigma }}_{i,j}$ and applying Lemma 1 to the conditional expectations in (8) and (9), we obtain

$$\mathrm{E}(z_{i,j}\mid {\mathit{z}}_{i,-j},x_{i,j};\widehat{ϴ},\widehat{\Omega })={\tilde{\mu }}_{i,j}+a_{i,j}{\tilde{\sigma }}_{i,j},$$ (12)

$$\mathrm{E}(z_{i,j}^2\mid {\mathit{z}}_{i,-j},x_{i,j};\widehat{ϴ},\widehat{\Omega })={\tilde{\mu }}_{i,j}^2+{\tilde{\sigma }}_{i,j}^2+2a_{i,j}{\tilde{\mu }}_{i,j}{\tilde{\sigma }}_{i,j}+b_{i,j}{\tilde{\sigma }}_{i,j}^2.$$ (13)

where

$$a_{i,j}=\frac{\varphi \left({\delta }_{i,j,x_{i,j}-1}\right)-\varphi \left({\delta }_{i,j,x_{i,j}}\right)}{\Phi \left({\delta }_{i,j,x_{i,j}}\right)-\Phi \left({\delta }_{i,j,x_{i,j}-1}\right)},b_{i,j}=\frac{{\delta }_{i,j,x_{i,j}-1}\varphi \left({\delta }_{i,j,x_{i,j}-1}\right)-{\delta }_{i,j,x_{i,j}}\varphi \left({\delta }_{i,j,x_{i,j}}\right)}{\Phi \left({\delta }_{i,j,x_{i,j}}\right)-\Phi \left({\delta }_{i,j,x_{i,j}-1}\right)}.$$

Next, we plug equations (12) and (13) into (8) and (9), respectively. Since ${\tilde{\mu }}_{i,j}$, a_i,j and b_i,j depend on the latent variables z_i,−j's, the outer expectations in (8) and (9) depend on $\mathrm{E}({\tilde{\mu }}_{i,j}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })$, $\mathrm{E}(a_{i,j}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })$, $\mathrm{E}(b_{i,j}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })$ and $\mathrm{E}(a_{i,j}{\tilde{\mu }}_{i,j}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })$. Note that ${\tilde{\mu }}_{i,j}$ is a linear function of z_i,−j and ${\tilde{\sigma }}_{i,j}$ is a constant irrelevant to the latent data. For each i = 1, …, n and j = 1, …, p, the conditional expectation of ${\tilde{\mu }}_{i,j}$ is

$$\mathrm{E}({\tilde{\mu }}_{i,j}\mid x_i;\widehat{\theta },\widehat{\Omega })={\widehat{\Sigma }}_{j,-j}{\widehat{\Sigma }}_{-j,-j}^{-1}\mathrm{E}(z_{i,-j}^{\mathrm{T}}\mid x_i;\widehat{\theta },\widehat{\Omega }).$$ (14)

However, a_i,j and b_i,j are nonlinear functions of ${\tilde{\mu }}_{i,j}$ and thus of z_i,−j. Using the first order delta method, we approximate their conditional expectations by

$$\mathrm{E}(a_{i,j}\mid x_i;\widehat{\theta },\widehat{\Omega })\approx \frac{\varphi \left({\tilde{\delta }}_{i,j,x_{i,j}-1}\right)-\varphi \left({\tilde{\delta }}_{i,j,x_{i,j}}\right)}{\Phi \left({\tilde{\delta }}_{i,j,x_{i,j}}\right)-\Phi \left({\tilde{\delta }}_{i,j,x_{i,j}-1}\right)}$$ (15)

$$\mathrm{E}(b_{i,j}\mid x_i;\widehat{\theta },\widehat{\Omega })\approx \frac{{\tilde{\delta }}_{i,j,x_{i,j}-1}\varphi \left({\tilde{\delta }}_{i,j,x_{i,j}-1}\right)-{\tilde{\delta }}_{i,j,x_{i,j}}\varphi \left({\tilde{\delta }}_{i,j,x_{i,j}}\right)}{\Phi \left({\tilde{\delta }}_{i,j,x_{i,j}}\right)-\Phi \left({\tilde{\delta }}_{i,j,x_{i,j}-1}\right)}$$ (16)

where ${\tilde{\sigma }}_{i,j,x_{i,j}}=[{\theta }_k^{\left(j\right)}-\mathrm{E}({\tilde{\mu }}_{i,j}\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega }]∕{\tilde{\sigma }}_{i,j}$. Finally, we approximate $\mathrm{E}(a_{i,j}{\tilde{\mu }}_{i,j}\mid {\mathit{x}}_i;\widehat{\theta },\widehat{\Omega })\approx \mathrm{E}(a_{i,j}\mid {\mathit{x}}_i;\widehat{\theta },\widehat{\Omega })\mathrm{E}({\tilde{\mu }}_{i,j}\mid {\mathit{x}}_i;\widehat{\theta },\widehat{\Omega })$. Therefore (8) and (9) can be approximated by

$$\mathrm{E}(z_{i,j}\mid x_i;\widehat{ϴ},\widehat{\Omega })\approx {\widehat{\Sigma }}_{j,-j}{\widehat{\Sigma }}_{-j,-j}^{-1}\mathrm{E}(z_{i,-j}^{\mathrm{T}}\mid x_i;\widehat{ϴ},\widehat{\Omega }+\frac{\varphi \left({\tilde{\delta }}_{i,j,x_{i,j}-1}\right)-\varphi \left({\tilde{\delta }}_{i,j,x_{i,j}}\right)}{\Phi \left({\tilde{\delta }}_{i,j,x_{i,j}}\right)-\Phi \left({\tilde{\delta }}_{i,j,x_{i,j}-1}\right)}{\tilde{\sigma }}_{i,j}$$ (17)

$$\begin{array}{cc}\hfill \mathrm{E}(z_{i,j}^2\mid x_i;\widehat{ϴ},\widehat{\Omega })& \approx {\widehat{\Sigma }}_{j,-j}{\widehat{\Sigma }}_{-j,-j}^{-1}\mathrm{E}(z_{i,-j}^{\mathrm{T}}{z}_{i,-j}\mid x_i;\widehat{ϴ},\widehat{\Omega }){\widehat{\Sigma }}_{-j,-j}^{-1}{\widehat{\Sigma }}_{j,-j}^{\mathrm{T}}+{\tilde{\sigma }}_{i,j}^2\hfill \\ \hfill & +2\frac{\varphi \left({\tilde{\delta }}_{i,j,x_{i,j}-1}\right)-\varphi \left({\tilde{\delta }}_{i,j,x_{i,j}}\right)}{\Phi \left({\tilde{\delta }}_{i,j,x_{i,j}}\right)-\Phi \left({\tilde{\delta }}_{i,j,x_{i,j}-1}\right)}\left[{\widehat{\Sigma }}_{j,-j}{\widehat{\Sigma }}_{-j,-j}^{-1}\mathrm{E}\right(z_{i,-j}^{\mathrm{T}}\mid x_i;\widehat{ϴ},\widehat{\Omega }\left)\right]{\tilde{\sigma }}_{i,j}\hfill \\ \hfill & +\frac{{\tilde{\delta }}_{i,j,x_{i,j}-1}^{\left(j\right)}\varphi \left({\tilde{\delta }}_{i,j,x_{i,j}-1}\right)-{\tilde{\delta }}_{i,j,x_{i,j}}\varphi \left({\tilde{\delta }}_{i,j,x_{i,j}}\right)}{\Phi \left({\tilde{\delta }}_{i,j,x_{i,j}}\right)-\Phi \left({\tilde{\delta }}_{i,j,x_{i,j}-1}\right)}{\tilde{\sigma }}_{i,j}^2\hfill \end{array}$$ (18)

Equations (17) and (18) establish the recursive relationships among the elements in $\mathrm{E}({\mathit{z}}_i\mid {\mathit{x}}_i;\widehat{ϴ},\widehat{\Omega })$ and $\mathrm{E}({z_i}^{⊺}{z}_i\mid {\mathit{x}}_i;\widehat{\Theta },\widehat{\Omega })$, respectively, giving a natural iterative procedure for estimating these quantities. Algorithm 1 summarizes the main steps of the proposed combined estimation procedure outlined in Sections 2.2 and 2.3.

Algorithm 1 The EM Algorithm for estimating Ω
1:	Initialize $\mathrm{E}(z_{i,j}\mid {\mathit{x}}_i;\widehat{\Theta },\widehat{\Omega })\approx \mathrm{E}(z_{i,j}\mid x_{i,j};\widehat{\Theta })$, $\mathrm{E}(z_{i,j}^2\mid {\mathit{x}}_i;\widehat{\Theta },\widehat{\Omega })\approx \mathrm{E}(z_{i,j}^2\mid x_{i,j};\widehat{\Theta })$ and $\mathrm{E}(z_{i,j}{z}_{i,j^{\prime }}\mid {\mathit{x}}_i;\widehat{\Theta },\widehat{\Omega })\approx \mathrm{E}(z_{i,j}\mid x_{i,j};\widehat{\Theta })\mathrm{E}(z_{i,j^{\prime }}\mid x_{i,j^{\prime }};\widehat{\Theta })$ for i = 1, …, n and j,j′ = 1, …,p;
2:	Initialize sj,j′ for 1 ≤ j,j′ ≤ p using the Line 1 above, and then estimate $\widehat{\Omega }$ by maximizing criterion (7); {Start outer loop}
3:	repeat
4:	E-step: estimate S in (6); {Start inner loop}
5:	repeat
6:	for i = 1 to n do
7:	if j = j′ then
8:	Update $\mathrm{E}(z_{i,j}^2\mid {\mathit{x}}_i;\widehat{\Theta },\widehat{\Omega })$ using RHS of equation (18) for j = 1, …, p;
9:	else
10:	Update $\mathrm{E}(z_{i,j}\mid {\mathit{x}}_i;\widehat{\Theta },\widehat{\Omega })$ using RHS of equation (17) for j = 1, …, p and then set $\mathrm{E}(z_{i,j}{z}_{i,j^{\prime }}\mid {\mathit{x}}_i;\widehat{\Theta },\widehat{\Omega })=\mathrm{E}(z_{i,j}\mid {\mathit{x}}_i;\widehat{\Theta },\widehat{\Omega })\mathrm{E}(z_{i,j^{\prime }}\mid {\mathit{x}}_i;\widehat{\Theta },\widehat{\Omega })$ for 1 ≤ j ≠ j′ ≤ p;
11:	end if
12:	end for
13:	Update $s_{j,j^{\prime }}=1∕n{\sum }_{i=1}^n\mathrm{E}(z_{i,j}{z}_{i,j^{\prime }}\mid {\mathit{x}}_i;\widehat{\Theta },\widehat{\Omega })$ for 1 ≤ j,j′ ≤ p;
14:	until The inner loop converges;
15:	M-step: update $\widehat{\Omega }$ by maximizing criterion (7);
16:	until The outer loop converges.

In Algorithm 1, Lines 1–2 initialize the conditional expectation E(z_i,j | x_i) and the parameter estimate $\widehat{\Omega }$. Lines 3–16 establish the outer loop which iteratively computes the E-step and the M-step. In the E-step, Lines 5–14 consist of the inner loop which recursively estimates the first and second moments of z_i,j conditional on x_i. The complexity of the inner loop is O(np²), which is the same as that of the graphical lasso algorithm in the M-step. Therefore, the overall complexity of Algorithm 1 is O(Mnp²), where M is the number of EM steps required for convergence. In our numerical studies, we found M is often smaller than 50. For a more concrete idea about the computational cost, we note that on a linux server with four 1G Dual-Core AMD Opteron Processors and 4GB RAM, it takes about 2 minutes for the proposed algorithm to complete the fitting on a simulated dataset in Section 3 with n = 200 observations and p = 50 variables.

2.4 Model selection

In the probit graphical model, the tuning parameter λ controls the sparsity of the resulting estimator and it can be selected using cross-validation. Specifically, we randomly split the observed data X into D subsets of similar sizes and denote the index set of the observations in the d-th subset by ${\mathcal{T}}_d(d=1,\dots ,D)$. For any pre-specified λ, we denote by ${\widehat{\Omega }}_{\lambda }^{[-d]}$ the maximizer of the criterion (4) estimated by Algorithm 1 using all observations except those in ${\mathcal{T}}_d$. We also denote by ${\widehat{\Theta }}^{[-d]}$ and ${\mathbf{S}}^{\left[d\right]}={\left(s_{j,j^{\prime }}^{\left[d\right]}\right)}_{p\times p}$ the analogs of $\widehat{\Theta }$ S in Section 2.2, but computed from the data in ${\mathcal{T}}_d^c$ and ${\mathcal{T}}_d$, respectively. In particular, an element of S^[d] is defined as $s_{j,j^{\prime }}^{\left[d\right]}={\mid {\mathcal{T}}_d\mid }^{-1}{\sum }_{i\in {\mathcal{T}}_d}\mathrm{E}(z_i,z_{i,j^{\prime }}\mid x_i;{\widehat{\Theta }}^{[-d]},{\widehat{\Omega }}_{\lambda }^{[-d]})$, for 1 ≤ j, j′ ≤ p, where $\mid {\mathcal{T}}_d\mid$ is the cardinality of ${\mathcal{T}}_d$. Given ${\widehat{\Theta }}^{[-d]}$ and ${\widehat{\Theta }}_{\lambda }^{[-d]}$, S^[d] can be estimated by the algorithm introduced in Section 2.3, i.e., the inner loop of Algorithm 1. Thus, the optimal tuning parameter can be selected by maximizing the following criterion:

$$\underset{\lambda }{\text{max}}\sum _{d=1}^D\log \text{det}\left({\widehat{\Omega }}_{\lambda }^{[-d]}\right)-\text{trace}\left(S^{\left[d\right]}{\widehat{\Omega }}_{\lambda }^{[-d]}\right)-p\log \left(2\pi \right).$$ (19)

We note that we have also considered the AIC and BIC type criteria for choosing the tuning parameter λ. We found that AIC performs the worst among the three due to estimating many zero parameters as non-zeros (Lian, 2011); BIC and cross-validation tend to have similar performances in estimating zero parameters as zeros, but BIC also tends to estimate the non-zero parameters as zeros. Therefore, we choose to use cross-validation. Due to space limitation, the results are not included.

3 Numerical Examples

In this section, we use two sets of simulated experiments to illustrate the performance of the probit graphical model. The first set aims at comparing the computational cost of the three methods that estimate the Q-function in the E-step; namely the direct computation, the MCMC sampling and the approximation algorithm. The second set compares the performance of the probit graphical model using the approximation algorithm to that of the Gaussian graphical model.

3.1 Computational cost and performance

Note that the computational costs of the direct estimation and the MCMC sampling are extremely high when p is even of moderate size. Therefore, in this experiment, we simulate a low-dimensional data set with p = 5 variables and n = 10 observations. Specifically, we define the underlying inverse covariance matrix Ω as a tri-diagonal matrix with 1's on the main diagonal and 0.5 on the first sub-diagonal. The corresponding covariance matrix is then scaled so that all the variances are equal to 1. Then, for i = 1, …, n, we generate the latent data z_i = (z_i,1, …, z_i,p) from N(0, Σ) and discretize them as follows: for each j = 1, …, p, set

$${\theta }_k^{\left(j\right)\theta }=\{\begin{array}{cc}-\infty ,\hfill & \text{if}k=0;\hfill \\ {\Phi }^{-1}\left(0.2\right)\hfill & \text{if}k=1;\hfill \\ {\Phi }^{-1}\left(0.4\right)\hfill & \text{if}k=2;\hfill \\ +\infty ,\hfill & \text{if}k=3.\hfill \end{array}\phantom{\}}$$ (20)

and $x_{i,j}={\sum }_{k=0}^{2}I(z_{i,j}\ge {\theta }_k^{\left(j\right)})$ (i = 1, …, n; j, …, p), i.e., the value of x_i,j is k if it locates in interval $[{\theta }_{k-1}^{\left(j\right)},{\theta }_k^{\left(j\right)})$.

The probit graphical model is applied using four estimation methods in the E-step, namely the direct computation, a standard Gibbs sampling, the Gibbs sampler proposed by Pakman and Paninski (2012) and the approximation algorithm proposed in this manuscript. The procedure is repeated for 20 times, and the computational costs are shown in Table 1. We can see that the median CPU time of the approximation algorithm is only about 1/1,000 of that of the Gibbs sampling and about 1/80,000 of that of the direct computation. To further compare the estimation accuracy of these methods, we use the Frobenius and entropy loss metrics that are defined next:

$$FL=\frac{\sum _{1\le j<j^{\prime }\le p}{({\omega }_{j,j^{\prime }}-{\widehat{\omega }}_{j,j^{\prime }})}^2}{\sum _{1\le j<j^{\prime }\le p}{\omega }_{j,j^{\prime }}^2}$$ (21)

$$EL=\text{trace}\left({\Omega }^{-1}\widehat{\Omega }\right)-\log \left[\text{det}\right({\Omega }^{-1}\widehat{\Omega }\left)\right]-p$$ (22)

where $\widehat{\Omega }$ denotes the estimated network.

Table 1.

The numbers are the mean CPU times for different tuning parameter values and 20 replications, with median absolute deviations in parentheses (in second). Direct: direct computation. Gibbs sampler: the regular Gibbs sampler; TMG: the Gibbs sampler proposed by Pakman and Paninski (2012) via the R package "tmg"; Proposed Approximation: the approximation approach proposed in our manuscript

Method	CPU time in seconds
Direct	3310.21 (199.95)
Gibbs sampler	46.17 (1.51)
TMG	303.94 (11.05)
Proposed Approximation	0.04 (0.03)

The performance of the three estimation methods is depicted in Figure 1. It can be seen that the direct computation and Gibbs sampling methods are fairly similar in performance (The result using the R package “tmg” is almost identical to that of the standard Gibbs sampling and not shown); this is expected since they can all be considered “exact” approaches. In terms of the Frobenius and entropy losses, the approximation algorithm lags slightly behind its competitors when the tuning parameter λ is relatively small, whereas for larger λ it outperforms them. This is due to the fact that in this simulation study, the true Ω is very sparse and the mean field approximation also happens to implicitly enforce a conditional independence structure on the S matrix. These findings suggest that the proposed approximation algorithm achieves its orders of magnitude computational savings over the competitors with minimal degradation in performance.

Figure 1.

Comparison of Frobenius loss and Entropy loss over different values of the tuning parameter. The direct computation, the MCMC sampling and the approximation algorithm are respectively represented by blue dotted, red dashed and black solid lines.

3.2 Experiments with different types of graphs

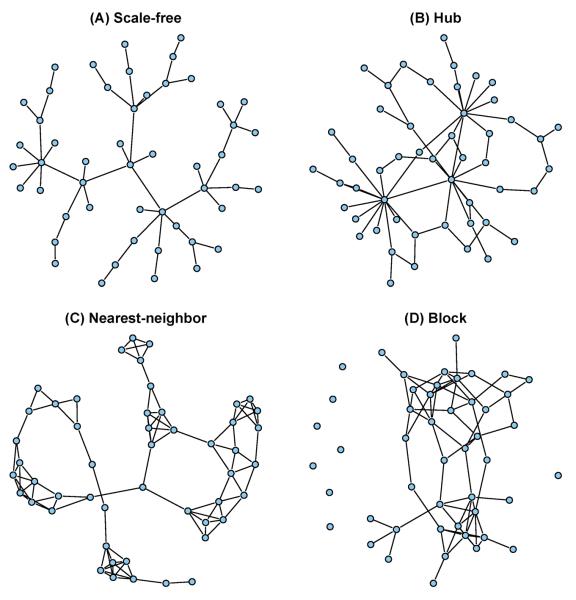
In this section, we evaluate the performance of the proposed method by simulation studies. These examples simulate four types of network structures: a scale-free graph, a hub graph, a nearest-neighbor graph and a block graph. Each network consists of p = 50 nodes. The details of these networks are described as follows:

• Example 1

  Scale-free graph. A scale-free graph has a power-law degree distribution and can be simulated by the Barabasi-Albert algorithm (Barabasi and Albert, 1999). A realization of a scale-free network is depicted in Figure 2 (A).

• Example 2

  Hub graph. A hub graph consists of a few high-degree nodes (hubs) and a large amount of low-degree nodes. In this example, we follow the simulation setting in Peng et al. (2009) and generate a hub graph by inserting a few hub nodes into a very sparse graph. Specifically, the graph consists of three hubs with degrees around eight, and the other 47 nodes with degrees at most three. An example of the hub graph is shown in Figure 2 (B).

• Example 3

  Nearest-neighbor graph. To generate nearest neighbor graphs, we slightly modify the data generating mechanism described in Li and Gui (2006). Specifically, we generate p points randomly on a unit square, calculate all p(p−1)/2 pairwise distances, and find the m nearest neighbors of each point in terms of these distances. The nearest neighbor network is obtained by linking any two points that are m-nearest neighbors of each other. The integer m controls the degree of sparsity of the network and the value m = 5 was chosen in the simulation study. Figure 2 (C) exhibits one realization of the nearest-neighbor network.

• Example 4

  Block graph. In this setting, we generate a graph using a random adjacency matrix generated from the stochastic block model. Specifically, for nodes 1–20 the probability of being linked is 0.2, for nodes 21–30 the probability of being linked is 0.5, whereas for all other pairs of nodes the probability of having a link is 0.02. Figure 2 (D) illustrates such a random graph.

Figure 2.

Illustration of the networks used in four simulated examples: scale-free graph, hub graph, nearest-neighbor graph and block graph.

The ordinal data are generated as follows. First, we generate the inverse covariance matrix Ω of the latent multivariate Gaussian distribution. Specifically, each off-diagonal element ω_j,j′ is drawn uniformly from [−1, −0.5] ⋃ [0.5, 1] if nodes j and j′ are linked by an edge, otherwise ω_j,j′ = 0. Further, the diagonal elements were all set to be 2 to ensure positive definiteness, and the corresponding covariance matrix is scaled so that all the variances are equal to 1. Second, we generate the latent data z_i = (z_i,1, …, z_i,p) as an i.i.d. sample from N(0, Σ). Finally, the continuous latent data z_i's are discretized into ordinal scale with three levels by thresholding. Specifically, for each j = 1, …, p, we set

$${\theta }_k^{\left(j\right)}=\{\begin{array}{cc}-\infty ,\hfill & \text{if}k=0;\hfill \\ {\Phi }^{-1}\left(0.1\right)\hfill & \text{if}k=1;\hfill \\ {\Phi }^{-1}\left(0.2\right)\hfill & \text{if}k=2;\hfill \\ +\infty ,\hfill & \text{if}k=3.\hfill \end{array}\phantom{\}}$$ (23)

and set $x_{i,j}={\sum }_{k=0}^{2}I(z_{i,j}\ge {\theta }_k^{\left(j\right)})$ (i = 1, …, n; j = 1, …, p). For each example, we considered different sample sizes, with n=50, 100, 200 and 500.

We compare the proposed probit graphical model with two other methods. One consists of direct application of the graphical lasso to the ordinal data X, ignoring their discrete nature. The second uses the graphical lasso on the latent continuous data Z. We refer to the first one as the naive method and the second one as an oracle method because it represents an ideal situation where Z is exactly recovered. Of course, the latter never occurs with real data, but serves as a benchmark for comparison purposes. The receiver operating characteristic curve (ROC) was used to evaluate the accuracy of network structure estimation. The ROC curve plots the sensitivity (the proportion of correctly detected links) against the false positive rate (the proportion of mis-identified zeros) over a range of values of the tuning parameter λ. The sensitivity and the false positive rate are defined as follows:

$$\text{Sensitivity}=\frac{\sum _{1\le j<j^{\prime }\le p}\mathcal{I}({\omega }_{j,j^{\prime }}\ne 0,{\widehat{\omega }}_{j,j^{\prime }}\ne 0)}{\sum _{1\le j<j^{\prime }\le p}\mathcal{I}({\omega }_{i,j^{\prime }}\ne 0)}$$ (24)

$$\text{False Positive Rate}=\frac{\sum _{1\le j<j^{\prime }\le p}\mathcal{I}({\omega }_{j,j^{\prime }}=0,{\widehat{\omega }}_{j,j^{\prime }}\ne 0)}{\sum _{1\le j<j^{\prime }\le p}\mathcal{I}({\omega }_{j,j^{\prime }}=0)}$$ (25)

where $\mathcal{I}(\cdot )$ is an indicator function whose value is one if the statement in the parenthesis is true, and is zero if it is false. In addition, the Frobenius loss and the entropy loss defined in (21) were used to evaluate the performance of parameter estimation.

Figure 3 shows the ROC curves for all simulated examples. The curves are averaged over 50 replications. The oracle method provides a benchmark curve for each setting (blue dotted line in each panel). We can see that when the sample size is relatively small (n=50, 100 or 200), the probit model (dark solid line) dominates the naive method (red dashed line). When the sample size gets larger, the two methods exhibit similar performance.

Figure 3.

The ROC curves estimated by the probit graphical model (solid dark line), the oracle method (dotted blue line) and the naive method (dashed red line). The oracle method and the naive method simply apply the graphical lasso algorithm to the latent continuous data Z and the observed discrete data X, respectively.

Table 2 summarizes the parameter estimation measured by the Frobenius loss and the entropy loss. The results were again averaged over 50 repetitions and the tuning parameter λ was selected using the cross-validation introduced in Section 2.4. The oracle method evidently performs the best, as it should. Comparing the two methods based on the observed data X, we can see that the Frobenius losses from the probit model are consistently lower than those from the naive method. The advantage is more significant when the sample size is moderate (n=100 or 200). In terms of the entropy loss, we can see that the probit model outperforms the naive method for relatively large sample sizes, such as n=200 and 500.

Table 2.

The Frobenius loss and the entropy loss estimated by the probit graphical model, the oracle method and the naive method. The oracle method and the naive method simply apply the graphical lasso algorithm to the latent continuous data Z and the observed discrete data X, respectively. The results are averaged over 50 repetitions and the corresponding standard deviations are recorded in the parentheses.

Example	n	Frobenius Loss			Entropy Loss
		Gaussian	Oracle	Probit	Gaussian	Oracle	Probit
Scale-free	50	2.3 (0.12)	0.7 (0.05)	2.2 (0.13)	12.0 (0.73)	3.1 (0.29)	23.1 (1.83)
	100	2.2 (0.13)	0.4 (0.08)	1.7 (0.09)	9.4 (0.68)	1.9 (0.29)	10.1 (0.45)
	200	1.7 (0.12)	0.3 (0.02)	1.2 (0.04)	6.4 (0.33)	1.1 (0.10)	5.4 (0.26)
	500	0.9 (0.05)	0.1 (0.01)	0.7 (0.04)	3.3 (0.19)	0.5 (0.05)	2.7 (0.19)
Hub	50	1.2 (0.06)	0.3 (0.02)	1.1 (0.04)	21.2 (1.32)	5.8 (0.70)	29.4 (1.76)
	100	1.1 (0.10)	0.1 (0.01)	0.8 (0.03)	15.9 (1.03)	3.2 (0.27)	15.1 (0.64)
	200	0.8 (0.05)	0.1 (0.01)	0.6 (0.01)	11.9 (0.39)	1.8 (0.23)	10.4 (0.33)
	500	0.6 (0.02)	0.0 (0.00)	0.5 (0.01)	9.1 (0.16)	0.7 (0.06)	7.5 (0.16)
Nearest-neighbor	50	1.4 (0.04)	0.6 (0.02)	1.3 (0.06)	16.5 (0.80)	5.6 (0.30)	25.6 (2.04)
	100	1.3 (0.08)	0.4 (0.02)	1.0 (0.02)	12.1 (0.52)	3.5 (0.36)	12.4 (0.76)
	200	1.0 (0.04)	0.2 (0.01)	0.7 (0.03)	8.6 (0.32)	2.0 (0.11)	7.5 (0.17)
	500	0.6 (0.03)	0.1 (0.01)	0.5 (0.02)	5.5 (0.12)	0.8 (0.02)	4.5 (0.19)
Random-block	50	1.8 (0.05)	0.7 (0.05)	1.7 (0.04)	14.8 (1.04)	4.7 (0.46)	23.5 (1.76)
	100	1.6 (0.16)	0.4 (0.02)	1.3 (0.03)	10.7 (1.10)	2.9 (0.27)	11.3 (0.46)
	200	1.3 (0.05)	0.2 (0.03)	0.9 (0.05)	7.2 (0.19)	1.6 (0.11)	6.3 (0.32)
	500	0.7 (0.03)	0.1 (0.01)	0.6 (0.03)	4.1 (0.15)	0.7 (0.06)	3.5 (0.13)

4 Data Examples

4.1 Application to movie rating records

In this section, we apply the probit graphical model to Movielens, a data set containing rating scores for 1682 movies by 943 users. The rating scores have five levels, where 1 corresponds to strong dissatisfaction and 5 to strong satisfaction. More than 90% of the entries are missing in the full data matrix; for this reason, we consider a subset of the data containing 193 users and 32 movies, with 15% missing values. The missing values were imputed by the median of the observed movie ratings.

The estimated network for these 32 movies is shown in Figure 4. We can see that the estimated network consists of a large connected community as well as a few isolated nodes. The large community mainly consists of mass marketed commercial movies, dominated by science fiction and action films. These movies are characterized by high production budgets, state of the art visual effects, and famous directors and actors. Examples in this data subset include the Star Wars franchise (“Star Wars” (1977), “The Empire Strikes Back” (1980) and “Return of the Jedi” (1983), directed/produced by Lucas), the Terminator series (1984, 1991) directed by Cameron, the Indiana Jones franchise (“Raiders of Lost Ark” (1981), “The Last Crusade” (1989), directed by Spielberg), the Alien series, etc. As expected, movies within the same series are most strongly associated. Further, “Raiders of the Lost Ark” (1981) and “Back to the Future” (1985) form two hub nodes each having 16 connections to other movies and their common feature is that they were directed/produced by Spielberg.

Figure 4.

The network estimated by the probit graphical model. The nodes represent the movies labeled by their titles. The area of a node is proportional to its degree and the width of a link is proportional to the magnitude of the corresponding partial correlations.

On the other hand, isolated nodes tend to represent “artsier” movies, such as crime films and comedies whose popularity relies more on the plot and the cast than on big budgets and special effects, many with cult status among their followers. Examples include “Pulp Fiction” (1994) (one of the most popular Tarantino movies), “Fargo” (1996) (a quintessential Coen brothers movie), “When Harry Met Sally” (1989) and “Princess Bride” (1987). These films have no significant connections in the network, either with each other or with the commercial movies in the large community. This is likely due to two reasons: (1) we restricted the dataset to movies rated by a substantial fraction of the users, so while there probably are connections from “Fargo” to other Coen brothers movies, the other ones did not appear in this set; and (2) there is a greater heterogeneity of genres in this set than among the large group of science-fiction and action films. In other words, liking “When Harry Met Sally” (a romantic comedy) does not make one more likely to enjoy “Silence of the Lambs” (a thriller/horror movie), whereas liking “Terminator” suggests you are more likely to enjoy “The Alien”. A more complete analysis of this dataset is an interesting topic for future work and requires a more sophisticated way of dealing with missing data, which is not the focus of the current manuscript.

4.2 National education longitudinal survey study

The data for the second example come from the National Educational Longitudinal Study of 1988 (NELS:88), whose objective was to assess student attitudes towards a number of questions about their school, education, and activities. The data used were obtained from the study's website http://nces.ed.gov/surveys/nels88/ and correspond to a sample of 12144 students of eighth-graders. We selected 218 questions with ordinal and/or binary responses that focused on diverse issues, including school, work and home experiences, educational and occupational aspirations, access to educational resources and other support, as well as student background and school characteristics. Ordinal responses were chosen from the following options: “OFTEN”, “SOMETIMES”, “RARELY”, and “NEVER”, while binary ones corresponded to a ”YES/NO” answer. Figure 5 depicts the histogram of the frequency of options in 218 survey questions.

Figure 5.

Histogram of the number of options in 218 survey questions.

The estimated network of the selected 218 survey questions is shown in Figure 6. It is apparent that the estimated network exhibits a strong clustering structure. For example, the set of the following nodes “F1S33A”, “F1S33B”, “F1S33C”, “F1S33D”, and “F1S33E” forms a cluster, separated from the remaining nodes. These five questions are a part of a sequence of similar questions, focusing on vocational coursework. Specifically, the question inquires whether “In your most recent or current VOCATIONAL course, how much emphasis did/does your teacher place on the following objectives?” and the specific objectives are listed in Table 3. It can be seen that questions “F1S33A”–“F1S33E” reflect different aspects of knowledge and analytical ability that a student should acquire from a vocational course, and therefore it is reasonable that they form a tight cluster. Similar clustering patterns can be observed in other parts of the graph, for example, serial “F1S7”, serial “F1S8”, serial “F1S12”, serial “F1S25”, etc.

Figure 6.

Layout of the network estimated by the proposed probit graphical model. The nodes represent the survey questions labeled by their code. The area of a node is proportional to its degree and the width of a link is proportional to the magnitude of the corresponding partial correlations. The red lines represent positive associations, while the light green lines negative ones.

Table 3.

Objectives in survey questions “In your most recent or current vocational course, how much emphasis did/does your teacher place on the following objectives?”.

F1S33A	Teaching you skills you can use immediately
F1S33B	Teaching you facts, rules, and steps
F1S33C	Helping you understand how scientific ideas and mathematics are used in work
F1S33D	Thinking about what a problem means and the ways it might be solved
F1S33E	Helping you to understand mathematical and scientific ideas by helping you to manipulate physical objects (tools, machines, lab equipment)

Next, we focus on broad patterns revealed by the model, as depicted in Figure 6. The upper right corner captures relationships between serial questions broadly related to coursework (F1S22–F1S25) in various disciplines (mathematics, science, English, computer education), whereas in the lower left corner there are questions related to overall attitude and study patterns regarding mathematics and science classes (F1S26–F1S32). It is interesting to observe that the model does not discover any relationships between these two question clusters. In the center of the plot we find questions related to various life aspects and being successful/accomplishing them (F1S46) which is negatively associated with a cluster of questions related to working hard in school for good grades (F1S11). In the center, we also find a cluster of serial questions related to different ways of interacting with friends (F1S44) which is negatively correlated to questions related to students awards (F1S8). In the upper left corner we see the serial cluster on grades performance (F1S39) which is also negatively correlated with some of the questions related to amount of coursework in various subjects (F1S22 and F1S24). Finally, in the bottom right corner we encounter questions related to school attendance and attitude towards it (F1S10, F1S12).

Overall, the model reveals interesting and informative patterns, much more so than its Gaussian counterpart shown in Figure 7.

Figure 7.

Layout of the estimated network by the graphical lasso algorithm. The nodes represent the survey questions labeled by their code. The area of a node is proportional to its degree and the width of a link is proportional to the magnitude of the corresponding partial correlations. The red lines represent positive associations, while the light green lines negative ones.

Next, we examined pairs of questions exhibiting the largest positive partial correlations (based on the theory of Gaussian graphical models, the partial correlation of variables j and j′ is defined as ${\rho }_{j,j^{\prime }}=-{\omega }_{j,j^{\prime }}∕\sqrt{{\omega }_{j,j}{\omega }_{j^{\prime },j^{\prime }}}$). The results are shown in Table 4. Among the top five ones, four pairs correspond to serial questions. The only exception is pair “F1S44D—F1S43”, although it inquires about extra reading, outside school. Analogously, Table 5 lists the pair of questions exhibiting the strongest negative partial correlations. Note that question pairs “F1S8F—F1S8A”, “F1S15B—F1S15A”, “F1S16B—F1S16D” are composed of two opposite questions. It is interesting to observe that the model identifies the pair `F1S10B—F1S12B”, which can be interpreted that although students may skip class often they do not feel good about their action. A similar negative partial correlation is present in pair “F1S10A—F1S12A” that addresses a “coming to school late” issue. Overall, the proposed model identifies strong clustering patterns in the questions being asked in this survey, which primarily correspond to series of related in intent and purpose questions, thus indirectly validating its usefulness.

Table 4.

List of pairs of questions with strongest positive partial correlations.

Connection	Partial Correlation	Description
F1S44D—F1S43	0.617981	F1S44D: How often do you spend time on reading for pleasure?
		F1S43: How much additional reading do you do each week on your own outside of school - not in connection with schoolwork?
F1S45A—F1S45B	0.443995	F1S45A: During the school year, how many hours a day do you on weekdays?
		F1S45B: During the school year, how many hours a day do you on weekends?
F1S36E1—F1S36E2	0.416786	F1S36E1: How much time do you spend on History homework in school each week?
		F1S36E2: How much time do you spend on History homework out of school each week?
F1S44E—F1S44F	0.398257	F1S44E: How often do you spend time on going to the park, gym, beach, or pool outside of school?
		F1S44F: How often do you spend time on playing ball or other sports with friends outside of school?
F1S12D—F1S12E	0.388861	F1S12D: How often do you feel it is “OK” for you to cheat on tests?
		F1S12E: How often do you feel it is “OK” for you to copy someone else's homework?

Table 5.

The list of pairs of questions with strongest negative partial correlations.

Connection	Partial Correlation	Description
F1S8F—F1S8A	−0.376025	F1S8F: Did you win any special recognition for good grades or honor roll?
		F1S8A: Haven't you won any awards or received recognition?
F1S10B—F1S12B	−0.281428	F1S10B: How many times did you cut or skipped classes?
		F1S12B: How often do you feel it is “OK” for you to cut a couple of classes?
F1S15B—F1S15A	−0.259550	F1S15B: If does anyone from school called my home on your last absence from school.
		F1S15A: The school did not do anything on your last absence from school.
F1S10A—F1S12A	−0.216677	F1S10A: How many times were you late for school in the first half of the current school year?
		F1S12A: How often do you feel it is “OK” for you to be late for school?
F1S16B—F1S16D	−0.214770	F1S16B: When you came back to school after your last absence, other students helped you catch up on the work you missed.
		F1S16D: When you came back to school after your last absence, you didn't need to catch up on work.

5 Summary and Discussion

Ordinal data occur often in practice and are usually treated as continuous for most analyses, including estimating dependencies between the variables under consideration by fitting a graphical model. Our proposed model, explicitly takes into account the ordinal nature of the data in the graphical modeling step. While direct computation for the proposed model is expensive, the approximations employed allow us to efficiently fit high-dimensional models. On those datasets that the model can be fitted directly, our numerical results show that the approximations we make result in a minimal loss of accuracy. We leave the theoretical properties of both the exact estimator and its approximate version as a topic for future work.

The method proposed in this paper can also be extended to fit the multivariate ordinal regression model, where multiple ordinal responses are fitted on a number of covariates. Specifically, suppose W_j1, …, W_jmj are the covariates associated with the jth response. Following the notation in Section 2.1, let X_j denote the jth response, which is an ordinal variable, and Z_j the corresponding latent continuous variable. We may assume Z_j = α_j0 + α_j1W_j1 + … + α_jmjW_jmj + ∊_j, where α_j0 is the intercept, and α_j1, …, α_jmj are regression coefficients. In addition, we assume that ∊₁, …, ∊_p jointly follow a Gaussian distribution with mean zero and covariance matrix Σ = Ω⁻¹. To estimate the regression coefficients, we may modify the M-step in Section 2.2 to estimate Ω and α_jℓ's simultaneously. Rothman et al. (2010) discussed a similar problem as the modified M-step, and the algorithm there can be directly applied.