Bi-Component T₂* Analysis of Bound and Pore Bone Water Fractions Fails at High Field Strengths

Abstract

Osteoporosis involves degradation of bone’s trabecular architecture, cortical thinning, and enlargement of cortical pores. Increased cortical porosity is a major cause of the decreased strength of osteoporotic bone. The majority of cortical pores, however, are below the resolution limit of MRI.

Recent work has shown that porosity can be evaluated by MRI-based quantification of bone water. Bi-exponential T₂* fitting and adiabatic inversion preparation are the two most common methods purported to distinguish bound and pore water in order to quantify matrix density and porosity.

To assess the viability of T₂* bi-component analysis as a method for quantifying bound and pore water fractions, we have applied this method to human cortical bone at 1.5T, 3T, 7T, and 9.4T, and validated the resulting pool fractions against μCT-derived porosity and gravimetrically-determined bone densities. We also investigated alternative methods: 2D T₁–T₂* bi-component fitting by incorporating saturation-recovery, 1D and 2D fitting of CPMG echo amplitudes, and deuterium inversion recovery.

Short-T₂* pool fraction was moderately correlated with porosity (R² = 0.70) and matrix density (R² = 0.63) at 1.5T, but the strengths of these associations were found to diminish rapidly as field strength increases, falling below R² = 0.5 at 3T. Addition of the T₁ dimension to bi-component analysis only slightly improved the strengths of these correlations. T₂*-based bi-component analysis should therefore be used with caution.

Performance of deuterium inversion-recovery at 9.4T was also poor (R² = 0.50 versus porosity and R² = 0.46 versus matrix density). CPMG-derived short-T₂ fraction at 9.4T, however, is highly correlated with porosity (R² = 0.87) and matrix density (R² = 0.88), confirming the utility of this method for independent validation of bone water pools.

1. Introduction

Osteoporosis is a common bone disease which involves deterioration of trabecular bone architecture (1) and thinning and enlargement of pores in cortical bone (2). This increased cortical porosity is a major cause of the impaired strength of osteoporotic bone (3,4). Measurement of cortical porosity is, therefore, of great interest for assessment of bone health.

Micro-computed tomography (μCT), due to its exquisite spatial resolution on the order of microns, is a gold-standard method for direct visualization of pores and quantification of cortical porosity (5,6), but is applicable only ex vivo, and segmentation of pore spaces depends on selection of an appropriate intensity threshold. Dual-energy x-ray absorptiometry (DXA) is a standard in vivo screening tool that measures apparent areal bone mineral density, which varies inversely with porosity as long as mineralization density is constant. This density is ‘apparent’ in that it represents mineral per total bone area, including both matrix and pore spaces. DXA density is therefore affected both by changes in porosity (mesoscopic scale) and tissue mineralization (microscopic scale). Due to its two-dimensional nature, it is also affected by bone thickness. Quantitative computed tomography (QCT) adds a third dimension, but is still subject to the other limitations of DXA.

NMR and MRI methods have recently been used to study bone density and porosity. Unfortunately, the majority of cortical pores are smaller than the spatial resolution achievable by in vivo MRI, necessitating other approaches that do not rely on resolution of pore spaces. The NMR ¹H signal in bone arises from three major pools. Water in bone is partitioned into two compartments: mobile water within the Haversian and lacunocanalicular pore system (7), and water which is hydrogen-bonded to bone matrix collagen (8–10). The third pool consists of protons in collagen and mineral (11).

As bone substance is lost and pore spaces expand, pore water concentration increases (9,10,12–17). Bound water concentration, which should parallel collagen density (8), is proportional to bone density and, therefore, is inversely proportional to porosity (9,10,12–14,18–22). Total water concentration, the sum of bound and pore water concentrations, is also weakly associated with porosity (9,13,16,23–26).

The three ¹H signal pools can be separated based on their T₂ relaxation times (8): pore water has T₂ > 1 ms, bound water has T₂ ~ 300–400 μs, and collagen has T₂ < 60 μs. These components are shown in a schematic T₂ spectrum (Figure 1). Due to its extremely short transverse relaxation time, the collagen and mineral ¹H signal is beyond the reach of clinical MRI hardware, even with specialized solid-state pulse sequences.

Figure 1.

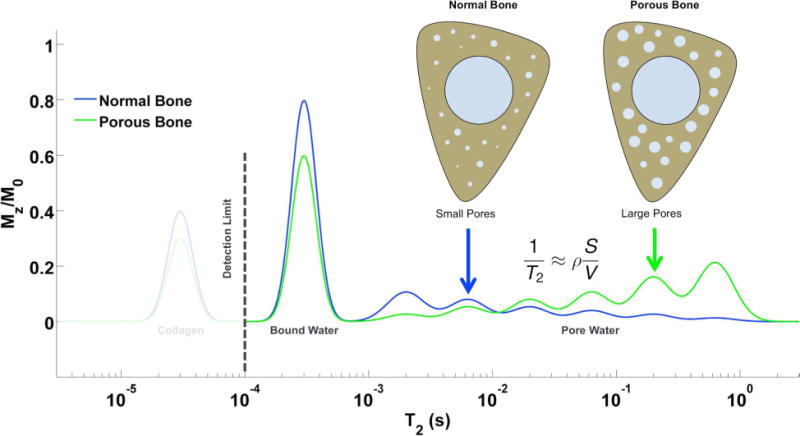
Cartoon T₂ relaxation spectrum diagramming the three major ¹H NMR signal pools in bone. Pore water has T₂ > 1 ms, while bound water has T₂ ~ 300–500 μs. Collagen signal, at T₂ ~ 40–60 μs, is below the detection limit at clinical field strengths, but becomes visible using micro-imaging and spectroscopic hardware. As porosity increases, collagen and bound water decrease, while pore water increases and shifts to longer T₂ values due the smaller surface-to-volume ratio of enlarged pores. This figure is adapted from Li et al. (16).

There are two main NMR methods in routine use for distinguishing between bound and pore water: bi-exponential T₂* fitting and T₂-selective magnetization preparation. The former involves acquisition of signals at several TEs and fitting of a sum of two weighted exponential functions to the resulting decaying signals. The weights of each exponential have been hypothesized to represent bound and pore water signal amplitudes (12,22). The latter method uses an adiabatic RF pulse to selectively invert long-T₂ pore water magnetization while saturating short-T₂ bound water magnetization (13,18,21,27–29). After a specific inversion-recovery time (TI), pore water’s longitudinal magnetization (M_z) will be nulled while bound water magnetization will have recovered to M_z > 0.

T₂* of pore water, however, is shortened due to strong internal magnetic field gradients arising from the difference in magnetic susceptibility between water and bone tissue (∆χ ~ 2.5 ppm SI) (30). The reduced separation between bound and pore water T₂* values, illustrated in Figure 2, complicates separation via bi-component fitting, which, as a form of inverse Laplace transformation, is an ill-posed problem (31). Because the strength of the induced magnetic fields increases linearly with field strength, this effect becomes more severe at higher field strengths.

Figure 2.

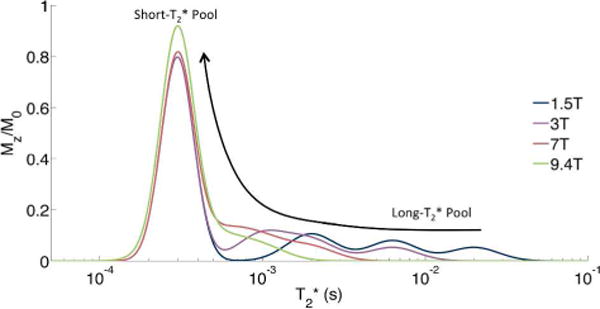
Cartoon ¹H NMR T₂* relaxation spectrum of bone at multiple field strengths. Note that as field strength increases, the T₂* of pore water becomes shorter and merges with the short- T₂* bound water pool.

To assess the viability of T₂* bi-component analysis as a method for quantifying bound and pore water fractions in humans, we have scanned a set of human cortical bone specimens at 1.5T, 3T, 7T, and 9.4T, and validated bi-exponential fitting of the resulting FIDs against μCT-derived porosity and gravimetrically-determined bone densities. These specimens are expected to vary widely in bone density and porosity. We also compared T₂* bi-component analysis at these four field strengths to T₂ bi-exponential fitting of CPMG echo amplitudes (8) and deuterium inversion-recovery NMR (9) at 9.4T.

2. Materials and Methods

2.1. Specimen Source and Preparation

The tissue examined consisted of 15 specimens of cortical bone taken from the tibial mid-shaft of previously frozen male and female human donors, aged 27–97 years (National Disease Research Interchange, NDRI). Donors with bone demineralizing disorders were excluded; only age-related structural bone loss is expected. A 4-mm slice was cut from each thawed tibia with a rotating blade at the region of maximum cortical bone thickness, 38% of the length of the tibia from the medial malleolus to the medial condyle. A rectangular beam was cut from the longest of the three faces of the roughly triangular bone slice, and trimmed to fit into a 5-mm NMR tube. The direction of the long axis of the bone was indicated on the end of each beam by cutting a notch parallel to the bone’s axis. Specimens were stored individually in phosphate-buffered saline.

2.2. ¹H NMR Spectroscopy

1.5T, 3T, and 7T experiments were performed on whole-body human MRI scanners (Siemens, Erlangen, Germany) using custom-built ¹H-free solenoidal radiofrequency (RF) coils (to eliminate signal contamination from the coil), 10 mm in diameter and 25 mm in length. Each coil was constructed of two parallel six-turn windings of copper wire on a polytetrafluoroethylene (PTFE) tube, mounted to a PTFE board, and tuned and matched capacitively. Coils were connected to the transmit/receive interface box (Stark Contrast, Erlangen, Germany) using PTFE-dielectric and -insulated coaxial cable. At 9.4T, experiments were performed on a vertical-bore NMR spectrometer and micro-imaging system (Avance III, Bruker, Billerica, MA) using a standard commercially-available 5-mm broadband inverse (BBI) probe with a 1-axis gradient.

Each bone was removed from its storage solution, gently blotted dry, placed quickly into a small, air-tight NMR tube with minimum interior air volume to prevent evaporation of free water, and scanned with a saturation-recovery (SR) pulse sequence, shown in Figure 3a. Longitudinal magnetization was saturated by a train of 90° pulses followed by spoiler gradients, and the partially-recovered magnetization was measured after each of 12 saturation recovery times (T_SR) arrayed logarithmically from 3 ms to 6 s. 32 signal acquisitions were averaged, and scan time for this sequence was 6 min.

Figure 3.

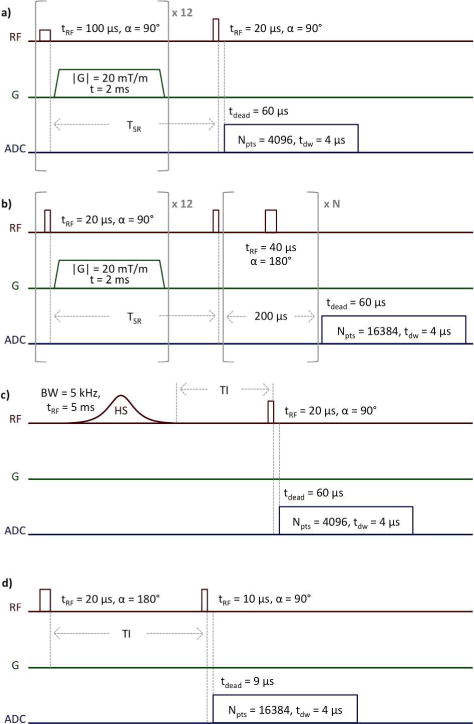
¹H SR-FID (a), SR-CPMG (b), SIR-FID (c), and ²H IR-FID (d) NMR pulse sequences. In (a) and (b), the saturation-recovery time, T_SR, is arrayed logarithmically from 3 ms to 6 s in 12 steps. In (b), the number of refocusing pulses, N, is arrayed logarithmically from 0 to 5000 in 20 steps.

An equation consisting of the sum of two decaying exponentials plus a noise offset term,

$$f(t)=M_S\exp \left(\frac{-t}{T_{2S}^{\ast }}\right)+M_L\exp \left(\frac{-t}{T_{2L}^{\ast }}\right)+n,$$ [1]

was fitted using non-linear least squares (NLLS) to the magnitude free induction decay (FID) data after the longest T_SR. Short-T₂* fraction is given by M_S/(M_S+M_L), and the corresponding short T₂* relaxation time by T_2S*. Similarly, long-T₂* fraction is given by M_L/(M_S+M_L) and the long T₂* relaxation time by T_2L*.

Two-dimensional bi-component T₁–T₂* fitting, which has been shown to improve accuracy (32), was also performed by fitting a similar equation,

$$f(T_{SR},t)=M_S\left(1-\exp \left(\frac{-T_{SR}}{T_{1S}}\right)\right)\exp \left(\frac{-t}{T_{2S}^{\ast }}\right)+M_L\left(1-\exp \left(\frac{-T_{SR}}{T_{1L}}\right)\right)\exp \left(\frac{-t}{T_{2L}^{\ast }}\right)+n,$$ [2]

to the set of saturation recovery-prepared magnitude FIDs. Here, the short-T₂* fraction is given by M_S/(M_S+M_L), the short T₂* relaxation time by T_2S^*, and the short- T₂* pool’s T₁ relaxation time by T_1S; fractions and relaxation times are analogous for the long- T₂* pool. All reconstruction and fitting was performed in Matlab (Mathworks, Natick, MA).

Additionally, taking advantage of the lack of specific absorption rate (SAR) limitations and the availability of high-powered hardware at 9.4T, each bone was scanned using a SR-prepared Carr-Purcell-Meiboom-Gill (SR-CPMG) pulse sequence (33), shown in Figure 3b. T_SRs were arrayed identically to the SR-FID sequence, and the number of refocusing pulses, N, was arrayed logarithmically from 0 to 5000 in 20 steps, and one signal acquisition was performed. Scan time for this sequence was 29 min. Analysis was performed similarly to the 1D and 2D bi-exponential fitting of FIDs, with FIDs simply substituted for arrays of echo amplitudes, using the following equations:

$$f\left(TE\right)=M_S\exp \left(\frac{-TE}{T_{2S}}\right)+M_L\exp \left(\frac{-TE}{T_{2L}}\right)+n$$ [3]

and

$$f\left(T_{SR},TE\right)=M_S\left(1-\exp \left(\frac{-T_{SR}}{T_{1S}}\right)\right)\exp \left(\frac{-TE}{T_{2S}}\right)+M_L\left(1-\exp \left(\frac{-T_{SR}}{T_{1L}}\right)\right)\exp \left(\frac{-TE}{T_{2L}}\right)+n.$$ [4]

Finally, each bone was scanned with a single adiabatic inversion recovery-prepared FID (SIR-FID) pulse sequence, shown in Figure 3c, at all fields. Adiabatic inversion pulses may be designed with both long duration and broad bandwidth, and are thus T₂-selective, rather than T₂*-selective. Inversion time (TI) was stepped from 10 to 270 ms at TR = 300 ms. All other parameters were identical to SR-FID. The magnitude FID from each TI was processed by fitting a sum of two exponentials in a similar manner as 1D FID data, but with the relaxation times of the two pools instead set as fixed constants equal to the fitted values from 2D T₁–T₂* bi-component analysis. The TI at which the long-T₂* pool fraction was minimized was selected for each bone as the optimal inversion-nulling time for pore water signal.

2.3. ²H NMR Spectroscopy

Labile protons, consisting predominantly of bound and pore water, were exchanged with ²H by immersion in deuterium oxide (D₂O). Bones were blotted dry and placed in a 20-fold volume excess of 99.9% purity D₂O-saline for six days, and were removed and transferred to a container with the same volume of fresh D₂O-saline on days two and four to ensure full exchange.

Following full deuterium exchange, specimens were scanned using ²H inversion-recovery (IR) (9). A ²H spectrum of bone at 9.4T consists of a narrow central peak with long T₁ flanked by a doublet with short T₁. The narrow single peak corresponds to bone water residing in the pore system of bone and whose motion is unimpeded by interaction with bone collagen. The doublet peak with splitting of 4.8 kHz results from quadrupole interaction of the deuteron with the electric field gradient along the O-²H bond in bone water that is hydrogen-bonded to matrix collagen (34–36).

The pulse sequence and relevant parameters are shown in Figure 3d. TI was stepped in 10 ms increments in order to capture the null point of the narrow pore water peak, the post-acquisition delay was 1 s to ensure return to equilibrium longitudinal magnetization, and 48 signal acquisitions were averaged. Scan time for this sequence was 21 minutes. A fully relaxed spectrum was also acquired. The integral of the fully-relaxed spectrum represents total bone water, the integral of the spectrum with the narrow pore water signal nulled represents bound water only, and the difference between these two represents pore water only. Bound and pore water fractions were calculated by dividing the integral of the pore water-nulled spectrum or the difference spectrum, respectively, by the integral of the fully relaxed spectrum.

2.4. μCT Imaging

Bone specimens were scanned on a Scanco μCT35 scanner (Scanco, Brüttisellen, Switzerland) at 18.5-μm isotropic resolution. Bone exteriors were masked by 3D active snakes using the ITK-SNAP software package (37), and pores were segmented from this masked 3D image by thresholding. Porosity was calculated as pore (segmented) volume divided by total (masked) volume.

2.5. Gravimetry

Fully hydrated bone specimens were removed from liquid, gently blotted dry, and weighed to establish their initial mass. The bones were then placed in tared crucibles and dried at 105° C for 110 hr to remove all bound and pore bone water. Completion of drying was verified by no change in mass over a 24-hour period. Bones were again weighed and the dry mass was recorded. The bones were then incinerated at 600° C for 30 hr to burn off all organic matrix, and the residual ash was weighed again. Total water mass was then obtained as the difference between initial and dry mass, total matrix mass was the difference between dry and ash mass, and total mineral mass was equal to the ash mass. These masses, divided by total bone volume obtained from the μCT bone exterior mask, yield total water, matrix, and mineral densities.

3. Results

3.1. ¹H NMR Spectroscopy

The measured NMR pool fractions by bi-exponential fitting, along with validation measurements by μCT, ²H IR NMR, and gravimetry, are shown in Table 1. Short- T₂* fraction at 1.5T was 69.6±12.7% (37.7–82.6%) (mean ± standard deviation and range (min-max)). At 3T, the mean short- T₂* fraction was similar to 1.5T at 68.1%, but the standard deviation and range were larger, at 21.9% and 17.0–98.6%, respectively. Short- T₂* fractions at 7T and 9.4T were 82.3±14.0% (49.8–99.9%) and 55.1±28.7% (18.6–98.3%).

Table 1.

Bone properties measured by μCT, ²H IR, gravimetry, SR-CPMG NMR at 9.4T, SR-FID NMR at four field strengths, and SIR-FID NMR at three field strengths. Bone labels are composed of the two-digit age and one-letter gender of the donor.

Bone	27F	30F	37M	49M	53M	53F	65F	69M	74F	75M	82F	83F	83M	93M	97F	Mean	StDev
μCT Porosity	3.70	3.06	4.77	4.08	5.56	3.78	5.57	5.18	20.38	4.51	17.31	33.53	4.94	5.18	12.92	8.96	8.61
2H IR Bound Fraction (%)	72.1	68.8	61.7	77.9	60.7	72.0	75.6	68.9	50.4	62.1	56.2	48.7	58.8	56.0	49.4	62.62	9.56
Mineral Density (mg/cc)	1197	1208	1163	1207	1159	1192	1161	1172	930.7	1175	1015	751.2	1159	1219	1058	1118	129.6
Organic Density (mg/cc)	525.2	520.7	494.9	514.3	513.1	527.5	513.0	511.2	472.4	510.3	479.0	437.0	520.1	515.2	501.2	503.7	24.3
Water Density (mg/cc)	287.4	292.3	316.2	281.4	294.6	294.8	297.3	302.7	405.0	298.8	394.5	435.6	317.2	318.7	356.2	326.2	48.4
9.4T Short T1–T2 Fraction (%)	86.6	86.2	78.4	83.8	82.9	86.6	81.2	79.3	62.4	80.1	66.4	55.4	77.3	77.6	71.4	77.0	9.3
9.4T Short T2 Fraction (%)	87.4	86.7	78.9	83.9	83.4	87.4	82.3	79.6	64.7	80.6	68.1	59.0	77.8	78.5	73.1	78.1	8.5
1.5T Short T2* Fraction (%)	82.6	82.4	72.2	77.1	75.0	80.7	75.5	72.9	50.5	75.2	74.7	37.7	58.6	68.9	59.5	69.6	12.7
3T Short T2* Fraction (%)	80.0	81.0	72.5	73.2	71.2	94.5	76.9	75.2	37.8	75.6	98.6	17.0	62.9	67.2	37.2	68.1	21.9
7T Short T2* Fraction (%)	87.3	91.7	86.4	87.3	83.6	88.5	84.9	89.1	58.1	94.0	90.8	64.6	99.9	78.2	49.8	82.3	14.0
9.4T Short T2* Fraction (%)	19.4	95.0	59.4	79.4	95.5	18.6	43.0	49.0	38.8	80.7	31.2	60.7	21.8	98.3	35.2	55.1	28.7
1.5T Short T1–T2* Fraction (%)	82.6	81.9	71.9	76.8	75.2	81.0	76.2	73.5	51.1	75.1	64.4	41.5	64.0	69.5	62.3	69.8	11.6
3T Short T1–T2* Fraction (%)	80.3	80.5	73.7	73.2	72.0	57.1	76.9	75.9	49.1	75.2	44.9	37.3	64.5	69.0	55.1	65.6	13.7
7T Short T1–T2* Fraction (%)	84.3	85.4	83.4	85.9	82.9	85.4	83.4	86.0	58.0	87.6	81.6	52.4	33.1	75.6	61.5	75.1	16.2
9.4T Short T1–T2* Fraction (%)	14.3	91.4	62.7	79.1	72.6	16.1	49.5	53.8	39.0	79.6	33.8	32.3	33.2	34.4	45.9	49.2	23.6
1.5T Optimal TI (ms)	70	70	80	80	70	60	90	100	110	100	130	120	90	90	110	91.3	20.3
3T Optimal TI (ms)	50	50	80	60	60	70	80	90	110	80	110	130	100	70	80	81.3	23.3
7T Optimal TI (ms)	140	180	180	160	140	130	160	200	160	220	190	170	240	160	180	174	30

Short- T₂* pool relaxation times were 401±119 (301–762) μs, 389±116 (249–768) μs, 368±76 (302–613) μs, and 302±150 (125–615) μs at 1.5T, 3T, 7T, and 9.4T, respectively. Long- T₂* relaxation times decreased more dramatically at higher field strength: 4110±1230 (1840–7170) μs, 4350±8570 (980–35300) μs, 1300±420 (380–1860) μs, and 886±525 (410–2160) μs at 1.5T, 3T, 7T, and 9.4T, respectively. Short- and long- T₂* relaxation times and short- T₂* pool sizes are plotted in Figure 4. If one outlier, 35300 μs, is excluded from this mean and standard deviation at 3T, the long- T₂* relaxation time becomes 2150±540 (980–2940) μs. This outlier was a result of poor fitting due to oscillations in the magnitude FID; this phenomenon, which appeared in several specimens at multiple fields, will be discussed in detail in the discussion section.

Figure 4.

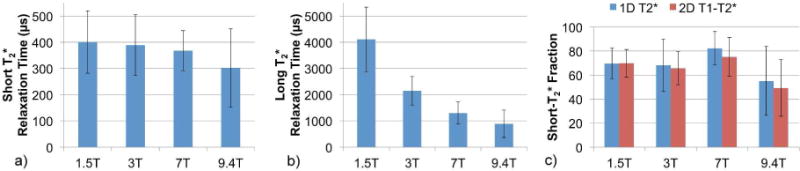
Bar graphs showing trends in average (a) short- T₂* relaxation times and (b) long- T₂* relaxation times by 1D T₂* bi-component fitting of FIDs, and (c) short- T₂* fractions by 1D T₂* and 2D T₁–T₂* bi-component fitting at four field strengths. Error bars indicate standard deviation.

Addition of the T₁ dimension reduced the standard deviations of 2D short- T₂* fractions relative to 1D, particularly at 3T, but average pool fractions and T₂* relaxation times were unchanged. T₁ relaxation times of the short- T₂* fractions were 82.6±10.4 (62.2–97.3) ms, 145±25 (103–186) ms, 400±68 (206–496) ms, and 358±240 (93–565) ms at 1.5T, 3T, 7T, and 9.4T, respectively, and T₁s of the long- T₂* fractions were 651±273 (379–1210) ms, 880±281 (465–1470) ms, 1790±470 (898–2470) ms, and 1300±370 (751–1940) ms.

Short-T₂ fractions by bi-component T₂ fitting of CPMG echo amplitudes at 9.4T were generally larger than short- T₂* fractions by FID fitting: 1D short-T₂ fraction was 78.1±8.5% (59.0–87.4%), and 2D short-T₂ fraction was 77.0±9.3% (55.4–86.6%). Relaxation times for short- and long-T₂ fractions were 540±150 (430–960) μs and 77±53 (22–220) ms, respectively, for 1D fitting. Short-T₂ relaxation time for 2D fitting was unchanged at 540±150 (430–980) μs, while long-T₂ relaxation time was 55±38 (17–161) ms. The corresponding T₁ relaxation times of short- and long-T₂ fractions obtained by 2D fitting were 480±80 (320–560) ms and 1210±300 (880–1910) ms, respectively.

Average signal to noise ratios (SNRs), defined as the magnitude of the first data point of the FID signal divided by the standard deviation of the magnitude of the final 25 data points, were 4130, 3040, 15600, and 34300 at 1.5T, 3T, 7T, and 9.4T, respectively. The noise terms, n, in Equations 1 and 2 for 1D and 2D bi-component T₂* fitting were on the order of 0.1% of total signal (M_S+M_L) or less at all field strengths, and were therefore inconsequential. In Equations 3 and 4 for 1D and 2D bi-component T₂ fitting of CPMG data, the noise terms, n, were 2–3% of total signal. This larger value of n is a result of the overly simple assumption of two discrete pools; the presence of a small fraction of signal that has T₂ much longer than the fitted long-T₂ value appears to the bi-component fitting method as a non-zero noise level.

Three example 2D relaxation spectra of a bone specimen taken from a 37 year old male donor are shown in Figure 5: T₂*–T₂ and T₁–T₂ spectra at 9.4T, and a T₁–T₂* spectrum at 3T. Relaxation times given in the labels next to each pool represent the centroid of each pool. T₂ values were distributed across three orders of magnitude (horizontal axis in Figure 5a and 5b), while T₂* values spanned less than two (vertical axis in Figure 5a and horizontal axis in Figure 5c).

Figure 5.

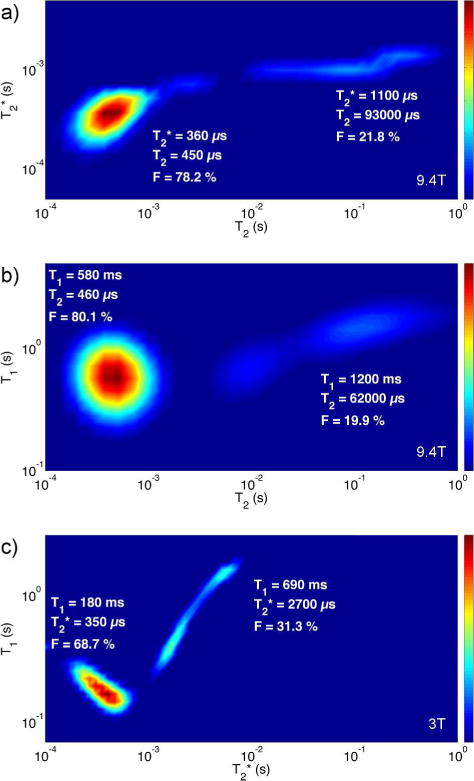
2D T₂*–T₂ and T₁–T₂ ¹H relaxation spectra at 9.4T, and 2D T₁–T₂* relaxation spectrum at 3T, generated using the MERA software package (43). Spectra are from a bone specimen taken from a 37 year old male donor. The T₂*–T₂ spectrum is generated from CPMG data, the T₁–T₂ spectrum from SR-CPMG data, and the T₁–T₂* spectrum from SR-FID data.

Optimal inversion times were 91.3±20.3 (60–130) ms at 1.5T, 81.3±23.3 (50–130) ms at 3T, and 174±30 (130–240) ms at 7T. These TIs resulted in short- T₂* signal fractions of 99.3±0.6% (97.7–100%) at 1.5T, 99.2±0.6% (98.1–100%) at 3T, and 99.7±0.2% (99.3–100%) at 7T.

3.2. ²H NMR Spectroscopy

Deuterium-exchanged ²H IR bound water fraction was 62.6±9.6% (48.7–77.9%). Mean T₁ of the bound water pool was 11.2±1.7 (9.8–15.9) ms, and mean T₁ of the pore water pool was 197±42 (129–282) ms. The mean inversion-recovery time to achieve nulling of the central pore water peak was 142±31 (92–206) ms. An example plot in Figure 6 shows the fully relaxed, pore water-nulled, and subtracted pore water-only spectra taken from the specimen from a 27 year old female donor.

Figure 6.

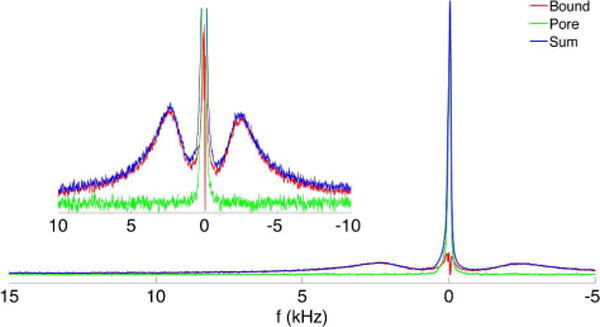
²H spectra showing the bound and pore D₂O components (inset is magnified vertically and truncated). Pore water (narrow central peak in green) is calculated by subtracting the bound water spectrum obtained by inversion-recovery nulling of pore water (the split peaks shown in red) from the fully relaxed spectrum (shown in blue). This spectrum is taken from a specimen from a 27 year old female donor with the osteonal axis orthogonal to B₀. Splitting of 4.8 kHz is observed, consistent with the orientation-dependent splitting observed by Ong et al. (9).

3.3. μCT and Gravimetry

Porosity measured from μCT image segmentation was 8.96±8.61% (3.06–33.53%). Gravimetric mineral density was 1118±130 (751–1219) mg/cc and organic matrix density was 503.7±24.3 (437.0–527.5) mg/cc, consistent with previous observations in porcine femoral cortical bone by Cao et al. (18,38). Total water density, including both bound and pore water, was 326.2±48.4 (281.4–435.6) mg/cc. A matrix of R² values for inter-parameter correlations is given in Table 2. Porosity and matrix density were highly negatively correlated (R² = 0.91), supporting the notion that any increase in porosity occurs at the expense of a loss of matrix volume.

Table 2.

Inter-parameter correlations (R²) of measured bone properties. All correlations are statistically significant (p < 0.05) unless italicized.

	μCT Porosity	Organic Density	1.5T 1D T2* Short- T2* Fraction	1.5T 2D T1–T2* Short- T2* Fraction	3T 1D T2* Short- T2* Fraction	3T 2D T1–T2* Short- T2* Fraction	7T 1D T2* Short- T2* Fraction	7T 2D T1–T2* Short- T2* Fraction	9.4T 1D T2* Short- T2* Fraction	9.4T 2D T1–T2* Short- T2* Fraction	9.4T 1D T2 Short-T2 Fraction	9.4T 2D T1–T2 Short-T2 Fraction
9.4T 2H IR Bound Fraction	0.50	0.46	0.61	0.68	0.46	0.51	0.40	0.40	0.00	0.05	0.67	0.66
9.4T 2D T1–T2 Short-T2 Fraction	0.90	0.89	0.77	0.94	0.50	0.74	0.39	0.35	0.03	0.08	1.00
9.4T 1D T2 Short-T2 Fraction	0.87	0.88	0.77	0.94	0.49	0.72	0.37	0.35	0.02	0.07
9.4T 2D T1–T2* Short- T2* Fraction	0.10	0.02	0.08	0.08	0.01	0.24	0.04	0.14	0.55
9.4T 1D T2* Short- T2* Fraction	0.02	0.00	0.02	0.02	0.00	0.12	0.00	0.11
7T 2D T1–T2* Short- T2* Fraction	0.25	0.16	0.66	0.54	0.47	0.30	0.12
7T 1D T2* Short- T2* Fraction	0.40	0.31	0.42	0.41	0.62	0.31
3T 2D T1–T2* Short- T2* Fraction	0.76	0.61	0.54	0.69	0.26
3T 1D T2* Short- T2* Fraction	0.50	0.44	0.83	0.67
1.5T 2D T1–T2* Short- T2* Fraction	0.84	0.80	0.93
1.5T 1D T2* Short- T2* Fraction	0.70	0.63
Organic Density	0.91

1D short- T₂* pool fraction was moderately negatively correlated with porosity and positively with matrix density at 1.5T (R² = 0.70 and 0.63, respectively), but the strengths of these associations diminished rapidly as field strength increased. In fact, at 9.4T, no statistically significant correlation was observed. Scatter plots displaying 1D short- T₂* pool fractions versus matrix density are shown in Figure 7. In general, addition of the T₁ dimension improved the strengths of these correlations (except at 7T), but this improvement still did not raise the correlations at 9.4T to the level of statistical significance.

Figure 7.

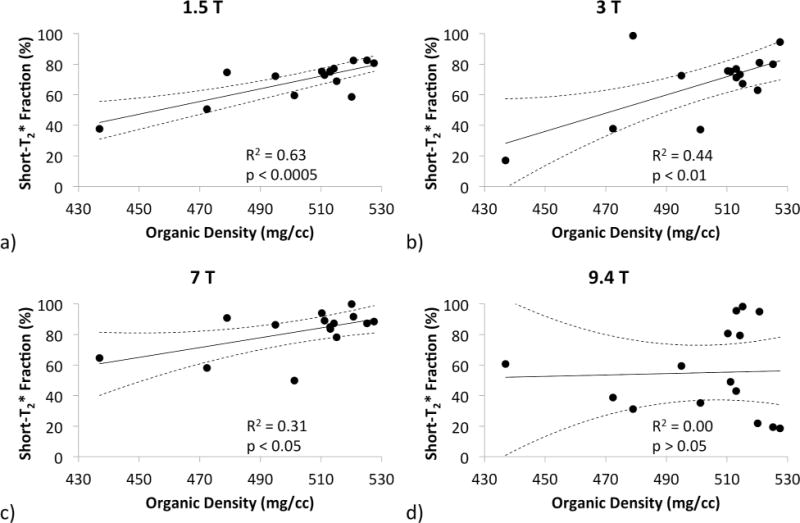
Scatter plots displaying the correlations of the 1D bi-component short- T₂* ¹H signal fraction to organic matrix density measured by gravimetry. Correlations become significantly worse as field strength increases.

Fitted pool fractions by bi-component T₂ fitting of CPMG echo amplitudes at 9.4T were generally better correlated with porosity and matrix density than were those derived from T₂* fitting of FIDs and ²H IR. Coefficients of determination (R²) of short-T₂ fraction by 1D fitting of CPMG echo amplitudes to porosity and matrix density were 0.87 and 0.88, respectively; with the addition of the T₁ dimension, these increased slightly to 0.90 and 0.89, respectively. Bound water fraction by ²H IR, however, was only moderately correlated with porosity (R² = 0.50) and matrix density (R² = 0.46), but correlations of ²H IR bound water fraction with short- T₂* fraction by 1D FID and 2D SR-FID fitting showed the same trend of reduced association as field strength increases.

4. Discussion

Bi-exponential fitting is applicable as long as the as the time constants representative of the two pools are sufficiently separated from one another. Due to the ill-posed nature of the inverse Laplace transform, significant errors may arise in the fitted pool fractions and time constants once the two time constants become similar. Because T₂* of pore water is substantially shortened by dephasing due to internal magnetic field gradients arising from the large susceptibility difference between water and bone tissue (∆χ_v ~ 2.5 ppm SI) (30), resulting in decreased separation of bound and pore water relaxation times, T₂* bi-component fitting of FIDs is inferior to T₂ fitting of CPMG echo amplitudes (8). As field strength increases, these internal magnetic field gradients increase proportionally, and pore water T₂* further decreases, more severely impacting the ability of bi-component fitting of FIDs to distinguish bound and pore water. This is reflected in the reduced strength of the correlations of short- T₂* fractions versus porosity and matrix density as field strength increases. While the results are promising at 1.5T, less than half the variance in matrix density is explained by 1D short- T₂* fraction at 3T. The phase dispersion resulting from the static internal field inhomogeneity is refocused in the CPMG sequence, yielding greater separation in T₂ and improved fitting performance.

The measured short- T₂* component fractions of 69.6% and 68.1% at 1.5T and 3T, respectively, are nearly identical to the 68.5% and 69% measured by Li et al. (39) in bovine bone, but are slightly lower than the 74.4% and 75.9% measured in human bone at these same field strengths. The ages and pore volume fractions of the human bones studied by Li et al., however, are unknown. While Li et al. observed decreases in short T₂* relaxation time from 450 μs to 320 μs, and in long T₂* relaxation time from 7.17 ms to 3.02 ms, at 1.5T compared to 3T, the relaxation times presented here are relatively consistent at these two field strengths. Most importantly, however, no significant differences between 1.5T and 3T short- T₂* fraction are observed in the present results or in either of Li’s measurements.

At 3T and higher fields, oscillations appear in the magnitude FIDs of several bone specimens, presumably resulting from non-water off-resonant spins. Similar oscillations have previously been observed in bone (13) and tendon (19). In many cases, the amplitude of these oscillations is sufficient to disrupt the monotonic decrease of the FID, a condition that is not able to be fitted by a sum of monotonically decaying exponentials. An example of such an oscillatory FID at 7T of a bone specimen from a 53-year-old female donor, with attempted mono-exponential and bi-exponential fits, is shown in Figure 8a. These oscillations appear most regularly in bone from old female donors, who have greater porosity. Although care was taken in the preparation of these samples to remove marrow fat, some may remain trapped in the enlarged pore spaces of osteoporotic cortical bone. A small amount of lipid also exists within cortical bone matrix at the cement line surrounding each osteon (40).

Figure 8.

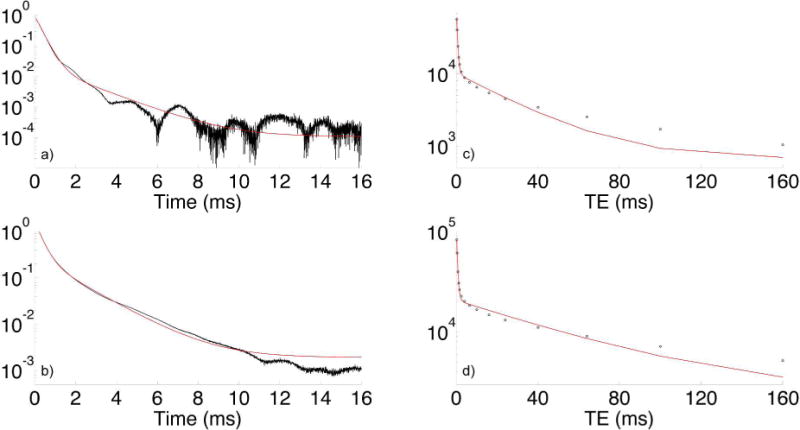
Log-magnitude FID at 7T of a cortical bone specimen from a 53 y/o female donor (a). Note the irregular oscillation of the signal, which causes failure of bi-exponential fitting (green line, R² = 0.999592): 97.4% short- T₂* signal fraction, versus 86.6% by 2D T₁–T₂ bi-exponential fitting at 9.4T. Fat at 7T is 1040 Hz off-resonance. A FID from a 53 y/o male donor (b) not exhibiting these oscillations is also shown for comparison (R² = 0.999901). Similar plots of fitted CPMG echo amplitudes for the same 53 y/o female (c) and male (d) donors are also shown.

Note also that the oscillation in Figure 8 does not appear to have a fixed period; rather, its period varies. If this signal were purely from the methylene resonance of fatty acid triglycerides, a frequency of 1040 Hz would be expected at 7T. It is possible that this oscillation arises from fat that exists in a spatially heterogeneous magnetic field due to susceptibility effects, from other non-fat sources within the same environment, or some combination of these effects (all of which would be refocused by the 180° pulses in CPMG), but further experimentation would be necessary to support any of these speculative hypotheses.

If bone specimens exhibiting these problematic oscillations are retrospectively excluded from correlation analyses (four females ages 53–97 years, one male age 83 years), the R² values describing the association of short- T₂* fraction with μCT porosity and matrix density in the remaining 10 specimens are substantially improved. At 1.5T, 3T, and 7T, R² = 0.87, 0.93, and 0.86, respectively, for correlations with μCT porosity, and 0.83, 0.78, and 0.61 for correlations with matrix density. At 9.4T, none of the samples yielded data judged suitable for fitting. It must be noted that the specimens removed from this analysis were predominantly from the population to which an MRI study of bone composition would be of greatest benefit, and it is not possible to know in advance of such a study whether the resulting data will be usable.

Short-T₂ fraction by 1D bi-component fitting of CPMG echo amplitudes outperforms bi-component fitting of FIDs at all field strengths. This is likely due to the much greater separation of bound and pore water T₂ relaxation times. Whereas the two pools are separated by only one order of magnitude in T₂*, the difference in T₂ is two orders of magnitude. This T₂-based method, however, is not applicable to clinical scanners due to SAR limitations and the requirement of extremely short, high-amplitude 180° refocusing pulses. Nevertheless, the method is suitable for independent determination of bound and pore water fractions.

Addition of a second dimension generally improves the stability and accuracy of bi-component fitting (32). In the present case, addition of T₁ to T₂* by incorporation of saturation-recovery into the sequence improves the strengths of correlations between fitted short- T₂* fraction and validation methods, except at 7T. Though it would be time-prohibitive to incorporate saturation-recovery into a spatially-resolved in vivo bi-component T₂* scanning protocol, this result suggests that methods which take advantage of differences in both T₁ and T₂ (or T₂*) may be superior to those relying solely on T₂*. An example of such an approach is single adiabatic inversion recovery (13,14,28,29,41), which selectively inverts long-T₂ pore water while saturating short-T₂ bound water. As the longitudinal magnetization of pore water (which was also found to have longer T₁ than bound water) passes through its null point, a solid-state imaging readout is performed to selectively image bound water.

The optimal inversion times calculated in this study from SIR-FID experiments are consistent with previous work at 3T by Li et al. (42), but calculation of these results utlizes the same 1D bi-component T₂* fitting method that is the main subject of this work. These TI results, therefore, should be interpreted with the same caution as 1D bi-component T₂* fitting for calculation of bound and pore water fractions in general. Specifically, the value at 1.5T is well supported by strong correlations between 1D short- T₂* fraction and both μCT porosity and gravimetric density, while the value at 3T is somewhat less well supported. Also consistent with Li et al., the long- T₂* fraction is very well-suppressed (to less than ~5%) in a range of approximately ±20 ms surrounding the optimal value for each bone, suggesting that the effectiveness of adiabatic inversion nulling of long- T₂* signal is not significantly decreased by even moderate deviations from the optimal TI.

Also note that the optimal inversion time of 174 ms at 7T is greater than one half of the TR = 300 ms used in this experiment. The spin dynamics, as predicted by the Bloch equations, preclude the possibility of a signal pool being nulled by inversion in steady-state at a TI greater than half the TR. Primarily on the basis of this observation, and secondarily due to the weak correlations between 7T 1D short- T₂* fraction and the two confirmatory measurements, we have no confidence in this calculated optimal TI at 7T.

²H IR was found to be less effective in separating the two water (i.e. deuterium oxide) pools than bi-component T₂ fitting of CPMG data. Bound water fraction obtained by this ²H IR method were considerably less strongly correlated with μCT porosity and matrix density than was short-T₂ fraction by fitting of CPMG amplitudes. Correlations of short- T₂* fraction at 1.5T with these same validation methods were also stronger than those of ²H IR bound water fraction. This unexpectedly inferior performance may be due to a distribution of T₁ values within pore D₂O, thereby preventing complete nulling of the central pore water peak. These results suggest that bi-component fitting of CPMG data is a more reliable NMR-based method for quantification of bound and pore water fractions than ²H IR.

It is important to keep in mind that bi-component analysis, whether based on T₂* or T₂, and whether performed in one or two dimensions, involves one major, and incorrect, assumption: the existence of two pools with discrete relaxation times. T₂ values are instead distributed continuously over several orders of magnitude. While deviations from this assumption may not have severe consequences at low field, where relaxation times of bound and pore water are well-separated and, thus, well-approximated by this two-pool model, the results are more severely impacted as the relaxation times converge. Non-negative least squares methods, such as the MERA software package (43), do not require an assumption of the number of pools, but demand careful regularization to generate a valid relaxation spectrum, which may have any number of peaks. As bound and pore water relaxation times converge, this method often fails to distinguish multiple pools, instead returning a single peak containing 100% of ¹H signal.

The T₁ values obtained for the long- T₂* fraction by 2D T₁–T₂* fitting at 7T and 9.4T (1790 ms and 1300 ms, respectively) are greater than 1200 ms and, therefore, greater than T_SR/5. If these values are accurate, this may cause the magnetization after T_SR = 6 s to be slightly below the equilibrium magnetization. As a consequence, long- T₂* longitudinal magnetization at 7T measured by 1D T₂* fitting may be attenuated by 3.5%, and the resulting 1D short- T₂* fraction may be higher than the actual fraction by approximately 1%. It is unlikely that this effect is responsible for the large (>10%) difference in 1D T₂* pool sizes at 7T compared to other field strengths. Also, the more reliable T₁-T₂ results at 9.4T show a long-T₂ fraction T₁ value of 1210 ms, which is sufficient for assumption of full longitudinal relaxation (T_SR = 5T₁).

This study has several limitations. First, we focus only on cortical bone, whereas in vivo examinations will likely target both cortical and trabecular bone. Though we expect our results to be generalizable (the important difference between trabecular and cortical bone being the predominance of pore versus bound water, respectively), this may benefit from further investigation into the effects of marrow fat. Also, we examine bi-component T₂ fitting of CPMG echo amplitudes at only one field strength, 9.4T. Although this is a widely available field strength for spectroscopic hardware, it would be instructive to examine whether short-T₂ fraction is also sensitive to field strength. Finally, the source of the oscillations in magnitude FIDs remains unclear. Further investigation, possibly by chemical removal of fat or a complementary method to quantify lipid and protein content, would likely yield additional insight into this phenomenon.

5. Conclusion

T₂* bi-component fitting for quantification of bound and pore water fractions performs moderately well at 1.5T, but becomes less reliable as field strength increases. It should therefore be used with caution, and other methods for distinguishing between bone water fractions, namely those based on adiabatic inversion-recovery or dual-band saturation should be considered for use in in vivo examinations. For validation of bound and pore water fractions, bi-component fitting of CPMG echo amplitudes is superior to ²H IR, and is on par with μCT as a method of investigating bone porosity within a single specimen.

Abbreviations

μCT

micro-computed tomography

CPMG

Carr-Purcell-Meiboom-Gill

DXA

dual-energy x-ray absorptiometry

QCT

quantitative computed tomography

TI

inversion time

M_z

longitudinal magnetization

RF

radiofrequency

PTFE

polytetrafluoroethylene

BBI

broadband inverse

SR

saturation-recovery

T_SR

saturation-recovery time

NLLS

non-linear least-squares

FID

free induction decay

SAR

specific absorption rate

SIR

single adiabatic inversion recovery

TI

inversion time

D₂O

deuterium oxide

IR

inversion-recovery

χ_v

volume magnetic susceptibility