Glaucoma progression detection using nonlocal Markov random field prior

Abstract.

Glaucoma is neurodegenerative disease characterized by distinctive changes in the optic nerve head and visual field. Without treatment, glaucoma can lead to permanent blindness. Therefore, monitoring glaucoma progression is important to detect uncontrolled disease and the possible need for therapy advancement. In this context, three-dimensional (3-D) spectral domain optical coherence tomography (SD-OCT) has been commonly used in the diagnosis and management of glaucoma patients. We present a new framework for detection of glaucoma progression using 3-D SD-OCT images. In contrast to previous works that use the retinal nerve fiber layer thickness measurement provided by commercially available instruments, we consider the whole 3-D volume for change detection. To account for the spatial voxel dependency, we propose the use of the Markov random field (MRF) model as a prior for the change detection map. In order to improve the robustness of the proposed approach, a nonlocal strategy was adopted to define the MRF energy function. To accommodate the presence of false-positive detection, we used a fuzzy logic approach to classify a 3-D SD-OCT image into a “non-progressing” or “progressing” glaucoma class. We compared the diagnostic performance of the proposed framework to the existing methods of progression detection.

1. Introduction

Glaucoma is a leading cause of visual impairment and blindness around the world.¹ It is characterized by structural changes in the optic nerve head (ONH) (neuroretinal rim and retinal nerve fiber layer (RNFL) thinning and optic nerve cupping are usually the first visible signs), and visual field defects. Glaucoma is painless and gradually damages the optic nerve, which makes patients not aware of any visual loss until the optic nerve is severely damaged. Untreated it can cause an irreversible vision loss, and hence it is critical to early detect glaucoma and to monitor its progression in order to avoid permanent damage to the ONH.

It has now been more than 150 years since physicians were able to visualize damages in the ONH associated with glaucoma using an ophthalmoscope. However, clinical examination of the ONH remains subjective, qualitative, and often with higher variabilities among observers.²

Over the past three decades, advances in technology for ocular imaging using the optical properties of the optic nerve and RNFL layer have gained widespread use in the diagnosis and management of glaucoma patients. In particular, the Heidelberg retina tomograph (HRT) (Heidelberg Engineering, Heidelberg, Germany), a confocal scanning laser technology, has been commonly used for glaucoma diagnosis since its commercialization 20 years ago.³ Several strategies have been proposed for automated change detection using HRT images. One strategy, the proper orthogonal decomposition,⁴ indirectly utilizes the spatial relationship among voxels by controlling the family-wise type I error rate. The Markov model was used in Ref. 5 to model the inter/intra observations dependency allowing a better glaucoma regression detection rate. However, because HRT imaging is limited to ONH surface topography, it cannot directly measure the RNFL thickness.⁶

In order to overcome this drawback, the three-dimensional (3-D) spectral domain optical coherence tomography (SD-OCT), an optical imaging technique, is now the standard of care for obtaining images of both the ONH and RNFL thicknesses. Several studies have been proposed for glaucoma diagnosis using SD-OCT images. Most of the studies use the peripapillary RNFL thickness measurements (i.e, circular B-scans (3.4-mm diameter, 768 A-scans) centered at the optic disk were automatically averaged to reduce speckle noise)^7–11 or the ONH measurements (e.g, rim area, minimum rim width, etc.)^12–14 which are either provided by the commercially available spectral-domain optical coherence tomographers or manually calculated by experts.¹³ In Ref. 15, authors used the 3-D volume to extract the whole RNFL thickness map instead of the peripapillary RNFL thickness and proposed a variable-size super pixel segmentation to improve the discrimination between early glaucomatous and healthy eyes. In Ref. 16, authors used the RNFL thickness map to identify and to quantify glaucoma defects. Because of the high reproducibility of the SD-OCT, many studies used the peripapillary RNFL measurements for glaucoma change detection.^17–19 In Ref. 20, authors showed that the instrument built-in segmentation software is relatively robust to the image quality and the noise may lower the accuracy of the RNFL layer thickness estimation. However, the detection of glaucoma progression with optical coherence tomography (OCT) remains a challenge because when assessing structural changes over time, it is difficult to discriminate between glaucomatous structural damage and measurement variability.

In this paper, we propose a new strategy for glaucoma progression detection using 3-D SD-OCT images. This strategy is divided into two steps:

• 1.Change detection step: it consists of detecting changes between a baseline image and a follow-up image. In contrast to previous works that use the RNFL thickness measurement provided by commercially available instruments, we consider the whole 3-D volume for change detection. Note that to the best of our knowledge, this is the first time that the whole 3-D SD-OCT volume is considered for glaucoma progression detection. In this work, we propose a fully Bayesian framework for change detection. Bayesian methods are relatively simple and offer efficient tools to include priori through a posteriori probability density functions (PDF). In this work, we propose the use of the Markov random field (MRF) to exploit the statistical correlation of intensities among the neighborhood voxels.²¹ In particular, consider the use of a nonlocal framework for the MRF energy function definition which has been proposed for the image denoising task.²² Indeed, the nonlocal approach has been successfully applied in several image processing applications such as image restoration²³ and image segmentation.²⁴The main idea of the nonlocal approach is to exploit repetitive structures in the image which leads to a multi-model approach using only a single observation. Moreover, in order to develop a noise robust algorithm, we propose the consideration of the change detection problem as a missing data problem where we jointly estimate the noise hyperparameters and the change detection map. Because we used the MRF model with the change detection map as the prior for the change detection map, the optimization step is intractable. Hence, we propose the use of a Monte Carlo Markov chain (MCMC) technique.²⁵
• 2.Classification step: it consists of classifying an SD-OCT image into the “non-progressing” and the “progressing” glaucoma classes using the estimated change detection map. For this, a threshold-based classification method is generally used to accommodate the presence of false-positive detection.⁴ However, the choice of the threshold may affect the robustness of the classification method. We will show that the classification results are better when we use a fuzzy set-based classifier compared with other classifiers.

This paper is divided into four sections. In Sec. 2, the proposed glaucoma change detection scheme is presented. In Sec. 3, we describe the classification scheme. Then, in Sec. 4 results obtained by applying the proposed scheme to real data are presented. Specifically, we compare the diagnostic accuracy, robustness, and efficiency of this novel proposed approach to the two existing progression detection RNFL-based approaches: the artificial neural network classifier (ANN) and the support vectors machine classifier.

2. Change Detection

Let us consider the detection of changes in a pair of 3-D SD-OCT images. The change detection problem is formulated as a multihypotheses testing problem by denoting the “no-change,” “increase change” (i.e., ONH hypertrophy), and “decrease change” (i.e., ONH atrophy) hypotheses as $H_0$, $H_1$, and $H_2$, respectively. We denote by $I_0$ and $I_1$ two images acquired over the same eye at times $t_0$ and $t_1$, respectively ($t_1>t_0$), and co-registered. In this paper, we assume that the noise is additive, white, and normally distributed, whereas the noise-free SD-OCT images follow a gamma distribution. Indeed, the gamma distribution $\mathcal{G}$ is widely used for fitting non-negative data such as the synthetic aperture radar images²⁶ and the high resolution magic angle spinning nuclear magnetic resonance images²⁷ due to its shape hyperparameters $(\alpha >0,\beta >0)$, which allow us to fit spectral data that may present a background.²⁸ The direct model for both images $I_0=[I_0(i)|i=1,\dots ,M]$ and $I_1=[I_1(i)|i=1,\dots ,M]$, where $M$ is the number of voxels, is then given by

$$I_0=X_0+N_0;I_1=X_1+N_1,$$ (1)

where $X_0=[X_0(i)|i=1,\dots ,M]$, $X_0(i)\sim \mathcal{G}({\alpha }_0,{\beta }_0)$, and $X_1=[X_1(i)|i=1,\dots ,M]$, $X_1(i)\sim \mathcal{G}({\alpha }_1,{\beta }_1)$ are the noise-free 3-D SD-OCT ONH images and $N_0=[N_0(i)|i=1,\dots ,M]$, $N_0(i)\sim \mathcal{N}(0,{\sigma }_0)$, $N_1=[N_1(i)|i=1,\dots ,M]$, and $N_1\sim \mathcal{N}(0,{\sigma }_1)$ are the Gaussian additive noises. As no simple expression of the distribution of the difference of two gamma distribution variables exists, we adopted for image an ratioing approach instead of the differencing image approach, which generates a ratio image $R$ resulting in the following direct model:

$$R=\frac{I_0}{I_1}=\frac{X_0+N_0}{X_1+N_1},$$ (2)

where $R=(R(i),i=1\dots M)$. This model is unfortunately intractable. To overcome this problem, we propose a hierarchical change detection framework which consists of estimating the noise-free SD-OCT images ${\widehat{X}}_0$ and ${\widehat{X}}_1$ and then using the image ratio approach for change detection. The new direct model is then given by $R={\widehat{X}}_0/{\widehat{X}}_1$. The gamma ratio distribution is expressed as

$$p(R(i);{\alpha }_0,{\beta }_0,{\alpha }_1,{\beta }_1)=\frac{\mathrm{\Gamma }({\alpha }_0+{\alpha }_1)}{\mathrm{\Gamma }({\alpha }_0)\mathrm{\Gamma }({\alpha }_1)}{R(i)}^{{\alpha }_0-1}{\left(\frac{{\beta }_0}{{\beta }_1}\right)}^{{\alpha }_0}{(R(i)+\frac{{\beta }_0}{{\beta }_1})}^{-({\alpha }_0+{\alpha }_1)}.$$ (3)

Proof.

The PDF of the ratio $R=(X_0/X_1)$ is given by

$$p(R(i);{\alpha }_0,{\beta }_0,{\alpha }_1,{\beta }_1)={\int }_0^{\infty }\mathcal{G}(X_1(i)R(i),{\alpha }_0,{\beta }_0)\mathcal{G}(X_1(i),{\alpha }_1,{\beta }_1)X_1(i)d{X}_1(i)=\frac{{R(i)}^{{\alpha }_0-1}}{\mathrm{\Gamma }({\alpha }_1){\beta }_1^{{\alpha }_1}}\frac{1}{\mathrm{\Gamma }({\alpha }_0){\beta }_0^{{\alpha }_0}}\hspace{0.17em}{(\frac{R(i)}{{\beta }_0}+\frac{1}{{\beta }_1})}^{{\alpha }_0+{\alpha }_1}\mathrm{\Gamma }({\alpha }_1+{\alpha }_0)\times {\int }_0^{\infty }\frac{1}{{(\frac{R(i)}{{\beta }_0}+\frac{1}{{\beta }_1})}^{{\alpha }_0+{\alpha }_1}\mathrm{\Gamma }({\alpha }_1+{\alpha }_0)}{X}_1^{{\alpha }_0+{\alpha }_1-1}\exp (-X_1(i)(\frac{r}{{\beta }_0}+\frac{1}{{\beta }_1}\left)\right)d{X}_1=\frac{\mathrm{\Gamma }({\alpha }_0+{\alpha }_1)}{\mathrm{\Gamma }({\alpha }_0)\mathrm{\Gamma }({\alpha }_1)}{R(i)}^{{\alpha }_0-1}{\left(\frac{{\beta }_0}{{\beta }_1}\right)}^{{\alpha }_0}{(R(i)+\frac{{\beta }_0}{{\beta }_1})}^{-({\alpha }_0+{\alpha }_1)},$$ (4)

since the PDF integrates to 1.

For the sake of simplicity, we assume that ${\alpha }_0={\alpha }_1=\alpha$ and $\beta ={\beta }_0/{\beta }_1$, $p(R(i);\alpha ,\beta )$ is then given by

$$p(R(i);\alpha ,\beta )=\frac{\mathrm{\Gamma }(2\alpha )}{{\mathrm{\Gamma }(\alpha )}^2}r{(i)}^{\alpha -1}{\beta }^{\alpha }{(r(i)+\beta )}^{-2\alpha }.$$ (5)

The change detection is handled through the introduction of change class assignments $Q=[Q(i)|i=1,\dots ,M]$. Hence, the posterior probability distribution of change detection map $Q$ at each voxel location (i.e., $Q(i)$) is given by

$$p(Q_i=H_j|R,\mathrm{\Theta })=\frac{1}{Z}\exp (-U(q_i=H_j|R,\mathrm{\Theta })),$$ (6)

where $Z$ is the normalization constant, $\mathrm{\Theta }$ consists of the model hyperparameters and $U(H_j|R,\mathrm{\Theta })$, and $j\in \{\mathrm{0,1},2\}$ is the energy function of the MRF model. In the case of an isotropic Potts model-type prior,²⁹ the corresponding posterior energy to be minimized is

$$U(Q_i=H_j|R,{\alpha }_j,{\beta }_j,\zeta )=\sum _{l\in S_i}\{\log [p_l(R(l)|Q(l)=H_j;{\alpha }_j,{\beta }_j)]\}+\zeta \sum _{l\in S_i\setminus i}\delta (q_i,q_l),$$ (7)

where $p_l(R(l)|Q(l)=H_j)$ is the gamma ratio probability density function of the $l$’th amplitude ratio $R(l)$ belonging to the source neighboring system $S_i$ given the class $H_j$, $({\alpha }_j,{\beta }_j)$ is the set of the gamma ratio distribution hyperparameters of the class $H_j$, $j\in \{\mathrm{0,1},2\}$, $\delta$ is the delta Kroneker function, and $\zeta$ is a positive parameter. Note that we opted for the 3-D eight-connexity neighboring system.

In this work, we adopt a nonlocal approach to define the energy function. The nonlocal approach aims to take advantage of the redundancy presented in the images by extending the neighboring system. This is based on the assumption that a given neighborhood around a voxel may be similar to the neighborhoods around other voxels in the same image. Figure 1 presents an example of the classical and the nonlocal neighboring systems. In contrast to the classical approach, the nonlocal approach allows us to exploit the information available in other neighborhoods called patches. The contribution of each new neighborhood or patch depends on the similarity between the main neighborhood $Si$ and the other patches $S{i}_d$ where $i_d$ is the center of the patch [Fig. 1(b)]. The more similar they are, the greater their contribution is. To this end, a weighted graph $G$ that links together voxels over the image is calculated. In Ref. 30, authors showed that the Euclidean distance is sufficient to reliably measure the similarity. Hence, the similarity between two voxels $i$ and $i_d$, based on the pairwise Euclidean distance, is expressed as follows:

$$G_{i_d,i}=\sum _{l_1\in S_{i_1},l\in S_i}{(R(l_1)-R(l))}^2.$$ (8)

Fig. 1.

Comparison of (a) the classical approach (b) the nonlocal approach where the different neighborhoods/patches $S{i}_{d,d\in \{\mathrm{1,2},\mathrm{3,4},\mathrm{5,6}\}}$ will contribute to the estimation of the voxel $i$ based and the their similarities $G{i}_d,i$.

The new energy function, which integrates the non-local weights $G$ associated with different patches around the voxel of interest $i$ and located in an extended neighborhood $N{S}_i$, is expressed as follows:

$$U(Q_i=H_j|R,{\alpha }_j,{\beta }_j,\zeta ,\eta )=\eta \sum _{S_n\in N{S}_i}{G}_{n,i}\sum _{l\in S_n}\{\log [p_l(R(l)|q(l)=H_j,{\alpha }_j,{\beta }_j)]\}+\zeta \sum _{l\in S_i\setminus i}\delta (Q_i,Q_l).$$ (9)

The first part of the energy function models the a priori we have on the image ratio $R(l)$ conditioned to change and no-change hypotheses as well as the information available in other patches (information fusion). The second part models the spatial dependency by the use of the second-order isotropic Potts model with parameter $\zeta$. Hence, the definition of the energy function favors the generation of homogeneous areas reducing the impact of the speckle noise, which could affect the classification results of the SD-OCT images.³¹ The hyperparameters $\zeta ,\eta$ handle the importance of the energy terms. On one hand, $\zeta$ allows us to tune the importance of the spatial dependency constraint. In particular, high values of $\zeta$ correspond to a high spatial constraint. On the other hand, $\eta$ models the reliability of the patches and is usually assumed to take on values in [0, 1]. This constraint can easily be satisfied by choosing the appropriate a priori distribution for $\eta$.

The whole set of the model hyperparameters is then given by $\mathrm{\Theta }=\{{\sigma }_{\mathrm{0,1}},{\alpha }_{\mathrm{0,1}},{\beta }_{\mathrm{0,1}},{\alpha }_j,{\beta }_j,\eta ,\zeta \}$. Without information prior knowledge, the following priors are retained: $p({\sigma }_0^2)=\frac{1}{{\sigma }_0}$, $p({\sigma }_1^2)=\frac{1}{{\sigma }_1}$. The non-negativity of the the hyperparameters $\{{\alpha }_{\mathrm{0,1}},{\beta }_{\mathrm{0,1}},{\alpha }_j,{\beta }_j,\eta ,\zeta \}$ is guaranteed through the use of the exponential densities: $p({\alpha }_0,{\beta }_0)=\frac{1}{\phi }\exp (-{\alpha }_0/\phi )\hspace{0.17em}\frac{1}{\vartheta }\exp (-{\beta }_0/\vartheta )$, $p({\alpha }_1,{\beta }_1)=\frac{1}{\phi }\exp (-{\alpha }_1/\phi )\hspace{0.17em}\frac{1}{\vartheta }\exp (-{\beta }_1/\vartheta )$, $p({\alpha }_j,{\beta }_j)=\frac{1}{\phi }\exp (-{\alpha }_j/\phi )\hspace{0.17em}\frac{1}{\vartheta }\exp (-{\beta }_j/\vartheta )$, $p(\eta )=\frac{1}{\kappa }\exp (-\eta /\kappa )$, and $p(\zeta )=\frac{1}{\kappa }\exp (-\zeta /\kappa )$. Note that the values of $\{\phi ,\vartheta ,\kappa \}$ are empirically fixed but do not really influence the results. The hierarchical approach we proposed and the prior knowledge we opted for our model lead to an intractable posterior distribution $p(Q,\mathrm{\Theta }|R)$. Therefore, we propose the use of an MCMC procedure to estimate the model parameters and hyperparameters. Indeed, the principle of the MCMC method is to generate samples drawn from the posterior densities and then to be able to achieve parameter estimation. We use a Gibbs sampler based on a stationary ergodic Markov chain allowing us to draw samples whose distribution asymptotically follows the a posteriori densities. Indeed, the Gibbs sampler decomposes the problem of generating a sample from a high dimension PDF by simulating each variable separately according to its conditional PDF. Since no classical expressions for the posterior PDFs are available, there is no direct simulation algorithm for them. To overcome this problem, we perform Hastings–Metropolis steps within the Gibbs sampler²⁵ to ensure that all convergence properties are preserved.³² Moreover, since no knowledge on the posterior definition is available, we have opted for the random walk version of the Hastings–Metropolis algorithm. The proposal distribution $p$ is then defined as $p(.|Y)=Y+p^{\prime }(.)$ where $p^{\prime }$ is a distribution which does not depend on $Y$ and is usually centered on 0. Hence, at each iteration, a random move is proposed from the actual position. The choice of a good proposal distribution is crucial to obtain an efficient algorithm, and the literature suggests that, for low dimension variables, a good proposal should lead to an acceptance rate of 0.5.²⁵ The determination of a good proposal distribution can be solved by using a standard Gaussian distribution with an adaptive scale technique.³³ The main Gibbs sampler steps are described in Algorithm 1. We used a burn-in period of $h_{\min }=500$ iterations followed by another 1000 iterations for convergence ($h_{\max }=1500$). The change detection map $Q$ is estimated using the maximum a posteriori MAP estimator: $\widehat{Q}=\underset{H_l}{\mathrm{argmax}}{\overline{p}}_{H_l}$, where ${\overline{p}}_{H_1}=\frac{1}{h_{\max }-h_{\min }}\sum _{h=h_{\min }+1}^{h_{\max }}{p}^{[h]}(Q=H_1|R^{[h]},{\mathrm{\Theta }}^{[h-1]})$, ${\overline{p}}_{H_2}=\frac{1}{h_{\max }-h_{\min }}\sum _{h=h_{\min }+1}^{h_{\max }}{p}^{[h]}(Q=H_2|R^{[h]},{\mathrm{\Theta }}^{[h-1]})$ and ${\overline{p}}_{H_3}=1-{\overline{p}}_{H_3}-{\overline{p}}_{H_1}$.

Algorithm 1.

Sampling Algorithm.

1. Initialization of $X_0^{[0]},X_1^{[0]},Q^{[0]}$ and ${\mathrm{\Theta }}^{[0]}$

2. For each iteration $h$ repeat:

i) Sampling $X_0^{[h]}$ from $p(X_0|I_0,{\mathrm{\Theta }}^{[h-1]})$

ii) Sampling $X_1^{[h]}$ from $p(X_1|I_1,{\mathrm{\Theta }}^{[h-1]}$

iii) Calculating $R^{[h]}=X_0^{[h]}/X_1^{[h]}$

iv) Creating a configuration of $Q$ basing on $R^{[h]}$

v) Calculating $p^{[h]}(Q=H_l|R^{[h]},{\mathrm{\Theta }}^{[h-1]})$

vi) Sampling ${\mathrm{\Theta }}^{[h]}$ from $p(\mathrm{\Theta }|X_0^{[h]},X_1^{[h]},I_0,I_1)$

vii) Until convergence criterion is satisfied

3. Classification

This step aims at classifying an image into the nonprogressor or the progressor classes based on the estimated change detection map. In contrast to Ref. 4, we considered two-layer fuzzy classifier rather than a threshold-based classifier. Indeed, the fuzzy set theory is used to quantify the membership degrees of a given image to each class (i.e, progressor and nonprogressor).

As in Ref. 4, we considered two features as input for the classifier: (1)feature 1: the number of changed sites and (2) feature 2: the ratio image intensity $R$ of changed sites. In this work, only the loss of retinal height in neighboring areas is considered change due to glaucomatous progression because an increase in retinal height is considered improvement (possibly due to treatment or tissue rearrangement).

We now calculate the elementary membership degree to the nonprogressor class given each feature ${\gamma }_{\mathrm{nor},o\in \{\mathrm{feature}1,\mathrm{feature}2\}}$ using an $S$-membership function $f$ whose expression is given in Eq. (10). Note that the range $[a,c]$ defines the fuzzy region.

$$f(x;a,b,c)=\{\begin{array}{ll}0& x<a\\ \frac{{(x-a)}^2}{(b-a)(c-a)}& a\le x<b\\ 1-\frac{{(x-c)}^2}{(c-b)(c-a)}& b\le x<c\\ 1& \text{otherwise}\end{array},$$ (10)

where $a<b<c$.

$${\gamma }_{\mathrm{nor}}={\gamma }_{\mathrm{nor},\mathrm{feature}1}\times {\gamma }_{\mathrm{nor},\mathrm{feature}2},$$ (11)

where ${\gamma }_{\mathrm{nor},\mathrm{feature}1}=f(N_c;a_1,b_1,c_1)$, ${\gamma }_{\mathrm{nor},\mathrm{feature}2}=f(\sum _{i\in C}{R}_i;a_2,b_2,c_2)$, $N_c$ and $C$ stand for the number of changed sites and the changed site class, respectively, and $(a_1,b_1,c_1,a_2,b_2,c_2)$ are the hyperparameters of the $S$-membership functions. The hyperparameters $(a_1,b_1,c_1,a_2,b_2,c_2)$ are estimated with the genetic algorithms³⁴ using longitudinal SD-OCT data from a training dataset which contains 10 normal eyes, 5 nonprogressing eyes, and 10 progressing eyes. Note that the training dataset is independent of the test dataset described in Sec. 4.1.

The membership degree to the glaucoma class ${\gamma }_{\mathrm{glau}}$ is given by

$${\gamma }_{\mathrm{glau}}=1-{\gamma }_{\mathrm{nor}}.$$ (12)

To decide if a given SD-OCT image belongs to the glaucoma progressor class, another membership function is used. We opted for the trapezoidal function denoted by $g$ as a membership function. The expression of $g$ is given by

$$g(x;a_3,b_3,c_3,d_3)=\{\begin{array}{ll}\left(\frac{x-a_3}{b_3-a_3}\right)& a_3\le x<b_3\\ 1& b_3\le x<c_3\\ \left(\frac{d_3-x}{d_3-c_3}\right)& c_3\le x<d_3\\ 0& \text{otherwise}\end{array},$$ (13)

where $a_3<b_3<c_3<d_3$. Alternately, the genetic algorithm was used to estimate this quadruple. The decision to classify an image into the glaucoma class depends on the output of the function $g({\gamma }_{\mathrm{glau}})$. As can be observed, the $g$ function depends on the quadruple $(a_3,b_3,c_3,d_3)$ as well as on $(a_2,b_2,c_2)$ and $(a_1,b_1,c_1)$. If $g({\gamma }_{\mathrm{glau}})=1$ the image is assigned to the glaucoma progressor class. Note that an eye is considered as a progressor if one follow-up image is a progressor.

4. Experiments

The different datasets used for validation are described in the next sub-section 4.1. Then, change detection results on simulated and semi-simulated datasets are presented in sub-section 4.2. Finally, the classification results on clinical datasets are presented in sub-section 4.3.

4.1. Datasets

The proposed framework was experimentally validated on simulated, semi-simulated, and clinical datasets. Our clinical datasets consist of 117 eyes of 75 participants. Table 1 presents a description of the clinical dataset. Specifically, the first clinical dataset consists of 27 eyes from 27 participants with glaucoma progression. The glaucomatous progression was defined based on: (1) likely progression by visual field³⁵ or (2) progression by stereo-photographic assessment of the optic disk.³⁶ A third observer adjudicated any differences in assessment between these two observers. The second clinical dataset consists of 40 eyes from 23 healthy participants. The third clinical dataset consists of 50 eyes from 26 participants considered stable (each participant was imaged once a week for five consecutive weeks). All eligible participants were recruited from the University of California, San Diego Diagnostic Innovations in Glaucoma Study (DIGS) with at least five good quality visual field exams to ensure an accurate diagnosis. Note that for each exam, the baseline image and the follow-up image are automatically co-registered with built in instrument software. Specifically, the Spectralis SD-OCT (Heidelberg Engineering GmbH, Heidelberg, Germany) instrument features two different options to enhance reproducibility. A real-time eye-tracking device (eye tracker) compensates for involuntary eye movements during the scanning process, and a retest function assures that follow-up measurements are taken from the same area of the retina as the baseline examination. Many studies demonstrate that the retest recognition and eye tracker options led to high reproducibility and accurate and repeatable alignment of the baseline and the follow-up images.^36–38

Table 1.

Description of the clinical dataset used to assess the diagnosis accuracy of the proposed framework.

	Number of patients	Number of eyes	Follow-up duration (median/interquartile range)
Normal group	23	40	2.03 (1.8) years
Stable glaucoma group	50	26	5 (0) weeks
Progressing glaucoma group	27	27	2.4 (1.6) years

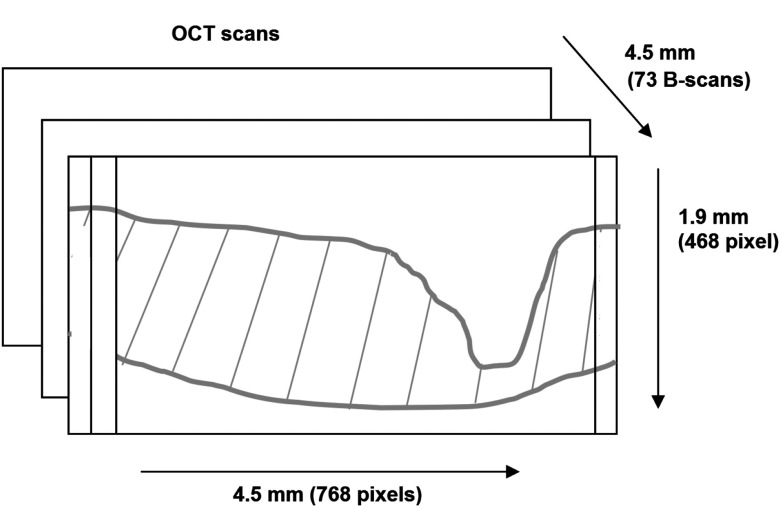
Because the performance of any change detection algorithm can be affected by the OCT instrument specifications³⁹ (axial/lateral resolution, voxel sizes, etc.), a test with low measurement variability is important for detecting change during longitudinal analysis. This is of particular importance in the evaluation of glaucoma progression where visit-to-visit changes may be very small. Several studies have shown that Spectralis SD-OCT can reliably measure very small changes.^37,40,41 Using the high resolution mode and a ($4.5\times 1.9\times 4.5\mathrm{mm}$) pattern size centered on the ONH, we obtained an axial and lateral resolution of 3.87 and $5.84\mu \mathrm{m}$, respectively, where the distance between two consecutive B-scans is $62\mu \mathrm{m}$ (c.f, Fig. 2). Therefore, each 3-D OCT images consists of ($768\times 468\times 73$) voxels. All experiments were performed on a workstation with Intel Core i7, 1.6 GHz CPU and 16 GB RAM memory. MATLAB® 7.14.0 (R2012a) and C++ were used for processing. The processing time is approximately 5 min per image.

Fig. 2.

Dimension of the three-dimensional (3-D) optical coherence tomography (OCT) images.

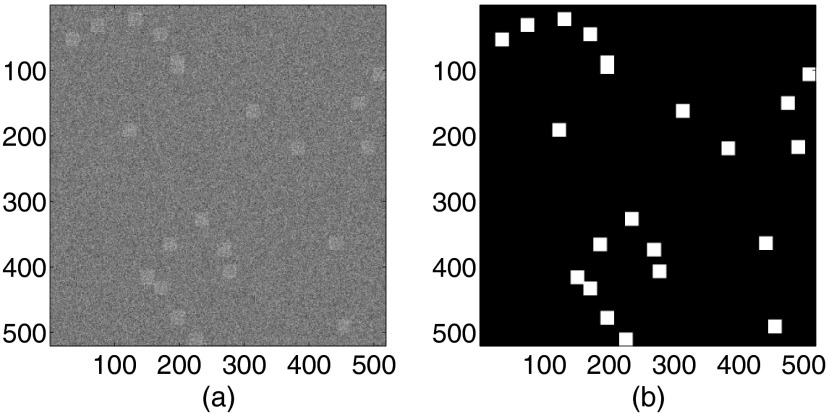
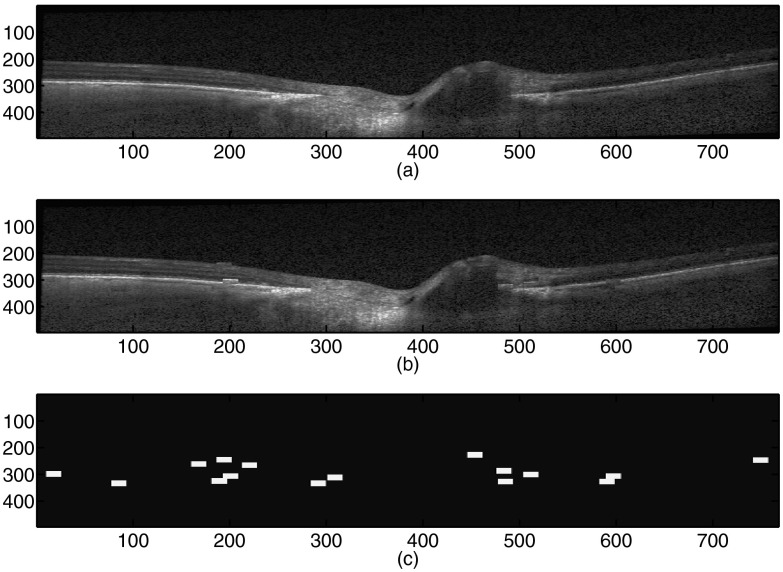
Because no ground truth for glaucomatous change in the 3-D SD-OCT images is available, we generated simulated and semi-simulated datasets to assess the proposed change detection method. The simulated dataset consists of 100 images generated according to the proposed model with different values of peak signal to noise ratio (PSNR) (30, 25, 20, and 15 dB) ($\mathrm{PSNR}=10{\log }_{10}\{\max {(\mathrm{Image})}^2/E[{(\mathrm{Noise})}^2]\}$). Figure 3 presents an example of a simulated image. The semi-simulated dataset was constructed from 100 normal 3-D SD-OCT images. Changes were simulated (1) by the permuting 1%, 2%, 3%, and 5% of image regions in the images, respectively, and (2) by modifying the intensities of each $15\times 15\times 3$ voxel-sized region in the images randomly with 0.5%, 0.75%, 1%, and 1.25% probabilities, respectively. The intensities were randomly modified by multiplying the real intensities by 0.5, 0.75, 1.5, or 2 with a 0.25% probability. In order to emphasize the robustness of the proposed approach, an additive Gaussian noise with different values of PSNR (30, 25, 20, and 15 dB) was added to both the original image and the semi-simulated images. Figure 4 presents an example of a semi-simulated image. Table 2 summarizes the simulated and semi-simulated datasets.

Fig. 3.

Simulated image: (a) the simulated image ($\mathrm{PSNR}=20\mathrm{dB}$) and (b) the ground truth; the white boxes represent the changes.

Fig. 4.

Semi-simulated image by the permutation of image regions: (a) the original B-scan image, (b) the simulated B-scan image, (c) the ground truth: the white boxes represent the changes.

Table 2.

Description of the simulated and semi-simulated dataset used to evaluate the proposed nonlocal Bayesian Markovian approach for change detection.

	Number of images
Simulated dataset	100
Semi-simulated dataset by region permutation	100
Semi-simulated dataset by intensity modification	100

4.2. Change Detection Algorithm Assessment

In order to emphasize the benefit of the proposed change detection approach called the nonlocal Bayesian Markovian approach and particularly the use of the nonlocal approach to define the MRF energy function, we compared the proposed nonlocal Bayesian Markovian approach with three change detection methods:

• 1.The proposed method with a classic MRF neighboring system
• 2.The kernel $k$-means algorithm⁶ with the RBF Gaussian kernel
• 3.A Bayesian threshold-based method.⁴²

To perform the change detection evaluation, we use the percentage of false alarm (PFA), the percentage of missed detection (PMD) and the percentage of total error (PTE) measurements defined by

$$\mathrm{PFA}=\frac{\mathrm{FA}}{N_F}\times 100\%;\mathrm{PMD}=\frac{\mathrm{MD}}{N_M}\times 100\%;\mathrm{PTE}=\frac{\mathrm{MD}+\mathrm{FA}}{N_M+N_F}\times 100\%,$$

where FA stands for the number of unchanged voxels that were incorrectly determined as changed ones, $N_F$ stands for the total number of unchanged voxels, MD stands for the number of changed voxels that were mistakenly detected as unchanged ones, and $N_M$ stands for the total number of changed voxels. The kappa coefficient of agreement between the ground truth and the change detection map was also calculated. The kappa statistic was originally developed by Cohen⁴³ in order to discern the amount of agreement that could be expected to occur through chance. A detailed description of the kappa coefficient of agreement can be found.⁴⁴ Strength of agreement can be categorized according to the method proposed in Ref. 45: $0=\mathrm{poor}$, 0 to $0.20=\mathrm{slight}$, 0.21 to $0.40=\mathrm{fair}$, 0.41 to $0.60=\mathrm{moderate}$, 0.61 to $0.80=\mathrm{substantial}$, and 0.81 to $1.00=\mathrm{almost}$ perfect. Table 3 shows the results of the change detection on simulated and semi-simulated datasets. The nonlocal Bayesian Markovian approach ($\mathrm{kappa}=0.84$) tends to perform better than the kernel $k$-means ($\mathrm{kappa}=0.71$), classic MRF approach ($\mathrm{kappa}=0.78$), and the Bayesian threshold-based ($\mathrm{kappa}=0.64$) methods. This means that the proposed nonlocal Markov priori we considered improves the change detection results by modeling the spatial dependency of voxels as well as the redundancy presented in the images by extending the neighboring system.

Table 3.

Mean and standard deviation (SD) of false detection, missed detection, total errors, and the kappa coefficient resulting from the proposed nonlocal Bayesian Markovian approach, the classic Markov random field (MRF) approach, the kernel $k$-means method and the threshold method using simulated and semi-simulated.

Semi-simulated datasets	False detection ($\pm \mathrm{SD}$)	Missed detection ($\pm \mathrm{SD}$)	Total errors ($\pm \mathrm{SD}$)	Kappa
Nonlocal Bayesian Markovian approach	0.37 ($\pm \mathbf{0.14}$) %	3.12 ($\pm \mathbf{0.65}$) %	0.61 ($\pm \mathbf{0.13}$) %	0.84
Classic MRF approach	0.54 ($\pm \mathrm{0.21}$) %	5.62 ($\pm 1.03$) %	0.91 ($\pm 0.20$) %	0.78
Kernel $k$-means	0.89 ($\pm 0.41$) %	8.03($\pm 2.75$) %	2.03($\pm 0.51$) %	0.71
Threshold	2.14($\pm 0.71$) %	10.52($\pm 3.14$) %	3.45($\pm 1.24$) %	0.64
Simulated dataset	False detection ($\pm \mathrm{SD}$)	Missed detection ($\pm \mathrm{SD}$)	Total errors ($\pm \mathrm{SD}$)	Kappa
Nonlocal Bayesian Markovian approach	0.84 ($\pm \mathrm{0.24}$) %	5.17 ($\pm 1.05$) %	0.97 ($\pm 0.17$) %	0.82
Classic MRF approach	1.24 ($\pm 0.35$) %	7.05 ($\pm 1.95$) %	1.51 ($\pm 0.34$) %	0.72
Kernel $k$-means	1.65 ($\pm 0.63$) %	8.89 ($\pm 2.87$) %	2.38 ($\pm 2.44$) %	0.69
Threshold	3.78 ($\pm 1.47$) %	15.25 ($\pm \mathrm{SD}4.17$) %	6.41 ($\pm 2.74$) %	0.53

Note: Bold values correspond to the best values.

4.3. Classification Results

This section describes the glaucoma progression detection results obtained with the proposed scheme. In order to perform the classification evaluation, we have retained the area under the receiver operating characteristic area under the receiver operating characteristic curve (AUROC), the sensitivity and the specificity measurements:

$$\mathrm{sensitivity}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}};\mathrm{specificity}=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}},$$

where TP stands for the number of true positive identifications, FN stands for the number of false-negative identifications, and FP stands for the number of false-positive identifications.

The proposed framework was experimentally validated with clinical datasets. It is important to note that we used independent training and test sets to estimate the diagnostic accuracy of the methods. Specifically, we trained our classifiers, as well as the other classifiers used for the comparison, on 10 normal eyes, 5 stable glaucoma eyes, and 10 progressor eyes. In order to emphasize the benefit of the proposed glaucoma progression detection scheme, we have compared the proposed framework called as nonlocal Bayesian-fuzzy detection scheme (BFDS) to six other methods:

• 1.The support vector machine (SVM) classifier of the RNFL thickness. As in Ref. 46, we used the radial basis function as a kernel. The SVM was trained by a variation of Platt’s sequential minimal optimization algorithm.⁴⁷ The SVM hyperparameters were determined by a global optimization technique based on simulated annealing⁴⁸ (RNFL-SVM).
• 2.The ANN classifier of the RNFL thickness. As in Ref. 46, we used the multiayer perceptrons version of the ANN⁴⁹ (RNFL-ANN).
• 3.The proposed method with the classic MRF a priori knowledge on the change detection map standard BFDS.

Results are presented in Table 4. The nonlocal BFDS method with the use of the whole 3-D SD-OCT volume instead of the RNFL measurements results in high specificity in both normal and stable glaucoma eyes (94% and 94% respectively) while maintaining good sensitivity (70%). This can be explained by the fact that we take the noise for change detection instead of the machine measurements which strongly depend on the image quality. Moreover, the nonlocal approach led to a better sensitivity compared to the classic approach. This is due to the accuracy of the changes detection of the nonlocal approach. It is important to note that the specificity is generally considered more important in glaucoma progression detection than the sensitivity since glaucoma is a slow disease⁵⁰ and false negatives (people falsely identified as nonprogressing) can be eliminated in the next follow-up visits. However, if the specificity is low, this would lead to substantial follow-up costs, unnecessary treatment (e.g., surgery) and may cause much distress for people who are not progressing.

Table 4.

Diagnostic accuracy of the nonlocal BFDS, the standard BFDS, the RNFL-ANN, and the RNFL-SVM methods.

	Progressing glaucoma group sensitivity (%)	Normal group specificity (%)	Stable group specificity (%)	AUROC
Nonlocal BFDS	70	94	94	0.87
standard BFDS	64	90	92	0.83
RNFL-ANN	69	71	78	0.69
RNFL-SVM	52	68	79	0.60

Note: Bold values correspond to the best values.

5. Conclusion

A new framework for glaucoma progression detection has been proposed. We particularly focus on the formulation of the change problem as a missing data problem. The task of inferring the glaucomatous changes is tackled with a hierarchical MCMC algorithm that is used for the first time to our knowledge in the glaucoma diagnosis framework. The new nonlocal approach we proposed to define the MRF energy function increased the robustness of the proposed change detection scheme compared to the classic method. The validation using clinical data of the proposed approach has shown that it has a high diagnostic accuracy for detecting glaucoma progression compared with other methods.

Biographies

Akram Belghith received his PhD degree in computer science from University of Strasbourg. He is an assistant scientist at the Hamilton Glaucoma Center, University of California, San Diego, California, USA. His current research interests include machine learning, image processing, pattern recognition, and data analysis.

Christopher Bowd received his PhD degree from Washington State University, Pullman, Washington, USA. Currently, he is a research scientist at the Hamilton Glaucoma Center, University of California, San Diego, California, USA. His current work involves early detection and monitoring of glaucoma with structural imaging of the optic nerve, visual function, and electrophysiological testing using standard and machine learning classifier-based analyses.

Felipe A. Medeiros received the graduate degree and residency from the University of Sao Paulo. He is a professor of ophthalmology and the medical director of the Hamilton Glaucoma Center, University of California San Diego, California, USA. He is also the director of vision function research at the same institution.

Madhusudhanan Balasubramanian received his PhD degree from Louisiana State University, USA. Currently, he is an assistant professor in the Department of Electrical and Computer Engineering at the University of Memphis, Tennessee, USA. His research interests include the intersection of computational science and engineering, biosolid mechanics and biofluid dynamics with emphasis in studying ocular structures, and dynamics, and the mechanism of vision loss in glaucoma.

Robert N. Weinreb received his electrical engineering degree from the Massachusetts Institute of Technology, USA, and his MD degree from Harvard Medical School, Massachusetts. He is a clinician, a surgeon, an educator, and a scientist. He is the distinguished professor of ophthalmology and the chairman of the Department of Ophthalmology at the University of California, San Diego, California, USA.

Linda M. Zangwill received her MS degree from the Harvard School of Public Health and her PhD degree from Ben-Gurion University of the Negev. She is a professor of ophthalmology at the University of California, San Diego, California, USA. Her research interests include studying the relationship between structural and functional changes in the aging and glaucoma eye, and developing computational techniques to improve glaucomatous change detection.