Abstract.
In x-ray imaging, contrast information content varies with photon energy. It is, therefore, possible to improve image quality by weighting photons according to energy. We have implemented and evaluated so-called energy weighting on a commercially available spectral photon-counting mammography system. The technique was evaluated using computer simulations, phantom experiments, and analysis of screening mammograms. The CNR benefit of energy weighting for a number of relevant target-background combinations measured by the three methods fell in the range of 2.2 to 5.2% when using optimal weight factors. This translates to a potential dose reduction at constant CNR in the range of 4.5 to 11%. We expect the choice of weight factor in practical implementations to be straightforward because (1) the CNR improvement was not very sensitive to weight, (2) the optimal weight was similar for all investigated target-background combinations, (3) aluminum/PMMA phantoms were found to represent clinically relevant tasks well, and (4) the optimal weight could be calculated directly from pixel values in phantom images. Reasonable agreement was found between the simulations and phantom measurements. Manual measurements on microcalcifications and automatic image analysis confirmed that the CNR improvement was detectable in energy-weighted screening mammograms.
Keywords: digital mammography, energy weighting, spectral x-ray imaging, contrast-to-noise ratio, photon counting, dose efficiency
1. Introduction
The advent of spectral x-ray imaging enables a number of applications that take advantage of differences in x-ray attenuation as a function of energy.1,2 In mammography, spectral imaging has been investigated for detecting iodine contrast agent,3,4 improving lesion visibility,5,6 measuring breast density,7 discriminating between lesion types,8 and measuring the x-ray attenuation of breast tissue.9 Another application of spectral imaging is energy weighting, which was pioneered by Tapiovaara and Wagner,10 and later investigated for mammography application by Cahn et al.11 Subsequent studies have investigated energy weighting for mammography and projection imaging in more detail,12–15 but the studies are so far limited to theoretical and/or laboratory environments.
Energy weighting improves the pixel-to-pixel contrast-to-noise ratio (CNR) by assigning a higher weight to low-energy photons. Thus, the dose efficiency is effectively improved, which enables a higher CNR at a constant patient dose, or a lower dose at a constant CNR. The effect follows as a logical consequence of the fact that the x-ray contrast drops with increasing photon energy, which holds true in energy regions dominated by the photoelectric effect, including most, or possibly all, (unenhanced) mammography applications.11 The technique can be viewed as a special case of optimally combining images acquired at different mean energies for a specific imaging task, where the task function in this case is constant at all spatial frequencies, i.e., corresponding to a delta function.14
A photon-counting mammography system has recently been developed that allows for one-shot spectral imaging by electronic spectrum splitting.16,17 It is likely that one-shot spectral imaging will be an enabling factor for implementing energy weighting in clinical practice as the relatively moderate CNR improvement will probably not justify the additional effort and alignment problems caused by acquisition of multiple images at different beam qualities. It is interesting to note that photon counting in itself improves the CNR compared to energy integrating systems as the intrinsic energy weighting of photon counting (equal weights to all photons) is closer to optimal than that of energy integration (lower weight to low-energy photons).10,11
This work aims at investigating the practical potential of energy weighting to improve the CNR in screening mammography using the spectral photon-counting mammography system. The technique is evaluated using computer simulations, phantom experiments, and analysis of screening mammograms acquired with the system.
2. Materials and Methods
2.1. Spectral Mammography System
Philips MicroDose SI (Philips Healthcare, Solna, Sweden) spectral mammography systems were used for all image acquisitions. The spectral system is in many respects similar to the nonspectral Philips MicroDose system.18 It comprises a tungsten-target x-ray tube with aluminum filtration, a precollimator, and an image receptor, which is scanned across the object [Fig. 1(a)]. The image receptor consists of photon-counting silicon strip detectors with a pixel pitch of and corresponding slits in the precollimator [Fig. 1(b)]. This multislit geometry rejects virtually all scattered radiation.19
Fig. 1.
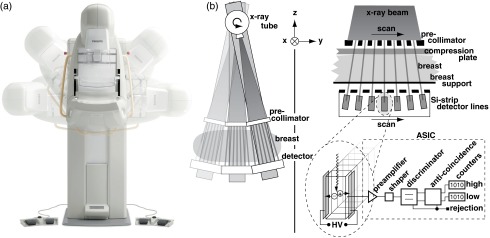
(a) Schematic of the Philips MicroDose SI Mammography system. (b) The spectral image receptor and electronics.
Photons that interact in the detector are converted to electronic pulses with amplitude proportional to the photon energy. As opposed to the nonspectral system, two thresholds are implemented in the detector electronics: one low-energy threshold at that discriminates against electronic noise and one high-energy threshold that sorts the detected pulses into two bins according to energy.17 Each acquisition, therefore, produces two images with pixel values proportional to the count rates in two different energy intervals of the impinging photons. Anticoincidence logic rejects coincident counts in adjacent detector elements in order to mitigate the effect of charge sharing.
2.2. Theoretical Background
An energy-weighted image with signal can be formed as a linear combination of the energy-resolved photon counts according to
| (1) |
where are the weight factors and is the energy bin index. The trivial choice of a signal combination is uniform weighting (i.e., ), which corresponds to conventional photon counting, but can take on any value that maximizes a figure-of-merit.
A conceivable figure-of-merit for optimization is the signal-to-noise ratio (SNR) defined as
| (2) |
where is the expectation value and is the variance of the signal . SNR is maximized using weights10,20
| (3) |
If are ideal photon counts, they are Poisson distributed, i.e., , and uniform weighting maximizes the SNR.
However, CNR is a more comprehensive measure of image quality than SNR as it also includes the contrast between relevant structures.21 CNR can be defined as
| (4) |
where superscripts and refer to the target and background areas, respectively. Comparing Eqs. (2) and (4), it is clear that CNR is equivalent to the SNR of the difference signal (). In accordance with Eq. (3), the CNR is, therefore, maximized for weights:
| (5) |
Even if the background and target signals are samples of a Poisson distribution, the difference signal is generally not Poisson distributed. Rather, the optimal weight factors will be higher for lower energies, where the difference in x-ray attenuation is larger. Note that maximization of the CNR may come at the expense of a lower SNR. It is also important to note that the CNR is task dependent, i.e., it depends on the (nontrivial) choice of the target and background. Optimal weight factors will also depend on incident x-ray spectrum, detector energy resolution, and system nonidealities.
The imaging system considered in this study (c.f. Sec. 2.1) discriminates between high- and low-energy photons, i.e., , and Eq. (1) can be reduced to
| (6) |
where . The weight factor that maximizes the CNR is, therefore [c.f. Eq. (5)],
| (7) |
All components of Eq. (7) can be estimated experimentally from region-of-interest (ROI) measurements in images, which provides a convenient avenue for finding optimal weights in practice. Equation (7) can also be directly derived [not via Eq. (5)] by inserting Eq. (6) into Eq. (4) and maximizing with respect to .
2.3. Simulations
An analytical framework was set up for computer simulations of energy weighting. Incident x-ray spectra at all acceleration voltages available in the MicroDose system (listed in Table 1) were simulated as generic tungsten spectra22 with corresponding count rates measured on the system. The spectra were filtered by 0.5 mm of aluminum (corresponding to the filter), 3 mm of polymethyl methacrylate (PMMA, corresponding to the compression plate), and 1 mm of carbon (corresponding to the breast support). Attenuation was calculated according to the Beer-Lambert law using elemental attenuation coefficients from the XCOM database.23
Table 1.
Simulation parameters as a function of acceleration voltage.
| Tube voltage (kV) | High-energy threshold (keV) | Breast thickness (mm) | PMMA thickness (mm) |
|---|---|---|---|
| 26 | 18 | 30 | 28 |
| 29 | 19 | 40 | 36 |
| 32 | 20 | 50 | 43 |
| 35 | 21 | 60 | 51 |
| 38 | 22 | 70 | 57 |
Note: PMMA, polymethyl methacrylate.
Four different contrast objects were simulated.
-
1.
Target: A embedded microcalcification (). Background: 25% glandular and 75% adipose tissue. Skin: 3 mm.
-
2.
Target: 5 mm of embedded tumor tissue (attenuation coefficient approximated as muscle). Background: 25% glandular and 75% adipose tissue. Skin: 3 mm.
-
3.
Target: 5% glandular and 95% adipose tissue. Background: 100% adipose tissue. Skin: 3 mm.
-
4.
Target: 0.1 mm of added aluminum. Background: PMMA.
The breast compression height was chosen as a typical value at each acceleration voltage (Table 1). Corresponding PMMA thicknesses were calculated to match the transmission of the background of contrast objects 1 and 2. This conversion is specific for the current simulation and may not be generally applicable. To take geometrical effects into account, the target was assumed to be located at a distance of 60 mm from the chest wall. The attenuation coefficients of breast tissue were calculated from the elemental composition.24
The detection process was simulated based on a previously described detector model,17 which includes quantum efficiency, charge sharing, electronic noise, thresholding, pile-up, and the anticoincidence logic. The high-energy threshold is a function of the acceleration voltage and was set at five discrete levels (Table 1).
CNR values for energy weighting and uniform weighting were calculated according to Eq. (4) using a range of weight factors larger than or equal to unity. The optimal weight for energy weighting was taken to be the one that maximized the CNR, i.e., a numerical equivalence to Eq. (7).
2.4. Phantom Measurements
Phantom images were acquired with PMMA plates of varying height as background with an additional 0.1-mm aluminum sheet as the target (corresponding to contrast object 4 in Sec. 2.3). Acquisition parameters were set automatically by the automatic exposure control and the optimal weight factor for each acquisition was calculated according to Eq. (7). Some degree of system ideality is assumed by Eq. (7), e.g., uncorrelated energy bins, and the validity of Eq. (7) was, therefore, verified by comparing the calculated weight factor with the one corresponding to the maximum CNR improvement for a range of weight factors. The measurements were conducted between pairs of ROIs obtained from ROI grids in adjacent target and background areas. The average and standard deviation of values obtained from all nine ROI pairs were used as expectation values and error estimates of optimal weight factor and CNR improvement.
In order to cross-check measurements and simulations, all phantom measurement setups were simulated using the framework presented in Sec. 2.3.
2.5. Analysis of Screening Mammograms
Two methods were used to evaluate the image-quality improvement in energy-weighted mammograms: (1) manual measurement of the CNR of microcalcifications and (2) automatic measurements of the CNR in a large number of uniformly distributed ROIs.
Anatomical structures may interfere with CNR measurements in mammograms, and great care was taken to minimize the impact of this so-called anatomical noise when analyzing the mammograms. The power spectrum of anatomical noise exhibits a strong dependence on spatial frequency, commonly approximated by a power law, which is radically different from white quantum noise with no frequency dependence.25 Burgess et al. found that the detection threshold in anatomical backgrounds behaved as in white noise for targets (reduced threshold with increasing target size),26 but observed the opposite behavior for targets (increasing threshold with increasing size), which indicates that anatomical noise dominates at spatial frequencies in standard mammograms (the crossing between the power spectra of anatomical and quantum noise can be expected to occur close to this frequency). Therefore, in the following analysis, we have chosen to use ROI sizes well below 1 mm, which can be expected to minimize the impact of anatomical noise on the measurement because the noise power spectrum inside the ROI is a convolution with the Fourier transform of the aperture.
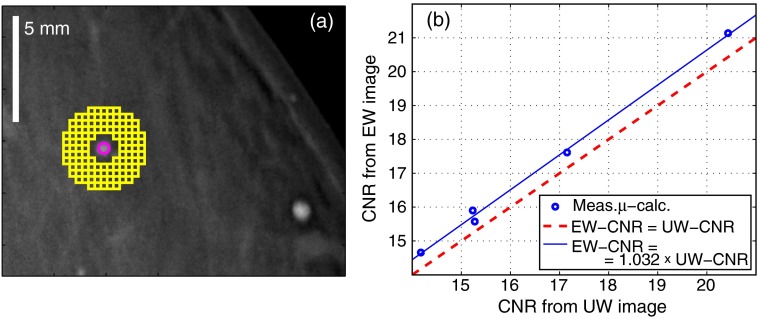
A mammogram of a 71-mm-thick breast acquired at a 35 kV acceleration voltage was used for the manual evaluation of CNR improvement. The mammogram contained five large microcalcifications with approximate diameters ranging from 1.0 to 1.7 mm. A circular target ROI with a diameter of 0.5 mm was placed at the center of each microcalcification. A grid of small background ROIs, each of size , was placed around the target ROI, see Fig. 3(a) for a drawing. The CNR was calculated as the difference between the target ROI mean and the average of all background ROIs, divided by the mean standard deviation in the background ROIs. This scheme, averaging many small background ROIs, was selected to mitigate the influence from low-frequency anatomical noise. The target ROI was not included in the estimation of the noise [as in Eq. (4)] because the microcalcifications were not uniform.
Fig. 3.
(a) Layout of regions of interest (ROIs) for the manual measurement of microcalcification contrast-to-noise ratio (CNR). (b) Measured microcalcification CNR-pairs in the uniformly weighted (UW) and the energy-weighted (EW) images. Also shown is the best proportional fit.
For the automatic CNR measurements, 71 mammograms were randomly selected from a screening population with patients aged 40 to 74 years (patients with implants were not included). The compressed breast thickness distribution in the selected group ranged from 21 to 92 mm with a mean of 55 mm. The median acceleration voltage for the mammograms was 32 kV.
Energy weighting was applied retrospectively on the mammograms. The weight factor for each compressed breast thickness and acceleration voltage was determined by simulation of contrast object 4 in Sec. 2.3 (PMMA-aluminum contrast) with a PMMA thickness chosen to match the transmission of the compressed breast (i.e., the background of contrast objects 1 and 2 in Sec. 2.3).
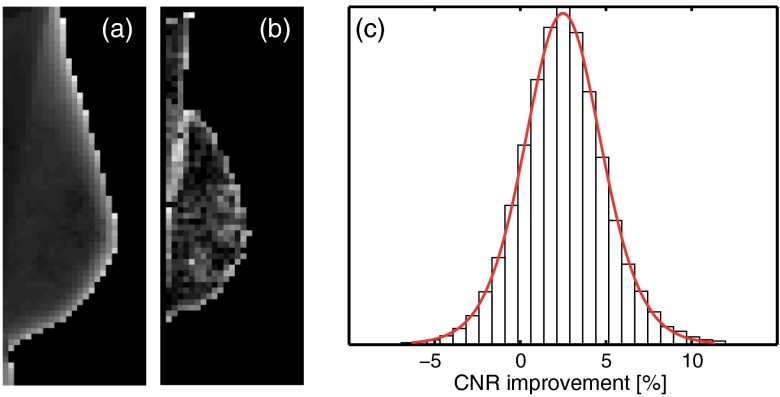
Each mammogram was automatically subdivided into ROIs. The CNR was calculated as the mean absolute difference between the mean pixel values in the center ROI and in the surrounding ROIs, over the mean pixel standard deviation in all ROIs. An ROI size of was chosen as a compromise between excluding anatomical noise and a large-enough ROI for a reliable calculation of the pixel standard deviation. The distance between ROIs (the pitch), on the other hand, was set to 4 mm in order to increase the probability of picking up a reasonably large signal difference. Figures 4(a) and 4(b) illustrate the ROI segmentation for a typical mammogram.
Fig. 4.
Automatic CNR measurements between neighboring regions of interest (ROIs) in 71 energy-weighted screening mammograms. Illustration of the ROI segmentation of an exemplary mammogram in MLO view. (a) The mean signal. (b) The CNR for each ROI compared to its neighbors. (c) Histogram of the CNR improvement for energy weighting gathered from 30,280 ROIs with fit to a location-scale distribution. Note that a large number of the displayed measurements of mean signal were excluded in the calculation of CNR to avoid, for instance, the steep thickness gradient toward the edge.
To measure the signal difference and background standard deviation, surrounding ROIs were selected from the eight-neighborhood of the center ROI. ROIs fulfilling any of the following criteria were excluded from the measurement: top-three highest standard deviation (to avoid an excessive amount of anatomical noise); lowest standard deviation (to somewhat compensate for a potential bias introduced by the first criterion); highest signal difference (to avoid thickness gradients); lowest signal difference (to avoid flat areas). The calculation of standard deviation included the center ROI under the condition that it did not meet any of the exclusion criteria.
Further, measurements with high mean, high standard deviation, or high signal difference values were discarded in order to restrict the CNR calculations to areas with low levels of anatomical noise, but with reasonable signal differences and located within the compressed breast regions. Histograms of the mean and standard deviation values both exhibited bimodal distributions, and upper limits were set approximately at the valley points of the bimodal distributions; the upper parts were assumed to belong to areas with high levels of anatomical noise (high standard deviation values) or to areas outside the compressed breast region (high mean and standard deviation values). The limits of signal difference were set to exclude approximately the 10% lowest and 30% highest values, which was found to be a reasonable compromise between excluding extreme contrast values and keeping enough measurements for a meaningful analysis.
Identical ROI selection was applied to the energy-weighted and the uniformly weighted mammograms to enable a one-to-one comparison on an ROI basis. The ROI selection algorithm was applied to the uniformly weighted image, but similar results were obtained when ROI selection was performed in the energy-weighted image. Pectoralis segmentation of mammograms in the mediolateral oblique (MLO) view was not implemented, but it was assumed that the result of energy weighting within the muscle area is approximately equivalent to that within the breast area.
3. Results
3.1. Simulations
The simulated CNR improvement as a function of weight is shown in Fig. 2 for three of the examined types of contrast object (microcalcification/breast, tumor/breast, and aluminum/PMMA). The glandular/adipose contrast object was found to closely correspond to the tumor/breast contrast object and is, therefore, not shown in Fig. 2. A maximum CNR improvement for each acceleration voltage between 2.2 and 5.2% was obtained using weight factors between 1.5 and 2.0. CNR improvement and optimal weight both increased with acceleration voltage. However, a weight of would result in a near-optimal performance for all the simulated cases. Optimal weights as well as the CNR improvements were similar for the aluminum/PMMA setup and the mammography-related setups.
Fig. 2.
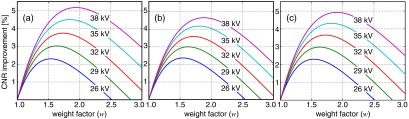
Simulated contrast-to-noise ratio (CNR) improvement by energy weighting over uniform weighting as a function of weight (): (a) microcalcification embedded in breast tissue, (b) 5-mm tumor embedded in breast tissue, and (c) 0.1 mm aluminum on polymethyl methacrylate (PMMA). Breast compression heights and PMMA thicknesses were chosen as a function of acceleration voltage according to Table 1.
3.2. Phantom Measurements
The optimal weight factor calculated using Eq. (7) and the CNR improvement by energy weighting over uniform weighting as measured in the phantom images are shown in Table 2. In summary, using a weight factor of improved the CNR by close to 4% on average. Scanning the weight factor over a range of values yielded slightly lower optima than Eq. (7) (and higher CNR improvements), but as the differences were minor ( in optimal weight on average), the detailed results are not given in Table 2. Simulations of the phantom experiments resulted in slightly lower optimal weight factors, combined with slightly lower CNR improvements (Table 2). Although the discrepancies to simulations were in all cases significant (at the 5% significance level, determined by one-sample tests), they were relatively small, and equal trends were observed for the measurements and simulations (i.e., a peak in weight factor and CNR improvement at 50 mm PMMA and 35 kV).
Table 2.
Optimal weight factor and contrast-to-noise ratio (CNR) improvement for 0.1 mm aluminum on PMMA: phantom measurements and simulated phantom measurements. The optimal weight from Eq. (7) was used to calculate the CNR improvement in the measurements. For the simulations, the weight was scanned to find an optimum. Numbers in parenthesis refer to one standard deviation, and percentage points are abbreviated as pp.
| Measurements | Simulations | ||||
|---|---|---|---|---|---|
| PMMA thickness (mm) | Acceleration voltage (kV) | Optimal weight, | CNR improvement | Optimal weight, | CNR improvement |
| 20 | 29 | 1.68 (0.02) | (0.17 pp) | 1.62 | |
| 30 | 32 | 1.75 (0.01) | (0.11 pp) | 1.72 | |
| 40 | 32 | 1.75 (0.02) | (0.16 pp) | 1.73 | |
| 50 | 35 | 1.84 (0.03) | (0.27 pp) | 1.82 | |
| 60 | 35 | 1.82 (0.03) | (0.28 pp) | 1.79 | |
| 70 | 35 | 1.79 (0.02) | (0.17 pp) | 1.77 | |
| Mean | 1.77 | 1.74 | |||
3.3. Analysis of Screening Mammograms
The microcalcification CNR values for the uniformly weighted image and the energy-weighted image are plotted in Fig. 3(b). Also shown is the best proportional fit with a coefficient of 1.032, i.e., the CNR improvement of energy weighting was 3.2%. This CNR difference was not found to be visible in printed images, and the example in Fig. 3(a), therefore, shows only the energy-weighted image.
Figure 4(c) shows a histogram of the CNR improvement of energy-weighted ROIs compared to uniformly weighted ROIs from the automatic image analysis. Out of a total of 76,750 measurements inside the segmented breast areas, 30,280 measurements were included for CNR calculation after excluding measurements with high mean and standard deviation values. The mean number of included ROIs in each measurement was 4.7 (including the center ROI). The measured CNR improvements were fitted to a location-scale distribution, i.e., a standard student’s distribution with location and scaling parameters in addition to the usual degrees-of-freedom parameter.27 The mean of the fit was 2.49% (95% confidence intervals: [2.46% 2.52%]), and the standard deviation of the distribution was 2.2 percentage points (pp).
4. Discussion
Three different methods were used to evaluate energy weighting: computer simulations, phantom experiments, and analysis of screening mammograms. Reasonable agreement was found between the simulations and phantom measurements in terms of CNR improvement and weight factor (c.f. Table 2, in particular, the mean values), which gives some confidence in using simulations to predict the performance for various tasks. Further, in the phantom experiments, scanning the weight factor yielded close-to-identical results as Eq. (7), which validates the equation.
The CNR improvement measured in the mammograms was slightly lower than expected from simulations; we could expect a CNR improvement of from the manual measurement (compared to the microcalcification in Fig. 2 and 60 mm PMMA in Table 2) and an average of 3 to 4% from the automatic analysis (includes a range of compression heights and tube voltages, centered around 55 mm and 32 kV, and mainly adipose/glandular contrast, which is similar to the tumor target in Fig. 2).
The deviation in mean CNR improvement observed in the mammograms can partly be explained by small amounts of anatomical noise that have prevailed and interfered with the measurement. As anatomical noise is caused by contrast between breast structures, it is affected by energy weighting in a similar way as is the target contrast and would, therefore, reduce the measured improvement toward zero. One additional reason for the deviation in the automatic analysis is that constant weight factors were used for the entire breasts, although there are natural variations in thickness, glandularity, and tissue types. A future solution to this may be to locally adapt the weight factor within the image.
Except for the deviation in mean CNR improvement, the automatic analysis exhibited a large spread of measured improvements [c.f. Fig. 4(c)]. This spread was not a real effect but a measurement artifact, which is explained in the following. In most cases, the propagation of Poisson-distributed image noise through the measurement is close to linear and we can expect a close-to-normal distribution of measured values. This expectation was verified by repeating the phantom experiment that resembled most the average properties of the mammograms (0.1 mm Al, 40 mm PMMA, 32 kV in Table 2) using ROI sizes that corresponded to the automatic analysis. The result of this measurement was a normal distribution with a standard deviation of 1.5 pp, which is somewhat smaller but of the same order as the standard deviation of the distribution in Fig. 4(c). However, Fig. 4(c) exhibits heavier tails than a normal distribution, i.e., there are outliers toward both the positive and negative ends, and a location-scale distribution provided a better fit. The origin of the outliers was investigated on a case-by-case basis and was found to be a combination of nonlinearity and exaggerated noise at extreme values in signal difference. For instance, if the signal difference is close to zero, the CNR will be close to zero and errors or noise in the measurement will be amplified in the assessment of CNR improvement. The limits that were put on signal difference were chosen as a tradeoff between mitigating this effect and keeping enough measurements for a meaningful analysis. Nevertheless, we verified that the distribution became close to normal when the limits were tightened to include only the 10% of measurements closest to the median signal difference.
We make the following observations and conclusions from the results of this study:
-
•
The simulations, phantom measurements, and the analysis of screening mammograms all indicated a CNR benefit in the range of 2.2 to 5.2% when using an optimal weight factor in the range of 1.5 to 2.0.
-
•
The CNR benefit translates to a potential dose reduction at a constant CNR in the range of 4.5 to 11%.
-
•
Referring to Fig. 2, the CNR optimum was quite flat (not very sensitive to weight near the optimum), and the optimal weight was similar for all clinically relevant tasks, which simplifies the choice of weight in practical implementations. This result is in analogy with previous studies on energy weighting11 and with the fact that the optimal incident energy in mammography is similar for clinically relevant targets.28
-
•
Further, the simulations indicate that the PMMA-aluminum contrast serves as a good proxy for clinically relevant tasks, which justifies the use of aluminum/PMMA phantoms to find optimal weights in practice.
-
•
The optimal weight found by the image-based, or calibration-based, method [Eq. (7)] agreed well with the optimal weight found in simulations (Table 2). Hence, the optimal weight can be calculated with good precision directly from the pixel values in phantom images, which further facilitates the choice of weight in practice.
-
•
The benefit of energy weighting increases with tube voltage, and the cost of using a higher-than-optimal tube voltage would, therefore, be smaller for energy weighting compared to uniform weighting. Furthermore, the optimal tube voltage increases for energy-weighted images. (This is also the case for uniform weighting—photon counting—compared to energy integrating detection.)
-
•
It has previously been shown that the optimal weight factor approximately follows the inverse of the cube of the photon energy,11 which is consistent with the finding here that the weight factor increases with tube voltage.
-
•
In general, the benefit of energy weighting can be expected to drop with increased material thickness (breast or PMMA) at a constant acceleration voltage because beam hardening narrows the spectrum. This effect was clearly seen at 35 kV (Table 2), but was not evident at 32 kV, likely because of a narrower incident spectrum.
It has previously been recognized that quantum noise is not the dominant noise source for some imaging tasks in mammography, but rather the anatomical noise, which is in magnitude proportional to the contrast.14,25,26,29 An improvement in pixel CNR would be of limited importance for these tasks, but, as the anatomical noise has a strong spatial-frequency dependence, the benefit would be larger for tasks that include detection and discrimination of small details, e.g., microcalcifications, fine tissue structures and spiculations, and edges of larger structures, such as solid tumors.
Several previous studies have investigated energy weighting in mammography at the limit of infinite energy resolution. Cahn et al. reported a CNR improvement of for microcalcifications and a 30 kV tungsten spectrum;11 Giersch et al. reported a CNR improvement of for microcalcifications and a 35 kV molybdenum spectrum.12 These results are of the order of twice the improvements presented here. However, studies with a realistic energy resolution are more relevant for comparison. Lundqvist calculated a CNR improvement of 4 to 5% for a tumor target in 5- to 8-cm breasts, using 28- to 34-kV tungsten spectra, and an ideal detector with two energy bins (the improvement was reduced substantially when charge sharing was included in the calculation);13 Karg et al. reported a CNR improvement of 2.2% for measurements of water targets in PMMA, using a 60-kV tungsten spectrum and a Medipix2 detector with five energy bins and substantial charge sharing;30 Fredenberg et al. calculated a CNR improvement of 1 to 2% for microcalcifications in a 5-cm breast, using a 30-kV tungsten spectrum and a detector model similar to the one used in the present study, but under the influence of anatomical noise and with a slightly worse energy resolution.14
5. Conclusions
To the best of our knowledge, this study is the first to show the feasibility and benefit of energy weighting on a clinical mammography system. Energy weighting improved the CNR of several relevant target-background combinations by 2.2 to 5.2%, which translates to a potential dose reduction at a constant CNR in the range of 4.5 to 11%. These results are in line with the expectations from previous studies under relevant experimental conditions. We expect the choice of weight factor in practical implementations to be straightforward because the CNR was relatively insensitive to weight and target-background combination, and can be calculated directly from the pixel values of aluminum/PMMA phantom images. Manual measurements of the CNR of microcalcifications and automatic analysis of energy-weighted screening mammograms confirmed that an image-quality improvement is detectable in practice.
Biography
Biographies of the authors are not available.
References
- 1.Alvarez R. E., Macovski A., “Energy-selective reconstructions in x-ray computerized tomography,” Phys. Med. Biol. 21(5), 733–744 (1976). 10.1088/0031-9155/21/5/002 [DOI] [PubMed] [Google Scholar]
- 2.Lehmann L. A., et al. , “Generalized image combinations in dual KVP digital radiography,” Med. Phys. 8(5), 659–667 (1981). 10.1118/1.595025 [DOI] [PubMed] [Google Scholar]
- 3.Lewin J. M., et al. , “Dual-energy contrast-enhanced digital subtraction mammography: feasibility,” Radiology 229(1), 261–268 (2003). 10.1148/radiol.2291021276 [DOI] [PubMed] [Google Scholar]
- 4.Fredenberg E., et al. , “Contrast-enhanced spectral mammography with a photon-counting detector,” Med. Phys. 37(5), 2017–2029 (2010). 10.1118/1.3371689 [DOI] [PubMed] [Google Scholar]
- 5.Johns P. C., Yaffe M. J., “Theoretical optimization of dual-energy x-ray imaging with application to mammography,” Med. Phys. 12, 289–296 (1985). 10.1118/1.595766 [DOI] [PubMed] [Google Scholar]
- 6.Kappadath S. C., Shaw C. C., “Quantitative evaluation of dual-energy digital mammography for calcification imaging,” Phys. Med. Biol. 53(19), 5421–5443 (2008). 10.1088/0031-9155/53/19/010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ding H., Molloi S., “Quantification of breast density with spectral mammography based on a scanned multi-slit photon-counting detector: a feasibility study,” Phys. Med. Biol. 57(15), 4719–4738 (2012). 10.1088/0031-9155/57/15/4719 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Norell B., et al. , “Lesion characterization using spectral mammography,” Proc. SPIE 8313, 83130I (2012). 10.1117/12.913032 [DOI] [Google Scholar]
- 9.Fredenberg E., et al. , “Measurement of breast-tissue x-ray attenuation by spectral mammography: first results on cyst fluid,” Phys. Med. Biol. 58(24), 8609–8620 (2013). 10.1088/0031-9155/58/24/8609 [DOI] [PubMed] [Google Scholar]
- 10.Tapiovaara M. J., Wagner R. F., “SNR and DQE analysis of broad spectrum x-ray imaging,” Phys. Med. Biol. 30, 519–529 (1985). 10.1088/0031-9155/30/6/002 [DOI] [Google Scholar]
- 11.Cahn R. N., et al. , “Detective quantum efficiency dependence on x-ray energy weighting in mammography,” Med. Phys. 26(12), 2680–2683 (1999). 10.1118/1.598807 [DOI] [PubMed] [Google Scholar]
- 12.Giersch J., Niederlohner D., Anton G., “The influence of energy weighting on x-ray imaging quality,” Nucl. Instrum. Meth. A 531(1–2), 68–74 (2004). 10.1016/j.nima.2004.05.076 [DOI] [Google Scholar]
- 13.Lundqvist M., “Silicon strip detectors for scanned multi-slit x-ray imaging,” Ph.D. Thesis, Royal Institute of Technology (KTH), Stockholm, Sweden (2003). [Google Scholar]
- 14.Fredenberg E., et al. , “Observer model optimization of a spectral mammography system,” Proc. SPIE 7622, 762210 (2010). 10.1117/12.845480 [DOI] [Google Scholar]
- 15.Shikhaliev P. M., “Projection x-ray imaging with photon energy weighting: experimental evaluation with a prototype detector,” Phys. Med. Biol. 54(16), 4971–4992 (2009). 10.1088/0031-9155/54/16/009 [DOI] [PubMed] [Google Scholar]
- 16.Bornefalk H., et al. , “Single-shot dual-energy subtraction mammography with electronic spectrum splitting: feasibility,” Eur. J. Radiol. 60(2), 275–278 (2006). 10.1016/j.ejrad.2006.08.004 [DOI] [PubMed] [Google Scholar]
- 17.Fredenberg E., et al. , “Energy resolution of a photon-counting silicon strip detector,” Nucl. Instrum. Meth. A 613(1), 156–162 (2010). 10.1016/j.nima.2009.10.152 [DOI] [Google Scholar]
- 18.Åslund M., et al. , “Physical characterization of a scanning photon counting digital mammography system based on Si-strip detectors,” Med. Phys. 34(6), 1918–1925 (2007). 10.1118/1.2731032 [DOI] [PubMed] [Google Scholar]
- 19.Åslund M., et al. , “Scatter rejection in multi-slit digital mammography,” Med. Phys. 33, 933–940 (2006). 10.1118/1.2179122 [DOI] [PubMed] [Google Scholar]
- 20.Schmidt T. G., “Optimal ‘image-based’ weighting for energy-resolved CT,” Med. Phys. 36(7), 3018–3027 (2009). 10.1118/1.3148535 [DOI] [PubMed] [Google Scholar]
- 21.Wagner R. F., Brown D. G., “Unified SNR analysis of medical imaging-systems,” Phys. Med. Biol. 30(6), 489–518 (1985). 10.1088/0031-9155/30/6/001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Boone J. M., Seibert J. A., “Accurate method for computer-generating tungsten anode x-ray spectra from 30 to 140 kV,” Med. Phys. 24(11), 1661–1670 (1997). 10.1118/1.597953 [DOI] [PubMed] [Google Scholar]
- 23.Berger M. J., et al. , “XCOM: photon cross section database,” 2005, http://physics.nist.gov/xcom (June 2009).
- 24.Hammerstein G. R., et al. , “Absorbed radiation dose in mammography,” Radiology 130(2), 485–491 (1979). 10.1148/130.2.485 [DOI] [PubMed] [Google Scholar]
- 25.Fredenberg E., et al. , “Optimization of mammography with respect to anatomical noise,” Proc. SPIE 7961, 796112 (2011). 10.1117/12.877985 [DOI] [Google Scholar]
- 26.Burgess A. E., Jacobson F. L., Judy P. F., “Human observer detection experiments with mammograms and power-law noise,” Med. Phys. 28(4), 419–437 (2001). 10.1118/1.1355308 [DOI] [PubMed] [Google Scholar]
- 27.Lange K. L., Little R. J. A., Taylor J. M. G., “Robust statistical modeling using the t distribution,” J. Am. Stat. Assoc. 84(408), 881–896 (1989). [Google Scholar]
- 28.Fahrig R., Yaffe M. J., “Optimization of spectral shape in digital mammography: dependence on anode material, breast thickness, and lesion type,” Med. Phys. 21(9), 1473–1481 (1994). 10.1118/1.597191 [DOI] [PubMed] [Google Scholar]
- 29.Bochud F. O., et al. , “Estimation of the noisy component of anatomical backgrounds,” Med. Phys. 26(7), 1365–1370 (1999). 10.1118/1.598632 [DOI] [PubMed] [Google Scholar]
- 30.Karg J., et al. , “Using the Medipix2 detector for energy weighting,” Nucl. Instrum. Meth. A 546(1–3), 306–311 (2005). 10.1016/j.nima.2005.03.033 [DOI] [Google Scholar]