Abstract.
An analytical framework is presented for evaluating the equivalence of parenchymal texture features across different full-field digital mammography (FFDM) systems using a physical breast phantom. Phantom images (FOR PROCESSING) are acquired from three FFDM systems using their automated exposure control setting. A panel of texture features, including gray-level histogram, co-occurrence, run length, and structural descriptors, are extracted. To identify features that are robust across imaging systems, a series of equivalence tests are performed on the feature distributions, in which the extent of their intersystem variation is compared to their intrasystem variation via the Hodges–Lehmann test statistic. Overall, histogram and structural features tend to be most robust across all systems, and certain features, such as edge enhancement, tend to be more robust to intergenerational differences between detectors of a single vendor than to intervendor differences. Texture features extracted from larger regions of interest (i.e., ) and with a larger offset length (i.e., ), when applicable, also appear to be more robust across imaging systems. This framework and observations from our experiments may benefit applications utilizing mammographic texture analysis on images acquired in multivendor settings, such as in multicenter studies of computer-aided detection and breast cancer risk assessment.
Keywords: digital mammography, parenchymal pattern, robust texture features
1. Introduction
Breast cancer is the most commonly diagnosed cancer in American women after skin cancer, with about one in eight expected to develop invasive breast cancer over the course of their lifetime.1 With the advent of early cancer detection through screening and treatment, the five-year survival rate for women diagnosed with breast cancer in western countries is currently up to 89%.2 Approximately 95% of screening centers in the United States utilize full-field digital mammography (FFDM) systems as their primary screening tool,3 which rapidly replaced screen-film mammography over the last decade due to advantages of FFDM systems, such as improved image contrast and dynamic range.4 Mammographic images have extensively been used in the literature to generate image-based features for examining the potential risk for breast cancer.5–20 For example, mammographic percent density (PD%)5,6,15 has been repeatedly shown to be a strong risk factor for breast cancer. In addition, it has also been suggested in more recent studies that parenchymal texture features,7,8 which are measures of the local distribution of the parenchymal tissue, may also provide complementary information regarding an individual woman’s risk for breast cancer.
For studies analyzing parenchymal texture features for breast cancer risk assessment, one additional factor that needs to be accounted for is the mammography system used for image acquisition. With the wide-scale implementation of screening programs utilizing FFDM systems, large clinical data sets typically include images acquired from several commercial FFDM systems built with different detector technologies and image acquisition parameters. Differences between x-ray systems introduce inherent differences to the acquired images, which subsequently affect extracted mammographic features, such as breast density21 and, as a result, higher-order measures of breast parenchymal texture. This effect can be more pronounced for more granular type of features that directly depend on the variation of image intensity values, such as texture features, compared to more global image measures, such as breast PD%. For example, Manduca et al.8 noted that accounting for the parameters used to acquire images from different mammography systems is important, specifically with regards to affecting the numerical values of texture features. This could, in turn, bias any subsequent investigation of associations between such features and any related outcomes of interest, such as the risk of developing breast cancer.
Motivated by this problem, we propose a statistical framework to evaluate the robustness of texture features across FFDM systems from different vendors, focusing on the effect of different x-ray systems on image intensity and texture. We use a physical breast phantom (Gammex 169 “Rachel,” Madison, Wisconsin), which enables the imaging of a consistent (i.e., ground truth) parenchymal tissue pattern across different systems, allowing us to directly evaluate any added system-induced effects on image intensity and texture. To demonstrate proof-of-concept and be applicable to the clinical setting, we compare three FFDM systems (Senographe 2000D and Senographe DS, General Electric Medical Systems, Milwaukee, Wisconsin; and Selenia Dimensions, Hologic Inc., Bedford, Massachusetts) operated at the clinical automated exposure control setting and design a series of experiments to evaluate whether the distributions of a panel of different texture features are robust and statistically equivalent across these different imaging systems. While our framework is presented here using three specific imaging systems from two vendors and a selected set of texture features previously used for breast cancer risk assessment, our method can, in principal, generalize across a broader range of image acquisition systems and features. As such, it could have value for studies utilizing mammographic feature analysis in a multivendor setting, such as studies focusing on breast cancer risk assessment, breast tissue characterization, and computer-aided diagnosis.
2. Materials and Methods
2.1. Breast Phantom Imaging
An anthropomorphic breast phantom22 (Gammex 169 “Rachel,” Madison, Wisconsin) was imaged on three FFDM systems. The first two systems, the Senographe 2000D and DS, utilize equal-sized, indirect flat panel detectors with a common spatial resolution of , although the GE DS has a smaller x-ray tube relative to GE 2000D. In contrast to these systems, the Selenia Dimensions utilizes an amorphous selenium direct flat panel detector with a higher spatial resolution of . Last, the three units have different automated exposure control systems, resulting in different dose performances.
To account for system noise effects and better assess intersystem differences, digital mammograms of the Rachel phantom were acquired five times on each FFDM unit, with no physical movement of the phantom during the image acquisition process. The raw (FOR PROCESSING) images stored at the common vendor-specified 14-bit gray-level depth were used for subsequent analysis. The GE systems utilized an Rh/Rh target/filter combination and the Hologic system utilized a W/Rh combination. Acquisition parameters were and for GE 2000D, and for the GE DS system, and and for the Hologic Selenia Dimensions, when using the automated exposure control setting for each model digital mammography machine.
2.2. General Statistical Framework for Robust Feature Identification
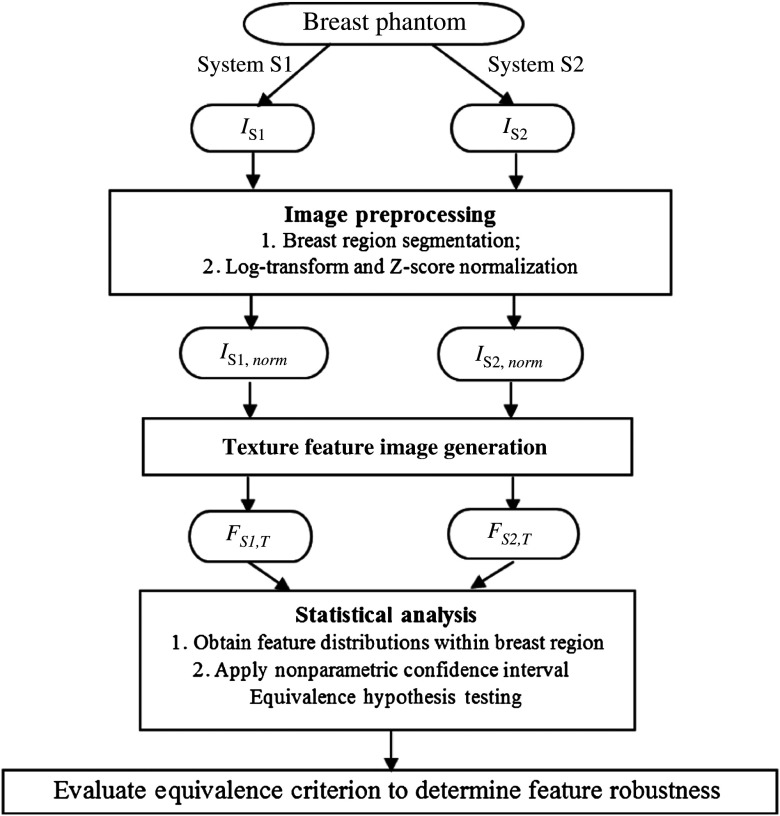
For the purposes of our study, we define a robust texture feature to be a feature for which the distributions of the corresponding feature images from a given pair of systems are statistically equivalent. Specifically, given a texture feature, the process to identify whether it is robust can be divided into three main steps (Fig. 1). First, a series of phantom images are acquired from all mammography systems and the breast region is segmented. Image intensity values are first log-transformed to account for the relationship between raw gray-level values and exposure, then inverted so that radio-opaque foreground objects (i.e., the breast) are of a higher pixel intensity than the background (i.e., air), and, finally, are normalized by a z-score transformation23 within the breast region. Briefly, z-score normalization is a linear transformation of image pixels, or more generally any distribution, so that the average value of the distribution of image pixels is made to be zero and the standard deviation of the distribution of values is one. In practice, z-score normalization has the effect of aligning different histograms of different images without altering the shape of their distribution.24
Fig. 1.
Workflow of our statistical framework for texture feature equivalence assessment. , digital mammography image acquired from system ; , after image intensity normalization; , texture feature image for system , texture feature .
For each log-transformed, z-score normalized image, texture features are generated using automated computerized analysis25,26 from each of the five images acquired on each digital mammography system, generating a set of five pixel-value distributions per each texture-parameterization-system combination. Next, these distributions are compared across acquisition systems via a series of nonparametric equivalence tests,27 testing the hypothesis that the median of the differences in texture feature values across acquisition systems is within a prespecified equivalence range.27 Details of the procedure are provided in Sec. 2.6. All statistical analysis in this study was performed with SAS 9.4 statistical computing software.
2.3. Image Preprocessing
As the region occupied by the breast phantom covers only a fraction of the total image field [Fig. 2(a)], we perform a preprocessing step to (1) remove the phantom bounding box from any subsequent analysis and (2) segment the breast region [Figs. 2(b) and 2(c)]. The bounding box is cropped based on the detection of the box boundary [shown in Fig. 2(a)]. Given the differences in the edge response and spatial resolution between the three systems, the breast region is segmented by using intensity thresholding in each phantom image, which is then used for the analysis of all images acquired by that system.
Fig. 2.
Raw digital mammogram of the Rachel phantom acquired on GE 2000D: (a) the original raw phantom image, (b) exclusion of the breast phantom bounding box, shown after the inverse-log transformation for visualization, and (c) the binary mask of the breast region.
2.4. Texture Feature Generation
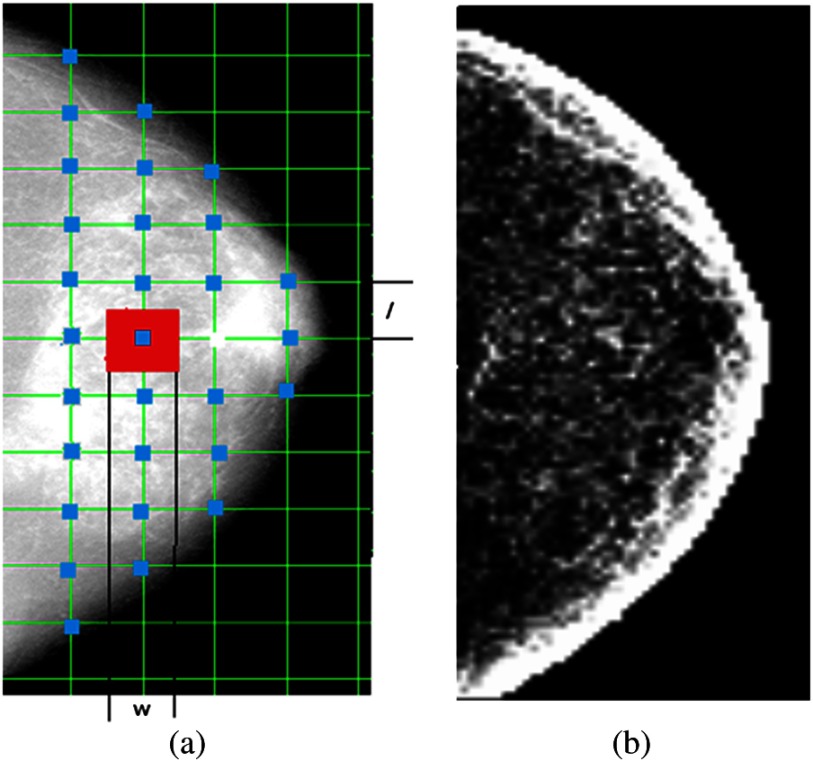
We used an automated image analysis pipeline25 that can generate a corresponding texture feature image for each texture descriptor. Specifically, we use a lattice-based strategy, where at each lattice point [shown in blue in Fig. 3(a)], a texture feature value is calculated within the local square region [shown in red in Fig. 3(a)] surrounding the lattice point. Both the lattice size (i.e., the distance between neighborhood lattice points) and the local window size are parameters that can be optimized for texture feature generation. In our study, the lattice size and the local window size are set to be equal. Five different window sizes , equal to 15, 31, 63, 127, and , were evaluated to capture parenchymal texture patterns at different granularities.
Fig. 3.
(a) The lattice scheme for texture image generation and (b) a gray-level histogram (STD) image.
The texture features used in our study can be broadly categorized into four groups: (1) gray-level histogram features;28 (2) co-occurrence features;29,30 (3) run-length features;31,32 and (4) structural features.20,33–35 All features and their corresponding shorthand notations are summarized in Table 1 (detailed mathematical notations are also included in the Appendix). These features were selected in our study for two main reasons. First, most of these features have been widely used for mammographic image analysis and shown to have value specifically for breast tissue characterization in breast cancer risk assessment.17,34,36 Second, features capturing the local tissue architecture, such as the local binary pattern (LBP)33 and the edge enhancing index,35,37 are relatively more recent texture features. Traditionally, these features have been used in computer vision,33,37,38 while recently they have also been applied for mammographic pattern analysis and breast cancer risk assessment.35
Table 1.
A list of all texture features analyzed in our study.
| Feature class | Feature name | Notation |
|---|---|---|
| Group 1 Gray-level histogram | Max | MAX |
| Min | MIN | |
| Mean | MEAN | |
| Sum | SUM | |
| Entropy | ETP | |
| Kurtosis | KTS | |
| Sigma | STD | |
| Skewness | SKEW | |
| 5th percentile | 5TH | |
| 5th mean | 5THM | |
| 95th percentile | 95TH | |
| 95th mean | 95THM | |
| Group 2 Co-occurrence | Cluster shade | CSD |
| Energy | ENG | |
| Entropy | CETP | |
| Inertia | INT | |
| Correlation | COR | |
| Haralick correlation | HCOR | |
| Inverse difference moment | IDM | |
| Group 3 Run length | Grey-level nonuniformity | GLN |
| Run-length nonuniformity | RLN | |
| Run percentage | RP | |
| High gray-level run emphasis | HGLRE | |
| Long run emphasis | LRE | |
| Low gray-level run emphasis | LGLRE | |
| Short run emphasis | SRE | |
| Group 4 Structural features | Local binary pattern | LBP |
| Edge enhancing index | EEI | |
| Fractal dimension | FD |
2.5. Parameters in Texture Feature Generation
These texture features are computed using certain parameters, summarized into two main categories: (1) parameters that are involved in the numerical implementation and can be decided depending on numerical precision, computational cost, and related factors and (2) parameters introduced in the mathematical computation directly related to inherent properties captured by the feature (e.g., co-occurrence pixel distance, etc.).
In general, there is no single best choice for parameters within the first category, due to trade-offs between precision and efficiency. Features in groups 1 to 3 in Table 1 all depend upon such a parameter, specifically the number of histogram bins. In this study, this parameter was set to a fixed value of 128 based on previous studies.28 For features with parameters in the second category, we describe in detail our approach for the co-occurrence, LBP, and edge enhancing index features.
Co-occurrence features describe the spatial relationship between pixels and are based on the gray-level co-occurrence matrix (GLCM).29 Given an image , an by GLCM matrix is defined as
| (1) |
where is the number of gray levels used to describe image , is the pixel offset length, and is the offset angle. is commonly chosen as a power of 2, typically between 16 and 256. In our experiments, was chosen equal to 128 to balance computational precision with efficiency. The combination of parameters and determines the search direction and the neighborhood size of each pixel pair. Features are typically calculated using the same offset length along four directions (0, 45, 90, and 135 deg) and then averaged, based on the assumptions that these features are orientation invariant39,40 and that one single direction might not give sufficient texture information.30 With respect to the offset length , in several studies, it is chosen by default to be equal to 1 pixel, however, this is not always justified based on its actual physical dimensions.7,41 Here we theorize that the proper selection of is important for the robustness of the corresponding texture features, as it may be associated with the blurring effect, and therefore, artificially introduced texture, in FFDM systems using an indirect-conversion detector. To evaluate such effects, we varied the offset length from 1 to 13 pixels (i.e., 0.1 mm up to 1.3 mm) by using 2-pixel increments.
LBPs33,38 capture the relationship between central and neighboring pixels. Given an image , the value at pixel is defined as
| (2) |
The two parameters, neighborhood size and number of neighborhood pixels , define the LBP.18 Previous studies have shown that the performance of LBP features in pattern detection varies with the change of parameters and . The common choices of in previous studies in computer vision include 1, 2, and 3 pixels.33 In our study, three pairs of values were used, namely (1, 8), (2, 20), and (3, 36) pixels.
Finally, the edge enhancing index is based on edge enhancing diffusion,42 which preserves and enhances edge structures within an image. The flow-like structures within the breast tissue suggest that this type of feature could be an appropriate descriptor for characterizing the structural properties of the parenchymal pattern.
Given an image , the edge enhancing index is defined as
| (3) |
Here, and with are eigenvalues of the diffusion tensor matrix defined as
When , , and when , and is an empirical normalizing factor set equal to 10 for this study. The parameter evaluated in our study is the Gaussian kernel size . Gaussian smoothing (i.e., ) is used as a common image preprocessing step to remove image noise before image analysis and the kernel size determines the degree of smoothing (i.e., the extent of image details that are preserved). In our study, was varied from 1 to 15 pixels.
2.6. Statistical Analysis
To assess the robustness of texture features across any two FFDM systems (i.e., pair-wise comparison), the distributions of texture feature values were compared via a series of nonparametric equivalence tests, testing the hypothesis that the median of the differences, , in texture feature values across the two acquisition systems is within an equivalence range equal to the maximum intrasystem variation of the two systems being compared pair-wise. For each system, the intramachine variation was determined by the maximum 95% confidence interval (CI) resulting from the intrasystem comparisons. The test statistic is computed as follows: given observations from two independent acquisition systems, for and for , respectively, a difference is calculated between each pair . There are such differences. The test statistic is equal to and is equivalent to the Hodges–Lehmann statistic.43
Intra- and intersystem comparisons for each different window size utilized different numbers of observations. Comparisons of values derived from the larger window sizes (e.g., 255 and ) resulted in smaller sample sizes. This is because as the lattice size increases, larger amounts of the image (in intensity space) are represented by each pixel in feature space, thus resulting in a smaller number of feature space pixels needed to represent the entire image. These smaller sample size comparisons were carried out via a nonparametric equivalence test procedure in which data-derived confidence intervals were utilized.27 The derivation of these confidence intervals can be briefly described as follows. First, an empirical distribution for the independent difference is computed as , where , , 0 for , , , respectively. General U-statistic theory implies the asymptotic standard normality of the statistic, for any with . Confidence interval bounds are then defined as
| (4) |
| (5) |
where denotes the () percentile of the standard normal distribution. Computing the distribution of the independent differences directly from the data and utilizing them to build the CIs for the test statistic allows us to assess distributional differences without making any assumptions regarding their shape. Finally, comparisons for the smaller window sizes (i.e., 63, 31, and ) resulted in much larger sample sizes rendering the empirical procedure computationally intractable, thus, asymptotically derived CIs for the Hodges–Lehmann statistic43 were utilized.
Intersystem robustness was assessed according to the following four category scale: (1) features for which the intermachine CI was entirely contained within the specified equivalence bounds were deemed very robust (VR), implying that the variation between the systems being compared is not significantly different from the intramachine variation; (2) cases in which the intermachine CIs were not fully contained within the equivalence bounds, but still crossed [indicating that the test statistic is not significantly (at ) different from zero, thus implying no significant difference in texture feature distributions across systems] and for which the intermachine test statistic was contained in the intramachine CI, were deemed robust (R); (3) cases for which only one of the criteria described in (1) or (2) were met were deemed less robust (LR); and (4) cases that did not meet any of the criteria described in (1), (2), and (3) were deemed not robust (NR).
3. Results
Results of the equivalence assessment comparing the distributions of all texture features between each pair of systems are provided, where the degree of feature equivalence between the GE 2000D-GE DS, Hologic Selenia Dimensions-GE 2000D, and Hologic Selenia Dimensions-GE DS comparisons are shown in Tables 2, 3, and 4, respectively.
Table 2.
Feature robustness between the GE 2000D and GE DS systems. VR, very robust; R, robust; LR, less robust; NR, not robust.
| Feature group | Feature | Parameter | Window size (, pixel) | ||||
|---|---|---|---|---|---|---|---|
| 15 | 31 | 63 | 127 | 255 | |||
| Gray-level histogram | 5TH | R | R | R | R | R | |
| 5THM | NR | R | R | R | VR | ||
| 95TH | R | R | R | VR | VR | ||
| 95THM | R | R | R | VR | VR | ||
| ETP | NR | NR | R | VR | VR | ||
| KTS | NR | NR | R | VR | VR | ||
| MAX | NR | R | R | R | R | ||
| MEAN | R | R | R | VR | VR | ||
| MIN | NR | LR | R | R | VR | ||
| STD | NR | NR | R | R | R | ||
| SKEW | LR | R | R | VR | VR | ||
| SUM | R | R | R | VR | VR | ||
| Co-occurrence | CSD | Offset length | NR | R | R | R | VR |
| COR | NR | NR | NR | R | R | ||
| ENG | NR | NR | NR | NR | R | ||
| ETP | NR | NR | NR | NR | NR | ||
| HCOR | NR | NR | R | R | VR | ||
| INT | NR | NR | NR | NR | NR | ||
| IDM | NR | NR | NR | NR | NR | ||
| Run length | GLN | LR | LR | R | R | R | |
| HGLRE | R | NR | R | VR | VR | ||
| LRE | NR | NR | NR | NR | LR | ||
| LGLRE | NR | NR | NR | VR | VR | ||
| RLN | NR | NR | NR | NR | NR | ||
| RP | NR | NR | NR | NR | LR | ||
| SRE | NR | NR | NR | NR | LR | ||
| Structural | LBP | , | VR | VR | VR | R | R |
| , | VR | R | VR | R | R | ||
| , | VR | R | R | R | VR | ||
| EEI | NR | LR | R | R | R | ||
| R | R | R | VR | NR | |||
| R | R | R | R | R | |||
| LR | R | R | R | VR | |||
| FD | NR | NR | NR | VR | NR | ||
Table 3.
Feature robustness between the Hologic Selenia Dimensions and GE 2000D systems. VR, very robust; R, robust; LR, less robust; NR, not robust.
| Feature group | Feature | Parameter | Window size (, pixel) | ||||
|---|---|---|---|---|---|---|---|
| 15 | 31 | 63 | 127 | 255 | |||
| Gray-level histogram | 5TH | VR | VR | VR | VR | R | |
| 5THM | R | VR | VR | VR | VR | ||
| 95TH | R | R | R | R | R | ||
| 95THM | R | R | R | R | R | ||
| ETP | NR | NR | NR | R | R | ||
| KTS | NR | NR | R | R | R | ||
| MAX | R | R | R | LR | R | ||
| MEAN | R | R | R | R | R | ||
| MIN | NR | R | VR | VR | R | ||
| STD | NR | NR | NR | LR | R | ||
| SKEW | NR | R | R | VR | VR | ||
| SUM | R | R | R | R | R | ||
| Co-occurrence | CSD | Offset length | NR | LR | NR | R | R |
| COR | NR | R | NR | LR | R | ||
| ENG | NR | NR | NR | NR | R | ||
| ETP | NR | NR | NR | NR | LR | ||
| HCOR | R | NR | NR | R | R | ||
| INT | NR | NR | NR | NR | NR | ||
| IDM | NR | NR | NR | NR | NR | ||
| Run length | GLN | NR | NR | NR | R | R | |
| HGLRE | NR | R | NR | VR | R | ||
| LRE | NR | NR | NR | NR | R | ||
| LGLRE | NR | NR | NR | NR | LR | ||
| RLN | NR | NR | NR | NR | R | ||
| RP | NR | NR | NR | NR | NR | ||
| SRE | LR | NR | NR | NR | NR | ||
| Structural | LBP | , | VR | VR | VR | VR | NR |
| , | VR | VR | VR | VR | NR | ||
| , | VR | VR | VR | VR | NR | ||
| EEI | NR | LR | R | LR | LR | ||
| NR | NR | NR | NR | NR | |||
| NR | NR | NR | LR | LR | |||
| NR | NR | NR | LR | LR | |||
| FD | NR | NR | NR | VR | LR | ||
Table 4.
Feature robustness between the Hologic Selenia Dimensions and GE DS systems. VR, very robust; R, robust; LR, less robust; NR, not robust.
| Feature group | Feature | Parameter | Window size (, pixel) | ||||
|---|---|---|---|---|---|---|---|
| 15 | 31 | 63 | 127 | 255 | |||
| Gray-level histogram | 5TH | R | R | R | VR | VR | |
| 5THM | R | R | R | R | R | ||
| 95TH | NR | R | R | R | R | ||
| 95THM | NR | LR | LR | NR | R | ||
| ETP | NR | NR | NR | VR | VR | ||
| KTS | VR | R | R | R | R | ||
| MAX | NR | NR | NR | NR | LR | ||
| MEAN | VR | R | R | R | R | ||
| MIN | LR | R | R | R | R | ||
| STD | NR | NR | NR | NR | R | ||
| SKEW | NR | NR | R | VR | VR | ||
| SUM | VR | R | R | R | R | ||
| Co-occurrence | CSD | Offset length | NR | NR | R | VR | VR |
| COR | NR | NR | NR | NR | R | ||
| ENG | NR | NR | NR | NR | R | ||
| ETP | NR | NR | NR | NR | R | ||
| HCOR | NR | NR | NR | LR | R | ||
| INT | NR | NR | NR | LR | R | ||
| IDM | NR | NR | NR | LR | R | ||
| Run length | GLN | NR | NR | NR | R | R | |
| HGLRE | NR | NR | R | R | VR | ||
| LRE | NR | NR | NR | R | VR | ||
| LGLRE | NR | LR | R | NR | VR | ||
| RLN | NR | NR | NR | VR | R | ||
| RP | LR | NR | NR | R | R | ||
| SRE | LR | NR | NR | R | R | ||
| Structural | LBP | , | VR | VR | VR | R | LR |
| , | VR | R | VR | R | R | ||
| , | VR | R | VR | R | R | ||
| EEI | NR | NR | LR | VR | R | ||
| NR | NR | NR | NR | VR | |||
| NR | NR | NR | LR | LR | |||
| NR | NR | NR | LR | LR | |||
| FD | R | R | VR | VR | LR | ||
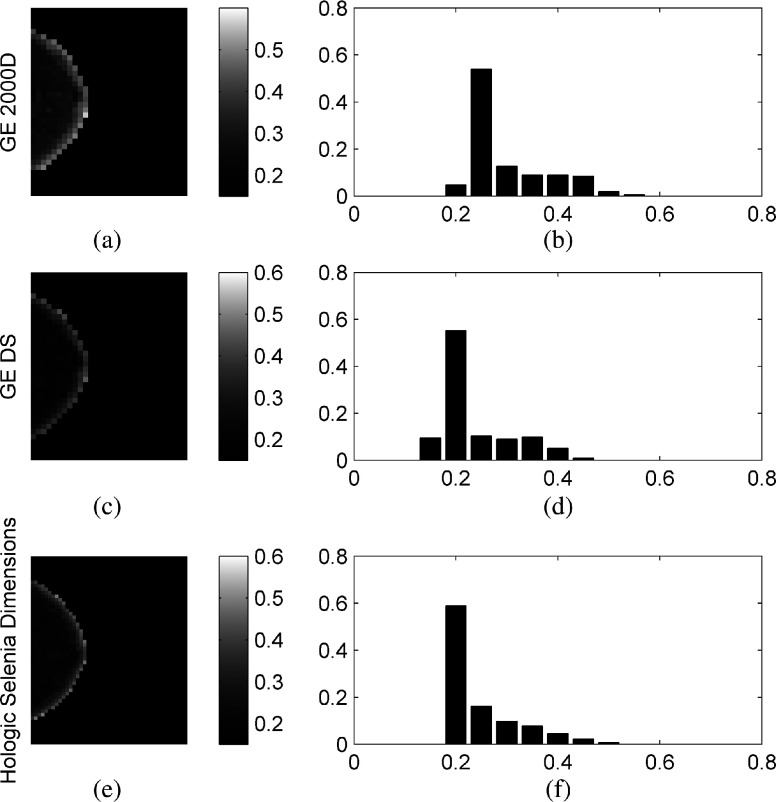
In general, gray-level histograms and structural features appear to be more robust than co-occurrence and run-length texture features, while smaller window sizes tend to result in fewer robust texture features. Larger window sizes (i.e., ) appear to provide generally more robust texture features. The majority of structural texture features found to be VR appear in the LBP subcategories of all three tables. The effect of increased window size is most evident in the co-occurrence and run-length features of all three comparisons, but is also apparent in the gray-level histogram features of the GE 2000D-GE DS comparison, which exhibits VR features for window sizes of 127 and . The fractal dimension feature also appears to benefit from increased window size as the majority of the VR features for this section are for the 63 and larger window sizes. The edge enhancing index features are least robust across the Selenia-GE 2000D systems, marginally more robust for the Selenia-GE DS systems, and most robust for the GE 2000D-GE DS comparison. Last, few co-occurrence features were found to be robust when computed at an offset length of 1. Figure 4 provides texture maps and histograms of the inverse difference moment features on the three systems computed at offset length 1 and window size 63, illustrating this finding.
Fig. 4.
Example feature maps [(a), (c), and (e)] and feature-value histograms [(b), (d), and (f)] of the co-occurrence inverse difference moment feature computed on the GE 2000D [(a) and (b)], GE DS [(c) and (d)], and Hologic Selenia Dimensions [(e) and (f)] digital mammography systems using a window size of and offset of .
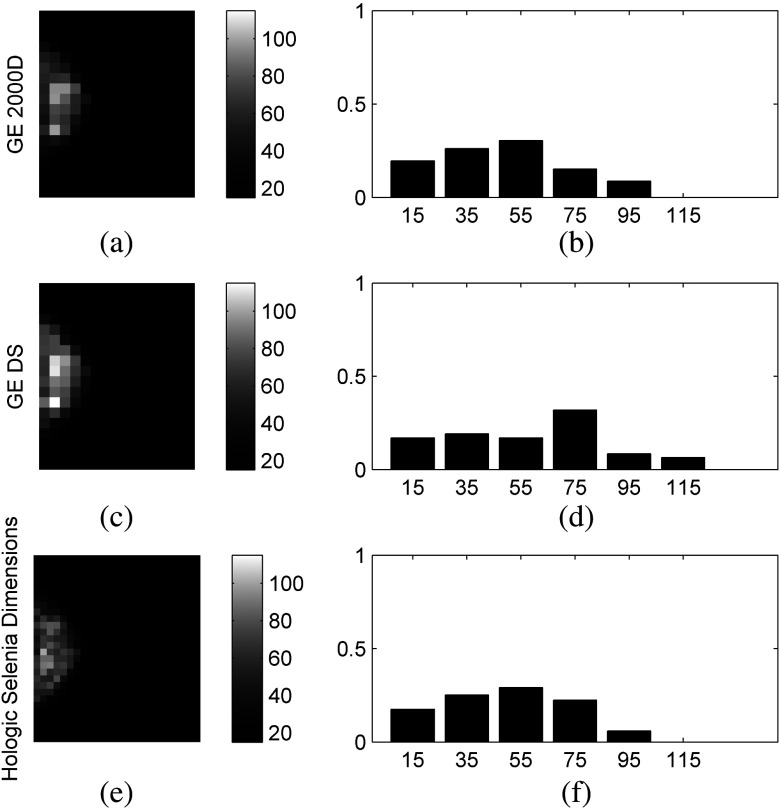
Tables 5–7 show the effect of the offset length parameter, , used in the computation of the GLCM for the co-occurrence texture features, when a representative window size is fixed at for the three pair-wise system comparisons. Overall, co-occurrence features tend to be more robust across the Selenia-GE 2000D comparison, where VR designations appear for the majority of features and for all offset lengths. While cluster shade and Haralick correlation are robust across all comparisons and for all offset lengths, the correlation feature is least robust across the Selenia-GE DS comparison where the feature is found to be NR for all offset lengths except 1. Increasing the offset length appears to benefit robustness among the entropy, energy, inertia, and inverse difference moment features, and is most apparent across the Selenia-GE DS and GE 2000D-GE DS comparisons. Figure 5 provides texture maps and histograms of the inertia feature on the three systems computed at offset length 7 and window size 127.
Table 5.
Effect of offset length, , on feature robustness between the GE 2000D and GE DS systems for the co-occurrence texture features computed at window size 127. VR, very robust; R, robust; LR, less robust; NR, not robust.
| Feature | Offset length (, pixel) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | ||
| Co-occurrence | CSD | R | R | R | R | R | R | R |
| COR | R | R | R | R | R | R | R | |
| ENG | NR | NR | NR | R | R | R | R | |
| ETP | NR | NR | LR | R | R | R | R | |
| HCOR | R | R | R | R | R | R | R | |
| INT | NR | NR | NR | R | R | R | R | |
| IDM | NR | NR | LR | R | R | R | R | |
Table 6.
Effect of offset length, , on feature robustness between the Hologic Selenia Dimensions and GE 2000D systems for the co-occurrence texture features computed at window size 127. VR, very robust; R, robust; LR, less robust; NR, not robust.
| Feature | Offset length (, pixel) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | ||
| Co-occurrence | CSD | R | R | R | R | R | R | R |
| COR | LR | NR | NR | NR | NR | NR | NR | |
| ENG | NR | R | R | R | LR | LR | LR | |
| ETP | NR | R | VR | R | R | R | R | |
| HCOR | R | R | R | R | R | R | R | |
| INT | NR | LR | VR | VR | VR | VR | VR | |
| IDM | NR | NR | VR | R | LR | LR | LR | |
Table 7.
Effect of offset length, , on feature robustness between the Hologic Selenia Dimensions and GE DS systems for the co-occurrence texture features computed at window size 127. VR, very robust; R, robust; LR, less robust; NR, not robust.
| Feature | Offset length (, pixel) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | ||
| Co-occurrence | CSD | VR | VR | VR | VR | VR | VR | VR |
| COR | NR | NR | NR | NR | NR | NR | NR | |
| ENG | NR | NR | NR | NR | NR | NR | NR | |
| ETP | NR | NR | NR | NR | NR | NR | LR | |
| HCOR | LR | LR | LR | LR | LR | LR | LR | |
| INT | LR | LR | LR | LR | R | R | R | |
| IDM | LR | VR | VR | R | R | R | R | |
Fig. 5.
Example feature maps [(a), (c), and (e)] and feature-value histograms [(b), (d), and (f)] of the co-occurrence inertia (INT) feature computed on the GE 2000D [(a) and (b)], GE DS [(c) and (d)], and Hologic Selenia Dimensions [(e) and (f)] digital mammography systems using a window size of and offset of .
4. Discussion
The question of how to most appropriately normalize mammographic images obtained from different vendor systems and acquisition physics parameters for subsequent image analysis and feature extraction is an important active area of research. In our study, z-score normalization was applied to the log-transformed images in order to remove linear differences in gray-level intensities between the various FFDM systems evaluated. Both log-transformation and z-score normalization are commonly utilized preprocessing steps when dealing with raw, FOR PROCESSING, mammograms as a means to alleviate interscan differences between studies via histogram alignment, while still maintaining the overall pattern, spatial relationship, and relative contrast of the pixels,24 all of which are important in texture analysis. Our results suggest that the framework proposed in this work will be beneficial for studies utilizing texture analysis in digital mammography in clinical, multisite, multivendor data sets, including studies investigating breast cancer risk assessment, tissue classification, and computer-aided diagnosis.
As our study focuses on the effect of detector differences on texture quantification and not necessarily on classification tasks such as risk assessment using such textures, it is difficult to compare our extracted texture measures directly to prior work, although comparison of parameter selection choices can be reported. In previous studies using co-occurrence features, the offset length was generally chosen heuristically. For example, in mammographic imaging research, is often chosen between 1 and 10 pixels with 1 being the most common value, such as in the work by Khuzi et al.30 for mass identification and Li et al.7 for texture analysis of mammographic parenchymal patterns. Our results suggest that if the offset length is gradually increased to 7 pixels or larger, the majority of inherent system effects can be alleviated. The effects of the window size and the offset length on the texture feature images are shown in Figs. 6 and 7. For smaller window sizes, more granular features are obtained, while for larger windows, more smoothed (i.e., blurred) texture images are generated.
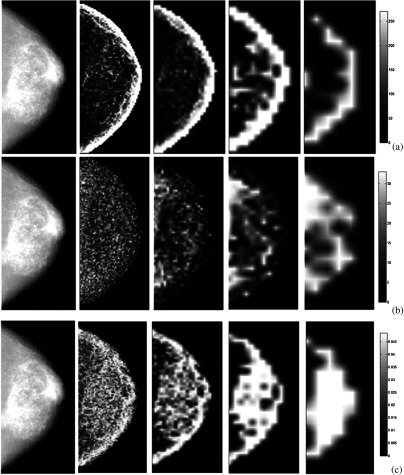
Fig. 6.
Illustration of the effect of the window size () on the texture feature images. Representative examples shown in each row, from left to right, for GE 2000D raw images (after -log transformation) and corresponding texture feature images with increasing window sizes of 15, 31, 63, and for texture features (a) STD (gray-level histogram); (b) GLN (run length); (c) EEI (structural). The texture feature images are generated from z-score normalized raw images acquired on the GE 2000D system.
Fig. 7.
Co-occurrence feature energy with varying window size and offset length. Each row indicates one window size (31, 63, ) and each column indicates one offset length (1, 5, 9 pixels).
This observation may be partly explained via examination of the modulation transfer function (MTF) of the imaging system,44 a measure of its inherent spatial resolution. The MTF is unity at the lowest spatial frequency and drops with increasing spatial frequency. Both of the GE systems in our study use indirect conversion detectors (i.e., cesium phosphor with thin-film transistor). Compared to a direct conversion process, such as the one utilized in the Hologic Selenia Dimensions system evaluated in our study, blurring effects are introduced by phosphor luminescence and can cause loss of the spatial resolution, which may be alleviated by the use of smoothed (i.e., less granular) texture features that do not consider the spatial relation of pixels (e.g., first-order histogram statistics), intensity-invariant structure-based features, and larger lattice window sizes. Furthermore, when taking this blurring effect into consideration, the differences between texture images for the two GE systems, and between the GE and Hologic systems, can potentially be enhanced within relatively small pixel neighborhood sizes, as pixels within such a small neighborhood can be highly spatially correlated, which could be the case when choosing a small offset length (e.g., pixel) in the co-occurrence texture feature calculation. This interpixel correlation is also likely to affect the robustness of many of the gray-level run-length features: as the correlation properties differ between images, so will the gray-level runs in an image as they are, in essence, representative of pixel-adjacency relationships. Similarly, as the lattice window size increases, more features are labeled as robust between the three systems. This does not necessarily imply that features generated using a coarser lattice scheme (e.g., 63 pixels or larger) or larger co-occurrence offset length will perform better in tissue characterization or breast cancer risk assessment. As the images are essentially smoothed when analyzed with such coarser parameters, image noise may be removed, implying less confounding results due to system effects; however, the performance of these features for tissue characterization may be reduced, and this will need to be further investigated in future research studies.
One interesting finding from our study is the impact of vendor normalization on apparent gray-level values in an image. One potential explanation is that these differences are due to the fact that x-ray projection images are inherently not calibrated, as are most medical imaging modalities with a few exceptions, such as computed tomography images. In practice, this leads to vendor-specific mapping of observed x-ray attenuation values to gray-level pixel values using proprietary algorithms. This mapping can vary between the different generations of a given system, as is observed in this study, as well as between different vendors of a given modality. The existence of such differences demonstrates the necessity of running studies such as ours and the use of a consistent normalization scheme (i.e., log-transformation followed by z-score normalization) when investigating imaging features dependent on gray-level values, especially when images are acquired from a variety of data sources, in order to ensure that observed differences in an imaging feature are not affected by underlying confounding and bias.
One should note that although the phantom was not moved between the five acquisitions of a single system, it was physically moved between the three systems, and thus, the mammograms taken by the three systems were not spatially aligned in any systematic way, as, for example, by the means of image registration. In that context, our results also suggest that when a whole-breast texture analysis approach is taken, the exact alignment of the lattice regions of interest, and to a lesser extent, the dose and system resolution differences, seem to have a negligible impact on the robustness of a significant subset of features. This is likely due to the fact that any small variations in texture over the breast are averaged out when analyzing the entire breast, and supports the notion and utility of whole-breast texture analysis. One limitation of our study is that while we do compare several detectors with different technological properties, two of the three systems evaluated, specifically the GE 2000D and DS, were developed by the same manufacturer. In addition, we only evaluate a single system with a direct detector, the Hologic Selenia Dimensions, and only utilize one physical phantom as ground truth for parenchymal texture in our analysis.
Last, one issue common to studies evaluating many metrics simultaneously is that of multiple comparisons. However, hypothesis testing for equivalence via a CI-based approach somewhat mitigates this multiplicity issue. A multiple-comparison adjustment (e.g., a Bonferroni type of approach) in this setting would imply the use of a wider CI for interscanner differences than the commonly used 95% CI. However, based on the definitions of robustness defined in our work, the use of wider CIs would have systematic effects on the results that would most likely and for the most part leave our findings unchanged. Specifically, given any arbitrarily wider CI as a multiple-comparisons correction, VR features would at most become R as the test statistic would still remain in the intrasystem CI and the wider CI would remain crossing even if the entire CI was no longer contained within the intrasystem CI. In contrast, NR feature CIs could at most become LR by crossing , but a wider CI will not alter the point estimate of the test statistic nor allow for the CI to shift to be entirely contained within the intrasystem CI if it was not already. As such, even in the presence of multiple comparisons correction, the relative robustness categories of the features would likely hold, particularly in the case of NR features as they cannot, by definition, meet the criterion for R or VR features. The fact that data-driven, feature-specific margin parameters are used to define equivalence also minimizes the multiple-comparisons issue as the number of family-wise comparisons is drastically reduced relative to the case where only a single, study-wide margin is utilized.
Overall, the comparison between these imaging systems with a specific phantom serves as a proof-of-concept for the utility of our approach, and in principal, our proposed statistical framework could generalize to additional imaging systems and breast phantoms. For example, while the Rachel phantom used in this work was designed as a craniocaudal view phantom, extension of this analysis to include mediolateral-oblique view mammograms and phantoms, which may include the chest wall, would primarily depend on accurate delineation of the breast area so as to exclude the pectoralis muscle and would require no alterations to the proposed framework itself. Furthermore, while our experiments focus on detector differences when mammograms are acquired using an x-ray dose estimated using the standard automated exposure control setting, there exists the option to also perform low-dose analyses, such as with tomosynthesis projection data, or to acquire texture from other breast screening modalities altogether, such as with MRI and whole-breast ultrasound. As such, future work will, therefore, need to consider dose and intermodality differences in addition to model and detector differences within a given modality. In addition, our framework could also be used to examine a broader range of texture features and other parenchymal descriptors for different computation parameters than those considered in this work. Ultimately, optimization of these features should also consider the specific context of the clinical application at hand, as for example examining the performance of these features in breast cancer risk assessment for different feature extraction parameters.
5. Conclusion
We proposed a statistical framework to evaluate the robustness of texture features across different FFDM imaging systems, focusing specifically on the effect of different x-ray systems on image intensity and texture. Our results suggest that proper choice of feature extraction parameters is crucial in generating robust texture features. The z-score normalization can alleviate linear differences in intensity profiles between different imaging systems. Once the images are normalized, gray-level histograms and structural features appear to be more robust than co-occurrence and run-length texture features. For all texture features, larger window sizes (i.e., ) tend to result in more robust texture features. Specifically for co-occurrence texture features, a larger offset length (i.e., ) also appears to generate features more robust to inherent imaging system effects. The framework proposed in this work will be beneficial for studies utilizing texture analysis in digital mammography in clinical, multisite, multivendor data sets, including studies investigating breast cancer risk assessment, tissue classification, and computer-aided diagnosis.
Acknowledgments
This work was supported by an American Cancer Society (ACS) Research Scholar Grant (RSGHP-10-108-01-CPHPS), by research grants from the National Institutes of Health/National Cancer Institute (1U54CA163313-01, R01-CA161749-01A1), and by a Breast Cancer Alliance Young Investigator Research Grant.
Biographies
Brad M. Keller received his PhD from Cornell University in 2011. Currently, he is a research associate in the Computational Breast Imaging Group of the Department of Radiology at the University of Pennsylvania. His current research interest focuses on quantitative medical image analysis, applied epidemiological and statistical analysis of quantitative analytical software, and development of image-derivable biomarkers of the pathophysiology underlying breast density and its association to breast cancer risk.
Andrew Oustimov received his MPH (biostatistics) from the University of South Florida in 2014, after which he joined the Computational Breast Imaging Group in the Department of Radiology at the University of Pennsylvania. With expertise in pattern recognition, predictive modeling, analysis of survival, categorical, and longitudinal/multilevel data, he is currently interested in causal inference, biomedical image analysis, cancer genomics, and predictive modeling with respect to personalized screening, diagnosis, prognosis, and treatment of breast cancer.
Yan Wang received her PhD from the University of Pennsylvania in 2013. Her research primarily focused on the study of image-based local scale structure using nonlinear diffusion in various medical imaging modalities. She is currently a health economist with Grey Healthcare Group.
Jinbo Chen is an associate professor of biostatistics at the University of Pennsylvania. Her primary areas of research include the development of statistical methods for designing and analyzing two-phase epidemiologic studies, methodological and collaborative work in genetic association studies of complex diseases, and the development and evaluation of risk prediction models.
Raymond J. Acciavatti received his PhD from the University of Pennsylvania in 2013. He is currently a postdoctoral researcher in the Department of Radiology Physics Section of the University of Pennsylvania. His research focuses on image acquisition physics and the development of new techniques to improve image resolution.
Yuanjie Zheng received his PhD from Shanghai Jiaotong University in 2006. He is currently a senior research investigator in the Penn Image Computing & Science Lab at the University of Pennsylvania. His research focuses on the enhancement of patient care via the creation of algorithms for automatically quantifying and generalizing the information latent in various medical images for tasks such as disease analysis and surgical planning.
Shonket Ray received his PhD from the University of California, Davis, in 2012. He is currently a postdoctoral researcher in the Computational Breast Imaging Group at the University of Pennsylvania School of Medicine. His research interests focus on the development of novel techniques using advanced biomedical image analysis and processing, such as image segmentation, classification, and feature extraction using various breast imaging modalities.
James C. Gee is an associate professor of radiologic science and computer and information science, and director of the Penn Image Computing and Science Laboratory at the University of Pennsylvania. His research interests are broadly in bio/medical image analysis and computing, with active work in all of the quantitative methods represented, including segmentation, registration, morphometry, and shape statistics, as applied to a variety of organ/model systems and the major modalities in biological and medical imaging.
Andrew D. A. Maidment is an associate professor of radiology at the Hospital of the University of Pennsylvania and chief of the Physics Section of the Department of Radiology. His research currently focuses on the development of advanced imaging modalities to improve breast cancer detection and clinical care.
Despina Kontos is an assistant professor of radiology and head of the Computational Breast Imaging Group at the University of Pennsylvania. Her current research focuses on assessing the role of imaging as a quantitative biomarker for improving personalized clinical decision making for breast cancer screening, prognosis, and treatment.
References
- 1.Siegel R., Naishadham D., Jemal A., “Cancer statistics, 2013,” CA Cancer J. Clin. 63, 11–30 (2013). 10.3322/caac.v63.1 [DOI] [PubMed] [Google Scholar]
- 2.American Cancer Society, “Breast cancer facts and figures 2011–2012,” 2011, http://www.cancer.org/acs/groups/content/@epidemiologysurveilance/documents/document/acspc-030975.pdf (17 March 2015).
- 3.FDA, “MQSA National Statistics,” 2014, http://www.fda.gov/Radiation-EmittingProducts/MammographyQualityStandardsActandProgram/facilityScorecard/ucm113858.htm (21 January 2015).
- 4.Suryanarayanan S., et al. , “Flat-panel digital mammography system: contrast-detail comparison between screen-film radiographs and hard-copy images,” Radiology 225(3), 801–807 (2002). 10.1148/radiol.2253011736 [DOI] [PubMed] [Google Scholar]
- 5.Boyd N., et al. , “The association of breast mitogens with mammographic densities,” Br. J. Cancer 87(8), 876–882 (2002). 10.1038/sj.bjc.6600537 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Boyd N. F., et al. , “Mammographic densities and breast cancer risk,” Cancer Epidemiol. Biomarkers Prev. 7(12), 1133–1144 (1998). [PubMed] [Google Scholar]
- 7.Li H., et al. , “Computerized texture analysis of mammographic parenchymal patterns of digitized mammograms,” Acad. Radiol. 12(7), 863–873 (2005). 10.1016/j.acra.2005.03.069 [DOI] [PubMed] [Google Scholar]
- 8.Manduca A., et al. , “Texture features from mammographic images and risk of breast cancer,” Cancer Epidemiol. Biomarkers Prev. 18(3), 837–845 (2009). 10.1158/1055-9965.EPI-08-0631 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wolfe J. N., “Risk for breast cancer development determined by mammographic parenchymal pattern,” Cancer 37(5), 2486–2492 (1976). 10.1002/(ISSN)1097-0142 [DOI] [PubMed] [Google Scholar]
- 10.McCormack V. A., dos Santos Silva I., “Breast density and parenchymal patterns as markers of breast cancer risk: a meta-analysis,” Cancer Epidemiol. Biomarkers Prev. 15(6), 1159–1169 (2006). 10.1158/1055-9965.EPI-06-0034 [DOI] [PubMed] [Google Scholar]
- 11.Heine J. J., Malhotra P., “Mammographic tissue, breast cancer risk, serial image analysis, and digital mammography. Part 1. Tissue and related risk factors,” Acad. Radiol. 9(3), 298–316 (2002). 10.1016/S1076-6332(03)80373-2 [DOI] [PubMed] [Google Scholar]
- 12.Heine J. J., Malhotra P., “Mammographic tissue, breast cancer risk, serial image analysis, and digital mammography. Part 2. Serial breast tissue change and related temporal influences,” Acad. Radiol. 9(3), 317–335 (2002). 10.1016/S1076-6332(03)80374-4 [DOI] [PubMed] [Google Scholar]
- 13.Byrne C., et al. , “Mammographic features and breast cancer risk: effects with time, age, and menopause status,” J. Natl. Cancer Inst. 87(21), 1622–1629 (1995). [DOI] [PubMed] [Google Scholar]
- 14.Byrne C., et al. , “Effects of mammographic density and benign breast disease on breast cancer risk (United States),” Cancer Causes Control 12(2), 103–110 (2001). 10.1023/A:1008935821885 [DOI] [PubMed] [Google Scholar]
- 15.Fabian C. J., Kimler B. F., “Mammographic density: use in risk assessment and as a biomarker in prevention trials,” J. Nutr. 136(10), 2705–2708 (2006). [DOI] [PubMed] [Google Scholar]
- 16.Tice J. A., et al. , “Mammographic breast density and the Gail model for breast cancer risk prediction in a screening population,” Breast Cancer Res. Treat. 94(2), 115–122 (2005). 10.1007/s10549-005-5152-4 [DOI] [PubMed] [Google Scholar]
- 17.Li H., et al. , “Computerized analysis of mammographic parenchymal patterns for assessing breast cancer risk: effect of ROI size and location,” Med. Phys. 31, 549 (2004). 10.1118/1.1644514 [DOI] [PubMed] [Google Scholar]
- 18.Li H., et al. , “Computerized texture analysis of mammographic parenchymal patterns of digitized mammograms,” Acad. Radiol. 12(7), 863–873 (2005). 10.1016/j.acra.2005.03.069 [DOI] [PubMed] [Google Scholar]
- 19.Li H., et al. , “Power spectral analysis of mammographic parenchymal patterns for breast cancer risk assessment,” J. Digit. Imaging 21(2), 145–152 (2008). 10.1007/s10278-007-9093-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Li H., et al. , “Fractal analysis of mammographic parenchymal patterns in breast cancer risk assessment,” Acad. Radiol. 14(5), 513–521 (2007). 10.1016/j.acra.2007.02.003 [DOI] [PubMed] [Google Scholar]
- 21.Kim W. H., et al. , “Variability of breast density assessment in short-term reimaging with digital mammography,” Eur. J. Radiol. 82(10), 1724–1730 (2013). 10.1016/j.ejrad.2013.05.004 [DOI] [PubMed] [Google Scholar]
- 22.Caldwell C. B., Yaffe M. J., “Development of an anthropomorphic breast phantom,” Med. Phys. 17, 273 (1990). 10.1118/1.596506 [DOI] [PubMed] [Google Scholar]
- 23.Marx M. L., Larsen R. J., Introduction to Mathematical Statistics and Its Applications, Pearson/Prentice Hall, Upper Saddle River, New Jersey: (2006). [Google Scholar]
- 24.Keller B. M., et al. , “Estimation of breast percent density in raw and processed full field digital mammography images via adaptive fuzzy c-means clustering and support vector machine segmentation,” Med. Phys. 39(8), 4903–4917 (2012). 10.1118/1.4736530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zheng Y., et al. , “A fully-automated software pipeline for integrating breast density and parenchymal texture analysis for digital mammograms: parameter optimization in a case-control breast cancer risk assessment study,” Proc. SPIE 8670, 86701B (2013). 10.1117/12.2008155 [DOI] [Google Scholar]
- 26.Ibanez L., et al. , “The ITK software guide,” 2003, http://www.itk.org/ItkSoftwareGuide.pdf (9 August 2014).
- 27.Meier U., “Nonparametric equivalence testing with respect to the median difference,” Pharm. Stat. 9(2), 142–150 (2010). 10.1002/pst.384 [DOI] [PubMed] [Google Scholar]
- 28.Amadasun M., King R., “Textural features corresponding to textural properties,” Trans. Syst. Man Cybern. 19, 1264–1274 (1989). 10.1109/21.44046 [DOI] [Google Scholar]
- 29.Haralick R. M., Shanmugam K., Dinstein I. H., “Textural features for image classification,” IEEE Trans. Syst. Man Cybern. 3(6), 610–621 (1973). 10.1109/TSMC.1973.4309314 [DOI] [Google Scholar]
- 30.Khuzi A. M., et al. , “Identification of masses in digital mammogram using gray level co-occurrence matrices,” Biomed. Imaging Interv. J. 5(3), e17 (2009). 10.2349/biij.5.3.e17 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Galloway M. M., “Texture analysis using gray level run lengths,” Comput. Graph. Image Process. 4(2), 172–179 (1975). 10.1016/S0146-664X(75)80008-6 [DOI] [Google Scholar]
- 32.Chu A., Sehgal C., Greenleaf J., “Use of gray value distribution of run lengths for texture analysis,” Pattern Recognit. Lett. 11(6), 415–419 (1990). 10.1016/0167-8655(90)90112-F [DOI] [Google Scholar]
- 33.Ojala T., Pietikainen M., Maenpaa T., “Multiresolution gray-scale and rotation invariant texture classification with local binary patterns,” IEEE Trans. Pattern Anal. Mach. Intell. 24(7), 971–987 (2002). 10.1109/TPAMI.2002.1017623 [DOI] [Google Scholar]
- 34.Caldwell C. B., et al. , “Characterisation of mammographic parenchymal pattern by fractal dimension,” Phys. Med. Biol. 35(2), 235 (1990). 10.1088/0031-9155/35/2/004 [DOI] [PubMed] [Google Scholar]
- 35.Karemore G., et al. , “Anisotropic diffusion tensor applied to temporal mammograms: an application to breast cancer risk assessment,” in Annual Int. Conf. of the Engineering in Medicine and Biology Society, pp. 3178–3181 (2010). 10.1109/IEMBS.2010.5627183 [DOI] [PubMed] [Google Scholar]
- 36.Huo Z., et al. , “Computerized analysis of digitized mammograms of BRCA1 and BRCA2 gene mutation carriers,” Radiology 225(2), 519–526 (2002). 10.1148/radiol.2252010845 [DOI] [PubMed] [Google Scholar]
- 37.Weickert J., “Coherence-enhancing diffusion filtering,” Int. J. Comput. Vis. 31(2), 111–127 (1999). 10.1023/A:1008009714131 [DOI] [Google Scholar]
- 38.Ahonen T., Hadid A., Pietikainen M., “Face description with local binary patterns: application to face recognition,” IEEE Trans. Pattern Anal. Mach. Intell. 28(12), 2037–2041 (2006). 10.1109/TPAMI.2006.244 [DOI] [PubMed] [Google Scholar]
- 39.Holmes Q. A., Nuesch D. R., Shuchman R. A., “Textural analysis and real-time classification of sea-ice types using digital SAR data,” IEEE Trans. Geosci. Remote Sens. GE-22(2), 113–120 (1984). 10.1109/TGRS.1984.350602 [DOI] [Google Scholar]
- 40.Soh L.-K., Tsatsoulis C., “Texture analysis of SAR sea ice imagery using gray level co-occurrence matrices,” IEEE Trans. Geosci. Remote Sens. 37(2), 780–795 (1999). 10.1109/36.752194 [DOI] [Google Scholar]
- 41.Mohanty A. K., Beberta S., Lenka S. K., “Classifying benign and malignant mass using GLCM and GLRLM based texture features from mammogram,” Int. J. Eng. Res. Appl. 1(3), 687–693 (2011). [Google Scholar]
- 42.van den Boomgaard R., “Algorithms for non-linear diffusion,” Technical Report no.1, Intelligent Sensory Information Systems, University of Amsterdam, The Netherlands.
- 43.Hodges J., Lehmann E. L., “Hodges-Lehmann estimators,” in Encyclopedia of Statistical Sciences, Kotz S., Johnson N. L., Read C. B., Eds., Vol. 3, pp. 463–465, John Wiley & Sons, New York: (1983). [Google Scholar]
- 44.Yaffe M. J., “Detectors for digital mammography,” in Digital Mammography, Bick U., Diekmann F., Eds., pp. 13–31, Springer, Berlin, Heidelberg: (2010). [Google Scholar]