Abstract.
Magnetic resonance imaging is a technique for the diagnosis and classification of brain tumors. Discrete compactness is a morphological feature of two-dimensional and three-dimensional objects. This measure determines the compactness of a discretized object depending on the sum of the areas of the connected voxels and has been used for understanding the morphology of nonbrain tumors. We hypothesized that regarding brain tumors, we may improve the malignancy grade classification. We analyzed the values in 20 patients with different subtypes of primary brain tumors: astrocytoma, oligodendroglioma, and glioblastoma multiforme subdivided into the contrast-enhanced and the necrotic tumor regions. The preliminary results show an inverse relationship between the compactness value and the malignancy grade of gliomas. Astrocytomas exhibit a mean of , whereas oligodendrogliomas exhibit a mean of . In contrast, the contrast-enhanced region of the glioblastoma presented a mean of , and the necrotic region presented a mean of . However, the volume and area of the enclosing surface did not show a relationship with the malignancy grade of the gliomas. Discrete compactness appears to be a stable characteristic between primary brain tumors of different malignancy grades, because similar values were obtained from different patients with the same type of tumor.
Keywords: neuromorphometry, discrete compactness, magnetic resonance imaging, gliobastoma multiforme, brain tumors
1. Introduction
At the present time, magnetic resonance imaging (MRI) is the leading noninvasive imaging tool. In the framework of brain tumors, MRI acquisition and postprocessing techniques have become the state-of-the-art technique for the diagnosis and classification of tumors.1–4 By using morphological information, obtained with the current software applications and MRI techniques available, it is possible to determine the approximate three-dimensional (3-D) architecture, level of infiltration, and evolution of a tumor. One of the pitfalls of using MRI for brain tumors is the inability to objectively measure a tumor’s borders, grade of malignancy, and sites of infiltration. Moreover, there is the fact that this technique is always observer-dependent; a tumor’s assessment is subjective and to some extent even biased. In this context, the development of new mathematical tools that allows the quantification of some morphological aspects of the tumors, such as the volume, enclosing surface, and compactness, may be beneficial to obtain a better understanding of brain tumors through imaging and their relationship with biological characteristics.2,3
Tumor volume is easily measured by actual MRI techniques; however, an increase in tumor volume is not necessarily related to its grade of malignancy. Malignancy is more closely related to the grade of tumor infiltration.5 Because infiltration usually occurs at the periphery of the tumor, a morphological variable, such as tumor compactness, could indicate that a less-compact tumor should be a more aggressive one. This hypothesis is supported by the observations found by Braumann et al.6 and Einenkel et al.7 through their analysis and quantification of the invasion of carcinoma from the uterine cervix based on a 3-D tumoral reconstruction of the tissue data. This group showed an inverse correlation between the compactness and the grade of tumor infiltration; the more compact, the less invasive. In other types of tumors, the group of Moon et al.8 attempted to develop a novel computer-aided diagnosis system for the classification of breast cancer using 3-D features and morphological variables with the objective of classifying benign and malignant tumors from ultrasound images. Huang et al.9 proposed a computer-aided diagnosis of mass-like lesions in breast MRI to distinguish between benign and malignant tumors from a differential analysis of 3-D morphology. Thus, the aforementioned studies suggest that other types of morphological measures may be a new variable to consider when studying brain tumors through MRI. Because MRI is a potent imaging tool that delivers high-resolution digital images, the measurement of morphological variables, such as discrete compactness (), is possible. Hence, we aimed to measure the level of compactness of different brain tumor types and brain tumor grades in the case of glioblastoma multiforme (GBM). GBM images can normally be divided in two areas: the contrast-enhancement region and the necrosis region. Therefore, it would be interesting to determine whether there is a correlation between the malignancy grade of gliomas and their level of compactness.
1.1. Neuromorphometric Parameters
1.1.1. Volume
The volume is one of the inherent characteristics used to describe a 3-D object. Volumetric representations are used for rigid solids through spatial occupancy arrays. Thus, in the case of digital images, the discretized objects are represented as one 3-D array of voxels.
If a 3-D object is composed of voxels, where each voxel has a volume equal to one, the volume () corresponds to the sum of all voxels that comprise the 3-D object.
1.1.2. Area of enclosing surface
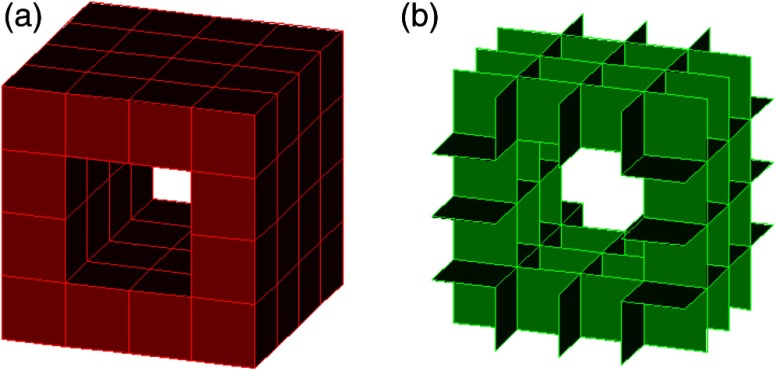
To introduce the concept of the area of the enclosing surface (), we defined the concept of contact surface area () of a 3-D object composed of a finite number of voxels. The contact surface area () corresponds to the sum of the areas of the surfaces that are common to two voxels. An example of a 3-D voxel-based object is shown in Fig. 1(a). This object is composed of 48 voxels, i.e., . The contact surface area () of the 3-D object is equal to 84, i.e., , which corresponds to the contact faces of the object; these are illustrated in Fig. 1(b). Note that the area of all of the faces of the voxels is considered equal to one.
Fig. 1.
(a) An example of a voxel-based object composed of voxels and (b) the contact faces of the object, where .
Next, considering the same discretized 3-D object composed of a finite number of voxels, the area of the enclosing surface () corresponds to the sum of the areas of the external plane polygons of the voxels that form the visible faces of the solid. Therefore, according to Theorem 2 defined by Bribiesca,10 the area of the enclosing surface () is expressed as follows:
| (1) |
where is the contact surface area, is the area of the face of a voxel (in this case is equal to one, which means that all sides of the voxels are a unit value), and is the number of voxels. The number 6 in Eq. (1) indicates the number of faces of the voxel, which in this case is a cube. Therefore, the area of the enclosing surface () of the aforementioned 3-D object, which is shown in Fig. 1, is equal to 120, i.e., , which corresponds to the visible faces of the object. Note that the relationship between the areas described in Eq. (1) is preserved for solids with holes and inner holes.
1.1.3. Discrete compactness
The classical compactness () is an important intrinsic property of objects. In 3-D objects, this property relates the enclosing surface area () with the volume (), which is dimensionless and minimized by a sphere. However, in the digital domain, most objects have no well-defined enclosing surface, a phenomenon that may produce noisy enclosing-surfaces and consequently large values, which will affect the measure of the classical compactness.8 In contrast, the discrete compactness () depends in large part on the sum of the contact surface area of the neighboring voxels of 3-D objects;10–12 thus, this discrete measure is more robust than the classical measure. The measure of is an intrinsic property of objects; therefore, it is invariant under translation, rotation, and scaling.
The unique simple equation for computing the measure of for 3-D objects composed of voxels is defined by the following equation,9 which was normalized:
| (2) |
The measure of of a 3-D objects is dimensionless and maximized by a digital cube, i.e., its values vary continuously from 0 to 1. Thus, the value of the minimum measure of for a 3-D object of voxels is zero. In contrast, the value of the maximum measure is one, which corresponds to a digital cube. In this study, the measure of was normalized such that its values vary continuously from 0 to 1000.
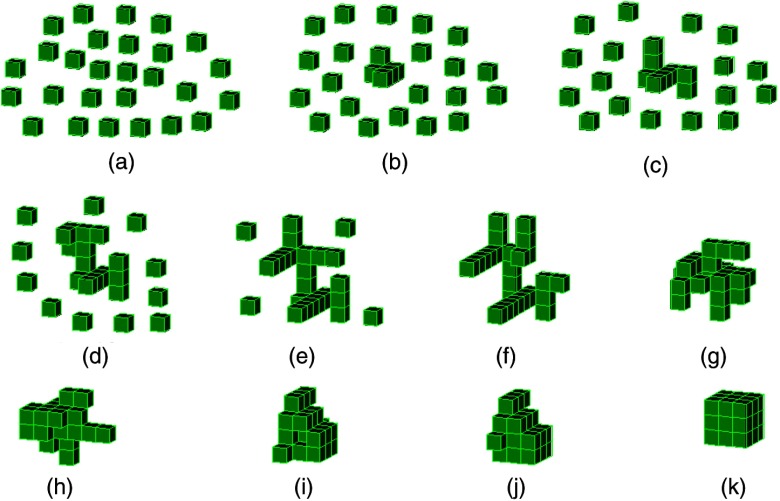
Figure 2 illustrates some interesting examples of progressive measures of compactness of some 3-D objects composed of 27 voxels; their values of contact surface areas are shown. Figure 2(a) shows a 3-D fragmented object, which has a compactness measure equal to 0; i.e., it has no contact surface area. Thus, Figs. 2(b)–2(k) present examples of progressive measures of compactness. Notice that the minimum measure of compactness corresponds to Fig. 2(a) (). On the other hand, the maximum measure of compactness corresponds to Fig. 2(k) (). This measure of varies discretely, which is an important advantage in 3-D objects analysis because it allows us to classify 3-D shapes. Thus, this measure may be a useful tool for the detection of morphological dissimilarities between 3-D objects.
Fig. 2.
Examples of objects with various measures of compactness and their values of contact surface areas; each object is composed of 27 voxels. (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , ; (g) , ; (h) , ; (i) , ; (j) , ; and (k) .
1.2. Brain Tumor Characteristics
A combination of morphological information and technical medical characteristics of brain tumors derived from MRI data may help the development of image processing algorithms and the quantification of neuromorphometric parameters.
Figure 3 shows magnetic resonance (MR) images of different glioma types. The technical characteristics of the different gliomas are depicted in the images.
Fig. 3.
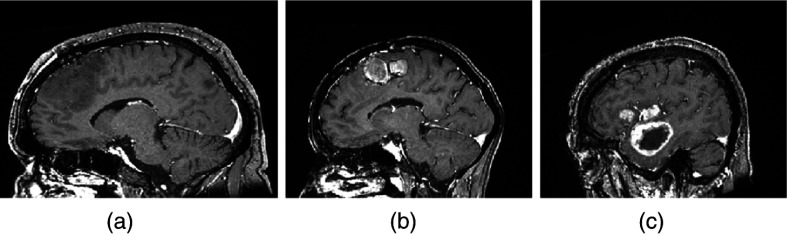
T1w gadolinium-enhanced magnetic resonance (MR) images of the sagittal view of gliomas: (a) grade II glioma [astrocytoma (astro)], (b) grade III glioma [oligodendroglioma (oligo)], and (c) grade IV glioma [glioblastoma multiforme (GBM)].
By definition, contrast enhancement is absent in gliomas of grade II [e.g., the astrocytoma that is shown in Fig. 3(a)]. Their intensity often resembles that of gray matter, which is darker than the surrounding white matter. Their contour cannot always be clearly delimited. Grade III gliomas [e.g., the oligodendroglioma shown in Fig. 3(b)] can be fully enhanced (i.e., bright due to gadolinium enhancement) or show only some areas of enhancement. Grade IV gliomas [e.g., the GBM shown in Fig. 3(c)] commonly have both regions of enhancement and regions of necrosis (dead cells), the latter of which indicates fast-growing tumors, and surrounding edema.13
In particular, the most important clue for the diagnosis of GBM is the MRI-based identification of a thick, irregularly enhancing ring of neoplastic tissue surrounding the necrotic core,3,14–16 which is regularly localized on the supratentorial white matter.15
There are some helpful magnetic resonance sequences for GBM, such as the following:
-
(a)
T1-weighted images, where a GBM can be observed as an irregular isointense/hypo-intense mass of white matter and presents a region of necrosis or the presence of cysts in the interior and irregular contours;
-
(b)
T2-weighted images, which present the GBM as a heterogeneous and hyperintense mass with adjacent tumor infiltration and a vasogenic edema, although necrotic regions, cysts, haemorrhages, and neovascularity may also be observed;
-
(c)
Fluid-attenuated inversion recovery (FLAIR) images, which show the GBM as a heterogeneous and hyperintense mass with adjacent tumor infiltration and a vasogenic edema; and
-
(d)
Fast low-angle shot or spoiled gradient recalled echo (SPGR) images, which show GBM as an irregular hyperintense mass accompanied by a region of necrosis and irregular contours, which allows us to differentiate the enhancement region and necrotic region of GBM.
1.3. Aim of the Study
We are interested in studying brain tumors, particularly grade IV gliomas, through neuromorphometric analysis. The morphological parameter proposed in this work is , which was proposed as a parameter that can be used to identify and quantify the grade of malignancy between different types of gliomas. The impact of as a neuromorphometric measure for the diagnostic of gliomas is the final goal of this research study.
2. Methods
2.1. Patients and Tumor Characteristics
The data used in this article consists of 20 biopsy-proven tumors from seven women and 13 men with a mean age of and an age range of 31 to 76 yr. As the most common type of primary brain tumors, gliomas were the only type of tumor included in this study: five low-grade gliomas (LGG) of grade II and 15 high-grade gliomas (HGG) ranked grade III or IV. Table 1 further divides the gliomas into subtypes: astrocytomas (astro), oligodendrogliomas (oligo), and GBM.
Table 1.
Overview of brain tumor cases included in this study: patients’ number, sex, age, hemisphere, and lobe in which the tumor was located, general tumor type, and specific tumor subtype.
| Patient no. | Sex | Age | Tumor location | Tumor grade | Tumor subtype |
|---|---|---|---|---|---|
| 1 | M | 49 | Left temporal | LGG | Astro grade II |
| 2 | M | 37 | Right frontal | LGG | Astro grade II |
| 3 | M | 50 | Right frontal | HGG | Oligo grade III |
| 4 | M | 74 | Left parietal | HGG | GBM |
| 5 | F | 64 | Right temporal | HGG | GBM |
| 6 | F | 63 | Left frontal | HGG | GBM |
| 7 | F | 59 | Left parietal | HGG | GBM |
| 8 | M | 42 | Left temporal | HGG | GBM |
| 9 | M | 69 | Right parietal | HGG | GBM |
| 10 | M | 49 | Right frontal | HGG | GBM |
| 11 | F | 53 | Left frontal | HGG | GBM |
| 12 | M | 31 | Right frontal | LGG | Astro grade II |
| 13 | F | 40 | Right frontal | LGG | Astro grade II |
| 14 | M | 70 | Right temporal | LGG | Astro grade II |
| 15 | M | 39 | Left frontal | HGG | Oligo grade III |
| 16 | F | 49 | Left frontal | HGG | Oligo grade III |
| 17 | F | 42 | Right frontal | HGG | GBM |
| 18 | M | 70 | Left parietotemporal | HGG | GBM |
| 19 | M | 40 | Left frontal | HGG | GBM |
| 20 | M | 76 | Right parietal | HGG | GBM |
In this study, we included five astro cases, three oligo cases, and 12 GBM cases. Table 1 also indicates the patient data (identification number, sex, and age) and shows the hemisphere and lobe in which the tumor was located, the general tumor type, and the specific tumor subtype.
2.2. Data Acquisition
The data from whole-brain MRI were acquired from two different datasets. The first MRI dataset was acquired from a retrospective study of 11 patients admitted to the National Institute of Neurology and Neurosurgery “Manuel Velasco Suárez” in Mexico City. All of the images were T1w gadolinium-enhanced MR acquired on a 1.5 T GE Signa HDxt (GE Medical System) using 3-D axial SPGR sequences, where the sequences have different slice thickness (1.4, 1.5, and 1.6 mm) and pixel size (, , and ); however, all images were resampled to 1.0 mm isotropic resolution in a standardized axial orientation, by linear interpolation with the use of MATLAB® tools. These images correspond to the MRIs of the first 11 patients cited in Table 1.
The second MRI dataset includes data from nine patients and was received from the Montreal Neurological Institute’s Brain Images of Tumors for Evaluation database.11 All of the images were acquired on a 1.5T GE Signa EXCITE (General Electric, Milwaukee, Wisconsin) with 1-mm slice thickness and in-plane pixel size (3-D axial SPGR sequences, , , and , and the voxel size was normalized to . These images correspond to the MRIs of the last nine patients cited in Table 1.
The images were neither corrected for intensity nonuniformities nor normalized in any way because this was not judged necessary.
2.3. Tumor Segmentation
A semiautomatic method of segmentation by thresholding was applied for segmentation of the tumor (Anatomist—Brainvisa 4.0.2.—CEA/NeuroSpin/SHFL on a Linux PC) from gadolinium-enhanced MRI axial SPGR sequences. The tumor segmentation was realized and validated by one neuroradiologist and three neurosurgeons from the National Institute of Neurology and Neurosurgery “Manuel Velasco Suárez” and the Neurological Center—ABC Medical Center.
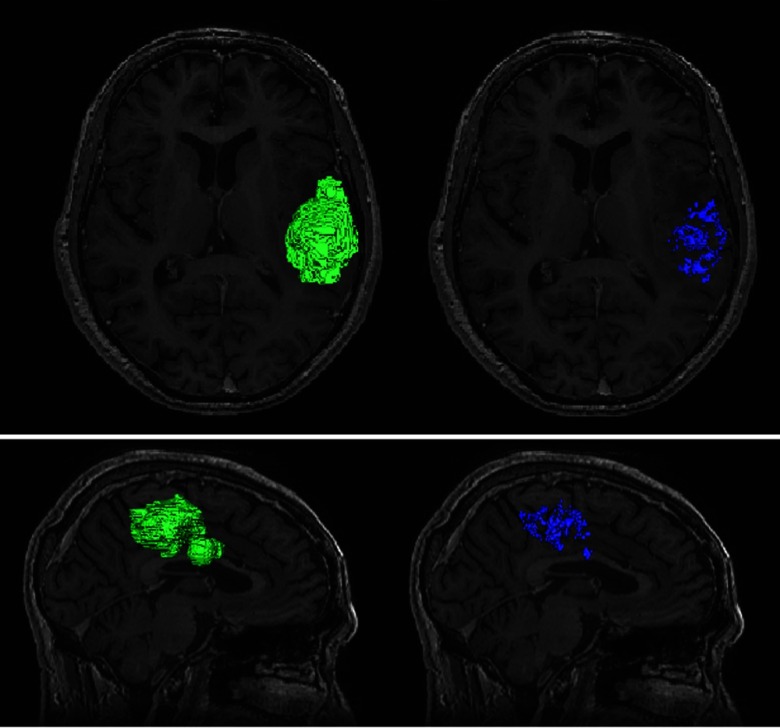
In the case of astrocytomas and oligodendrogliomas, the region of interest was the whole region of the tumor (V1), and in the case of GBM, we considered two regions of interest, namely: the enhanced region (V2) and the necrotic region (V3). Figure 4 shows axial and sagittal views of the segmentation and a 3-D reconstruction of the two regions of interest (V2 and V3) from a patient with GBM.
Fig. 4.
Three-dimensional segmentation and reconstruction of the enhanced-region (in green) and necrotic region (in blue) of a patient with GBM.
2.4. Feature Analysis
After segmentation (whole tumor region—V1, enhancement region (GBM)—V2, and necrotic region (GBM)—V3), some features were proposed to describe the morphological characteristics of the tumors. These morphological features were the volume (), the area of enclosing surface (), and the discrete compactness (). To quantify , we calculated the volume and the area of enclosing surface. In this study, the measure of was normalized such that the values vary from 0 to 1000.
A quantification of these morphological variables (, , and ) was obtained from the whole tumor in the case of astrocytomas and oligodendrogliomas. Because GBM commonly has both a region of enhancement and a region of necrosis, we calculated the values of the morphological variables for both regions. All of the algorithms used to measure the morphological variables were implemented with a high-level language and interactive environment for numerical computation, visualization, and programming (MATLAB®—2013a, version 8.1).
3. Results
3.1. Feature Analysis
The values of the volume (), area of enclosing surface (), and discrete compactness () for all of the patients are listed in Table 2.
Table 2.
Values of the morphological features of the brain tumors in the dataset (astro, oligo, and GBM): volume (), area of enclosing surface (), and discrete compactness ().
| Patient no. | Tumor subtype | Volume () | Area of enclosing surface () | Discrete compactness |
|---|---|---|---|---|
| 1 | Astro grade II | 7.99 | 31.58 | 957 |
| 2 | Astro grade II | 161.10 | 188.52 | 984 |
| 3 | Oligo grade III | 126.35 | 79.24 | 947 |
| 4 | GBM | 30.81 | 161.15 | 947 |
| 5.10 | 80.01 | 817 | ||
| 5 | GBM | 68.03 | 610.40 | 823 |
| 52.56 | 414.24 | 855 | ||
| 6 | GBM | 48.55 | 309.68 | 868 |
| 20.89 | 188.38 | 809 | ||
| 7 | GBM | 45.83 | 133.89 | 945 |
| 9.39 | 76.00 | 825 | ||
| 8 | GBM | 43.98 | 212.48 | 931 |
| 6.81 | 91.14 | 776 | ||
| 9 | GBM | 75.91 | 586.09 | 922 |
| 26.68 | 330.18 | 872 | ||
| 10 | GBM | 28.61 | 174.69 | 868 |
| 37.54 | 81.59 | 967 | ||
| 11 | GBM | 15.25 | 121.71 | 927 |
| 5.83 | 53.31 | 921 | ||
| 12 | Astro grade II | 69.34 | 383.44 | 966 |
| 13 | Astro grade II | 41.85 | 119.47 | 990 |
| 14 | Astro grade II | 32.31 | 174.71 | 970 |
| 15 | Oligo grade III | 0.20 | 3.89 | 919 |
| 16 | Oligo grade III | 7.91 | 60.28 | 961 |
| 17 | GBM | 1.95 | 20.24 | 951 |
| 0.12 | 4.17 | 795 | ||
| 18 | GBM | 43.82 | 256.60 | 965 |
| 9.22 | 83.35 | 947 | ||
| 19 | GBM | 16.87 | 190.67 | 924 |
| 15.22 | 108.38 | 946 | ||
| 20 | GBM | 23.90 | 185.12 | 952 |
| 2.97 | 47.65 | 897 |
For all of the GBM cases, the value on top corresponds to the enhanced region and the value on the bottom corresponds to the necrotic region.
In the Sec. 2.2, we mentioned that the MRI sequences were obtained from two different studies: (1) a retrospective study in which the MRI sequences were not the same, due to variations in the pixel size and slice thickness (group I); and (2) a study in which all of the MRI sequences were acquired using the same acquisition protocol (group II). However, note that is scale-invariant. Therefore, we compared the mean values of these morphological variables between both studies.
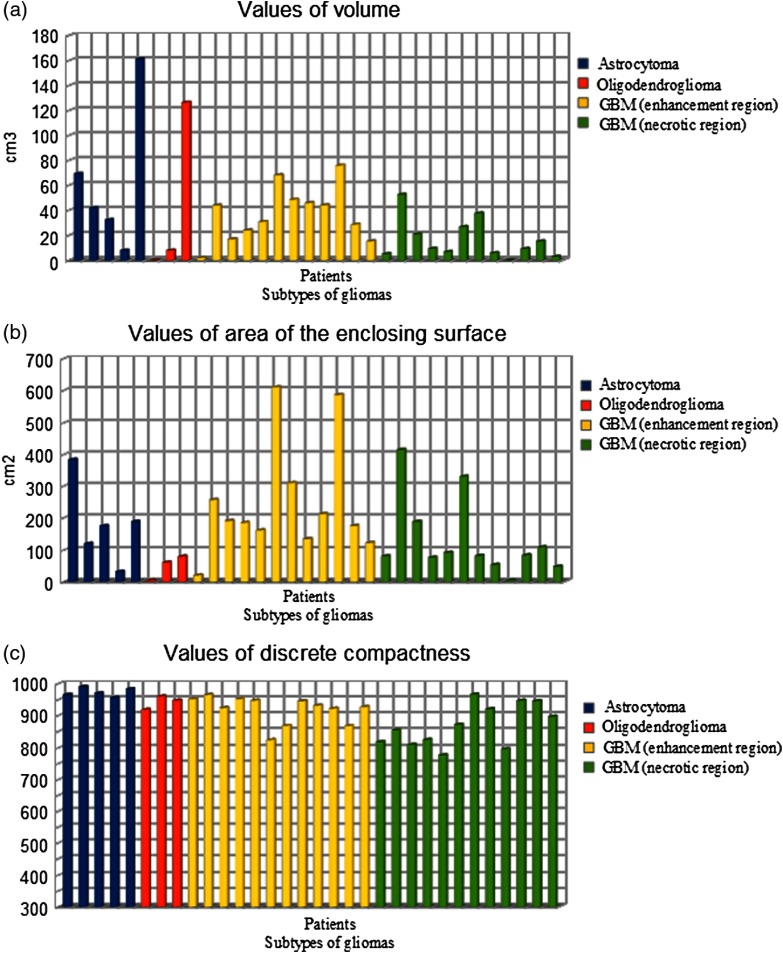
Table 3 shows the mean values of volume (), enclosing surface (), and discrete compactness () of both groups I and II. For all glioma subtypes, the mean values of volume and area of enclosing surface were different, but the mean values of were similar in both groups, as shown in Table 3 and Fig. 5.
Table 3.
Mean values of volume (), enclosing surface (), and discrete compactness () of group I and II for each glioma subtype: astrocytoma (whole tumor region), oligodendroglioma (whole tumor region), and GBM (enhancement region and necrotic region).
| Group | Astrocytoma (whole tumor region) | Oligodendroglioma (whole tumor region) | GBM (enhanced region) | GBM (necrotic region) |
|---|---|---|---|---|
| I | ||||
| II | ||||
Fig. 5.
Values of , , and for each region and subtype of gliomas (astro, oligo, enhancement region of GBM, and necrotic region of GBM). (a) Values of volume, (b) values of area of the enclosing surface, and (c) values of discrete compactness.
3.2. Tumor Classification
As mentioned in the previous paragraph, the values of were found to be similar between both MRI datasets for the different subtypes of gliomas. Thus, we consider both datasets as a single group for the following statistical analyses. The mean values of volume (), area of enclosing surface (), and discrete compactness () for all patients are shown in Table 4.
Table 4.
Mean values of volume (), enclosing surface (), and discrete compactness () for all patients included in the dataset and all glioma subtypes: astrocytoma (whole tumor region), oligodendroglioma (whole tumor region), and GBM (enhancement region and necrotic region).
| Astrocytoma (whole tumor region) | Oligodendroglioma (whole tumor region) | GBM (enhanced region) | GBM (necrotic region) |
|---|---|---|---|
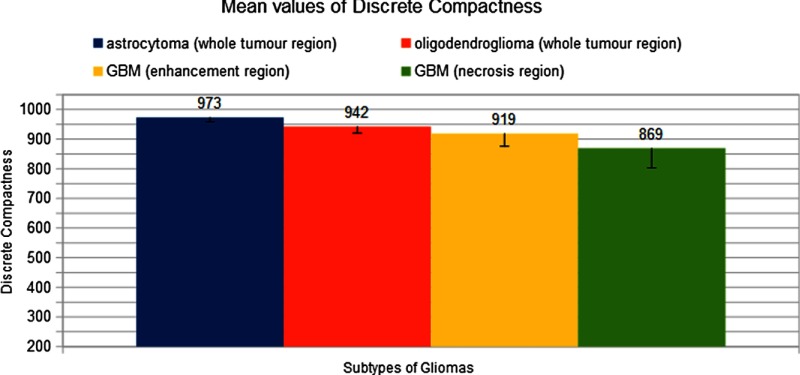
One of the aims of this work was to propose a morphological variable that can be used to identify differences between various types of brain tumors or to characterize the development of one subtype of gliomas. Figure 6 shows the values of for each analyzed region of the different gliomas. The comparison of the values revealed that these values follow a decreasing pattern in the different glioma subtypes: the most compact glioma subtype was the astrocytoma group (), followed by the oligodendroglioma group (), the GBM enhancement region (), and then the GBM necrotic region ().
Fig. 6.
Mean values of for each subtype/region of gliomas (astro, oligo, enhancement region of GBM, and necrotic region of GBM).
The preliminary results show an inverse correlation between the compactness value and the malignancy grade of gliomas (, ). The correlation between the volume and the malignancy grade, and the area of enclosing surface and the malignancy grade were not significant.
4. Discussion
Tumor resection is a crucial part of treatment, as shown by the fact that the majority of patients have better outcomes after gross total resection.1,4,16,17 In particular, GBM aggressiveness makes it imperative to perform an extensive resection of the tumor.1,2 Therefore, the aim of the surgery is to maximize tumor resection without affecting the surrounding brain structures in order to avoid postsurgery neurological deficits.1,4 The size, localization, and extent of the tumor can be identified by conventional MRI,18 and advanced MRI techniques render it possible to characterize the anatomical and functional properties of the tumor and its surroundings before tumor resection. When a brain tumor is detected, several MRI tools are used, including perfusion-weighted imaging analysis, spectroscopy, and FLAIR.19–21 All of these techniques provide detailed information about the eloquent brain areas adjacent to the tumor as well as the apparent tumor edges and morphology, although the intrinsic characteristics of the tumor, such as the sites of necrosis and neovascularization, are not well-identified. Until now, information regarding this kind of tumor is obtained using the aforementioned MRI techniques and through correlation with postsurgery histopathological reports.
Therefore, a measurement of the tumor compactness may be beneficial to understanding the level of tumor growth and may be useful for grading the malignancy of different types of tumors. Because this is an early report on the measure of in brain imaging, it is necessary to evaluate the correlation between the values within a histopathological standardized diagnosis in a significant number of patients. The establishment of a correlation between compactness and tumor activity could be beneficial for the planning of tumor resection, for determining the characteristics of tumor growth and response to treatment, and for comparisons between cases. In this first approach, we found that may be a morphological variable capable of distinguishing different subtypes of gliomas, as shown in Table 4. In fact, Table 4 demonstrates that astrocytoma has a high value of and is the type of glioma with the lowest malignancy grade. In contrast, the regions of GBM (enhancement region and necrotic region) show the lowest values of but these subtypes of gliomas present a high malignancy level. In particular, the values of in the necrotic region show decrease in comparison with the values observed in the enhancement region, as shown in Fig. 6.
It should be noted that this work presents some limitations associated with the acquisition of the images. However, the glioma subtype differences were similar across two datasets. A semiautomatic method of segmentation by thresholding is not the best method because this is operator-dependent, which is why we are currently working on implementation of an automatic segmentation method.
5. Conclusion
The neuromorphometric parameter of discrete compactness () may have the potential to differentiate gliomas of different malignancy grade (e.g., astrocytomas, oligodendrogliomas, and GBM) and may therefore be a useful MRI-postprocessing method for the analysis of brain tumors. Our preliminary results show that this morphological variable is a stable neuromorphometric characteristic of tumors, as demonstrated by the finding that the quantified values of all of the regions of interest are very similar according to the type of tumor in all of the patients. Differences in the value of were found among intrinsic regions of the same tumor (enhancement region and necrotic regions in GBM). The measure of can be standardized by computer software such that it is user-independent. Further studies on histopathological correlations are needed to thoroughly understand this phenomenon.
Acknowledgments
Pedro I. Rodriguez-Perez thanks the CONACyT for his PhD scholarship, which made this research possible.
Biographies
Nidiyare Hevia-Montiel received her BSc degree in electric engineering from the Universidad Autónoma del Estado de Morelos. She received her MSc degree in electric engineering from the Universidad Nacional Autónoma de México, and she received her PhD degree in physics from the Université de Paris XI–Orsay. Currently, she is an associate researcher at the Instituto de Investigaciones en Matemáticas Aplicadas y en Sistemas at the Universidad Nacional Autónoma de México. Her research areas are medical image processing and pattern recognition.
Pedro I. Rodriguez-Perez received his BSc degree in computer engineering from the Universidad Nacional Autónoma México. Currently, he is a PhD student in computer science and engineering at the Instituto de Investigaciones en Matemáticas Aplicadas y en Sistemas of the Universidad Nacional Autónoma de México.
Paul J. Lamothe-Molina started his career in electronics engineering and medicine. He was always drawn to medical research so he decided to pursue his PhD degree in biomedical sciences at the Universidad Nacional Autónoma de México. At the moment, he is a postdoctoral fellow in optogenetics at the Eppendorf University Clinic in Hamburg, Germany.
Alfonso Arellano-Reynoso received her BSc degree in medicine from the Universidad Nacional Autónoma de México and special studies in stereotactic and functional neurosurgery from the Université de Paris, France. Currently, he is neurosurgeon at the Instituto Nacional de Neurología y Neurocirugía and at the Centro Médico ABC in Mexico, where his research areas are brain tumors and general neurology.
Ernesto Bribiesca received his BSc degree in electronics engineering from the Instituto Politécnico Nacional. He received his PhD degree in mathematics from the Universidad Autónoma Metropolitana. He was a researcher at the IBM Latin American Scientific Center, and at the Dirección General de Estudios del Territorio Nacional. He is associate editor of the Pattern Recognition journal. He has twice been chosen as Honorable Mention winner of the Annual Pattern Recognition Society Award. Currently, he is a professor at the Instituto de Investigaciones en Matemáticas Aplicadas y en Sistemas at the Universidad Nacional Autónoma de México.
Marco A. Alegria-Loyola received his BSc degree in medicine from the Escuela Medico Militar UDEFA and the Hospital Central Militar in Mexico City. He received special studies in neurology from the Cleveland Clinic Foundation, Cleveland, Ohio. He is member of the Colegio de Medicina Interna de México, Colegio Nacional de Médicos Militares, American Academy of Neurology, and Panamerican Society of Neurovirology. Currently, he is a neurosurgeon at the Centro Médico ABC in Mexico, where his research areas are stroke, brain tumors, and general neurology.
References
- 1.Gupta A., et al. , “Imaging of brain tumors: functional magnetic resonance imaging and diffusion tensor imaging,” Neuroimaging Clin. North Am. 20(3), 379–400 (2010). 10.1016/j.nic.2010.04.004 [DOI] [PubMed] [Google Scholar]
- 2.Bizzi A., “Presurgical mapping of verbal language in brain tumors with functional MR imaging and MR tractography,” Neuroimaging Clin. North Am. 19(4), 573–596 (2009). 10.1016/j.nic.2009.08.010 [DOI] [PubMed] [Google Scholar]
- 3.Clarke J. L., Chang S. M., “Neuroimaging: diagnosis and response assessment in glioblastoma,” Cancer J. 18(1), 26–31 (2012). 10.1097/PPO.0b013e318244d7c8 [DOI] [PubMed] [Google Scholar]
- 4.Lefranc F., et al. , “Present and potential future issues in glioblastoma treatment,” Expert Rev. Anticancer Ther. 6(5), 719–732 (2006). 10.1586/14737140.6.5.719 [DOI] [PubMed] [Google Scholar]
- 5.Sampetrean O., et al. , “Invasion precedes tumor mass formation in a malignant brain tumor model of genetically modified neural stem cells,” Neoplasia 13(9), 784–791 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Braumann U. D., et al. , “Three-dimensional reconstruction and quantification of cervical carcinoma invasion fronts from histological serial sections,” IEEE Trans. Med. Imaging 24(10), 1286–1307 (2005). 10.1109/TMI.2005.855437 [DOI] [PubMed] [Google Scholar]
- 7.Einenkel J., et al. , “Evaluation of the invasion front pattern of squasmous cell cervical carcinoma by measuring classical and discrete compactness,” Comput. Med. Imaging. Graphics 31(6), 428–435 (2007). 10.1016/j.compmedimag.2007.03.004 [DOI] [PubMed] [Google Scholar]
- 8.Moon W. K., et al. , “Computer-aided diagnosis for the classification of breast masses in automated whole breast ultrasound images,” Ultrasound Med. Biol. 37(4), 539–548 (2011). 10.1016/j.ultrasmedbio.2011.01.006 [DOI] [PubMed] [Google Scholar]
- 9.Huang Y. H., et al. , “Computer-aided diagnosis of mass-like lesion in breast MRI: differential analysis of the 3-D morphology between benign and malignant tumors,” Comput. Methods Programs Med. 112(3), 508–517 (2013). 10.1016/j.cmpb.2013.08.016 [DOI] [PubMed] [Google Scholar]
- 10.Bribiesca E., “An easy measure of compactness for 2D and 3D shapes,” Pattern Recognit. 41, 543–554 (2008). 10.1016/j.patcog.2007.06.029 [DOI] [Google Scholar]
- 11.Bribiesca E., “A measure of compactness for 3D shapes,” Comput. Math. Appl. 40, 1275–1284 (2000). 10.1016/S0898-1221(00)00238-8 [DOI] [Google Scholar]
- 12.Einenkel J., et al. , “Evaluation of the invasion front pattern of squamous cell cervical carcinoma by measuring classical and discrete compactness,” Comput. Med. Imaging Graphics 31, 428–435 (2007). 10.1016/j.compmedimag.2007.03.004 [DOI] [PubMed] [Google Scholar]
- 13.Mercier L., et al. , “Online database of clinical MR and ultrasound images of brain tumors,” Med. Phys. 39(6), 3253–3261 (2012). 10.1118/1.4709600 [DOI] [PubMed] [Google Scholar]
- 14.Prayson R. A., “Glial and glioneuronal: diffuse (fibrillary) astrocytomas,” Chapter 9 in Neuropathol. JR Goldblum, 2nd Ed., 461–468 (2012). [Google Scholar]
- 15.Louis D. N., et al. , “The 2007 WHO classification of tumours of the central nervous system,” in Acta Neuropathol 114(2), 97–109 (2007). 10.1007/s00401-007-0243-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Maldaun M. V., et al. , “Cystic glioblastoma multiforme: survival outcomes in 22 cases,” J. Neurosurg. 100, 61–67 (2004). 10.3171/jns.2004.100.1.0061 [DOI] [PubMed] [Google Scholar]
- 17.Lacroix M., et al. , “A multivariate analysis of 416 patients with GBM: prognosis, extent of resection, and survival,” J. Neurosurg. 95(2), 90–198 (2001). 10.3171/jns.2001.95.2.0190 [DOI] [PubMed] [Google Scholar]
- 18.Martin-Duverneuil N., Mokhtari K., “Gliomes du tronc cérébral,” in Les tumeurs intracraniennes de l'adulte, 1st ed., Sauramps Medical editorial, Paris, 114–116 (2009). [Google Scholar]
- 19.Fan G., et al. , “In vivo single voxel proton MR spectroscopy in the differentiation of high-grade gliomas and solitary metastases,” Clin. Radiol. 59, 77–85 (2004). 10.1016/j.crad.2003.08.006 [DOI] [PubMed] [Google Scholar]
- 20.Castillo M., Smith J. K., Kwock L., “Correlation of myo-inositollevels and grading of cerebral astrocytomas,” AJNR Am J Neuroradiol. 21(9), 1645–1649 (2000). [PMC free article] [PubMed] [Google Scholar]
- 21.Server A., et al. , “Quantitative apparent diffusion coefficients in the characterization of brain tumors and associated peritumoral edema,” Acta Radiol. 50(6), 682–689 (2009). 10.1080/02841850902933123 [DOI] [PubMed] [Google Scholar]