Enrollment in prescription drug insurance: the interaction of numeracy and choice set size

Abstract

Objective

To determine how choice set size affects decision quality among individuals of different levels of numeracy choosing prescription drug plans.

Methods

Members of an internet-enabled panel age 65 and over were randomly assigned to sets of prescription drug plans varying in size from 2 to 16 plans from which they made a hypothetical choice. They answered questions about enrollment likelihood and the costs and benefits of their choice. The measure of decision quality was enrollment likelihood among those for whom enrollment was beneficial. Enrollment likelihood by numeracy and choice set size was calculated. A model of moderated mediation was analyzed to understand the role of numeracy as a moderator of the relationship between the number of plans and the quality of the enrollment decision and the roles of the costs and benefits in mediating that relationship.

Results

More numerate adults made better decisions than less numerate adults when choosing among a small number of alternatives but not when choices sets were larger. Choice set size had little effect on decision making of less numerate adults. Differences in decision making costs between more and less numerate adults helped explain the effect of choice set size on decision quality.

Conclusions

Interventions to improve decision making in the context of Medicare Part D may differentially affect lower and higher numeracy adults. The conflicting results on choice overload in the psychology literature may be explained in part by differences across different types of people in their response to choice sets of varying sizes.

Studies have shown that numeracy, the ability to understand basic probability and other numerical concepts, improves decision quality. More highly numerate individuals are less likely to make mistakes such as to incorrectly apply the use of heuristics or to be prone to different biases when facing decision problems (Cokely & Kelley, 2009; Peters et al., 2006). Studies have also shown that numeracy improves the comprehension and use of health information, resulting in better medical decision making (Peters, Hibbard, Slovic, & Dieckmann, 2007; Reyna, Nelson, Han, & Dieckmann, 2009). Because numeracy-related tasks are common in health care, it is important to assess the effect of numeracy on health-related decisions (Rothman, Montori, Cherrington, & Pignone, 2008).

Other research examines the relationship between the decision making environment and decision outcomes, with many studies focusing on the effect of the number of alternatives facing the decision maker. Many studies document that decision conflict and trade-off difficulty increase with the number of options in the choice set, often resulting in lower likelihood of purchase (Iyengar & Lepper, 2000; Schwartz, 2004). While much of the literature focuses on the effects of extensive choice, Tversky and Shafir (1992) have shown that even with as few as two options, decision conflict can lead to negative outcomes. Szrek and Baron (2007), in contrast, demonstrate that a consumer’s willingness to pay for a product can be greater when the product is presented as one of two options rather than singly. Shah and Wolford (2007) showed that purchase likelihood resembles an inverse U-shaped curve, with purchasing initially increasing and later decreasing with choice set size.

This study considers the effect of the interaction of an individual difference, numeracy, and an environmental characteristic, choice set size, on decision quality. The analysis takes place in the context of Medicare Part D, a program of publicly subsidized prescription drug insurance for older adults and the disabled. In this program, insurance is provided exclusively by competing private insurers, and, in order to obtain publicly subsidized coverage, beneficiaries must choose from an average of 33 plans in their area (Hoadley, Cubanski, Hargrave, Summer, & Neuman, 2010). Approximately 60% of all potential beneficiaries enroll in Medicare Part D. While many beneficiaries have other sources of prescription drug coverage and some low-income beneficiaries are automatically enrolled into a plan, an estimated 10% of potential beneficiaries lack prescription drug coverage (Kaiser Family Foundation, 2011). Thus, while many enroll in the subsidized benefit, the factors influencing the decision not to enroll remain an important policy issue.

Consistent with the broader literature on numeracy and decision outcomes, studies in this setting find that more highly numerate older adults choose better plans (Tanius, Wood, Hanoch, & Rice, 2009), and that numeracy is a more important predictor than age in explaining decision outcomes (Szrek & Bundorf, 2011). As is found in other settings, studies also find that extensive choice set size can impede comprehension or lead to poor choices between drug plans (Hanoch, Miron-Shatz, Cole, Himmelstein, & Federman, 2010; Hanoch, Rice, Cummings, & Wood, 2009; Tanius et al., 2009; Wood et al., 2011). In particular, Wood et al. (2011) found that numeracy remained an important predictor of good financial decision making even after considering crystallized knowledge (vocabulary) and fluid intelligence (e.g., speed of processing and working memory. Our contribution is to examine the interaction of numeracy and choice set size on decision quality. The results highlight the interplay between the environment and individual differences in decision outcomes.

This analysis follows the Reutskaja and Hogarth (2009) conceptual framework in which having additional options generates both benefits and costs to the decision maker. The main benefit of choice is a greater likelihood of finding an ideal product, which is especially important when there is heterogeneity in consumer needs and preferences. Choice may also increase satisfaction with the decision or process. The costs of choice are due to the difficulty that having many options entails: increases in search time, the emotional costs of choice, and the possibility of error. The net benefit depends on the magnitude of the costs relative to the benefits. While both benefits and costs increase with choice set size, benefits increase more slowly than costs. The result is an inverse u-shape relationship between the number of options and the likelihood of purchase reflecting the relative rates of increase of the benefits and costs.

The main hypothesis of the current study is that the effects of choice set size on decision quality vary by individual numeracy. This hypothesis is developed by considering how the predictions of the above framework vary by numeracy. The benefits of additional options will be higher for more numerate adults compared to less numerate adults because more numerate adults can discern the benefits of additional options more readily. The incremental costs of additional options will be lower for more numerate adults because they will find evaluating the alternatives easier and can more easily ignore irrelevant alternatives. Taken together, this suggests that enrollment likelihood will increase more quickly with choice set size among individuals with stronger numeracy skills.

These effects, however, may depend on the calibration of the decision problem. If the problems are calibrated such that they are very difficult for all respondents, with even the easiest problem being too difficult for the less numerate, then more options could increase choice difficulty for the more numerate individuals (and not make a difference in the decision making costs of the less numerate). The net effect of having additional options then will be context-dependent and will depend on whether the benefits outweigh the costs for individuals of different numeracy levels.

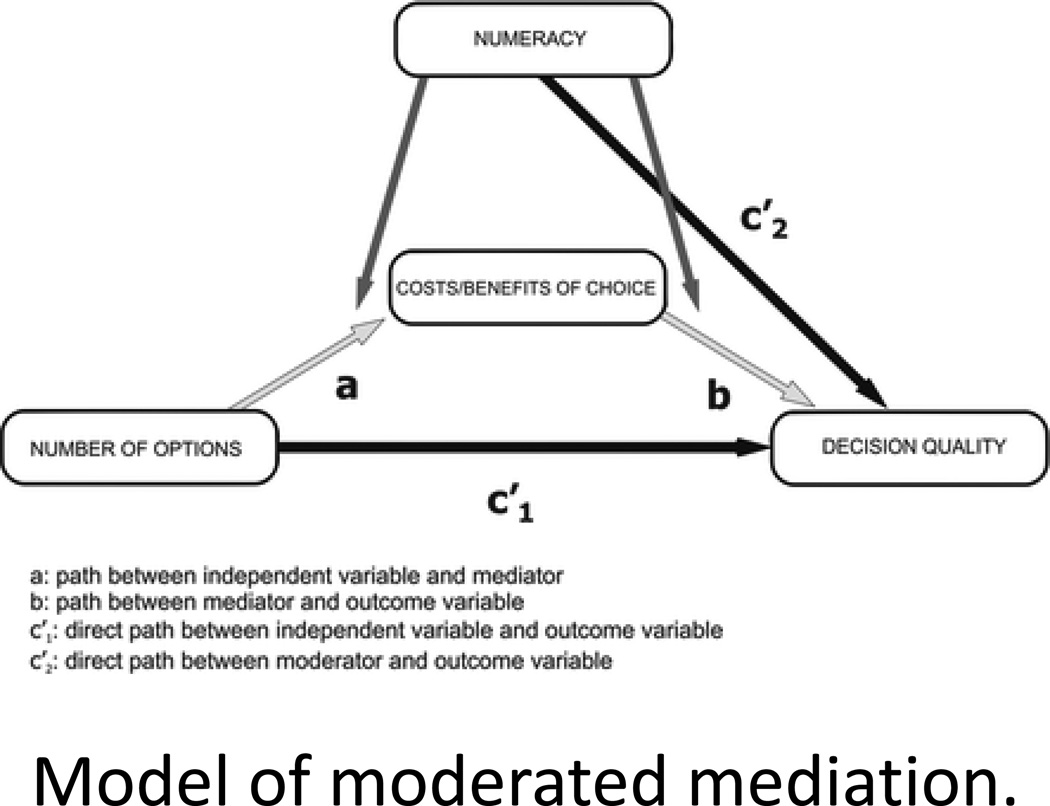
Thus, the hypothesized model is a model of moderated mediation in which numeracy moderates both the path between the independent variable (number of plans) and the mediator (costs/benefits) and the path between the mediator and dependent variable (enrollment likelihood). See Figure 1. The number of options has a direct effect on decision quality (c′₁) and an indirect effect on decision quality through perceptions of the costs and benefits of choice (path a*b). Numeracy has a direct effect on decision quality (c′₂) but also indirectly affects decision quality by moderating the a and b paths.

Figure 1.

Method

Participants

Responses were collected in December 2007, 11 months after the inception of Medicare Part D, from members of an internet-enabled panel age 65 and older (see knowledgenetworks.com). In total 534 individuals were contacted and of these 299 completed the study. We use data from 266 individuals who responded to the key questions of this study, reflecting a response rate of 50%. In order to restrict this analysis to those for whom enrollment is normatively optimal (see more detailed discussion in Measures section), 37 individuals who do not take prescription drugs regularly were eliminated, resulting in a study sample of 229 individuals.

All respondents consented to participating before they were allowed to take part in the study. They were required to check a box that they understood the benefits of participating as well as the potential risks, both of which were described to them. The Stanford University Institutional Review Board approved the study.

Materials and Procedure

The experiment was a simulation of enrollment in Medicare Part D in which participants made hypothetical choices among different prescription drug plans. Actual plan characteristics were modeled after information available on the Medicare website during the first year. By design, study participants chose among a set of nondominated plans; plans with lower deductibles, for example, had correspondingly higher premiums. A hedonic equation was estimated to determine the values of plan characteristics based on the market values (Simon & Lucarelli, 2006). Using this model, the plan premiums were adjusted to make all the potential plans from which respondents chose actuarially equivalent. Descriptions of plan characteristics and other stimuli were also modeled after the Medicare Part D website. This ensured that the study followed actual enrollment decisions as closely as possible. This approach contrasts with other related studies on Part D that are based on simplified problems which have a correct answer that is the same across respondents. Here respondents were given more realistic stimuli with the consequence that the decisions were more difficult.

Upon entry to the study web site, respondents were given information about the different plan characteristics, and randomly assigned to a choice set of two, five, ten, or sixteen different drug plans. See Online Appendix A for a screen shot of the choice screen with 10 drug plans. After making a choice between drug plans, respondents were asked some questions about their decision. They were then randomized, without replacement, to a second choice set size. For the set of two choices, respondents were randomized to different levels of variety: some choice sets had drug plans that were more similar to each other and others had drug plans that were more dissimilar. In this paper, only the first choice from each respondent is analyzed and the multivariate models control for the level of variety.

Measures

The main measure of decision quality is enrollment likelihood: “If presented with the choice of the above plans, how likely would you be to enroll in ANY plan (where the alternative is going without a plan)?” Possible responses ranged from 1 (Certain NOT to enroll), 4 (Equally likely to enroll and not to enroll), to 7 (Certain to enroll). The analysis was restricted to those who take at least one prescription drug. Heiss, McFadden, and Winter (2006) conclude that enrollment is beneficial for seniors who take at least one prescription drug regularly because the expected benefits of coverage are at least as large as the expected costs for this group and coverage also serves as insurance against catastrophic costs. While enrollment may be normatively optimal even for many older adults taking no prescription drugs due to the existence of a penalty associated with late enrollment (Heiss, McFadden, & Winter, 2008), optimality is based on a complicated calculation of the future economic implications of delaying enrollment. As a result, we took the more conservative approach of including the sample for whom optimality was conditional only on current period trade-offs. Other studies, in contrast, have focused on whether one plan is better than another when measuring decision quality (Hanoch et al., 2009; Tanius et al., 2009; Wood et al., 2011). While the question of which drug plan is optimal for a particular person is controversial, the desirability of enrolling in a Medicare drug plan is much less so. This approach also has the advantage of being more consistent with the choice overload literature in which purchasing likelihood is the main dependent measure.

Numeracy was measured using the three general numeracy items from Lipkus, Samsa, and Rimer (2001), which were modified from Schwartz, Woloshin, Black, and Welch (1997). These questions assess respondents’ ability to perform simple mathematical operations using percentages or proportions and to convert between them. This instrument, available in Online Appendix B, was adapted to the survey by making responses multiple choice. (Guessing introduces error that can make it harder to distinguish between levels of numeracy, potentially making it harder to find statistically significant effects.) While this study analyzes only numeracy, rather than using a broader measure of cognitive ability, we note that numeracy has been found to be the most important aspect of cognitive ability in this context (Wood et al., 2011). Demographic characteristics were provided by the survey company and additional information was collected from respondents, including the number of drugs they took regularly.

The costs of choice were measured by asking individuals, following their choice, how difficult the decision was. Benefits were measured by asking respondents how similar their chosen plan is to their ideal plan. Both variables were measured on a 1 to 7 Likert Scale.

Data Analysis

The costs of choice, benefits of choice, and enrollment likelihood were calculated both by numeracy score and by choice set size within each numeracy score. Tests of statistical significance in each outcome by numeracy score were calculated. To examine the hypothesized model in Figure 1, two separate moderated mediation models were fit to the data described above. One model uses costs as the mediator; the other uses benefits.

The moderated-mediation analysis follows the methods described by Preacher, Rucker and Hayes (2007) to identify the areas of the moderator (numeracy) in which mediation occurs. (Analyses are based on Model 5 from Preacher, Rucker, and Hayes (2007); UCLA Academic Technology Services Statistical Consulting Group (2012) provides useful documentation for Stata users.) More specifically, two sets of regressions were run for each mediator (costs or benefits). In one, enrollment likelihood (y) was regressed on costs (or benefits) (m), the number of plans (x), numeracy (w), costs (benefits) interacted with numeracy (mw), numeracy interacted with the number of plans (wx), and all control variables. In the second regression, the mediator m (costs or benefits) was regressed on the number of plans (x), numeracy (w), numeracy interacted with the number of plans (wx), and all control variables. The estimates allow for correlation of the error terms between the two regressions. The coefficients from these two models were then used to compute the full effect of x on y, which includes both its direct and indirect effect on y. First, the direct effect of the number of plans (x) on enrollment likelihood (y) at each level of the moderator (when numeracy=0, 1, 2, 3) was calculated. This is shown as c′₁ in Figure 1, but what is not obvious from the figure is that c′₁ depends on the level of numeracy. Second, the conditional indirect effects of the number of plans (x) on the enrollment likelihood (y) through each of the mediators (costs of choice, benefits of choice) at each level of the moderator (when numeracy=0, 1, 2, 3) were calculated. These conditional indirect effects are further decomposed into the a and b paths. The a path is the path from the number of plans (x) to the mediator (costs/benefits) which is the effect of the number of plans on the perceived costs/benefits of choice to the respondent. The b path is the path from the mediator (costs/benefits) to enrollment likelihood (y) – the effect of an increase in perceived costs/benefits on enrollment likelihood. The product a*b is the conditional indirect effect which shows the effect of x on y through the mediator variable at each level of the moderator (numeracy=0, 1, 2, or 3). Bootstrapping (5000 replications) was used to calculate 95% bias corrected confidence intervals. Linear models in which the moderator (numeracy) is linearly interacted with the number of plans (x) and in which the mediator (costs, benefits) interacts linearly with numeracy were run. The control variables in the regressions include individual characteristics that can effect demand for health insurance (Bundorf, 2002; Scanlon, Chernew, & Lave, 1997) or prescription drug insurance (Levy & Weir, 2010): age, gender, education, employment status, marital status, race, household income, the number of drugs taken regularly, and level of variety. The highest correlation among the variables included in the models was between education and numeracy (0.36).

Results

Respondents in the experiment are younger, more likely to be male, and more highly educated than those in a representative sample of Americans 65 and older (Bundorf & Szrek, 2010). As discussed earlier, for this analysis, 37 people who did not regularly take one prescription drug were dropped from analyses. In the resulting sample, 46% percent of respondents are 65–69 years old, 34% are 70–74, and 20% are 75 and over. Fifty-two percent are female, 10% have less than a high school education, 32% have a bachelor’s degree or higher (not shown in table), 20% are employed, 75% are married, and 14% are non-White. Table 1 shows demographic characteristics for the sample, responses to the main variables (choice difficulty, availability of the ideal plan, and enrollment likelihood), and actual enrollment statistics for our respondents. The number of plans in the choice set was a randomized variable as was the level of plan variety.

Table 1.

Study Sample Characteristic

Age	65–69	46
	70–74	34
	75 and over	20
Gender	Male	52
	Female	48
Education	Less than High School	10
	High School Graduate	32
	More than High School	58
Employment Status	Not Employed	80
	Employed	20
Marital Status	Married	75
	Not Currently Married	25
Race	White	86
	Other	14
Household Income	Less than $24,999	20
	$25,000–74,999	58
	More than 75,000	22
Number of Drugs Taken Regularly	1–2	28
	3–5	44
	6 or more	28
Number of Plans in Choice Set	2 plans	22
	5 plans	24
	10 plans	31
	16 plans	23
Level of Plan Variety	Low	46
	High	54
Number of Numeracy Questions Correct	0 correct	21
	1 correct	25
	2 correct	28
	3 correct	26
Choice Difficulty	1 (Not at all)	6
	2	7
	3	9
	4	11
	5	20
	6	27
	7 (Extremely)	19
Similarity to one's Ideal Plan	1 (Ideal plan would be very different)	9
	2	7
	3	16
	4	20
	5	26
	6	17
	7 (Plan is the ideal)	4
Enrollment Likelihood	1 (Certain NOT to enroll)	3
	2	5
	3	17
	4 (Equally likely to enroll and not to enroll)	30
	5	28
	6	14
	7 (Certain to enroll)	2
Prescription Drug Coverage (actual)	Medicare Part D only	32
	Medicare Part D & Other Drug Coverage	11
	Other Drug Coverage only	50
	No Prescription Drug Coverage	8

Note. Sample characteristics are shown in percentages. Due to rounding, numbers in some categories may not add up to 100. (N=229)

Numeracy, Choice Set Size, and Enrollment Likelihood

Numeracy is positively associated with enrollment likelihood (see last column of Table 2 where all choice set sizes are combined). Individuals with 1 or more correct numeracy questions have significantly higher enrollment likelihood than those with 0 correct. While those with 1 or more correct numeracy items are indistinguishable from each other in the unadjusted models, when controlling for demographics, those with 2 or 3 correct items are more likely to enroll than those with 1 correct item.

Table 2.

Enrollment likelihood, benefits, and costs by number of plans and numeracy questions correct

		2 Plans	SD	5 Plans	SD	10 Plans	SD	16 Plans	SD	All	SD
Enrollment Likelihood	0 correct	4.3	[1.77]	4.9	[1.31]	4.1	[2.03]	4.7	[1.23]	4.5	[1.62]
	1 correct	4.9	[1.97]	5.5	[1.73]	5.4	[1.96]*	5.5	[1.57]	5.4	[1.79]**
	2 correct	5.6	[1.85]*	5.7	[1.65]	6.3	[1.14]**	4.9	[2.06]	5.7	[1.72]**
	3 correct	5.8	[1.48]*	6.2	[0.86]**	5.5	[1.54]*	5.6	[1.64]	5.7	[1.41]**
Costs (Choice Difficulty)	0 correct	5.2	[1.94]	4.6	[1.68]	4.9	[1.98]	5.9	[0.83]	5.1	[1.71]
	1 correct	4.6	[1.69]	4.8	[1.82]	4.4	[2.26]	5.8	[1.49]	4.8	[1.92]
	2 correct	4.0	[1.91]	4.6	[2.14]	5.1	[1.45]	5.7	[1.29]	4.8	[1.79]
	3 correct	3.4	[1.90]*	4.9	[1.39]	5.4	[1.31]	5.2	[1.70]	4.9	[1.66]
Benefits (Closeness to Ideal Plan)	0 correct	4.0	[1.48]	3.3	[1.56]	3.9	[1.46]	5.1	[1.22]	4.0	[1.53]
	1 correct	4.7	[1.35]	3.7	[2.06]	4.2	[1.74]	4.1	[1.51]	4.1	[1.71]
	2 correct	4.1	[1.49]	3.8	[1.83]	4.8	[1.52]*	4.4	[1.79]	4.3	[1.64]
	3 correct	3.2	[1.75]	4.2	[1.70]	4.4	[1.71]	4.3	[1.28]	4.1	[1.63]

Note. Table shows mean enrollment likelihood, benefits, and costs by number of plans and number of numeracy questions correct. Standard deviations are shown in squared brackets, with asterics indicating if the mean is statistically different from the mean within the same number of plans and 0 correct. In the last two columns, data is pooled across choice set size (all choice set sizes are included) and tests show if the mean is different by numeracy questions correct from the mean with 0 correct.

Significance levels shown are ** p<0.01,

^*p<0.05.

The unadjusted analyses also indicate that the effect of numeracy depends on choice set size. Table 2 presents means and standard deviations for enrollment likelihood, benefits (similarity to the ideal plan), and costs (choice difficulty) by choice set size and numeracy score. Tests of significant differences, calculated using t-tests, are shown within each choice set size, for each numeracy level compared to 0 correct. In the right two columns, means and standard deviations of enrollment likelihood, costs, and benefits are shown by numeracy score, pooled across choice set size. The main finding is that enrollment likelihood increases with numeracy when there are fewer than 16 drug plans. At 16 drug plans, the differences in enrollment likelihood for individuals at different numeracy levels are no longer significant. (We note that the mean enrollment rate for those with numeracy scores of 2 exceeds that of those with numeracy scores of 3 at 10 plans, but this difference is not significant (p=.06). Also, at 16 plans the mean enrollment rate for individuals with a numeracy score of 1 exceeds the mean enrollment rate for individuals with numeracy scores of 2 and 3, but again these differences are not significant with p=.44 and p=.87, respectively.)

The results in Table 2 suggest that the costs of choice are lower for those with high levels of numeracy when choice set size is small but not when it is larger. When respondents chose between 2 plans, the costs of choice were significantly lower for respondents with 3 numeracy questions correct than for those with 0 correct. Additionally, in regressions not shown here, we found that costs increase linearly with choice set size but only for individuals in the higher numeracy groups, but not for those in the lower numeracy groups: Using OLS regression to predict costs separately for each numeracy group, the coefficient on number of plans is significant with p=.03 and p=.01 for models with numeracy scores of 2 and 3, respectively, but is not significant for models with numeracy scores of 0 or 1. Finally, we also explored the potential of learning in our task by analyzing whether respondents reported lower costs the second time they made a choice. We used data, not analyzed in this current study, on a second choice made by respondents. We found that only the highest numeracy group saw a significant reduction in costs the second time they made a choice (difference = .6, p=.03).

The results provide little evidence of systematic differences in benefits by numeracy level either within choice set size groups or when the responses are pooled over choice sets of difference sizes. The one statistically significant comparison is not consistent with a clear pattern of results within the choice set size category.

While other studies also show that older adults with higher numeracy make better decisions in this context (Tanius et al., 2009), the results on the interaction between numeracy and choice set size indicate that this difference depends on choice set size. The finding suggests that the “advantage” that individuals with higher numeracy possess that helps them make better quality decisions disappears when choice set sizes are large. The next section reports results from a framework for analyzing the mechanisms underlying this finding.

Moderated Mediation Models

Table 3 shows the direct and indirect effects of choice set size on enrollment likelihood for a model with costs as a mediating variable (Model 1) and for a model with benefits as a mediating variable (Model 2). See also Figure 1 for the hypothesized model and the description of the moderated mediation models above. All results are shown separately for each level of numeracy, and included are the estimates and confidence intervals for the direct effects, a path, b path, and a*b indirect effect.

Table 3.

Moderated-Mediation Model of the Effect of Choice Set Size on Enrollment Likelihood

	Numeracy as the Moderator
	Numeracy = 0		Numeracy = 1		Numeracy = 2		Numeracy = 3
Model 1: Costs as the Mediator	(n=48)		(n=57)		(n=63)		(n=59)
Cost measured by choice difficulty	Estimate	95% BC CI	Estimate	95% BC CI	Estimate	95% BC CI	Estimate	95% BC CI
Indirect Effect (a*b)	−0.008	(−0.040–0.005)	−0.012*	(−0.032–−0.001)	−0.016*	(−0.035– −0.004)	−0.021*	(−0.059– −0.003)
Choice set size on Enrollment via Costs
Path (a)	0.074	(−0.002–0.152)	0.084*	(0.034–0.134)	0.094*	(0.047–0.146)	0.104*	(0.030–0.184)
Choice set size on Costs
Path (b)	−0.107	(−0.337–0.120)	−0.138	(−0.283–0.009)	−0.170*	(−0.295– −0.043)	−0.201*	(−0.402– −0.023)
Costs on Enrollment Likelihood
Direct effect (c'1)	0.012	(−0.056–0.083)	0.003	(−0.044–0.052)	−0.005	(−0.055–0.042)	−0.014	(−0.089–0.055)
Choice set size on Enrollment Likelihood
	Numeracy = 0		Numeracy = 1		Numeracy = 2		Numeracy = 3
Model 2: Benefits as the Mediator	(n=47)		(n=57)		(n=62)		(n=59)
Benefits measured by similarity to ideal plan	Estimate	95% BC CI	Estimate	95% BC CI	Estimate	95% BC CI	Estimate	95% BC CI
Indirect Effect (a*b)	0.002	(−0.010–0.031)	0.005	(−0.002–0.024)	0.009*	(0.001–0.023)	0.012	(−0.002–0.040)
Choice set size on Enrollment via Benefits
Path (a)	0.047	(−0.025–0.116)	0.047*	(0.002–0.092)	0.047*	(0.004–0.088)	0.046	(−0.024–0.106)
Choice set size on Benefits
Path (b)	0.042	(−0.260–0.349)	0.113	(−0.074–0.308)	0.184*	(0.046–0.341)	0.255*	(0.051–0.483)
Benefits on Enrollment Likelihood
Direct effect (c'1)	0.009	(−0.067–0.80)	−0.011	(−0.062–0.036)	−0.031	(−0.080–0.011)	−0.051	(−0.127–0.011)
Choice set size on Enrollment Likelihood

Note. Separate models are shown for when costs (benefits) are the mediator. In both cases, the two regressions used were of the following form. In the first regression, y (enrollment likelhood) was regressed on costs (or benefits) (m), the number of plans (x), numeracy (w), costs (benefits) interacted with numeracy (mw), numeracy interacted with the number of plans (wx), and all control variables. In the second regression, the mediator m (costs or benefits) was regressed on the number of plans (x), numeracy (w), numeracy interacted with the number of plans (wx), and all control variables. The control variables used in the regression were age, gender, education, employment status, marital status, race, household income, and the number of drugs taken regularly. Estimates and 95% bias-corrected confidence intervals are shown.

The direct effect of the number of plans on enrollment likelihood

Table 3 shows that the direct effect of the number of plans on enrollment likelihood is not significant in either model at any level of numeracy.

The indirect effect of the number of plans on enrollment likelihood: costs as mediating variable

As hypothesized, as the number of plans increases, choice difficulty increases and decision quality (enrollment) declines. The magnitude of the effect increases with numeracy, although the confidence intervals overlap. At numeracy scores of 0, choice set size does not have a significant effect on decision quality through the indirect effect a*b. However, at numeracy scores of 1 or higher, the indirect effect is statistically significant. At numeracy scores of 2, an increase of 10 plans in the choice set increases choice difficulty by 15.7 percentage points ((0.094*10)/6) and reduces enrollment likelihood by 28 percentage points ((−0.170*10)/6). More generally, as shown in Table 3, increases in choice set size increase costs as numeracy increases (path a). This increase in costs consequently lowers enrollment likelihood (path b) for those with numeracy levels of 2 and 3, with the effect even stronger for the latter group.

The indirect effect of the number of plans on enrollment likelihood: benefits as mediating variable

There is less support for the hypothesized role of benefits as a mediator. It was expected that the benefits of choice, in the form of access to one’s ideal plan, and decision quality would increase as the number of plans increased. While the estimates of the indirect effects are consistent with this hypothesis, only at numeracy scores of 2, is there a statistically significant increased effect of the number of options on benefits and of benefits on decision quality. For numeracy scores of 3, the 95% bias corrected confidence interval of the indirect effect is from −0.002 to 0.040, which just includes 0 but is mostly positive. The separate indirect effects are worth mentioning. First, the effect of choice set size on benefits (path a) does not change with numeracy. Second, the effect of benefits on enrollment likelihood (path b) increases with numeracy.

The direct effect of numeracy on enrollment likelihood

Results from the moderated mediation analysis are consistent with those shown in Table 2. With choice difficulty as a mediator and for choice set sizes up to 10 plans, increases in numeracy increase enrollment likelihood from .36 to .48 (an increase in enrollment likelihood of 6–8%, result not shown in table). However, with 16 plans, changes in numeracy do not improve enrollment likelihood. In the benefits model, increases in numeracy generally do not significantly affect enrollment likelihood. The direct effect of numeracy on enrollment likelihood is calculated by taking the first derivative of enrollment likelihood with respect to numeracy and measuring the direct effect of numeracy for all combinations of numeracy levels and number of plans. As before, bootstrapping is used to derive confidence intervals around the estimates.

Models without the control variables

Given the relatively small sample size and potential collinearity between some variables, we chose to rerun the models without the control variables to see how this affected the results. In the costs model, we found the estimates of the indirect effects at numeracy levels 2 and 3 to increase slightly, and the indirect effect at numeracy level 1 was no longer significant. Similarly, in simpler regression models, we had previously found the numeracy group with 1 correct to be statistically indifferentiable from those with 0 correct until we accounted for individual characteristics. In the benefits model, estimates change only very slightly and statistical significance remains unchanged with the exclusion of the control variables.

Discussion

Consistent with previous work on individual differences, in this context and others, more numerate individuals make higher quality decisions when deciding whether or not to enroll in a prescription drug plan. It is shown, however, that the advantage of more numerate individuals dissipates when the environment changes – when the number of alternatives increases. This provides the first evidence that numeracy moderates the choice overload effect.

The moderated mediation analysis highlights the main mechanism that explains how numeracy moderates the choice overload effect in the setting examined: The costs of larger choice set sizes, as measured by self-reported decision difficulty, increase with numeracy. This results in choice set size having a larger negative effect on enrollment likelihood for individuals with higher numeracy compared to those with lower numeracy. Our results showed that these two separate effects (choice set size on choice difficulty, choice difficulty on enrollment likelihood) were not significant for individuals with the lowest numeracy levels. A simple interpretation of this is that, for individuals with lower numeracy, making choices amongst even small set sizes was difficult, so there was no difference across choice set size. The data are consistent with an explanation in which those with low numeracy reach a floor, in which choice difficulty does not increase further even with increases in choice set size and in which choice difficulty does not decrease even a second time a choice is made. Similarly, costs experienced by those randomized to two plans with 0 numeracy questions correct are already as high as costs for those randomized to 16 plans with 2 numeracy questions correct. For individuals with higher numeracy, there were differences in performance with set size because individuals found it significantly more difficult to make choices with larger set sizes and because this increase in costs translated into lower enrollment likelihood.

Although the indirect effect of choice set size via benefits on enrollment likelihood was generally not significant in the benefits model, our results suggest that further inquiry into this effect may be valuable. The effect of increases in choice set size on benefits did not vary by numeracy level, but the effect of increases in benefits on enrollment likelihood did. The former suggests that the differences in perceptions of benefits were relatively small, perhaps because the product was difficult for all respondents to evaluate in the first place. Perceptions of benefits may not be as easy to vary as actual benefits in a decision context as complex as this one. The latter result is interesting because it shows that higher numeracy respondents were more responsive to perceptions of benefits, thus providing some general support for the hypothesis that benefits differ by numeracy level. Future work could experimentally randomize the level of benefits or costs to explore the resulting effects on enrollment likelihood for respondents of different numeracy levels.

More generally, the moderated mediation analysis highlights two indirect effects of the number of choices on decision quality that run in opposite directions. When choice set size increases, both the costs and benefits of decision making rise. In this context, these effects were more pronounced among more highly numerate individuals. We did not find evidence that decision making costs increased with choice set size among less numerate individuals. While this was not what we hypothesized – we expected decision making costs to increase with choice set size among all respondents, it is not inconsistent with the conceptual framework. A potential explanation for the lack of a relationship between choice set size and decision making costs for individuals with low numeracy is that they did not increase their effort because the decision was very difficult even when they were choosing from only two plans. In other words, they experienced a floor effect. Another explanation, which builds on Dieckmann, Slovic, and Peters (2009), is that individuals with lower numeracy use different information than individuals with higher numeracy, which may lead them to hold different perceptions and make different decisions. This alternative approach would then separately consider individuals with lower and higher numeracy to understand what information they respond to and how they apply the cost-benefit framework. This study provides support for ex-ante hypotheses that suggest why we would expect different relationships amongst choice set size, costs, and benefits in these two groups, in particular in response to different numeric information.

More generally, the pattern of results observed in this context could be a function of the type of decision that was analyzed. How the costs and benefits of decision making vary by individual characteristics such as numeracy could vary across decisions and contexts. It is possible that some of the contradictory findings in the choice overload literature could be explained by analyzing these two opposing indirect effects (Zhao, Lynch, & Chen, 2010). Research that finds no effect of the number of options on satisfaction or purchase likelihood, as well as research that does find a direct effect, could potentially be reconciled by analyzing these two separate pathways. Future work will need to examine whether considering the costs and benefits of choice at different set sizes, moderated by numeracy, can help explain the contradictory findings in the literature on choice overload (Schebeihenne, Greifeneder, & Todd, 2010).

Policy Implications

The main policy implication from this study is that individuals with differing levels of numeracy may need different types of policies or different kinds of assistance in order to make effective choices. Higher numeracy respondents had difficulty with extensive choice, but the results also suggest that simply reducing the number of alternatives would not help improve decision quality for people with lower numeracy in this setting. Rather, they have trouble making a decision in the first place, as indicated by their much lower baseline enrollment rates when choice set size was two or five plans. Thus efforts to simplify the choice process, such as those advocated by Wrobel, Kling, Mullainathan, Shafir, and Vermeulen (2008), are likely to be most helpful for more numerate adults. Older adults with lower numeracy, in contrast, may benefit from more paternalistic policies, such as expert guidance or automatic enrollment into a default plan in the absence of an active choice. Consistent with this, we found that respondents with numeracy scores of 0 stated “It was too difficult to make a choice” as a frequent reason for not actually being enrolled in a drug plan in real life, which was not the case for the other numeracy groups. More generally, future work should consider what processes influence decisions of different numeracy groups in more detail.

This study has some limitations that should be considered when identifying the policy implications. First, the maximum choice set size in the study was 16 while in reality individuals have on average 33 plans from which to choose. Second, respondents were responding to a hypothetical task for which they would not be as motivated as with the real task. A study based on actual plan choices finds a similar main effect of cognition on enrollment in Medicare Part D (Levy & Weir, 2010), providing support that the results are not entirely driven by a lower level of motivation among those with lower numeracy in responding to this survey. In addition, people may have decision support from their family and friends, but the effects of this kind of support are not captured in this analysis. Again the study by Levy and Weir (2010) suggests that this type of assistance does not eliminate differences between people of different levels of cognitive ability.

Choice among competing health plans is an important policy issue in other settings as well. The 2010 health care reform in the U.S. extends this model of subsidized insurance more broadly by promoting the implementation of health insurance exchanges in which people would choose among competing private plans to obtain coverage. This model of providing subsidized health insurance is not restricted to the U.S. Both the Netherlands and Switzerland have health care systems in which consumers choose among competing plans to obtain publicly subsidized benefits. Thus, evidence on how different exchange design factors, such as the number of plans offered, affects different types of people is relevant beyond the context of this study.

Overall, more research that couples analysis of the environment and of individual decision making competencies is needed to help extend our understanding of decision making in naturalistic environments and of the kind of government policies that would be most effective for different types of people.