Continuum Modeling of Forces in Growing Viscoelastic Cytoskeletal Networks

Abstract

Mechanical properties of the living cell are important in cell movement, cell division, cancer development and cell signaling. There is considerable interest in measuring local mechanical properties of living materials and the living cytoskeleton using micromechanical techniques. However, living materials are constantly undergoing internal dynamics such as growth and remodeling. A modeling framework that combines mechanical deformations with cytoskeletal growth dynamics is necessary to describe cellular shape changes. The present paper develops a general finite deformation modeling approach that can treat the viscoelastic cytoskeleton. Given the growth dynamics in the cytoskeletal network and the relationship between deformation and stress, the shape of the network is computed in an incremental fashion. The growth dynamics of the cytoskeleton can be modeled as stress dependent. The result is a consistent treatment of overall cell deformation. The framework is applied to a growing 1-d bundle of actin filaments against an elastic cantilever, and a 2-d cell undergoing wave-like protrusion dynamics. In the latter example, mechanical forces on the cell adhesion are examined as a function the protrusion dynamics.

1 Introduction

Eukaryotic cells are constantly undergoing motion. In order to move, cells also exert significant traction forces on their underlying substrates (14; 11; 44), and protrusive forces on obstacles (39). At the molecular level, cell movements are driven by polymerization and depolymerization of cytoskeleton filaments and the action of molecular motors (38). What remains to be explained is the relationship between global cell shape and intracellular forces. Quantitation of intracellular forces is important in understanding how cells sense their mechanical environment, and how forces affect cell signaling. Toward this end, mechanical measurements on live cells using micromechanical techniques have emerged (52; 35; 50; 49; 17; 12; 7; 8). These measurements show that the cytoskeletal network inside cells are relatively soft and viscoelastic. Slow relaxation of cellular stress is probably due to complex internal dynamics of the cytoskeleton. The present paper develops a general framework that can relate changes in the global shape of the cytoskeleton network with mechanical forces in the cell. The framework takes into account growth and shrinking of the cytoskeleton and its viscoelastic properties. We show that given the growth dynamics of the network, internal stress in the network can be computed. The growth dynamics is also coupled to the stress in the network. The framework is applied to 1- and 2-dimensional proof-of-principle examples, including forces exerted on focal adhesions during wave-like growth of the cell leading edge.

At large enough length scales, the cytoskeletal network can be modeled as a continuum deformable body. A novel aspect of cytoskeletal networks, and indeed all living materials, is that their constitutive parts are not static but undergoing their own internal dynamics. Actin filaments are polymerizing and depolymerizing on time scales of seconds; branching proteins such as Arp2/3 and bundling proteins such as fascin change the network geometry dynamically (38). These remodeling activities can be classified into two types: Type one are changes that modify the local elastic properties of the cytoplasm, but do not change the shape of the cell. Activities such as polymer cross-linking and increases in filament density stiffen the network, but do not necessarily change the cell shape. Type two are changes that affect the material shape. Polymerization and depolymerization, which add and subtract material, fall into this category. In this paper, type one changes are equivalent with the term “remodeling” and type two changes are equivalent with the term “growth,” although it is important to note that both types of changes occur in the F-actin network in the living cell. There has been theoretical work on modeling the F-actin network constitutive law (45). This work analyzes the combined effects of mechanics and growth, which must be considered on an equal footing.

Dynamics of growing actin networks in vitro and in vivo have been studied extensively with experiments and modeling. In the context of a single filament, force generation by a growing stiff polymer was predicted theoretically (37), and single filament measurements of microtubule force generation have been performed (24; 43). Forces by growing actin filaments have been measured as well (25; 15). In the context of a moving cell, F-actin network growth drives the motility of eukaryotic cells, including the fish keratocyte where experiments and mathematical modeling have been performed (28; 27; 33; 42). F-actin protrusions such as the lamellipodium and filopodium are also involved in changing the cell shape (32; 34; 3; 2). Mechanics, shape changes and force generation in endothelial cells and neutrophils have been examined (21; 40). Mechanics and forces in a gel of cytoskeleton and motors have been studied (23; 47). For the bacterial cell Listeria monocytogenes, actin network growth occurs outside the cell body and propulsion of the F-actin comet tail has been described by continuum models and discrete filament simulations (46; 19; 18; 13; 1). Experiments on moving beads in a reconstituted F-actin network have also been performed (29). Force measurements on a reconstituted growing network have been studied recently (8; 36). Finally, cytoskeletal networks also drive the motion eukaryotic sperm cells where instead of actin, the protein MSP is known to be a major contributor (48; 51).

A major conclusion from this body of work is that the cytoskeletal network has diverse morphologies in different contexts. The cytoskeleton network is the critical element controlling the shapes and forces in the cell. For example, in the filopodium, F-actin is organized in parallel bundles. In the lamellipodium of fish keratocyte, the F-actin network forms a dendritic branched structure. Within a single cell, the network in the cell cortex is different from the network in cytoplasm. Structures such as stress fibers and contractility from internal molecular motors further complicates the description. The mechanism of growth and remodeling is also different in different contexts. Thus, it is desirable to develop a general framework to quantify the process of cytoskeleton growth and remodeling where any mechanical properties of the network and any growth and remodeling mechanism can be incorporated. It is also desirable to incorporate experimentally measured network mechanical properties, spatial heterogeneity and anisotropic effects. A general framework such as this will connect growth remodeling mechanisms with macroscopic shape changes of the cell, predict internal forces and stress in the cell, and compute forces exerted by the cell on extracellular objects such as the substrate or obstructions.

The method in this paper starts with a continuum kinematic framework developed by Rodriguez, Hoger and McCullor that decomposes the net deformation of a body into an elastic component and a growth component (41). This framework, in principle, is mathematically exact. When combined with a constitutive law for the body, a complete description of the internal forces and overall deformation is possible. The constitutive law can relate the molecular geometry of the cytoskeleton network with strains and/or strain velocities, and relate the strains and strain velocities to stress. And it is in the constitutive law where heterogeneous structures such as bundles and crosslinks can be incorporated. This paper applies this kinematic framework to viscoelastic materials which is more appropriate for cytoskeletal networks. We develop an incremental deformation approach to describe viscous stress, and analyze arbitrary growth dynamics and stress-dependent growth, and can model systems ranging from reconstituted networks to cells. The novel parts of our formulation are: 1) we incorporate small incremental growth and deformation, which converts an intrinsically nonlinear problem into a linear one with cumulative elastic quantities; 2) the deformation decomposition is developed for viscoelastic media which is applicable to the cytoskeletal network (Appendix); and 3) the development allows for coupling of any physically relevant phenomena such as the local stress in the material or local G-actin concentration with the growth tensor. The formulation is designed to be appropriate for biological systems. We apply the framework to several proof-of-principle 1- and 2-dimensional examples. For the 1-d example, we show that stress-dependent growth can explain the force exerted by a F-actin bundle against a cantilever. For the 2-d case, we show that it is possible to compute forces on focal adhesions from cytoskeletal dynamics at the leading edge. The developed framework is therefore a versatile tool for analyze a range of problems in different contexts.

2 The Model

In general, deformations must be described using tensor quantities. In the Appendix, we describe a general kinematic framework for examining incremental growth and deformation of a growing deformable body. We also develop a general relationship between the elastic and viscous stress with strain, strain velocity, and a spatially varying growth rate. We show that the growth rate of the network affect the stress in the network and can be computed using a finite deformation formulation. The growth rate is also affected by the stress internal to the body, much like how a single bond reaction rate is affected by forces. We propose a phenomenological relationship between the growth rate and stress. For a single bond in the static limit, the model reduces to Bell’s model of bond rapture rate (5).

For a 1-D situation, all the deformation and growth tensors are scalars. Equations in the Appendix simplify; the deformation from the (k–1)-th increment to the k-th increment in time is

$$F_k=A_k{G}_k=\frac{\partial x_k}{\partial x_{k-1}}$$ (1)

where G_k is the growth at the k-th time increment and A_k is the mechanical deformation. Here k = 0 is equivalent to t = 0. Also we have G₀ = A₀ = 1. The net growth and net mechanical deformations are (Fig. 1)

$$\begin{array}{cc}\hfill & G^{\left(k\right)}=G_k{G}_{k-1}\cdots G_1\equiv G,\hfill \\ \hfill & A^{\left(k\right)}=A_k{A}_{k-1}\cdots A_1\equiv A.\hfill \end{array}$$ (2)

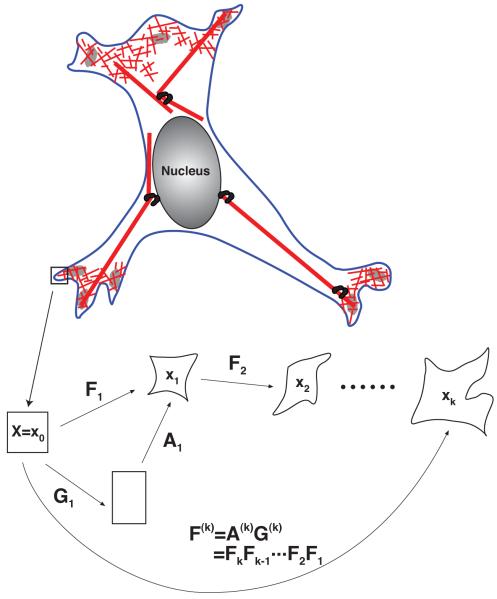
Fig. 1.

The dynamics of cytoskeleton networks can be described in a continuum framework using coordinate transformations. The cartoon shows incremental growth and deformation that produce successive material frames X ≡ x₀, x₁ …, x_k. At each step, the shape changes can be described by the deformation tensor, F_k = ∂x_k/∂x_k–1. Successive incremental deformations generate large overall deformations. The deformation is due to a combination of cytoskeletal growth/shrinking, and mechanical deformation. See the Appendix for a complete development of the mathematical framework.

We note that growth of the cytoskeleton can be substantial, therefore the net deformation due to growth, G, can be substantially different from unity. To properly account for large deformations, we must use finite deformation models. The stress in the cytoskeletal network is due to mechanical deformation, A, only. The cytoskeleton is a viscoelastic material. The stress can be written as σ = σ^e + σ^v where σ^e is the elastic part and σ^v is the viscous part. The appendix describes a general constitutive relationship that incorporates finite deformations. In 1-D, the results simplify and the net Cauchy stress is

$${\sigma }_k=\underset{\text{elastic part}:{\sigma }^e}{\underbrace{{\lambda }_0\ln A+{\mu }_0(A^2-1)}}+\underset{\text{viscous part}:{\sigma }^v}{\underbrace{{\mu }_1\frac{\partial A}{\partial t}{F}^{-1}}}$$ (3)

This forms of the stress will result in a nonlinear differential equation, and the solutions are growth-history dependent. A linear and simplified set of equations can be obtained by considering the deformation from (k – 1)-th increment to the k-th increment as small (see Appendix). We write F_k = 1+U_k where U_k is the gradient of the displacement, u_k,

$$U_k=\frac{\partial u_k}{\partial x_{k-1}}=\frac{\partial (x_k-x_{k-1})}{\partial x_{k-1}}$$ (4)

we obtain

$$\begin{array}{cc}\hfill {\sigma }_k& =\left({\lambda }_0+2{\mu }_0{A}^{{(k-1)}^2}\right)(U_k-g_k)\hfill \\ \hfill & +{\mu }_1{G}^{{(k-1)}^{-1}}(W_k-K_k)\hfill \\ \hfill & +{\mu }_0\left(A^{{(k-1)}^2}-1\right)+{\lambda }_0\ln A^{(k-1)}.\hfill \end{array}$$ (5)

where W_k is the gradient of the displacement velocity: W_k = U_k/Δt, g_k is the displacement gradient due to growth: G_k = 1+g_k and K_k is the growth rate K_k = g_k/Δt. A^(k–1) is the mechanical deformation up to the previous step. Because the increment is small, one can also assume x_k ≈ x_k–1 as in linear elastic theory. The equation for the displacement is obtained from force balance in the quasi-static (slow growth) limit where the drag from the surrounding fluid is negligible:

$$\frac{\partial {\sigma }_k}{\partial x_k}=0.$$ (6)

In the limit of small total deformation and no growth, i.e., A^(k) = F^(k) = 1+U where U is small, the above constitutive equation leads to the following conventional linear viscoelasticity

$$\sigma =\mathit{YU}+{\mu }_1\stackrel{.}{U}$$ (7)

where $U=\frac{\partial u}{\partial x}$ and Y denotes the Young’s modulus. Here, however, we see that the presence of growth modifies the stress and forces in the network.

The growth dynamics in the cell is generally time-dependent. When the cell is experiencing mechanical stress, the growth dynamics should be a function of the stress in the material, i.e.,

$$\frac{\partial G}{\partial t}=\mathit{KG}=K_0{e}^{\gamma \sigma (x,t)∕k_{\mathrm{B}}T}G\left(t\right)$$ (8)

Thus Eq. (8) must be solved in conjunction with Eq. (6) as a coupled system.

3 Forces in a Growing Cytoskeletal Bundle

Recent experiments have measured forces and shape change in a growing cytoskeletal bundle. Here we use our model to explain the measurement. We consider the geometry used in Ref. (8; 36), i.e., a 1-d bar of growing viscoelastic actin network subjected to a pressure at one end; and the other end is fixed (Fig. 2). Using Eqs. (B.1), (B.13), and (B.18), and a finite element method, we can solve the stress and length of the system under any pressure. The initial length and the cross-sectional area of the bar are denoted as L₀ and A_c, respectively. The boundary conditions are: u(x(X = 0, t)) = 0 and σ(x(X = L₀, t)) = P(t). The pressure on the boundary P(t) comes from the deflection of the AFM cantilever, and can be written as:

$$P\left(t\right)=\frac{C}{A_c}\left(L\right(t)-L_0)$$ (9)

where C is the stiffness of the cantilever and L(t) is the current length of the bundle, L₀ is the length before any deflection occurred. We assume that the newly added network material also has the same elastic and viscous response. For the elastic part, the network has Young’s modulus (Y) and Poisson’s ratio (ν), which are related to (μ₀, λ₀) as given in Eq. (B.5).

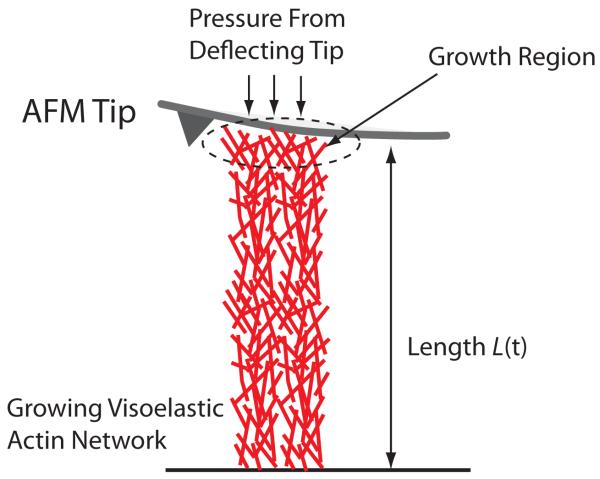
Fig. 2.

A growing bundle of F-actin pushing against an AFM cantilever. The lever exerts a pressure on the bundle due to elastic restoring force. However, the growing F-actin also exerts an upward force, and the measured force in the cantilever depends on the growth dynamics in the actin network. Growth does not occur uniformly in the bundle, rather growth is localized near the tip of the bundle.

The Young’s modulus of the actin bundle was measured independently in a micro-manipulation experiment (31). In the 1-D case, since there is no lateral information, we set ν = 0. In Table 1 we summarize these parameters.

Table 1.

Elastic and geometric parameters from Ref. (36). These parameters are not fitted, but are used as inputs of the model.

Description	Value
Young’s Modulus, Y, [kPa]	3.7
Poisson’s Ratio, ν	0.0
Cross Sectional Area, Ac [μm2]	381
Initial Bundle Length, L0, [μm]	3.0
Cantilever Stiffness, C, [nN/μm]	30

Given these physical parameters for this system, our framework allows us to compute the length and force in the bundle as a function of the growth dynamics. We model the growth rate at the tip of the bundle as

$$K\left(x\right)=K_0\delta (x-L(t\left)\right)e^{\gamma f\left(x\right)∕k_{\mathrm{B}}T}$$ (10)

where K₀ and γ are constants, and f(x) is the force at the tip of the bundle: f(x) = σ(x)A_c. Thus, there are three parameters γ, K₀ and μ₁ that will determine the stress in the bundle and the deflection of the cantilever as a function of time.

In the experiment, there is a force-independent regime at smaller loads. The exact growth mechanism in this regime is not known. Here we will model the force-dependent growth which occurs after the bundle. The actual calculation proceeds as follows. First we divide the initial cytoskeleton region into a finite element mesh. In this example, the 1-D domain of the initial bundle is divided into N elements. Spatially non-uniform growth is described by assigning displacement due to growth, u_g, at each finite element node. Recall that $u_g(x,t_k)={\int }_0^{x}K(y,t_k)\Delta \mathit{tdy}$. The deviatoric growth tensor g_k at the corresponding element is then obtained by using the finite element interpolation with the nodal values of u_g in that element. If we utilize linear finite element interpolation function as in (26), then we have

$$g_k=\frac{1}{{\Delta }_x}(-1,1)\left(\begin{array}{c}\hfill u_g(x_i,t_k)\hfill \\ \hfill u_g(x_{i+1},t_k)\hfill \end{array}\right)$$

at the element consisting of node iand i + 1. Using finite element procedure as summarized in the appendix, one can solve for u_k given g_k.

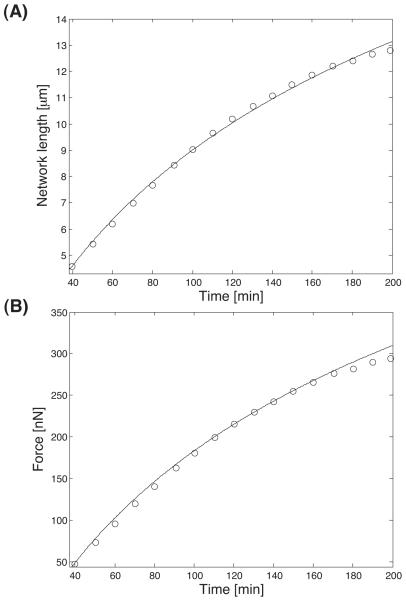
Fig. 3 shows the model results optimized with respect to the experimental data. Our model is able to capture the results quantitatively. An outcome of the modeling is that the viscous part of the stress, characterized by the constant μ₁, plays no role in the results. The results are insensitive to μ₁. For the other 2 parameters γ and K₀, we obtain K₀ = 0.0021s⁻¹ and γ = 1.3 × 10⁻⁸μm. Thus, with 2 parameters, we are able to explain the measurements. Physically, K₀ is the polymerization rate of actin under stress free conditions. This rate is a function of the concentration of actin monomer, the amount of free ends and the detailed growth mechanism. K₀ can be measured from a freely growing actin bundle.

Fig. 3.

A growing bundle of F-actin network against an elastic cantilever. The measured data are the circles and the model results are the lines. (A) Position of the cantilever as a function of time. (B) The force exerted by the growing bundle on the cantilever as a function of time. For these curves, two parameters are sufficient to explain the results (see text).

The significance of γ can be understood by considering the growth chemistry at the molecular level. According to Kramer’s result for chemical reaction rates, the rate of a single reaction, r, is roughly modified by a static force in the form

$$r=r_0{e}^{-\mathrm{f}\cdot {\mathrm{s}}^{\ast }∕k_{\mathrm{B}}T}$$ (11)

where f is the applied force vector and s is the reaction coordinate; s* is the location of the transition state along the reaction coordinate. r₀ is the rate without any forces. Thus, γ represent the component of the force in the direction of the reaction coordinate: γ = |s*| cos θ where θ is the angle between f and s. For typical molecular reactions, |s*| ≈ 0.1 – 1nm. In the present case, the stress and force at the growing tip are in the x-direction. We see that the component of the force in the direction of s is small.

Note that in this calculation, we have assumed that growth occurs at the very tip of the bundle, nucleated by the ActA complex. In realty, the growth mechanism can be more complicated. The obtained parameter K₀ is also proportional to the local concentration of G-actin, which may vary over time due to diffusion limited processes. The presence of branching proteins such as Arp2/3 could also change the local stiffness of the network. Nevertheless, even with a simple phenomenological growth law as in Eqs. (8) and (10), our model can roughly capture the behavior of the bundles and forces it exerts over the experimental time scale. If there is no cantilever at the tip, and the bundle is allowed to grow freely, the length of the bundle at the end of the calculation would reach 25μm. Compared to the length with the cantilever, 14μm, there are significant deformations. Therefore, a finite deformation formulation which incorporates the changes in the material frame is needed. Cytoskeletal networks are also significantly softer than other materials, we expect that the finite deformation formulation is applicable in general.

4 Contractile Forces from Shrinking Network

The above formalism can be generalized to multi-dimensions and used to understand shape and stress in viscoelastic bodies of arbitrary shape. A simple example is shown in Fig. 4 where an initially rectangular bar of 2-d viscoelastic body is held between 2 fixed ends. The Young’s modulus of this strip is 72 Pa (50). The Poisson ratio is taken to be 0.37. The dynamic viscosity, μ₁, is 30 Pa-s or 300 Poise. This situation models a viscoelastic cell adhered to a rigid substrate. We allow the material to shrink uniformly, i.e., the growth rate tensor as

$$K_{\mathit{xx}}\left(x\right)=-k_0$$ (12)

and K_xy = K_yx = K_yy = 0. The specification of growth tensor is modeling a network that is shrinking which can result from depolymerization of filaments. We see that the network becomes thinner in the middle and a tension is developed between 2 ends. The thinning behavior is a result of the Poisson ratio. At the molecular level, the force generation mechanism is similar to the depolymerization wench model (48). The network prefers to maintain a particular density of filaments. As material is removed, the network shrinks.

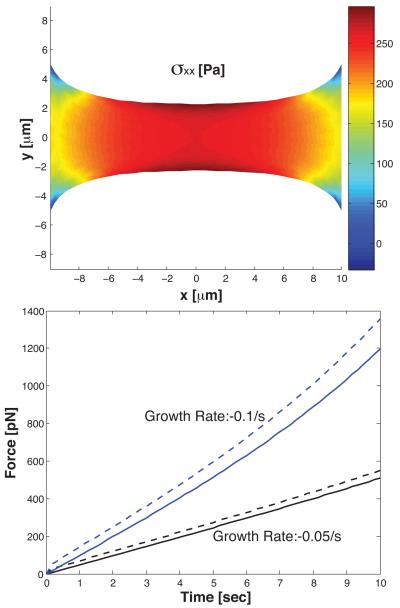
Fig. 4.

A shrinking strip of viscoelastic material is held between two fixed ends 20μm apart. The geometry of the strip and the xx-component of the stress tensor is shown. The material thins in the middle. The bottom plot shows the computed contractile force between the ends as a function of time for two shrinking rates. The solid line is when the dynamic viscosity, μ₁, is 0. The dashed line is when μ₁ = 30 Pa-s. We see that the viscous part of the stress makes a contribution if the relaxation time scale τ ≈ μ₁/Y is comparable to the growth time scale.

Using our model, it is possible to compare the effects of different constitutive laws on the developed force. For the same growth rate, stiffer material will develop more contractile force. In Fig. 4, we also see a difference between a viscoelastic material and an elastic material. The viscous part of the stress increases as the growth rate increases. The viscous part of the stress shows up on the time scale of τ ≈ μ₁/Y . If the material growth and shrinking is fast compared τ, then viscous part of the stress will be important.

5 Forces on Cell Adhesions During Leading Edge Growth

In this section, we apply the proposed framework to compute forces developed at focal adhesion sites during cytoskeleton growth. Typically, cell adhesions have been modeled as a drag force on the cell movement. However, over a short time scale, adhesions between the cell and substrate are regions where the cell body is fixed to the substrate. Dynamics in other areas of the cell will exert forces on the adhesions. These forces have been observed in experiments either using beads embedded in the substrate, or flexible poles as substrates. Using the present framework, the forces on the adhesions can be easily quantified. Note that in typical measurements, forces on cell adhesions is a result of both myosin motor activity and the dynamics of the cytoskeleton network. Here we only consider cytoskeleton dynamics. Motor activity can be incorporated by another term in the stress of Eq. (B.1). We also assume a phenomenological growth deformation, and do not consider the molecular mechanism that generates the ruffling motion. More detailed modeling can include local G-actin concentration and signaling molecules that activate actin polymerization. The molecular mechanism will give rise to the growth kinematics. Here, we focus on the strategy of computing forces on adhesions for a given growth kinematics.

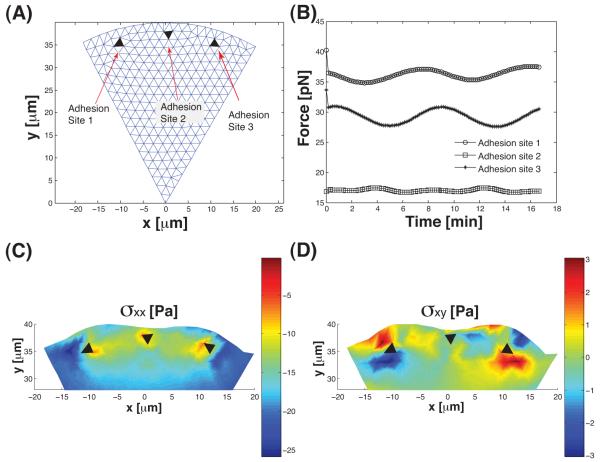
The geometry of the considered situation is shown in Fig. 5 and 6 where the filled triangles are the adhesion sites, roughly 1μm in size. The cell is contained within plasma membrane. Therefore, there is a pressure applied at the boundary which comes from the surface tension of the cell membrane. We take a pressure of approximately 20pN/μm² (10). The adhesion sites are fixed to the substrate, therefore, the boundary of the adhesion sites cannot move. Here, we do not consider the possibility of the boundary detaching or possible focal adhesion growth and shrinking dynamics which is observed in real cells. Generalization of the current procedure to include more realistic focal adhesion dynamics is straightforward. Here, we use this as a proof-of-principle example.

Fig. 5.

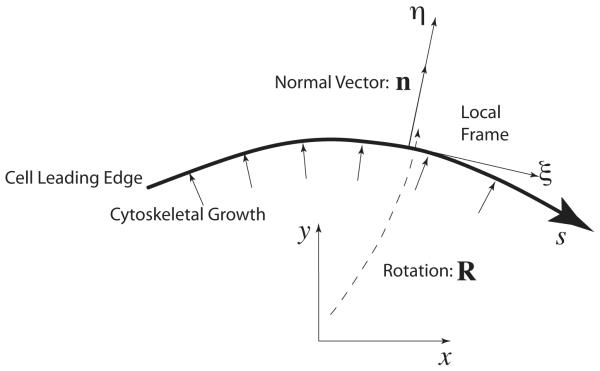
A simple way to specify cytoskeletal growth at the leading edge. A local coordinate frame at the leading edge, (η, ξ), describes the local growth dynamics which is in the normal direction, n. Therefore the growth tensor in the local frame. To obtain the growth tensor in the lab frame, a rotation transformation is needed. From the growth tensor, we can also derive the displacements at the boundary (see text).

Fig. 6.

(A) The geometry of the leading edge being considered. The black triangles are the adhesions which are fixed. The leading edge is undergoing wave-like growth dynamics. (B) The magnitude of forces on the adhesions as a function of time. The force is obtained by solving for the stress inside the cell (Eq. (19)). The oscillations follow the oscillations in the growth dynamics. (C, D) The components of the stress tensor, σ_xx and σ_xy, as functions of space. The oscillatory growth dynamics introduces nonuniform stress patterns in the cell. In particular the shear stress, σ_xy, is significant.

We now examine forces and stress in the cell body during leading edge ruffling where there is wave-like protrusion and shrinking of the actin network at the boundary of the cell. The displacement at the leading edge boundary due to actin network growth at (x, y), u_g(x, y), can be computed by the definition of the deformation (or displacement) gradient as

$${\mathrm{u}}_g(x,y)={\int }_{\Omega }\mathrm{g}(\stackrel{‒}{x},\stackrel{‒}{y})d\stackrel{‒}{\mathrm{x}}+{\int }_{\Gamma }\mathrm{g}(\stackrel{‒}{x},\stackrel{‒}{y})\mathrm{n}(\stackrel{‒}{x},\stackrel{‒}{y})d\Gamma$$ (13)

where Ω denotes the inner domain of the cell. The second term describes growth terms on the boundary, where Γ denotes the corresponding boundary and n denotes the normal vector at each point on that boundary. In our case, since growth occurs only at the frontal boundary, i.e., $\mathrm{g}={\mathrm{g}}_c\delta (\stackrel{‒}{x}-x)\delta (\stackrel{‒}{y}-y)$ where (x, y) ∈ Γ, only the second term remains:

$${\mathrm{u}}_g(x,y)=\mathrm{g}(x,y)\mathrm{n}(x,y).$$ (14)

We specify the cytoskeleton growth at the boundary as normal to the leading edge (28). For each point along the boundary, there is a local coordinate frame, (ξ, η) (Fig. 5). The unit vector n now becomes a normal vector parallel to the η-direction. Therefore, the growth tensor in the local coordinates, $\stackrel{‒}{\mathrm{g}}$, is defined as

$$\stackrel{‒}{\mathrm{g}}=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \alpha \hfill \end{array}\right].$$ (15)

That is to say, the growth tensor in the lab frame g has 0 and α as its eigenvalues and the eigenvector corresponding to α is n. Therefore, we have

$$\mathrm{gn}=\alpha \mathrm{n}.$$ (16)

At the boundary, we denote the arclength along the boundary as s, measured from the left to right. Hence, the displacement due to growth can be expressed as

$${\mathrm{u}}_g\left(s\right)=\alpha \left(s\right)\mathrm{n}\left(s\right).$$ (17)

In other words, the displacement field is now defined at each point on the boundary and normal to the surface at that point, which is coincident with the published growth kinematics of a cell (28).

We investigate ruffling-like movement at the frontal boundary. For our purposes, we define wave-like growth pattern at the leading edge by specifying the displacement at the boundary as

$${\mathrm{u}}_g=u_c\sin \left(\frac{4\pi s}{L_{\mathit{arc}}}-\omega t\right)\mathrm{n}$$ (18)

where ω denotes the frequency the wave-like motion along the arc. In this example we assume ω = 0.0125 which implies that the period of oscillation is 500 seconds. u_c denotes the amplitude of the growth displacement, which depends on the local G-actin concentration as well as the concentrations of other accessory molecules. As explained above, this is related to the growth rate along the normal direction to each point on the surface. Hypothetically, we have chosen u_c = 60nm and a growth velocity v_c = u_c/Δt = 6nm/s. n denotes a normal vector to the frontal arc. This displacement field gives a sine wave-like fluctuation at the frontal arc. The mechanical constants are unchanged from the previous example: Y = 72 Pa, ν = 0.37 and μ₁ = 30 Pa-s.

Fig. 6 shows the forces on the 3 adhesion sites and the stress in the cell body during the ruffling-like motion. The force is obtained from integrating around the boundary of the adhesions:

$$\mathrm{f}={\int }_{\Sigma }\sigma \cdot {\mathrm{n}}_{\Sigma }d\Sigma$$ (19)

where ∑ is the boundary around the adhesions and n_∑ is the normal vector of ∑. In this example, the viscous time scale is much smaller than the growth time scale, therefore, the forces are determined most by the elastic part of the stress. The forces on the adhesions are directly proportional to the Young’s modulus and the magnitude of growth fluctuations, u_c. The forces on the adhesions are on the order of 10s of pN. However, the stress distribution shows that the stress around the adhesion varies by magnitude and direction. σ_xx is around 10s of Pa. The force on the adhesion is the result of integrating the stress around the adhesion, and some cancellations occur. Fig. 6 also shows that the movement also induces significant shear stress in the cell. The force and stresses are also largely the result of the elastic part of the stress, and are directly proportional to the elastic modulus.

Fig. 7 shows the behavior of the forces on adhesions when the growth rate is varied. Interestingly, the average forces on the adhesions do not vary significantly with the growth rate. The average force is mostly determined by the geometry of the leading edge and the position of the adhesions. However, the variation in the adhesion force increases as the growth rate is increased. This result suggests that increasing local actin monomer concentration which increase the growth rate, would affect fluctuations in the adhesion force directly.

Fig. 7.

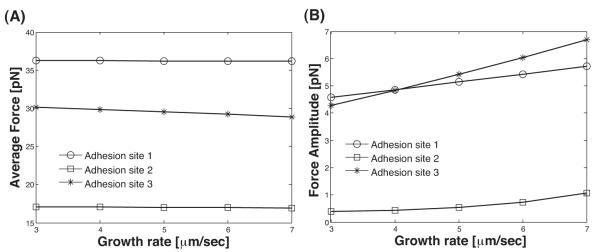
(A) The average force on the adhesions in Fig. 6 are plotted as a function of the growth rate, u_c/Δt. The average force on the adhesions are insensitive to the growth rate. (B) However, the variation in the adhesion forces is affected by the growth rate. The force amplitude is max(force)-min(force).

Note that in this calculation, no other forces are present and we have not considered stress stemming from molecular motors which can be included as another term in Eq. (B.1). Here we see that cytoskeleton dynamics alone can already generate significant intracellular stress. If the stress changes enzymatic reaction rates at the molecular level, then a direct relationship between forces and signaling can be examined (14).

6 Discussion and Conclusions

We have presented a general formalism to describe the shape changes of a growing viscoelastic body. We propose that growth and shrinking of filaments can be modeled using deformation tensors mapping the change in the coordinate frames of the deformable body. A component of the deformation is due to growth, the other component is due to mechanical response. We developed an incremental framework of growth and deformation that allows for arbitrary growth dynamics, and possibility that growth is coupled to internal stress on the body. We applied the formalism to examine forces and stress in growing viscoelastic bodies of simple geometries. The modeling formalism is able to explain an experimental force measurement on a growing bundle of actin filaments with 2 parameters. Extension of the modeling framework to 2-dimensions is able to describe complex dynamics observed in more realistic geometries.

In living cells, the actin network is not only viscoelastic, it is also heterogeneous and non-isotropic. Heterogeneous distribution of actin networks imply that material constants, μ₀, λ₀, μ₁, ν, are functions of space. Non-isotropic orientations actin filaments also imply that the simple constitutive laws introduced here are probably not adequate. The cell also actively changes the mechanical properties of the cytoskeletal network by modifying cross-linking and bundling. Thus, mechanical constants themselves should be treated as functions of time. Nevertheless, these increases in complexity can be introduced within this framework when more experimental data are available.

Measurements of contractile forces in cells typically show nano-newton forces. However, these measurements are made in the presence of myosin motors which exerts additional forces on the actin network. Action of motors can be included in our framework as another stress term in Eq. (B.1). Here, we showed that the forces generated by actin networks in absence of motors are directly related to the mechanical constants of the network. Stiffer material (both in terms of Young’s modulus and dynamic viscosity) will develop more forces. The growth rate of the material also influences the time course of force generation.

When our formalism is applied to adhered cells undergoing leading edge growth and shrinking, we see that the adhesions experiences substantial amount of force. It is known that focal adhesions undergo their own dynamics when forces are applied. Our work introduces the way to relate actin network dynamics with forces on the adhesions. The present framework is also applicable to any geometry and any configurations of adhesions. The method can be used to analyze motile cells as well as cells in 3-d. Considerable technology of finite element modeling can be applied to cell mechanics using our approach.

Finally, in micromechanical measurements on cytoskeletal networks, the network is typically undergoing internal polymerization and depolymerization. Therefore, the growth tensor, G, is not identity uniformly across the network. Typically, only the integral of G is identity:

$${\int }_{\Omega }\mathrm{G}\left(\mathrm{x}\right)d\mathrm{x}=\mathrm{I}$$ (20)

where Ω is the entire body. We see that growth affects the local stress in the body and therefore the net strain. The meaning of the measured strain in these experiments needs further careful consideration.

A.

A General Framework to Model Growing Viscoelastic Material

A.1 Incremental Kinematic Framework

Shape changes of a deformable body can be described by a mapping between material coordinate frames X and x, where X and x are coordinates of material points before and after the deformation, respectively. The central quantity that describes this shape change is the deformation gradient tensor, F = ∂x/∂X. Other quantities of interest such as the strain tensor, Cauchy-Green tensors can be directly defined from F. In the presence of growth, the net deformation of a body under stress can be decomposed into a part due to growth, and a part due to material response to external forces (41)

$$\mathrm{F}=\mathrm{AG},$$ (A.1)

where A denotes the deformation due to stress and applied forces, and G denotes the deformation due to growth. Both tensors A and G are also functions of space and time. The above decomposition is valid for finite size deformations, regardless of the extent of growth. However, since biological growth dynamics are generally functions of time, and may depend on the stress history, it is more natural to consider incremental growth and deformation where a large deformation is broken up into successive small deformations (20). For each step, growth and elastic deformation occur. Each increment can also be considered as an increment in time. Fig. 1 illustrates this concept in cartoon form. Here, x_k denotes the current configuration at k^th time increment. X is the reference configuration, which is also expressed as x₀. For the tensors F, A, and G, superscript (k) and subscript k denotes that the corresponding quantity is described in terms of frames X and x_k–1, respectively. The total deformation gradient tensor is then F^(k) = F_kF_k–1…F₂F₁, where F_k = A_kG_k. Thus, for each increment, the decomposition of deformation gradient tensor still holds. It is also possible to decompose the net deformation:

$${\mathrm{F}}^{\left(k\right)}={\mathrm{A}}^{\left(k\right)}{\mathrm{G}}^{\left(k\right)}.$$ (A.2)

To relate the net deformation to the current one, we factor out contributions from rigid body rotation (20; 41):

$${\mathrm{G}}^{\left(k\right)}={\left({\mathrm{A}}^{(k-1)}\right)}^{-1}{\mathrm{R}}_k^T{\mathrm{G}}_k{\mathrm{A}}^{(k-1)}{\mathrm{G}}^{(k-1)}$$ (A.3)

where G_k = V_kR_k is the left polar decomposition. The net elastic deformation is then ${\mathbf{A}}^{\left(k\right)}={\mathbf{F}}_k{\mathbf{G}}_k^{-1}{\mathbf{R}}_k{\mathbf{A}}^{(k-1)}$. The decomposition of growth tensor has been discussed more extensively by Hoger, Lubarta and others (22; 9).

In a calculation, we seek to find the displacement field u_k as a function of x_k–1. Since we are free to choose the size of the time increment, let us examine the limit where the incremental growth and deformation are small. In this limit, we have F_k = 1+U_k and G_k = 1+g_k, where the displacement gradient tensor U_k and the deviatoric growth tensor g_k are small. To first order, quantities such as u_k and G_k can be treated as functions of the current configuration x_k, as in Linearized Elasticity Theory. Indeed, quantities such as ${\mathbf{U}}_k=\frac{\partial \mathrm{u}k}{\partial {\mathrm{x}}_{k-1}}$, G_k and A^(k–1) can now all be approximated as functions of the current configuration x_k, for example, ${\mathbf{U}}_k=\frac{\partial \mathrm{u}k}{\partial {\mathrm{x}}_k}$. The next configuration is obtained by x_k = x_k–1 + u_k.

B Force Balance and Constitutive Equation

For typical cellular and experimental conditions, the length scale is microns and the time scale is seconds to minutes; the Reynold’s number in these situations is small, and inertia can be neglected when considering balance of forces. The dominant contributions to force balance are stresses in the cell body, drag forces with the surrounding fluid and forces from molecular motors or other applied forces. When defined with respect to the coordinate frame x_k, the equation of motion is then:

$${\nabla }_{{\mathrm{x}}_k}\cdot {\sigma }_k+{\mathrm{f}}_{{\mathrm{x}}_k}=\eta \mathrm{v}.$$ (B.1)

where σ is the stress tensor in the elastic body. f_xk is the body force in the current coordinate frame. This body force may include stretch and shear forces from internal molecular motors, or forces applied externally using nanomechanical instruments. The right hand side include viscous drag from the surrounding fluid where η is the drag coefficient and v is the velocity difference between the material points and the local fluid velocity. In this paper, we will concentrate on quasi-steady situations where drag forces from the fluid is negligible. Therefore, the right hand side of Eq. (B.1) is taken to be zero.

External boundary forces are included as a boundary condition σ_kn = −Pn, where P and n denote the pressure and the unit vector normal to the boundary of the current configuration, respectively. In a cell, the pressure naturally arise from membrane tension (Laplace pressure). However, pressure could also be applied from external instruments such as the cantilever of the AFM tip as in Section 3.

Now, let us consider a general linear viscoelastic material which has the constitutive relationship (4; 16)

$$\sigma (\mathrm{x},t)={\sigma }^e(\mathrm{x},t)+{\sigma }^v(\mathrm{x},t)$$ (B.2)

where σ^e is the elastic part of the stress which depends on the elastic deformation A, σ^v is the viscous part of the stress which depends on the deformation or strain velocity. As it is written now, the material is a viscoelastic solid which contains contribution from both types of stress. If σ^e or σ^v is zero, then the material is an elastic solid, or a viscoelastic fluid, respectively. Note that in addition to material stress, molecular motors can also generate stress within the network. The motor stress will be another term in Eq. (B.2), and σ(x, t) becomes σ(x, t) + σ^m(x, t) where σ^m is the stress due to molecular motors as a function of space and time.

We obtain the elastic stress part by first computing the 1^st Piola-Kirchhoff stress tensor, denoted as T, and then convert it into Cauchy stress, denoted as σ, by the following relationship (6)

$$\sigma =\frac{1}{\text{det}\mathrm{F}}{\mathrm{TF}}^T$$ (B.3)

where F denotes a deformation gradient tensor connecting from the reference configuration to the current configuration.

The elastic part of the stress with inclusion of deformation from growth has been discussed before (41; 20). In a finite deformation formulation, when we consider a compressible elastic material, the corresponding elastic energy in 3-D space is (6)

$$W\left(\mathrm{A}\right)=\frac{1}{2}{\lambda }_0{\left(\ln \right(\text{det}\mathrm{A}\left)\right)}^2-{\mu }_0\ln \left(\text{det}\mathrm{A}\right)+\frac{1}{2}{\mu }_0\left(\mathrm{Tr}\right({\mathrm{A}}^T\mathrm{A})-3)$$ (B.4)

where λ₀ and μ₀ denote Lamé constants. Relationships between these Lamé constants and the Young’s modulus (Y) and Poisson’s ratio (ν) are as follows

$${\lambda }_0=\frac{\nu Y}{(1+\nu )(1-2\nu )};{\mu }_0=\frac{Y}{2(1+\nu )}.$$ (B.5)

The 1^st Piola-Kirchhoff stress (with respect to the reference frame) then is computed as (20)

$$\mathrm{T}=\text{det}\mathrm{F}\frac{\partial W\left(\mathrm{A}\right)}{\partial \mathrm{F}}.$$ (B.6)

Using the fact that

$$\frac{\partial W\left(\mathrm{A}\right)}{\partial \mathrm{F}}=\frac{\partial W\left(\mathrm{A}\right)}{\partial \mathrm{A}}\cdot {\mathrm{G}}^{-T},$$ (B.7)

and by means of Eq. (B.3), one can obtain the expression for the so-called Cauchy stress (with respect to the current frame):

$${\sigma }^e(\mathrm{x},t)=({\lambda }_0\ln \text{det}\mathrm{A}-{\mu }_0)1+{\mu }_0\mathrm{B}$$ (B.8)

where B = AA^T.

The viscous part of the stress in general is linear in strain velocity, and may include memory effects. However, in a long time scale motion, which is often encountered in experiments, memory effects may be neglected. That is to say, we treat a viscous part of the network stress as a simple Newtonian fluid (30). With that in mind, we define the Cauchy stress as

$${\sigma }^v=\frac{{\mu }_1}{2}\left({\stackrel{.}{\mathrm{A}}}_t\left(t\right)+{\stackrel{.}{\mathrm{A}}}_t^T\left(t\right)\right)$$ (B.9)

where μ₁ is the viscous modulus (or dynamic viscosity) and A_t(τ) is the relative elastic deformation gradient (30). By using the following transformation rule

$${\stackrel{.}{\mathrm{A}}}_t\left(t\right)=\stackrel{.}{\mathrm{A}}\left(t\right){\mathrm{F}}^{-1}\left(t\right)$$ (B.10)

we have the following viscoelastic constitutive relation without terms of memory

$${\sigma }^v(\mathrm{x},t)=\frac{{\mu }_1}{2}\left(\stackrel{.}{\mathrm{A}}{\mathrm{F}}^{-1}+{\mathrm{F}}^{-T}{\stackrel{.}{\mathrm{A}}}^T\right)$$ (B.11)

Note that since we are considering a growing elastic material, the overall deformation, F, is not small. However, most of this deformation is due to growth, G. Therefore, the elastic part A which then defines the strain E and strain velocity ∂E/∂t, is small. Therefore, we expect that a linear dependence between stress and strain is valid, however, a finite deformation description of strain is necessary to describe the stress.

Now we discretize time: t ⇔ t_k. Also t₁ = 0. In the current context, F(t) = F(t_k) = F^(k), and accordingly the same notation is applied for A and G. Then the discretized version of the constitutive equation becomes

$$\begin{array}{cc}\hfill \sigma \left(\mathrm{x}\right(\mathrm{X},t_k\left)\right)& \equiv {\sigma }_k=({\lambda }_0\ln \text{det}{\mathrm{A}}^{\left(k\right)}-{\mu }_0)1+{\mu }_0{\mathrm{A}}^{\left(k\right)}{\mathrm{A}}^{{\left(k\right)}^T}\hfill \\ \hfill & +\frac{{\mu }_1}{2}\left({\stackrel{.}{A}}^{\left(k\right)}{\mathrm{F}}^{{\left(k\right)}^{-1}}+{\mathrm{F}}^{{\left(k\right)}^{-T}}{\left({\stackrel{.}{\mathrm{A}}}^{\left(k\right)}\right)}^T\right).\hfill \end{array}$$ (B.12)

Since the incremental deformation is small, we linearize the k^th step. That is to say, we ignore higher order terms of U_k and g_k. The elastic part of the constitutive equation becomes

$$\begin{array}{cc}\hfill {\sigma }_k^e& =\left({\lambda }_0\mathrm{Tr}({\mathrm{U}}_k-{\mathrm{g}}_k)+{\lambda }_0\ln \text{det}{\mathrm{A}}^{(k-1)}-{\mu }_0\right)1\hfill \\ \hfill & +{\mu }_0({\mathrm{Q}}^{(k-1)}+{\mathrm{U}}_k{\mathrm{Q}}^{(k-1)}+{\mathrm{Q}}^{(k-1)}{\mathrm{U}}_k^T\phantom{)}\hfill \\ \hfill & \phantom{(}-{\mathrm{g}}_k{\mathrm{Q}}^{(k-1)}-{\mathrm{Q}}^{(k-1)}{\mathrm{g}}_k^T)\hfill \end{array}$$ (B.13)

where

$${\mathrm{Q}}^{(k-1)}={\mathrm{R}}_k{\mathrm{A}}^{(k-1)}{\mathrm{A}}^{{(k-1)}^T}{\mathrm{R}}_k^T.$$

Now we apply the same technique to the viscous part. First of all, as for the time derivative, we utilize the following approximation;

$${\stackrel{.}{\mathrm{A}}}^{\left(k\right)}=\frac{{\mathrm{A}}^{\left(k\right)}-{\mathrm{A}}^{(k-1)}}{\Delta t}.$$ (B.14)

We also adopt the following assumption that with the current incremental quantities being small, the current growth tensor has its stretch and rotation parts as

$$\begin{array}{cc}\hfill & {\mathrm{V}}_k\approx 1+\frac{1}{2}({\mathrm{g}}_k+{\mathrm{g}}_k^T)=1+{\Lambda }_k\hfill \\ \hfill & {\mathrm{R}}_k\approx 1+\frac{1}{2}({\mathrm{g}}_k-{\mathrm{g}}_k^T)=1+{\Omega }_k.\hfill \end{array}$$ (B.15)

Now, let us define rates of the displacement and the growth tensor as

$${\mathrm{W}}_k=\frac{{\mathrm{U}}_k}{\Delta t},{\mathrm{K}}_k=\frac{{\mathrm{g}}_k}{\Delta t}.$$ (B.16)

From the second equation, we get

$${\Lambda }_k^r=\frac{1}{2}\left({\mathrm{K}}_k+{{\mathrm{K}}_k}^T\right).$$ (B.17)

This quantity involves symmetric parts of the rate of displacements due to growth. Again by ignoring the higher order terms of U_k and g_k and together with Eq. (A.3), we have

$${\sigma }_k^v=\frac{{\mu }_1}{2}\left[({\mathrm{W}}_k-{\Lambda }_k^r){\mathrm{Z}}^{(k-1)}+{\mathrm{Z}}^{{(k-1)}^T}\left({{\mathrm{W}}_k}^T-{\Lambda }_k^r\right)\right]$$ (B.18)

where Z^(k–1) = A^(k–1)F^(k–1)–1. Hence the stress becomes

$${\sigma }_k={\sigma }_k^e+{\sigma }_k^v.$$ (B.19)

Using Eq. (B.1), we obtain a closed equation for the unknown U_k or u_k. The equations obtained are valid for a general linear viscoelastic fluid in any dimension. Recursive applications of this equation determine the configuration at each time step.

Since growth requires adding material to available space, growth is affected by the stress in the material. For a single filament in a Brownian ratchet, the growth rate depends exponentially on the applied force. For a continuous body, the growth rate should depend on the stress tensor. The elements of the growth tensor becomes

$$K_{\mathit{ij}}=K_{0,\mathit{ij}}{e}^{{\gamma }_{\mathit{ij}}{\sigma }_{\mathit{ij}}∕k_{\mathrm{B}}T}$$ (B.20)

where K_0,ij is the growth rate in absence of any stress and γ_ij is a constant that has the dimension of volume, and represent the molecular volume of growth change. In 1-d, γ_ij becomes a molecular length times an area, and the above expression reduces to standard Bell’s model for reaction rates (5). Since the growth tensor is

$$\stackrel{.}{\mathrm{G}}=\mathrm{KG}$$ (B.21)

The growth equation (B.21) should be solved simultaneously with the force balance equation Eq. (B.1). Note that this dependence of the growth rate on stress suggests that extensional stress will increase the growth rate and compressional stress will slow down growth.

C Finite Element Formulation

This section explains the finite element implementation of Eq. (B.1). We follow the notation in (26) and explain it with a one-dimensional case as in the example of a 1-d bar. Two-dimensional finite element formulation is straight-forward. Details can be found in (26). We use Distmesh algorithm to generate the 2-d mesh (53). In general the Cauchy stress at the current time step is expressed as a linear combination of deformation gradient of the current displacement, current growth tensor, and the cumulative elastic quantities. We have the relation between stress and strain, without subscripts, as

$$\begin{array}{cc}\hfill \sigma \left(x\right)& =\left({\lambda }_0+2{\mu }_0{A}^{{(k-1)}^2}+\frac{{\mu }_1}{\Delta t}{G}^{{(k-1)}^{-1}}\right)\left(\frac{\partial u}{\partial x}-g\right)\hfill \\ \hfill & +{\mu }_0\left(A^{{(k-1)}^2}-1\right)+{\lambda }_0\ln A^{(k-1)}.\hfill \end{array}$$ (C.1)

Here u(x) is the displacement along x-direction at the current time. The equation of motion (Eq. (B.1)) in the quasi-static limit and no body forces is:

$$\frac{\partial \sigma }{\partial x}=0.$$ (C.2)

Let ω be a weighting (or trial) function. The weak form of the equilibrium equations is

$${\int }_0^L\omega \frac{\partial \sigma }{\partial x}\mathit{dx}=0$$ (C.3)

where L denotes the current length of a network. Integration by part gives

$${\int }_0^L{\phantom{\mid }\frac{\partial \omega }{\partial x}\sigma \mathit{dx}=\omega \sigma \mid }_0^L.$$ (C.4)

The right-hand side is determined from given boundary conditions. Now we apply the linear finite element to the above equation. The shape functions are defined as in (26). Then we can describe any quantity from the geometric information on this “finite element”. Eventually, this leads to a matrix-vector equation

$$\left[K\right]\left\{d\right\}=\left\{f\right\}$$ (C.5)

where {d} denotes the displacement at each node. [K] and {f} denote system matrix and vector containing all the information explained above. By solving this equation, we obtain the current geometry. By iteratively applying this, we can obtain a series of deformed geometries with time.