LOGISTIC NETWORK REGRESSION FOR SCALABLE ANALYSIS OF NETWORKS WITH JOINT EDGE/VERTEX DYNAMICS

Abstract

Change in group size and composition has long been an important area of research in the social sciences. Similarly, interest in interaction dynamics has a long history in sociology and social psychology. However, the effects of endogenous group change on interaction dynamics are a surprisingly understudied area. One way to explore these relationships is through social network models. Network dynamics may be viewed as a process of change in the edge structure of a network, in the vertex set on which edges are defined, or in both simultaneously. Although early studies of such processes were primarily descriptive, recent work on this topic has increasingly turned to formal statistical models. Although showing great promise, many of these modern dynamic models are computationally intensive and scale very poorly in the size of the network under study and/or the number of time points considered. Likewise, currently used models focus on edge dynamics, with little support for endogenously changing vertex sets. Here, the authors show how an existing approach based on logistic network regression can be extended to serve as a highly scalable framework for modeling large networks with dynamic vertex sets. The authors place this approach within a general dynamic exponential family (exponential-family random graph modeling) context, clarifying the assumptions underlying the framework (and providing a clear path for extensions), and they show how model assessment methods for cross-sectional networks can be extended to the dynamic case. Finally, the authors illustrate this approach on a classic data set involving interactions among windsurfers on a California beach.

1. INTRODUCTION

Change in network structure (i.e., network dynamics) has been a topic of extensive theoretical and methodological interest within the sociological community. Network dynamics may be viewed as a process of change in the edge structure of a network, in the vertex set on which edges are defined, or in both simultaneously. Although early studies of such processes were primarily descriptive (e.g., Coleman 1964; Newcomb 1953; Sampson 1968), recent work on this topic has increasingly turned to formal statistical models (e.g., Banks and Carley 1996; Krackhardt and Handcock 2007; Robins and Pattison 2001; Snijders 1996, 2001, 2005). Although showing great promise, many of these modern dynamic models are computationally intensive and scale very poorly in the size of the network under study, making them difficult or impossible to apply to large networks in practical settings. Likewise, currently used models focus on edge dynamics, with little support for endogenously changing vertex sets. Given this situation, there is a need for scalable approaches that, even if limited in various ways, can serve as a starting point for analysis of intertemporal network data with vertex dynamics at large scales.

In this article, we explore the use of the well-known logistic network regression framework as a simple basis for the modeling of joint edge/vertex dynamics with various orders of temporal dependence. We expand on past work showing how this family can be derived from the theory of exponential-family random graph (ERG) models (ERGMs; Butts 2008; Holland and Leinhardt 1981; Snijders 2002; Strauss and Ikeda 1990) via dependence assumptions in the dynamic case, and we discuss computational issues related to its use with large, sparse graphs. The ERGM framework represents an important methodological development for the sociological and social network communities, having been used to further our understanding of such important and diverse cases as preference in adolescent friendship networks (Goodreau, Kitts, and Morris 2009), racial mixing in online social networks (Wimmer and Lewis 2010), and in the study of interlocking directorates (Wang, Sharpe, et al. 2009). We discuss basic parameterization issues, including one approach to the treatment of cases with vertex set dynamics.

We follow this discussion with a case study in which we analyze the dynamics of interpersonal communication during 31 days of windsurfer interaction on a beach in Southern California: the famous “beach” data set collected by Freeman, Freeman, and Michaelson (1988), hereafter referred to as the beach network. Demonstrating several methods for assessing model adequacy, we evaluate the ability of the logistic family to capture the evolution of the beach network over the 31-day collection period. Informed by these results, we conclude by discussing some of the strengths and weaknesses of this approach for practical analysis of large-scale intertemporal data sets. As a practical framework for capturing both population and relational processes in dynamic networks, our approach has potential applications in a wide range of sociological contexts. Examples include the study of dynamic online social networks (such as Facebook and Twitter), interaction in small groups with free entry and exit, intraorganizational networks with personnel turnover, sexual contact networks with endogenous mortality (e.g., from human immunodeficiency virus infection), and emergent multiorganizational networks (e.g., in response to disasters or political events).

Although existing models for joint edge/vertex evolution are rare (an example being recent work by Krivitsky 2009 and Krivitsky and Handcock 2014),¹ basic statistical methods for edge prediction have been in the social network literature for several decades (e.g., see Krackhardt 1987a, 1987b, 1988). Much of this early work involved variations on ordinary least squares or logistic regression applied to adjacency matrices. Logistic regression per se has a long history of being applied to social network data (Lazega and van Duijn 1997; Pattison and Wasserman 1999; Robins, Pattison, and Wasserman 1999; Wasserman and Pattison 1996), both because it arises naturally from edgewise independence assumptions (see Holland and Leinhardt 1981) and because of the wide availability of existing implementations. Less appreciated have been the computational advantages of the logistic framework relative to more complex schemes; scalable methods for estimation of logistic models on large, sparse data sets are well developed (e.g., see Komarek 2004; Komarek and Moore 2003; Lin, Weng, and Keerthi 2008), in contrast with currently available methods for general ERGMs. We propose to take advantage of this latter property, formulating our models in a fashion that facilitates computation for even very large, sparse dynamic graphs.

We also make use of available exponential family theory to derive a minimal set of assumptions that leads immediately to a lagged logistic form for the joint evolution of edge structure and vertex set. This allows us to clarify what is being assumed in using such a model, thereby facilitating the assessment of its applicability in particular settings. Moreover, placing this family within the general family of dynamic ERGMs allows it to be readily expanded by the incorporation of alternative dependence assumptions (although not without computational cost). Key to our effort is the intuition that, in the dynamic case, the history of the evolving network will account for much of the (marginal) dependence among edges; thus, the assumption of conditional independence of edges in the present (given the past) may be a much more effective approximation for incremental snapshots of evolving networks than for typical cross-sectional and/or marginalized network data. By leveraging this approximation, we can potentially account for many aspects of network evolution for systems whose sizes would prove prohibitive to more elaborate models.

The overall structure of the article is as follows: We begin by describing the basic background and notation for our proposed modeling framework, following this with a derivation of the dynamic logistic regression family with vertex dynamics from the general family of dynamic ERGMs under specified independence assumptions. We then consider model fit assessment. We conclude with an illustration of the use of this approach (and of associated adequacy diagnostics) through an application to the evolution of interpersonal communication of windsurfers on a beach in Southern California in the late summer of 1986.

2. NOTATION AND CORE CONCEPTS

We begin by laying out the basic notation and statistical framework that underlies both the theoretical and methodological contributions of this work. This section first covers the necessary graph theoretic and matrix notation needed for defining the ERGMs. A brief review of core concepts from the ERGM literature follows and will be explored in the subsequent sections of this article.

2.1. Graph Notation

We here follow the common practice of representing structural concepts in a mixture of graph theoretic and statistical notation (e.g., see Butts 2008; Wasserman and Faust 1994). A graph in mathematical language is a relational structure consisting of two elements: a set of vertices or nodes (here used interchangeably) and set of vertex pairs representing ties or edges (i.e., a “relationship” between two vertices). Formally, this is often represented as G = (V, E), where V is the vertex set and E is the edge set. If G is undirected, then edges consist of unordered vertex pairs, with edges consisting of ordered pairs in the directed case; our development applies in both circumstances, unless otherwise noted.

We represent the number of elements in a given set with the cardinality operator | · |, such that |V| and |E| are the number of vertices and edges in G, respectively. The term for the number of vertices in a given graph in social network analysis is either order or size and is denoted n = |V|. As noted below, we will be considering cases in which neither E nor V is fixed but evolves stochastically through time. Throughout this discussion, however, we will treat n as finite with probability 1 and assume that the elements of V are identifiable.

A common representation of graph G is that of the adjacency matrix Y, such that Y = (y_ij)_{1≤i, j≤n}, where y_ij = 1 if i sends a tie to j and 0 otherwise. If G is undirected, then its adjacency matrix is by definition symmetric (i.e., y_ij = y_ji); if G is directed, then its adjacency matrix is not necessarily symmetric. It is common to assume that there are no self-ties (or loops), and thus the diagonal is represented either as all zeros (y_ii = 0, or treated as missing, y_ii = NA). This assumption is not necessary for the development that follows.

A necessary addition to this notation is that of an index for time, t, such that Y becomes a t-indexed vector of adjacency matrices, with Y_t being a convenient shorthand for the adjacency matrix at time t and Y_tij an indicator for the state of i, j edge at said time. We also apply this notation to graphs, such that G_t = (V_t, E_t) denotes the state of G at time t (an adjacency matrix version would be Z_t = (V_t, Y_t)). Noting that, we will use n_t = |V_t|, the cardinality of the vertex set at time t. Our development assumes that G is observed at a finite number of time points (i.e., we consider network evolution in discrete time).

2.2. Random Graph Models and Exponential-family Form

When modeling networks, it is helpful to represent their distributions via random graphs in exponential family form. The explicit use of statistical exponential families to represent random graph models was introduced by Holland and Leinhardt (1981), with important extensions by Frank and Strauss (1986) and subsequent elaboration by Wasserman and Pattison (1996) and others. Often misunderstood as a type of model per se, the ERG formalism is in fact a framework for representing distributions on graph sets, and it is complete for distributions with countable support (i.e., we can always write such a distribution in ERG form, albeit not always parsimoniously). The power of this framework lies in the extensive body of inferential, computational, and stochastic process theory (borrowed from the general theory of discrete exponential families) that can be brought to bear on models specified in its terms (e.g., see Brown 1986); in effect, the ERG form constitutes a general “language” for expressing and working with random graph models.

Given a random graph G on support , we may write its distribution in exponential family form as follows:

$$Pr(G=g\mid s,\mathrm{\theta })=\frac{exp\left({\mathrm{\theta }}^{T}s(g)\right)}{{\sum }_{g^{\prime }\in \mathcal{G}}exp\left({\mathrm{\theta }}^{T}s(g^{\prime })\right)}{\mathbb{I}}_{\mathcal{G}}(g),$$ (1)

where Pr (·) is the probability mass of its arguments, 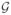is the support of G, g is the realized graph, s is the function of sufficient statistics, θ is a vector of parameters, and 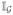is the indicator function (i.e., 1 if its argument is in the support of 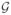, 0 otherwise). If | 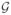| is finite, then the probability mass function (pmf) of G can be written with finite-dimensional s, θ; this is not necessarily true in the more general case, although a representation with s, θ of countable dimension still exists.

Although the extreme generality of this framework has made it attractive, model selection and parameter estimation are often difficult because of the normalizing factor in the denominator of equation (1), generally computationally intractable because of the superexponential growth in the number of terms in the sum of a function of n, except in special cases such as the Bernoulli and dyad-multinomial random graph families discussed in Holland and Leinhardt (1981). The first applications of this family (stemming from Holland and Leinhardt’s seminal 1981 article) focused on these special cases. Frank and Strauss (1986) introduced a more general estimation procedure on the basis of cumulant methods, but this proved too unstable for general use; emphasis then switched to approximate inference using maximum pseudolikelihood estimation (Besag 1974), as popularized in this application by Strauss and Ikeda (1990) and later by Wasserman and Pattison (1996). Although maximum pseudolikelihood estimation coincides with maximum likelihood estimation (MLE) in the limiting case of edgewise independence, the former was found to be a poor approximation to the latter in many practical settings, thus leading to a consensus against its general use (e.g., see Besag 2001; van Duijn, Gile, and Handcock 2009). The development of effective Markov-chain Monte Carlo strategies for simulating draws from ERGMs in the late 1990s (Anderson, Wasserman, and Crouch 1999; Snijders 2002) led to the current focus on MLE methods based either on first-order method of moments (which coincides with MLE for this family) or on importance sampling (Geyer and Thompson 1992). Algorithms for parameter estimation and model selection using these approaches are implemented in a number of software packages (e.g., see Handcock et al. 2003; Snijders et al. 2007; Wang, Robins, and Pattison 2009), and empirical applications are increasingly common (e.g., Goodreau et al. 2009; Robins and Pattison 2001).

This tension between the capacity of the ERGM framework to represent computationally difficult models with substantial dependence and the need for models that can be deployed in practical settings has been a defining theme of research in this area. In this article, our concern is primarily with the latter problem: We seek families of models for network dynamics that are computationally tractable and easily interpreted. At the same time, however, we recognize the power and flexibility of the ERGM representation, particularly as a tool for embedding simple models within a much broader family (thus paving the way for subsequent expansion). As such, we will draw heavily on the exponential family framework in our development, even when working with cases that can be represented in other ways (e.g., logistic regression).

3. MODELING NETWORK DYNAMICS WITH LOGISTIC REGRESSION

Consider a discrete time series …, Y₀, Y₁ …, where Y_i ∈ {0, 1}. One approach to modeling such a series is to posit that each Y_i arises as a Bernoulli trial whose parameter, ϕ_i, is the inverse logit of some given function of Y_i−1, Y_i−2, … (along, perhaps, with some vector of covariates X_i). This model family is equivalent to logistic regression of Y involving one or more “lagged” terms (i.e., functions of the prior values of Y), and it is thus referred to as lagged logistic regression (a natural analogue of the Gaussian AR process [Brockwell and Davis 2002; Shumway and Stoffer 2006]). Models with lagged logistic form have been used for studying network dynamics (Robins and Pattison 2001), but the family as a whole has a higher level of generality than has been exploited in the social network literature. In the development that follows, we review and extend the derivation of an analogous family of processes for dynamically evolving network data. In keeping with the analogy, we refer here to the models associated with these processes as dynamic network logistic regression or lagged network logistic regression models. Although this family lacks the full flexibility of the general ERGMs cited above, it has the advantage of being simple, scalable, and easily extensible to the case of network vertex dynamics (the “entry” and “exit” of vertices). These features make this model family a natural starting point for dynamic network modeling on large graph sequences. Even where the family proves inadequate unto itself, its extensibility provides a natural path for incorporation of more complex forms of dependence.

As noted, an important consideration in our development is scalability to graphs with large vertex sets. Recent innovations in data collection, as well as new forms of social interaction (e.g., online social networks), have greatly expanded the size of social networks available for study. Although this has been a boon to analysts, it has also posed significant challenges: The computational complexity of many basic network properties grows rapidly with the size of the vertex set, and the Monte Carlo procedures underlying conventional statistical techniques for network modeling require that such properties be evaluated a large number (perhaps even millions) of times. These complexity problems are exacerbated in the dynamic case by the need to perform such computations for multiple temporal cross-sections. It is worth noting that computational power and algorithmic efficiency both continue to improve with time; however, current implementations of general frameworks such as the actor-oriented models of Snijders (2001) or the dynamic ERGMs (Krackhardt and Handcock 2007; Krivitsky 2009) are often impractical to apply to networks having even a few thousand nodes. Although scalability is a challenge for virtually all nontrivial network models, simplifying assumptions can often allow efficiency gains that permit the analysis of data that would otherwise fall beyond the reach of statistical procedures. We now turn to a consideration of one such set of assumptions, which jointly imply a general conditional logistic structure for networks with jointly evolving edge and vertex sets.

3.1. The Core Dependence Structure

In the conventional, cross-sectional case in which V is fixed, logistic models arise from the assumption that all edges are independent conditional on a fully observed set of covariates (Wasserman and Robins 2005). Although potentially adequate in networks with very strong covariate effects (Butts 2003, 2011), such models are often poor approximations when covariate information is limited or when complex interactive processes are the primary drivers of tie formation and dissolution (Goodreau et al. 2009). Consider, however, the case of network “panel” data, in which an evolving network is measured at regular intervals during its evolution. Here, too, simultaneity can be a problem, and specialized modeling schemes such as those of Snijders (2001), Krackhardt and Handcock (2007), and Krivitsky (2009) have been proposed to capture this dependence. If the intervals over which we measure the network are suitably fine, however, very little simultaneous dependence is likely to occur: For many systems, much of what transpires over a short time interval can be treated as independent given the history of interaction as well as suitable covariates. (Indeed, taking this logic to its infinitesimal extreme results in the relational event framework of Butts [2008], which exploits this property to model the dynamics of event-based interaction in continuous time.) Where this assumption is reasonable, it may be possible to approximate the process of network evolution through an inhomogeneous Bernoulli graph process in which edge states at future times depend on the history of the network but not (conditionally) on other edges at the same time point. Such an approximation would allow us to leverage the substantial computational and interpretive advantages of the general linear model framework while still capturing the critical mechanisms of network evolution.

The model family we propose is one that leverages potentially complex dependence on the past together with conditional independence in the present to flexibly capture network evolution in a way that nonetheless reduces to lagged logistic regression. Specifically, we derive our model family from the core assumption that E_{t + 1} depends only on V_{t + 1} and (E_t, V_t), …, (E_t−k, V_t−k), and V_{t + 1} depends only on (E_t, V_t), …, (E_{t −k}, V_{t −k}), together with any exogenous covariates (see Figure 1). Intuitively, this can be thought of as specifying that today’s vertices are determined by the past network structure (out to some limit, k) and that today’s edges are determined by both this past structure and today’s vertices. One of the effects of this framework is that it allows uncertainty in network composition to be considered when making predictions. As we shall see, explicitly considering this aspect of network structure (which has been largely overlooked in prior research) leads to a very different view of network dynamics in contexts for which vertex entry and exit are possible.

Figure 1.

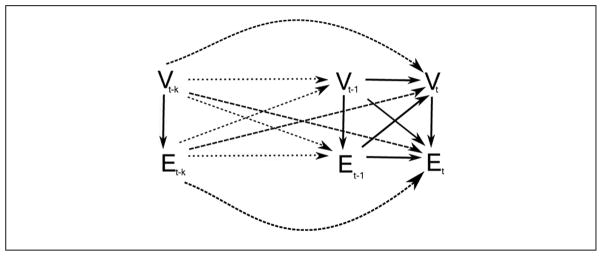
A dependence diagram showing the cross-sectional vertex and edge sets under the assumptions of Appendix A, where t represents time and k represents the number of lags. The solid lines represent dependence at time t, with dashed lines representing dependence over k lags. The thickness of dashes distinguishes between the t and t − 1 cases.

Although the aforementioned model family treats edges as conditionally independent within time steps, they may depend on past time steps via arbitrary functions of previous graph realizations (up to some finite order, k). We call such functions of previous network states lag terms (in analogy with time-series models), with the order of a lag term corresponding to the temporal difference between the earliest cross-section used by the term and the current cross-section. (Thus, a first-order term involves only the previous time step, the second involves at most the second, etc.) In general, our framework allows for the arbitrary choice of k (and thus dependence over arbitrarily long lags).

3.2. Dynamic Network Logistic Regression

The dependence structure proposed in section 3.1 leads immediately to a separable model, whereby we decompose the model structure into two conditionally independent parts. For a full derivation of the likelihood, see Appendix A, in which we describe the precise assumptions required to provide this dual-logistic structure (i.e., the necessary Markov, conditional independence, and homogeneity assumptions).

To obtain the dynamic logistic network regression representation for our process, we divide our derivation into two distinct parts. First, we specify the necessary assumptions for the likelihood of the relational structure of the graph given the vertex set; second, we set out the necessary assumptions to derive the fully logistic structure for modeling both the vertices and the edges as a lagged logistic regression model. Note that, unlike in the preceding sections in which we used the edge set notation (E), we apply adjacency matrix notation (Y) in the section that follows for greater flexibility in handling edge set decomposition.

We start by relaxing the temporal Markov and fixed vertex set assumptions of Hanneke and Xing (2007) and Hanneke, Fu, and Xing (2010), replacing them with weaker versions. We then impose some conditional edge and vertex independence assumptions, and last, we make some homogeneity assumptions. We formally specify these assumptions in Appendix A (sections A.1 and A.2), combining them to derive the likelihood of the dynamic network logistic regression model family.

This structure allows us two distinctive advantages over Hanneke and Xing (2007), Hanneke et al. (2010), and others. The first advantage is that unlike Hanneke and Xing and Hanneke et al., we do not require the vertex set to be fixed, and thus the number and identity of vertices may change endogenously with time (an important factor when modeling emergent networks, such as those that arise following disasters, in naturally occurring groups, etc.). The second important advantage is that we explicitly develop the dependence conditions needed for inhomogeneous Bernoulli structure, in comparison with Hanneke and Xing and Hanneke et al., whose computational examples implicitly assume Bernoulli structure but who do not elaborate the associated theoretical assumptions. This development facilitates the expansion of the present model family by relaxation of conditional independence, as necessary.

We consider first the evolution of edges, given the vertices present in the network. (For a more formal description, see section A.1.) Given a graph (Y_i, V_i) = Z_i and covariate set X_t (noting that X may contain covariate information from prior time points) with i ∈ 1, …, t, we formally specify our assumptions: (1) that the state of the network at any given time point depends only on the states of the networks over some previous k time points (the relaxed temporal Markov assumption); (2) the conditional independence of edges in the same time slice, given history and covariates; and (3 and 4) the temporal homogeneity of the stochastic process generating the network (given the covariates).

There are few inferential models in the social network literature that incorporate the vertex dynamics (i.e., vertex set change) of a social network; however, vertex dynamics can greatly influence the nature and characteristics of an evolving relational structure. We propose using the aforementioned dynamic logistic regression as a reasonable starting point. As with edge dynamics, logistic structure for vertex entry (“birth”) and exit (“death”) arises naturally given a series of simplifying conditional independence assumptions. Note that we do not require that vertices can enter or exit only once, although adding such an assumption may be appropriate in some settings. This can be done within the logistic framework used here, with the addition of appropriate support constraints.

To model vertex dynamics in a practical fashion, we propose the following additional simplifying assumptions. We begin with (5), which simply states that there exists a finite set that contains all vertices at risk for entering the network over the entire time period 1, …, t. Next, we make another conditional independence assumption (6) such that vertex set at time V_t is conditionally independent of network realizations prior to a fixed point in the past. We then assume (7)² that the indicator of vertex g is conditionally independent of the indicator of vertex h, h ≠ g (i.e., whether vertex g is present or not is conditionally independent of h) given the edges set at time t, the past realizations of the edge and vertex set, and exogenous covariates. Last, we make a homogeneity assumption (8) that parallels that of the edge case. For a more formal description, see section A.2.

This derivation allows us to divide the likelihood of the vertex portion of the model and the edge portion of the model into separable terms, where the vertex likelihood is given by

$$Pr(V_t\mid Z_{t-1},\dots ,Z_{t-k},X)=\prod _{i=1}^{n}B\left((\mathbb{I}{v}_i\in V_t)\mid {\text{logit}}^{-1}\left({\mathrm{\psi }}^{T}w(i,Z_{i-1},\dots ,Z_{i-k},X)\right)\right)$$ (2)

and the edge likelihood by

$$Pr(Y_t\mid V_t,Z_{t-1},\dots ,Z_{t-k},X)=\prod _{(i,j)\in V_t\times V_t}^{n}B\left(Y_{\mathit{tij}}\mid {\text{logit}}^{-1}({\mathrm{\theta }}^{T}u(i,j,V_t,Z_{i-1},\dots ,Z_{i-k},X))\right),$$ (3)

where B is understood to be the Bernoulli pmf, is the indicator function, X is a covariate set, u and w are sufficient statistics for the edge and vertex models (respectively), and θ, ψ are the respective edge and vertex parameter vectors. The joint likelihood of Z is then the product of the respective vertex and edge likelihoods. A useful computational side effect of this is that we may use a single logistic routine to fit the entire model, using the augmented vector of the adjacency matrix and the temporal vertex indicator set, as shown in equations (2) and (3).

The above provides a fairly flexible and highly tractable framework for modeling joint edge/vertex dynamics for the case in which the risk set of potentially appearing vertices is known (or can be approximated as such). In some cases, this risk set may be well approximated by the set of all vertices ever appearing in the network (e.g., that the chance of a vertex being effectively at risk and never actually appearing is small). In other cases, it may be desirable to consider a larger population of potential actors. (We assume at present that this set is bounded, although extensions using Dirichlet processes [Ferguson 1973] or the like could be used to generalize this framework to the unbounded case.) For inferential purposes, estimation for parameters of both vertex dynamics and edge dynamics is performed within the same logistic regression and is fully separable. In the case of simulation, however, the dependence structure illustrated in Figure 1 requires alternately sampling vertices and (conditionally) edges on those vertices. As this suggests, both edge and vertex submodels can interact in complex ways to create network structure, even when these models are inferentially distinct. An example of this interaction is shown in section 5.

3.3. Considerations for Implementation

As noted earlier, logistic regression is a popular and well-established technique for statistical analysis, and the development of scalable algorithms for logistic regression is an active area of research (e.g., Kiwiel 2001; Komarek 2004; Komarek and Moore 2003; Lin et al. 2008; McCullagh and Nelder 1999). Although the implementation of dynamic network logistic regression using standard techniques is in principle straightforward, it is worth noting a few practical observations and cautions about the use of conventional fitting algorithms in the network context per se.

The decomposable nature of dynamic network logistic regression (i.e., the separability of the edge and vertex sets) allows the edge and vertex set estimation to be computed simultaneously. In particular, these operations can be both divided (reducing the size of each problem) and parallelized (potentially reducing computation time). Other ways to speed up computation include the use of specialized data structures and result caching for the sufficient statistics of the model. (This is particularly important for model adequacy checking, for which it is necessary to compute multiple iterations for simulation purposes; see section 4.)

Last, we would like to provide a few words of caution about the use of subsampling methods, a popular family of approaches that seek to reduce computational time by carrying out regression using only a subset of the observed data. In implementing the models described here, we first attempted to use various standard subsampling methods (e.g., Manski and Lerman 1977; Prentice and Pyke 1979) for our optimization routine; however, we ran into issues related to the extreme sparsity of the network data sets we were considering that resulted in very unstable error estimation. Among the approaches used were classic methods for optimizing logistic regression in a rare-events framework, and they revolve around a clever post hoc stratified-sampling scheme (also known as endogenous stratified sampling or choice based in economics and as case-control design in epidemiology). Typically this involves “sampling” every rare event (i.e., a 1 in the case of sparse graphs), and subsampling the more common events (i.e., a 0 in the case of sparse graphs). This method has been used quite successfully in the social and public health fields (for a review, see King and Zeng 2001); however, in the case of dynamic logistic regression, it may be necessary to sample specific cells at high rates to obtain stable estimates, in a manner that is model dependent.

Ultimately, we obtained superior performance via classic weighted least squares methods for parameter estimation (which allow a high degree of scalability through sparse matrix data structures). This was then further improved upon with an expectation maximization algorithm developed by Gelman et al. (2008). Our experience suggests that although off-the-shelf methods are adequate for many purposes, the development of specialized techniques for efficient estimation of dynamic network models by modifying standard logistic regression algorithms would yield significant gains in performance.

4. MODEL ADEQUACY ASSESSMENT AND SIMULATION ANALYSIS

Model selection and assessment are common problems in all fields using mathematical and statistical models. In the present context, it is useful to begin by distinguishing between model selection (the identification of a best-fitting model on statistical grounds) and model assessment (evaluation of the adequacy of a selected model for scientific purposes). For the former problem, we recommend that the analyst start with standard model selection techniques based on penalized log-likelihood approaches such as the Bayesian information criterion (BIC; Schwarz 1978) or the Akaike information criterion (Akaike 1974) for deciding which model performs best within a collection of proposed models. This procedure follows standard statistical practice and is reasonably well developed; for further details, see Brockwell and Davis (2002) and Gelman et al. (2003). Assuming that research has identified the best overall candidate model, we then recommend performing simulation-based assessments of model adequacy to verify that the candidate captures the relevant properties of the original data; the approach to adequacy testing suggested here is an adaptation and extension of those applied in the computational Bayesian literature (Gelman et al. 2003) and the model assessment methods for cross-sectional network data (Hunter, Goodreau, and Handcock 2008).

Modern network analysis often applies simulation-based methods for analysis, prediction, exploration, or model diagnostics. Simulation is typically used in these cases because few network models lend themselves to analytical treatment. In this article, we use simulation methods to ascertain the model performance on a series of theoretically motivated network metrics (i.e., model adequacy assessment).

For purposes of this article, we focus on assessment by simulating n outcomes from the best-fitting model and then examining statistics of interest on the resulting distribution. We refer to this technique as an inhomogeneous Bernoulli prediction. The algorithm we use is as follows: For each time point (t) we predict Z_t|Z_t−1 = z_t−1, …, Z_t−k = z_t−k n times (i.e., we take n draws from the conditional distribution of the network at time t given the previous k observed time steps), where we first predict the vertex set (e.g., the vertices that we project to occur at time t), and then from the vertex set we predict the edge structure. For each realization $Z_t^{(i)}$, we summarize the resulting network through a set of (user-specified) graph level indices (GLIs; Anderson, Butts, and Carley 1999; Wasserman and Faust 1994), yielding a GLI distribution for each time point. This predictive GLI distribution is then used to study the properties of the underlying model.

Our reason for concentrating on GLI distributions is twofold. First, it is often difficult or impractical to inspect thousands of simulated networks visually or otherwise, nor are these easy to compare statistically in simple and practical terms without the use of descriptive indices. (This is particularly true given that vertex set composition will generally vary across realizations, requiring approaches to graph comparisons that do not depend on a fixed vertex set.) Second, it is typically the case that the analyst is not concerned with the occurrence of a single edge or vertex but rather with the overall macrolevel properties of the network (e.g., mean degree, triad census, centrality measures, connectedness measures). Examination of a limited set of index distributions accomplishes the latter goal while avoiding the former difficulty.

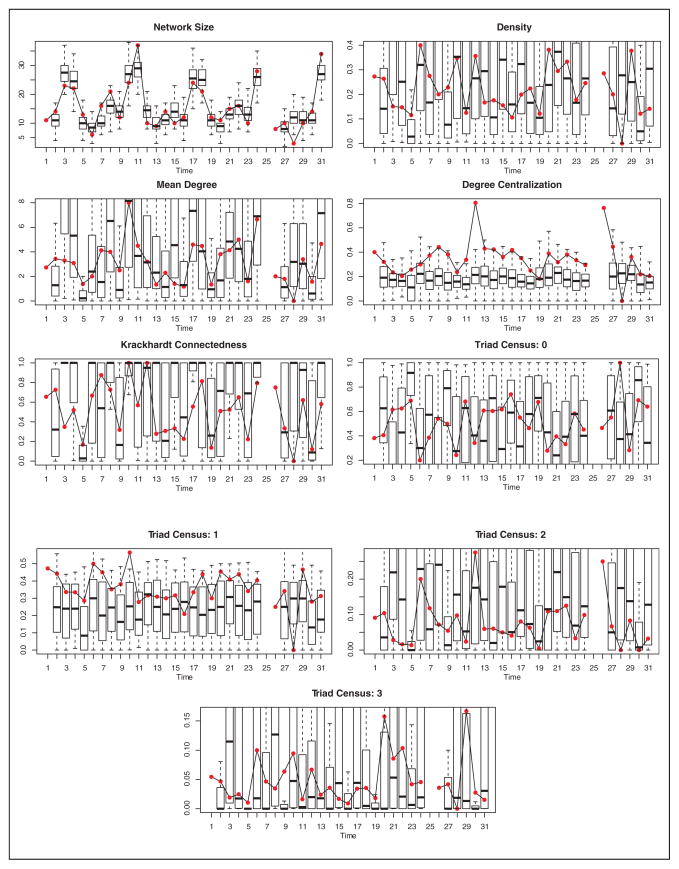
Although prediction of GLIs may at first blush seem to evaluate only the edge model, this is not the case. Because each Z_i consists of both edge and vertex sets, accurate structural prediction depends on the joint behavior of the edge and vertex models. In particular, recall that Y_i depends on V_i not only directly (via the support) but also indirectly (via any sufficient statistics that involve attributes or past interaction history of vertices within the network). The effects of the vertex model thus “cascade” into the edge model during prediction, despite the fact that the two are inferentially separable. One consequence of this phenomenon is that poor vertex modeling will result in the inability to correctly model GLIs of interest (a topic further discussed in section 6 and demonstrated in Figure 4); GLI-based evaluation is thus an effective way to evaluate the joint performance of the edge and vertex models as a combined whole.

Figure 4.

Graph level index (GLI) comparison for the one-step dynamic network logistic regression prediction under inhomogeneous Bernoulli prediction with the vertex set fixed to V_max = 95. Gray dots represent the observed GLI, and black box plots are the simulated distribution of the onestep prediction on the basis of the model 4 edge weights (100 simulated networks for each one-step prediction). Note that only 28 points are used in this analysis. This is because there is 1 missing time point, and we cannot perform one-step prediction on the first day of measurement or for the time point for which we lack the past day’s information.

After we perform the simulation procedure, we say that the proposed model “adequately” captures a given feature of the observed network at a specified level of precision α if the associated GLI value falls within the central α-coverage simulation interval for the model in question. The optimal case is naturally one in which the simulated GLI distribution is centered on the observed value, with little variation; for a simple model of a complex system, however, we may use a looser criterion (e.g., coverage by the 95 percent simulation interval for a certain fraction of time steps). Selection of both GLIs to study and adequacy criteria are necessarily dependent on substantive considerations (including the use to which the model is to be put). For example, if our central theoretical concern is the explanation of transitivity in an evolving network, then ensuring that this index is well accounted for by the model (in the sense of being reliably included in simulation intervals with α ≤ 0.95) would be critical. In the same context, we might be less concerned with capturing, say, mean degree, but may nevertheless show concern if such a basic property were not covered by wide (say, 99 percent) simulation intervals in a significant fraction of time points. For an extensive example of this procedure, see section 5.4.

5. SAMPLE APPLICATION: GOING TO THE BEACH

To illustrate the application of the dynamic network logistic regression approach, we use the methods discussed in this article to the analysis of a classic network data set, which involves a dynamically evolving network of interpersonal communication among individuals congregating on a beach in Southern California over a one-month observation period (Freeman 1992; Freeman et al. 1988). Interpersonal communication in small groups is a well-studied subfield in social psychology and social network analysis (Festinger and Thibaut 1951). The sociological study of interpersonal communication networks in a dynamic context was originally pioneered by Nordlie (1958) and Newcomb (1961). Here, we show how the dynamic logistic family allows us to flexibly model the evolving network, with particular emphasis on the interplay between tie structure and vertex set dynamics.

5.1. Software Implementation and Estimation Methodology

The particular implementation of dynamic logistic regression and simulation analysis used in this article was coded for the R statistical computing platform (R Development Core Team 2010). For parameter estimation we used the expectation maximization algorithm described by Gelman et al. (2008). All sufficient statistics were computed either using the sna package in R (Butts 2007) or implemented directly. For model adequacy assessment, we use the algorithms described in section 4.

Parameter estimates reported here were obtained via Bayesian posterior mode estimation with weakly informative Student’s t priors (specifically, independent and identically distributed t priors centered at 0 with a scale parameter of 2.5 and 1 degree of freedom, i.e., Cauchy distributions). Our approach follows that of Gelman et al. (2008), who recommended a t prior distribution as an effective default choice in conventional logistic regression settings. This choice of prior has the advantage of always yielding a well-defined posterior estimate and automatically applying more shrinkage to higher order interactions, while otherwise remaining diffuse. One may interpret the resulting estimator in either frequentist or Bayesian terms. From a Bayesian point of view, the estimator in our case is the mode of the posterior distribution in which all model parameters are viewed a priori multivariate t distributed, an estimator that is optimal under 0/1 loss. Within a frequentist framework, the use of a “prior” structure may be thought of as a bias reduction technique. Because past work (e.g., Gelman et al. 2008) on related models has suggested that estimates of uncertainty are often better behaved under this alternate procedure than estimates obtained from the Hessian of the deviance matrix, we recommend the use of the former in typical settings.

5.2. Data

The data analyzed in the sections that follow were originally collected and analyzed in aggregate by Freeman et al. (1988) and have since been used in a number of influential articles (e.g., see Cornwell 2009; Hummon and Doreian 2003; Zeggelink, Stokman, and van der Bunt 1996). Although this network is typically analyzed in aggregate, it was originally collected as a dynamically evolving network (in which the vertex set is composed of windsurfers and the edge set is composed of interpersonal communication). The network was collected daily (aggregated over a morning and an afternoon observation period) for 31 days (August 28, 1986, to September 27, 1986).³

Individuals were tracked with unique identifiers, and they were divided by Freeman et al. (1988) into those we will here call regulars (N = 54)—frequent attendees who were well integrated into the social life of the beach community—and irregulars (N = 41) on ethnographic grounds. The former category was further broken down by the researchers into two groups: group 1 (N = 22) and group 2 (N = 21), with 11 individuals not classified as belonging to either group 1 or group 2. Altogether, the union of vertex sets (V_max) consists of 95 individuals. On any given day during the observation period, the number of wind-surfers appearing on the beach ranged from 3 to 37, with the number of communication ties per day ranging from 0 to 96.

These basic characteristics are used in the illustrative analysis that follows, which centers on the question of what drives the evolution of interpersonal communication in this open, uncontrolled setting.

5.3. Mechanisms of Dynamic Interpersonal Communication

A number of distinct mechanisms may influence whether a windsurfer engages another windsurfer at any given time; however, two windsurfers clearly cannot interact if both do not appear simultaneously on the beach, and thus the first influences to be considered are those affecting the vertex set. For this illustrative analysis, we propose four basic mechanisms as governing the propensity of an individual to appear on a given day: (1) a regularity effect, (2) an inertial network effect (e.g., the lag term), (3) a three-cycle effect (here equivalent to a triangle term), and (4) seasonal effects (e.g., day of week). An intuitive summary of each mechanism follows.

Of the four mechanisms we consider as drivers of vertex set dynamics, the first is regularity, the notion that an individual is more likely to appear on any given day if he or she is one of the individuals who is classified (on ethnographic grounds) as belonging to the category of regulars who form the core of the beach community. This recognizes the fact (known from the observational accounts) that there is heterogeneity among the windsurfers, with certain individuals being much more active than others.

The second posited mechanism is one of persistence or inertia; that is, if an individual is active today, he or she is more likely to be active tomorrow. This is sometimes known in the social network literature as “behavioral inertia” and has been seen both empirically and experimentally in varied social network contexts (Corten and Buskens 2010).

The third mechanism is a triangle effect, whereby the number of three-cycles in which an individual is embedded at point t − k influences the likelihood of whether an individual will appear on day t. This may be thought of as capturing the effect of social participation, with the intuition that persons embedded in dense social groups (e.g., cliques) are more likely to have their attendance reinforced and thus to return to the beach.

The fourth mechanism is seasonality: the tendency for activity to show systematic variation over daily or weekly cycles. Cyclic phenomena are common in human systems, as has long been recognized in the time-series literature (Shumway and Stoffer 2006). Common seasonal effects in behavioral data include daily and hourly effects (e.g., differences between weekdays and weekends or between midnight and midday). Networks are no exception to this rule, as evidenced by Baker’s (1984) observation of daily variation in structure and activity within trading networks in a national securities market, and Butts and Cross’s (2009) finding that the volatility of evolving blog citation networks changes with time of day, day of week, and external events (in that particular case, phases of the 2004 U.S. electoral cycle). In the present case, a parallel phenomenon may occur through weekly cycles in the frequency of attendance at the beach (a reasonable expectation given the institutional context of work and leisure time for the study population during this period).

Once the vertex set arises, the influence of a new set of interpersonal communication mechanisms becomes relevant. Of the many potential mechanisms that could govern interpersonal communication in the study population, we here explore six: (1) regularity of beach use and other assortative mixing effects, (2) individual propensity effects for regularly occurring individuals, (3) contagious participation, (4) inertial network effects (e.g., the lag term),⁴ (5) embeddedness, and (6) seasonal effects. As with the vertex model, we briefly consider each of these in turn.

The first mechanism is assortative mixing between those identified as regular beachgoers and those who were classified as irregulars. In the social network literature, effects of a priori group partitioning on tie formation are often referred to as mixing effects. McPherson, Smith-Lovin, and Cook (2001) reviewed extensive evidence that individuals cluster in homophilous grounds, and thus we might expect that those more deeply embedded in the milieu of the beach environment (the regulars) will be more likely to talk with others of the same ilk (and, likewise, that outsiders will be more likely to interact with other outsiders). Furthermore, among the regulars, those identified as belonging to the same core groups by the ethnographic observers are conjectured to mix at higher rates, all else equal, than others.

The second mechanism consists of individual-level heterogeneity in the propensity of regular attendees to engage in communication with others. We might expect that idiosyncratic shyness or gregariousness of regularly occurring individuals may influence the amount of activity on a given day. Similar to the argument applied for the first mechanism, we might expect the basic propensity of a regular attendee to engage or not engage other beach members to be highly influential on the amount of activity on any given day.⁵

The third mechanism is contagious participation, based on the notion that high levels of beach-going activity at the group level are likely to translate into high levels of other activity (including communication). Thus, we take the number of persons present itself as a predictor of the propensity of individuals to communicate with others on the beach.

The fourth mechanism is inertia (or persistence); that is, if an individual is active or has a relationship today, he or she is more likely to be active or have a relationship tomorrow.

The fifth mechanism is embeddedness (see Granovetter 1985). A dyadic relationship that is embedded within a broader communicative context (e.g., in which three persons in question are linked by numerous past chains of communication) is likely stronger and more likely to persist at a later time point than one lacking such a context. We measure embeddedness by the number of k-cycles within which a pair was embedded on the prior day of interaction.

The sixth mechanism is seasonality, here in the propensity to form ties rather than the tendency to appear at the beach. This might arise for a number of reasons, such as systematic variation in the sorts of people who go on weekdays versus weekends and differences in activities pursued during weekday versus weekend excursions.

Each of the proposed mechanisms for both vertex formation and edge creation may or may not be important to the network structure, which brings up the necessary process of model selection and model adequacy assessment. In the sections that follow, we first use penalized deviation-based model assessment to select the best-fitting model. We then use a series of simulation-based model adequacy checks, as discussed in section 4, to assess the extent to which the selected model does or does not capture important features of the evolving network.

5.4. Model Selection and Adequacy

5.4.1. Parameterization

To implement our model, the impact of each of the mechanisms in section 5.3 is operationalized as a weight or parameter in the dynamic logistic regression framework. The first step in the model-building process is to select the vertex mechanisms, which are highly influential in this context because the vertex portion of the model predicts “who shows up to the party” (so to speak) and thus who is eligible to interact at a given time point. The importance of “who shows up” will greatly depend on the context and actor-specific covariates in a given dynamic network. For the beach data (as we will see), the most important attribute that an individual carries is whether or not he or she is a regular beach attendee (and which group within the regular attendees he or she is a part of). It should also be noted, however, that individuals carry more with them than their exogenous covariates: insofar as individuals’ interaction histories affect their probability of communicating with others, they are less substitutable with peers having different histories of interaction. Thus, correct prediction of individual attendance can be important even in settings for which exogenous covariates are limited (or altogether absent).

In addition to specifying putative mechanisms, our vertex model requires specification of the risk set (V_max), that is, the set of persons effectively at risk for showing up on a given day. Here, we treat all individuals observed at any time during the data collection window as our risk set, lacking other information on potential attendance. Although this is obviously a simplification, we view the total set of all persons appearing over an entire month as a reasonable proxy for the unobserved collection of persons with a nonsmall chance of appearing on any given day.

As with other exponential family models, we capture the effects of putative mechanisms by statistics that (together with their associated parameters) determine the probability that an edge or vertex will appear at a given point in time. For full details of the sufficient statistics applied in this application, see Appendix B.

5.4.2. Model Fit

Each mechanism proposed in section 5.3 may or may not influence whether a windsurfer arrives on a given day and/or, given that he or she arrives, whether he or she interacts with another windsurfer; a priori, we may suspect that any or all of these mechanisms may be active. To infer which of the proposed mechanisms are in fact present, we search the space of models for the combination that provides the best total accounting of the data (in a penalized likelihood sense). We interpret any mechanism not selected through this procedure as one that is not influential in this process net of other factors (i.e., we reject the hypothesis that the mechanism is a substantial factor in shaping the evolution of this network, given the other mechanisms). In our specific case, we perform model selection using the BIC score, selecting the model in which the BIC is lowest for the posterior mode. As will be shown in Tables 2 and 3, the full model containing all proposed effects is the best-fitting model under this criterion. We thus tentatively conclude that all of the putative mechanisms suggested here for attendance and edge evolution are active to some degree.

Table 2.

Vertex Portion of Models 1 to 4 Ranked by BIC Score

	Vertex Model
	Model 1	SE	Model 2	SE	Model 3	SE	Model 4	SE
BIC	8,166.2395*		7,929.2997*		7,699.5743*		7,689.1466*
Intercept	−1.5893*	(0.0517)	−1.9250*	(0.0536)
regular							0.9319*	(0.0650)
group 1							0.7803*	(0.0910)
Vt−1			1.5295*	(0.1016)	1.1312*	(0.1066)	0.7867*	(0.1107)
3-cyclet−1					0.3780*	(0.0605)	0.3520*	(0.0618)
Monday					−2.7044*	(0.1916)	−3.4522*	(0.1982)
Tuesday					−2.5047*	(0.1787)	−3.3754*	(0.1827)
Wednesday					−2.1569*	(0.1589)	−3.0218*	(0.1657)
Thursday					−2.0497*	(0.1497)	−2.8769*	(0.1559)
Friday					−2.2750*	(0.1426)	−3.0973*	(0.1466)
Saturday					−1.1718*	(0.1059)	−1.9258*	(0.1102)
Sunday					−1.5207*	(0.1446)	−2.2235*	(0.1491)

Note: t −1 indicates the lag interval, V_{t − 1} represents the lag term, the days of the week stand in for the intercept term in models 3 and 4, 3-cycle_{t − 1} represents the triangle effect, and indicates that a given variable is represented by a dummy variable. BIC = Bayesian information criterion.

^*p < .05.

Table 3.

Edge Portion of Models 1 to 4 Ranked by BIC Score

	Edge Model
	Model 1	SE	Model 2	SE	Model 3	SE	Model 4	SE
BIC	8,166.2395*		7,929.2997*		7,699.5743*		7,689.1466*
Intercept	−2.3162*	(0.0359)	−4.3081*	(0.0362)
Mixing regular (R)					1.1091*	(0.0430)	1.1389*	(0.0434)
Mixing ¬ R ↔ R					0.5560*	(0.0737)	0.5595*	(0.0742)
Mixing ¬ R					—	—	—	—
Indiv 06							−0.6563*	(0.0384)
Indiv 17							−0.9519*	(0.0397)
Indiv 16							−0.4602*	(0.0473)
Indiv 37							−0.4161*	(0.0459)
Indiv 39							−0.5880*	(0.0638)
Indiv 46							−0.7159*	(0.0502)
Indiv 05							0.5852*	(0.0485)
Indiv 07							−0.5901*	(0.0475)
Indiv 20							−0.8542*	(0.0497)
Indiv 40							0.7993*	(0.0552)
Indiv 15							−2.8539*	(0.0485)
Indiv 19							0.3049*	(0.0580)
Indiv 02							−0.8645*	(0.0624)
Indiv 26							−0.7884*	(0.0580)
Indiv 51							0.1373*	(0.0712)
Indiv 54							0.3120*	(0.0645)
Indiv 24							1.1369*	(0.0580)
Indiv 28							0.2357*	(0.0504)
Indiv 33							−0.1863*	(0.0623)
Indiv 42							−1.1086*	(0.0532)
Indiv 44							1.4785*	(0.0594)
Indiv 50							−0.6624*	(0.0801)
Indiv 08							0.2206*	(0.0569)
log (nt)			0.6394*	(0.0118)	0.3884*	(0.0120)	4.0946*	(0.0121)
Yt−1			0.8946*	(0.1019)	0.3120*	(0.1042)	0.2808*	(0.1052)
log (9-cyclet−1 + 1)					0.0880*	(0.0095)	0.1077*	(0.0095)
Monday					−5.9929*	(0.1768)	−12.2986*	(0.1776)
Tuesday					−4.1357*	(0.1665)	−9.5061*	(0.1643)
Wednesday					−3.7315*	(0.1225)	−10.6229*	(0.1248)
Thursday					−4.0714*	(0.1057)	−10.6006*	(0.1108)
Friday					−4.7021*	(0.1305)	−11.6135*	(0.1308)
Saturday					−4.2353*	(0.0564)	−11.4279*	(0.0569)
Sunday					−4.9328*	(0.0837)	−12.5474*	(0.0840)

Note: The lag term is t − 1. The days of the week stand in for the intercept term in models 3 and 4; indiv k indicates the density effect for individual k (as indexed in the data set); log (n_t) indicates the contagious propensity effect and is the log of the network size at time t; again, Y_t−1 represents the lag effect and log (9-cycle_t−1 + 1) is the embeddedness cycle statistic; and indicates that a given variable is represented via a dummy variable.

^*p <.05.

Summarizing this result in substantive terms, we find that the best-fitting model for the vertex process is one that incorporates differential base rates of attendance for regulars and (above and beyond this) for members of group 1, as well as simple inertia, prior participation in cohesive conversation subgroups, and weekly seasonality. For the edge process, we likewise find that all conjectured mechanisms—mixing, individual heterogeneity, contagious participation, inertia, prior embeddedness, and seasonality—are active in governing who communicates with whom (conditional on who shows up). Interpretation of model parameters is discussed below.

5.4.3. Model Adequacy

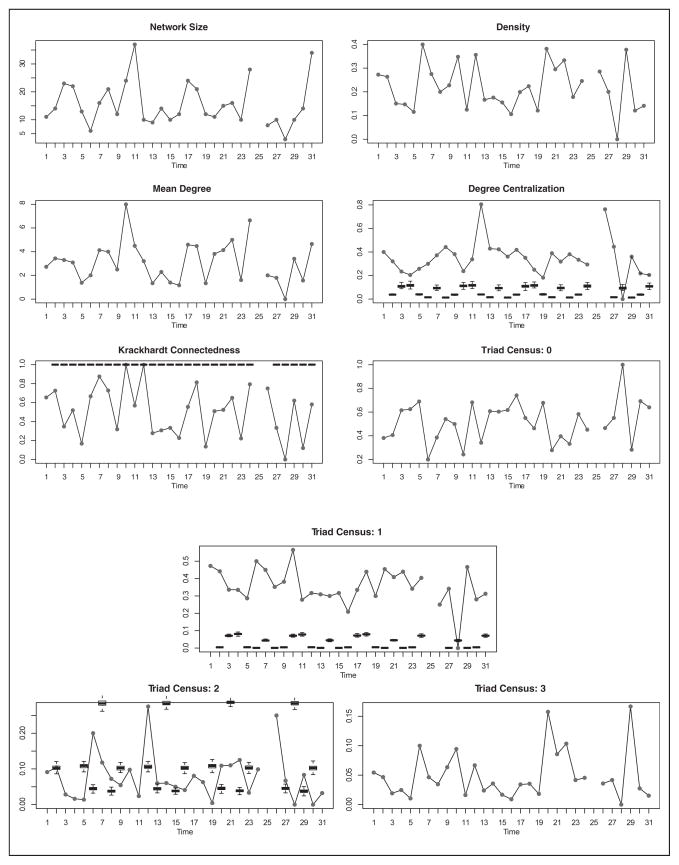
To evaluate the adequacy of the best-fitting model, we use simulation-based one-step prediction under an inhomogeneous Bernoulli predictor, as discussed in section 4. Although the selected model may be the best fitting of those proposed, we are also interested in assessing the extent to which it can effectively capture the properties of the evolving beach network per se; significant failures in this regard may suggest the need for further elaboration. In the present case, we begin with simple network features such as size and density (and, therefore, mean degree). In the context of interpersonal communication on a beach, capturing local group structure is also of interest; thus, we include the statistics of the undirected triad census (null, dyad, two-path, and triangle) as targets for evaluation.⁶ To evaluate our ability to capture inequality in communication, we include degree centralization (Freeman 1979). And, last, we may be interested in our ability to predict the extent to which the communication network formed on a given day will be well connected, a feature that we examine using the Krackhardt connectedness statistic (Krackhardt 1994). The simulation intervals for each GLI under the best-fitting model (model 4, Figure 2) perform reasonably well under the 95 percent coverage criterion suggested in section 4 (α ≤ 0.95). In Table 1, we see that the observed GLI falls within the interval over 26 of the 28 predicted time points for all but mean degree (and in fact falls within the interval all 28 times for six of nine GLIs).

Figure 2.

Graph level index (GLI) comparison for the one-step dynamic network logistic regression prediction under an inhomogeneous Bernoulli assumption for model 4. Gray dots represent the observed GLI, and black box plots are the simulated distribution of the one-step prediction on the basis of the model 4 weights (100 simulated networks for each one-step prediction). Note that only 28 points are used in this analysis. This is because there is 1 missing time point, and we cannot perform one-step prediction on the first day of measurement or for the time point at which we lack the past day’s information.

Table 1.

A GLI One-Step Prediction Simulation Count (α ≤ 0.95)

GLI	Fraction Correct
Network size	26/28
Density	28/28
Mean degree	28/28
Degree centralization	20/28
Krackhardt connectedness	28/28
Triad census: 0	28/28
Triad census: 1	27/28
Triad census: 2	28/28
Triad census: 3	28/28

Note: This is a check of whether the α ≤ 0.95 simulation interval contains a given GLI. Total possible correct is 28. GLI = graph level index.

It is worth pointing out at this juncture that the model adequacy method used is a quite stringent one, based on a fairly strict notion of prediction (specifically, forecasting). We might imagine different forms of dependence (either temporally or endogenously) that might affect the model’s ability to correctly predict macrolevel characteristics of the observed network at any given time point; however, the proposed model performs quite well at predicting the proposed network characteristics, and we thus regard the model as adequate for current purposes. Furthermore, the success of the model in predicting a variety of GLIs suggests that the conditional independence assumptions used in deriving the dual logistic regression structure for this model are not grossly violated in this case.

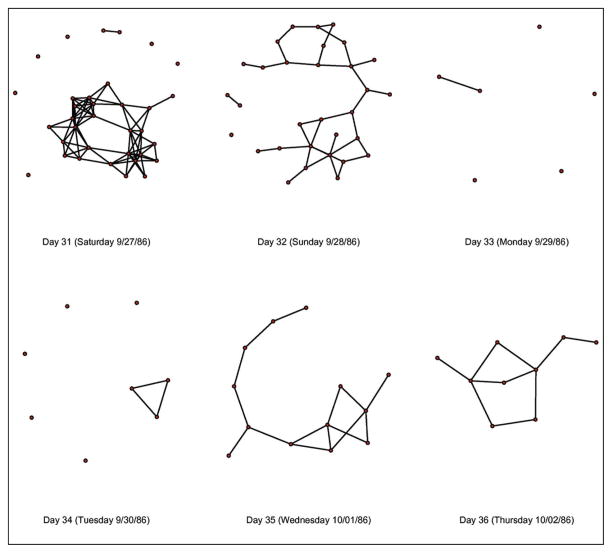
As a final test, we perform a five-step prediction of the complete network (Figure 3) as a form of visual analysis to verify that the model is not producing degenerate structures over several iterations of the model. These issues include, for example, those identified by Robins, Pattison, and Woolcock (2005), such as giant “clumps, ” so-called caveman graphs, or other highly clustered graphs. Such structures are largely considered pathological and unrepresentative of “real-world” social networks and (more important) do not resemble the types of networks arising within our observed data. Inspection of the graphs generated through the five-step prediction verifies that the networks predicted by the model are nonpathological, either in terms of converging to an unrepresentative canonical structure (as in the Robins et al. case) or in producing effectively random graphs with less structure than the observed data. Taken together with the GLI-based adequacy checks, these results suggest that the model is indeed doing a reasonable job of capturing the core features of the evolving network.

Figure 3.

A five-step projection of the windsurfer network by Freeman et al. (1988). The first of these six plots is the last observed network in Freeman et al.’s network (day 31). The next five plots represent a typical five-day projection via inhomogeneous Bernoulli prediction.

5.5. Parameter Interpretation

The parameter estimates presented in Tables 2 and 3 are interpreted in terms of the influence of the mechanisms proposed in section 5.3. To simplify this presentation, we discuss these mechanisms in two parts, starting with vertex mechanisms and proceeding to mechanisms associated with the edge set.

5.5.1. Vertex Mechanisms

We proposed three basic mechanisms for the vertex set dynamics in this particular context (Table 2, model 4). The first was that an individual’s group membership would be predictive of attendance. As expected, we find that being a regular has a significant and positive influence over whether an individual is likely to appear on any given day (vs. irregulars), with those in group 1 being even more likely to appear. The second mechanism was that being present at the beach on the prior day would make individuals more likely to appear at the beach on the next day, which is indeed what we find (the weight is again positive and significant). Similarly, if individuals are engaged in a conversational clique the day before, they are even more likely to appear the next day than if they are simply present; in fact, each three-clique in which they participate increases their conditional odds of subsequent attendance by over 40 percent. Finally, we see that beach attendance is indeed highly seasonal: with the exception of a slight bump on Thursday, weekends are substantially more popular times for beach-going than the workweek (Tuesdays in particular). These seasonal effects are comparable in magnitude with the effect of being a regular and exceed the effect of inertia (although inertia combined with participation in one or two conversation clusters has a similar overall effect).

5.5.2. Edge Mechanisms

We proposed five basic mechanisms (regularity, inertia, contagious participation, individual differences, and seasonality) as shaping whether a beachgoer was likely to engage in interpersonal communication (Table 3, model 4), starting with assortative mixing of regulars (and group members). The mixing hypothesis is confirmed such that regulars are more likely to interact with other regulars but refuted in the sense that irregulars are more likely to interact with regulars than with other irregulars. This suggests a core-periphery phenomenon, wherein irregulars are more likely to interact with “core” regulars who go to the beach more often and are more likely to be knowledgeable of the sport and area. The fourth mechanism, individual differences within the most influential group (high-attending regulars), is confirmed: All individuals are significantly more likely to interact or less likely to interact than the baseline. This occurs at substantially high levels (as much as + 1.5 times or down to as low as −2.9 times). The third mechanism, contagious participation, is highly influential and is both positive and significant. The inertial hypothesis is confirmed because the lag and the cycle term are positive and significant. (It should be pointed out that that the number of cumulative cycles up to nine that a dyad may be involved in can be quite large, e.g., in the thousands, and thus this term can be quite influential.)

For the fifth mechanism, it is important to point out that many of these terms cannot be interpreted independently. For example, everyone regardless of their categorization of “regularity” is influenced by the number of individuals on the beach on a given day. To put this in perspective, take the highest number of individuals to appear on the beach over the 31 days (37 individuals) so that log (37) · 4.09 = 14.77 and compare it with the lowest, log (3) · 4.09 = 4.49. To fully grasp how this interacts with the days of the week, it is important to note that network size is highly correlated with the day of the week, and thus we find that there are more individuals on the beach on a typical Saturday or Sunday than on a typical weekday (e.g., the lowest day occurs on a Wednesday and the highest day occurs on a Sunday), such that the total effect on baseline density at the high end is log (37) · 4.09–12.55 = 2.22 versus a total lowest day effect of log (3) · 4.09–10.62 = −6.12. Thus the baseline propensity for interaction is given almost eight times the boost (on a logit scale) on the day with the largest number of beachgoers versus the day with the smallest number of beachgoers. We therefore observe that, as the beach becomes more populated, the chance of interacting with any given individual increases, which supports the hypothesis of contagious participation.

5.6. Summary of Findings

In the context of the beach data, we find a number of distinct patterns in both presence and interaction. We find that features such as regularity, embeddedness, and seasonality greatly influence both the number of participants on a given day and who interacts with whom. All mechanisms discussed appear to play an important role in determining presence and interaction, as we find significant results for all of our hypothesized effects; in Table 4, we provide a summary of our findings.

Table 4.

Observed Direction and Significance of Each Vertex and Edge Hypothesis from Section 5.3

Hypothesis	Result
Vertex mechanisms
Regularity	+ *
Inertial network effects (e.g., the lag term)	+ *
Embeddedness (three-cycle effect)	+ *
Seasonal effects	−*
Edge mechanisms
Assortative mixing	+ *
Individual-level heterogeneity	−*, + *
Contagious participation	+ *
Persistence/inertia	+ *
Embeddedness (nine-cycle)	+ *
Seasonality	−*

Note: Minus and plus signs denote negative and positive effects, respectively.

^*Significant effect.

We begin our summary by noting that the baseline for participation on a given day varies by day of the week; that is, the participation rate on any given day ranges from a low of 0.03 on Monday to a high of 0.13 on Saturday. Furthermore, we find a positive influence on attendance on the basis of whether an individual is a regular attendee or in group 1; the effect of being a regular attendee increases an individual’s propensity of appearing on the beach from 0.07 to 0.27 (more than double the baseline), and if an individual is a regular attendee and a member of group 1, he or she has an increased range of 0.15 to 0.45. This likelihood of participation increases to a range of 0.28 to 0.64 if an individual was on the beach yesterday and this is further increased to 0.35 to 0.72 if he or she was embedded in a group the day before.

Similarly, the baseline interaction probability for two beachgoers varies by day of the week, number of participants on the beach on a given day (ranging from a low of three individuals on Wednesday to a high of 37 individuals on Saturday), and whether an individual is a regular; this is in turn heavily mediated by individual effects (e.g., whether a given individual is gregarious or not). Furthermore, we discover that individuals who were active in the past and/or embedded in groups of activity are more likely to be interacting. In total, the conditional probability of interaction can range from a low of nearly 0 (low level of activity, mixing between an irregular and low-activity individual who was also not active in the past) to a high of almost 1 (high-activity day, mixing between two regulars with high activity, who were both active in the past).

5.7. Discussion of Findings

The above case illustrates some of the insights that can be obtained via this modeling framework. Modeling vertex dynamics allows us to discover and interpret the mechanisms that influence individuals’ propensities to be present or absent (e.g., in our illustrative example, being both a regular and a member of group 1 or being embedded in multiple conversations the day before). After taking into account the vertex mechanisms, we can then interpret the factors influencing edge formation (e.g., given that actors A and B show up, how likely are they to interact) in a manner familiar to many social scientists (e.g., allowing a log-odds interpretation). Furthermore, we can examine temporal effects such as seasonality in both the vertex and edge context in a synthesized, coherent manner, as we might imagine that the day of the week could have a very different influence on attendance and interaction. Finally, we can consider the combined effect of attendance and interaction mechanisms on structural dynamics, allowing us to explain phenomena that cannot be well characterized in terms of either edge or vertex dynamics alone. For the study of emergent organizational networks, naturally occurring groups, and other systems with endogenous vertex dynamics, these capabilities may prove particularly useful.

6. DISCUSSION AND CONCLUSION

The dynamic network logistic regression framework proposed in this article builds on a number of well-established concepts in the social network literature. We have extended this prior work by incorporating vertex dynamics, clarifying the assumptions needed to model joint vertex/edge dynamics in logistic form, and addressing practical issues such as model assessment and scalability. Applying the resulting framework to a dynamic network, we illustrated how this approach allows us to identify mechanisms underlying both individual presence and absence and relationships in a straightforward fashion.

On the basis of our model adequacy checks, we find that our proposed model does a reasonable job of capturing many properties of the beach data, despite the lack of available covariates (e.g., age, race, prior relationships) that would undoubtedly facilitate prediction. Notwithstanding our model’s limitations, we find that the mechanisms most important to prediction of dynamic network collaboration in the Southern California beach data are assortative mixing, inertia (in a dyadic sense and in the number of cycles an individual is engaged in), individual differences of key players, the size of the network itself, and seasonality. As expected, we find that those identified ethnographically as core members of the beach community are more likely to be present on a given day, along with factors such as having been active on a previous day and having been previously involved in group interaction. We also find that the day of the week greatly influences the number of individuals who appear on any given day.

We have noted repeatedly throughout the article that a good vertex set model is key to effective prediction of joint vertex/edge set evolution, a fact that can be dramatically illustrated by comparing the model of section 5.4 with a similar model for which the vertex set is fixed to V_max (i.e., assuming all actors are eligible to interact) and the best edge model. The results are shown in Figure 4. Notice that the model simulation intervals never cover the observed statistics, and they are often so far from the observed values that they do not fall within the range of the observed statistics over the entire observation period (see again Figure 2). A naive approach to solving the vertex problem clearly will not work in this context.

Comparing the performance of our best-fit model with a naive model without a well-specified vertex component underscores the critical interaction between the size and composition of the vertex set and the structure of the resulting relationships. In particular, we find that models that do not accurately capture vertex set dynamics are deeply pathological for predicting other aspects of structure as well: We simply cannot get the edge set right without first modeling the vertex set. Because vertex set models are rarely used at present, this observation calls into question the trustworthiness of the current generation of dynamic network models. Although more research is certainly needed on this point, our experience thus far has strongly suggested that predictive adequacy for dynamic network models in realistic settings will depend as much or more heavily on capturing the factors that lead to individual presence and participation than on modeling the factors that lead participating individuals to interact. This implies a substantial rethinking of our current ideas regarding network evolution.

Although we believe that the logistic framework pursued here is both flexible and powerful, we end on a note of moderation. There may well be settings for which the available historical data do not adequately account for dependence among edges (or vertices) and for which the logistic approximation will perform poorly. Likewise, some research questions may require a degree of predictive accuracy that cannot be readily obtained without incorporating simultaneous dependence. For these problems, the framework presented here should be viewed as a “first cut” family of models, to be extended by the incorporation of additional dependence terms in a manner analogous to the extension of Bernoulli graph models in the cross-sectional ERGM case. That said, considerable progress may be made by beginning investigations with models based on conditional independence assumptions and adding dependence terms only as needed to obtain acceptable results. (Some recent promising developments by Desmarais and Cranmer 2012 suggest that parameter error estimation for the maximum pseudolikelihood estimation might be improved with bootstrap methods.) Because the dynamic logistic models can be easily manipulated (and understood), they are well suited to exploratory analysis and to tasks such as the identification of key covariates. They also scale readily to large data sets, making them applicable in settings for which models with edgewise dependence are too computationally expensive to be used. These advantages make the dynamic logistic family an important and useful tool in the analyst’s arsenal, as part of the growing family of techniques for modeling the dynamics of social structure.

Biographies

Zack W. Almquist is an assistant professor in the Department of Sociology and School of Statistics at the University of Minnesota. He is also an affiliate of the Minnesota Population Center. He received his PhD from the University of California, Irvine, where he also earned MAs in sociology and demography. He also holds a master’s degree in statistics from Northwestern University and a bachelor’s degree in mathematics from the University of Oregon. His current research focuses on modeling large-scale dynamic social networks; the structure of spatially embedded large-scale interpersonal networks, and spatial analysis more broadly; and the measurement and sampling of social network data.

Carter T. Butts is a professor in the departments of sociology and statistics and the Institute for Mathematical Behavioral Sciences at the University of California, Irvine. His research involves the application of mathematical and computational techniques to theoretical and methodological problems within the areas of social network analysis, mathematical sociology, quantitative methodology, and human judgment and decision making. Currently, his work focuses on the structure of spatially embedded large-scale interpersonal networks; models for informant accuracy, network inference, and graph comparison; representation and modeling of intertemporal relational data; and measurement and modeling of online social networks. He also studies social phenomena related to emergency situations and is involved in research that seeks to combine social science and information technology to improve group and organizational responses to disasters and other adverse events.

APPENDIX A. DERIVING THE LIKELIHOOD

A.1. Part 1: Edges Given the Vertex Set

We begin with the following assumptions using the notation introduced in section 3.2:

• 1For some specified k ≥ 0, Z_i | {Z_i−1, …, Z_i−k, X_t} is independent of Z_i−k−δ for all δ > 0.
• 2Y_ijk is independent of Y_igh given {V_i, Z_i−1, …, Z_i−k, X_t} for all j, k ≠ g, h.
• 3
  Let f_Y be the conditional pmf of Y_i (i.e., an arbitrary time slice of Y). For any realizable y, y₁, y₂, …, y_k, v, v₁, v₂, …, v_k then, for all i, j ∈ 1, …, t:

  $$f_Y(Y_i=y\mid V_i=v,Z_{i-1}=z_1,\dots ,Z_{i-k}=z_k,X_t=x_t)=f_Y(Y_j=y\mid V_j=v,Z_{j-1}=z_1,\dots ,Z_{j-k}=Z_k,X_t=x_t).$$
• 4
  Let f_V be the conditional pmf of V_i (i.e., an arbitrary time slice of V). For any realizable y₁, y₂, …, y_k, v, v₁, v₂, …, v_k then, for all i, j ∈ 1, …, t:

  $$f_V(V_i=v\mid Z_{i-1}=z_1,\dots ,Z_{i-k}=z_k,X_t=x_t)=f_V(V_j=v\mid Z_{j-1}=z_1,\dots ,Z_{j-k}=z_k,X_t=x_t).$$

From these assumptions, we can derive the joint likelihood of the network time series. We begin by applying assumption 1, which allows us to decompose the joint likelihood of the time series as a product of conditional distributions:

$$Pr((Y,V)=(y,v)\mid X_t)=\prod _{i=k}^{t}Pr(Z_i=z_i\mid Z_{i-1},\dots ,Z_{i-k},X_t).$$

Applying assumption 2, we can further decompose the joint likelihood into vertex and adjacency components, the latter written as products over individual edge variables:

$$\begin{array}{l}=\prod _{i=k}^{t}Pr(Y_i=y_i\mid V_i,Z_{i-1},\dots ,Z_{i-k},X_t)\times Pr(V_i=v_i\mid Z_{i-1},\dots ,Z_{i-k},X_t)\\ =\prod _{i=k}^{t}Pr(V_i=v_i\mid Z_{i-1}\dots ,Z_{i-k},X_t)\times {\prod }_{i=k}^t{\prod }_{(g,h)\in V_i^2}Pr(Y_{\mathit{igh}}=y_{\mathit{igh}}\mid V_i,Z_{i-1},\dots ,Z_{i-k},X_t).\end{array}$$ (A1)

Homogeneity assumptions 3 and 4 allow the above to be written in terms of the pmfs f_V and f_Y :

$$={\prod }_{i=k}^t{f}_V(v_i\mid Z_{i-1},\dots ,Z_{i-k},X)\times {\prod }_{i=k}^t{\prod }_{(g,h)\in V_i^2}{f}_Y(y_{\mathit{igh}}\mid V_i,Z_{i-1},\dots ,Z_{i-k},X_t),$$

which, by the completeness of the exponential family representation for binary variables, leads us to

$$\prod _{i=k}^t[f_V(v_i\mid Z_{i-1},\dots ,Z_{i-k},X_t)\times {\prod }_{i=k}^t{\prod }_{(g,h)\in V_i^2}B\left(Y_{\mathit{tij}}\mid {\text{logit}}^{-1}({\mathrm{\theta }}^{T}u(g,h,V_i,Z_{i-1},\dots ,Z_{i-k},X_t))\right).$$ (A2)

Thus, each adjacency snapshot is conditionally a logistic network model, and it is separable from the likelihood of V.

A.2. Part 2: Vertex Dynamics

As we did with the edge case, we begin with a series of assumptions:

• 5There exists some finite set V_max such that V_i ⊆ V_max for all i ∈ 1, …, t.
• 6V_i is independent of Z_i−k−δ given Z_i−1, …, Z_i−k, X_t for all δ>0.
• 7 (g ∈ V_i) is independent of (h ∈ V_i) given Z_i−1, …, Z_i−k, X_t for all g ≠ h.
• 8Let f_{V, i} be the conditional pmf of inclusion for some vertex i in some V_j. Then, given any realizable v₁, v₂, …, v_k, for all i ∈ 1, …, t and all g, h ∈ V_max,

$$f_{V_g}(\mathbb{I}(g\in V_i)=1\mid Z_{i-1}=Z_{i-1},\dots ,Z_{i-k}=Z_{i-k},X_t=x_t)=f_{V_h}(\mathbb{I}(h\in V_i)=1\mid Z_{i-1}=Z_{i-1},\dots ,Z_{i-k}=Z_{i-k},X_t=x_t).$$ (A3)

With assumptions 5 through 8 and the exponential family argument applied earlier, we may rewrite the left side of equation (A2):

$$\begin{array}{l}{f}_V(V_i\mid V_{i-1},\dots ,V_{i-k},X_t)=\prod _{i=k}^t\prod _{g\in V_{\mathit{max}}}{f}_V(\mathbb{I}(g\in V_i)\mid V_{i-1},\dots ,V_{i-k},X_t)\\ =\prod _{i=k}^t\prod _{g\in V_{\mathit{max}}}B(\mathbb{I}(g\in V_i)\mid {\text{logit}}^{-1}({\mathrm{\psi }}^{T}w(g,V_{i-1},\dots ,V_{i-k},X_t))).\end{array}$$ (A4)

Thus, with these additional constraints, we acquire a dual-logistic structure. We may then summarize the likelihood of the vertex portion of the model and the edge portion of the model in separable terms. The vertex likelihood is given by

$$Pr(V_t\mid Z_{t-1},\dots ,Z_{t-k},X)=\prod _{i=1}^{n}B(\mathbb{I}(v_i\in V_t)\mid {\text{logit}}^{-1}({\mathrm{\psi }}^{T}w(i,Z_{i-1},\dots ,Z_{i-k},X)))$$ (A5)

and the edge likelihood by

$$Pr(Y_t\mid V_t,Z_{t-1},\dots ,Z_{t-k},X)=\prod _{(i,j)\in V_t\times V_t}^{n}B(Y_{\mathit{tij}}\mid {\text{logit}}^{-1}({\mathrm{\theta }}^{T}u(i,j,V_t,Z_{i-1},\dots ,Z_{i-k},X))),$$ (A6)

with the joint likelihood being the product of the two. A useful computational side effect of this is that we may use a single logistic routine to fit the entire model, using the augmented vector of the adjacency matrix and the temporal vertex indicator set (equations A5 and A6).

APPENDIX B. Sufficient Statistics for the Beach Model

As with other exponential family models, we capture the effects of putative mechanisms through statistics that (together with their associated parameters) determine the probability that an edge or vertex will appear at a given point in time. In describing these statistics, we use the following notation. Within this section, t, i, and j jointly index the adjacency structure, for example, so that Y_tij represents the edge between the ith and jth vertices of V_max at time t. Time itself is indexed in integer increments from 1, …, T, for example, T = 31 for the beach network. We use w as the generic function for a sufficient statistic in the vertex set model and u as a generic function for the sufficient statistic in the edge set model.

We will frequently use k to represent lags, for example, with Y_t−k representing the state of the edge set at time t − k. The vertex and edge statistics within the model follow the basic form of Appendix A, with $w_{tp}^{.}(V,Y,X)$ being a generic function for a statistic at vertex p, and $u_{\mathit{tij}}^{.}(V,Y,X)$ being a generic function for a statistic at edge ij. Notice that in this context, V is the vertex set, Y is the adjacency matrix, and X is a generic placeholder for the covariate matrix (each of these terms may vary with time t). For the beach data, we use certain specific forms for the X variable. In some cases, we will express X in terms of component parts: X = (X^r, X^δ, …), that is, relevant covariates for a vertex or edge. For example, in the beach data, $X_p^r$ is a dichotomous variable for whether v_p is a regular (r) or an irregular (δ); $X_{ij}^{.}$ is a dichotomous variable for whether edge ij is regular (r), irregular (δ), or regular to irregular and vice versa (ϕ); and $X_{tp}^d$ is the day (Monday, …, Sunday) at time t for vertex v_i, and $X_{\mathit{tij}}^d$ is the day at time t for edge ij. For simplicity in notation, we also define two measures: (1) τ_tp = the count of triangles within which v_p is embedded at time t, and (2) ${\mathrm{\zeta }}_{\mathit{tij}}^{\mathrm{\epsilon }}$ = the count of ε-length cycles within which edge ij is embedded. Detailed descriptions of the sufficient statistics used in section 5 follow in the next two subsections.

B.1. Vertex Statistics

B.1.1. Vertex statistic 1

We use a series of dummy variables for whether an individual is in the regular category or in the group 1 category. We express this statistic in the following manner:

$$w_{tp}^r(V,Y,X)=X_p^r,$$ (B1)

where X is a dichotomous variable (i.e., 1 if in the group and 0 otherwise), p represents the index for vertex, and r represents the group (i.e., regular or group 1).

B.1.2. Vertex statistic 2

For the inertial mechanism, we use a single lag term with the basic interpretation that if this weight is positive, an individual is more likely to appear on a given day if he or she was at the beach the day before (i.e., 1 if the focal actor was present at time t − k and 0 otherwise). We express this statistic in the following manner:

$$w_{tp}^l(V,Y,X)=\mathbb{I}\{v_p\in V_{t-k}\},$$ (B2)

where is an indicator function, p is the vertex index, and t − k is lag term (k is 1 in the model in section 5).

B.1.3. Vertex statistic 3

For the triangle effect, we use a log of the three-cycle lag statistic with the interpretation that a vertex is more likely to appear on a given day if it was embedded in a triangle relation the day before (i.e., we count the number of three-cliques in which the focal actor participated at time t − k). We express this statistic in the following manner:

$$w_{tp}^{\mathrm{\Delta }}(V,Y,X)=log({\mathrm{\tau }}_{t-k,p}),$$ (B3)

where τ is count of three-cliques in which the focal actor participated at time t − k for vertex p (k is 1 in the model in section 5).

We use a dummy variable for each day of the week, thus allowing for a higher or lower likelihood of every individual appearing on a given day of the week (seasonality in this case represents the intercept or baseline term in this model). We express this statistic in the following manner:

$$w_{tp}^s(V,Y,X)=(\mathbb{I}\{X_{tp}^d=\mathit{Monday}\},\dots ,\mathbb{I}\{X_{tp}^d=\mathit{Sunday}\}),$$ (B4)

where is an indicator function, and $X_{tp}^d$ is variable representing the day of the week at time t for vertex p.

B.2. Edge Statistics

B.2.1. Edge statistic 1

The mechanism of assortative mixing between regulars and irregulars is implemented as a series of three dummy statistics. We express this statistic in the following manner:

$$u_{\mathit{tij}}^r(V,Y,X)=X_{ij}^r,$$ (B5)

$$u_{\mathit{tij}}^{\mathrm{\delta }}(V,Y,X)=X_{ij}^{\mathrm{\delta }},\text{and}$$ (B6)

$$u_{\mathit{tij}}^{\mathrm{\varphi }}(V,Y,X)=X_{ij}^{\mathrm{\varphi }},$$ (B7)

where the first statistic (denoted r) represents the baseline effect of regular-to-regular interaction, the second statistic (denoted δ) represents irregular-to-irregular interaction, and the last statistic (denoted ϕ) represents regular-to-irregular (and vice versa) interaction. It is worth pointing out that this term stands in place of the standard intercept term in this model.

B.2.2. Edge statistic 2

The mechanism of individual-level heterogeneity is implemented as a dummy variable for the regular group members who are also the most frequent attendees.⁷ We express this statistic in the following manner:

$$u_{\mathit{tij}}^h=\mathbb{I}\{v_{i}or{v}_j\in \text{Regular}\text{and}\text{frequent}\},$$ (B8)

where is an indicator function for whether vertex i or vertex j is in the regular group and appears more than f times over a given time period.

B.2.3. Edge statistic 3

The mechanism of contagious participation is implemented as a density effect that changes dynamically on the basis of the log of the number of individuals at the beach on the given day of interest (making use of the fact that, because each day’s edge realization is conditioned on that day’s vertex set, properties of the latter can be used to predict the former). We express this statistic in the following manner:

$$u_{\mathit{tij}}^c(V,Y,X)=log(\mid V_t\mid ),$$ (B9)

where |V_t| is the size of the vertex set at time t. We use log function to ensure numerical stability in our optimization routine.⁸

B.2.4. Edge statistic 4

The mechanism of inertia is implemented as a single lag term. We express this statistic in the following manner:

$$u_{\mathit{tij}}^l(V,Y,X)=Y_{t-k,ij},$$ (B10)

where Y is the ij edge at time t − k (k is 1 in the model in section 5).

B.2.5. Edge statistic 5

The embeddedness effect is implemented as the log of the dyadic count of the number of cycles (up to nine) of the lagged network, with the interpretation that a dyadic interaction is more or less likely if the edge existed yesterday and was in more or fewer cycles (depending on the sign of the weight). We express this statistic in the following manner:

$$u_{\mathit{tij}}^e(V,Y,X)=log({\mathrm{\zeta }}_{t-k,ij}^{\mathrm{\epsilon }}+1),$$ (B11)

where ζ is the count of cycles (up to ε) that edge ij at time t − k is embedded (k is 1, and ε is 9 in the model in section 5). We use log function again for numerical stability in our optimization algorithm.

B.2.6. Edge statistic 6

Seasonality is again implemented as a series of dummy variables for each day of the week (seasonality in this case represents the intercept or baseline term in this model). We express this statistic in the following manner:

$$u_{\mathit{tij}}^s(V,Y,X)=\mathbb{I}(\{X_{\mathit{tij}}^d=\mathit{Monday}\},\dots ,\mathbb{I}\{X_{\mathit{tij}}^d=\mathit{Sunday}\}),$$ (B12)

where is an indicator function, and $X_{tp}^d$ is variable representing the day of the week at time t for vertex p.