Improving Simulation-Based Algorithms for Fitting ERGMs

Abstract

Markov chain Monte Carlo methods can be used to approximate the intractable normalizing constants that arise in likelihood calculations for many exponential family random graph models for networks. However, in practice, the resulting approximations degrade as parameter values move away from the value used to define the Markov chain, even in cases where the chain produces perfectly efficient samples. We introduce a new approximation method along with a novel method of moving toward a maximum likelihood estimator (MLE) from an arbitrary starting parameter value in a series of steps based on alternating between the canonical exponential family parameterization and the mean-value parameterization. This technique enables us to find an approximate MLE in many cases where this was previously not possible. We illustrate these methods on a model for a transcriptional regulation network for E. coli, an example where previous attempts to approximate an MLE had failed, and a model for a well-known social network dataset involving friendships among workers in a tailor shop. These methods are implemented in the publicly available ergm package for R, and computer code to duplicate the results of this paper is included in the Supplemental Materials.

1 Introduction

Networks are a form of relational data, often represented as a set of pairs of individuals, called nodes, where each pair may be directed or undirected and is called an arc or an edge, respectively. Examples of networks include disease contact networks, where the nodes are individuals and the edges indicate some type of physical contact, and friendship networks, where the nodes are school students and an arc indicates that one student considers another to be a friend. These two examples are far from exhaustive; networks can involve all kinds of individuals, groups, organizations, objects, or concepts, and the scientific literature on networks is massive and growing quickly.

This article focuses on maximum likelihood estimation for a class of statistical network models called exponential-family random graph models (ERGMs). A large literature on ERGMs exists; for an introduction, we refer the interested reader to the survey article of Robins et al. (2007a) and the many references therein. Here, we present only the basic mathematical groundwork necessary to make this article self-contained.

We define the class of ERGMs for simple (no repeated edges), loopless (no self-edges) networks as follows:

$$P_{\mathit{\eta }}(\mathbf{Y}=\mathbf{y})=\frac{exp\{{\mathit{\eta }}^t\mathbf{g}(\mathbf{y})\}}{\kappa (\mathit{\eta })},\mathbf{y}\in \mathcal{Y},$$ (1)

where Y is a random network written as an adjacency matrix so that Y_ij is the indicator of an edge from node i to node j; g(y) is a vector of the network statistics of interest, which may include covariates that are measured on the nodes; η is the vector of parameters measuring, in some sense, the strengths of the effects of the corresponding entries in the vector g(y); κ(η) is the constant of proportionality that makes the probabilities sum to one; and is the space of allowable networks. Typically, 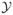includes only networks on a specific set of nodes; in particular, this means that each element of 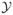typically has the same number of nodes. Letting n denote this number, we may always refer to Y as an n × n matrix of zeros and ones. For simplicity, we assume throughout this article that Y is undirected; that is, Y_ij = Y_ji, and so we will use the convention that i < j whenever we write Y_ij. There is no difficulty in extending our methods to directed networks.

Given an observed network y^obs, the log-likelihood function

$$\ell (\mathit{\eta })={\mathit{\eta }}^{\top }\mathbf{g}({\mathbf{y}}^{\text{obs}})-log\kappa (\mathit{\eta })$$ (2)

is, in general, very difficult to maximize due to the intractability of κ(η), which is evidently equal to the sum of exp{η^tg(y)} for all possible networks y. Since there may be $2^{\left(\begin{array}{c}n\\ 2\end{array}\right)}$ such networks even in the undirected case, κ(η) is not computable directly unless some mathematical simplification is possible. Nevertheless, approximate maximum likelihood may be accomplished using a simulation-based method as described by Geyer and Thompson (1992). Typically, such methods rely on Markov chain Monte Carlo (MCMC) to simulate random networks. We describe a standard MCMC algorithm and explain how approximate maximum likelihood estimation (MLE) may proceed in Section 2.

This article suggests two qualitatively distinct improvements to a standard MCMC MLE algorithm as described in Geyer and Thompson (1992). First, the standard approximation is replaced by a lognormal-based approximation. Second, we describe a “stepping” algorithm that moves step-by-step toward a maximizer of the loglikelihood. Though our improvements are still MCMC MLE algorithms and therefore rely on randomly simulated networks, we stress that this article does not discuss improvements to the MCMC sampler used for this purpose. In fact, as we demonstrate in Section 3, even a perfectly efficient sampler applied to the simplest of all network models cannot overcome the flaws inherent in the standard MCMC MLE method.

After describing the basic MCMC MLE idea and introducing a lognormal approximation to the loglikelihood (Section 2), we illustrate a major downfall of the basic method using a simple network model in Section 3. We then introduce a new “stepping” algorithm in Section 4 and discuss standard error estimation in Section 5. Finally, we demonstrate our methods on both the simplistic model used earlier (Section 6) and two network datasets from the literature (Section 7).

2 Approximate maximum likelihood estimation methods

Any approximate MLE method based on simulation relies on some form of random sampling of networks. Typically, this sampling is accomplished via MCMC based on the following derivation. For a particular ordered pair (i, j), we denote by ${\mathbf{Y}}_{ij}^c$ all entries in Y except for Y_ij. Furthermore, ${\mathbf{Y}}_{ij}^{+}$ and ${\mathbf{Y}}_{ij}^{-}$ are the networks obtained from Y by replacing Y_ij by 1 and 0, respectively. Calculating the odds from (1) of setting a particular Y_ij to 1 or 0 conditional on the rest of the network ${\mathbf{Y}}_{\mathbf{ij}}^{\mathbf{c}}$, we obtain

$$\frac{P_{\mathit{\eta }}(Y_{ij}=1\mid {\mathbf{Y}}_{ij}^c={\mathbf{y}}_{ij}^c)}{P_{\mathit{\eta }}(Y_{ij}=0\mid {\mathbf{Y}}_{ij}^c={\mathbf{y}}_{ij}^c)}=\frac{exp\{{\mathit{\eta }}^{\top }\mathbf{g}({\mathbf{y}}_{ij}^{+})\}}{exp\{{\mathit{\eta }}^{\top }\mathbf{g}({\mathbf{y}}_{ij}^{-})\}}=exp\{{\mathit{\eta }}^{\top }{\mathit{\delta }}_g{(\mathbf{y})}_{ij}\},$$ (3)

where ${\mathit{\delta }}_g{(\mathbf{y})}_{ij}=\mathbf{g}({\mathbf{y}}_{ij}^{+})-\mathbf{g}({\mathbf{y}}_{ij}^{-})$ denotes the change in g(y) when yij is changed from 0 to 1 and is sometimes called the vector of change statistics (Wasserman and Pattison, 1996). Equation (3) may be exploited to define a Markov chain with stationary distribution (1); the particular MCMC sampler we use is the one described by Hunter et al. (2008b) and implemented in the ergm package (Handcock et al., 2011) for R (R Development Core Team, 2010).

For certain choices of the g(y) vector, the indicators Y_ij are independent; that is, $P(Y_{ij}=1)=P(Y_{ij}=1\mid {\mathbf{Y}}_{ij}^c={\mathbf{y}}_{ij}^c)$ for all i < j. In such cases, we can estimate η simply by logistic regression with odds as defined in (3); that is, the vector of predictors for response Y_ij is δ_g (y^obs)_ij for each i < j. The resulting log-likelihood in this special case can be written as

$$\ell (\mathit{\eta })=\underset{i<j}{\sum \sum }[y_{ij}^{\text{obs}}{\mathit{\eta }}^{\top }{\mathit{\delta }}_g{({\mathbf{y}}^{\text{obs}})}_{ij}-log(1+exp\{{\mathit{\eta }}^{\top }{\mathit{\delta }}_g{({\mathbf{y}}^{\text{obs}})}_{ij}\})].$$ (4)

When the Y_ij are not independent, formula (4) is no longer the log-likelihood, but is called the (logarithm of the) pseudolikelihood, and its maximizer is the Maximum Pseudolikelihood Estimator, or MPLE. As discussed in Geyer and Thompson (1992), Robins et al. (2007a), and van Duijn et al. (2009), the MPLE can perform badly in some cases.

Since the behavior of the MPLE is unpredictable, it is preferable to maximize the true log-likelihood function (2) rather than the pseudolikelihood function. This is rarely an option in practice; for a network of more than a few nodes, the mere evaluation of the normalizing constant κ(η) is computationally intractable, and direct maximization over η is therefore impossible. An indirect alternative arises if we fix an arbitrary parameter value η₀ and note that for all η,

$$\ell (\mathit{\eta })-\ell ({\mathit{\eta }}_0)={(\mathit{\eta }-{\mathit{\eta }}_0)}^{\top }\mathbf{g}({\mathbf{y}}^{\text{obs}})-log{E}_{{\mathit{\eta }}_0}[exp\{{(\mathit{\eta }-{\mathit{\eta }}_0)}^{\top }\mathbf{g}(\mathbf{Y})\}],$$ (5)

where E_η0 denotes expectation with respect to the mass function (1) with η = η₀. A technical detail that we do not discuss in this article is the fact that when g(y^obs) happens to lie on the boundary of the convex hull of the set {g(y) : y ∈ 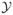} of all possible statistics, the MLE does not exist. This phenomenon is quite well-understood and is described in detail by Rinaldo et al. (2009) and Geyer (2009). It is qualitatively different from the vexing issue of model degeneracy, which we address in Section 7.1.

As first suggested in Geyer and Thompson (1992) and later developed for ERGMs by Snijders (2002), Robins and Pattison (2005), and Hunter and Handcock (2006), we can exploit equation (5) by randomly sampling networks Y₁, …, Y_m from P_η0 and approximating

$$\ell (\mathit{\eta })-\ell ({\mathit{\eta }}_0)\approx {(\mathit{\eta }-{\mathit{\eta }}_0)}^{\top }\mathbf{g}({\mathbf{y}}^{\text{obs}})-log\left[\frac{1}{m}\sum _{i=1}^{m}exp\{{(\mathit{\eta }-{\mathit{\eta }}_0)}^{\top }\mathbf{g}({\mathbf{Y}}_i)\}\right].$$ (6)

Iterating an approximate Fisher scoring method (Hunter and Handcock, 2006) until convergence gives a maximizer of the approximate log-likelihood ratio (6). We refer to Equation (6) is the “naive” approximation since it simply approximates a population mean by the sample mean. As Geyer and Thompson (1992) point out, this approximation is ineffective except for η close to η₀. We demonstrate in Section 3 how ineffective it can be even for a simplistic network.

One possibility for improving the approximation in Equation (6) arises from a loose distributional assumption that is reasonable in many cases. Suppose Z = (η − η₀)^⊤g(Y) is approximately normally distributed with mean μ = (η − η₀)^⊤m₀ and variance σ² = (η − η₀)^⊤Σ₀(η − η₀), where m₀ and Σ₀ are the mean vector and covariance matrix of g(Y) under P_η0. Then exp(Z) is lognormally distributed and log E_η(exp(Z)) = μ + σ²/2, which suggests

$$\ell (\mathit{\eta })-\ell ({\mathit{\eta }}_0)\approx {(\mathit{\eta }-{\mathit{\eta }}_0)}^{\top }[\mathbf{g}({\mathbf{y}}^{\text{obs}})-{\widehat{\mathbf{m}}}_0]-\frac{1}{2}{(\mathit{\eta }-{\mathit{\eta }}_0)}^{\top }{\widehat{\mathbf{\sum }}}_0(\mathit{\eta }-{\mathit{\eta }}_0),$$ (7)

which has maximizer ${\mathit{\eta }}_0+{\widehat{\mathbf{\sum }}}_0^{-1}[\mathbf{g}({\mathbf{y}}^{\text{obs}})-{\widehat{\mathbf{m}}}_0]$. In Equation (7), we take m̂₀ and Σ̂₀ to be the usual sample estimators of m₀ and Σ₀. Alternatively, we could use robust estimators to approximate log E_η(exp(Z)) based on μ̂ = median_1≤i≤m(η − η₀)^⊤g(Y_i) and

$${\widehat{\sigma }}^2=c\times {\text{median}}_{1\le i\le m}\mid {(\mathit{\eta }-{\mathit{\eta }}_0)}^{\top }\mathbf{g}({\mathbf{Y}}_i)-\widehat{\mu }\mid ,$$

where c is some appropriately chosen constant such as 1.483, the reciprocal median absolute value of a standard normal variable.

Regardless of the method of approximation used, the MCMC MLE approach gives values of ℓ(η) − ℓ(η₀) that are inaccurate unless η is near η₀, so using the maximizer of the approximation as an approximant of the true MLE η̂ can be perilous if η₀ lies far from η̂. In Section 4 we introduce a systematic method for moving closer to η̂ step by step.

3 Example: The Gilbert–Erdős–Rényi model

Proposed as early as Rapoport (1953), then later described independently by Gilbert (1959) and Erdős and Rényi (1959), this model assumes that all Y_ij are independent Bernoulli random variables with common mean b, so that the total number of edges in the network is binomial with parameters $N=\left(\begin{array}{c}n\\ 2\end{array}\right)$ and b.

The Gilbert–Erdős–Rényi model can be written as an ERGM by defining the scalar g(y) to be equal the number of edges of y. Since each edge exists independently with probability b,

$$P(\mathbf{Y}=\mathbf{y})={(b)}^{g(\mathbf{y})}{(1-b)}^{N-g(\mathbf{y})}={\left(\frac{b}{1-b}\right)}^{g(\mathbf{y})}{(1-b)}^N.$$ (8)

Setting e^η = b/(1 − b), Equations (8) and (1) match when we let κ(η) = (1 + e^η)^−N. To apply the simulation-based likelihood approximation methods of Section 2, we simply simulate g(y₁), …, g(y_m) as independent binomial random variables with parameters N and e^η₀/(1 + e^η₀).

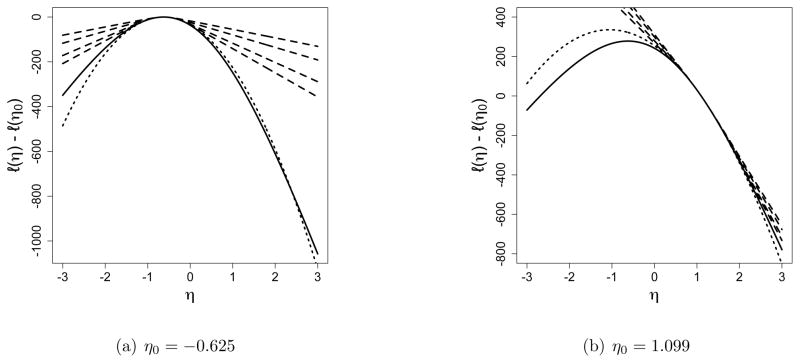
As an example, we consider a simulated 40-node network that has 272 edges out of a possible N = 780 dyads. The MLE for η in this case is η̂ = log(272/508) = −0.625. In our example, we may rewrite Equation (5) as

$$E_{{\eta }_0}[exp\{(\eta -{\eta }_0)g(\mathbf{Y})\}]=\sum _{j=0}^{780}{p}_{j}exp\{j(\eta -{\eta }_0)\},$$

where the p_j are simply the usual binomial probabilities. We may approximate (5) using the idea of Equation (6) but with an idealized sample of size m in which p_j is replaced by the closest multiple of 1/m to p_j. Figure 1 depicts the resulting approximations to (5) using various values of η₀ and m. Of particular note is that even for incredibly large m, such as m = 10¹⁵, the approximation to (5) is not good for η far from η_o. Also of note is that in Figure 1(b), even the enormous m = 10¹⁵ yields a sample consisting only of values larger than g(y^obs) = 272, so Equation (6) has no maximizer. Indeed, with η₀ = 1.099, a value like 272 is more than 25 standard deviations below the mean, so a random observation as extreme as 272 is exceptionally rare.

Figure 1.

Approximated values of ℓ(η) − ℓ(η₀). The solid line is the true loglikelihood (5), maximized at η̂ = −0.625. The dashed lines are Equation (6) with idealized sample sizes 10³, 10⁵, 10¹⁰, and 10¹⁵. The dotted line is Equation (7).

4 Partial stepping

The original MCMC MLE article by Geyer and Thompson (1992) recognized that “The theory of importance sampling leads to the conclusion that the best results are obtained when η₀ is near η̂.” (We have substituted our notation for theirs in the quotation.) Indeed, as demonstrated in Section 3 for even the simplest of exponential family models, the “arbitrary” value η₀ of equation (5) is not quite so arbitrary: The quality of approximations (6) and (7) degrades quickly as η moves away from η₀. As a remedy for this problem, Geyer and Thompson (1992) recommended maximizing the approximate loglikelihood subject to a restriction on the maximum allowable step, e.g., subject to ||η −η₀|| ≤ δ. However, they offered no guidance on how to choose an appropriate δ. In one numerical example, they state that all steps were constrained to a maximum step size of $\delta =\sqrt{2}$; however, they state that this value was “chosen arbitrarily, though several other runs showed it to be about the right size.” We do not use constrained optimization using a value of δ as suggested by Geyer and Thompson (1992). The alternative method that we introduce here is also a systematic method for moving η₀ closer to η̂ step by step, but it avoids the difficult problem of how to choose the δ parameter.

To explain our method, we first review a bit of exponential family theory. In common statistical parlance, the original ERGM parameterization (1), with η as parameter, is called the canonical parameterization. Standard theory (Barndorff-Nielsen, 1978; Brown, 1986) states that the MLE, if it exists, is the unique parameter vector η̂ such that E_η̂ g(Y) = g(y^obs). The so-called mean value parameterization is defined by ξ(η) = E_η(g(Y)). Therefore, calculating the maximum likelihood estimate using the ξ parameters is trivially easy: It is simply g(y^obs). However, this fact is of little practical value, since we cannot estimate standard errors or even simulate from the fitted model without knowing the inverse image η̂ of g(y^obs).

Our idea is to take partial steps toward g(y^obs) in mean value parameter space by pretending that the MLE is not g(y^obs) but rather some point in between g(y^obs) and our estimate of ξ(η₀). In the algorithm below, this intermediate point is denoted ξ̂_t at the tth iteration; because it will play the role of the observed data instead of g(y^obs), we may call it a “pseudo-observation”. This idea allows us to restrict our search for a maximizer of the approximate log-likelihood ratio, based on our pseudo-observation rather than the actual observed data, to a region where this approximation is reasonably accurate. As the algorithm proceeds, we will iteratively jump from canonical parameter space to mean value parameter space (by taking means of MCMC samples) and vice versa (by maximizing approximate log-likelihood functions) until we obtain a value of η₀ close enough to η̂ to allow one final MCMC-based maximization step.

Our algorithm proceeds as follows:

• Step 1: Set t, the iteration number, equal to zero and choose some initial parameter vector η₀. Often, η₀ is taken to be the MPLE.

• Step 2: Use MCMC to simulate samples Y₁, …, Y_m from P_ηt (Y).

• Step 3: Calculate the sample mean ${\overline{\mathit{\xi }}}_t=m^{-1}{\sum }_{i=1}^m\mathbf{g}({\mathbf{Y}}_i)$.

• Step 4: For some γ_t ∈ (0, 1], define the “pseudo-observation” ξ̂_t to be the convex combination

  $${\widehat{\mathit{\xi }}}_t={\gamma }_t\mathbf{g}({\mathbf{y}}^{\text{obs}})+(1-{\gamma }_t){\overline{\mathit{\xi }}}_t.$$ (9)
• Step 5: Replace g(y^obs) by ξ̂_t in Equation (6) or (7) and then maximize; in other words, in the case of Equation (7), let

  $$\begin{array}{l}{\mathit{\eta }}_{t+1}=arg\underset{\mathit{\eta }}{max}\left\{{(\mathit{\eta }-{\mathit{\eta }}_t)}^{\top }\left[{\widehat{\mathit{\xi }}}_t-{\overline{\mathit{\xi }}}_t\right]-\frac{1}{2}{(\mathit{\eta }-{\mathit{\eta }}_t)}^{\top }{\widehat{\mathbf{\sum }}}_t(\mathit{\eta }-{\mathit{\eta }}_t)\right\}\\ ={\mathit{\eta }}_t+{\widehat{\mathbf{\sum }}}_t^{-1}[{\widehat{\mathit{\xi }}}_t-{\overline{\mathit{\xi }}}_t],\end{array}$$ (10)

  where Σ̂ is an estimator of the covariance matrix of the g(Y_i) vectors.

• Step 6: Increment t and return to step 2.

The important decision to be made in step 4 is the choice of γ_t ∈ (0, 1]. If we decide to use approximation (6) instead of (7), then one important consideration is that γ_t must be chosen so that the resulting ξ̂_t is in the interior of the convex hull of the vectors g(Y₁), …, g(Y_m); otherwise, Equation (6) will have no maximizer. In practice, we use a modified version of this guideline, even when using approximation (7): We find the largest γ_t on a regular grid of points in (0, 1] such that even the point

$$1.05{\gamma }_t\mathbf{g}({\mathbf{y}}^{\text{obs}})+(1-1.05{\gamma }_t){\overline{\mathit{\xi }}}_t,$$ (11)

which is slightly farther from ξ̄_t than ξ̂_t of Equation (9), is in the interior of the convex hull of the sampled statistics. Ideally, we would like to be able to set γ_t = 1, and in fact when this is possible while simultaneously satisfying the convex hull criterion described here for two consecutive iterations, the “stepping” portion of the algorithm is judged to have converged. At this point, we may take η_t+1 to be the final MLE or, alternatively, simulate a much larger sample using this η_t+1 in one final iteration.

The question of whether the vector ξ̂_t is in the convex hull of the sample of vectors g(y₁), …, g(y_m) may be answered via the following linear programming problem (Fukuda, 2004):

$$\text{maximize}({\mathbf{z}}^{\top }{\widehat{\mathit{\xi }}}_t-z_0)\text{subject}\text{to}({\mathbf{z}}^{\top }\mathbf{g}({\mathbf{y}}_i)-z_0)\le 0\text{for}\text{all}i=1,\dots ,m.$$ (12)

Note that the maximum is always at least zero, since (z = 0, z₀ = 0) always satisfies the constraints. But if the maximum is strictly positive, then the hyperplane {x : z^⊤x = z₀} separates the sample points g(y_i) from the point ξ̂_t, so ξ̂_t cannot be in the convex hull of the sample points. In practice, we choose γ_t in Equation (9) as the largest value on a grid of points from 0 to 1 ensuring that ξ̂ is inside the convex hull of the sampled statistics, which we check in the ergm package by using the R interface to the GNU Linear Programming Kit package (Theussl and Hornik, 2010; Makhorin, 2006) to determine whether the maximizer in (12) is strictly positive. The computer code for all of the examples in this article is included in the Supplementary Materials.

5 Estimating Standard Errors

Standard error estimates for the approximate maximum likelihood estimator are necessary for performing statistical inference. Here, the error has two components: first is the usual error due to the sampling distribution, or the error inherent in estimating the true η by a maximizer of the likelihood function, η̂; and second is the MCMC error incurred when we approximate the true log-likelihood function using an equation such as (6) or (7) and accordingly approximate the true MLE, η̂, by an approximate MLE, which we denote here by η̃ to distinguish it from the true MLE. Using standard asymptotic theory, we estimate and invert the Fisher information matrix to estimate the sampling distribution error. The MCMC error is approximated as in Hunter and Handcock (2006); details are provided below.

For an exponential family, the Fisher information, I(η), is given by Var_ηg(Y). Furthermore, the variance of the sample statistics under η can be written Var_ηg(Y) = ∇² log κ(η), where κ(η) is the normalizing constant of equation (1). Hence, the inverse of the usual covariance matrix estimate for the sampling error is given by

$$\mathbf{I}(\widehat{\mathit{\eta }})={\text{Var}}_{\widehat{\mathit{\eta }}}(\mathbf{g}(\mathbf{Y}))={\nabla }^{2}log{\mathrm{E}}_{{\mathit{\eta }}_0}[exp\{{(\mathit{\eta }-{\mathit{\eta }}_0)}^{\top }\mathbf{g}(\mathbf{Y})\}]{\mid }_{\mathit{\eta }=\widehat{\mathit{\eta }}}.$$ (13)

Using the naive approximation for the required expectation as in (6), we obtain

$$\mathbf{I}(\widehat{\mathit{\eta }})\approx \widehat{\mathbf{I}}(\stackrel{\sim }{\mathit{\eta }})\stackrel{\text{def}}{=}\sum _{i=1}^m{w}_i\mathbf{g}({\mathbf{y}}_i){\mathbf{g}}^{\top }({\mathbf{y}}_i)-\left[\sum _{i=1}^m{w}_i\mathbf{g}({\mathbf{y}}_i)\right]{\left[\sum _{i=1}^m{w}_i\mathbf{g}({\mathbf{y}}_i)\right]}^{\top },$$ (14)

where the weights w_i ∝ exp{(η̃ − η₀)^⊤g(y_i)} are normalized so that Σ_i w_i = 1.

If we use the lognormal approximation as in (7), then simply Var_ηg(Y) ≈ Σ₀, the covariance for g(Y), which depends on η₀ but not η. This underscores the importance of choosing η₀ close to η̂, since both approximations to ℓ(η̂) − ℓ(η₀) are best when η₀ = η̂. Indeed, after the approximate MLE η̃ has been determined, it is sensible to estimate I(η̂) using the sample covariance for a separate sample g(Y₁), …, g(Y_m), drawn independently (or as close to independently as practical) from the distribution using η̃.

The approximate MCMC standard errors may be derived by first Taylor-expanding the approximate gradient around the point η̃:

$$\nabla \widehat{\ell }(\widehat{\mathit{\eta }})\approx \nabla \widehat{\ell }(\stackrel{\sim }{\mathit{\eta }})+{\nabla }^2\widehat{\ell }(\stackrel{\sim }{\mathit{\eta }})(\widehat{\mathit{\eta }}-\stackrel{\sim }{\mathit{\eta }})=0+{\nabla }^2\widehat{\ell }(\stackrel{\sim }{\mathit{\eta }})(\widehat{\mathit{\eta }}-\stackrel{\sim }{\mathit{\eta }}),$$

which results in

$$\sqrt{m}(\stackrel{\sim }{\mathit{\eta }}-\widehat{\mathit{\eta }})\approx -{[{\nabla }^2\widehat{\ell }(\stackrel{\sim }{\mathit{\eta }})]}^{-1}[\sqrt{m}\nabla \widehat{\ell }(\widehat{\mathit{\eta }})].$$ (15)

Conditional on the data, the true MLE is fixed and so Expression (15) measures the MCMC-based variability inherent in estimating η̂ by η̃. From expression (15), we obtain

$$\text{Var}(\stackrel{\sim }{\mathit{\eta }}\mid \text{data})\approx \frac{1}{\mathrm{m}}{[{\nabla }^2\ell (\stackrel{\sim }{\mathit{\eta }})]}^{-1}\text{Var}[\sqrt{\mathrm{m}}\nabla \widehat{\ell }(\widehat{\mathit{\eta }})]{[{\nabla }^2\widehat{\ell }(\stackrel{\sim }{\mathit{\eta }})]}^{-1}\approx \frac{1}{\mathrm{m}}{\left[\widehat{\mathbf{I}}(\stackrel{\sim }{\mathit{\eta }})\right]}^{-1}\stackrel{\sim }{\mathbf{V}}{\left[\widehat{\mathbf{I}}(\stackrel{\sim }{\mathit{\eta }})\right]}^{-1},$$ (16)

where

$$\stackrel{\sim }{V}=\frac{1}{m^2}{\left[\sum _{i=1}^{m}exp\left\{{({\mathit{\eta }}_0-\stackrel{\sim }{\mathit{\eta }})}^{\top }\mathbf{g}({\mathbf{Y}}_i)\right\}\right]}^2$$

is an estimate of the variance of $\sqrt{m}\nabla \widehat{\ell }(\widehat{\mathit{\eta }})$, assuming that the Y_i are drawn sufficiently far apart in the Markov chain to be considered roughly independent. See Geyer (1994) and Hunter and Handcock (2006) for additional details on the Ṽ estimator, in particular regarding how to take correlations between successive sampled points into account.

6 Application to a Gilbert–Erdős–Rényi model

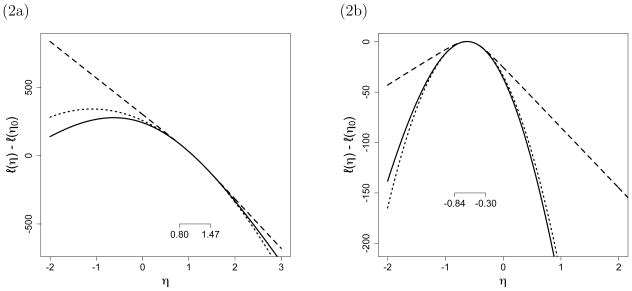
We illustrate our algorithm on the Gilbert–Erdős–Rényi example in Section 3. This network has 272 edges, with MLE η̂ = log(272/508) = −0.625. Starting from η₀ = 1.099 as depicted in Figure 1(b), corresponding to b₀ = .75, we sample 100 random binomial(780, b₀) variables, each of which can be viewed as the number of edges in a randomly generated Gilbert–Erdős–Rényi network with η₀ = 1.099. The mean of the sample is ξ̄₀ = 584.46, while the minimum and maximum are 556 and 616. As in Figure 1(c), the naive approximation (6) will not have a maximizer; this is due to the fact that g(y^obs) = 272 is not in the interval (556, 616).

With g(y^obs) = 272 and ξ̄₀ = 584.46, a simplistic step-halving scheme for selecting γ₀ proceeds by testing the midpoint 428.23 (corresponding to γ₀ = 1/2, followed by 506.35, 545.40, and finally 564.93 (corresponding to γ₀ = 1/4, 1/8, and 1/16) before finding a value of ξ̂₀ contained in (556, 616), which is the interior of the convex hull of sampled statistics in this case. We thus take ξ̂₀ = 564.93 as the new “observed” value of the network statistic and find the maximum of the corresponding (naive) log-likelihood ratio

$$\ell (\eta )-\ell ({\eta }_0)\approx (\eta -1.099)\times 564.93-log\left[\frac{1}{100}\sum _{i=1}^{100}exp\{(\eta -1.099)\times g({\mathbf{Y}}_i)\}\right].$$

This maximum occurs at η = 0.909, which becomes the value of η₁, and we iterate.

After 10 such iterations, we finally achieve ξ̂₁₀ = 272, which means that the random sample using η₁₀ = −0.571 includes values both larger and smaller than 272. Using the resulting value of η₁₁ = −0.632, we then take one final, much larger sample of size m = 10⁵ and, based on this sample, we find a final approximate MLE of η̂ = −.6246 (compared to the true MLE η̂ = −.625). In this example, this process took ten steps to find an η_t value that produced a sample containing η̂_∞. The first and last iterations of this process are depicted in Figure 2.

Figure 2.

The solid line is the true log-likelihood ratio function, the dotted line is Approximation (6), and the dashed line is Approximation (7). The values of η₀ are 1.099 in (a) and −0.571 in (b). Since the closed-form map from mean-value parameters ξ to canonical parameters η is known, the range of η values corresponding to the range of sampled statistics is shown as a short segment with its endpoints marked in each plot.

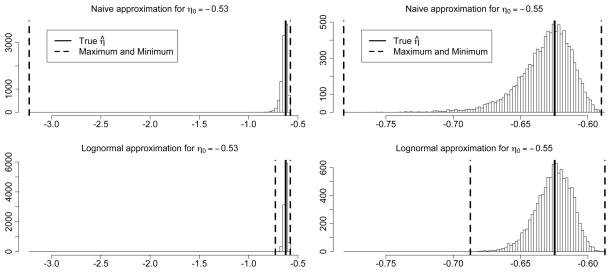
Figure 2 suggests that the naive approximation used in our illustration above might not perform as well as the lognormal approximation (7). In fact, Equation (7) in this example amounts to the normal approximation to the binomial. To compare the performance of the two approximations, we focus on the final step of our Gilbert–Erdős–Rényi example. Figure 3 shows histograms of 10,000 values of η̂ obtained from a hypothetical “final” step of the example, taking η₀ = −0.53 in the left column and η₀ = −0.55 in the right column.

Figure 3.

Distribution of the approximate MLE for the final step of the example, for the naive approximation (top) and the lognormal approximation (bottom), for η₀ = −.53 (on left) and η₀ = −.55 (on right). The thick dashed lines indicate the minimum and maximum values found by each approximation, and the thick solid line marks the true MLE.

The true MLE corresponding to g(y^obs) = ξ̂ = 272 is η̂ = −0.625. The approximations for several nearby values for η₀ are shown in Table 1. When η₀ = −0.625, the MLE, both estimates are quite similar, as are their variances. When η₀ moves away from the MLE, however, the estimate from the naive approximation deteriorates, and the standard deviation of the naive approximation begins to explode in comparison to the standard deviation of the lognormal approximation.

Table 1.

Compare means to the true MLE, −0.6246769. In some of the 10,000 samples drawn for each η₀, ξ̂ = g(y^obs) is not in the convex hull of the sampled statistics, so, when necessary, we show the results with these cases removed for both approximations.

η0	Sample size	Mean η̃naive	Mean η̃lognormal	StDev η̃naive	StDev η̃lognormal
−0.625	10000	−0.625	−0.625	0.0078	0.0077
v.57	10000	−0.628	−0.625	0.0134	0.0110
−0.56	10000	−0.629	−0.626	0.0162	0.0122
−0.55	10000	−0.632	−0.626	0.0199	0.0134
−0.54	10000	−0.635	−0.626	0.0267	0.0146
−0.53	10000	−0.639	−0.626	0.0422	0.0158
−0.52	9999	−0.647	−0.626	0.0728	0.0171
−0.51	9985	−0.660	−0.625	0.1158	0.0182
−0.5	9948	−0.683	−0.625	0.2069	0.0196
−0.45	6615	−0.979	−0.617	0.7830	0.0231
−0.4	1360	−1.106	−0.601	0.9614	0.0264

7 Application to network datasets

7.1 A biological network

Here, we consider the E. coli transcriptional regulation network of Shen-Orr et al. (2002), based on the RegulonDB data of Salgado et al. (2001) and depicted in Figure 4. This network is analyzed using ERGMs, along with other biological networks, by Saul and Filkov (2007). In this network, the nodes represent operons and the edges indicate a regulating relationship between two nodes. Specifically, a directed edge from A to B means that A encodes a transcription factor that regulates B. Self-regulation is possible and occurs for 59 nodes. We call these “self-edges” or simply “loops.”

Figure 4.

E. coli transcriptional regulation network of Shen-Orr et al. (2002), with self-regulating nodes depicted as triangles.

Although the network is directed and contains self-edges, here we will mimic the analysis of Saul and Filkov (2007) and treat it as undirected with 519 edges and 418 nodes, ignoring the self-loop information (the Saul and Filkov article deleted five of the original 423 nodes because they had no edges other than self-edges). For comparison, we then include an analysis that includes the self-loop information as a nodal covariate.

Saul and Filkov (2007) fit an ERGM in which the statistics g(y) are those listed in Table 2, though they used MPLE to produce parameter estimates because approximate maximum likelihood estimates proved unobtainable. We nearly duplicate their MPL estimates here, obtaining the results shown in column 3 of Table 2. It was not possible to duplicate the results exactly because Saul and Filkov (2007) do not report the value of the θ_s parameter they used for the GWDeg statistic, though we came close using θ_s = 3.75.

Table 2.

Model terms and MPLEs for the E. coli dataset of Shen-Orr et al. (2002). The first model is the model specified and fit in Saul and Filkov (2007). The second model is our adaptation to avoid issues of degeneracy.

Term(s)	Description:	Model 1	Model 2
Edges	# of Edges	2.82	−5.35
2-Deg	# of nodes with degree 2, D2(y)	−1.20	−2.58
3-Deg	# of nodes with degree 3, D3(y)	−1.75	−3.06
4-Deg	# of nodes with degree 4, D4(y)	−1.45	−2.39
5-Deg	# of nodes with degree 5, D5(y)	−1.34	−1.85
2-Star	# of pairs of edges with one end in common, S2(y)	0.01
GWDeg	Weighted sum of 1-Deg, 2-Deg, …, (n − 1)-Deg, with weights tending to 1 at a geometric rate: $u(\mathbf{y};{\theta }_s)=e^{{\theta }_s}{\sum }_{i=1}^{n-1}\left\{1-{(1-e^{{\theta }_s})}^i\right\}{D}_i(\mathbf{y})$ with θs = 3.75; with θs = 0.25	−3.89	8.13

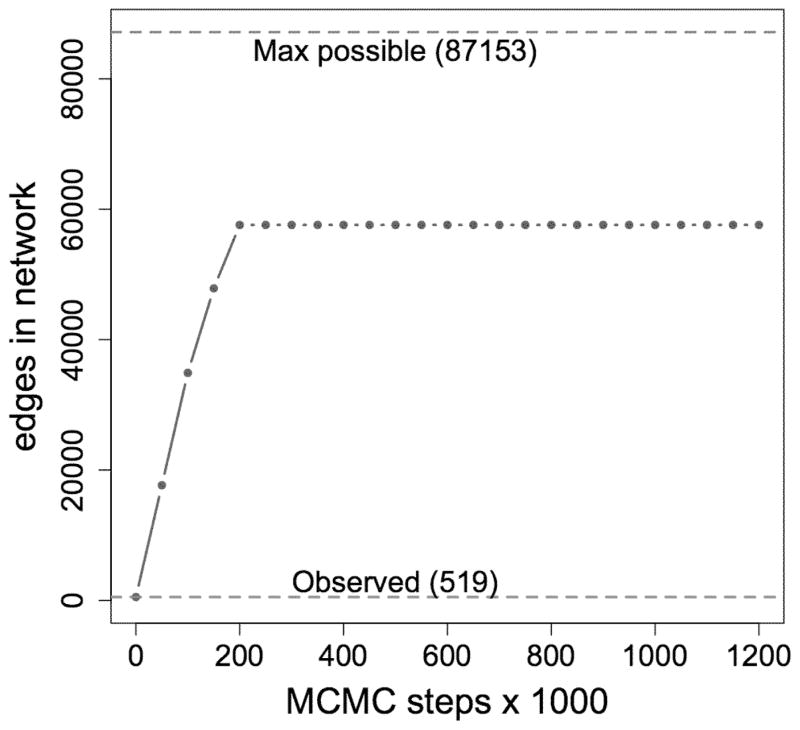
When we run a Markov chain to simulate from the first model of Table 2, we encounter problems: Figure 5 is a time-series plot of the edge-count of 25 networks sampled at intervals of 50,000 iterations from the Markov chain: The chain yields only networks that are very dense, nothing like the observed network. The problem here is the presence of the 2-star term in the model: For a high-degree node, adding one edge can increase the 2-star count by a lot. Thus, when the 2-star coefficient is positive as in this case, the Markov chain tends to favor networks with more and more edges. This problem, which afficts models that contain certain types of terms such as the 2-star, is called model degeneracy by Handcock (2003). A full treatment of the topic of degeneracy is beyond the scope of this article, but Schweinberger (2010) describes in detail how certain terms, when included among the g(y) statistics, have the effect of essentially reducing the dimension of the space of parameter values for which this degeneracy behavior does not occur. As a result, models containing these problematic terms essentially render simulation-based estimation methods useless. On the other hand, terms such as GWDeg (and GWESP and GWDSP as described in Section 7.2), when used with positive θ_s parameters as we have here, allow modelers to circumvent these vexing model degeneracy problems. Further discussion of the GWDeg, GWESP, and GWDSP terms is provided by Hunter (2007) and Robins et al. (2007b). Since Model 1 cannot be fit using simulation-based methods, we drop the 2-star term and fit a new model, using a different value of θ_s = 0.25 for the GWDeg term.

Figure 5.

The model including a 2-star term and fit using MPLE produces unrepresentative random networks.

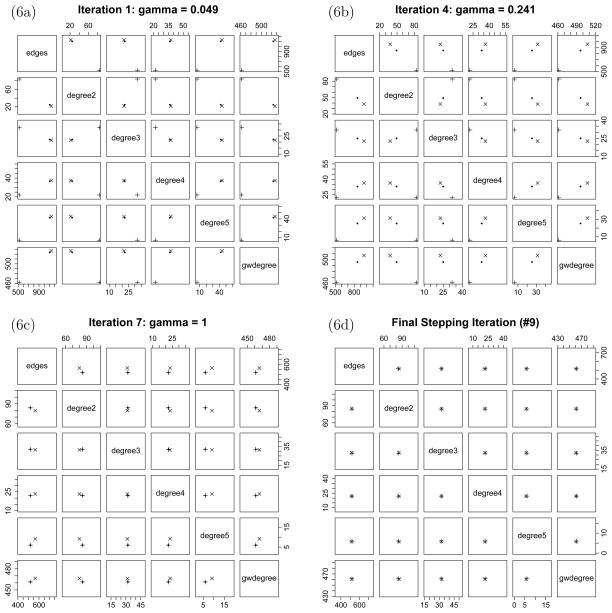
Taking the MPLE as the inital value η₀ in fitting Model 2, the stepping procedure using the lognormal approximation (7) finds an approximate MLE in seven stepping iterations, plus a final iteration using the true observed statistics (see Figure 6). The naive approximation (6) gives parameter estimates very similar to those of the lognormal approximation, so we omit them from Table 3, which also gives standard error estimates. There is a large discrepancy between the MPLE and the approximate MLEs. In addition, it is apparent in Figure 6a that the sample generated from the MPLE does not correspond very closely to the observed statistics. In contrast, Figure 6d shows that the mean of the sample generated from the approximate MLE is quite close to the observed statistics.

Figure 6.

Plots of the sampled statistics from selected iterations, showing that ξ̂_t (the black dot) is moving from the mean of the sample (the x) towards the observed statistics (the plus) without leaving the convex hull of the sample. In the final plot, ξ̂_t is always the same as the observed statistics and so it is not plotted.

Table 3.

Approximate MLEs (with standard errors and MCMC standard errors in parentheses) obtained using the stepping algorithm and the lognormal approximation (7). Model 2 is based on the analysis of Saul and Filkov (2007) but omits the problematic 2-star term.

Parameter	Model 2	Model 2 plus self-edges
Edges	−5.07 (0.027, 0.012)	−5.83 (0.067, 0.013)
2-Deg	−1.47 (0.126, 0.025)	−1.36 (0.141, 0.014)
3-Deg	−2.36 (0.192, 0.027)	−2.03 (0.206, 0.010)
4-Deg	−2.30 (0.229, 0.020)	−1.79 (0.239, 0.009)
5-Deg	−2.91 (0.415, 0.183)	−2.32 (0.409, 0.035)
GWDeg(.25)	1.86 (0.174, 0.094)	2.32 (0.336, 0.050)
noself↔self	—	1.55 (0.037, 0.0002)
self↔self	—	1.21 (0.118, 0.002)

Although Saul and Filkov (2007) did not use the self-regulation information in the E. coli dataset, we may consider it in a simplistic manner by adding two additional terms to Model 2. The noself↔self and self↔self coefficients are estimates of the additional log-odds of an edge corresponding to node pairs in which one is a self-regulator and the other is not, in the first case, and in which both are self-regulators, in the second. Here, the case in which neither node is a self-regulator serves as a “baseline” to which the other cases are compared. This analysis could be improved if the MCMC algorithm were expanded to allow for the creation and deletion of self-edges, since currently the sample space 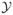of possible networks disallows these loops. Since the ergm package does not currently allow for this type of simulation, we do not present such an analysis here.

7.2 A Sociological Dataset

We analyze a well-known social network dataset involving “sociational” (friendship and socioemotional) interactions among a group of 39 workers in a tailor shop in Zambia. The data were collected from June 1965 to August 1965, the first of two time periods during which Kapferer (1972) collected data on these individuals; but we do not analyze the dataset for the second period here. In fact, there are actually 43 individuals in the network for the first time period, but we only consider the 39 who occur in both time periods here (missing are the workers named Lenard, Peter, Lazarus, and Laurent), since the smaller dataset is much better-known. In this network, an edge between two individuals indicates an interactional relationship, which in most cases is a reciprocal relationship. Originally, Kapferer also recorded some asymmetrical interactional relationships in which one individual received more than he gave; however, here we simply consider such asymmetric relationships as symmetric, which is common practice for this particular dataset.

This network has of 158 edges, which means it has density $158/\left(\begin{array}{c}39\\ 2\end{array}\right)=0.213$ and average degree 158/39 = 4.05. Typically, increasing the number of nodes of a social network does not dramatically increase the average degree, which means that larger networks tend to have smaller densities. Yet they also tend to be harder to fit using MCMC MLE techniques due to the fact that the Markov chain cannot easily visit as large a proportion of the sample space. On the other hand, for degenerate models, even small networks can cripple MCMC MLE algorithms. In addition to the 2-star term described in Section 7, terms such as the number of k-stars (for general k > 2) and the number of triangles can also result in degeneracy, as explained in Schweinberger (2010). Thus, ERG models containing these terms are not viable despite their theoretical appeal (Frank and Strauss, 1986).

Alternatives to these terms are introduced by Snijders et al. (2006) and expressed by Hunter (2007) as the “geometrically weighted” terms GWDegree, GWESP, and GWDSP. Roughly speaking, these terms capture the spread of the degree distribution, the tendency to transitive closure, and the preconditions for transitivity, respectively. More detailed explanations of these terms are given by Snijders et al. (2006), where they are discussed in their alternative forms: alternating k-stars, alternating k-triangles, and alternating k-twopaths, respectively. For now, we mention only that these geometrically weighted statistics are shown by Schweinberger (2010) to lead to models free from degeneracy as long as the special parameter associated with each term is greater than −ln 2. In the models that follow, we set these parameters at 0.25 for each of the three statistics.

We illustrate the use of the GWDegree, GWESP, and GWDSP terms in a model by providing R commands and output that can be used to fit a model with these four terms, along with the edges terms. These commands are intended to be used in conjunction with the ergm package version 2.4-3:

> data(kapferer)
> kformula <- kapferer ~ edges + gwdegree(0.25, fixed=TRUE) +
                         gwesp(0.25, fixed=TRUE) + gwdsp(0.25, fixed=TRUE)
> kap1 <- ergm(kformula, maxit=1, seed=123,
           control=control.ergm(stepMCMCsize=1000,
           style=“Stepping”, metric=“lognormal”))
> summary(kap1)
...
Monte Carlo MLE Results:
                 Estimate  Std. Error  MCMC s.e.  p-value
edges            -3.17598   0.05925       0.058   <1e-04 ***
gwdegree         0.43127   1.08510       1.868    0.691
gwesp.fixed.0.25   1.53531   0.02042       0.010   <1e-04 ***
gwdsp.fixed.0.25   -0.11757   0.00636      0.000   <1e-04 ***

The output reveals that the GWDegree effect does not appear to be statistically significant; thus, we may refit the model without this term:

> kformula2 <- kapferer ~ edges + gwesp(0.25, fixed=TRUE) +
                          gwdsp(0.25, fixed=TRUE)
> kap2 <- ergm(kformula2, maxit=1, seed=123,
           control=control.ergm(stepMCMCsize=1000,
           style=“Stepping”, metric=“lognormal”))
> summary(kap2)
...
Monte Carlo MLE Results:
                 Estimate  Std. Error  MCMC s.e.  p-value
edges           -3.016163  0.455807       0.384   <1e-04 ***
gwesp.fixed.0.25   1.444937  0.322320       0.272   <1e-04 ***
gwdsp.fixed.0.25  -0.123964  0.006169       0.000   <1e-04 ***

Roughly speaking, these parameter values reveal a propensity to completion of triads in this network but no overall tendency to form two-paths except those that lead to completed triads. These models are each fit using the stepping algorithm together with the lognormal approximation to the log-likelihood.

7.3 Comparison with standard MCMC MLE

A standard Markov chain Monte Carlo algorithm for finding approximate maximum likelihood estimates, implemented in the ergm package, simply attempts to maximize equation (6), where η₀ is the parameter vector defining the stationary ERGM distribution of the networks generated by the Markov chain Y₁, …, Y_m. Once the maximizer, say η̂, is found, it becomes the value of η₀ for the next iteration of the algorithm. One of the modifications suggested here is to replace equation (6) by (7). The other is the stepping idea that replaces the observed statistics in the approximate loglikelihood by an alternative vector of statistics that is closer to the observed sample mean of the statistics.

It is difficult to succinctly and fairly compare an algorithm employing both modifications with a standard MCMC MLE procedure. For example, the number of iterations that should be employed in a standard MCMC MLE algorithm, or an algorithm using equation (7) without the stepping idea, is a bit of an open question. The ergm package default value of three iterations is almost certainly too low for some applications, though it is easy to override the default when using this software. On the other hand, our stepping method provides a relatively simple criterion: As explained following Equation (11), convergence is declared whenever the vector of observed statistics is well within the convex hull of the randomly η₀-generated statistics.

For the Kapferer dataset using either of the two models considered in Section 7.2, both a standard MCMC MLE algorithm and a modified algorithm replacing Equation (6) by (7) produce reasonable parameter estimates. Here, “reasonable” is a vague term, construed essentially to mean that networks generated from the estimated model have statistics that surround the observed network statistics. We use this concept since, in the context of this article, finding parameter values with this property is an intermediate goal of the proposed methods. It is also possible to define alternative notions of reasonableness of estimates, such as the related but more general notion of “goodness of fit” explored in Hunter et al. (2008a). However, this notion encompasses not only the quality of the coefficient estimate but the appropriateness of the model statistics themselves, so we do not explore it here.

In contrast, Model 2 for the E. coli dataset of Section 7.1 creates serious problems for the standard MCMC MLE algorithm, and increasing the number of iterations does not help. The standard algorithm, using the MPLE as the starting value of η₀, is essentially not applicable to this problem. Substituting approximation (7) for (6), however—which is actually currently default behavior for the $\stackrel{̑}{\text{er}}\text{gm}$ function in the ergm package—does work, though typically only after quite a few iterations. This phenomenon is illustrated in Figure 7, where we see two figures side by side, showing the edge and gwdegree statistics for 500 randomly generated networks using the parameter values obtained after fifteen iterations (on the left) and twenty iterations (on the right) of the MCMC MLE algorithm modified to use the lognormal approximation (7). A similar plot using the full stepping algorithm is in the lower left panel of Figure 6d.

Figure 7.

Edge and gwdegree statistics for a modified MCMC MLE algorithm using the lognormal approximation (7), but without the stepping improvement, for Model 2 of Section 7.1. The observed values are shown as a circled X.

8 Discussion

The procedure in this article addresses the serious problem encountered when implementing approximate maximum likelihood techniques to find estimates for model parameters in exponential-family random graph models (assuming that the Y_ij variables are not independent): A law-of-large-numbers approximation (6) to the log-likelihood ratio ℓ(η) − ℓ(η₀) tends to be poor when η is far from η₀. Our algorithm moves η₀, step by step, closer to η̂ until the MCMC sample generated from η₀ does in fact cover g(y^obs). By combining this stepping procedure with the lognormal approximation described in Equation (7) of Section 2, we are able to estimate approximate MLEs in many scenarios in which this was not possible using a standard algorithm. The techniques described here are implemented in the ergm package of Handcock et al. (2011).

One potential benefit of our method is that it could alleviate the necessity for MCMC MLE algorithms to choose an initial value η₀ that is already close to the true MLE. Currently there are no better options in the literature than starting at the MPLE, which is problematic for at least two reasons. First, multiple authors have shown that the MPLE may have poor statistical properties. Second, sometimes we may wish to fit an ERGM based solely on the vector g(y^obs) of network statistics; after all, the ERGM of Equation (1) depends on the network only through g(y). However, finding an MPLE requires an actual network that actually possesses the given network statistics. Such a network might not exist if g(y^obs) arises as some vector of theoretical interest rather than from a network dataset—for instance, sometimes g(y) must consist of integers (as it does for all but the GWDeg statistic in our Section 7 example) but we might want to estimate the model parameters using a non-integer-valued vector of “observed” statistics. Even when possible, finding such a network introduces a potentially unnecessary additional computational step. Furthermore, the vector g(y) does not uniquely determine a network, which means that diffierent possible “observed” networks could produce g(y^obs) and there is no guarantee that all of these will yield the same MPLEs. For all of these reasons, approximate methods for finding the true maximum likelihood estimator are preferable to MPLE methods; and these approximate methods continue to improve with algorithmic refinements such as those we present here.

Several extensions and improvements to the techniques presented here are possible. For instance, instead of choosing γ in Section 4 so that the new “observed” statistics are just barely inside the convex hull of sampled statistic vectors, we might make the choice based on some notion of data depth within these statistics (Liu et al., 2006). Or we could start the algorithm by fixing some of the parameters at zero, bringing others on target one at a time or in groups using the steplength routine. Finally, it is possible that our algorithm, or indeed any simulation-based algorithm, would work better if the underlying MCMC sampler were improved. Although improving the MCMC algorithm is not the focus of our current article, this is certainly an interesting topic of research unto itself. We do not claim that the current algorithm is a panacea, capable of moving straight to an approximate MLE for any model, from any starting parameter value; however, it represents one more tool to employ in the tricky task of estimating these models, and our experience is that it has succeeded in certain problems that were formerly intractable.