Abstract.
Hepatocellular carcinoma (HCC) is the most common histological type of primary liver cancer. HCC is graded according to the malignancy of the tissues. It is important to diagnose low-grade HCC tumors because these tissues have good prognosis. Image interpretation-based computer-aided diagnosis (CAD) systems have been developed to automate the HCC grading process. Generally, the HCC grade is determined by the characteristics of liver cell nuclei. Therefore, it is preferable that CAD systems utilize only liver cell nuclei for HCC grading. This paper proposes an automated HCC diagnosing method. In particular, it defines a pipeline-path that excludes nonliver cell nuclei in two consequent pipeline-modules and utilizes the liver cell nuclear features for HCC grading. The significance of excluding the nonliver cell nuclei for HCC grading is experimentally evaluated. Four categories of liver cell nuclear features were utilized for classifying the HCC tumors. Results indicated that nuclear texture is the dominant feature for HCC grading and others contribute to increase the classification accuracy. The proposed method was employed to classify a set of regions of interest selected from HCC whole slide images into five classes and resulted in a 95.97% correct classification rate.
Keywords: cancer grading, hepatocellular carcinoma histological images, multifractal computation, multifractal measures, textural feature descriptor, segmentation, classification
1. Introduction
Liver cancer is a leading cause of worldwide cancer death, and hepatocellular carcinoma (HCC) is the most common histological type of primary liver cancer that develops in liver cells.1 Histopathology—the microscopic examination of human tissues—is one HCC diagnostic technique. Histopathological investigations identify benign or malignant lesions and estimate the histological types and grades of tumors. In particular, histological grading is used as a scale for estimating tumor malignancies. Generally, low-grade tumors have good prognoses, whereas high-grade tumors indicate low survival rates. Edmondson and Steiner’s grading is a commonly used standard for determining the grade of HCC.2 It defines the following four tumor grades: G1, G2, G3, and G4, where G1 is the lowest grade and G4 is the highest grade. In practice, cancerous regions may be extracted from non-neoplastic tissue regions. Therefore, we incorporated the images of non-neoplastic tissues and categorized them as G0. Figure 1 shows these five categories of HCC histological images. It is very difficult for pathologists to diagnose low-grade tumors correctly because of the uneven tumor growth and similar structural appearances within different tumor grades. Image interpretation-based computer-aided diagnosis (CAD) systems partially circumvent these limitations and improve the reliability of manual diagnosis results. Many valuable studies have been reported on the computational tumor grading of different types of cancers, such as prostate carcinoma,3–6 renal cell carcinoma,7,8 and brain tumor astrocytoma.9,10 However, few studies have been reported on the computer-assisted tumor grading of HCC.11,12
Fig. 1.
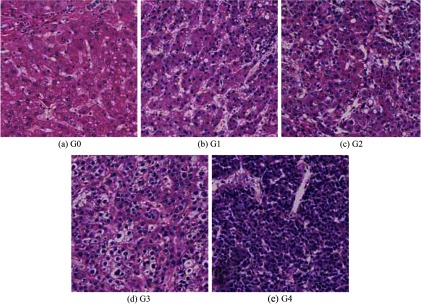
Five categories of hematoxylin and eosin (HE)-stained hepatocellular carcinoma (HCC) biopsy specimen images. (a) Non-neoplastic tissues: G0. (b)–(e) HCC tumors, Grade 1 to 4: G1–G4.
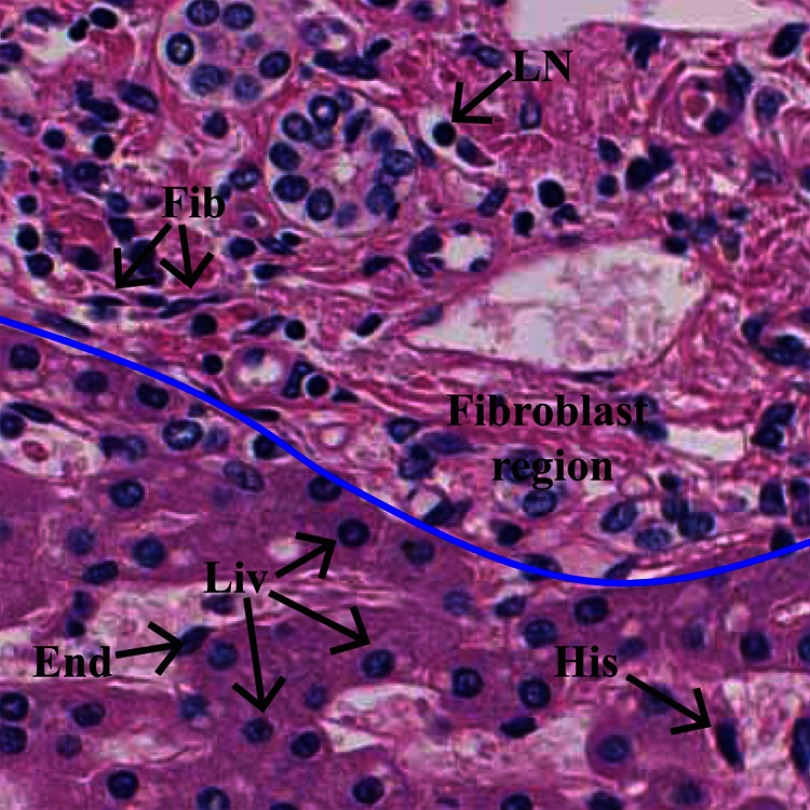
In a whole slide image (WSI) of a biopsy specimen, tumor regions are erratically distributed, and a selected region of interest (ROI) may contain different types of cells, such as liver cells, fibroblasts, lymphocytes, endothelial cells, and histiocytes. Figure 2 shows annotations of the different types of cell nuclei in an ROI of a hematoxylin and eosin (HE)-stained liver biopsy specimen. Generally, most of the image processing-based CAD systems first segment the nuclei and utilize their features for tumor classification.8,10,11 Nuclear segmentation can be accomplished by supervised or nonsupervised methods.13 These methods segment every possible nucleus in the images because the nuclei in HE-stained biopsy images often appear darker in a pink background. Since manual HCC grading is performed based on characteristics of liver cell nuclei, it is important that the computational HCC grading systems classify liver cell nuclei related to all the segmented nuclei.
Fig. 2.
Description of HE-stained liver biopsy image. The image contains different types of cell nuclei and cellular components. Five types of nuclei have been annotated: Liv: liver cell nucleus, Fib: fibroblast cell nucleus, LN: lymphocyte, End: endothelium, and H: histiocyte. Upper part of the blue colored line indicates fibrous region.
This paper proposes a technique that can be used for classifying liver cell nuclei and grading HCC histological images. An overview of the proposed method is given in Fig. 3. It contains five modules. First, a textural feature extraction module computes the pixel-wise textural characteristics using our previously proposed multifractal textural feature description method.12 The computed textural features are used in the four succeeding modules. The nuclear segmentation module segments every possible nucleus, including liver cell nuclei, fibroblast nuclei, endothelial nuclei, histiocytes, lymphocytes, and so on. The shapes of the nuclei in fibrous regions are irregular and are located very close to each other or are bound (see Fig. 2). Moreover, liver cells are not found within fibrous regions. Therefore, the fibrous region detection and processing module detects the fibrous regions and excludes the segmented nuclei within these regions. The results may contain liver cell nuclei, endothelial nuclei, histiocytes, lymphocytes, and so on. The liver cell nuclei classification module classifies these nuclei into two classes, i.e., liver cell nuclei and others. The tumor classification module computes the following four categories of liver cell nuclear feature: inner texture, geometry, spatial distribution, and surrounding texture (part of cytoplasm), and uses them to classify a given ROI into specific HCC grades.
Fig. 3.
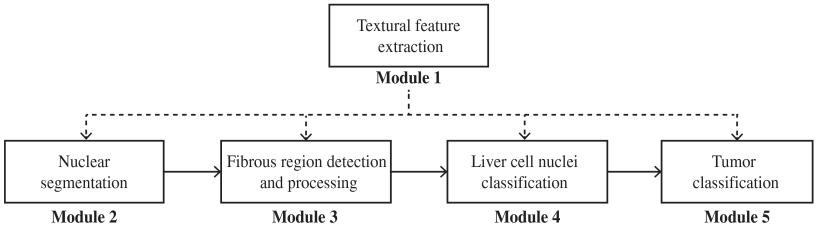
Overview of the proposed method.
In the proposed method, modules 3 and 4 subsequently exclude the nonliver cell nuclei. We investigate the effectiveness of these modules for HCC tumor classification (refer Sec. 5.3). In particular, we extract four categories of features: inner texture, geometry, spatial distribution, and surrounding texture from the outcome of the modules 2, 3, and 4 separately and employ these features to discriminate HCC images into two classes: non-neoplastic versus neoplastic. The experimental results indicate that modules 3 and 4 significantly contribute to an increase in the correct classification rate (CCR).
Finally, we define an HCC grading framework based on the proposed method by considering domain specific information such as irregular distribution of several tumors in an ROI and specific nuclei structure in G4 tumors (refer Sec. 4.6). Accordingly, the HCC grading framework classifies a given ROI in two stages using a random patch-based majority voting method (refer Sec. 4.6 for details). We utilized this HCC grading framework to classify a set of HCC ROIs and obtained approximately 95% average CCR.
The paper is organized as follows: Sec. 2 reviews related works of nuclear segmentation, nuclear classification, and the computational grading of HCC images. Section 3 describes the basic materials used in the proposed method. Section 4 illustrates the proposed method, including the textural feature descriptor, nuclear segmentation, fibrous region detection, liver cell nuclei classification, nuclear feature extraction, and HCC grading. Section 5 provides the implementation details, experimental results, and discussion. Section 6 presents the conclusion of the study.
2. Previous Studies
This section briefly describes recent studies related to nuclear segmentation, nuclear classification, and HCC histological image grading methods.
2.1. Nuclear Segmentation
Nuclear segmentation is one of the important operations in histological imaging-based CAD systems. A number of nuclear segmentation methods have been reported in the past.13 They can be categorized as supervised or nonsupervised schemes. In general, supervised methods classify image pixels or regions to localize the nuclei. In addition, they may generate probability maps by using the classifier’s probability of each pixel or region for the nuclear class. Nonsupervised methods may utilize one or more image processing techniques, such as edge detection, intensity-based thresholding, and mathematical morphology. Both approaches may utilize contour detection methods, such as active contour, gradient vector flow, watershed, and level-set to extract the edges of the segmented regions.
Naik et al.14 proposed a method to segment lumen, cytoplasm, and nuclei regions of prostate histological images. They used RGB color intensities to describe the pixel’s characteristics (three-dimensional feature vector) and estimated the parameters of a Bayesian classifier using an annotated dataset. Subsequently, they computed the pixel-wise likelihood for each pixel and obtained probability maps for each lumen, cytoplasm, and nuclei regions. The boundaries of the classified regions were computed by the level-set method.
Veillard et al.15 described the cell nuclei segmentation method for HE-stained breast cancer histological images. First, they performed HE-deconvolution16 on an RGB image. The HE-deconvolution produced a hematoxylin image, an eosin image, and a residual image. They utilized several textural feature descriptors and computed a 180-dimensional feature vector to describe the pixels’ characteristics. They estimated the probability associated with the feature vector of each pixel using the softmax function. Consequently, a gray-scale image was obtained, where the normalized value of each pixel indicated its probability of belonging to the nuclear class. Finally, the nuclear boundaries were computed by using an active contour model with a nuclear shape prior.17 Results indicated that this method segmented nearly round-shaped nuclei.
Naik et al.14 utilized only the color intensities to describe the pixels’ features. However, it is required to acquire pixels’ local characteristics to improve the robustness and consistency of the system. Veillard et al.15 showed that the characteristics of hematoxylin image were not adequate to segment the nuclei. As a consequence, they utilized all decomposed images in the feature computation. In fact, histological examinations are based on visual characteristics of the cellular components. Color deconvolution may distort some important visual characteristics. This paper proposes a supervised learning-based segmentation method. It overcomes the limitations of Naik et al.14’s method by incorporating the pixels’ local characteristics. We compute pixels’ characteristics by utilizing a multifractal feature multifractal feature descriptor. In general, the shapes of liver cell nuclei are varied for different tumor grades. Therefore, no shape prior information is used in the segmentation process.
2.2. Nuclear Classification
Histological images contain different types of cells. However, pathological examination is performed based on a specific type or several types of cells. Therefore, it is necessary that the CAD system discriminates the cells before applying diagnostic rules. In practice, most of the cells are distinguished based on their nuclear characteristics. Several studies have been reported for nuclear classification in histological images.
Fuchs et al.18 proposed a nuclear detection and segmentation method for tissue microarrays of renal clear cell carcinoma. They segmented the true nuclei and nuclei-like structures (false positive segmented blobs) using a morphological object-based segmentation method. Then, they computed eight features—size, ellipticity, shape regularity, nucleus intensity, inner intensity, outer intensity, inner homogeneity, outer homogeneity, and intensity difference—from the segmented regions and classified the true nuclei. The authors showed that the result is important for improving the efficiency of the manual diagnosis process. However, they classified the nuclei for the purpose of excluding the false segmentation regions.
A nuclei classification framework was proposed by Kong et al.19 for HE-stained histological images of diffuse gliomas. They used a mathematical morphology operation to separate foreground (nuclei) from background regions. Subsequently, nuclei regions were extracted by a straightforward thresholding method and the overlapped nuclei were separated using the watershed technique. For nuclear classification, they computed four categories of feature sets such as nuclear morphometry, region texture, intensity, and gradient statistics from the nuclei regions. In addition, they utilized characteristics of cytoplasmic regions by computing textural, intensity, and gradient statistics from the nuclear surrounding regions. Totally, they have used a 74-dimensional feature vector to describe the characteristic of a nucleus. They obtained significant classification accuracy for a large nuclei dataset. In addition, results indicated that the cytoplasmic texture also contributed to improve the classification accuracy.
Cell nuclear classification is domain oriented process. The objective of this paper is to perform tumor grading based on characteristics of the liver cell nuclei. Therefore, we should classify every possible liver cell nuclei despite to the tumor grade. In general, shapes of liver cell nuclei are varied with the tumor grade. Considering the visual observations of HCC histological images, we empirically decided to used only nuclear textural feature for classifying liver cell nuclei.
2.3. Computational Grading of HCC
A few studies have been reported for classifying HCC histological images.
Huang and Lai11 proposed a method to classify HCC histological images on the basis of morphological and textural characteristics of the nuclei. They performed a mathematical morphology-based segmentation method followed by the watershed and active contour method to segment the nuclear regions. Subsequently, they computed the feature vector for the entire image by using the characteristics of the segmented regions. In particular, they extracted three categories of features from the segmented nuclei, including the geometric relationship between the nucleus and the cytoplasm, the geometry of the nuclei, and the texture of the nuclei. They used five grades of ROI images of HE-stained HCC biopsies. Each ROI was divided into 12 nonoverlapping subimages and the majority of the predictions were used to classify the ROI. With a support vector machine-based decision-graph classifier, they obtained a 94.54% CCR.
Our earlier study, Atupelage et al.,12 proposed a textural feature-based HCC classification method. Textural features were utilized to classify HCC images into five categories (non-neoplastic and four grades of tumors). The textural features were extracted by using multifractal computation. A bag-of-feature (BOF)-based classification model was utilized to derive a description for the entire image. The classification model generated a 300-dimensional feature vector (histogram) for a given image. Fifty sample patches were selected from a given ROI and the majority of the predictions (threshold-based majority voting rule) was taken as the prediction for the entire ROI. Result showed that 95.03% CCR was obtained for five classes of annotated dataset.
Huang and Lai’s11 method utilized all segmented nuclei for grading the HCC images. Their results may have been influenced by the characteristics of nonliver cell nuclei, such as fibroblast, endothelium, and histiocyte. In addition, they assumed that the region between neighboring nuclei is entirely occupied by cytoplasm. In an HCC hitological ROI, a number of tissue components may exist in between neighboring cells such as fat and fibrosis. Therefore, the features computed from the geometric relationship between nuclei and cytoplasm may affect the accuracy of the entire system. Our earlier study, Atupelage et al.,12 utilized the entire texture of the image. The feature description obtained for an image may contained the characteristics of noninformative regions, such as muscles, fiber, and fat. Compared to the aforementioned two HCC grading methods, the present work consists of a more sophisticated description for the structural behavior of HCC histological images. Our method utilized only the liver cell nuclei in the computation. We defined a liver cell nuclei feature extraction method following the pathological HCC grading rules. In particular, we computed nuclear inner texture, geometry, spatial distribution features. Additionally, textural features of nuclear surrounding regions (cytoplasmic textural features) were also incorporated for tumor classification. Our random patch-based majority voting method increases the robustness of the entire framework for different tissue structures, such as existence of multiple graded tumors in an ROI and large regions of fibrosis or fat.
3. Materials
The textural feature descriptor was extended from our earlier study that utilized multifractal computations in texture analysis.6,12 In this study, we also used multifractal computation to extract textural features. These features were used in various modules throughout the entire system. In addition, we incorporated a BOF-based classification model to describe the textural characteristics of segmented regions.
3.1. Fractal and Multifractal
The fractal dimension (FD) of an object is a noninteger exponent that strictly exceeds the topological dimension and is computed using the Hausdorff-Besicovitch definition.20
Let be a bounded subset of , and be the minimum number of balls (spheres) of radius that are required to cover . When tends to 0, the limiting values of follow the power law , where is a constant, i.e., the FD of
| (1) |
Deterministic structures (that are mathematically generated by recursively applying the same rule) can be characterized by the same fractal dimension in all scales. In contrast, natural structures are nondeterministic. Therefore, a single FD may not be adequate to characterize such structures. Multifractal analysis is a generalization of fractal analysis that characterizes irregular natural structures as a spectrum of FDs, i.e., a multifractal spectrum. Generally, multifractal computations are performed in two consecutive steps.
In the first step, we find the local irregularity of a function called the “multifractal measure” at a point of set , as a noninteger exponent, which is described by a Hölder Exponent ,
| (2) |
where denotes the closed ball of radius centered at .
The multifractal analysis of set involves computing FDs of different sizes of level sets of ,
| (3) |
where is a set of points whose exponents are equal to . In the second step, we estimate FD of for different of , and form a spectrum , i.e., multifractal spectrum of ,21
| (4) |
where represents the FD of the set .
3.2. Multifractal Analysis of Digital Images
A digital gray-scale image is a two-dimensional real and non-negative function; , where and are discrete spatial coordinates of the image. Therefore, the fractal and multifractal definitions given in Sec. 3.1 are modified to be appropriate for the discrete digital imaging domain. As a consequence, in Eq. (2), become a square-window of side length . and are replaced by and , respectively,
| (5) |
where represents the window of side length , which is centered at .
The computation of is described in the following. We set the values, for , and computed for a particular (definitions of selected multifractal measures are given in Sec. 4.1). Subsequently, is plotted against and the gradient of the linear regression line is estimated as . Similarly, we repeat the computation for every pixel in the reference image and obtain a matrix having the same dimension, which is called feature matrix (or -image).
In the next step, the entire range of (from minimum to maximum) is quantized into discrete subranges. Let be all of the values quantized into the ’th subrange. may form a binary value matrix , which has the same dimensions as the matrix
| (6) |
where and represent the lower and upper limits of the ’th subrange, and is the value at point in the matrix.
Then, we compute the FD for each , according to Hausdorff–Besicovitch definition. Many algorithms have been proposed to compute the FD. Each method has its own theoretic basis for estimating the parameter according to Eq. (1).22 Among them, the algorithm “box-counting” is chosen because of its efficiency, accuracy, and ease of implementation.23 The box-counting algorithm estimates the FD as follows. The entire image may be covered using a grid of side length , then count the number of nonempty boxes . We defined the FD of as
| (7) |
We compute for , and plot them in a log-scale. Subsequently, is estimated by computing the gradient of the linear regression line, which is the FD of . Similarly, we obtain the FD for every binary image that corresponds to each , and form the multifractal spectrum. In addition, for each element in the matrix, there is a value (FD) in the multifractal spectrum which leads to a matrix called the feature matrix (or -image) having the same dimension as the matrix.
The computation showed that the features observed the pixel’s local behavior with respect to the neighborhood and the features contained the pixel’s spatial characteristics.
3.3. BOF-Based Classification Model
BOF-models are a promising approach for characterizing the visual content of the images (or regions). The key ideas behind the BOF classification model are the construction of a codebook and representation of the image by a simple frequency analysis of the codewords in the image. Generally, a codebook is a collection of distinct feature vectors that are called codewords, in which the most representative patterns are coded. These codewords are used to represent the pixel’s characteristics. In particular, every pixel is assigned to a certain index of the codeword, where the codeword has a minimum Euclidean distance to the pixel’s feature vector. This process may be called labeling. The frequency analysis of the codewords in an image or a region results in a histogram, in which each bin represents a codeword in the codebook and its value indicates the frequency of the codeword (labels) contained in the image. If different sizes of images or image regions are used, the areas of the histograms are different. Therefore, it is necessary to normalize the histograms. From a statistical point of view, this normalization turns the histogram into a probability distribution function, in which the sums of the total observations are equal to 1.
The codebook should contain an optimal number of discriminative codewords to obtain a higher classification performance in the classifier. Different codebook optimization (feature-selection) methods have been reported.24–26 Among them, we empirically selected the mutual information (MI) codebook optimization technique. Definition of the MI method is described as follows. For a given classes of dataset and number of codewords (codebook), indicates the correlation between codeword and class .25 We compute the class-specific scores for each codeword as , where represents the prior probability that the observed data falls in class . Subsequently, we obtained most discriminative codewords by eliminating the codewords whose class-specific scores are less than a given threshold (see Yang et al.24 for detailed information).
The proposed method used different codebooks for the fibrous region detection, liver cell nuclei classification, and nuclear feature extraction modules.
4. Methodology
This study describes an extended version of our previously proposed liver cell nuclei classification and HCC grading techniques.27 There are several contributions of the proposed method, such as utilizing multifractal computations for nuclear segmentation, fibrous region detection, and liver cell nuclei classification. Furthermore, we extracted the following four categories of nuclei features: inner texture, geometry, spatial distribution, and surrounding texture and utilized them for HCC grading. To the best of our knowledge, there have been no studies that have performed liver cell nuclei classification and used them for grading HCC histological images.
This section illustrates the details of each module shown in Fig. 3 and that of the HCC grading framework.
4.1. Textural Feature Extraction Module
The features presented in and matrices are dependent on the multifractal measure used in Eq. (5). Therefore, different multifractal measures can be utilized to describe the texture from different viewpoints. In this study, we utilized the following four multifractal measures: maximum: , minimum: , summation: , and Ndiff: as defined in Eqs. (8), (9), (10), and (11), respectively.28,29 These four measures observed the disparity of the gray intensities from four different viewpoints:
| (8) |
| (9) |
| (10) |
| (11) |
where represents the measurement at point . is the square window with side length centered at point . represents all of the nonzero pixels of . is the gray intensity at point .
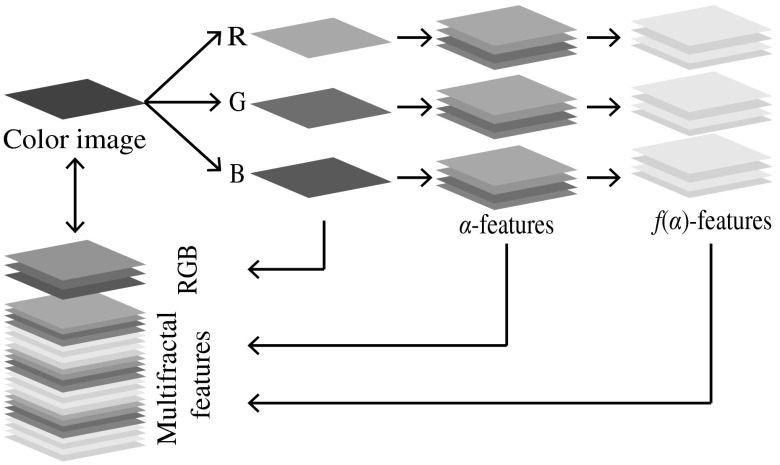
In this study, we computed and for each R, G, and B color channel using four multifractal measures, which yielded a 24-dimensional feature space. Subsequently, we combined the R, G, and B color intensities with the multifractal features and constructed a 27-dimensional feature space. As a consequence, each pixel of an image can be characterized by a 27-dimensional feature vector in the feature space. The proposed feature description is graphically illustrated in Fig. 4.
Fig. 4.
Textural feature description.
4.2. Nuclear Segmentation Module
Nuclear segmentation was performed as a supervised learning scheme for pixel-based classification. We utilized a training dataset, in which the nuclear and background regions were manually annotated by several experts. The annotated nuclei were selected from different types of cells and the background regions were randomly selected. We computed the features of each pixel in the annotated regions and trained a random forest classifier for two classes , where and stand for the nuclear and background classes, respectively. Let be the feature vector of a given image pixel. and are the classifier’s probabilities that belongs to and , respectively, where . We computed for every in the given image and visualized these values to gray scale [0, 255], in which high intensity values represent the nuclear regions and vice versa. Subsequently, we eliminated noises and refined the nuclear boundaries using a morphological closing operator with a 3-pixel radius disk-shaped structural element. The boundaries of the detected nuclear regions were computed using the level-set contour estimation method.30 We further refined the segmentation results by eliminating the regions of size (number of pixels) . Intermediate results of nuclei segmentation process are graphically illustrated in Fig. 5.
Fig. 5.
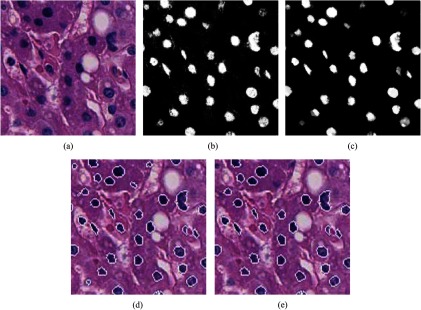
Nuclear segmentation (intermediate results). (a) Input image. (b) Pixels’ prediction probabilities for nuclear class (probability map). (c) Result of morphological closing operator. (d) Nuclear contours. (e) Final refined result of nuclear segmentation.
4.3. Fibrous Region Detection and Processing Module
Fibrous region detection was performed as a supervised learning scheme for patch-based classification. Images in the training dataset were divided into nonoverlapping patches and annotated into the following two classes: fibrous and other (background). The textural features of a patch were encoded as a histogram using the BOF model. We trained a random-forest classifier with the annotated dataset. A given image was divided into nonoverlapping patches and each patch was classified using the trained classifier. The noises (false positives) contained in the results were further refined with a nonlinear filtering approach as follows.
Let the outcomes of the classifier be . The probability of a given patch being classified to class is . Let eight neighborhoods of be , . The refined prediction, is defined as
| (12) |
We illustrated the intermediate steps of fibrous region detection graphically in Fig. 6.
Fig. 6.
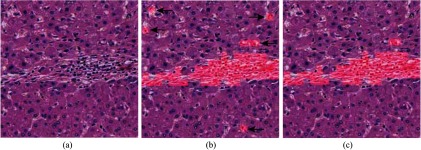
Fibrous regions segmentation. (a) Input image. (b) Classifier predictions (shaded in red). The black arrows shows the noise. (c) Final refined result.
Subsequently, all segmented nuclei that overlap with the fibrous regions are eliminated.
4.4. Liver Cell Nuclei Classification Module
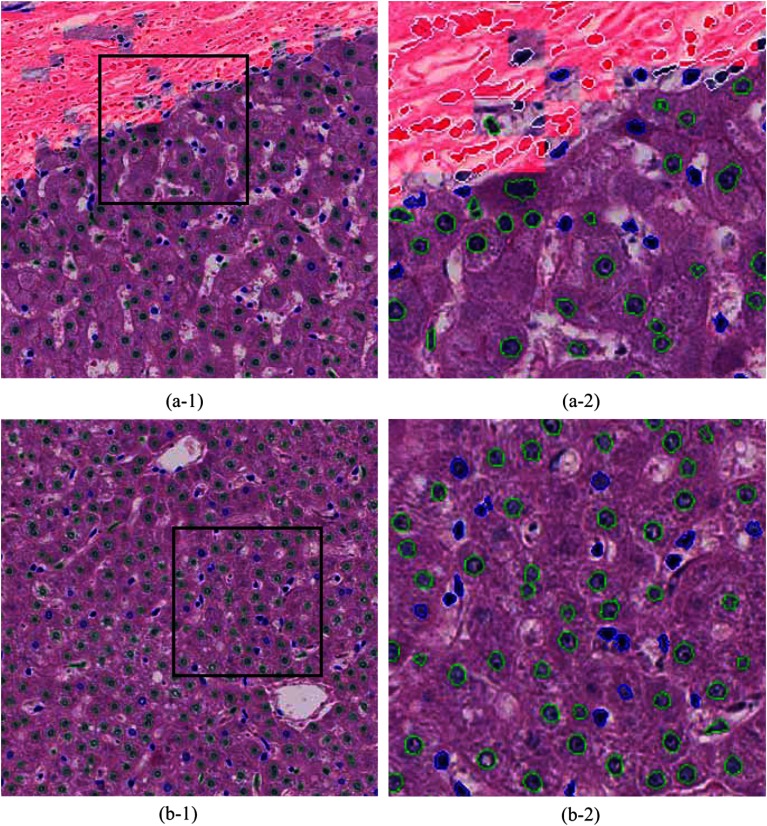
The outcome of the previous module may contain liver cell nuclei, lymphocyte, histiocytes, endothelial cell nuclei, and so on. This module classifies these segmented nuclei regions into two classes: liver cell and other nuclei. An annotated dataset (a set of nuclei that was labeled as liver cells and others) is utilized for training the classifier. We empirically decided to use only the textural features of the segmented regions. As a consequence, the texture of each annotated nucleus was coded into a normalized histogram using the BOF model. These histograms were used to train a random-forest classifier. The trained classifier was used to classify segmented nuclei in the experimental dataset. A graphical example of classified nuclei is shown in Fig. 7.
Fig. 7.
Computational annotations of nuclei segmentation and classification. (a-1) and (b-1) HCC images of . (a-2) and (b-2) High resolution images of the selected regions (black square) in (a-1) and (b-1), respectively. Fibrous regions are shaded in red. Annotations of nuclear contours; fibroblast nuclei: white, liver cell nuclei: green, and other nuclei: blue.
4.5. Nuclear Feature Extraction
A histopathological investigation of HCC grading is performed according to the different characteristics of the liver cell nuclei. We generalized these characteristics into the following three categories: texture (chromatin structures), geometry, and spatial distribution. Furthermore, this investigation incorporated the textural characteristics of the nuclear surrounding areas. With these four categories, we computed 115 features for a given HCC histological image.
4.5.1. f1: Textural features
The textural features of the segmented nuclear regions were extracted using the BOF model. We computed the textural features of the segmented regions (nuclei) in a given image and normalized histogram using 50 codewords of a codebook. As a consequence, we obtained a a 50-dimensional feature vector to describe the nuclear texture in the entire image.
4.5.2. f2: Geometrical features
We observed the geometrical features from the size, shape, and circularity of individual nuclei. For a given nucleus, the area is the total number of pixels in the segmented region, the perimeter is the length (number of pixels) of the nuclear contour, and the circularity is . Typically, a sample image (size: ) contains a large number of nuclei and the segmented (and classified) results may contain a few false positives (outliers). Therefore, we computed three percentiles; 5%, 50%, and 95% for each geometrical feature. Consequently, a nine-dimensional feature vector was obtained to describe the geometrical features of the nuclei in the entire image.
4.5.3. f3: Spatial distribution features
Pathologists often observe the spatial distributions of liver cell nuclei for diagnosing the HCC. We observed these features from two different parameters; density (= number of nuclei/area) and FD (= complexity of the configuration patterns of the nuclear distribution). A given HCC histological image may have contained regions of fiber, fat, muscle, and so on. These regions may interrupt the spatial distributions of the liver cells in an ROI. To minimize the effect of these regions in the computation, we randomly located 50 subwindows that were sized within the image and computed the density and FD for each patch. This computation is summarized as follows:
; //total number of patches
while do
;
;
if patch overlaps with fibrous region then
overlapped area = number of overlapped pixels;
overlapped ratio = overlapped area / area;
if overlapped ratio then
continue to next patch;
end if
area = area − overlapped area;
end if
density = number of nuclei/area;
FD = compute FD for the patch;
;
end while
For a given patch, we obtained a nuclear configuration pattern as a binary image (nuclear region: 1 and background: 0) and computed the FD using a box-counting method. This feature described the complexity of the nuclear configuration patterns over the entire patch.
We computed three percentiles; 5%, 50%, and 95% for each density and the FD features. As a consequence, a six-dimensional feature vector was generated to describe the spatial distribution patterns of the nuclei in the entire image.
4.5.4. f4: Surrounding textural features
Generally, the nucleus is covered by the cytoplasm. The outer margin of the cytoplasm defines the cell membrane. During tumor progression, the nuclear region becomes larger and the cytoplasm region becomes narrower. In addition, the cytoplasmic texture may also vary during tumor progression. These changes may be visually observed. Utilizing the textural characteristics of cytoplasmic texture may be significant for increasing the accuracy of HCC grading. Since it is very difficult to precisely locate cell membranes in HE-stained images, we acquired a region of fixed-distance radius surrounding the nucleus.
The segmented nuclear region is eroded using a disk-shaped structural element with a 10-pixel radius and the eroded region is used to compute the surrounding textural features. The similar textural feature extraction process is used as described in Sec. 4.5.1. Consequently, the surrounding textural features were also represented as a 50-dimensional feature vector.
4.6. HCC Grading
Generally, different grades of tumors are arbitrarily distributed in a WSI. A selected ROI may also contain several tumor cells. Pathologists examine the entire ROI and assign a label (tumor grade) on the basis of the majority of tumor tissues that appeared in the ROI. For example, an ROI that is annotated as G2 may contain G1 and G3 tumors, as well as smaller amounts of intermediate grade tumor cells that are between G1 and G2 and G2 and G3. In addition, the same class of tissues is often localized (e.g., small regions of G3 tumors may exist in an ROI that labeled as G2). By observing these circumstances, we incorporate a patch-based classification and a threshold-based majority voting technique into the HCC grading framework. As a consequence, a given ROI is classified as described below.
We select 16 nonoverlapped patches of size to cover the ROI and 34 patches of the same size from randomly selected locations. Based on the prediction of each patch in the ROI, we estimate the final prediction (grade) of the ROI using a threshold-based majority voting rule.
Let be the total number of predictions of class out of 50 samples in an ROI. The percentage of the probability of that ROI being categorized into class is
| (13) |
For a given threshold , if , then the ROI is labeled as class , otherwise it is labeled as non.
In practice, G4 tumors can be easily detected because of their specific structural appearances such as relatively larger nuclei and very narrow cytoplasm. In most cases, it is difficult to see the boundary of the nuclei because they visually overlap each other. This behavior overburdens the nuclear segmentation process. Nuclear shape estimation and postsegmentation methods may partially solve this problem.15,19 However, estimating the nuclear morphological features, spatial distribution features, and surrounding textural features using these methods may not be accurate for G4 tumors. To circumvent this limitation, we perform the HCC grading in two stages; (i) stage 1: a given ROI is classified using nuclear textural features () into two classes; G4 (G4 tumors) and O (stands for “Others,” in which G0, G1, G2, and G3 are categorized into one class) and (ii) stage 2: If the ROI is classified into class O in stage 1, then it performs a multiclass classification (G0, G1, G2, and G3) using the textural (), morphological (), spatial distribution (), and surrounding textural () features. We applied the threshold-based majority voting rule at each stage.
5. Experiments and Results
This section describes the experimental dataset, implementation, evaluation strategies, and discussion of the results.
5.1. Data Acquisition
A set of HE-stained liver biopsy specimens were obtained from 109 HCC patients. Each specimen was scanned as a WSI at a magnification of using a scanner (Nano-Zoomer; Hamamatsu Photonics K.K., Hamamatsu City, Shizuoka, Japan). The size of the WSI was . Several experienced pathologists examined the WSIs and selected several ROIs from neoplastic and non-neoplastic tissue regions. ROIs selected from non-neoplastic regions were grouped as G0 and others were grouped into four classes; G1, G2, G3, and G4 according to Edmondson and Steiner’s HCC definition.2 We selected several ROIs from the G0, G1, G2, and G3 categories for annotations. The rest of the images contained 93, 72, 67, 48, and 25 ROIs for the G0, G1, G2, G3, and G4 categories, respectively. ROI selection, grading, and annotation (nuclear region, fibrous regions, and liver cell nuclei) were performed in parallel by the pathologists. Ambiguous ROIs and annotated regions were clarified and confirmed by an association of several pathologists.
5.2. Implementation
The multifractal features of the nuclear textures were computed according to the definitions given in Sec. 3.2. In particular, -features were computed according to Eq. (5) by setting as 1, 3, 5,…, 13 and normalizing to the range [0, 1]. Subsequently, the range (minimum to maximum) was quantized into 70 discrete subranges and 70 binary images were obtained. The FD of each binary image was computed according to Eq. (7) by setting as 1, 2, 4, …, 16. and features were computed for each R, G, and B color channel using the multifractal measures defined in Sec. 4.1.
To detect fibrous regions, the codebook was computed using the annotations of the fibrous and background regions. We randomly selected 50,000 pixels from fibrous and background regions and their feature vectors were clustered into 500 clusters using a -means algorithm. The most discriminative 50 codewords were selected using the MI feature selection method (see Sec. 3.3). In particular, we compared the classification accuracies and the computational performance of the classifier with different sizes of codebooks. Experimental results indicated that 50 codewords of the codebook provide optimal result for fibrous regions classification. A similar approach was used to generate the codebook for liver cell nuclei classification, in which the annotations of the liver cells and other nuclei were used.
For feature extraction, we selected 50,000 nuclear pixels from the G0 to G4 categories and clustered them into 500 clusters. The optimal 50 codewords were selected with the MI feature selection method for the five classes (G0 to G4). Since we utilized for classifying G4 versus the others (G0 to G3), the codebook construction of incorporated G4 images. The codebook for was computed in a similar manner as that for , in which randomly selected pixels of the nuclear-surrounding areas of the G0 to G3 categories were used. During the codebook optimization, we performed several classification experiments using a small dataset for different sizes of codebooks. We selected the optimal codebooks by comparing the efficiency and accuracy.
For the and feature computation and liver cell nuclei classification, we normalized the histograms by dividing the frequency of each bin by the total observations (number of pixels in the region). The MATLAB random forest implementation method31 was used for classification throughout the entire experiment.
In the evaluation, a -fold cross-validation was performed with respect to the ROIs. In addition, sample patches that were obtained from an ROI were indexed into a single fold to separate the training and testing datasets.
We computed CCR, precision, recall, and -measures as evaluation statistics for the experiments.32,33
5.3. Evaluation of the Proposed Method
The proposed method contains multiple processing modules (see Fig. 3). This section describes several experimental evaluations that confirm the significance of the processing modules and the entire approach.
We primarily evaluated modules 3 and 4 individually. In module 3, we utilized 14,520 fibrous region blocks and 55,383 background blocks. Using the textural features of each block, we performed two-class classification and obtained the average precision and recall of the cross-validation as 80.72% and 74.10%, respectively. The annotated dataset of module 4 contained 2585 liver cells and 2027 other types of nuclei. We computed the textural features of the segmented regions (of the annotations) and performed two-class classification. Results showed the average precision and recall for cross-validation are 95.17% and 97.13%, respectively.
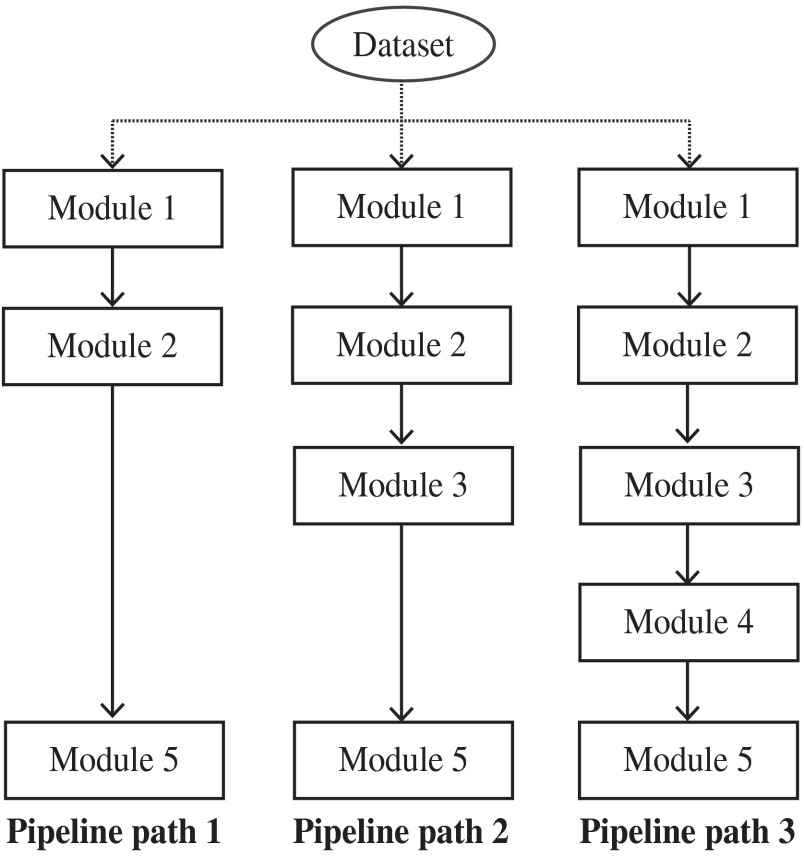
In the proposed method, module 1 extracts the textural features and they are used in every other module. Module 2 segments all possible nuclei, module 3 refines the results of module 2 by excluding the nuclei in fibrous regions and module 4 classifies the liver cell nuclei. Module 5 computes the nuclear characteristics and performs the tumor classification. In particular, modules 3 and 4 consecutively exclude the nuclei that are not examined by pathologists in HCC grading. Therefore, it is necessary to evaluate the impact of modules 3 and 4 for tumor classification. We experimentally evaluated the significance of modules 3 and 4 by utilizing the outcomes of modules 2, 3, and 4 in tumor classification. This process is graphically illustrated in Fig. 8. It contains three pipe-line paths; each path acquires the outcomes of module 2, 3, and 4 and performs tumor classification. In addition, we described four categories of nuclear features for tumor classification; : inner texture, : geometry, : spatial distribution, and : surrounding texture. Module 5 computes these nuclear features from the outcomes (segmented regions) of its preceding module.
Fig. 8.
Overview of the evaluation framework. The dataset is classified in three pipeline paths. Each pipeline component indicates a corresponding module in Fig. 3. Module 1: textural feature extraction, module 2: nuclear segmentation, module 3: fibrous region detection and processing, module 4: liver cell nuclei classification, and module 5: tumor classification.
In practice, it is difficult to accurately segment the nuclei in G4 (see Sec. 4.6). Therefore, we excluded G4 ROI in this evaluation. For simplicity, each pipeline path performs a two-class classification of non-neoplastic (G0) versus neoplastic tissues (G1, G2, and G3). To acquire higher efficiency in the experiments, each ROI was divided into four nonoverlapping subimages of and a 1120 images dataset was used.
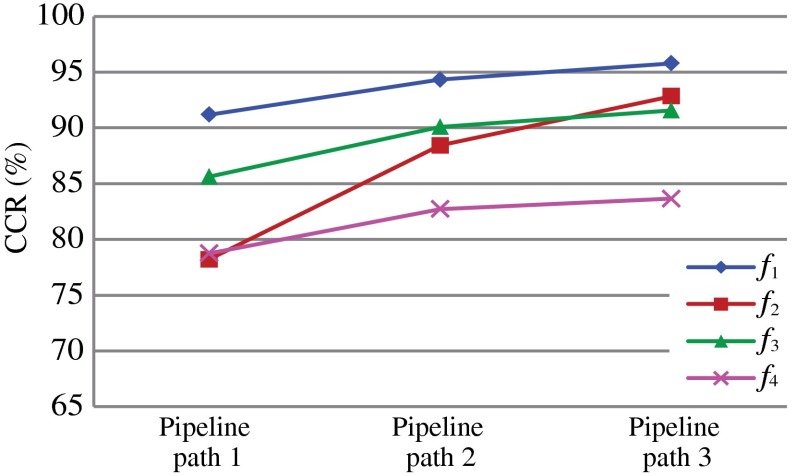
In the first experiment, we investigated the significance of each feature set, while comparing the classification results of each pipeline path. Detailed results of the first experiment are tabulated in Table 1 and the summary is given in Fig. 9.
Table 1.
Two-class classification results of three pipeline paths for each feature set.
| Feature set | CCR (%) | Precision/recall | ||
|---|---|---|---|---|
| Pipeline path 1 |
0.90 | |||
| 0.77 | ||||
| 0.83 | ||||
|
|
|
|
0.78 |
|
| Pipeline path 2 |
0.93 | |||
| 0.87 | ||||
| 0.88 | ||||
|
|
|
|
0.83 |
|
| Pipeline path 3 | 0.94 | |||
| 0.90 | ||||
| 0.91 | ||||
| 0.83 |
Fig. 9.
Two-class classification for each pipeline path using each feature set.
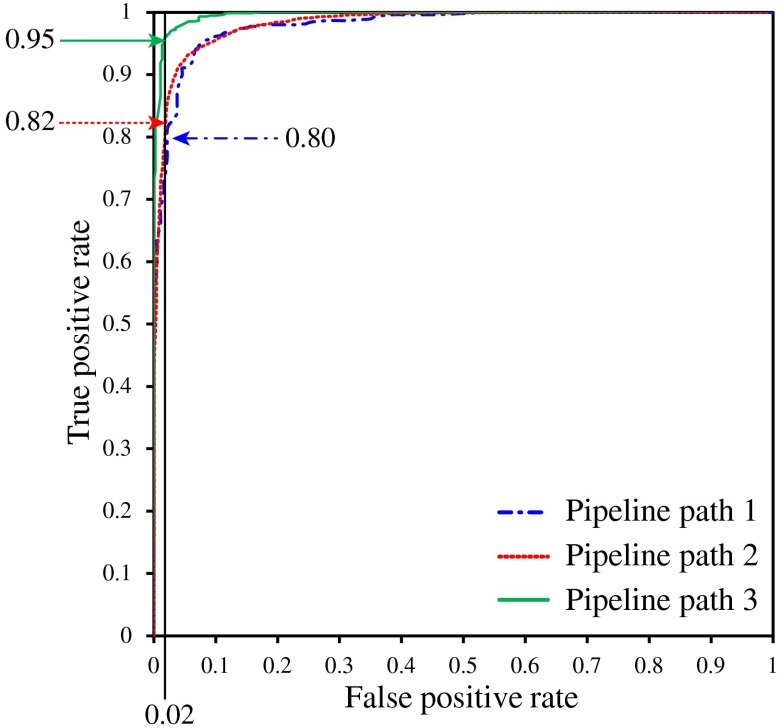
In the second experiment, we utilized combined nuclear features (see Sec. 4.5). The numerical results and receiver operator characteristic (ROC) curves of this experiment are shown in Table 2 and Fig. 10, respectively.
Table 2.
Two-class classification results for pipeline paths 1, 2, and 3.
| CCR (%) | Precision/recall | ||
|---|---|---|---|
| Pipeline path 1 | 0.93 | ||
| Pipeline path 2 | 0.93 | ||
| Pipeline path 3 | 0.97 |
Fig. 10.
Receiver operator characteristic curves for pipeline paths 1, 2, and 3.
The last experiment performed HCC classification according to the description given in Sec. 4.6. The five classes of the ROI image dataset were used for this experiment (see Sec. 5.1). G4 ROIs were classified in the first stage and other ROIs (G0 to G3) were classified in the second stage. ROI’s classified as “O” (see Sec. 4.6) in stage 1 were elected for stage 2 classification. In each fold of the cross-validation in stage 2, we explicitly excluded the misclassified G4 ROI from the training process. To maintain consistency in the experimental results, we employed the misclassified G4 ROIs into a randomly selected iteration of the cross-validation. Final classification results for threshold, are shown in a confusion matrix form in Table 3. The second column shows the total number of images used in each class, and the spanned column “Predictions” shows the predictions of each subimage. For example, the third row indicates that 67 ROIs were labeled as G2; there were 63 ROIs that were correctly classified, one ROI was classified as G1, two ROIs were classified as G3, and one was categorized as non. Thus, the CCR that was obtained for the G2 category was 94.03%.
Table 3.
HCC grading classification results for ROIs ().
| Grade | # of ROIs | Predictions | ||||||
|---|---|---|---|---|---|---|---|---|
| G0 | G1 | G2 | G3 | G4 | non | CCR (%) | ||
| G0 | 93 | 90 | 2 | 0 | 0 | 0 | 0 | 96.77 |
| G1 | 72 | 1 | 70 | 0 | 1 | 0 | 0 | 97.22 |
| G2 | 67 | 0 | 1 | 63 | 2 | 0 | 1 | 94.03 |
| G3 | 48 | 0 | 0 | 2 | 46 | 0 | 0 | 95.83 |
| G4 |
25 |
0 |
0 |
0 |
1 |
24 |
0 |
96.00 |
| Total | 305 | 95.97 | ||||||
5.4. Discussion
The individual performances of modules 3 and 4 were examined using fibrous regions and liver cell nuclei annotations, respectively. The precision and recall obtained for module 3 are slightly smaller: 80.72% and 74.10%. Marking the exact boundaries of fibrous regions is a very difficult process (see Fig. 2). We performed block-based detection to maintain the performance of the system. In this approach, the blocks located on the boundary of fibrous regions may be misclassified. The nuclei located in these regions may be excluded in module 4. Therefore, falsely detected fibrous regions may not affect the final tumor grading results. Liver cell nuclei classification is performed by using only the textural features. The liver cell nuclei classification module obtains very high precision and recall as 95.17% and 97.13%, respectively, for the annotated dataset. Considering the overall performance of the classifier (latency and accuracy), we decided to use only textural features for discriminating liver cell nuclei.
In manual HCC investigations, the characteristics of liver cell nuclei are mainly examined because they are significantly varied with tumor progression. The proposed method segmented every possible nucleus and subsequently excluded the nonliver nuclei in modules 3 and 4. The impact of excluding insignificant information should improve the accuracy of the classification and this was obvious in the experimental results. As indicated in Table 1 and Fig. 9, the CCR and other statistics of each feature set increased continuously from pipeline path 1 to pipeline path 3. Furthermore, the ROC curves in Fig. 10 indicated that for a false positive rate of 0.02, pipeline paths 1, 2, and 3 have obtained true positive rates of 0.80, 0.82, and 0.95, respectively. In addition, Table 2 shows that pipeline paths 1, 2, and 3 achieved 93.21%, 94.38%, and 97.85% CCRs, respectively. These results implied that excluding nuclei within fibrous regions contributed to improve the accuracy by a small degree and eliminating nonliver cell nuclei also contributed to improve the accuracy by a slightly larger degree. In fact, it is difficult to isolate the nuclei in fibrous regions because these nuclei may be very closely located or bound together. Utilizing these nuclei for liver cell nuclei classification (module 4) may increase the false detections of the classifier. Therefore, it is important to exclude the segmented nuclei in fibrous regions prior to the liver cell nuclei classification module. The results suggested that every processing module contributed significantly to improve tumor classification.
Table 1 and Fig. 9 further describe the significance of the proposed nuclear feature extraction method. The nuclear texture feature () achieved the highest classification accuracy for each pipeline path. The CCR of geometrical features () achieved the highest increment. In fact, different types of nuclei had different geometrical properties, e.g., fibroblast nuclei are shown as thin-long shapes and lymphocytes are shown as small-circular shapes. These characteristics highly influenced the features and this was clear from the results as well. Generally, the nuclear surrounding texture (cytoplasmic texture) is not employed for manual HCC grading. However, our investigation indicated that feature set contained significant discriminant information with respect to tumor classification by achieving approximately 83.66% CCR for pipeline path 3.
In practice, regions of WSIs are investigated by pathologists. Since WSIs are extremely large, the ROIs should be reasonably large for investigation. These ROIs may contain different grades of tissues. Pathologists grade these ROIs based on the majority of tumor grade present within the ROI. We imitate this mechanism by incorporating a threshold-based majority voting rule into our HCC grading system. It is intuitive that utilizing only nonoverlapped patches for majority voting may not be reasonable, because some important tissue patterns (structures) may be divided among these patches. Therefore, we additionally selected 36 randomly located patches from an ROI. Table 3 shows the classification results of the ROIs. It shows the significance of the proposed methodology for practical usage. The proposed HCC classification framework derives an interactive CAD system in which the pathologists can change the threshold in real-time and perform sophisticated investigation before the final decision. In addition, it requires manual investigation for the ROIs that are categorized as “non.” Therefore, incorporating a threshold-based majority voting method improves the reliability of the entire system.
6. Conclusion
HCC tumor grading is important because low-grade tumors have good prognosis and low-grade cancer patients have high survival rates. Manual low-grade HCC tumor diagnosing is crucial because these tumors have similar characteristics to non-neoplastic tissues. Image interpretation-based CAD systems have been developed to automate the HCC diagnosing and improve the consistency of the diagnostic results. Generally, HCC is graded according to the characteristics of liver cell nuclei. Therefore, it is important that the CAD system utilizes the characteristics of the liver cell nuclei in the computational HCC grading.
This paper proposed a liver cell nuclei classification and nuclei feature extraction method for the grading of HCC histological images. For a given histological HCC ROI, the proposed method segmented every possible nucleus and classified the liver cell nuclei. Subsequently, it computed four categories of features: texture, geometry, spatial distribution, and surrounding texture from the liver cell nuclei and used them for HCC grading. Results showed the significance of excluding liver cell nuclei for HCC grading. In addition, we evaluated the significance of nuclear features and results indicated that nuclear texture contained the dominant characteristics for HCC grading. Other features also contributed to an increase in the accuracy. We defined the automated HCC classification framework by considering the domain-specific information. In particular, we classified the patches in a given ROI. The decision was obtained by the threshold-based majority voting rule. In particular, the ROIs drawn under the threshold require manual pathological investigation. These routines improve the reliability and practical usage of the proposed method. Finally, the proposed method was utilized for grading a set of annotated HCC ROIs into five classes and obtained approximately 95.97% CCR.
Acknowledgments
This research is supported by the New Energy and Industrial Technology Development Organization in Japan under the research and development project of Pathological Image Recognition.
Biographies
Chamidu Atupelage received a BSc degree from the University of Colombo, Sri Lanka, in 2004, an MEng degree from Hiroshima University in 2009, and a PhD degree from Tokyo Institute of Technology in 2013. At present, he is a research fellow at Imaging Science and Engineering Laboratory, Tokyo Institute of Technology. He is a member of Information Processing Society of Japan. His research interest includes utilizing image processing and machine learning methods for quantitative biomedical image analysis.
Hiroshi Nagahashi received his BS and Dr. Eng. degrees from Tokyo Institute of Technology in 1975 and 1980, respectively. Since 1990, he has been with Imaging Science and Engineering Laboratory, Tokyo Institute of Technology, where he is currently a professor. His research interests include pattern recognition, image processing, and computer vision. He is a member of IEEE Pattern Analysis and Machine Intelligence Society, the Institute of Electrical Engineers of Japan, and the Information Processing Society of Japan.
Fumikazu Kimura received his PhD degree from the Department of Pathology, Kitasato University in 2010. Since 2011, he has been with the Global Scientific Information and Computing Center, Tokyo Institute of Technology, where he works as a researcher. His research interests include texture analysis, cell cycle differentiation for malignant tumor diagnosis. He is a member of Japanese Society of Clinical Cytology, Japanese Society of Pathology and International Academy of Cytology (C.M.I.A.C).
Masahiro Yamaguchi received his BS, MEng, and PhD degrees from Tokyo Institute of Technology in 1987, 1989, and 1994, respectively. He is a professor in the Global Scientific Information and Computing Center, Tokyo Institute of Technology since 2011. He worked as research associate and associate professor Tokyo Tech and project sub-leader in Akasaka Natural Vision Research Center, Telecommunication Advancement Organization (TAO), Japan. He interests on multispectral imaging, holography, medical image processing, and the information security.
Abe Tokiya received his PhD degree in 2005 from Tokyo Institute of Technology. After the graduation he worked as a postdoctoral researcher at Imaging Science and Engineering Laboratory in Tokyo Institute of Technology, Research Center for Frontier Medical Engineering, Chiba University, and Department of Pathology at Massachusetts General Hospital. From 2010, he has been working as a research associate at Department of Pathology, Keio University. His research interests are multispectral and histopathological image processing.
Akinori Hashiguchi received MD and PhD degrees from the School of Medicine, Keio University, Tokyo, Japan, in 1995 and 2011, respectively. He has worked as an instructor in the Department of Pathology, Keio University, since 1995 and is now engaged in research on digital pathology and pathology informatics.
Michiie Sakamoto received a PhD degree from Keio University, School of Medicine in 1991. He was the chief in Pathology Division, National Cancer Center Research Institute in Tokyo in 1999. He is currently a professor at the Department of Pathology, Keio University. He is an editor-in-chief of Pathology International and on the editorial boards of many international journals. His research interests are molecular pathology of cancer: multistep-carcinogenesis, early cancer, invasion and metastasis, and pathology informatics.
References
- 1.Ishak K., Goodman Z., Stochker T., Tumors of the Liver and Intrahepatic Bile Ducts (Atlas of Tumor Pathology), 3rd Series, American Registry of Pathology Press, Silver Spring, Maryland: (2001). [Google Scholar]
- 2.Edmondson H., Steiner P., “Primary carcinoma of the liver: a study of 100 cases among 48,900 necropsies,” Cancer 7(3), 462–503 (1954). 10.1002/(ISSN)1097-0142 [DOI] [PubMed] [Google Scholar]
- 3.Tahir M., Bouridane A., Kurugollu F., “An FPGA based coprocessor for GLCM and haralick texture features and their application in prostate cancer classification,” Analog Integr. Circuits Signal Process. 43(2), 205–215 (2005). 10.1007/s10470-005-6793-2 [DOI] [Google Scholar]
- 4.Tabesh A., et al. , “Multifeature prostate cancer diagnosis and Gleason grading of histological images,” IEEE Trans. Med. Imaging 26(10), 1366–1378 (2007). 10.1109/TMI.2007.898536 [DOI] [PubMed] [Google Scholar]
- 5.Huang P., Lee C., “Automatic classification for pathological prostate images based on fractal analysis,” IEEE Trans. Med. Imaging 28(7), 1037–1050 (2009). 10.1109/TMI.2009.2012704 [DOI] [PubMed] [Google Scholar]
- 6.Atupelage C., et al. , “Classification of prostate histopathology images based on multifractal analysis,” IEICE Trans. Inf. Process. E95-D(12), 3037–3045 (2012). 10.1587/transinf.E95.D.3037 [DOI] [Google Scholar]
- 7.Kim T., et al. , “Study on texture analysis of renal cell carcinoma nuclei based on the Fuhrman grading system,” in Proc. of 7th Int. Workshop on Enterprise Networking and Computing in Healthcare Industry, 2005 (HEALTHCOM 2005), pp. 384–387, Piscataway, Busan, Korea: (2005). [Google Scholar]
- 8.Novara G., et al. , “Grading systems in renal cell carcinoma,” J. Urol. 177(2), 430–436 (2007). 10.1016/j.juro.2006.09.034 [DOI] [PubMed] [Google Scholar]
- 9.McKeown M., Ramsay D., “Classification of astrocytomas and malignant astrocytomas by principal components analysis and a neural net,” J. Neuropathol. Exp. Neurol. 55(12), 1238–1245 (1996). 10.1097/00005072-199612000-00007 [DOI] [PubMed] [Google Scholar]
- 10.Glotsos D., et al. , “A hierarchical decision tree classification scheme for brain tumour astrocytoma grading using support vector machines,” in Proc. of the 3rd Int. Symposium on Image and Signal Processing and Analysis, 2003 (ISPA 2003), Vol. 2, pp. 1034–1038, IEEE, Rome, Italy: (2003). [Google Scholar]
- 11.Huang P., Lai Y., “Effective segmentation and classification for HCC biopsy images,” Pattern Recognit. 43(4), 1550–1563 (2010). 10.1016/j.patcog.2009.10.014 [DOI] [Google Scholar]
- 12.Atupelage C., et al. , “Computational grading of hepatocellular carcinoma using multifractal feature description,” Comput. Med. Imaging Graphics 37(1), 61–71 (2013). 10.1016/j.compmedimag.2012.10.001 [DOI] [PubMed] [Google Scholar]
- 13.Irshad H., et al. , “Methods for nuclei detection, segmentation, and classification in digital histopathology: a review-2014—current status and future potential,” IEEE Rev. Biomed. Eng. 7, 97–114 (2014). 10.1109/RBME.2013.2295804 [DOI] [PubMed] [Google Scholar]
- 14.Naik S., et al. , “Automated gland and nuclei segmentation for grading of prostate and breast cancer histopathology,” in 5th IEEE Int. Symposium on Biomedical Imaging: From Nano to Macro, 2008 (ISBI 2008), pp. 284–287, IEEE, Paris, France: (2008). [Google Scholar]
- 15.Veillard A., Kulikova M., Racoceanu D., “Cell nuclei extraction from breast cancer histopathologyimages using colour, texture, scale and shape information,” Diagn. Pathol. 8(1), 1–3 (2013). 10.1186/1746-1596-8-S1-S523298385 [DOI] [Google Scholar]
- 16.Ruifrok A. C., Johnston D. A., “Quantification of histochemical staining by color deconvolution,” Anal. Quant. Cytol. Histol. 23(4), 291299 (2001). [PubMed] [Google Scholar]
- 17.Kulikova M., et al. , “Nuclei extraction from histopathological images using a marked point process approach,” Proc. SPIE 8314, 831428 (2012). 10.1117/12.911757 [DOI] [Google Scholar]
- 18.Fuchs T., et al. , “Weakly supervised cell nuclei detection and segmentation on tissue microarrays of renal clear cell carcinoma,” Pattern Recognit. 5096, 173–182 (2008). 10.1007/978-3-540-69321-5_18 [DOI] [Google Scholar]
- 19.Kong J., et al. , “A comprehensive framework for classification of nuclei in digital microscopy imaging: an application to diffuse gliomas,” in 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, pp. 2128–2131, IEEE, Chicago, Illinois: (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mandelbrot B., The Fractal Geometry of Nature, WN Freeman, New York: (1983). [Google Scholar]
- 21.Barral J., Seuret S., “Combining multifractal additive and multiplicative chaos,” Commun. Math. Phys. 257(2), 473–497 (2005). 10.1007/s00220-005-1328-3 [DOI] [Google Scholar]
- 22.Lopes R., Betrouni N., “Fractal and multifractal analysis: a review,” Med. Image Anal. 13(4), 634–649 (2009). 10.1016/j.media.2009.05.003 [DOI] [PubMed] [Google Scholar]
- 23.Russell D., Hanson J., Ott E., “Dimension of strange attractors,” Phys. Rev. Lett. 45(14), 1175–1178 (1980). 10.1103/PhysRevLett.45.1175 [DOI] [Google Scholar]
- 24.Yang J., et al. , “Evaluating bag-of-visual-words representations in scene classification,” in Proc. of the Int. Workshop on Workshop on Multimedia Information Retrieval (MIR’07), pp. 197–206, ACM, New York: (2007). [Google Scholar]
- 25.Yang Y., Pedersen J., “A comparative study on feature selection in text categorization,” in Proc. of the Fourteenth Int. Conf. on Machine Learning (ICML 1997), pp. 412–420, Morgan Kaufmann, Tennessee: (1997). [Google Scholar]
- 26.Cruz-Roa A., Caicedo J. C., González F. A., “Visual pattern mining in histology image collections using bag of features,” Artif. Intell. Med. 52(2), 91–106 (2011). 10.1016/j.artmed.2011.04.010 [DOI] [PubMed] [Google Scholar]
- 27.Atupelage C., et al. , “Multifractal computation for nuclear classification and hepatocellular carcinoma grading,” in Proc. of the IASTED Int. Conf. on Biomedical Engineering (BioMed 2013), pp. 415–420, ACTA Press, Innsbruck, Austria: (2013). [Google Scholar]
- 28.Stoji T., Reljin I., Reljin B., “Adaptation of multifractal analysis to segmentation of microcalcifications in digital mammograms,” Physica A 367, 494–508 (2006). 10.1016/j.physa.2005.11.030 [DOI] [Google Scholar]
- 29.Grski A., “Pseudofractals and the box counting algorithm,” J. Phys. A 34(39), 7933–7940 (2001). 10.1088/0305-4470/34/39/302 [DOI] [Google Scholar]
- 30.Vese L. A., Chan T. F., “A multiphase level set framework for image segmentation using the Mumford and Shah model,” Int. J. Comput. Vision 50(3), 271–293 (2002). 10.1023/A:1020874308076 [DOI] [Google Scholar]
- 31.Jaiantilal A., “Classification and regression by randomforest-matlab,” https://code.google.com/p/randomforest-matlab (16May2009).
- 32.Lee W., Chen Y., Hsieh K., “Ultrasonic liver tissues classification by fractal feature vector based on m-band wavelet transform,” IEEE Trans. Med. Imaging 22(3), 382–392 (2003). 10.1109/TMI.2003.809593 [DOI] [PubMed] [Google Scholar]
- 33.Singhal A., “Modern information retrieval: a brief overview,” IEEE Data Eng. Bull. 24(4), 35–43 (2001). [Google Scholar]