Control of the Coupled Motion of a 6 DoF Robotic Arm and a Continuum Manipulator for the Treatment of Pelvis Osteolysis

Abstract

The paper addresses the coupled motion of a 6 degree of freedom robot and a snake-like dexterous manipulator (SDM) designed for the treatment of bone defects behind the implant during total hip arthroplasty revision surgery. We have formulated the problem as a weighted, multi-objective constraint, linear optimization. A remote center of motion (RCM) acts as a virtual constraint for the robot. The coupled robot kinematics does not assume piecewise-constant curvature for the SDM. We have evaluated our method by simulating the coupled system inside a potential lesion area.

I. Introduction

We have developed a snake-like dexterous manipulator (SDM) for medical applications with a focus on orthopaedic surgery [1, 2]. One motivating application is the treatment of osteolysis (bone degradation) behind the well-fixed acetabular component of a total hip arthroplasty (THA). The SDM is composed of superelastic nitinol with a 4mm open lumen for inserting different tools (e.g., curette, drill, auger, pincer, brush, vacuum). The notches cut on the body constrain the SDM to bend in a single plane. The SDM is designed to fit through the screw holes of the acetabular implant of the THA (6mm OD) and actuated using independent solid stainless steel cables passing through its walls [1].

In the envisioned application, the SDM will be positioned in the workspace by a robotic arm with at least six degrees of freedom (DoF) and uses screw holes in the acetabular implant as its entry to the patient’s body (Fig. 1). Controlling snake tip position requires concurrent control of the coupled SDM–robotic arm system. In this procedure, the screw hole acts as a RCM point, reducing the DoF of the robot. This RCM point can be created through hardware (e.g., the Laparoscopic Assistant Robot, LARS, [3]) or through virtual fixtures [4, 5].

Figure 1.

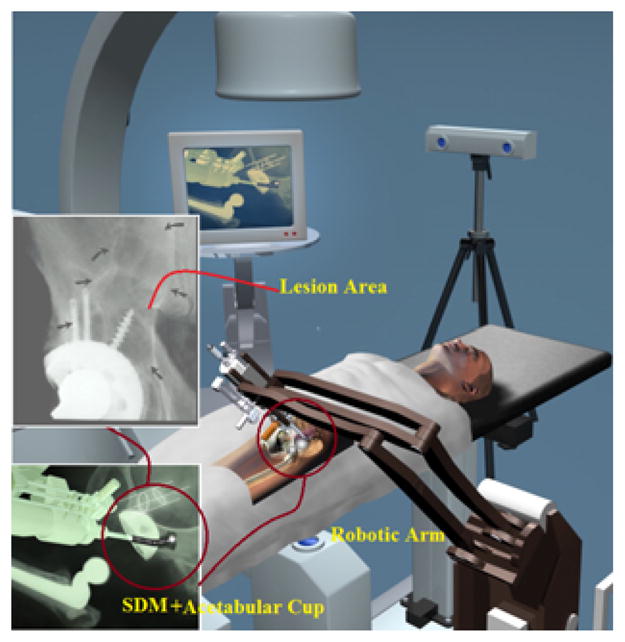
Positioning of the SDM in workspace using a robotic arm and its access to the osteolytic lesion through the screw hole of the acetabular implant [1].

For general applications using robotic arms without a mechanical RCM (e.g., UR5, Universal Robotics), recent literature suggests approaches developing a library of virtual fixtures for task primitives. These virtual fixtures were utilized for controlling the JHU steady hand robot [3], robotically-assisted sinus surgery [6], and suturing for minimally invasive surgery of the throat and upper airways [7]. These works formulated a constrained optimization problem where the goal was to obey the defined virtual fixtures and follow the desired motion as close as possible.

Controlling a coupled dexterous manipulator with a robotic arm using a constrained optimization algorithm has been done in [7]. This approach, however, utilized a robotic arm with a mechanical RCM and a complete kinematic model of their dexterous manipulator to control the system. In this work we modify this approach through the introduction of virtual fixtures for robots without a mechanical RCM. Moreover, our SDM is not well-characterized by the piecewise-constant curvature assumption reviewed by Webster et al. [8], requiring an experimentally-derived kinematic model [9]. Section II briefly describes the kinematics of the coupled manipulator. Section III introduces the constraints and objective functions for our constrained optimization control method. The simulation results are presented in Section IV.

II. Kinematic Model

A. UR5 Robot

Our system couples a UR5 [10] (Universal Robotics, Denmark) and the SDM (Fig. 2). The UR5 has a non-spherical wrist with six revolute joints and a spherical workspace. The D-H (Denavit-Hartenberg) parameters of the UR5 define six joint coordinate systems (Fig. 3). Using these D-H parameters forward kinematics can be calculated through (1):

$$T_{\mathit{Snakebase}}^w=T_1^w·T_2^1·T_3^2·T_4^3·T_5^4·T_6^5·T_{\mathit{Snakebase}}^6$$ (1)

Figure 2.

Snake-like Dexterous Manipulator(Left), UR5 robot [10](Right).

Figure 3.

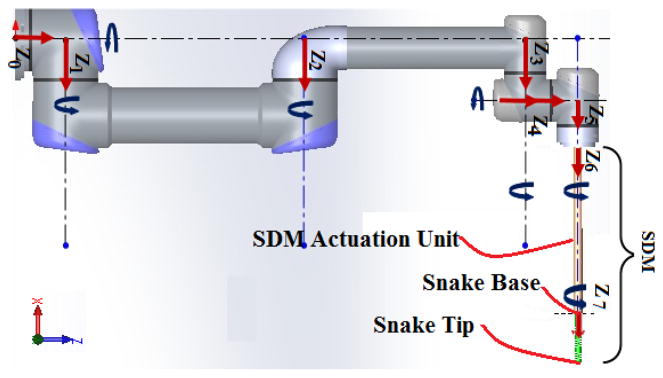
Defined D-H joint coordinate systems on the coupled robots

${\mathrm{T}}_{\mathrm{i}}^{\mathrm{j}}$ is a transformation from i^th coordinate to j^th coordinate. The velocity of the base of the SDM is related to the UR5 joint angles via the instantaneous direct kinematic Jacobian, J_UR5 ∈ ℝ^6×6, as:

$${\stackrel{.}{x}}_{\mathit{Snakebase}}^w=J_{UR5}·{\stackrel{.}{q}}_{UR5}=\left[\begin{array}{c}{J}_{vUR5}\\ J_{\omega UR5}\end{array}\right]·{\stackrel{.}{q}}_{UR5}$$ (2)

B. Snake-Like Dexterous Manipulator (SDM)

A series of experimental tests identified the relation between cable length (l) and tip position (p) [9]. In this method, nonlinear least-squares optimization has been used to fit a linear combination of Bernstein basis polynomials to the data for determining p_x. Afterward, p_z has been calculated based on p_x as sum of three sinusoids.

$$\begin{array}{l}{p}_x=f_1(\widehat{l})=B_n(\widehat{l})\\ p_y=0\\ p_z=f_2(p_x)=\sum _{i=1}^3{a}_{i}sin(b_i.p_x+c_i)\\ p_{\mathit{Snaketip}}^{\mathit{Snakebase}}=\left(\begin{array}{c}{p}_x\\ p_y\\ p_z\end{array}\right)=\left(\begin{array}{c}{f}_l(\widehat{l})\\ 0\\ f_2(f_1(\widehat{l}))\end{array}\right)\end{array}$$ (3)

l̂ is the normalized string length and B_n is an n^th order Bernstein polynomial. Coefficients a_i, b_i, and c_i represent the fit parameters for the i^th sinusoid. Differentiating (3) gives end-effector linear velocity, V, as:

$$V_{\mathit{Snaketip}}^{\mathit{Snakebase}}={\stackrel{.}{p}}_{\mathit{Snaketip}}^{\mathit{Snakebase}}=\left(\begin{array}{c}{\stackrel{.}{p}}_x\\ {\stackrel{.}{p}}_y\\ {\stackrel{.}{p}}_z\end{array}\right)=\left(\begin{array}{c}{\stackrel{.}{f}}_1(\widehat{l})\\ 0\\ {\stackrel{.}{f}}_2(f_1(\widehat{l}))\end{array}\right)$$ (4)

Where ṗ_x, ṗ_y, and ṗ_z are linear velocities of SDM tip. Fig. 4 shows the SDM tip position and velocity as a function of normalized string length.

Figure 4.

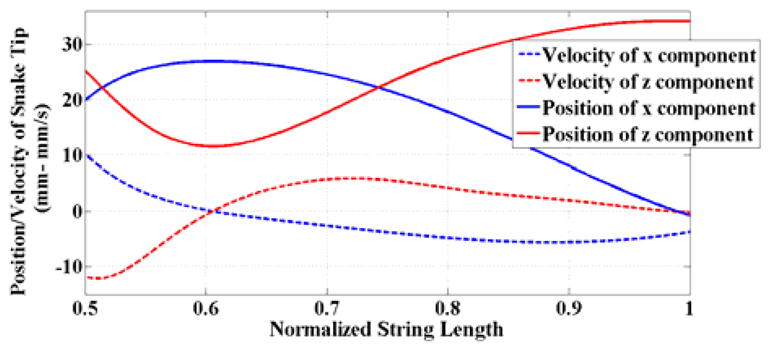
Components of tip velocity and position of SDM based on normalized string length. The characterized range of normalized string length is between 0.5 and 1 based experimental tests and SDM bending [9]

C. Kinematics model of the coupled manipulators

The forward kinematics and Jacobian of the coupled manipulators can be calculated using these relations:

$$\begin{array}{l}{p}_{\mathit{Snaketip}}^w=T_{\mathit{Snakebase}}^w·p_{\mathit{Snaketip}}^{\mathit{Snakebase}}\\ {\omega }_{\mathit{Snaketip}}^w={\omega }_{\mathit{Snakebase}}^w\\ V_{\mathit{Snaketip}}^w=V_{\mathit{Snakebase}}^w+R_{\mathit{Snakebase}}^w·V_{\mathit{Snaketip}}^{\mathit{Snakebase}}+{\omega }_{\mathit{Snakebase}}^w\times R_{\mathit{Snakebase}}^w·p_{\mathit{Snaketip}}^{\mathit{Snakebase}}\end{array}$$ (5)

Where $T_{\mathit{Snakebase}}^w$ is the transformation from snake base to world coordinate that is known using (1), and $R_{\mathit{Snakebase}}^w$ is the rotation matrix from snake base to world coordinate. $p_{\mathit{Snaketip}}^{\mathit{Snakebase}}$ is the value of (3). $V_{\mathit{Snaketip}}^w$ is the tip velocity of the SDM in world coordinate which is calculated using (4).

The coupled system has 7 independent variables, six for the UR5 (θ_UR5) and one for the SDM (q_SDM): q = [θ_UR5 q_SDM]. Using this definition the combined Jacobian matrix and linear and angular velocity of SDM ( ${\stackrel{.}{x}}_{\mathit{snake}}^W$) is:

$$\begin{array}{l}{J}_{\mathit{combined}}=[\begin{array}{cc}{J}_{UR5}& J_{\mathit{Snake}}\end{array}];J_{UR5}\in {ℝ}^{6\times 6},J_{\mathit{Snake}}\in {ℝ}^{6\times 1}\\ {\stackrel{.}{x}}_{\mathit{snake}}^W=J_{\mathit{combined}}·\stackrel{.}{q};J_{\mathit{combined}}\in {ℝ}^{6\times 7},\stackrel{.}{q}\in {ℝ}^{7\times 1}\end{array}$$ (6)

III. CONSTRAINED OPTIMIZATION CONTROL

During the procedure, the SDM will be positioned in the workspace by a UR5 robot and will access the lesion through the screw holes of an acetabular implant (Fig. 1). Ensuring the snake enters through the screw hole is achieved through the use of a virtual RCM applied to the UR5. Intraoperative control requires satisfying the RCM constraint while ensuring the SDM tip achieves the desired configuration. Solving this constrained optimization problem finds the joint angles of the coupled robots while minimizing the difference between the desired and actual robot tip [3]. In this work we use linear approximations of these nonlinear constraints to improve efficiency and allow robust computation [5].

A. Control Algorithm

For this preliminary work we assume that the SDM has passed through one of the holes of accetabular cup and the snake is completely inside the body. Also, we assume that there is no external force changing the snake configuration. With known initial joint angles of the UR5 and string length of SDM we can calculate the initial position of the tip. Therefore, we divide the control algorithm into these steps:

1. Estimate position of the coupled robots using (1) and (4).

2. Calculate desired incremental motion in Cartesian space

   $${\mathrm{\Delta }}_{\mathit{pos}}:{\mathrm{\Delta }}_{\mathit{pos}}=\mathit{Estimated}\mathit{Position}-\mathit{Deseried}\mathit{Position}$$
3. Consider Δt as a small time increment and use linear relations to approximate the incremental motion in Cartesian space, Δx as:

   $${\stackrel{.}{x}}_{\mathit{snake}}^W=J_{\mathit{combined}}·\stackrel{.}{q}\to \frac{\mathrm{\Delta }{x}_{\mathit{Snake}}^W}{\mathrm{\Delta }t}=J_{\mathit{combined}}·\frac{\mathrm{\Delta }q}{\mathrm{\Delta }t}\to \mathrm{\Delta }{x}_{\mathit{snake}}^W=J_{\mathit{combined}}·\mathrm{\Delta }q$$
4. Solve this constrained optimization problem minimizing the Euclidian error between desired and actual incremental motions through minimum joint motions of UR5 and SDM:

   $$\begin{array}{l}\mathrm{\Delta }q=arg\underset{\mathrm{\Delta }q}{min}({\Vert \mathrm{\Delta }x-{\mathrm{\Delta }}_{\mathit{pos}}\Vert }_2^2+{\Vert w·\mathrm{\Delta }q\Vert }_2^2);\mathrm{\Delta }q\in {ℝ}^{7\times 1}\\ s.t.A·\mathrm{\Delta }x\le b\end{array}$$ (7)

   Where Δq is desired incremental motions of the 7 DOF of the coupled robots, w is a diagonal matrix for weights. A and b matrices define the virtual RCM constraint and SDM string length constraint, respectively.

5. Update the robot state:

   $$q_{\mathit{New}}=q_{\mathit{Old}}+\mathrm{\Delta }q$$

B. Defining Constraints

1) Virtual RCM constraint

The RCM limits movement perpendicular to the shaft axis of the SDM. This means that the distance between the closest point on the shaft axis to the RCM in each time step should be less than a small value of ε. By this definition we confine movements in a virtual cylinder around the shaft axis of the SDM with radius of ε (Fig. 5). We estimate this cylinder by a polygon with m sides, where m defines the degree of approximation of a circle by a polygon. According to Fig. 5 and using this approximation, the RCM constraint must perform two tasks:

Figure 5.

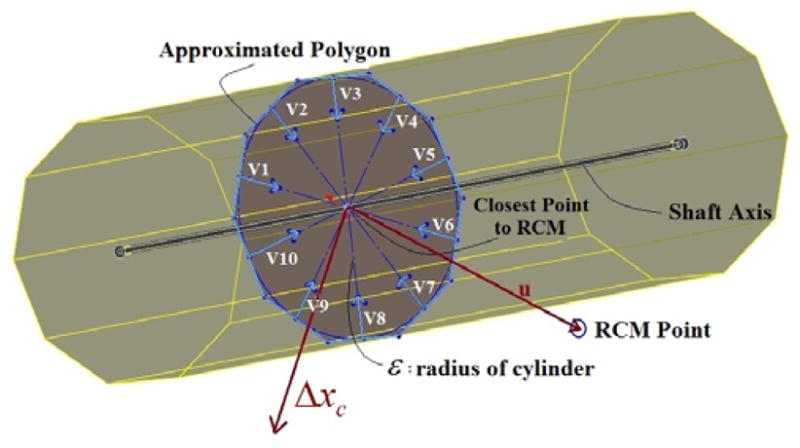
Defining RCM constraint based on approximated polygon

1. Maintaining the closest point on the shaft axis to the RCM inside the approximated cylinder with radius ε when the shaft passes through the RCM.

2. Minimizing movements of the closest point to the RCM along the shaft axis when the shaft is off the RCM and during new incremental movements.

Therefore we can write these constraints as:

$$\begin{array}{l}\underset{A_1}{\underbrace{\left[\begin{array}{c}{v}_1\\ ⋮\\ v_m\end{array}\right]}}·\mathrm{\Delta }{x}_c\le \underset{b_1}{\underbrace{\left[\begin{array}{c}\epsilon +v_1·u\\ ⋮\\ \epsilon +v_m·u\end{array}\right]}};\\ \mathrm{\Delta }{x}_c=J_{\mathit{closest}\text{point}}·\mathrm{\Delta }{q}_{UR5};\mathrm{\Delta }{q}_{UR5}\in {ℝ}^{6\times 1}\end{array}$$ (8)

Where Δx_c is the incremental Cartesian motion of the closest point on the shaft and J_{closest point} is the Jacobian matrix of this point. Vector u is the vector between the RCM and the closest point on the shaft, vectors v_i are normal vectors of each side of the polygon which approximates the cylinder with radius ε.

2) Constraint on SDM string length

Considering a single-cable bend, the model of the SDM requires the total string length not exceed 9 mm (i.e., the maximum the strings can be pulled) and no less than 0 mm (i.e., the string is fully relaxed). Therefore, we can write this constraint as:

$$\begin{array}{l}0mm\le q_{\mathit{SDM}}+\mathrm{\Delta }{q}_{\mathit{SDM}}\le 9mm\\ \underset{A_2}{\underbrace{\left[\begin{array}{c}1\\ -1\end{array}\right]}}·\mathrm{\Delta }{q}_{\mathit{SDM}}\le \underset{b_2}{\underbrace{\left[\begin{array}{c}9mm-q_{\mathit{SDM}}\\ q_{\mathit{SDM}}\end{array}\right]}}\end{array}$$ (9)

Where q_SDM is the string length and Δq_SDM ∈ ℝ^1×1 is incremental change in cable length.

3) Combining constraints as matrix A and b

The resulting constraints of (8) and (9) can be realized as a block diagonal matrix, A, and a vector, b:

$$\left[\begin{array}{cc}{A}_1& 0\\ 0& A_2\end{array}\right]·\left[\begin{array}{c}{J}_{\mathit{closest}\text{point}}\\ 1\end{array}\right]·\mathrm{\Delta }q\le \left[\begin{array}{c}{b}_1\\ b_2\end{array}\right];\mathrm{\Delta }q\in {ℝ}^{7\times 1}$$ (10)

IV. Simulation

We considered a 3D path for the snake that is a specific boundary of a simulated lesion and is inside a confined cubic space with sides of 7 cm (Fig. 6). The flexible portion of the SDM is 35 mm and the actuation unit has a length of 30 cm. The radius ε of the virtual cylinder (Fig. 5) was 5 mm, which is equal to the radius of the screw holes in the acetabular cup (the outer radius of the SDM is 3 mm). The coupled system should be able to cover the simulated lesion while satisfying constraints described in the previous section.

Figure 6.

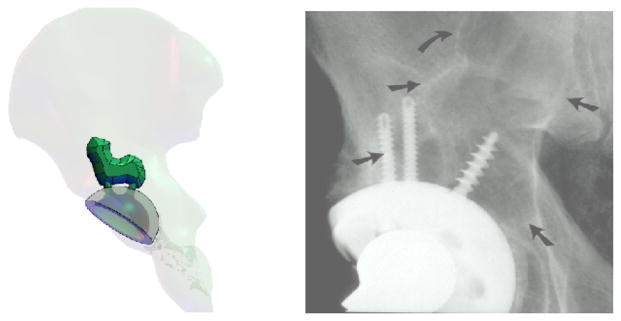
The simulated lesion area (left) and an example real x-ray image of a lesion (right). Note that the simulated lesion geometry does not correspond to the example geometry.

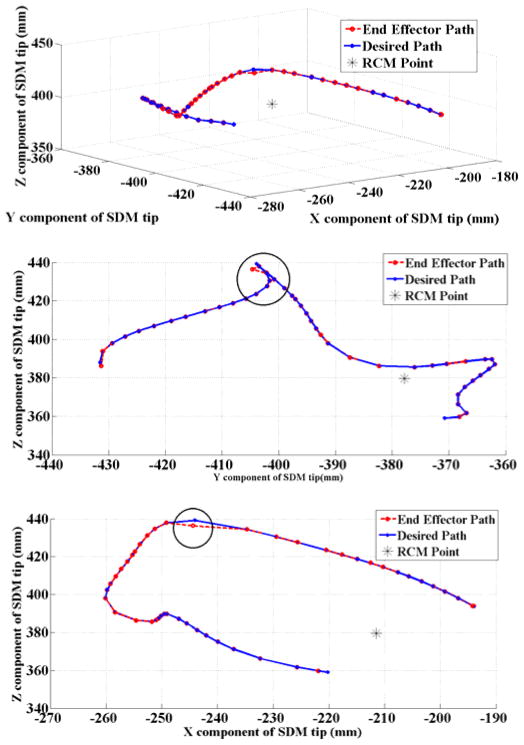
In this preliminary work we assumed that the flexible snake region is inside the body and no external force is applied to the tip of the SDM. For solving the constrained linear least-squares problem we have used lsqlin function in Matlab (The MathWorks Inc, Natick, MA). Note that the constraints in this problem can be nonlinear; however, in this work we have used linear approximation because computation for a linear constrained quadratic optimization problem is efficient and robust [5]. Overall, the control architecture tracked the desired path well (Fig. 7) with an average error of 4.2±2.1mm. The maximum tip position error was 10 mm, which occurred due to a sharp change in the path (Fig. 7).

Figure 7.

3D view (up), X-Z view (middle), and Y-Z view (down)of desired path and achieved positions by snake tip. The circle demonstrates the location of maximum deviation from the path.

In this simulation we have considered 4cm of snake base inside the body. Example snake configurations are presented in Fig. 8. According to this figure, the robot changes its configuration such that with minimum joint movements the desired goal could be achieved while satisfying the RCM constraint.

Figure 8.

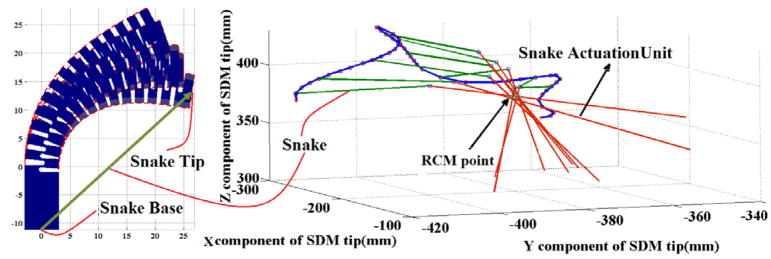
Optimization result for configuration (Left) and orientation of the snake and actuation unit (Right) in some points of the desired path.

V. Conclusion

In this work we have modified the constrained optimization algorithm and virtual fixture method of [5] to control the position of a coupled continuum robot and 6 DoF robotic arm inside a confined space. For modeling the kinematics of the SDM we have used the results of experiments in [9] to derive the relation between cable length change and tip velocity. The errors found during this simulation are largely due to the complex path. Considering only a smooth path, we find average error of 1.5±1.03. Moreover, the surgeon is interested in sweeping through the lesion. Doing so may not require exact control of the tip of the manipulator and, thus, larger errors may be acceptable.

While the model showed satisfactory accuracy for free bending, the presence of external forces applied to the body or the tip of the SDM may require extending the model to incorporate additional inputs such as introduction of opposing cable tension to increase SDM stiffness, real-time measurement of cable tension as well as opposing cable lengths, etc. Additionally, real-time novel technologies for SDM tip (or shape) sensing can also improve the presented approach for the control of the SDM. To that end we are currently investigating and addressing the challenges associated with the application of Fiber Bragg Grating (FBG) optical sensors [11]. It is also notable that during the proposed surgical application, we acquire intermittent x-ray images at the request of the surgeon. Anytime such images are obtained, the model can then reset to the actual pose of the SDM obtained through a deformable 2D/3D registration [12] to avoid accumulation of pose error during the procedure.