Simulation-Guided DNA Probe Design for Consistently Ultraspecific Hybridization

Abstract

Hybridization of complementary sequences is one of the central tenets of nucleic acid chemistry; however, the unintended binding of closely related sequences limits the accuracy of hybridization-based approaches for analyzing nucleic acids. Thermodynamics-guided probe design and empirical optimization of reaction conditions have been used to enable discrimination of single nucleotide variants, but typically these approaches provide only an approximate 25-fold difference in binding affinity. Here we show that simulations of the binding kinetics are both necessary and sufficient to design nucleic acid probe systems with consistently high specificity as they enable the discovery of an optimal combination of thermodynamic parameters. Simulation-guided probe systems designed against 44 different target single nucleotide variants sequences showed between 200- and 3000-fold (median 890) higher binding affinity than their corresponding wildtype sequences. As a demonstration of the usefulness of this simulation-guided design approach we developed probes which, in combination with PCR amplification, we use to detect low concentrations of variant alleles (1%) in human genomic DNA.

Detecting small changes in nucleic acid sequence is crucial in genomics research and in personalized medicine [1]. In particular, single-nucleotide variants (SNVs) at low variant allele frequency (VAF) have gained recent prominence as biomarkers for cancer molecular diagnostics [2–4]. Technology platforms developed to analyze nucleic acid sequence variations include next generation sequencing [5], specialized digital PCR [6], isothermal amplification assays [7–10], microarrays [11, 12], multiplexed barcode assays [13, 14], differential electrophoretic systems [15], and allele-specific PCR [16]. Crucially, all of these nucleic acid assays rely on the specificity of Watson-Crick base pairing at some step of their workflow, such as primer hybridization to a genomic DNA template.

Even in empirically optimized reaction conditions (e.g. temperature), discrimination of nucleic acids differing by a single nucleotide is challenging, with median hybridization-affinity difference of between 5 and 26 [17–21]. The relatively poor specificity of hybridization thus necessitates the more advanced and complex instrument platforms to detect intended target at low VAFs. As complementary or competing technologies, modifications in nucleic acid chemistry [22–24] have also been employed for rare nucleic acid detection [25–27]. Finally, chemicals additives such as formamide have been used to reduce nonspecific interactions in certain applications [28].

In applications where the sequences of both the target SNV and the corresponding wildtype (WT) are known, hybridization selectivity can be improved through the use of sequence-specific blocking agents to reversibly or irreversibly bind the WT molecules, in the same solution as primers or probes specific to the target SNV sequence [16, 17, 19, 29]. The homogeneous nature of their reaction with a heterogeneous sample makes the use of such Competitive Compositions (a target-specific Probe and a WT-specific Sink, here both DNA molecules) convenient for analytical and diagnostic applications. However, even Competitive Compositions struggle to consistently achieve high binding selectivity for all SNV/WT sequence pairs, even in assays where enzymes are used to further improve specificity [16, 29].

Here, we show that there exists an optimal combination of thermodynamic parameters of Probe and Sink that attains extremely high (1000+) selectivity, quantitated as the fold-change binding affinity difference between the SNV and the WT sequences to the Probe. These optimal parameters vary based on the sequences of the SNV and WT, on the design architecture of the Probe and Sink, and on reagent concentrations and assay conditions. In this manuscript, we constructed a kinetic reaction model of the underlying hybridization processes to predict the optimal parameter values. Experimentally, our simulation-informed Competition Compositions achieved a median 890-fold selectivity for 44 cancer-related DNA SNVs, with a minimum of 200; this represents at least a 30-fold improvement over previous hybridization-based assays (Table 1). Furthermore, we have additionally applied this technology to assay low VAF sequences from human genomic DNA following PCR, as well as directly to synthetic RNA sequences. By achieving these results without experimental optimization, we have shown the sufficiency of kinetic simulations to guide nucleic acid reagent design; the fact that the results we attained are significantly better than previous studies and reports show the necessity of such a model-informed approach.

Table 1.

Selective Detection Systems

System	Design Method	Median SNV Fold-Change
Molecular Beacons [16]	Empirical (Temperature, Loop Length)	10
Yin-Yang Probes [18]	Formulaic (7nt toehold)	10
Toehold Probes [20]	Thermodynamic (ΔG° ≈ 0)	26
Competitive Compositions (this work)	Simulation (kinetic modeling)	890

Theory and Modeling Results

Here, we consider the use of Competitive Compositions for detecting a SNV sequence in the presence of WT sequence, the latter of which may be in excess. A generalized Competitive Composition schematic is shown in Fig. 1a; both the Probe and the Sink may adopt any of a large number of architectures, such as those reported in literature [17, 19–21]. We believe our analysis and approach to hold regardless of specific implementation. Of the four reactions shown, the two involving the Probe lead to a downstream detection or amplification event; the design process thus seeks Probe and Sink constructions which maximize the Signal while minimizing Noise.

Figure 1. Detection of rare nucleic acid variants by Competitive Compositions.

(a) A Competitive Composition comprises a Target-specific Probe and a Wildtype-specific Sink molecule.

Potential architectures of the Probe and Sink are shown in the exploded panel. The state energies of different products are shown; Single nucleotide variant (SNV) and Wildtype (WT) molecules bound to Probe produce detectable signal. (b) Energy level diagram of the Competitive Composition system describes the equilibrium distribution according to a statistical mechanics model. The occupancy of each state is determined by the state's energy E, which is in turn determined by the sequence design of the Probe and Sink, as well as the reaction conditions. (c) The specificity and sensitivity of the Competitive Composition depend on values of E₁ and E₂; shown are analytic results assuming ΔΔG°₁ = 3 kcal/mol and ΔΔG°₂ = 4 kcal/mol at 37 °C. Discrimination factor is the fold-change difference in yield of the SNV and the WT in binding to the Probe. Qualitatively similar results are observed for other values of ΔΔG°. (d) The normalized fold-change β metric expresses a combination of system specificity and sensitivity. When [SNV]₀ = 0.5 nM, [WT]₀ = 1500 nM, and Background = 0.04 nM, there is a ray-shaped parameter space that yields optimal β at equilibrium.

Equilibrium analysis

We begin by considering the thermodynamics of the system, which predicts equilibrium behavior. To simplify the analysis, we first assume that the reactions of the Probe and Sink are independent and do not affect one another. This assumption allows us to use a statistical mechanics model of the equilibrium distribution (Fig. 1b). Each Target (SNV) molecule can exist in one of three states: unbound, bound to the Probe, or bound to the Sink. We can assign an energy (E) to each of the three states, and for convention define the unbound state to possess E = 0; the energies of the other two states (E₁ and E₄) will depend on the favorability of the Probe and Sink in reacting with Target.

The occupancies of each state follows a Boltzmann distribution with probability e^(−E₁ / Rτ) / Z_SNV, where Z_SNV ≅ e⁰ + e^(−E₁ / Rτ) + e^(−E₄ / Rτ) is the partition function, R is the ideal gas constant, and τ is the temperature in Kelvin.

Each Wildtype (WT) molecule likewise occupies one of three states: unbound (0), bound to Probe (E₃), or bound to Sink (E₂). Due to the sequence similarity between the SNV and the WT, the values of E₃ and E₄ are linked to E₁ and E₂, respectively, via:

$$E_3=E_1+\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}°}_1$$

$$E_4=E_2+\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}°}_2$$

where ΔΔG° refers to the thermodynamics of a single base mismatch relative to a perfect match (Section S1). The values of ΔΔG° vary depending on sequence, temperature, and buffer conditions, but are typically between 1 and 6 kcal/mol.

Two crucial metrics of goodness for molecular assay are specificity and sensitivity; for a Competitive Composition, these are quantitated as:

$$\text{Sensitivity}(\text{Yield})\cong [\mathrm{S}\mathrm{N}\mathrm{V}•\text{Probe}]/{[\mathrm{S}\mathrm{N}\mathrm{V}]}_0=\mathrm{e}^(-E_1/\mathrm{R}\mathrm{\tau })/{\mathrm{Z}}_{\mathrm{S}\mathrm{N}\mathrm{V}}$$

$$\text{Specificity}(\text{Discrimination Factor})\cong ([\mathrm{S}\mathrm{N}\mathrm{V}•\text{Probe}]/{[\mathrm{S}\mathrm{N}\mathrm{V}]}_0)/([\mathrm{W}\mathrm{T}•\text{Probe}]/{[\mathrm{W}\mathrm{T}]}_0)=(\mathrm{e}^(-E_1/\mathrm{R}\mathrm{\tau })/{\mathrm{Z}}_{\mathrm{S}\mathrm{N}\mathrm{V}})/(\mathrm{e}^(-E_3/\mathrm{R}\mathrm{\tau })/{\mathrm{Z}}_{\mathrm{W}\mathrm{T}})$$

where [SNV]₀ and [WT]₀ represent the initial concentrations of SNV and WT molecules, respectively.

Fig. 1c shows the equilibrium specificity and sensitivity as functions of E₁ and E₂ (here, ΔΔG°₁ = 3 and ΔΔG°₂ = 4 kcal/mol). Probe/Sink thermodynamic parameters that are conducive to high sensitivity are not favorable for high specificity, and vice versa. However, both specificity and sensitivity are important for real-world assays. To consider an appropriate tradeoff between specificity and sensitivity, we introduce a new metric, the normalized fold-change β, mathematically expressed as:

$$\mathrm{\beta }\cong ([\mathrm{S}\mathrm{N}\mathrm{V}•\text{Probe}]/\mathrm{V}\mathrm{A}\mathrm{F})/(\text{Background}+[\mathrm{W}\mathrm{T}•\text{Probe}])$$

where the variant allele frequency (VAF) is defined as VAF ≅ [SNV]₀ / [WT]₀, and the Background is a constant. Background could represent the aggregate of all sources of unavoidable detection signal (e.g. detector dark current, autofluorescence, ambient noise, other artifacts), or it could represent a minimal signal needed based on the detection mechanism.

Note that in the limit of Background = 0, β becomes identical to specificity (discrimination factor); consequently, β accounts for specificity. For a positive Background value, its presence in the denominator causes β to decrease in the limit of decreasing Yield, so β likewise accounts for sensitivity. Fig. 1d shows that there is a ray-shaped parameter space of E₁ and E₂ that yields optimal β at equilibrium. The position of the optimal ray and its corresponding maximum β vary based on ΔΔG° values, temperature, concentrations of SNV and WT, and the value of the Background, but the qualitative ray-shaped optimal parameter space generally holds.

Kinetics and simulations

The thermodynamics (statistical mechanics) model of Competitive Compositions fails to account for kinetics; Competitive Compositions with highly negative E₁ and E₂ do not practically reach equilibrium (e.g. half-life of years). Additionally, the model assumes a large excess concentration of Probe and Sink, and furthermore assumes that the reactions of SNV and WT have no impact on one another. To address these inaccuracies of the statistical mechanics model and provide quantitative guidance to Competitive Composition designs, we construct an ordinary differential equation model of the four reactions involved (Section S1 for details).

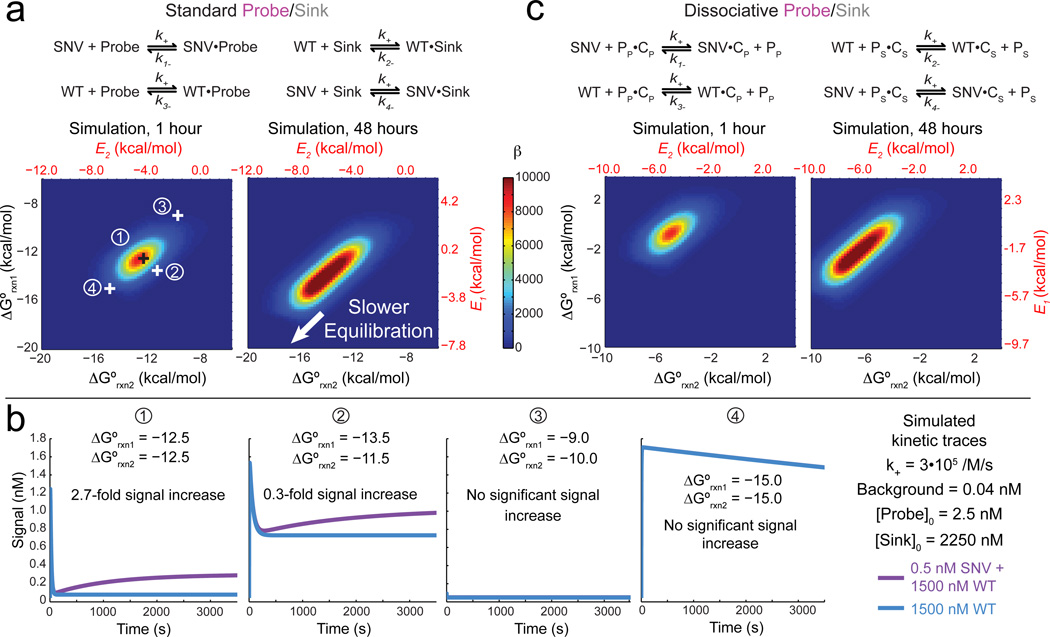
Accurate kinetic modeling requires knowledge of the architecture of the Probe and Sink, which can be broadly classified as either standard or dissociative (Fig. 2ac). Unlike standard probes (e.g. Taqman), dissociative probes [19, 21, 30] release an auxiliary species upon hybridization to their target. Although more complex, dissociative probes possess advantages in robustness to temperature and buffer conditions [21], so we explicitly model these as well as standard probes.

Figure 2. Kinetic simulations of Competitive Compositions.

(a) Reactions and simulations of standard (non-dissociative) Probe and Sink architectures. At t = 1 hr, there is a single optimal combination of ΔG°_rxn1 and ΔG°_rxn2 that yield highest β; corresponding E values are plotted in red. At t = 48 hr, the parameter space yielding high β broadens slightly; the lower left corner (highly negative ΔG°_rxn1 and ΔG°_rxn2) is slow to achieve equilibrium. Four representative combinations of ΔG°_rxn1 and ΔG°_rxn2 are shown; 1 represents the optimal combination, 2 represents a suboptimal combination with significantly lower selectivity, 3 represents a grossly incorrect combination, and 4 represents a combination that would have produced high selectivity after significantly longer reaction time. (b) Example simulation traces for different combinations of ΔG°_rxn1 and ΔG°_rxn2. (c) Reaction schemes and simulations for dissociative Probe and Sink architectures that release an auxiliary protector species P upon binding. P_P refers to protector for the Probe, and P_S refers to the protector for the Sink; P_P•C_P refers to the dissociative probe and P_S•C_S refers to the dissociative sink. Optimal parameter values are shifted relative to dissociative Probes, but there is likewise a single optimal combination of ΔG°_rxn1 and ΔG°_rxn2 that yield highest β at t = 1 hr.

Fig. 2ab show kinetic simulation results for standard probes. The rate constants of all forward reactions are assumed to be k₊ = 3 • 10⁵ M⁻¹ s⁻¹, based on literature [30, 31], and the rate constants of the reverse reactions are calculated based on equilibrium constants and the assumed forward rate constant.

The standard free energies ΔG°_rxn1 of the Probe hybridizing to SNV and ΔG°_rxn2 of Sink hybridizing to WT correspond to specific values of E₁ and E₂, respectively. Their effects on the β after 1 hour or 48 hours of reactions are shown; here, Background value was set at the equivalent of 0.04 nM, or roughly 1.6% of the maximum yield.

At t ≤ 1 hr, there is a single optimal combination of ΔG°_rxn1 and ΔG°_rxn2 that yields a maximum β value. At t = 48 hr, the parameter space of ΔG°_rxn1 and ΔG°_rxn2 that yields high β values broadens to a linear combination spanning roughly 3 kcal/mol. As reaction time approaches infinity, our simulations predict the optimal parameter space yielding maximal β will continue to expand to the lower left (more negative values of ΔG°_rxn1 and ΔG°_rxn2).

The optimal parameter space for (ΔG°_rxn1, ΔG°_rxn2) is rather small, with a radius of about 1 kcal/mol. In comparison, the average ΔG° of a single base stack is roughly 1.4 kcal/mol at 37 °C [32]. Fig. 2b shows that a 1 kcal/mol offset in ΔG°_rxn1 and ΔG°_rxn2 can produce a notable (9-fold) reduction in β. Competitive Compositions designed naively without simulation guidance exhibit poor, if any, discrimination between SNV and WT; for example, the ΔG°_rxn1 and ΔG°_rxn2 values selected in panel (4) of Fig. 2b exhibit no significant discrimination at t = 1 hr, despite exhibiting high β at t = 48 hr and at equilibrium.

Dissociative Probe/Sink pairs show qualitatively similar simulation results, but the optimal ΔG° values are significantly different (Fig. 2c). When the simulation results are plotted against state energy E values instead (red scales in Fig. 2ac), the predicted β landscape becomes quantitatively similar. For example, at t = 1 hr, the optimal combination of (E₁, E₂) are (−0.6, −5.0) for standard Probe/Sink, and (−0.5, −5.4) for dissociative Probe/Sink.

Our kinetic simulations thus suggest the optimal ΔG°_rxn of the Probe and Sink, which in turn guides sequence-level design; Fig. 4a shows a typical design workflow. Because of the similarity of the optimal (E₁, E₂) values from the statistical mechanics model as from kinetic simulations, the reader may be tempted to use the former to inform Probe and Sink design (i.e. picking the most positive E₁ and E₂ values from the high β region of the optimal ray). This is not recommended, because the mapping between ΔG°_rxn and E values depend sensitively on the exact concentration of the species, the structure of the reactions, and the sequences of the SNV and WT. For some ΔΔG° values, the deviations between the kinetics and statistical mechanics model are 2 kcal/mol (Section S1, Fig. S1–2).

Figure 4. Design workflow and experimental demonstration of Competitive Composition.

(a) Competitive Composition design workflow. (b) ΔΔG° (kcal/mol) of the two mismatch bubbles at 37 °C, in 1M Na⁺. (c) The Competitive Composition here consists of a target-specific X-Probe and a WT-specific Sink, with near-optimal ΔG°_rxn values (kcal/mol). (d) Sink architecture and sequence; the sequences of the X-Probe, Target, and WT are the same as in Fig. 3a. (e) Experimental time-based fluorescence response of Competitive Composition to different variant allele frequencies (VAF) of the target. β is higher for experiments at lower VAF due to the relatively smaller contribution of background fluorescence f_B.

Experimental results

X-Probes

Simulation-guided design of Competitive Compositions should yield high β values for discriminating SNV and WT sequence regardless of the exact architecture of the Probes and Sinks.

We decided to initially validate our simulation-guided probe design using conditionally fluorescent probes, in which binding yield can be accurately mapped to observed fluorescence. Molecular beacons [17] and toehold probes [21] both would have been reasonable choices for probe architecture, but are not ideal because rigorous testing on tens of different SNV/WT pairs would have required many different fluorophore- and quencher-labeled species, and have been very expensive.

To combat high oligonucleotide synthesis costs, we developed the X-Probe (Fig. 3a), a conditionally fluorescent nucleic acid probe in which the two functionalized oligonucleotides (F and Q) have sequences decoupled from the SNV/WT sequence. Thus, the same F and Q species could be used for any number of X-Probe designs targeting different sequences. The marginal cost of a new X-probe is only that of the two component oligonucleotides, P and C, with sequence dependent on the SNV sequence. Both P and C are unmodified, do not require post-synthesis purification, and in total cost less than $20 from typical oligonucleotide providers. From our experiments, the averaged price of each X-Probe was more than 80% lower than that of a molecular beacon.

Figure 3. The X-Probe is a dissociative probe that conditionally fluoresces upon hybridization to its DNA target.

Its construction utilizes universal functionalized strands F and Q; only the regions in green and red are target-specific. (a) Sequences of the X-probe targeting the EGFR-L858R (c.2573T>G) mutation; ROX denotes carboxy-X-rhodamine, and RQ denotes the Iowa Black Red Quencher. The polymorphic nucleotide (shown in red) can also exist in the double-stranded specific region for some probe designs (Section S3). (b) Experimental time-based fluorescence response of 10 nM X-Probe to 20 nM Target (red) and to 20 nM WT (light green); triplicate experimental traces are displayed. All triplicate experiments, including X-Probe to 5 other target sequences, show less than 5% variability (Section S5).

All experiments were performed at 37 °C in 5× PBS buffer. (c) Fluorescence response of 10 nM X-Probe to 500 nM WT (100% variant allele frequency (VAF), dark green) and to 500 nM WT plus 5 nM Target (1% VAF, yellow). Triplicate experimental traces are displayed. Normalized fold-change β is calculated from the VAF, the background fluorescence f_B, control fluorescence due to the WT f_C, and the additional fluorescence due to the SNV f_A.

The reaction mechanism of the X-Probe and its intended target (the SNV) is similar to that of the toehold probe [21] (Section S2). When the X-Probe reacts with its target molecule, the PQ sub-species is displaced, and the quencher on Q (black dot) is delocalized from the fluorophore on F (purple star), resulting in an increase of fluorescence. The strand displacement process is an enzyme-free process based on a number of individual single-base breakage and formation events; this process has been well-studied [30, 33–35] and has been characterized to be very fast, with half-life of under 1 second for oligonucleotides of under 100 nucleotides. Using standard DNA-DNA hybridization thermodynamic parameters [32], we designed P and C sequences resulting in X-Probes that react with their intended targets with optimal ΔG°_rxn1 informed by simulation.

Fig. 3b shows the time-based fluorescence response of the X-Probe targeting the EGFR-L858R (c.2573T>G) mutation to a synthetic oligonucleotide with the EGFR-L858R sequence, and to the same concentration of a synthetic oligonucleotide bearing the EGFR wildtype (WT) sequence. Fig. 3c shows the X-probe response to a larger concentration of the WT EGFR sequence, and to the same WT concentration with 1% variant allele frequency (VAF) of the EGFR-L858R target. Here, the reactions are judged to have reached equilibrium at t = 45 min, and β = 145 is estimated from the fluorescence data as:

$$\mathrm{\beta }=(f_{\mathrm{A}}/\mathrm{V}\mathrm{A}\mathrm{F})/(f_{\mathrm{B}}+f_{\mathrm{C}})$$

where f_B is the background fluorescence due to incomplete quenching and nonspecific fluorescence, f_C is the additional fluorescence induced by the wildtype, and f_A is the additional fluorescence induced by the target. Section S4 shows similar fluorescence results for 44 X-Probes to their corresponding DNA or RNA targets and their corresponding β values. The observed β values are similar to and consistent with the discrimination factors observed for toehold probes [21].

Competitive Compositions

For our Competitive Composition components, we use the X-Probe architecture for the Probe and the toehold probe [21] architecture for the Sink. We designed 44 Competitive Compositions based on the design workflow as outlined in Fig. 4a (see Section S6), against 44 different SNV/WT pairs. The SNVs are selected from frequently observed driver mutations in COSMIC cancer sequence database [36]. Recall that optimal ΔG°_rxn1 and ΔG°_rxn2 depend sensitively on the values of ΔΔG°₁ and ΔΔG°₂, corresponding respectively to the thermodynamic penalties of WT bound to Probe, and SNV bound to Sink. For the 44 WT/SNV sequence pairs we tested in this work, optimal ΔG°_rxn1 and ΔG°_rxn2 values varied from −1.6 to −0.6 kcal/mol and from −6.4 to −2.8 kcal/mol, respectively (Fig. S6-4).

Fig. 4bcd shows an example Competitive Composition construction targeting the EGFR-L858R (c.2573T>G) / EGFR-WT pair. Fig. 4e shows the time-based fluorescence traces of the Competitive Composition reacting with samples containing different VAFs of the EGFR-L858R SNV sequence.

The observed β values for Competitive Compositions are significantly higher than that of the X-Probe alone (Fig. 3c), supporting our theoretical and simulation analysis of the Competitive Composition.

The calculated values of β are higher for experiments with lower VAF because f_B is small compared to f_C, leading the value of β to approach that of the discrimination factor. Section S7 for results using fluorophore-labeled Sinks to further verify successful binding of the WT to the Sink.

The fluorescence observed maps accurately to the total concentration of Probe bound to either SNV or WT, but the concentration of [Probe • SNV] is not linear with the initial concentration of SNV. In experiments ranging from 0.1 to 300 nM SNV, in the presence of 100 nM WT, we observe a monotonic, sub-linear increase in signal with SNV concentration as expected (Section S8). Accurate quantitation would thus require a calibration curve.

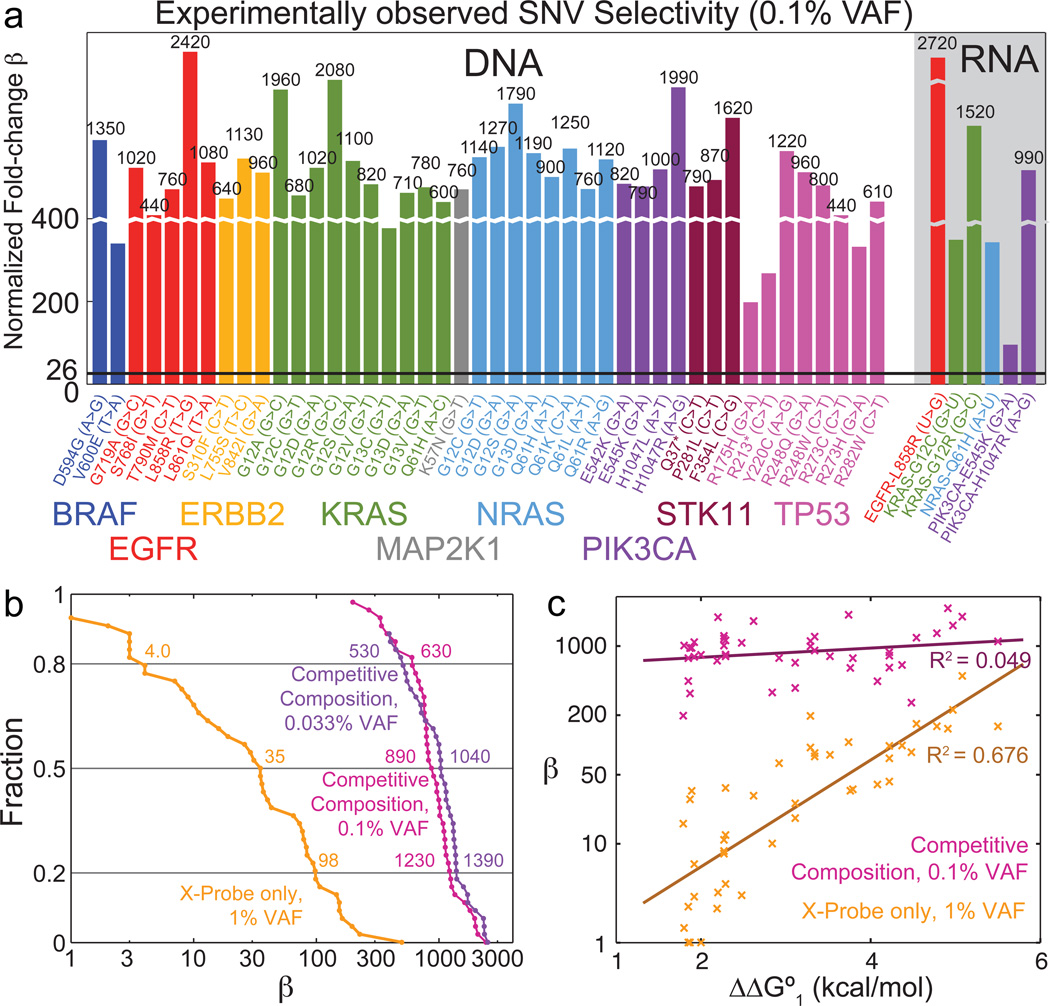
Fig. 5a summarizes experimental β values for Competitive Compositions to all 44 Competitive Compositions we test against all 44 corresponding DNA SNV/WT sequence pairs, as well as against 6 representative RNA SNV/WT sequence pairs. We performed fewer experiments on RNA due to the high cost of synthetic RNA oligonucleotides. RNA SNV/WT pairs generally produced lower β than their corresponding DNA pairs because the Competitive Compositions were designed based on ΔΔG° values for DNA. ΔΔG° values for RNA are incomplete in literature [37, 38]. Raw fluorescence traces for all Competitive Composition experiments are shown in Sections S9–S11.

Figure 5. Summary of Competitive Composition experimental results on synthetic targets.

(a) Experimentally observed normalized fold-change β for Competitive Compositions designed to 44 SNV cancer mutation sequences across 9 genes [36], and their corresponding WT sequences. The black horizontal line shows β = 26, the previous best median β demonstrated [20]. (b) Distribution of β for X-Probes only and Competitive Compositions. Also shown is Competitive Composition results with 0.033% VAF (Section S10). The 60% confidence interval for X-Probes' β is roughly 4 to 100, and for Competitive Compositions' is roughly 600 to 1300. (c) Scatter plot and linear fits of β versus literature-reported ΔΔG°₁ for X-Probe only and for Competitive Compositions. Competitive Compositions consistently result in high β regardless of mismatch identities.

Fig. 5b shows the distribution of β for the 44 different DNA targets for X-Probes only at 1% VAF, Competitive Compositions at 0.1% VAF, and Competitive Compositions at 0.033% VAF. The median β for X-Probes is 35, and the median β values for Competitive Compositions are 890 for experiments at 0.1% VAF and 1040 for experiments at 0.033% VAF. Thus Competitive Compositions improved median β by more than 25-fold. Importantly, the β values for Competitive Compositions showed significantly smaller coefficient of variation (standard deviation divided by mean) than X-Probes, indicating higher reliability: all β values observed for Competitive Compositions were greater than 200.

Fig. 5c plots experimental β values against the literature-predicted value of ΔΔG°₁ (of Probe binding to WT) [32]. X-Probes (by themselves) show strong linear correlation between the logarithm of β and ΔΔG°₁, consistent with our understanding of the biophysics and earlier studies [21]. In contrast, Competitive Compositions show much weaker correlation between the logarithm of β and ΔΔG°₁, and consistently yields β ≈ 1000 regardless of the exact sequence of the SNV and WT. This desirable feature is due to the significant anti-correlation that exists between ΔΔG°₁ and ΔΔG°₂ (R² = 0.56, Section S6). Traditional enzyme-based allele-specific approaches also exhibit sequence bias due to different enzyme preferences; thus, Competitive Compositions may possess a unique advantage in consistent detection of many different rare allele sequences.

Importantly, the Competitive Compositions designed here followed the workflow shown in Fig. 4a and represent our first try designs with no optimization of either sequence design or experimental conditions. Our simulations, using literature values of ΔΔG°₁ and ΔΔG°₂, predict a median β value of 8,200 for the 44 Competitive Compositions we tested (with β ranging between 3,200 and 16,000). We believe the 10-fold discrepancy between the experimental results and simulation results to be primarily due to (1) errors in literature thermodynamics values, (2) DNA oligonucleotide synthesis impurities, and (3) differences in rate constants among the different reactions.

Based on our experience, software-predicted values of ΔG°_rxn for DNA oligonucleotides between 20 and 30 nt possess roughly 1 kcal/mol of standard deviation; values of ΔΔG° likely have a similar level of inaccuracy. Errors in ΔΔG°₁ or ΔΔG°₂ values will shift the optimal values ΔG°_rxn1 and ΔG°_rxn2 for maximizing β, and Fig. 2b showed that 1 kcal/mol errors in ΔG°_rxn1 and ΔG°_rxn2 can lead to 10-fold reduction of β.

Truncation and deletion products exist in chemically synthesized oligonucleotides despite advances in synthesis technology; we estimate that roughly 10% of the molecules harbor one or more base deletions (for the given length oligonucleotides) [35]. While many of the (n−1)-mer products are benign and have no significant impact on β, adversarial base truncations or combinations thereof could lead to a subpopulation of Probe that binds more favorably to WT than to SNV, and a subpopulation of Sink that binds more favorably to SNV than to WT. Given that experimental β ≈ 1000, adversarial deletions at even the 1 part in 10,000 level could have significant impact on β.

Kinetics of DNA hybridization and strand displacement are notoriously difficult to predict from sequence, and even the best models today can only, under limited circumstances, predict rate constants to within a factor of 2 [30, 31]. For simplicity, our ordinary differential equation models assumed that all forward rate constants had value k₊ = 3 • 10⁵ M⁻¹ s⁻¹. In reality, forward rate constants will be influenced by secondary structure, G/C content, temperature, salinity, and nonspecific interactions. Real rate constants differing from our simulation assumptions would lead to both different predicted optimal β and different values of ΔG°_rxn1 and ΔG°_rxn2 that lead to this β.

Human genomic DNA analysis

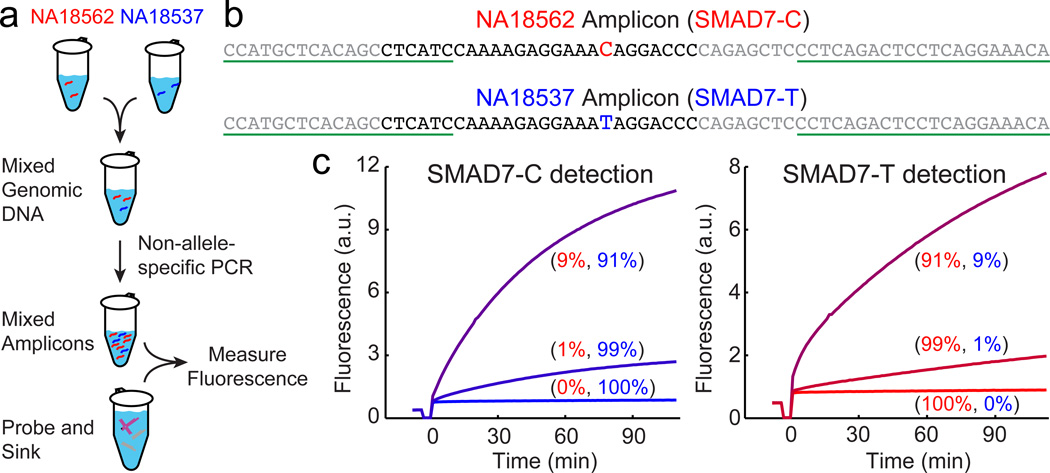
To demonstrate practicality for biotechnological use, we next applied our conditionally fluorescent Competitive Composition to PCR amplicons from human genomic DNA. Two extracted DNA samples from Coriell Cell Repository (NA18537 and NA18546) bearing different alleles (homozygous C/C and homozygous T/T, respectively) at SMAD7 gene locus are mixed, and amplified by non-allele specific asymmetric PCR (Fig. 6, see also Methods). The relative stoichiometry of the two alleles should be roughly preserved through the amplification process.

Figure 6. Competitive Composition assays on PCR amplicons of human genomic DNA samples.

(a) Experimental workflow. Two extracted DNA samples from Coriell Cell Repository (NA18537 and NA18546) bearing single nucleotide polymorphisms at the SMAD7 locus are mixed at 100:0, 99:1, 90:10, 10:90, 1:99, and 0:100 ratios to total concentrations of 2ng/µL (50 µL), and amplified by asymmetric non-allele-specific PCR to generate single-stranded amplicon. Competitive Compositions are designed to each allele; the rarer allele is assayed with the appropriate design. (b) Sequences of the SMAD7 amplicons. The Probe- and Sink-binding regions are shown in black; the forward PCR primer sequence and reverse PCR primer binding sites are underlined. (c) Fluorescence responses of Competitive Composition to each SNP. In each experiment, 0.5 nM Probe and 10 nM Sink were reacted with 40 µL PCR product. Allele frequencies of SMAD7-C and SMAD7-T in genomic DNA mixture prior to PCR are displayed in parentheses.

Two different Competitive Compositions were designed; the first has an X-Probe targeting the SMAD7-C allele (treating the SMAD7-T allele as wildtype), and the second has an X-Probe targeting the SMAD7-T allele. Both Competitive Compositions were able to produce a significant fluorescence signal when their intended target alleles were present at 1% and 10% VAF in the initial genomic template mixture (Fig. 6c); the value of β for both are above 100. Thus, we have shown that Competitive Compositions function even in a complex background of genomic DNA and can be integrated with PCR amplification.

We did not pursue significantly lower VAF detection on PCR amplicons, because we believe we would be limited by Taq polymerase fidelity, reported to be 1 error per 3700 nucleotide incorporate events [39, 40]. This means that, in each amplification cycle, roughly 0.01% of the amplicons generated have an adversarial misincorporation event that "mutates" the WT allele into the SNV allele. PCR amplification effectively ends after roughly 20–25 cycles (due to pyrophosphate inhibition, dNTP depletion, or pH change), corresponding to a total "mutation rate" of roughly 0.2%. That is to say, a pure WT template should, after non-allele-specific amplification, yield roughly 0.2% SNV amplicon. High fidelity polymerases such as NEB's Q5 may be more suitable for post-amplification analysis. Alternatively, the use of Competitive Compositions as PCR primers may suppress the amplification of WT amplicons in the first place.

Discussion

One major conceptual advance presented here is the systematic use of kinetic simulations to inform the thermodynamic and sequence design of DNA Probes and Sinks. Our first-try Competitive Composition designs succeeded in generating normalized fold-changes (β) in excess of 200 for all 44 SNV targets we tested, suggesting the sufficiency of ordinary differential equation simulations to generate high molecular specificity. The fact that the median β is unprecedented and over a factor of 30 higher than all previous demonstrates shows the necessity of ordinary differential equation simulations that consider kinetics in achieving high molecular specificity. Together, our results suggest a new paradigm for design of molecular reagents and diagnostics.

A practical advance presented in this manuscript is the X-Probe, which decouples functionalized oligonucleotides from the target-specific regions. The fact that the same functionalized oligonucleotides may be used for all X-Probe designs offers significant advantages both in synthesis cost (especially per design for research/prototyping purposes) and in manufacturing reliability (larger, more uniform lots). Although here X-Probes are presented as conditionally fluorescent probes for nucleic acid detection, the same principles can be applied to other expensive functionalizations, such as biotins, thiols, and haptens.

Competitive Compositions presented here with high β find natural application in the rare allele detection problem. Detection of low variant allele frequency (VAF) single nucleotide variants (SNVs) in DNA and RNA is clinically important for early cancer detection [4, 36], infectious disease subtyping [41, 42], and infectious disease drug resistance identification [43]. Presently, rare allele detection typically occurs via (1) deep sequencing [44], (2) enzymatic assays with specialized reagents [24, 28, 29], or (3) specialized instruments and reagents [6, 15, 45, 47], with respectively increasing levels of mutation sensitivity. Members of the last group, although capable of detecting rare alleles down to the 1 in 100,000 VAF levels, are not yet broadly adopted due to the bulk and expense of the instruments.

We envision that X-Probe and Competition Compositions technologies will find adoption by many sectors of nucleic acid biotechnology and diagnostics, as many current assays involve DNA or RNA hybridization in at least one step. For example, primer-mediated enzymatic amplification assays [7–9, 46, 47] all rely on proper primer hybridization, and intense efforts in bioinformatics-based primer design are currently employed to enable multiplexing (e.g. Ion AmpliSeq) and rare allele detection (e.g. BEAMing assays). Adapting our technology as ultraspecific primers that, at the chemistry level, hybridize only to the intended templates could alleviate the primer design problem and enable high sensitivity rare mutation detection.

In this work, our efforts were solely focused on improving the molecular specificity of hybridization interactions; molecular sensitivity (i.e. how few rare allele molecules can be detected) is not directly addressed. The demonstrated success of applying Competitive Composition to human genomic DNA subsequent to PCR indicates the potential of integrating this technology with other enzymatic amplification in biological sample detection [7–9, 48, 49]. Alternatively, readout modalities with single-molecule sensitivity, such as certain in situ hybridization techniques [50] and barcoded single-molecule assays [13, 14] may be able to directly apply Competitive Compositions for high selectivity nucleic acid detection.

In experiments on PCR amplicons of human genomic DNA, we added the Competitive Compositions solution after PCR amplification; such an "open tube" procedure would not be practical for diagnostic applications due to possibilities of contamination. Use of Competitive Compositions as a real-time or endpoint readout probe (similar to Taqman) would require chemical modifications, such as 3' dideoxynucleotides, to prevent polymerase activity. We believe that such adaptations may require a little optimization, but should be feasible.

In addition to single-base point changes, there are other genetic signatures of clinical importance, such as gene fusions, translocations, insertions, and deletions. These larger scale genetic changes involve more nucleotide differences, and hence possess greater ΔΔG° values. Although we did not explore these experimentally here, our theory and simulations indicate that these larger changes can be easily detectable at rare mutation loads of 1 in a million or lower.