Study of tissue oxygen supply rate in a macroscopic photodynamic therapy singlet oxygen model

Abstract.

An appropriate expression for the oxygen supply rate (${\mathrm{\Gamma }}_{\mathrm{s}}$) is required for the macroscopic modeling of the complex mechanisms of photodynamic therapy (PDT). It is unrealistic to model the actual heterogeneous tumor microvascular networks coupled with the PDT processes because of the large computational requirement. In this study, a theoretical microscopic model based on uniformly distributed Krogh cylinders is used to calculate ${\mathrm{\Gamma }}_{\mathrm{s}}=g$ ($1-[{{}^3\mathrm{O}}_2]/{[{{}^3\mathrm{O}}_2]}_0$) that can replace the complex modeling of blood vasculature while maintaining a reasonable resemblance to reality; $g$ is the maximum oxygen supply rate and $[{{}^3\mathrm{O}}_2]/{[{{}^3\mathrm{O}}_2]}_0$ is the volume-average tissue oxygen concentration normalized to its value prior to PDT. The model incorporates kinetic equations of oxygen diffusion and convection within capillaries and oxygen saturation from oxyhemoglobin. Oxygen supply to the tissue is via diffusion from the uniformly distributed blood vessels. Oxygen can also diffuse along the radius and the longitudinal axis of the cylinder within tissue. The relations of ${\mathrm{\Gamma }}_{\mathrm{s}}$ to ${[}^3{\mathrm{O}}_2]/{{[}^3{\mathrm{O}}_2]}_0$ are examined for a biologically reasonable range of the physiological parameters for the microvasculature and several light fluence rates ($\varphi$). The results show a linear relationship between ${\mathrm{\Gamma }}_{\mathrm{s}}$ and ${[}^3{\mathrm{O}}_2]/{{[}^3{\mathrm{O}}_2]}_0$, independent of $\varphi$ and photochemical parameters; the obtained $g$ ranges from 0.4 to $1390\mu \mathrm{M}/\mathrm{s}$.

1. Introduction

Photodynamic therapy (PDT) is a photochemical treatment modality used to treat malignant and nonmalignant conditions.¹ It is generally believed that the therapeutic effect in PDT is mainly attributed to the production of singlet oxygen (${}^1{\mathrm{O}}_2$), which involves the interaction of light, photosensitizer (PS), and ground-state oxygen (${}^3{\mathrm{O}}_2$) in the target tissue.¹ To evaluate the efficacy in generating ${}^1{\mathrm{O}}_2$, direct monitoring of ${}^1{\mathrm{O}}_2$ in vivo via singlet oxygen luminescence (SOL) at 1270 nm is preferable, but also technically challenging because of the short lifetime of ${}^1{\mathrm{O}}_2$ in real biological environments.^2–4 Hence, the progress in transferring this direct approach to the clinic has not been significant in the past decade since the successful in vivo detection of SOL in 2002.⁵ Alternatively, explicit measurements of one or all three components in PDT are more feasible although an ideal approach still requires continuous measurements during PDT. Studies have been conducted to investigate the effects of light [including total delivered light fluence and fluence rate ($\varphi$)] and PS concentration on PDT efficacy both in vitro and in vivo (PDT dosimetry).^1,6–13 The effect of oxygenation is much more easily examined in the in vitro model,¹⁴ because it is relatively difficult to monitor and quantify the spatial distribution of oxygen continuously and noninvasively in a real biological system.

To completely characterize the PDT treatment outcomes and interpret experimental results, mathematical modeling of the complex PDT mechanisms and the production of ${}^1{\mathrm{O}}_2$ are suggested.¹³ The basic mathematical descriptions of the photochemical and photophysical reactions during PDT can then be adopted into an in vitro and/or in vivo biological environment to calculate the temporal and spatial distributions of PDT components (PS, ${}^3{\mathrm{O}}_2$ and ${}^1{\mathrm{O}}_2$ concentrations and $\varphi$).^13,15–17 A macroscopic PDT model was developed to extract the so-called reacted singlet oxygen [${({{}^1\mathrm{O}}_2)}_{\mathrm{rx}}$] threshold dose at tumor tissue necrotic distances by fitting the calculated ${}^1{\mathrm{O}}_2$ profile to measured necrosis induced by interstitial PDT.¹³ This model considers light diffusion and a set of PDT kinetics equations incorporating the oxygen consumption rate per $\varphi$ and PS concentration ($\xi$), the probability ratio of an ${}^1{\mathrm{O}}_2$ molecule reacting with ground-state PS compared to the ${}^1{\mathrm{O}}_2$ molecule reacting with a cellular target ($\sigma$), and the ratio of the monomolecular decay rate of the triplet state (T) PS to the bimolecular rate of the triplet PS quenching by ${}^3{\mathrm{O}}_2$ ($\beta$), which can be potentially used as clinically practical dosimetry quantities. In this macroscopic model, the molecular oxygen supply rate to the target tissue was hypothesized as a linear function of fractional ${}^3{\mathrm{O}}_2$ concentration (the ratio of volume average oxygen concentration to its initial value prior to PDT) with a maximum supply rate ($g$), as shown in Eq. (1).

$${\mathrm{\Gamma }}_{\mathrm{s}}=g[1-\frac{[{}^3{\mathrm{O}}_2]}{[{}^3{\mathrm{O}}_2](t=0)}].$$ (1)

Preliminary results were presented on fitting the necrotic radius induced by interstitial Photofrin-mediated PDT to obtain model parameters ($\xi$, $\sigma$, $\beta$, and $g$) and ${[{{}^1\mathrm{O}}_2]}_{\mathrm{rx}}$. Then, the sensitivity of the model parameters to calculated ${[{{}^1\mathrm{O}}_2]}_{\mathrm{rx}}$ profiles has been explored for different light source geometries and PSs in in vivo interstitial conditions.¹³ A comparison of the computed ${[{{}^1\mathrm{O}}_2]}_{\mathrm{rx}}$ distributions showed that the model can be potentially correlated to differences in PDT efficacy.

In the current study, a microscopic model incorporating biological blood vasculature distribution is used to investigate an appropriate simple expression for oxygen supply which can be used in our macroscopic model. Due to the large computational requirement, modeling of the heterogeneity of tumor microvascular networks coupled with the PDT processes is at present impractical. The ultimate objective of this study is to replace the complex modeling of blood vasculature with a simplified expression for oxygen supply to tissue while maintaining reasonable accuracy. The findings of the present studies justify that our previously hypothesized linear expression in the macroscopic PDT model is sufficient to replace microscopically modeling oxygen supply in tissue. The values of $g=0.7-2.0\mu \mathrm{M}/\mathrm{s}$ as determined in the literature^13,18 for a number of PSs are also found to be within the range of $g$ values calculated in this study for the range of the physiological parameters being tested.

2. Theory and Method

2.1. Macroscopic Model for Photodynamic Therapy

The macroscopic PDT model is briefly described in this section, as well as the definitions of the five parameters to be optimized during the process of fitting in the in vivo experimental results. The intention of this work is to investigate the oxygen supply term in the model using a microscopic model instead of fitting experimental results to derive parameters. More detailed descriptions of the model and the fitting routine can be found elsewhere.¹³

In the macroscopic model,¹³ spatial distribution of $\varphi$ in the tumor is calculated via Eq. (2) based on the diffusion approximation. Temporal and spatial distributions of PS ($S_0$), $\left[{}^3{\mathrm{O}}_2\right]$ and $\left[{}^1{\mathrm{O}}_2\right]$ concentrations are obtained by solving a set of coupled time-dependent differential Eqs. (3) to (5). The cumulative concentration of ${[{{}^1\mathrm{O}}_2]}_{\mathrm{rx}}$ can then be derived by the integration of Eq. (5) over time ($t$). In Eq. (4), the symbol ${\mathrm{\Gamma }}_{\mathrm{s}}$ denotes the rates at which ${}^3{\mathrm{O}}_2$ is supplied to the surrounding tissue, which is the term to be examined in this study.

$${\mu }_{\mathrm{a}}\varphi -\nabla ·(\frac{1}{3{{\mu }_{\mathrm{s}}}^{\prime }}\nabla \varphi )=S,$$ (2)

$$\frac{d[S_0]}{dt}+\left[\xi \sigma \frac{\varphi ([S_0]+\delta )[{}^3{\mathrm{O}}_2]}{[{}^3{\mathrm{O}}_2]+\beta }\right][S_0]=0,$$ (3)

$$\frac{d[{}^3{\mathrm{O}}_2]}{dt}+\left\{\xi \frac{\varphi [S_0][1+\sigma ([S_0+\delta ])]}{[{}^3{\mathrm{O}}_2]+\beta }\right\}[{}^3{\mathrm{O}}_2]={\mathrm{\Gamma }}_{\mathrm{s}},$$ (4)

$$\frac{d{[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}}{dt}-f·\left[\xi \frac{\varphi ([S_0][{}^3{\mathrm{O}}_2])}{[{}^3{\mathrm{O}}_2]+\beta }\right]=0.$$ (5)

The parameters ${{\mu }_{\mathrm{s}}}^{\prime }$ and ${\mu }_{\mathrm{a}}$ represent optical scattering and absorption coefficients, respectively. $\delta$ is the low concentration correction parameter and $S$ describes the light source. The mathematical definitions of all parameters are given in Tables 1 and 2. Some reported values of the photochemical parameters for Photofrin are shown in Table 1.¹³

Table 1.

Photodynamic therapy (PDT) photochemical parameters used for calculations for Photofrin.¹³

Parameters	Values	Definitions
$\xi$ (${\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$)	$3.70\times {10}^{-3}$	$S_{\mathrm{\Delta }}{k}_5/(k_3+k_5)\epsilon /h\upsilon /(k_6/k_7[A]+1)$
$\sigma$ ($\mu {\mathrm{M}}^{-1}$)	$7.60\times {10}^{-5}$	$k_1/(k_7[A])$
$\delta$ ($\mu \mathrm{M}$)	33.00	Low concentration correction
$\beta$ ($\mu \mathrm{M}$)	11.90	$k_4/k_2$
${{\mu }_{\mathrm{s}}}^{\prime }$ (${\mathrm{cm}}^{-1}$)	13.46	Optical reduced scattering coefficient
${\mu }_{\mathrm{a}}$ (${\mathrm{cm}}^{-1}$)	1.03	Optical absorption coefficient

Table 2.

Definitions of the photochemical parameters.

Symbols	Definitions	Units
$k_1$	Photobleaching rate	$1/\mu \mathrm{M}·\mathrm{s}$
$k_2$	Reaction rate of ${{}^3\mathrm{O}}_2$ with T	$1/\mu \mathrm{M}·\mathrm{s}$
$k_3$	Rate of $S_1$ to $S_0$	$1/\mathrm{s}$
$k_4$	Rate of T to $S_0$	$1/\mathrm{s}$
$k_5$	Rate of $S_1$ to T	$1/\mathrm{s}$
$k_6$	Rate of ${{}^1\mathrm{O}}_2$ to ${{}^3\mathrm{O}}_2$	$1/\mathrm{s}$
$k_7$	React. rate of ${{}^1\mathrm{O}}_2$ and tissue	$1/\mu \mathrm{M}·\mathrm{s}$
$\epsilon$	Extinction coefficient	${\mathrm{cm}}^{-1}\mu {\mathrm{M}}^{-1}$
$g$	Maximum oxygen supply rate	$\mu \mathrm{M}/\mathrm{s}$
$[S_0]$	Ground state sensitizer concentration	$\mu \mathrm{M}$
$[S_1]$	Singlet excited state sensitizer concentration	$\mu \mathrm{M}$
$[T]$	Triplet excited state sensitizer concentration	$\mu \mathrm{M}$
$[{{}^3\mathrm{O}}_2]$	Triplet ground state oxygen concentration	$\mu \mathrm{M}$
$[{{}^1\mathrm{O}}_2]$	Singlet excited state oxygen concentration	$\mu \mathrm{M}$
$S_{\mathrm{\Delta }}$	Fraction $[{{}^1\mathrm{O}}_2]$ from $[T]$ and $[{{}^3\mathrm{O}}_2]$ reaction	Dimensionless

2.2. Microscopic Model for Photodynamic Therapy

A microscopic PDT model was developed based on the Krogh cylinder model.¹⁹ In the model, the tumor has uniformly spaced cylindrical blood capillaries (with a radius of $R_{\mathrm{c}}$) in parallel with the linear light source. The inter-capillary distance between two adjacent capillaries is assumed to be large enough so that each capillary can supply oxygen only to its immediate concentric surrounding tissue. The oxygen concentration in the oxygen supply term as expressed in Eq. (1) will be an average value over the entire tissue element volume. Due to the values of both inter-capillary distance ($R_{\mathrm{t}}$) and capillary length ($l_{\mathrm{z}}$) used in this study, it is reasonable to assume that $\varphi$ within the small tissue element in Fig. 1 is constant. Figure 1 shows the schematic of the cylindrical Krogh model. Note that a three-dimensional Krogh model can be simplified as a 2-D cylindrical symmetric model given the above assumptions.

Fig. 1.

(a) A schematic of the Krogh cylinder model. (b) three-dimensional (3-D) mesh plot of the Krogh cylinder model. The light fluence rate within the Krogh model is considered to be a constant because the spatial scale of light transport ($\sim 1$ to 10 mm) is much larger than the spatial scale of the Krogh model ($<0.4\mathrm{mm}=400\mu \mathrm{m}$). The incident direction of light is randomly distributed.

Before introducing the governing equations for oxygen and its carrier, oxyhemoglobin (HbO), some basic physiological assumptions are discussed first. Oxygen is normally present in the blood in two forms: chemically bound to hemoglobin forming HbO, and free molecules dissolved in the plasma. Most oxygen is bound to form HbO, which is contained in the red blood cell (RBC). However, there is still a small fraction of oxygen dissolved in the liquid media such as blood plasma and RBC water. The concentration of these free oxygen molecules can be represented using a quantity called oxygen partial pressure ($P$). The relation between them can be defined using Henry’s law in Eq. (6), where $\alpha$ is the oxygen solubility coefficient:

$$[{{}^3\mathrm{O}}_2]=\alpha P.$$ (6)

When $P$ decreases in the surrounding environment, HbO will release oxygen and vice versa. The percentage of hemoglobin that is saturated with oxygen is usually referred to as hemoglobin oxygen saturation (${\mathrm{SaO}}_2$). The relationship between $P$ and ${\mathrm{SaO}}_2$ is described by Hill’s oxygen dissociation curve. A mathematic expression for ${}^3{\mathrm{O}}_2$ dissociation is Hill’s equation, as shown in Eq. (7):¹⁶

$$\mathrm{Sa}=\frac{P^n}{P^n+P_{50}^n},$$ (7)

where $P_{50}$ represents the half maximum hemoglobin saturation pressure. $n$ is the Hill coefficient representing the degree of co-operativity.

Oxygen molecules can diffuse freely from RBC into the blood stream due to negligible resistance in the membrane.¹⁹ Therefore, the first assumption is that released oxygen from HbO can instantaneously be present in blood plasma (i.e., ignoring the diffusion from RBC). The second assumption is that RBCs are uniformly distributed in the blood.

Given the above assumptions, the time-dependent governing equations for ${}^3{\mathrm{O}}_2$ and HbO transport inside the capillary are given in Eqs. (8) and (9). First, note that the concentration of ${}^3{\mathrm{O}}_2$ is hereafter expressed using the partial pressure of ${}^3{\mathrm{O}}_2$ ($P$) based on Eq. (6) because of the continuity boundary conditions that will be discussed later. Second, Sa in Eq. (9) is the hemoglobin oxygen saturation describing the percentage of HbO concentration to total hemoglobin concentration.

$${\alpha }_{\mathrm{c}}\frac{\partial P}{\partial t}={\alpha }_{\mathrm{c}}{D}_{\mathrm{c}}{\nabla }^{2}P-v·{\alpha }_{\mathrm{c}}\nabla P+{\mathrm{\Gamma }}_{\mathrm{rec}},$$ (8)

$$C_{\mathrm{H}}\frac{\partial \mathrm{Sa}}{\partial t}=C_{\mathrm{H}}{D}_{\mathrm{H}}{\nabla }^2\mathrm{Sa}-v·C_{\mathrm{H}}\nabla \mathrm{Sa}-{\mathrm{\Gamma }}_{\mathrm{rec}}.$$ (9)

The product of Sa and $C_{\mathrm{H}}$ (total hemoglobin concentration in capillary) is the HbO concentration. The first terms on the right hand sides of Eqs. (8) and (9) are the diffusion terms of ${}^3{\mathrm{O}}_2$ and hemoglobin, respectively; the second terms describe the convection processes. The third term (${\mathrm{\Gamma }}_{\mathrm{rec}}$) is the so-called “reaction” term representing the ${}^3{\mathrm{O}}_2$ loading/unloading from deoxyhemoglobin/oxyhemoglobin. The parameters $D_{\mathrm{c}}$ and $D_{\mathrm{H}}$ represent the diffusion coefficients of ${}^3{\mathrm{O}}_2$ and hemoglobin in the capillary, respectively. ${\alpha }_{\mathrm{c}}$ is the solubility of ${}^3{\mathrm{O}}_2$ in plasma and $v$ is the blood velocity in the capillary.

By manipulating Eqs. (7) to (9), one can derive the main governing Eq. (10) for $P$ in the capillary, where $K$ and $M$ are defined in Eqs. (11) and (12), respectively.

$$({\alpha }_{\mathrm{c}}+K{C}_{\mathrm{H}})\frac{\partial P}{\partial t}=({\alpha }_{\mathrm{c}}{D}_{\mathrm{c}}+K{C}_{\mathrm{H}}{D}_{\mathrm{H}}){\nabla }^{2}P-({\nu }_{\mathrm{z}}{\alpha }_{\mathrm{c}}+{\nu }_{\mathrm{z}}K{C}_{\mathrm{H}})\frac{\partial P}{\partial z}+C_{\mathrm{H}}{D}_{\mathrm{H}}M[{\left(\frac{\partial P}{\partial r}\right)}^2+{\left(\frac{\partial P}{\partial z}\right)}^2],$$ (10)

$$K=\frac{n{P}^{n-1}{P}_{50}^n}{{(P^n+P_{50}^n)}^2},$$ (11)

$$M=\frac{n(n-1)P_{50}^n{P}^{n-2}(P^n+P_{50}^n)-2n^2{P}^{(2n-2)}{P}_{50}^n}{{(P^n+P_{50}^n)}^3},$$ (12)

where $r$ and $z$ are the radial and axial variables, respectively. $v_{\mathrm{z}}$ is the axial blood flow velocity.

The boundary conditions in the microscopic model are summarized in Eqs. (13) to (16). The bottom end of the capillary (i.e., $z=0$) is the entrance of blood flow, which is assumed to have a constant ${}^3{\mathrm{O}}_2$ partial pressure $P_{\mathrm{ts}}$. On the boundary between capillary and tissue, both ${}^3{\mathrm{O}}_2$ flux and $P$ are continuous as shown in Eqs. (14) and (15). Other boundaries are considered as insulation.

$${P|}_{\mathrm{z}=0,r\in [0,R_{\mathrm{c}}]}=P_{\mathrm{ts}},$$ (13)

$$D_{\mathrm{c}}{\alpha }_{\mathrm{c}}{\nabla P|}_{r=R_{\mathrm{c}}^{-}}=D_{\mathrm{t}}{\alpha }_{\mathrm{t}}{\nabla P|}_{r=R_{\mathrm{c}}^{+}},$$ (14)

$${P|}_{r=R_{\mathrm{c}}^{-}}={P|}_{r=R_{\mathrm{c}}^{+}},$$ (15)

$${\nabla P|}_{\text{other}}=0.$$ (16)

The parameters ${\alpha }_{\mathrm{t}}$ and $D_{\mathrm{t}}$ are the solubility and diffusion coefficients of oxygen in tissue, respectively.

The governing equation for $\left[{}^3{\mathrm{O}}_2\right]$ in tissue during PDT in the microscopic model is given by Eq. (17), which has the same terms on the left-hand side as Eq. (4) to describe PDT consumption of oxygen. The right-hand side of the equation contains both ${}^3{\mathrm{O}}_2$ diffusion (the first term) and the metabolic consumption (the second term). However, only a general oxygen supply term ${\mathrm{\Gamma }}_{\mathrm{s}}$ is used in the macroscopic model [as shown in Eq. (4)].

$$\frac{\partial [{}^3{\mathrm{O}}_2]}{\partial t}+\left\{\xi \frac{\varphi [S_0][{}^3{\mathrm{O}}_2][1+\sigma ([S_0]+\delta )]}{[{}^3{\mathrm{O}}_2]+\beta }\right\}=D_{\mathrm{t}}{\nabla }^2[{}^3{\mathrm{O}}_2]-q_0\frac{[{}^3{\mathrm{O}}_2]}{[{}^3{\mathrm{O}}_2]+{\alpha }_{\mathrm{t}}{P}_{\mathrm{m}}}.$$ (17)

The parameter $q_0$ represents the maximum metabolic ${}^3{\mathrm{O}}_2$ consumption rate and $P_{\mathrm{m}}$ is the half-maximum oxygen consumption.

Table 3 presents the magnitude of the physiological parameters based on the literature values for the normal and tumor tissues by either measurements (in both living animals and fixed tissues) or theoretical studies.^16,19–25 The normal capillaries appear as fine, nearly parallel vessels that are served by orderly branching arterial and venous trees.²¹ In contrast, the tumor vessels are disorganized, leaving large, irregular avascular spaces.²¹ We tried to cover the existing wide range data sets representing both normal and cancer tissues in our study.

Table 3.

Physiological parameters in the microscopic PDT model. The standard values are considered as the benchmark condition for the comparison.

Parameters	Ranges	Standard values	Description
$R_{\mathrm{t}}$	18–6019,20,21	60	Radius of cylindrical tissue ($\mu \mathrm{m}$)
$R_{\mathrm{c}}$	2.5–1019,20,21	4	Radius of cylindrical capillary ($\mu \mathrm{m}$)
$D_{\mathrm{t}}$		170019	${{}^3\mathrm{O}}_2$ diffusion coefficient in tissue ($\mu {\mathrm{m}}^2/\mathrm{s}$)
$D_{\mathrm{c}}$		124024	${{}^3\mathrm{O}}_2$ diffusion coefficient in capillary ($\mu {\mathrm{m}}^2/\mathrm{s}$)
${\alpha }_{\mathrm{t}}$		1.29519	${{}^3\mathrm{O}}_2$ solubility in tissue ($\mu \mathrm{M}/\mathrm{mmHg}$)
${\alpha }_{\mathrm{c}}$		1.52719	${{}^3\mathrm{O}}_2$ solubility in plasma ($\mu \mathrm{M}/\mathrm{mmHg}$)
$v_{\mathrm{z}}$	50–20019,24	10024	Blood flow velocity ($\mu \mathrm{m}/\mathrm{s}$)
$P_{50}$		2616	Half maximum hemoglobin saturation pressure (mmHg)
$C_{\mathrm{H}}$		250026,*	Total hemoglobin concentration in capillary ($\mu \mathrm{M}$)
$q_0$	0.9–6	2.419	${{}^3\mathrm{O}}_2$ maximum metabolic consumption rate ($\mu \mathrm{M}/\mathrm{s}$)
$n$		2.4624	Hill constant
$P_{\mathrm{m}}$		0.38624	$p{\mathrm{O}}_2$ at half maximum oxygen consumption concentration (mmHg)
$P_{\mathrm{ts}}$	50, 10019,25,27	10025	Artery ${{}^3\mathrm{O}}_2$ partial pressure (mmHg)
$D_{\mathrm{H}}$		1419	Hemoglobin diffusion coefficient in capillary ($\mu {\mathrm{m}}^2/\mathrm{s}$)
$l_{\mathrm{z}}$	100–40019,20	220	Length of capillary ($\mu \mathrm{m}$)

Note: * The hemoglobin concentration in a red blood cell is $5000\mu \text{M}$.¹⁶ Thus the hemoglobin concentration is $2500\mu \text{M}$ after we factor in the fraction of the red blood cell, ie. hematocrit, in blood is about 50%.²⁶

2.3. Simulation, Procedures, and Initial Conditions

The microscopic model was simulated by the finite element method (FEM) analysis, solver, and simulation software package COMSOL Multiphysics v4.3b (Comsol AB, Stockholm, Sweden), which was run on an iMAC OSX version 10.9.5 (Processor 3.1 GHz Intel Core 17 and Memory 16 GB 1600 MHz DDR3). LiveLink for MATLAB® was also used to work with COMSOL Multiphysics in combination with MATLAB R2013a (64-bit, Massachusetts).

The first step was to examine an expression for oxygen supply. For this purpose, the instantaneous total change rates of ${}^3{\mathrm{O}}_2$ in tissue [i.e., the sum of the two terms on the right-hand side of Eq. (17)] were calculated, and then plotted as a function of the instantaneous oxygen concentration at the corresponding time normalized to its value prior to PDT ($[{}^3{\mathrm{O}}_2]/{[{}^3{\mathrm{O}}_2]}_0$). These simulations were first performed for a range of $\varphi$ (25 to $150\mathrm{mW}/{\mathrm{cm}}^2$), and some typical treatment conditions for Photofrin-, mTHPC-, BPD-, and HPPH-mediated PDT. Different photochemical parameters $\xi$ ($3.7\times {10}^{-3}-76\times {10}^{-3}{\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$), $\sigma$ ($1.55\times {10}^{-5}-7.6\times {10}^{-5}\mu {\mathrm{M}}^{-1}$) and $\beta$ (8.7 to $11.9\mu \mathrm{M}$) were used in this step. The results were analyzed together to see the $\varphi$, $\xi$, $\sigma$, and $\beta$ dependence.

The main objective of the second step was to find $g$ values in Photofrin-mediated PDT for a range of physiological microenvironments at $\varphi =150\mathrm{mW}/{\mathrm{cm}}^2$. The initial Photofrin concentration in the tissue was assumed to be $7\mu \mathrm{M}$ and total treatment time was chosen to be 100 min. The standard values of the PDT photochemical and physiological parameters, reported by the other studies, were used as shown in Tables 1 and 3.^16,19–25 The radius of the capillary ($R_{\mathrm{c}}=2.5$, 4.0 or $10\mu \mathrm{m}$), the length of the capillary ($l_{\mathrm{z}}=100$, 220 or $400\mu \mathrm{m}$), the density of blood vessels ($R_{\mathrm{t}}=18$, 30 or $60\mu \mathrm{m}$), the blood flow velocity ($v_{\mathrm{z}}=50$, 100 or $200\mu \mathrm{m}/\mathrm{s}$), and maximum ${{}^3\mathrm{O}}_2$ metabolic consumption rate ($q_0=0.9$, 2.4 or $6\mu \mathrm{M}/\mathrm{s}$) were set at three different values, which cover the existing data sets representing both normal and tumor vasculatures.^19–24 The magnitude of $P_{\mathrm{ts}}$ was set at two different values of 50 and 100 mmHg representing ${{}^3\mathrm{O}}_2$ partial pressure in both tumor and normal arteries.^{19,22–25, 27} For the simulations, the physiological parameters were first set at their standard values and then the magnitude of $R_{\mathrm{c}}$, $R_{\mathrm{t}}$, $v_{\mathrm{z}}$, $q_0$, $P_{\mathrm{ts}}$ and $l_{\mathrm{z}}$ were varied from their standard values. The varied parameters with their values are listed in Table 4 along with the fitted results in the next section.

Table 4.

Physiological parameters varied for the range of microenvironment examined for $g$.

$P_{\mathrm{ts}}$ ($\mathrm{mmHg}$)	$q_0$ ($\mu \mathrm{M}/\mathrm{s}$)	$v_{\mathrm{z}}$ ($\mu \mathrm{m}/\mathrm{s}$)	$l_{\mathrm{z}}$ ($\mu \mathrm{m}$)	$g$ ($\mu \mathrm{M}/\mathrm{s}$)
				$R_{\mathrm{c}};R_{\mathrm{t}}$ ($\mu \mathrm{m}$)
				2.5;60	4;60	2.5;30	10;60	4;30	2.5;18	4;18	10;30	10;18
100	0.9	50	220	0.9	2.3	4.0	8.6	6.6	8.3	16.8	28.3	80.1
		100	220	2.0	4.4	7.0	17.2	14.9	15.5	29.1	51.9	147.0
		200	220	4.2	7.9	11.9	27.2	23.1	26.1	56.0	104.2	279.6
	2.4	50	220	0.9	2.1	4.1	10.6	8.8	9.1	18.5	28.8	82.7
		100	220	2.0	4.9	8.3	17.7	15.4	17.3	31.2	61.1	149.1
		200	220	3.9	7.9	13.9	36.4	30.6	31.7	87.2	104.9	282.7
	6	50	220	0.9	2.0	4.1	12.1	9.2	9.5	23.3	35.7	89.9
		100	220	2.0	4.9	9.2	20.0	15.9	18.2	33.2	68.7	155.7
		200	220	4.4	7.8	14.5	31.1	26.1	29.0	55.8	109.9	286.1
50	0.9	50	220	0.6	2.3	4.2	10.8	10.8	12.4	25.5	49.1	151.7
		100	220	1.9	4.6	8.2	18.8	18.7	23.0	44.0	93.8	297.5
		200	220	3.4	8.1	14.4	37.6	34.0	48.7	89.0	167.1	601.5
	2.4	50	220	0.9	2.2	3.9	10.8	11.3	14.5	27.4	51.2	152.2
		100	220	1.9	4.6	8.9	20.4	17.9	25.4	49.0	93.9	305.6
		200	220	3.4	7.5	15.2	37.7	30.8	45.7	88.2	167.2	604.6
	6	50	220	1.0	2.3	4.4	11.0	10.7	14.9	33.5	55.8	161.8
		100	220	1.9	4.6	7.4	20.7	16.0	25.8	52.2	94.3	325.5
		200	220	3.6	5.5	15.7	45.5	30.7	54.0	86.4	168.5	606.9
100	2.4	100	100	4.9	7.7	13.0	37.7	29.7	30.7	75.4	111.2	277.3
		100	220	2.0	4.9	8.3	17.7	15.4	17.3	31.2	61.1	149.1
		100	400	1.0	2.3	5.1	9.5	10.7	11.0	19.9	30.2	88.1
50	2.4	100	100	3.1	7.7	16.5	38.9	36.7	51.4	99.6	158.9	642.3
		100	220	1.9	4.6	8.9	20.4	17.9	25.4	49.0	93.9	305.6
		100	400	0.9	2.2	3.8	9.7	8.9	13.2	32.6	57.7	204.2

3. Results and Discussions

3.1. Linear Correlation and $g$ Calculation for Different Photochemical Parameters and Fluence Rates in a Capillary with Standard Physiological Parameters

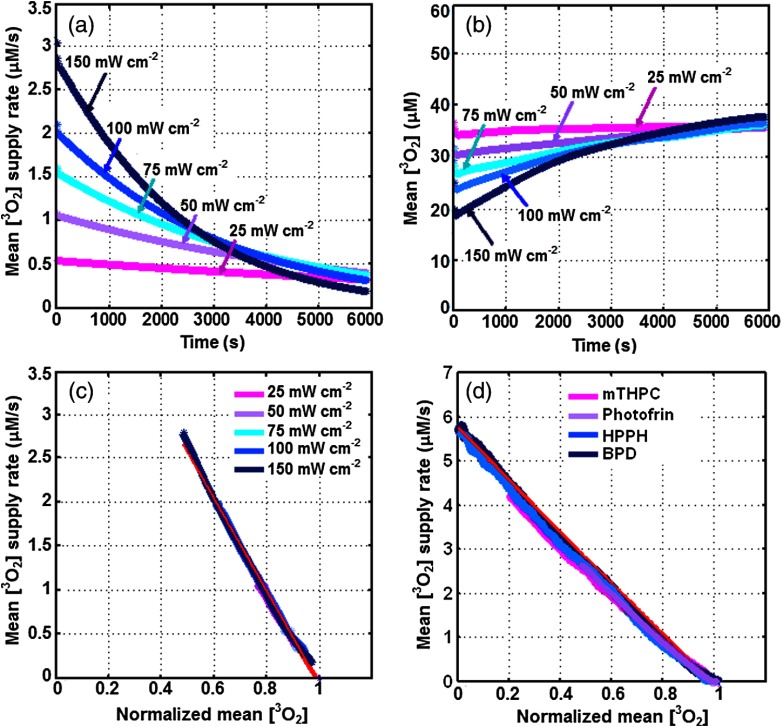
Figures 2(a) and 2(b) show the volume-averaged oxygen supply rate and ${{}^3\mathrm{O}}_2$ concentration over the whole Krogh cylinder as a function of time, calculated using the microscopic model for standard values presented in Table 3 and $\varphi =25$, 50, 75, 100, and $150\mathrm{mW}/{\mathrm{cm}}^2$. Based on our calculations, the initial volume-averaged oxygen concentration ${[{{}^3\mathrm{O}}_2]}_0$, prior to Photofrin-mediated PDT (with $\xi =3.7\times {10}^{-3}{\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$, $\sigma =7.6\times {10}^{-5}\mu {\mathrm{M}}^{-1}$, $\beta =11.9\mu \mathrm{M}$, $\delta =33\mu \mathrm{M}$), was around $39.41\mu \mathrm{M}$. The corresponding volume-averaged oxygen supply rate versus $[{{}^3\mathrm{O}}_2]/{[{{}^3\mathrm{O}}_2]}_0$ is presented in Fig. 2(c), which is “zero” prior to PDT and shows a linear correlation independent of $\varphi$. A linear fit to these data (has an intercept at 1 on $x$-axis) results in a slope of about $4.9\pm 0.1$, which represents the $g$ value in $\mu \mathrm{M}/\mathrm{s}$ with the standard deviation of the mean (STDM). The simulations were also performed for different PSs: mTHPC (with $\xi =30\times {10}^{-3}{\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$, $\sigma =2.97\times {10}^{-5}\mu {\mathrm{M}}^{-1}$, $\beta =8.7\mu \mathrm{M}$, $\delta =33\mu \mathrm{M}$), BPD (with $\xi =51\times {10}^{-3}{\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$, $\sigma =1.7\times {10}^{-5}\mu {\mathrm{M}}^{-1}$, $\beta =11.9\mu \mathrm{M}$, $\delta =33\mu \mathrm{M}$) and HPPH (with $\xi =76\times {10}^{-3}{\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$, $\sigma =1.55\times {10}^{-5}\mu {\mathrm{M}}^{-1}$, $\beta =11.9\mu \mathrm{M}$, $\delta =33\mu \mathrm{M}$) at $\varphi =150\mathrm{mW}/{\mathrm{cm}}^2$. The volume-averaged oxygen supply rate versus $[{{}^3\mathrm{O}}_2]/{[{{}^3\mathrm{O}}_2]}_0$ is presented in Fig. 2(d) and shows a linear correlation independent of $\xi$, $\sigma$ and $\beta$. The linear fit to these data results in a $g$ value of about $5.1\pm 0.2\mu \mathrm{M}/\mathrm{s}$ ($g$ is presented with STDM). While the $g$ value is extremely sensitive to change in the physiological parameters and ${{}^3\mathrm{O}}_2$ concentration, the results show that $g$ is independent of $\varphi$ and PS photochemical parameters.

Fig. 2.

(a) Oxygen supply rate [right-hand side of Eq. (17)] and (b) oxygen concentration, defined as the volumetric average around each vessel versus time. The plots are for $\varphi =25$, 50, 75, 100, and $150\mathrm{mW}{\mathrm{cm}}^{-2}$. (c) The mean oxygen supply rate versus normalized mean oxygen for different $\varphi$. A linear fit to the spectra (as shown with red lines) results an average slope of about $4.99\pm 0.10$, which is $g(\mu \mathrm{M}/\mathrm{s})\pm \mathrm{STDM}$. (d) The mean oxygen supply rate versus normalized oxygen for different photosensitizers (PSs), Photofrin ($\xi =3.7\times {10}^{-3}{\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$, $\sigma =7.6\times {10}^{-5}\mu {\mathrm{M}}^{-1}$, $\beta =11.9\mu \mathrm{M}$, $\delta =33\mu \mathrm{M}$), mTHPC ($\xi =30\times {10}^{-3}{\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$, $\sigma =2.97\times {10}^{-5}\mu {\mathrm{M}}^{-1}$, $\beta =8.7\mu \mathrm{M}$, $\delta =33\mu \mathrm{M}$), BPD ($\xi =51\times {10}^{-3}{\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$, $\sigma =1.7\times {10}^{-5}\mu {\mathrm{M}}^{-1}$, $\beta =11.9\mu \mathrm{M}$, $\delta =33\mu \mathrm{M}$) and HPPH ($\xi =76\times {10}^{-3}{\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$, $\sigma =1.55\times {10}^{-5}\mu {\mathrm{M}}^{-1}$, $\beta =11.9\mu \mathrm{M}$, $\delta =33\mu \mathrm{M}$). A linear fit to the spectra (as shown with red lines) results $g=5.12\pm 0.17\mu \mathrm{M}/\mathrm{s}$. The data are plotted for the physiological parameters with standard values presented in Table 3. Normalized mean oxygen is defined as the volumetric average of ${{}^3\mathrm{O}}_2$ around each vessel divided by ${[{{}^3\mathrm{O}}_2]}_0$, which is the initial mean oxygen before PDT.

3.2. Representative g Value Tests on More Than One Varying Parameter

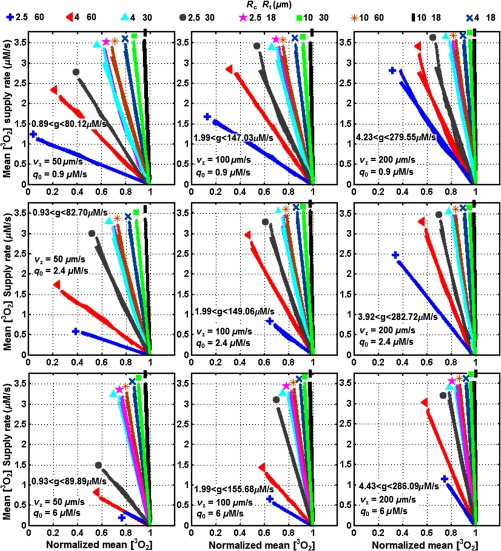
The $g$ values were calculated for Photofrin-mediated PDT and a range of physiological parameters at $\varphi =150\mathrm{mW}/{\mathrm{cm}}^2$. In our model, the blood vessel network forms uniformly distributed Krogh cylinders and the spacing between vascular cylinders $R_{\mathrm{t}}$ varies between 18 and $60\mu \mathrm{m}$. The cylindrical blood capillary has $R_{\mathrm{c}}$ in the range of 2.5 to $10\mu \mathrm{m}$ and $l_{\mathrm{z}}$ in the range of 100 to $400\mu \mathrm{m}$. For both tumor and normal vasculatures, the maximum ${{}^3\mathrm{O}}_2$ metabolic consumption rate ($q_0$) and blood velocity in capillary ($v_{\mathrm{z}}$) are in the ranges of 0.9 to $6\mu \mathrm{M}/\mathrm{s}$ and 50 to $200\mu \mathrm{m}/\mathrm{s}$, respectively (see Table 3). The oxygen pressure at the aortal entrance of the blood vessel ($P_{\mathrm{ts}}$) is assumed to be in the range of 50 or 100 mmHg.^19,25,27 The linear correlation between the volume-averaged oxygen supply rate and $[{{}^3\mathrm{O}}_2]/{[{{}^3\mathrm{O}}_2]}_0$ as well as their respective $g$ values is presented in Figs. 3 to 5 and Table 4. The linear fits to the data result in $g$ values in the ranges of 0.9 to $286.1\mu \mathrm{M}/\mathrm{s}$ for $P_{\mathrm{ts}}=100\mathrm{mmHg}$ and $0.6-606.9\mu \mathrm{M}/\mathrm{s}$ for $P_{\mathrm{ts}}=50\mathrm{mmHg}$.

Fig. 3.

Calculated mean oxygen supply rate [right side of Eq. 17] versus normalized mean oxygen, $[{{}^3\mathrm{O}}_2]/{[{{}^3\mathrm{O}}_2]}_0$. The data are plotted for artery oxygen partial pressure $P_{\mathrm{ts}}=100\mathrm{mmHg}$, capillary length $l_{\mathrm{z}}=220\mu \mathrm{m}$ as well as different blood flow $v_{\mathrm{z}}$ and maximum metabolic oxygen consumption rate $q_0$. Each plot contains nine combinations of cylindrical tissue radius $R_{\mathrm{t}}(18,30,60\mu \text{m})$ and capillary radius $R_{\mathrm{c}}(2.5,4,10\mu \text{m})$ as presented with different colors and symbols. The 3 plots for the left column are for $v_{\mathrm{z}}=50\mu \text{m}/\text{s}$ and $q_0=0.9,2.4,\text{\hspace{0.17em}and\hspace{0.17em}}6\mu \text{M}/\text{s}$, respectively; the 3 plots for the middle column are for $v_{\mathrm{z}}=\text{\hspace{0.17em}100\hspace{0.17em}\hspace{0.17em}}\mu \text{m}/\text{s}$ and $q_0=0.9,2.4,\text{\hspace{0.17em}and\hspace{0.17em}}6\mu \text{M}/\text{s}$, respectively; the 3 plots for the right column are for $v_{\mathrm{z}}=200\mu \text{m}/\text{s}$ and $q_0=0.9,2.4,\text{\hspace{0.17em}and\hspace{0.17em}}6\mu \text{M}/\text{s}$, respectively. The calculated $g$ values are in the range of 0.89–$286.09\mu \mathrm{M}/\mathrm{s}$.

Fig. 4.

Calculated mean oxygen supply rate [right side of Eq. 17] versus normalized mean oxygen, $[{{}^3\mathrm{O}}_2]/{[{{}^3\mathrm{O}}_2]}_0$. The data are plotted for artery oxygen partial pressure $P_{\mathrm{ts}}=50\mathrm{mmHg}$, capillary length $l_{\mathrm{z}}=220\mu \mathrm{m}$ as well as different blood flow $v_{\mathrm{z}}$ and maximum metabolic oxygen consumption rate $q_0$. Each plot contains nine combinations of cylindrical tissue radius $R_{\mathrm{t}}(18,30,60\mu \text{m})$ and capillary radius $R_{\mathrm{c}}(2.5,4,10\mu \text{m})$ as presented with different colors and symbols. The 3 plots for the left column are for $v_{\mathrm{z}}=50\mu \text{m}/\text{s}$ and $q_0=0.9,2.4,\text{\hspace{0.17em}and\hspace{0.17em}}6\mu \text{M}/\text{s}$, respectively; the 3 plots for the middle column are for $v_{\mathrm{z}}=\text{\hspace{0.17em}100\hspace{0.17em}\hspace{0.17em}}\mu \text{m}/\text{s}$ and $q_0=0.9,2.4,\text{\hspace{0.17em}and\hspace{0.17em}}6\mu \text{M}/\text{s}$, respectively; the 3 plots for the right column are for $v_{\mathrm{z}}=200\mu \text{m}/\text{s}$ and $q_0=0.9,2.4,\text{\hspace{0.17em}and\hspace{0.17em}}6\mu \text{M}/\text{s}$, respectively. The calculated $g$ values are in the range of 0.59–$606.96\mu \mathrm{M}/\mathrm{s}$.

Fig. 5.

Calculated mean oxygen supply rate [right side of Eq. 17] versus normalized mean oxygen, $[{{}^3\mathrm{O}}_2]/{[{{}^3\mathrm{O}}_2]}_0$. The data are plotted for blood flow $v_{\mathrm{z}}=100\mu \text{m}/\text{s}$, maximum metabolic oxygen consumption rate $q_0=2.4\mu \text{M}/\text{s}$ as well as different artery oxygen partial pressure $P_{\mathrm{ts}}$ and capillary length $l_{\mathrm{z}}$. Each plot contains 9 combinations of cylindrical tissue radius $R_{\mathrm{t}}(18,30,60\mu \text{m})$ and capillary radius $R_{\mathrm{c}}(2.5,4,10\mu \text{m})$ as shown with different colors and symbols. The 3 plots for the left column are for $P_{\mathrm{ts}}=100\mathrm{mmHg}$ and $l_{\mathrm{z}}=100,220,\text{and\hspace{0.17em}}400\mu \mathrm{m}$, respectively; the 3 plots for the right column are for $P_{\mathrm{ts}}=50\mathrm{mmHg}$ and $l_{\mathrm{z}}=100,220,\text{and\hspace{0.17em}}400\mu \mathrm{m}$, respectively. The $g$ values are in the ranges of 1.01–$277.33\mu \mathrm{M}/\mathrm{s}$ and 0.93–$642.25\mu \mathrm{M}/\mathrm{s}$ for $P_{\mathrm{ts}}=100\text{\hspace{0.17em}and\hspace{0.17em}}50\mathrm{mmHg}$, respectively.

3.3. Formulation of $g$ Directly from Blood Vessel Physiological Parameters

The convective oxygen delivery ($Q$) is related to the product of blood flow ($v_{\mathrm{z}}\pi R_{\mathrm{c}}^2$) and oxygen concentration by Fick’s principle:²⁸

$$Q=\pi R_{\mathrm{c}}^2{v}_{\mathrm{z}}[{{}^3\mathrm{O}}_2]\mathrm{.}$$ (18)

Oxygen continuously diffuses from the plasma to the tissue (with the volume of $\pi R_{\mathrm{t}}^2{l}_{\mathrm{z}}$) where it is consumed. If one assumes that all the capillaries perfusing the tissue are identical and that the oxygen consumption is uniform within the small tissue element shown in Fig. 1(a), then the amount of ${{}^3\mathrm{O}}_2$ removed from the volume of blood per unit length along the capillary ($\pi R_{\mathrm{c}}^2$) is constant. The amounts of oxygen moving across the capillary wall is proportional to that consumed by tissue which is supplied by the capillary:²⁸

$$\pi R_{\mathrm{c}}^2{v}_{\mathrm{z}}[{{}^3\mathrm{O}}_2]\propto g\pi R_{\mathrm{t}}^2{l}_{\mathrm{z}}=\mathrm{const}\mathrm{.}$$ (19)

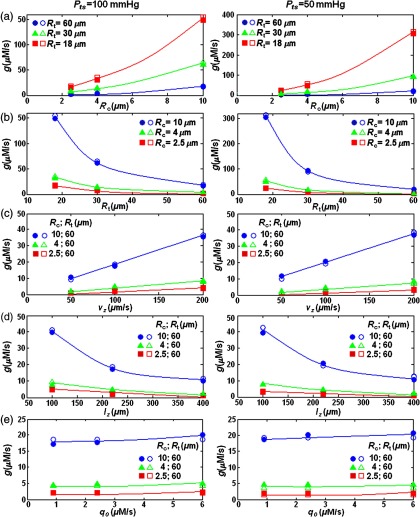
Figures 3 to 5 describing the changes of $g$ with $v_{\mathrm{z}}$, $R_{\mathrm{c}}$, $R_{\mathrm{t}}$, and $l_{\mathrm{z}}$ show close agreement with Fick’s principles. While with the same conditions of $R_{\mathrm{t}}$ and $R_{\mathrm{c}}$, the resulting $g$ values decreased roughly by $1/l_{\mathrm{z}}$, $g$ linearly increased with $v_{\mathrm{z}}$; $g$ showed a nonlinear relationship with $R_{\mathrm{c}}$, $R_{\mathrm{t}}$, and $q_0$. On the basis of the reduced chi-squared ($0.96\le {\chi }^2\le 1$), the $g$ values versus $R_{\mathrm{c}}$ [Fig. 6(a)], $R_{\mathrm{t}}$ [Fig. 6(b)], $v_{\mathrm{z}}$ [Figs. 6(c)], and $l_{\mathrm{z}}$ [Figs. 6(d)] were best fitted with a second-order polynomial, second power decay, linear, and first power decay curves, respectively. The fitting equations were used to obtain an empirical Eqs. (20) and (21) that can calculate $g$ directly from $v_{\mathrm{z}}$, $R_{\mathrm{c}}$, $R_{\mathrm{t}}$, $l_{\mathrm{z}}$, and $q_0$ for two $P_{\mathrm{ts}}$ conditions:

$$P_{\mathrm{ts}}=100\mathrm{mmHg}:g[\mu \mathrm{M}/\mathrm{s}]=\frac{1200v_{\mathrm{z}}[\mu \mathrm{m}/\mathrm{s}]R_{\mathrm{c}}[\mu \mathrm{m}](R_{\mathrm{c}}[\mu \mathrm{m}]+[\frac{{100}^2+q_0^2[\mu \mathrm{M}/\mathrm{s}]}{{(50)}^2-q_0^2[\mu \mathrm{M}/\mathrm{s}]}\left]\right),}{l_{\mathrm{z}}[\mu \mathrm{m}]{(R_{\mathrm{t}}[\mu \mathrm{m}]+4.2)}^2}$$ (20)

$$P_{\mathrm{ts}}=50\mathrm{mmHg}:g[\mu \mathrm{M}/\mathrm{s}]=\frac{1200v_{\mathrm{z}}[\mu \mathrm{m}/\mathrm{s}]R_{\mathrm{c}}[\mu \mathrm{m}](R_{\mathrm{c}}[\mu \mathrm{m}]+[\frac{{50}^2+q_0^2[\mu \mathrm{M}/\mathrm{s}]}{{(50)}^2-q_0^2[\mu \mathrm{M}/\mathrm{s}]}\left]\right)}{l_{\mathrm{z}}[\mu \mathrm{m}]{(R_{\mathrm{t}}[\mu \mathrm{m}]-4.2)}^2}.$$ (21)

Fig. 6.

$g$ versus (a) $R_{\mathrm{c}}$, (b) $R_{\mathrm{t}}$, (c) $v_{\mathrm{z}}$, (d) $l_{\mathrm{z}}$, and (e) $q_0$ for $P_{\mathrm{ts}}=100\mathrm{mmHg}$ (in the left column) and $P_{\mathrm{ts}}=50\mathrm{mmHg}$ (in the right column). The vasculature conditions assumed to have the standard values presented in Table 3. The actual $g$ values (filled-set symbols) are compared with those calculated by using Eqs. (20) and (21) (empty-set symbols). On the basis of the reduced chi-squared ($0.96\le {\chi }^2\le 1$), the $g$ values versus $R_{\mathrm{c}}$, $R_{\mathrm{t}}$, $v_{\mathrm{z}}$, and $l_{\mathrm{z}}$ were best fitted with second-order polynomial, second power decay, linear and first power decay curves, respectively.

The relationship between $g$ and $q_0$ as well as the constant values were obtained and optimized manually based on the relative errors of the actual $g$ and those obtained by Eqs. (20) and (21). For the range of microenvironments shown in Table 3, Eqs. (20) and (21) determine $g$ values in the ranges of 0.6 to $685.3\mu \mathrm{M}/\mathrm{s}$ for $P_{\mathrm{ts}}=100\mathrm{mmHg}$ and 0.4 to $1390\mu \mathrm{M}/\mathrm{s}$ for $P_{\mathrm{ts}}=50\mathrm{mmHg}$. The maximum $g$ value of $1390\mu \mathrm{M}/\mathrm{s}$ is obtained for $R_{\mathrm{c}}=10\mu \mathrm{m}$, $R_{\mathrm{t}}=18\mu \mathrm{m}$, $v_{\mathrm{z}}=200\mu \mathrm{m}/\mathrm{s}$, $P_{\mathrm{ts}}=50\mathrm{mmHg}$, $q_0=6\mu \mathrm{M}/\mathrm{s}$, and $l_{\mathrm{z}}=100\mu \mathrm{m}$. The minimum $g$ value of $0.4\mu \mathrm{M}/\mathrm{s}$ is calculated for $R_{\mathrm{c}}=2.5\mu \mathrm{m}$, $R_{\mathrm{t}}=60\mu \mathrm{m}$, $v_{\mathrm{z}}=50\mu \mathrm{m}/\mathrm{s}$, $P_{\mathrm{ts}}=50\mathrm{mmHg}$, $q_0=0.9\mu \mathrm{M}/\mathrm{s}$, and $l_{\mathrm{z}}=400\mu \mathrm{m}$. Table 5 shows the results of Eqs. (20) and (21) for the physiological parameters listed in Table 3. The $g$ values are presented with the standard deviations obtained from the actual FEM results and the calculated values from Eqs. (20) and (21). The relative errors were also measured as the percentages of the deviations divided by the FEM calculated $g$ values. The maximum error of 27% occurs for the blood vessel with $P_{\mathrm{ts}}=100\mathrm{mmHg}$, $q_0=0.9\mu \mathrm{M}/\mathrm{s}$, $v_{\mathrm{z}}=200\mu \mathrm{m}/\mathrm{s}$, $l_{\mathrm{z}}=220\mu \mathrm{m}$, $R_{\mathrm{c}}=2.5\mu \mathrm{m}$, and $R_{\mathrm{t}}=18\mu \mathrm{m}$; the minimum error of 0.03% occurs for the blood vessel with $P_{\mathrm{ts}}=100\mathrm{mmHg}$, $q_0=6\mu \mathrm{M}/\mathrm{s}$, $v_{\mathrm{z}}=100\mu \mathrm{m}/\mathrm{s}$, $l_{\mathrm{z}}=220\mu \mathrm{m}$, $R_{\mathrm{c}}=10\mu \mathrm{m}$ and $R_{\mathrm{t}}=18\mu \mathrm{m}$.

Table 5.

The calculated $g$ values using Eqs. (20) and (21) for the same microenvironment ranges examined for the actual $g$ obtained by FEM simulation. The values are presented with the standard deviations obtained from the actual FEM results and the calculated values from Eqs. (20) and (21). The maximum relative (standard) deviation of the fits is 12.82%.

	$v_{\mathrm{z}}$ ($\mu \mathrm{m}/\mathrm{s}$)	$l_{\mathrm{z}}$ ($\mu \mathrm{m}$)	$g$ ($\mu \mathrm{M}/\mathrm{s}$) calculated from Eqs. (20) and (21)
			$R_{\mathrm{c}};R_{\mathrm{t}}$ ($\mu \mathrm{m}$)
			2.5;60	4;60	2.5;30	10;60	4;30	2.5;18	4;18	10;30	10;18
$P_{\mathrm{ts}}=100\mathrm{mmHg}$$q_0=0.9\mu \mathrm{M}/\mathrm{s}$	50	220	$1.0\pm 0.1$	$2.1\pm 0.1$	$3.8\pm 0.2$	$9.3\pm 0.5$	$7.5\pm 0.6$	$9.0\pm 0.5$	$17.7\pm 0.6$	$32.6\pm 3.1$	$77.5\pm 1.9$
	100	220	$2.2\pm 0.1$	$4.2\pm 0.1$	$7.6\pm 0.4$	$18.5\pm 0.9$	$14.9\pm 0.1$	$18.0\pm 1.7$	$35.4\pm 4.5$	$65.3\pm 9.5$	$155.0\pm 5.6$
	200	220	$4.3\pm 0.1$	$8.5\pm 0.4$	$15.2\pm 2.3$	$37.1\pm 7.0$	$29.9\pm 4.8$	$36.0\pm 7.0$	$70.9\pm 10.5$	$130.6\pm 18.7$	$309.9\pm 21.5$
$P_{\mathrm{ts}}=100\mathrm{mmHg}$$q_0=2.4\mu \mathrm{M}/\mathrm{s}$	50	220	$1.1\pm 0.1$	$2.1\pm 0.01$	$3.8\pm 0.2$	$9.3\pm 0.9$	$7.5\pm 0.9$	$9.0\pm 0.1$	$17.7\pm 0.5$	$32.7\pm 2.7$	$77.5\pm 3.7$
	100	220	$2.2\pm 0.1$	$4.2\pm 0.4$	$7.6\pm 0.5$	$18.5\pm 0.6$	$14.9\pm 0.3$	$18.0\pm 0.5$	$35.5\pm 3.0$	$65.3\pm 3.0$	$155.1\pm 4.3$
	200	220	$4.3\pm 0.3$	$8.5\pm 0.4$	$15.2\pm 0.9$	$37.1\pm 0.5$	$29.9\pm 0.5$	$36.0\pm 3.1$	$70.9\pm 11.5$	$130.7\pm 18.2$	$310.2\pm 19.4$
$P_{\mathrm{ts}}=100\mathrm{mmHg}$$q_0=6.0\mu \mathrm{M}/\mathrm{s}$	50	220	$1.1\pm 0.1$	$2.1\pm 0.1$	$3.8\pm 0.2$	$9.3\pm 2.0$	$7.5\pm 1.2$	$9.1\pm 0.3$	$17.9\pm 3.8$	$32.8\pm 2.1$	$77.9\pm 8.5$
	100	220	$2.2\pm 0.1$	$4.3\pm 0.4$	$7.8\pm 1.0$	$18.6\pm 1.0$	$15.1\pm 0.6$	$18.2\pm 0.02$	$35.7\pm 1.8$	$65.6\pm 2.2$	$155.8\pm 0.1$
	200	220	$4.4\pm 0.1$	$8.6\pm 0.5$	$15.3\pm 0.6$	$37.2\pm 4.4$	$30.1\pm 2.8$	$36.4\pm 5.2$	$71.5\pm 11.1$	$131.3\pm 15.1$	$311.5\pm 18.0$
$P_{\mathrm{ts}}=50\mathrm{mmHg}$$q_0=0.9\mu \mathrm{M}/\mathrm{s}$	50	220	$0.8\pm 0.1$	$1.8\pm 0.4$	$3.6\pm 0.5$	$9.6\pm 0.8$	$8.2\pm 1.9$	$12.5\pm 0.1$	$28.7\pm 2.2$	$45.1\pm 2.8$	$157.5\pm 4.1$
	100	220	$1.5\pm 0.2$	$3.5\pm 0.8$	$7.2\pm 0.7$	$19.3\pm 0.4$	$16.4\pm 1.6$	$25.1\pm 1.5$	$57.3\pm 9.4$	$90.1\pm 2.6$	$315.1\pm 12.4$
	200	220	$3.1\pm 0.2$	$7.0\pm 0.7$	$14.3\pm 0.1$	$38.5\pm 0.7$	$32.8\pm 0.9$	$50.1\pm 1.0$	$114.6\pm 18.1$	$180.3\pm 9.3$	$630.2\pm 20.2$
$P_{\mathrm{ts}}=50\mathrm{mmHg}$$q_0=2.4\mu \mathrm{M}/\mathrm{s}$	50	220	$0.8\pm 0.1$	$1.8\pm 0.3$	$3.6\pm 0.2$	$9.9\pm 0.6$	$8.2\pm 2.2$	$12.6\pm 1.4$	$28.7\pm 0.9$	$45.1\pm 4.3$	$157.6\pm 3.8$
	100	220	$1.5\pm 0.3$	$3.5\pm 0.8$	$7.2\pm 1.2$	$19.3\pm 0.8$	$16.4\pm 1.1$	$25.1\pm 0.2$	$57.3\pm 5.9$	$90.2\pm 2.6$	$315.2\pm 6.8$
	200	220	$3.1\pm 0.2$	$7.0\pm 0.3$	$14.4\pm 0.6$	$38.6\pm 0.6$	$32.8\pm 1.4$	$50.2\pm 3.2$	$114.7\pm 18.7$	$180.4\pm 9.3$	$630.4\pm 18.2$
$P_{\mathrm{ts}}=50\mathrm{mmHg}$$q_0=6.0\mu \mathrm{M}/\mathrm{s}$	50	220	$0.8\pm 0.1$	$1.8\pm 0.4$	$3.6\pm 0.6$	$9.7\pm 1.0$	$8.2\pm 1.7$	$12.6\pm 1.6$	$28.8\pm 3.3$	$45.2\pm 7.5$	$158.0\pm 2.7$
	100	220	$1.6\pm 0.2$	$3.5\pm 0.8$	$7.2\pm 0.1$	$19.3\pm 1.0$	$16.5\pm 0.4$	$25.3\pm 0.3$	$57.6\pm 3.8$	$90.4\pm 2.8$	$315.9\pm 6.8$
	200	220	$3.1\pm 0.3$	$7.1\pm 1.1$	$14.5\pm 0.9$	$38.6\pm 4.9$	$33.0\pm 1.6$	$50.5\pm 2.5$	$115.2\pm 20.4$	$180.8\pm 8.7$	$631.8\pm 17.6$
$P_{\mathrm{ts}}=100\mathrm{mmHg}$$q_0=2.4\mu \mathrm{M}/\mathrm{s}$	100	100	$4.7\pm 0.1$	$9.3\pm 1.1$	$16.7\pm 2.6$	$40.8\pm 2.2$	$32.9\pm 2.2$	$39.6\pm 6.3$	$78.0\pm 1.9$	$143.8\pm 23.1$	$341.2\pm 45.1$
	100	220	$2.2\pm 0.1$	$4.2\pm 0.4$	$7.6\pm 0.5$	$18.5\pm 0.6$	$14.9\pm 0.3$	$18.0\pm 0.5$	$35.5\pm 3.0$	$65.3\pm 3.0$	$155.1\pm 4.3$
	100	400	$1.2\pm 0.1$	$2.3\pm 0.1$	$4.3\pm 0.6$	$10.2\pm 0.5$	$8.2\pm 1.7$	$9.9\pm 0.8$	$19.5\pm 0.3$	$35.9\pm 4.1$	$85.3\pm 2.0$
$P_{\mathrm{ts}}=50\mathrm{mmHg}$$q_0=2.4\mu \mathrm{M}/\mathrm{s}$	100	100	$3.4\pm 0.2$	$7.7\pm 0.01$	$15.8\pm 0.5$	$42.4\pm 2.5$	$36.1\pm 0.4$	$55.2\pm 2.7$	$126.1\pm 18.8$	$198.4\pm 27.9$	$693.4\pm 36.2$
	100	220	$1.5\pm 0.3$	$3.5\pm 0.8$	$7.2\pm 1.2$	$19.3\pm 0.8$	$16.4\pm 1.1$	$25.1\pm 0.2$	$57.3\pm 5.9$	$90.2\pm 2.6$	$315.2\pm 6.8$
	100	400	$0.8\pm 0.1$	$1.9\pm 0.2$	$4.0\pm 0.1$	$10.6\pm 0.6$	$9.0\pm 0.1$	$13.8\pm 0.4$	$31.5\pm 0.7$	$49.6\pm 5.7$	$173.4\pm 21.8$

4. Conclusion

The accurate estimation of the maximum oxygen supply rate, $g$, is very important for the mathematical investigation of complex PDT mechanisms. In this study, we suggested a simplified expression for $g$ that can replace the complex modeling of blood vasculature while maintaining reasonable accuracy. Using the microscopic model, the relationship of the oxygen supply rates versus $[{{}^3\mathrm{O}}_2]/{[{{}^3\mathrm{O}}_2]}_0$ has been examined for Photofrin-mediated PDT treated at $\varphi$ ranging from 25 to $150\mathrm{mW}/{\mathrm{cm}}^2$; the slope of the linear fit to these data represents the $g$ value in $\mu \mathrm{M}/\mathrm{s}$. The simulations have been also tested for different photochemical parameters corresponding to mTHPC-, BPD-, and HPPH-mediated PDT. The obtained results showed a linear relationship independent of $\varphi$, $\xi$, $\sigma$, and $\beta$. The possible $g$ values in Photofrin-mediated PDT were then calculated for a broad range of physiological parameters that have been measured in the past for normal and tumor vasculatures. Examination reveals that the $g$ values can range from 0.4 to $1390\mu \mathrm{M}/\mathrm{s}$ depending on the actual physiological environment. The maximum $g$ value of $1390\mu \mathrm{M}/\mathrm{s}$ was obtained for blood vessels with $R_{\mathrm{c}}=10\mu \mathrm{m}$, $R_{\mathrm{t}}=18\mu \mathrm{m}$, $v_{\mathrm{z}}=200\mu \mathrm{m}/\mathrm{s}$, $P_{\mathrm{ts}}=50\mathrm{mmHg}$, $q_0=6\mu \mathrm{M}/\mathrm{s}$, and $l_{\mathrm{z}}=100\mu \mathrm{m}$. The minimum $g$ value of $0.41\mu \mathrm{M}/\mathrm{s}$ was calculated for $R_{\mathrm{c}}=2.5\mu \mathrm{m}$, $R_{\mathrm{t}}=60\mu \mathrm{m}$, $v_{\mathrm{z}}=50\mu \mathrm{m}/\mathrm{s}$, $P_{\mathrm{ts}}=50\mathrm{mmHg}$, $q_0=0.9\mu \mathrm{M}/\mathrm{s}$, and $l_{\mathrm{z}}=400\mu \mathrm{m}$.

Based on Fick’s principle,²⁸ if all the capillaries perfusing the tissue are identical and the oxygen consumption is uniform within the tissue element, the amount of oxygen moving across the capillary wall is proportional to that consumed by tissue which is supplied by the capillary ($v_{\mathrm{z}}\pi R_{\mathrm{c}}^2[{{}^3\mathrm{O}}_2]\propto g\pi R_{\mathrm{t}}^2{l}_{\mathrm{z}}$). This is in close agreement with our simulation outcome which estimates $g$ to increase with decreasing $l_{\mathrm{z}}$ (first power decay) and $R_{\mathrm{t}}$ (second power decay) and increasing $R_{\mathrm{c}}$ (quadratic second-order polynomial enhancement), and $v_{\mathrm{z}}$ (linear enhancement). Our model also anticipates $g$ to increase nonlinearly and slowly with $q_0$.

A comparison of our estimated $g$ values with those obtained by the previous in vivo studies shows that our calculation is accurate and the $g$ value can be potentially used for our macroscopic model [Eqs. (1–5)].

Biographies

Timothy C. Zhu received his PhD degree in 1991 in physics from Brown University. He is currently a professor in the Department of Radiation Oncology at the University of Pennsylvania. His current research interests include explicit PDT dosimetry, singlet oxygen explicit dosimetry (SOED), integrated system for interstitial and intracavitory PDT, diffuse optical tomography, in vivo dosimetry, and external beam radiation transport.

BaochangLiu received his PhD degree in medical physics in 2012 from McMaster University, where he specialized in photodynamic therapy (PDT) dosimetry. He continued his research as a postdoctoral fellow in the Department of Radiation Oncology at the University of Pennsylvania. His research interests include modeling PDT dosimetry and oxygen transport in tissue, in vivo explicit dosimetry for interstitial PDT, developing direct ${{}^1\mathrm{O}}_2$ dosimetry system, and tissue optics.

RozhinPenjweini received her PhD degree in 2012 in physics from the University of Vienna. She is currently a postdoctoral researcher in the Department of Radiation Oncology at the University of Pennsylvania. Her current research interest is in vivo explicit PDT and singlet oxygen dosimetry. She also has practical experience in various fluorescence microscopy techniques for studying the structure, transport, and stability of nanomedicines for PDT treatment of cancer.