A direct method to evaluate the time-dependent predictive accuracy for biomarkers

Summary

Time-dependent receiver operating characteristic (ROC) curves and their area under the curve (AUC) are important measures to evaluate the prediction accuracy of biomarkers for time-to-event endpoints (e.g., time to disease progression or death). In this paper, we propose a direct method to estimate AUC(t) as a function of time t using a flexible fractional polynomials model, without the middle step of modeling the time-dependent ROC. We develop a pseudo partial-likelihood procedure for parameter estimation and provide a test procedure to compare the predictive performance between biomarkers. We establish the asymptotic properties of the proposed estimator and test statistics. A major advantage of the proposed method is its ease to make inference and to compare the prediction accuracy across biomarkers, rendering our method particularly appealing for studies that require comparing and screening a large number of candidate biomarkers. We evaluate the finite-sample performance of the proposed method through simulation studies and illustrate our method in an application to AIDS Clinical Trials Group 175 data.

1. Introduction

Recent developments in genomic and medical research have generated a large number of candidate biomarkers that have potential use in predicting an individual's future health status. These biomarkers are often biochemical or genetic measurements on a continuous scale that calibrate the progression of patients’ responses to the treatment of a disease, e.g., gene expression profiling and protein mass spectrometry (Cai and Moskowitz, 2004) and molecular biomarkers (Ransohoff, 2004). Before adopting biomarkers into clinical use, it is crucial to evaluate their accuracy (i.e., sensitivity and specificity) in predicting the likelihood of a patient experiencing a future event of interest (e.g., disease onset, disease progression and death).

One major challenge in evaluating the prediction accuracy of biomarkers arises from the fact that in many applications, the primary endpoint is the time to an event, and the risk of a patient developing the event of interest often changes over time given the baseline measure of biomarkers. For example, in a prostate cancer study, investigators analyzed data collected from samples of prostate-specific antigen and found that the test with the longest lead time did not necessarily correspond to a better diagnostic score (Pearson et al., 1994, 1996; Etzioni et al., 1999). Hence, they recommended evaluating the prediction performance of tests over a range of time rather than at the time of diagnosis. In this situation, the use of the conventional binary outcome-based receiver operating characteristic (ROC) methods and the area under the ROC curve (AUC) is not suitable and may lead to misleading results.

To address this issue, several time-dependent measures have been proposed in the literature, including time-dependent sensitivity, specificity, ROC and AUC (Heagerty et al., 2000; Heagerty and Zheng, 2005). In this article, we consider the incident/dynamic (I/D) time-dependent ROC, which was first defined by Heagerty and Zheng (2005), and focus on estimating its time-dependent AUC. One major advantage of the I/D definition over other types of time-dependent ROCs (e.g., cumulative/dynamic) is that it gives a natural way to define a weighted time-averaged summary of AUC, which is called IAUC. Moreover, Heagerty and Zheng (2005) showed that IAUC is equivalent to the global concordance summary with a proper weight function.

Two types of methods have been proposed to estimate time-dependent AUC and IAUC. The first type of methods, which might be called “indirect” methods, focus on modeling time-dependent ROC curves, and obtain the estimate of the AUC as a byproduct. Heagerty and Zheng (2005) considered time-dependent ROC estimation based on a Cox model for survival time. Cai et al. (2006) used generalized linear models to estimate time-dependent sensitivity and specificity. In Song and Zhou (2008), a covariate-specific ROC estimator was constructed by including baseline covariates in the modeling of hazard functions. Zheng et al. (2008, 2010) considered positive predictive value curve estimation based on flexible regression-type method, which was extended thereafter in the presence of competing risks (Zheng et al., 2012). An extension of the time-dependent ROC for competing risks has been considered by Saha and Heagerty (2010). For the purpose of estimating the time-dependent AUC and IAUC, the “indirect” methods have some drawbacks. For example, most ROC-estimation procedures rely on strong parametric assumptions such as proportional hazards, which may lead to potential bias due to the misspecification of the time-to-event model. In addition, because these methods are “indirect”, they are not particularly efficient and require unnecessary intensive computation.

The second type of methods, which are called “direct” methods, bypass the step of estimating ROC curves, and directly estimate the time-dependent AUC. Song et al. (2012) considered a flexible nonparametric estimation procedures based on the proportion of concordance pairs, and adopted the inverse-probability-of-censoring weighting technique (Robins et al., 1994) to handle the censored outcomes. Recently, Saha-chaudhuri and Heagerty (2013) proposed estimating the AUC nonparametrically by a locally weighted mean rank (WMR) kernel-based method with a bandwidth selected by cross-validation or other data-driven methods. The resulting WMR estimate is essentially a smoothed version of the proportion of concordant case-control pairs in the risk set and hence bypasses the need to model the distribution of the event time, and handles censoring in a simple way.

In modern biomarker studies, we often face the challenge of comparing and screening a large number of candidate biomarkers generated by high-throughput methods. It is highly desirable to have a direct method that is computationally easy, so that we can perform fast screening and comparison of the predictive accuracy of candidate biomarkers based on time-dependent AUC and IAUC. The WMR method of Saha-chaudhuri and Heagerty (2013) may not be particularly suitable for this task because the choice of bandwidth is often computationally intensive. In addition, it is not obvious how one should estimate and make inference of the IAUC under the WMR method, which mainly focuses on point-wise estimates of AUC(t) at a given time point t.

The goal of this paper is to propose a new direct method that provides straightforward inference for AUC(t) and IAUC. Our method directly models AUC(t) as a function of time t using a flexible and yet parsimonious parametric model, namely, the fractional polynomials model proposed by Royston and Altman (1994). We construct and maximize a pseudo partial-likelihood function to obtain the estimates of model parameters. We show that the resulting estimating equations can be viewed as U-statistics and derive asymptotic variance of the estimates. Under the proposed approach, it is convenient to obtain the confidence bands for the AUC(t), and estimate and compare the IAUC across biomarkers. These characteristics render our method particularly appealing for studies that require comparing and screening a large number of candidate biomarkers.

The rest of the paper is organized as follows. In Section 2, we introduce a pseudo partial- likelihood approach to estimate the time-dependent AUC and derive its large-sample properties. We construct a testing procedure to compare multiple biomarkers in Section 2.4. We report some simulation results in Section 3 that illustrate our methodology. We also discuss a real data example in Section 4, and provide technical proofs and additional numerical results in the online supplementary file.

2. Method

2.1 Notation and estimand

Suppose that there are n subjects in the study. For subject i, we denote event time and censoring time by T_i and C_i, and assume that C_i is independent of T_i. Define the observed event time Z_i = min(T_i, C_i) and the failure indicator δ_i = 1l(T_i ≤ C_i), where 1l(·) is the indicator function. Denote R(t) = {j : Z_j ≥ t} as the risk set at time t. We consider independently distributed biomarkers M₁, . . . , M_n, and assume that higher marker values are related to higher disease levels and shorter event times.

Because an ROC curve is completely determined by the set of combinations of true-positive (TP) and false-positive (FP) rates, it suffices to extend the definitions of TP and FP rates to accommodate the time-dependent setting. Different time-dependent extensions of the TP and FP rates have been proposed in the literature. Here, we have adopted the one proposed by Heagerty and Zheng (2005):

$${\mathrm{TP}}_t\left(m\right)=\mathrm{P}(M_i>m\mid T_i=t),{\mathrm{FP}}_t\left(m\right)=\mathrm{P}(M_i>m\mid T_i>t),$$

where TP_t(m) (i.e., sensitivity) measures the expected fraction of subjects with a biomarker value greater than m among the subpopulation of individuals who experience the event of interest at time t, while 1 FP_t(m) (i.e., specificity) measures the fraction of subjects with a biomarker value less than or equal to m among those who survive beyond time t. Heagerty and Zheng (2005) refer to these measures as time-dependent incidence sensitivity and dynamic specificity, respectively. Under this definition, the time-dependent ROC is defined as

$${\mathrm{ROC}}_t\left(p\right)={\mathrm{TP}}_t\left\{{\left[{\mathrm{FP}}_t\right]}^{-1}\left(p\right)\right\},\text{for}p\in [0,1],$$

and the corresponding AUC(t) is given by

$$\mathrm{AUC}\left(t\right)=\mathrm{P}(M_i>M_j\mid T_i=t,T_j>t).$$ (1)

2.2 Model AUC(t) using fractional polynomials

To model the AUC(t), a nonparametric method, such as the WMR estimate (Saha-chaudhuri and Heagerty, 2013), is flexible and imposes few assumptions on the functional form. However, the fitting process (e.g., selecting a bandwidth) can be computationally intensive, and estimating and making inference for the IAUC is diffcult with this type of method. In this article, we model the AUC(t) using a flexible parametric model that is parsimonious, and easy to fit and to use in making inference.

Specifically, letting η(·) denote a link function, e.g., logistic function, we directly model the AUC(t) as a parametric function of time t using fraction polynomials of K degrees as follows:

$$\eta \left(\mathrm{AUC}\left(t\right)\right)=\sum _{k=0}^K{\beta }_k{t}^{\left(p_k\right)},$$

where for k = 1, . . . , K,

$$t^{\left(p_k\right)}=\{\begin{array}{cc}{t}^{p_k}\hfill & \text{if}{p}_k\ne 0\hfill \\ \ln \left(t\right)\hfill & \text{if}{p}_k=0\hfill \end{array}\phantom{\}},$$ (2)

where p₁ ≤ . . . ≤ p_K are real-valued powers, and β₀, . . . , β_K are unknown regression parameters. Royston and Altman (1994) showed that unlike conventional polynomials, for which lower order polynomials offer a limited family of shapes and high order polynomials may fit poorly at the extreme values of the covariates, fractional polynomials have considerable flexibility and can mimic most function shapes we encounter in practice. The fractional polynomial regression provides an attractive alternative approach to conventional nonparametric methods, such as spline and kernel smoothers, while keeping the model parsimonious and inference straightforward given the closed-form variance formulae derived in the next subsection. According to Royston and Altman (1994), we will adopt the choice of powers p₁, . . . , p_K in a set {−2, −1, −1/2, 0, 1/2, 1, 2}, which will be good enough for most applications. For notational simplicity, we denote our estimator of the AUC(t) as ρ(t, β).

Our strategy of estimating ρ(t, β) is based on the fact that the conditional event in equation (1) is the same event that has being used to construct the risk function at time t in the partial-likelihood. More specifically, let s₁, ..., s_H be the ordered unique event times for z₁, ..., z_n. For each event time s_h, we denote its risk set by R(s_h). Motivated by equation (1), we consider two types of events conditional on each risk set R(s_h) derived from the observed data, denoted by

$$\begin{array}{cc}\hfill e_1(M_i,M_j,Z_i,Z_j)=& \{M_i>M_j\mid Z_i=s_h,{\delta }_i=1,j\in R\left(s_h\right)\},\hfill \\ \hfill e_2(M_i,M_j,Z_i,Z_j)=& \{M_i\le M_j\mid Z_i=s_h,{\delta }_i=1,j\in R\left(s_h\right)\}.\hfill \end{array}$$

Event e₁(M_i, M_j, Z_i, Z_j) occurs if subject j has a smaller biomarker value compared with that of subject i, given that subject j has longer survival than subject i, so we call it a “concordant” event. Event e₂(M_i, M_j, Z_i, Z_j) occurs if subject j has a larger biomarker value compared with that of subject i, given that subject j has longer survival than subject i; we similarly call this a “discordant” event.

For each event time s_h, the counts of two types of events are

$$\begin{array}{cc}\hfill n_1\left(s_h\right)=& \sum _{j}1\mathrm{l}\{j:M_i>M_j\mid Z_i=s_h,{\delta }_i=1,j\in R\left(s_h\right)\},\hfill \\ \hfill n_2\left(s_h\right)=& \sum _{j}1\mathrm{l}\{j:M_i\le M_j\mid Z_i=s_h,{\delta }_i=1,j\in R\left(s_h\right)\}.\hfill \end{array}$$

Note that AUC(t) = P(M_i > M_j|T_i = t, T_j > t), thus at each event time point s_h, conditional on risk set R(s_h), the count n₁(s_h) follows a binomial distribution with a probability of AUC(s_h). Motivated by this fact, we construct a pseudo partial-likelihood by multiplying all probabilities of observing the concordant or discordant counts over all of the risk sets from the observed event times. Synthesizing this information, we have the pseudo partial-likelihood as

$$L\left(\beta \right)\propto {\Pi }_{h=1}^H\rho {(s_h;\beta )}^{n_1\left(s_h\right)}{\{1-\rho (s_h;\beta )\}}^{n_2\left(s_h\right)},$$ (3)

Maximizing this pseudo partial-likelihood, or alternatively solving the corresponding score equations, yields parameter estimate $\widehat{\beta }$. Then, by using (2), we obtain the time-dependent AUC estimate ρ(t, β) as a smooth function of time t and β.

Notice that the above pseudo partial-likelihood L(β) is not a true likelihood function because the probabilities of observing the concordant or discordant counts conditional on the risk sets are multiplied together without accounting for the possible correlations between observed information from different risk sets. Nevertheless, since each term in L(β) is a legitimate conditional probability, the corresponding score equation is an unbiased estimating equation for β and the corresponding maximum pseudo partial-likelihood estimator can be shown to be consistent and asymptotically normal. In fact, the proposed pseudo partial-likelihood belongs to the family of composite likelihoods (Lindsay, 1988; Cox and Reid, 2004), for which (weighted) conditional or marginal densities are multiplied, whether or not they are independent. For more discussion on the composite likelihood methods, we refer to the excellent review paper by Varin et al. (2011) and the references therein.

In practice, it is also often of interest to estimate the IAUC, defined as

$$C\left(\tau \right)={\int }_0^{\tau }w(t;\tau )\mathrm{AUC}\left(t\right)dt,$$ (4)

where w(t, τ) is a non-negative weight function that integrates to 1 on the observation time period [0, τ]. The IAUC provides a global summary of the prediction accuracy for biomarkers, and can be used to compare the prediction performance between biomarkers and screen a pool of candidate biomarkers. Heagerty and Zheng (2005) showed that when w(t, τ) is proportional to the product of the density function and the survival function of t, C(τ) is equivalent to the global dependence measure, Kendall's tau. Under the proposed framework, the estimation of C(τ) is computationally simple, and a “plug-in” estimator of C(τ) is given by

$$C(\widehat{\beta };\tau )={\int }_0^{\tau }w(t;\tau )\rho (t;\widehat{\beta })dt.$$ (5)

When the weight function w(t, τ) is invariant to time, e.g., w(t, τ) = 1/τ, the IAUC C(τ) can be viewed as the global average of the AUC curve.

Computationally, our method estimates the whole curve of AUC(t) as a function of β by maximizing the proposed pseudo-partial likelihood. Then the global measures such as IAUC and its standard error can be conveniently estimated as by-products, since these quantities can be obtained as closed-form functions of β. In contrast, the nonparametric methods (Song et al., 2012; Saha-chaudhuri and Heagerty, 2013) give point-wise estimate of the AUC(t) and require repeated calculations at different grid points of time to obtain the whole curve of AUC(t). Consequently, one would need to repeat point-wise calculation many times to estimate the global measures such as IAUC. The tuning of smoothing parameters may also be cumbersome since an optimization of the IMSE is required according to Saha-chaudhuri and Heagerty (2013).

So far we have assumed that no two patients have the same failure event time in the data, which is an assumption that may be violated in practice. In the presence of such ties in failure times, without loss of generality, we assume the observed event times of the ith and jth patients are the same. Without any knowledge of the true ordering of the failure event times of patients i and j, we have to consider all possible orderings. There are 2 possible orderings in this case. We can construct two sets of unique failure event times by adding a small amount (e.g. 10⁻⁵) to Z_i or Z_j. Then the likelihood is constructed by adding two likelihoods under two sets of unique failure event times together. This method, called the exact method, can be computationally intensive. For example, suppose there are d_j tied failure event times at the s_j distinct time, then d_j! different orderings have to be considered and the likelihood is the sum of d_j! different terms. To handle such computational diffculties in the case of many ties, we can approximate the likelihood under the exact method by randomly choosing one possible ordering from the observed data and maximizing the corresponding likelihood under this chosen ordering.

2.3 Inference: Asymptotic results

When making inferences about the proposed estimators of the parameters, the major challenge lies in the fact that the proposed pseudo partial-likelihood cannot be treated as either a classical partial-likelihood function or a regular likelihood function. Specifically, the asymptotic variance of the estimators is not the inverse of the negative second derivative of the pseudo partial-likelihood. To evaluate the asymptotic behavior of the proposed estimators, we will further study the score equations that correspond to the proposed likelihood. We re-write the log-likelihood in the following way:

$$l\left(\beta \right)=\sum _{i=1}^n\sum _{j=1}^n{\delta }_{i}1\mathrm{l}(Z_j>Z_i)\{1\mathrm{l}(M_i>M_j)\log \left(\rho (Z_i;\beta )\right)+1\mathrm{l}(M_i\le M_j)\log (1-\rho (Z_i;\beta ))\}.$$

By taking the derivative, we obtain the score function as

$$U\left(\beta \right)=\sum _{i=1}^n\sum _{j=1}^n{\delta }_{i}1\mathrm{l}(Z_j>Z_i)\left\{1\mathrm{l}(M_i>M_j)\frac{{\nabla }_{\beta }\rho (Z_i;\beta )}{\rho (Z_i;\beta )}-1\mathrm{l}(M_i\ge M_j)\frac{{\nabla }_{\beta }\rho (Z_i;\beta )}{1-\rho (Z_i;\beta )}\right\},$$

where ∇_β f(β) is the first order derivative of a function f with respect to a vector β. Denote $\widehat{\beta }$ as a solution of U(β) = 0 and β ₀ as the true value of β. By Taylor's expansions of U(β) around β ₀ to the second order, we can show consistency of $\widehat{\beta }$. Moreover, based on the exchangeable structure in the score equation, we obtain the conclusion that $\widehat{\beta }$ is asymptotically normally distributed under certain regularity conditions using U-statistic projection theory. We summarize these results in the following theorem.

Theorem 1

Under the regularity conditions (A1) – (A3) listed in the supplementary file, the estimator $\widehat{\beta }$, at which the local maxima of L(β) occurs, converges to β₀. Moreover, is asymptotically normal with mean β₀ and covariance matrix $\mathit{V}={\Sigma }_1^{-1}{\Sigma }_2^{}{\Sigma }_1^{-1}$, where

$$\begin{array}{cc}\hfill & {\Sigma }_1=E\{-{\nabla }_{\beta }{f}_{12}\left(\beta \right);{\beta }_0\},{\Sigma }_2=4cov\{g_{12}\left(\beta \right),g_{13}\left(\beta \right);{\beta }_0\},g_{ij}\left(\beta \right)=\{f_{ij}\left(\beta \right)+f_{ji}\left(\beta \right)\}∕2,\hfill \\ \hfill & f_{ij}\left(\beta \right)={\int }_0^{\tau }{\int }_0^{\tau }1\mathrm{l}(t>s)\left\{1\mathrm{l}(M_i>M_j)\frac{{\nabla }_{\beta }\rho (s;\beta )}{\rho (s;\beta )}-1\mathrm{l}(M_i\le M_j)\frac{{\nabla }_{\beta }\rho (s;\beta )}{1-\rho (s;\beta )}\right\}d{N}_i\left(s\right)d{N}_j\left(t\right),\hfill \end{array}$$

and {N_i(t), t ≥ 0} is a right-continuous counting process that records the number of events occuring over [0, t].

The covariance matrix V can be consistently estimated by ${\widehat{\Sigma }}_1^{-1}{\widehat{\Sigma }}_2{\widehat{\Sigma }}_1^{-1}$, where

$$\begin{array}{c}\hfill {\widehat{\Sigma }}_1=-\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n{\delta }_{i}1\mathrm{l}(Z_j\ge Z_i){\nabla }_{\beta }\left\{1\mathrm{l}(M_i>M_j)\frac{{\nabla }_{\beta }\rho (Z_i;\widehat{\beta })}{\rho (Z_i;\widehat{\beta })}-1\mathrm{l}(M_i\le M_j)\frac{{\nabla }_{\beta }\rho (Z_i;\widehat{\beta })}{1-\rho (Z_i;\widehat{\beta }}\right\},\hfill \\ \hfill \text{and}{\widehat{\Sigma }}_2=\frac{4}{n(n-1)(n-2)}\sum _{i=1}^n\sum _{j\ne j^{\prime },j,j^{\prime }\ne i}{g}_{ij}\left(\widehat{\beta }\right)g_{i{j}^{\prime }}{\left(\widehat{\beta }\right)}^T.\hfill \end{array}$$

The asymptotic behavior of the estimated AUC curve and its integration, which follows that of $\widehat{\beta }$, are summarized in the next corollary.

Corollary 1

Under the regularity conditions (A1)–(A3), $\rho (t;\widehat{\beta })$ is a consistent estimator of AUC(t). Given that the weight function w is continuous on [0, τ], it follows that

$$\sqrt{n}(C(\widehat{\beta };\tau )-C({\beta }_0;\tau ))\stackrel{d}{\to }N(0,V),$$

The variance V can be consistently estimated by

$$\widehat{V}=\frac{4}{n(n-1)(n-2)}\sum _{i=1}^n\sum _{j\ne j^{\prime },j,j^{\prime }\ne i}{s}_{ij}\left(\widehat{\beta }\right)s_{i{j}^{\prime }}\left(\widehat{\beta }\right).$$

2.4 Testing: comparing the predictive accuracy of biomarkers

Rapid progress in biomedical technology has allowed the scientific community to identify numerous biomarkers, such as those for cancer diagnosis and prognosis. With such a large number of candidate biomarkers, it is highly important to select the most useful biomarkers based on their prediction performances. In this section, we use AUC curves and their integration measures to address the scientific question, “How do we compare the prediction accuracies of two biomarkers, M^A and M^B?” . We consider ρ(t, β^A) − ρ(t, β^B) as a quantitative measure of the prediction difference between M^A and M^B and derive its asymptotic distribution, as presented in Corollary 2. Moreover, we construct a test statistic based on a global measure of the prediction difference between two markers across the entire study period. In this subsection, we will use the respective superscripts A and B to denote the corresponding asymptotic quantities of M^A and M^B derived in the previous subsection.

Corollary 2

Under the regularity conditions (A1) – (A3) listed in the supplementary file, $\rho (t;{\widehat{\beta }}^A)-\rho (t;{\widehat{\beta }}^B)$ is asymptotically normal with mean AUC^A(t) AUC^B(t) and variance V ^AB(t), where

$$\begin{array}{c}\hfill V^{AB}\left(t\right)=4cov\{h_{12}({\beta }^A,{\beta }^B,t),h_{13}({\beta }^A,{\beta }^B,t);{\beta }_0^A,{\beta }_0^B\},\hfill \\ \hfill and{h}_{ij}({\beta }_0^A,{\beta }_0^B,t)={\nabla }_{\beta }^T\rho (t;{\beta }_0^A){\left({\Sigma }_1^A\right)}^{-1}{g}_{ij}^A\left({\beta }_0\right)-{\nabla }_{\beta }^T\rho (t;{\beta }_0^B){\left({\Sigma }_1^B\right)}^{-1}{g}_{ij}^B\left({\beta }_0\right).\hfill \end{array}$$

Moreover, $C({\widehat{\beta }}^A;\tau )-C({\widehat{\beta }}^B;\tau )$ is asymptotically normal with mean $C({\beta }_0^A;\tau )-C({\beta }_0^B;\tau )$ and variance V ^AB, where

$$\begin{array}{c}\hfill V^{AB}=4cov\{r_{12}({\beta }^A,{\beta }^B),r_{13}({\beta }^A,{\beta }^B);{\beta }_0^A,{\beta }^B\}and\hfill \\ \hfill r_{ij}({\beta }^A,{\beta }^B)={\int }_0^{\tau }w(t;\tau ){\nabla }_{\beta }^T\rho (t;{\beta }^A)dt{\left({\Sigma }_1^A\right)}^{-1}{g}_{ij}^A\left({\beta }^A\right)-{\int }_0^{\tau }w(t;\tau ){\nabla }_{\beta }^T\rho (t;{\beta }^B)dt{\left({\Sigma }_1^B\right)}^{-1}{g}_{ij}^B\left({\beta }^B\right).\hfill \end{array}$$

The variance V ^AB(t) of $\rho (t;{\widehat{\beta }}^A)-\rho (t;{\widehat{\beta }}^B)$ can be consistently estimated by V̂ ^AB(t), which is given by

$$\frac{4}{n(n-1)(n-2)}\sum _{i=1}^n\sum _{j\ne j^{\prime },j,j^{\prime }\ne i}{h}_{ij}({\widehat{\beta }}^A,{\widehat{\beta }}^B,t)h_{i{j}^{\prime }}({\widehat{\beta }}^A,{\widehat{\beta }}^B,t).$$

Similarly, the variance V ^AB of $C({\widehat{\beta }}^A;\tau )-C({\widehat{\beta }}^B;\tau )$ can be consistently estimated by

$$\widehat{V}=\frac{4}{n(n-1)(n-2)}\sum _{i=1}^n\sum _{j\ne j^{\prime },j,j^{\prime }\ne i}{r}_{ij}({\widehat{\beta }}^A,{\widehat{\beta }}^B)r_{i{j}^{\prime }}({\widehat{\beta }}^A,{\widehat{\beta }}^B).$$

One hypothesis of interest for the overall predictive equivalence of biomarkers M^A and M^B can be formulated as $H_0:C({\beta }_0^A;\tau )=C({\beta }_0^B;\tau )$. Following Corollary 2, we can accordingly construct a Wald-type test statistic, termed T ^AB, as

$$T^{AB}=\frac{C({\widehat{\beta }}^A;\tau )-C({\widehat{\beta }}^B;\tau )}{\sqrt{{\widehat{V}}^{AB}}},$$ (6)

which converges to a standard normal distribution under the null hypothesis H₀.

It is straightforward to generalize the proposed two-biomarker test statistic (6) for simultaneous testing of multiple markers {M¹,..., M^K}. Specifically, we wish to test for

$$H_0^K:C(\nabla {\beta }_0^1;\tau )=C({\beta }_0^2;\tau )=\cdots =C({\beta }_0^K;\tau ).$$

Accordingly, we can extend the test statistic (6) by considering $T^K=C_K^T{\left({\widehat{V}}^K\right)}^{-1}{C}_K$, where C_K is a (K − 1)-dimensional vector:

$$C_K={\left(C({\widehat{\beta }}^1;\tau )-C({\widehat{\beta }}^2;\tau ),C({\widehat{\beta }}^1;\tau )-C({\widehat{\beta }}^3;\tau ),\dots ,C({\widehat{\beta }}^1;\tau )-C({\widehat{\beta }}^K;\tau )\right)}^T,$$

and V̂^K is a (K − 1) × (K − 1) matrix, the (s, t)-th element of which is

$$v_{s,t}=\frac{4}{n(n-1)(n-2)}\sum _{i=1}^n\sum _{j\ne j^{\prime },j,j^{\prime }\ne i}{r}_{ij}({\widehat{\beta }}^1,{\widehat{\beta }}^{s+1})r_{i{j}^{\prime }}({\widehat{\beta }}^1,{\widehat{\beta }}^{t+1}).$$

Under the null hypothesis $H_0^K$, the test statistic T ^K converges to a standard ${\chi }_{K-1}^2$ distribution.

3. Simulation

To explore the theoretical results empirically, we conducted several simulation studies for the proposed estimators of the AUC(t) and the test that compares the predictive accuracy of biomarkers. In particular, we considered a logistic link function and chose the power of the polynomials as {−2, −1, −1/2, 0, 1/2, 1, 2}.

3.1 Estimating the AUC(t) of a single biomarker

We first considered estimating the AUC(t) of a single biomarker. Following the settings of Heagerty and Zheng (2005), we generated 200 pairs of survival time T and marker M, in which (log T, M) follows a bivariate normal distribution with means 0, variances 1 and correlation -0.7. In addition, we generated an independent censoring time uniformly from (0, τ*) such that either 20% or 40% of the subjects were censored. We calculated the estimated values of the AUC(t) at various time points based on N = 1000 replications and compared the fitting results obtained by the nonparametric kernel estimator (WMR) with bandwidth of n^−1/5, as reported by Saha-chaudhuri and Heagerty (2013).

Table 1 lists the empirical bias (Bias), empirical standard error (SD), average of the model-based standard error estimates (SE) and the coverage probability (CP) of the 95% confidence intervals for the estimates. Under both 20% and 40% censoring rates, we nd good estimation of the AUC(t) by the proposed method in that the biases of the estimates are small and the empirical standard errors are close to the averages of the model-based standard error estimates. The empirical coverage probabilities based on the 95% estimated confidence intervals are close to the nominal value of 0.95, especially when we have sufficient data around the given time points, i.e., −1.5 ≤ log T ≤ 0.5. Compared to the WMR, the proposed method has smaller biases and empirical standard deviations (i.e., about 10% smaller), except at the tails (log T = 1), due partly to the use of a regression-type function, ρ, in our method.

Table 1.

Simulation results for estimation of AUC of a single biomarker, comparing the proposed method with the WMR method cited from Table 1 of Saha-chaudhuri and Heagerty (2013). SD and SE are the empirical and model-based standard error estimates. CP is the calculated coverage probability of 95% confidence intervals.

		WMR			Proposed method
Log time	AUC(t)	Bias	SD	CP(%)	Bias	SD	SE	CP(%)
			20% censoring
–2.0	0.884	–0.008	0.055	90.2	–0.001	0.051	0.056	87.9
–1.5	0.833	–0.005	0.040	93.4	–0.001	0.037	0.041	94.1
–1.0	0.782	–0.002	0.037	93.2	–0.001	0.032	0.036	96.1
–0.5	0.734	0.000	0.035	94.1	0.000	0.029	0.035	98.2
0.0	0.693	0.002	0.037	94.0	0.000	0.032	0.037	97.0
0.5	0.660	0.004	0.047	94.9	0.002	0.042	0.046	96.4
1.0	0.634	0.004	0.066	93.0	0.004	0.075	0.074	93.1
C(β; τ)	0.741	–0.003	0.020	89.6	0.001	0.022	0.026	95.0
			40% censoring
–2.0	0.884	–0.008	0.056	89.9	–0.001	0.054	0.057	87.2
–1.5	0.833	–0.005	0.041	92.9	–0.001	0.039	0.042	94.0
–1.0	0.782	–0.001	0.038	92.7	–0.001	0.035	0.038	94.3
–0.5	0.734	0.001	0.039	94.3	–0.001	0.034	0.039	97.0
0.0	0.693	0.003	0.044	93.5	0.000	0.040	0.044	95.7
0.5	0.660	0.006	0.061	92.6	0.006	0.062	0.065	94.3
1.0	0.634	0.006	0.108	91.8	–0.027	0.235	0.285	85.8
C (β; τ)	0.741	–0.002	0.023	88.3	0.001	0.025	0.032	94.0

We considered another example in which the data (log T, M) were generated from a mixture of normal distributions ZN(−1.5, −1.5, 1, 1, 0) + (1 − Z)N(0, 0, 1, 1, −.8), where Z follows a Bernoulli distribution with success probability 0.2. An independent censoring time was generated such that 20% of the patients were censored. We summarize the estimated AUC(t) and compare the results with those of the WMR method in Table 2. It can be seen that the proposed method has comparable estimation bias and more accurate coverage probabilities than the WMR method.

Table 2.

Simulation results for estimation of AUC of a single biomarker, comparing the proposed method with the WMR method cited from Table 3 of Saha-chaudhuri and Heagerty (2013). SD and SE are the empirical and model-based standard error estimates. CP is the calculated coverage probability of 95% confidence intervals.

		WMR			Proposed method
Log time	AUC(t)	Bias	SD	CP(%)	Bias	SD	SE	CP(%)
–2.5	0.378	–0.002	0.109	87.7	0.000	0.104	0.111	91.9
–2.0	0.481	–0.004	0.083	91.1	0.006	0.077	0.085	95.2
–1.5	0.591	0.004	0.062	92.0	0.000	0.059	0.065	96.0
–1.0	0.673	0.001	0.048	91.6	–0.006	0.043	0.047	96.0
–0.5	0.709	–0.001	0.035	93.7	–0.001	0.040	0.041	95.6
0.0	0.709	0.001	0.030	94.8	0.005	0.037	0.039	95.0
0.5	0.691	0.001	0.034	92.5	–0.003	0.054	0.051	93.0
1.0	0.669	0.000	0.042	93.9	–0.002	0.088	0.102	96.2

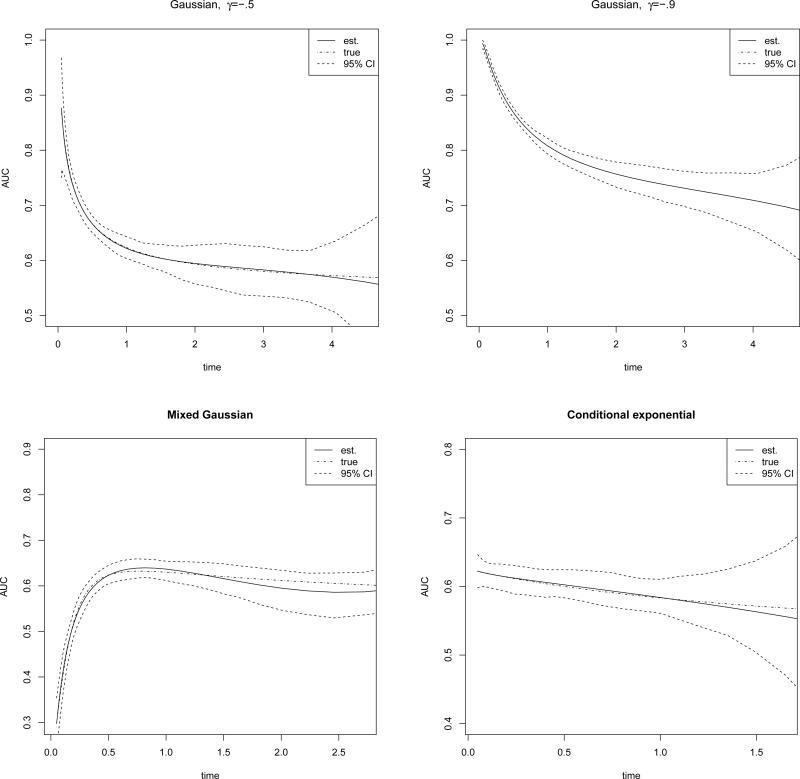
Note that our method is computationally easy and straightforward in producing confidence bands by using the delta method. In Figure 1, we plot the estimated AUCs and the corresponding 95% confidence bands under several data generating mechanisms. For the first two subplots, (log T, M) follows a bivariate normal distribution N(0, 0, 1, 1,γ) with γ = .5 and −.9. For the third subplot, we generate (log T, M) from a mixture of normal distributions ZN(−1.5, −1.5, 1, 1, 0) + (1 − Z)N(0, 0, 1, 1, −.6), where Z follows a Bernoulli distribution with success probability 0.2. For the fourth subplot, we generate M from an exponential distribution with mean one, and let T follow another exponential distribution with mean (1 + M)⁻¹ given fixed M. It can be seen that the estimated curve shows good agreement with the true curve in each of the four scenarios.

Figure 1.

Estimated AUC with 95% confidence intervals.

3.2 Testing predictive performance between two biomarkers

We next considered estimating the difference in the AUC(t) between two markers, M^A and M^B. For each of N = 1000 replications, we generated n = 200 realizations of (log T, M^A, M^B) from a three-dimensional Gaussian distribution with means zero, variances one and corr(log T, M^A) = −0.7, corr(log T, M^B) = −0.5, corr(M^A, M^B) = 0.8. An independent censoring time was generated uniformly from (0, τ*) such that either 20% or 40% of the observations were censored. As summarized in Table 3, in estimating the AUC(t), the performance of the proposed method is comparable to that of the WMR; whereas the empirical standard deviation of the proposed estimator is 10% smaller than that of the WMR. The estimated coverage probabilities based on 95% confidence intervals are close to the nominal value of 95% (range: 94.4% – 96.9%), except when the time point t is close to the boundary of the study period due to the limited observed information. The lengths of the confidence intervals increased with time, and sharply increased at the tails, which was due to the decreasing sizes of the risk sets over time. We also calculate the difference in IAUC of two biomarkers. For the 20% censoring rate, the estimation bias is .001, with an estimated standard error of .020, an empirical standard error of .021 and a coverage probability of 93.5%. For 40% censoring, the estimation bias is .001, with an estimated standard error of .023, an empirical standard error of .025 and a coverage probability of 90.8%.

Table 3.

Simulation results for estimated difference between AUCs of two biomarkers, comparing the proposed method with the WMR method as cited from Table 2 of Saha-chaudhuri and Heagerty (2013). dAUC(t) is the true value of difference in AUCs at time point t. SD and SE are the empirical and model-based standard error estimates. CP is the calculated coverage probability of 95% confidence intervals.

		WMR			Proposed method
Log time	dAUC(t)	Bias	SD	CP(%)	Bias	SD	SE	CP(%)
			20% censoring
–2.0	0.101	–0.002	0.062	88.8	0.001	0.060	0.063	88.7
–1.5	0.098	–0.002	0.040	94.5	0.000	0.036	0.041	96.6
–1.0	0.091	–0.001	0.032	94.6	–0.001	0.028	0.033	96.4
–0.5	0.080	–0.002	0.029	94.8	0.000	0.025	0.029	96.2
0.0	0.070	–0.001	0.030	94.9	–0.001	0.027	0.030	96.0
0.5	0.060	0.000	0.037	93.2	0.000	0.037	0.037	96.9
1.0	0.051	0.002	0.054	93.3	0.001	0.069	0.061	91.1
			40% censoring
–2.0	0.101	–0.002	0.062	88.8	0.000	0.068	0.063	89.0
–1.5	0.098	–0.002	0.041	94.7	0.000	0.039	0.042	95.3
–1.0	0.091	–0.001	0.033	95.0	–0.001	0.031	0.034	96.0
–0.5	0.080	–0.001	0.031	94.8	–0.001	0.030	0.032	96.4
0.0	0.070	0.001	0.035	94.5	–0.002	0.032	0.036	96.9
0.5	0.060	0.001	0.048	94.8	0.003	0.055	0.053	94.4
1.0	0.051	0.002	0.100	93.3	–0.008	0.258	0.266	85.8

We also consider another example where M^A and M^B follow a bivariate normal distribution and the survival time T is generated from a Cox model. More details and relevant results are presented in the supplementary material.

We then evaluated the performance of the test statistic proposed in (6), including the size and power. We generated (log T, M^A, M^B) from a normal distribution with means zero, variances one and correlations corr(log T, M^A) = γ_A , corr(log T, M^B) = γ_B and corr(M^A, M^B) = 0. We fixed γ_B = −0.4 and then let γ_A take a set of different values in {−0.4, −0.5, . . . , −0.9}. We calculated the probabilities of rejecting the null hypothesis $H_0:C({\beta }_0^A;\tau )=C({\beta }_0^B;\tau )$ based on percentiles (0.025 and 0.975) of the standard normal distribution. We based the calculation of the size of the test on 5000 Monte Carlo replications, and that of the power on 1000 replications. When the null hypothesis is true (i.e., γ_A = −0.4), the sizes of the proposed test were in a reasonable range: 0.052-0.083 under all scenarios considered. This suggests that the asymptotic approximation for the test statistic (6) is adequate for moderate sample sizes. As expected, the powers of the test increased with decreasing values of γ_A. The power decreased with an increase in the degree of censoring, indicating that the censoring percentage has an impact on the power.

4. Real data application

We applied the proposed methodology to the data collected from the AIDS Clinical Trials Group (ACTG) 175 study (Hammer et al., 1996). This study enrolled 2139 individuals and equally randomized them into one of four treatment arms that provided either single drug or combination treatments involving zidovudine (AZT), didanosine (ddI) and zalcitabine (ddC). Here, we focus on the combination treatment arm of AZT and ddC. Among 524 patients randomized to that treatment arm, 109 patients developed AIDS or died before the end of the study. The outcome of interest is the time to the development of AIDS. The follow-up time ranged from 14 days to 1231 days, with a median time of 997 days. Our goal here is to assess the ability of two biomarkers, CD4 and CD8 T cell counts (Catalfamo et al., 2011), to predict the risk of developing AIDS. Specifically, we are interested in two assessments: how well do the two biomarkers discriminate between patients who are at high risk of the progression of HIV infection to AIDS or death and those who are not; and which biomarker better discriminates the patients at higher risk.

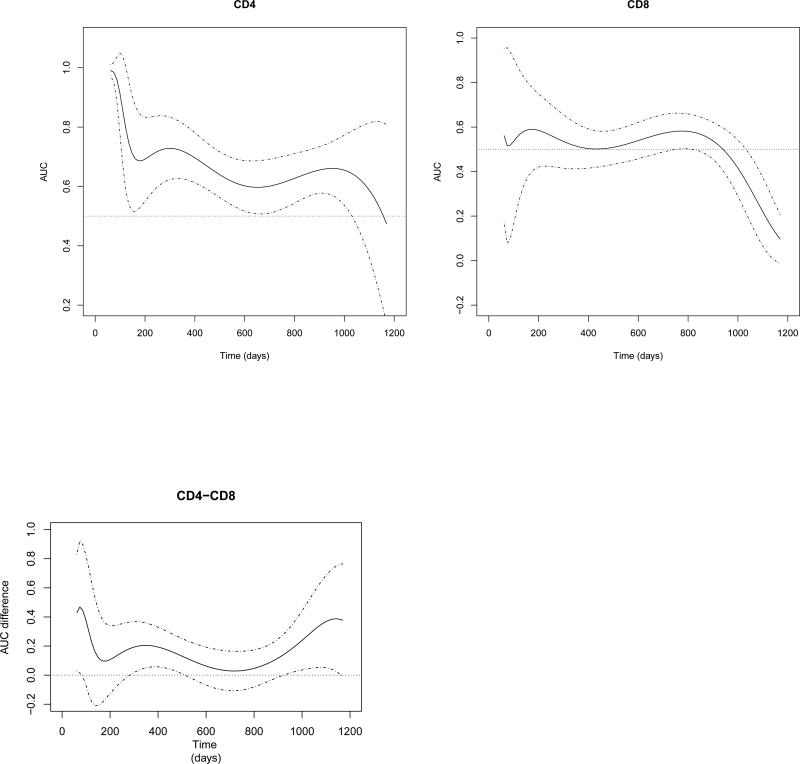
We made the first assessment by using the proposed method to estimate the respective AUC(t) of two biomarkers. We applied a logistic link function with the power of the polynomials as {−2, −1, −1/2, 0, 1/2, 1, 2}. We present two estimated AUC curves and their 95% confidence bands for the two biomarkers in the first two subplots of Figure 2. These two AUC curves decrease steadily over time. Specifically, over the first 400 days of follow-up, the value of the AUC(t) of CD4 is above 0.7, implying that for any time t before day 400, the probability of a patient who has a progression of AIDS on day t having a CD4 counts larger than a patient who survives beyond day t is at least 0.7. In contrast, the estimated AUC values of CD8 are between 0.5 and 0.6, implying that the predictive probability is close to non-informative value (0.5). It can been seen that estimates of the two AUC curves become increasingly variable with increasingly wider confidence intervals at the tails of the study period. Specifically, 10 out of 524 (1.9%) subjects died or were censored before day 200, and only 22.7% of the patients remained in the study at day 1100.

Figure 2.

Estimated AUC curves/associated 95% confidence intervals of CD4, CD8 and their AUC difference.

We performed the second assessment by testing the difference between the two estimated AUC curves. We present our estimates of the difference in the AUCs in the last subplot of Figure 2. It can be seen that the difference is always positive, indicating that CD4 has a better predictive performance than CD8 most of the time, although the lower confidence bound is below 0 around days 150 and 750. To determine whether such advantage is statistically significant when accounting for the estimation variation, we tested the difference in the IAUCs between the two markers. We chose the cut-off endpoint τ to be the 95th percentile of the observed survival time to avoid unnecessary variability. The estimated difference in the IAUC is 0.110, with a standard error of 0.037, which leads to the conclusion that CD4 has a significantly better prediction accuracy than that of CD8, with a p-value of 0.002. We performed the same analysis for the other three study arms and found a similar prediction superiority for CD4 compared to CD8. These results agree with the previous ndings of Catalfamo et al. (2011).

5. Discussion

In this paper, we have proposed a semi-parametric estimator of time-dependent AUC curve and have constructed a test procedure to compare the performances of biomarkers in terms of risk prediction. The pseudo partial-likelihood approach we proposed for estimation and inference readily and advantageously handles censoring. Compared to the time-dependent ROC estimation methods available in the literature, our approach is robust as it does not require any assumptions on the underlying survival time. One major difference between our method and existing nonparametric methods is that our method estimates the entire curve as a function of β and t through the fractional polynomial function, while the non-parametric methods use a point-wise approach to estimate the AUC. Consequently, our method is computationally very convenient for obtaining global statistics such as IAUC and the confidence band plot (e.g., Figure 1) through an analytic expression. In contrast, nonparametric methods would have to repeat the kernel-based estimation procedure N times, including the selection of bandwidths, in order to estimate AUC(t) at N different time points t. In addition, estimating the summary statistics would be computationally intensive. For example, to decrease the computational burden, Saha-chaudhuri and Heagerty (2013) calculated IAUC as the average of AUC(t) at 10 time points, which inevitably will lead to some approximation errors. Conceptually, our method may be easily understandable or interpretable for practitioners, since it is a “regression-type” method, with covariates being functions of time. Note that the inference results we developed apply to other types of basis functions as well, such as wavelets and local polynomials, which may be more appealing when modeling non-smooth AUC curves with local changes. In the future, it might be of interest to develop methods to nd optimal choice of orders of fractional polynomials and the related link functions.

In this paper, our focus is to develop a computationally convenient evaluation of the predictive ability of a single biomarker, and deal with the challenge of comparing and screening a large number of candidate biomarkers generated by high-throughput methods. A more clinically meaningful question is how to build a scoring system based on multiple biomarkers and covariates selected from our evaluation. Developing rigorous statistical tools for such scoring systems is beyond the scope of this paper, and is a worthy objective for future research.

Although our semi-parametric model employs a parametric regression form of time, strong modeling assumptions are avoided by using sufficiently flexible functions of time, such as fractional polynomial functions. In the numerical studies, we conducted a sensitivity analysis by trying a few different choices of parametric form for ρ and basis functions, including adding t³ to the basis defined by (2) and considering a more general transformation by replacing the number 1 in the logistic function with an additional parameter. We found that the results were not sensitive to these changes. Another issue in practice is the choice of τ, which depends on the range of accurate estimation of the AUC curves. In this paper, since we specify ρ as a logistic-regression-type function, we recommend picking τ as data-dependent, for example, as the 90%th percentile of the observed survival time points. We found that our test results when comparing C(β , τ) did not vary much for different values of τ. For example, in the ACTG data study, when we chose τ to be the 80%th, 90%th or 95%th percentile of the observed survival time, each resulting p-value did not differ much within each treatment group.

Table 4.

Empirical rejection rates (%) for comparing biomarkers' predictive accuracy with null hypothesis $H_0:C({\beta }_0^A;\tau )=C({\beta }_0^B;\tau )$.

sample size	γA = –.4	γA = –.5	γA = –.6	γA = –.7	γA = –.8	γA = –.9
			20% censoring
100	7.4	10.3	25.3	54.5	86.9	99.7
200	5.4	12.8	43.3	83.0	99.4	100
300	5.2	18.5	63.0	94.8	100	100
			40% censoring
100	8.3	11.1	21.0	43.4	74.4	96.2
200	6.3	12.9	36.0	71.0	94.6	100
300	5.6	15.1	50.8	87.1	99.7	100