A marching-walking hybrid induces step length adaptation and transfers to natural walking

Abstract

Walking is highly adaptable to new demands and environments. We have previously studied adaptation of locomotor patterns via a split-belt treadmill, where subjects learn to walk with one foot moving faster than the other. Subjects learn to adapt their walking pattern by changing the location (spatial) and time (temporal) of foot placement. Here we asked whether we can induce adaptation of a specific walking pattern when one limb does not “walk” but instead marches in place (i.e., marching-walking hybrid). The marching leg's movement is limited during the stance phase, and thus certain sensory signals important for walking may be reduced. We hypothesized that this would produce a spatial-temporal strategy different from that of normal split-belt adaptation. Healthy subjects performed two experiments to determine whether they could adapt their spatial-temporal pattern of step lengths during the marching-walking hybrid and whether the learning transfers to over ground walking. Results showed that the hybrid group did adapt their step lengths, but the time course of adaptation and deadaption was slower than that for the split-belt group. We also observed that the hybrid group utilized a mostly spatial strategy whereas the split-belt group utilized both spatial and temporal strategies. Surprisingly, we found no significant difference between the hybrid and split-belt groups in over ground transfer. Moreover, the hybrid group retained more of the learned pattern when they returned to the treadmill. These findings suggest that physical rehabilitation with this marching-walking paradigm on conventional treadmills may produce changes in symmetry comparable to what is observed during split-belt training.

walking must be highly adaptable to new environments in order to be useful—people quickly learn new calibrations of their walking pattern to account for ice, sand, or even high heels. One novel environment used for studying human walking adaptation is the split-belt treadmill, which has two belts that can move at different speeds (Reisman et al. 2005). During split-belt adaptation where one treadmill belt moves faster than the other, people initially walk with a limp (unequal step lengths) and adapt over hundreds of strides to equalize their step lengths. When the treadmill belts are returned to the same speed, they limp in the opposite direction, indicating that they stored a new walking pattern and this pattern must be actively deadapted (Reisman et al. 2005).

Split-belt adaptation leads to changes in the movement of both legs to reestablish step length symmetry (Choi and Bastian 2007; Reisman et al. 2005). Recently, it has been shown that step length symmetry can be decomposed into spatial (i.e., where to step), temporal (i.e., when to step), and perturbation contributions (Finley et al. 2015). In split-belt walking, the perturbation term is a result of the belts moving at different speeds. To walk with symmetric step lengths, the spatial and temporal terms must adapt to counteract this perturbation.

Here we asked whether spatial and temporal adaptation can occur if a person walks in place with one leg (i.e., marches) on a stationary treadmill belt while walking with the other leg on a moving belt (i.e., marching-walking hybrid). This marching-walking hybrid pattern is interesting for several reasons. First, it allows us to determine whether unilateral alteration of some of the sensory information known to be important in walking (e.g., stretch of the hip flexors, limb loading, and body weight transfer) (Anderson and Grillner 1981, 1983; Duysens and Pearson 1980; Grillner and Rossignol 1978; Pang and Yang 2000) modulates the process of adaptation. For example, it is possible that adaptation might be disrupted with the decrease of some of these essential sensory cues. Second, the marching-walking hybrid hypothetically should not allow the leg on the stationary belt to dramatically change its stepping location. Thus it could reduce the availability of the spatial learning strategy in adapting leg motions toward symmetry.

Third, this type of locomotion is similar to previous research in a reduced gait. In a reduced gait, one limb is walking on a moving surface while the other limb steps in place and is required to remain “stiff” to reduce joint movement (Faist et al. 1999; Van de Crommert et al. 1996). Reflex and EMG analysis of the reduced gait indicated that there were similar patterns of phase-dependent modulation in the lower limbs (Faist et al. 1999; Van de Crommert et al. 1996). This suggests that the marching-walking hybrid may partially activate overlapping neural adaptation circuits to that of split-belt walking.

Finally, understanding whether adaptation can occur in a marching-walking hybrid condition might have clinical implications for individuals who have suffered a stroke and walk with asymmetric step lengths (Allen et al. 2011; Balasubramanian et al. 2007; Hall et al. 2012; Patterson et al. 2010). We have previously shown that stroke survivors can learn to correct their step length asymmetry from long-term training on a split-belt treadmill (Reisman et al. 2013). However, split-belt treadmills are generally expensive and are not universally available for rehabilitation. Therefore, it would be important to know whether they could benefit from adaptation with the marching-walking hybrid, as rehabilitation could be completed on a single-belt treadmill.

A couple of studies have assessed whether unilateral stepping affects over ground walking—one study showed that it transfers to over ground walking much less than split-belt walking in control subjects (Huynh et al. 2014), and another study showed it produces modest over ground changes after long-term training in stroke survivors (Kahn and Hornby 2009). However, in unilateral stepping one foot remains on the ground the entire time and the other steps on and off a moving surface (similar to a pattern that would be used to propel a skateboard). We hypothesize that a pattern that more closely matches normal walking with alternating single limb supports, such as a walking-marching hybrid, might lead to greater adaptive changes in walking.

Here we tested whether a marching-walking hybrid pattern can induce adaptation and deadaptation similar to split-belt walking. We then asked whether the adapted marching-hybrid pattern would transfer to more natural, over ground walking in a similar way as results from split-belt adaptation. Furthermore, we are interested in understanding how the nervous system solves this spatial-temporal balance compared with that of split-belt walking. The results presented here are important for expanding our understanding of locomotor adaptation, which potentially could be beneficial for walking rehabilitation.

METHODS

Subjects.

Fifty-seven healthy naive subjects (31 men, 26 women; 23.6 ± 0.65 yr old) participated in this study. The Johns Hopkins Institutional Review Board approved all protocols, and all subjects gave informed written consent before participating.

Data collection.

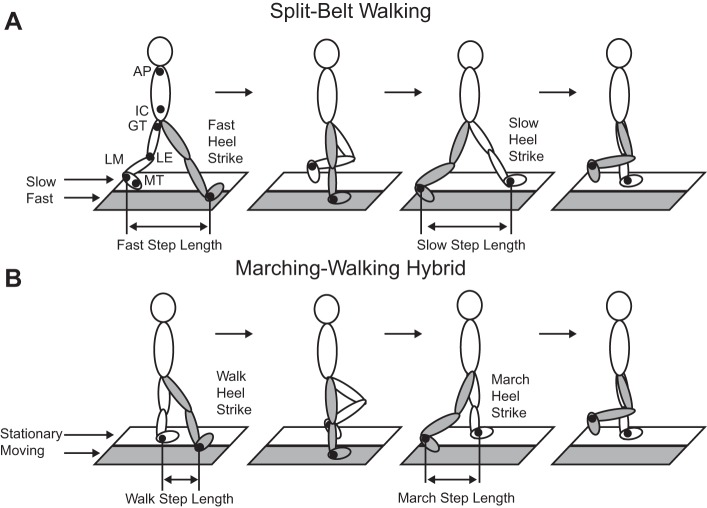
Infrared-emitting markers were placed bilaterally on each subject's body over the fifth metatarsal head, lateral malleolus, lateral femoral epicondyle, greater trochanter, iliac crest, and acromion process as shown in the first image of Fig. 1A. During treadmill (Woodway Split-Belt treadmill) walking, the three-dimensional position of the markers was recorded at 100 Hz with an Optotrak (Northern Digital) motion capture system. Vertical ground reaction forces were collected at 1,000 Hz from the force plate under each belt while the subjects were on the treadmill, and these forces were synchronized with the kinematic data. These forces were used to compute heel strike and toe-off events, and were not otherwise included in our analysis. For the over ground portions of the walking experiment, the time and location of heel strike were recorded with a Zeno Walkway (ProtoKinetics, Havertown, PA) 6 m in length. The over ground walking was recorded in a different area of the lab, and Optotrak markers were not recorded during those portions of the experiment.

Fig. 1.

Illustrations of step length and marker positions for split-belt walking (A) and the marching-walking hybrid (B). Step length is defined as the anterior-posterior distance between the ankle markers at heel strike. Fast (walk) step length occurs at heel strike on the fast (walk) belt, and slow (march) step length occurs at heel strike on the slow (march) belt. Infrared emitting markers were placed bilaterally on the fifth metatarsal head (MT), lateral malleolus (LM), lateral femoral epicondyle (LE), greater trochanter (GT), iliac crest (IC), and acromion process (AP).

Overall protocol.

Subjects walked on the split-belt treadmill with one foot on each belt. The treadmill belt speeds were independently controlled with custom software (Vizard, WorldViz). Sometimes the treadmill belts moved at the same speed (“tied belts”), and sometimes they moved at different speeds (“split belts”). During split-belt walking, the faster belt was always under the right foot. A thin divider was placed between the belts to prevent subjects from stepping on the opposite belt. Subjects wore a non-weight-bearing safety harness attached to the ceiling. They were given instructions to hold on to the treadmill's handrail when the belts started moving and then let go and cross their arms within the first few seconds. Near the end of each trial they were instructed to hold on to the handrail before the belts stopped moving. While they were walking, subjects were told not to look at their feet and to watch a self-selected movie or show on a TV screen placed in front of them.

In experiment 1, 29 subjects (16 men, 13 women; 22.8 ± 0.9 yr old) completed the protocol shown in Fig. 2 to assess differences between a marching-walking hybrid and split-belt training. The subjects were randomly divided into two groups. The SPLIT_TM group (n = 15) performed a standard split-belt experiment (Fig. 2A) with the slow belt moving at 0.5 m/s and the fast belt moving at 1.5 m/s. This type of walking can be seen in Fig. 1A. The MARCH_TM group (n = 14) performed the protocol in Fig. 2B with the marching-walking hybrid discussed above: the slow belt was stationary, and the fast belt moved at 1.0 m/s. The marching-walking hybrid can be seen in Fig. 1B. Note that all belt speeds at 0 m/s are marching. Thus the difference in belt speeds (fast − slow) was 1.0 m/s for both groups. During adaptation, the subjects in the MARCH_TM group were instructed to march with one foot on the stationary belt and walk with the other foot on the moving belt. To prevent unilateral stepping, subjects were asked to maintain a reciprocal gait pattern in which stance on one leg occurred during swing on the other and vice versa. However, they were not instructed how fast to alternate feet or how high to lift their marching foot. No explicit instructions were given to the SPLIT_TM group during split-belt walking.

Fig. 2.

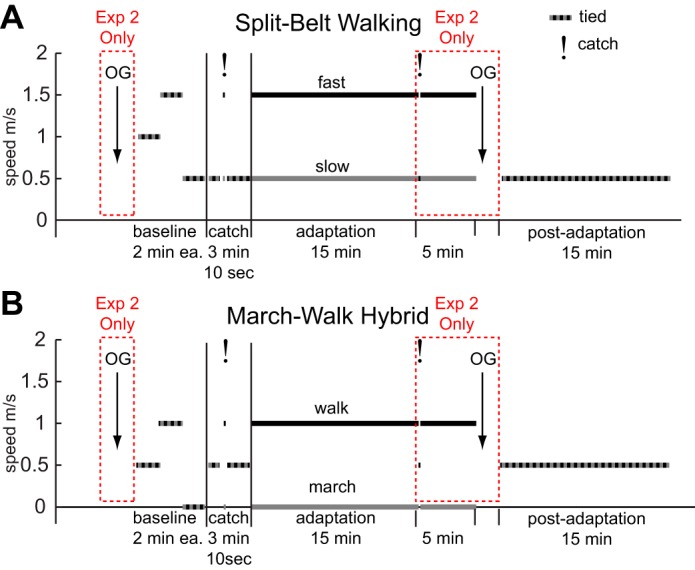
Experimental paradigms with belt speeds for split-belt walking (A) and the marching-walking hybrid (B). Experiments began with baseline walking at 3 different speeds for 2 min each. The subjects then walked at 0.5 m/s for 1 min, experienced a brief 10-s exposure (catch) to the belts moving at different speeds, and then walked again at 0.5 m/s for 2 min. This was followed by an adaptation phase with the belts moving at different speeds for an extended period. In experiment 1, subjects adapted for 15 min and then deadapted on the treadmill for 15 min. In experiment 2, subjects adapted for 15 min, experienced a 10-s tied-belt catch trial, adapted for 5 more minutes, walked over ground for ten 6-m walks, and then returned to the treadmill for washout. For all belt speeds at 0 m/s, the subjects were instructed to march; 10-s catch trials are indicated with an exclamation mark.

Both groups in this experiment began with a 2-min warm-up at 1.0 m/s followed by three 2-min baselines at tied speeds (mean, fast and slow speeds). The subjects again walked at 0.5 m/s for 1 min before they experienced an initial exposure to the belts moving at different speeds for 10 s. The purpose of the initial exposure was to eliminate startle effects associated with experiencing split-belt walking for the first time (Finley et al. 2014). Although the subjects were not told that the belts would be moving at different speeds, they were instructed to hold the handrail during this portion of the experiment. This brief exposure was followed by 2 min of walking on tied belts at 0.5 m/s. All subjects then underwent the adaptation portion of the experiment for 15 min with the belts moving at different speeds, followed by a postadaptation portion for 15 min with tied belts. The postadaptation speed was 0.5 m/s for both groups because previous work has shown that the largest aftereffects for split-belt training are seen at the slow speed (Vasudevan and Bastian 2010).

In experiment 2, 28 new subjects (15 men, 13 women; 24.4 ± 0.9 yr old) were recruited and randomly divided into two groups to assess the differences in transfer to over ground walking from the marching-walking hybrid versus standard split-belt walking. The SPLIT_OG group (n = 14) and MARCH_OG group (n = 14) adapted to the same speeds as in experiment 1 in a similar paradigm as shown in Fig. 2 (note that this experiment includes the red dashed segments in Fig. 2). Before the treadmill portion began, the subjects walked 10 times over ground on a 6-m Zeno Walkway, which recorded the time and position of over ground foot falls. After 15 min of adaptation on the treadmill, they experienced a 10-s tied-belt catch trial (without holding on), in which both belts moved at 0.5 m/s, to assess their learning on the treadmill. After the catch trial, they readapted for 5 more minutes. Within a few minutes of completing the adaptation portion, subjects were then pushed in a wheelchair to the Zeno Walkway, where they walked 10 times over the 6-m walkway. To measure how much over ground walking washed out treadmill adaptation, subjects were then returned with the wheelchair to the treadmill and walked for 15 min at 0.5 m/s. If there exist overlapping adaptive neural circuits between the marching-walking hybrid and natural walking, we should see over ground transfer following adaptation and we should see that the postadaptation over ground walking washes out the adaptive learning (Choi and Bastian 2007; Reisman et al. 2009).

Data analysis.

In this study, step length is defined as the difference in ankle marker positions at heel strike of each leg. The heel strikes were determined from vertical ground reaction forces as crossing of a threshold corresponding to ∼10% of each subject's weight. The fast step length corresponds to heel strike with the foot on the fast belt, and the slow step length corresponds to heel strike with the foot on the slow belt as shown in Fig. 1A. The difference in step lengths (fast − slow) is defined as step length difference. For the marching-walking hybrid, the fast leg is the walking leg and the slow leg is the marching leg as shown with step lengths in Fig. 1B. A step length difference value of 0 means that the step lengths are equal, a positive value means that the fast step length is longer than the slow step length, and a negative value means that the fast step length is shorter than the slow step length.

Time frames of interest for treadmill walking.

In experiment 1, we analyzed adaptation and postadaptation periods in three separate time frames: initial (mean of first 5 strides), early (mean of strides 5–200), and late (mean of last 30 strides). The early measure provides a method for comparing rates of adaptation and deadaptation between groups. This method is agnostic in that it does not assume a specific model (e.g., single or double exponential) but still allows us to robustly distinguish between groups with different rates of learning (Jayaram et al. 2012; Malone et al. 2011). Note that the baseline step length difference for each subject was calculated as the mean step length difference across the 2-min 0.5 m/s tied-belt baseline since all groups deadapted at this speed. The mean of this baseline period was subtracted from all subsequent analysis so that all values are expressed relative to baseline.

Over ground transfer and washout indexes.

In experiment 2, step length difference treadmill learning was defined as the difference between the mean of the first 5 strides in the tied-belt catch trial (TM_catch) and the mean of 2-min 0.5 m/s tied-belt baseline (TM_baseline, ∼50 strides). Baseline over ground walking (OG_baseline) was defined as the average step length difference over all ten 6-m walks before walking on the treadmill. The postadaptation over ground aftereffect (OG_after) was defined as the average step length difference of the first postadaptation over ground 6-m walk (∼4 strides). The over ground transfer was then defined as the difference between the over ground aftereffect and over ground baseline. The subjects were then returned to the treadmill to assess how over ground walking washed out the treadmill learning. The treadmill washout was defined as the difference in step length difference between TM_catch and the mean of the first 5 strides of postadaptation on the treadmill (TM_after). These quantities were defined mathematically as

$$\text{Treadmill}\hspace{0.17em}{\text{Learning}=\text{TM}}_{\text{catch}}{-\text{TM}}_{\text{baseline}}$$

$$\text{Over}\hspace{0.17em}\text{Ground}\hspace{0.17em}{\text{Transfer}=\text{OG}}_{\text{after}}-O{G}_{baseline}$$

$$\text{Treadmill}\hspace{0.17em}{\text{Washout}=\text{TM}}_{\text{catch}}{-\text{TM}}_{\text{after}}$$

Similarly, over ground transfer and treadmill washout as percentages of treadmill learning were defined as

$$\text{\%Over}\hspace{0.17em}\text{Ground}\hspace{0.17em}\text{Transfer}=\hspace{0.17em}\frac{\text{Over}\hspace{0.17em}\text{Ground}\hspace{0.17em}\text{Transfer}}{\text{Treadmill}\hspace{0.17em}\text{Learning}}\text{×}100$$

$$\text{\%Treadmill}\hspace{0.17em}\text{Washout}=\hspace{0.17em}\frac{\text{Treadmill}\hspace{0.17em}\text{Washout}}{\text{Treadmill}\hspace{0.17em}\text{Learning}}\text{×}100$$

These metrics for over ground transfer are similar to those in previous split-belt experiments (Torres-Oviedo and Bastian 2010, 2012).

Spatial and temporal contributions to adaptation.

It was shown previously that split-belt treadmill walking induces independent adaptation in the spatial domain and in the temporal domain (Malone et al. 2012). To further understand the differences between split-belt walking and the marching-walking hybrid, we decomposed step length difference into spatial, temporal, and perturbation contributions with the following equations (Finley et al. 2015):

$$\text{Step}\hspace{0.17em}\text{Length}\hspace{0.17em}\text{Difference}=\text{Fast}\hspace{0.17em}\text{Step}\hspace{0.17em}\text{Length}-\text{Slow}\hspace{0.17em}\text{Step}\hspace{0.17em}\text{Length}=\hspace{0.17em}\text{Spatial}+\text{Temporal}+\text{Perturbation}$$

where

$$\text{Spatial}=\hspace{0.17em}\left({\alpha }_{\text{f}}-{\alpha }_{\text{s}}\right),\hspace{0.17em}Temporal=\frac{{\upsilon }_{\mathrm{s}}+{\upsilon }_{\mathrm{f}}}{2}\left(t_{\mathrm{s}}-t_{\mathrm{f}}\right),\hspace{0.17em}and\hspace{0.17em}Perturbation=\frac{{\upsilon }_{\mathrm{s}}-{\upsilon }_{\mathrm{f}}}{2}\left(t_{\mathrm{s}}+t_{\mathrm{f}}\right)$$

Here α_s is a spatial variable that indicates where the slow foot is placed relative to the previous fast foot placement, v_s is the approximate speed of the slow ankle relative to the body while it is on the slow moving belt, and t_s is the slow step time. Similarly, α_f is a spatial variable that indicates where the fast foot is placed relative to the previous slow foot placement, v_f is the approximate speed of the fast ankle relative to the body while it is on the fast moving belt, and t_f is the fast step time. The step time was defined as the time between opposite heel strikes, as done previously by Malone et al. (2012). The derivation of this model has been described in detail elsewhere (Finley et al. 2015) and is summarized in the appendix for clarity.

In this model for step length difference, the spatial contribution is due to differences in foot placements relative to the body, the temporal contribution is due to differences in step times, and the perturbation contribution is largely due to differences in treadmill belt speeds. Under normal treadmill walking, individuals do not experience the perturbation term because both feet are moving at the same speed (v_s = v_f). During split-belt walking, this term can be thought of as a perturbation to step length difference as it changes almost instantly to a nonzero value when the belts begin moving at different speeds. The temporal and spatial components must cancel this perturbation to have symmetric step lengths; therefore, we also calculated the sum of the temporal and spatial components. Baseline values from the 0.5 m/s tied baseline for each of these components were subtracted to account for any offset. Since each subject has a slightly different perturbation size, we also calculated the relative contribution of the temporal and spatial components with respect to the perturbation size.

Statistical analysis.

In experiment 1, a mixed-model repeated-measures ANOVA with time frame (initial adaptation, early adaptation, late adaptation, initial postadaptation, early postadaptation, and late postadaptation) and group (split-belt walking or marching-walking hybrid) as fixed effects and subject as a random effect was utilized to test for differences in step length during the experiment. When there was statistical significance in this ANOVA, post hoc analyses were used to compare between time frames (1-sample t-tests) and between groups (2-sample t-tests). One subject from the SPLIT_TM group was removed from all analyses since the subject experienced an initial adaptation step length difference that exceeded 3 standard deviations of the other SPLIT_TM subjects. For the model analysis, one-sample t-tests were used to compare between time frames within a group and two-sample t-tests were used to compare between the groups for each of the model components for several time frames. In experiment 2, two-sample t-tests were used to analyze the over ground metrics discussed above. All statistical analysis was conducted in MATLAB, and P values < 0.05 were considered as significant.

RESULTS

Time frame analysis.

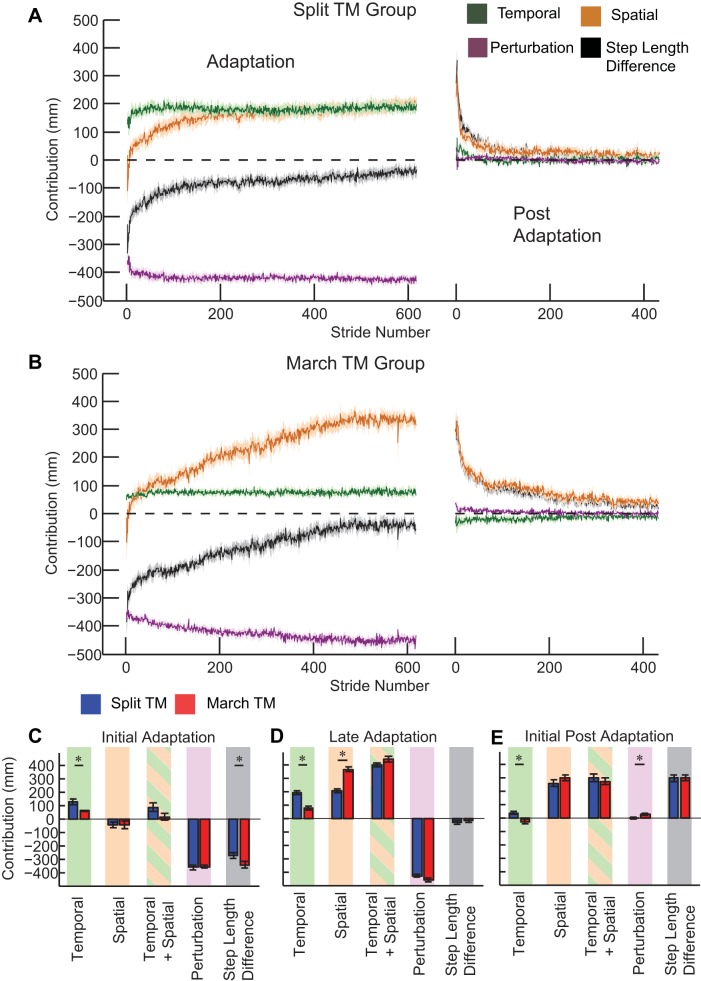
We found that the marching-walking hybrid induces adaptation and aftereffects of step length difference, similar to those seen with split-belt walking. Figure 3A shows the group means (±SE) on a stride-by-stride basis for step length difference for experiment 1. Both groups had similar step length differences during baseline tied-belt walking at 0.5 m/s (P = 0.41) that were not different from 0 (P = 0.14), i.e., symmetric walking. Therefore, baseline step length difference was removed on an individual basis. The initial, early, and late time frames for adaptation and postadaptation are shown in Fig. 3B. A mixed-model repeated-measures ANOVA showed that there was not a significant group effect [F(1,26) = 0.77, P = 0.38] but there was a significant time frame effect [F(5,130) = 408, P < 0.001] and a group × time frame interaction effect [F(5,130) = 8.8, P < 0.001]. These effects indicate that the step length differences varied across time frames and that these changes across time frames depended on the group. Post hoc t-tests showed that the MARCH_TM group had a larger step length difference during initial adaptation (P = 0.04), early adaptation (P < 0.001), and early postadaptation (P = 0.002) compared with the SPLIT_TM group, whereas no differences were observed for late adaptation (P = 0.52), initial postadaptation (P = 0.88), and late postadaptation (P = 0.46). A striking finding is that it took the marching-walking hybrid group longer to reduce the step symmetry errors in both adaptation and postadaptation as shown by the differences in the early time frames.

Fig. 3.

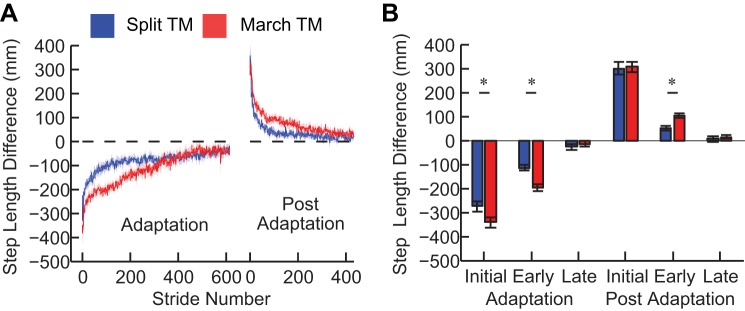
Experiment 1 results. A: mean (±SE) stride-to-stride step length difference for the SPLIT_TM and MARCH_TM groups. The step length difference is baseline subtracted on an individual basis. During adaptation, the step length difference is initially perturbed and then slowly adapted to near baseline values. During postadaptation, the belts are returned to the same speed and an aftereffect is observed in the opposite direction. B: analysis for initial adaptation, early adaptation, late adaptation, initial postadaptation, early postadaptation, and late postadaptation. *Significant differences (P < 0.05).

Step length difference model analysis.

We applied the step length difference model described in methods to determine whether there were differences in the temporal, spatial, and perturbation components across time frames or between groups. Stride-by-stride adaptation and postadaptation group mean (±SE) for the spatial, temporal, and perturbation components as well as step length difference for the SPLIT_TM and MARCH_TM groups are shown in Fig. 4, A and B, respectively. This figure demonstrates that the temporal component adapts much quicker for both groups whereas the spatial component changes much slower. Also note that the SPLIT_TM group has approximate equal contributions from the spatial and temporal components at the end of adaptation, whereas the MARCH_TM group has a much greater contribution from the spatial component.

Fig. 4.

Model results, experiment 1. The step length difference, fast − slow, can be decomposed into spatial, temporal, and perturbation contributions. A: split-belt walking group averages ± SE. B: marching-walking hybrid group averages ± SE. The perturbation (largely negative) occurs when the treadmill belts are driven at different speeds. The temporal term adapts faster in both groups and is much greater in the split-belt group. The spatial term adapts slower and is greater in the marching-walking hybrid group. C–E: temporal, spatial, sum (temporal + spatial), perturbation, and step difference components were analyzed for initial adaptation (C), late adaptation (D), and initial postadaptation (E) of experiment 1.

With this model, we can explain the differences in experiment 1 observed in initial adaptation in step length difference. There was no significant difference between the groups during initial adaptation in the spatial component (P = 0.97), the sum of the spatial and temporal components (P = 0.11), or the perturbation (P = 0.84), but there was a significant difference in the temporal component (P = 0.005) as shown in Fig. 4C. This indicates that the initial difference observed in step length difference (P = 0.04) is due to the temporal component. Recall that the temporal component is the product of the average belt speed and the step time difference. Although there was no difference in the step time difference (P = 0.80) during initial adaptation, the average speed was significantly different (P < 0.001) near 0.5 m/s for the marching-walking hybrid and near 1.0 m/s for the split-belt walking. As a result, it appears that the difference between these two groups in initial adaptation step length difference (Fig. 3B) was due to the difference in average belt speed, since all other components of this model were not significantly different.

We observed that different spatial and temporal strategies can achieve symmetric stepping in late adaptation for the two groups. Figure 4D shows the different model components of step length difference for late adaptation. Over the course of 15 min, both groups increased their spatial component (late − initial adaptation both P < 0.001) but to different extents, as the MARCH_TM group has a much larger value compared with the SPLIT_TM group (P < 0.001). In addition, the MARCH_TM group did not significantly change its temporal component (late − initial adaptation, P = 0.15), whereas the SPLIT_TM group significantly increased its temporal component (late − initial adaptation, P < 0.001). However, these spatial and temporal changes balance out, since the sum of the two components in late adaptation are not significantly different (P = 0.13). Although the perturbation is not significantly different between the two groups at late adaptation (P = 0.07), the perturbation has increased slightly (both P < 0.001), most likely because of a settling of the stride times. During late adaptation, the sum of the temporal and spatial components is almost equal and opposite to the amplitude of the perturbation, so the groups ultimately reach a similar step length difference (P = 0.52). Figure 5 shows the relative contributions of the temporal and spatial components to offsetting the perturbation during late adaptation. These results indicate that individual subjects can use different combinations of the spatial and temporal components to achieve symmetric stepping. It appears that subjects performing the marching-walking hybrid utilize a strategy that is mostly spatial whereas the subjects walking with the split belts use a more even mixture of temporal and spatial. However, subjects in either group could vary in their strategy.

Fig. 5.

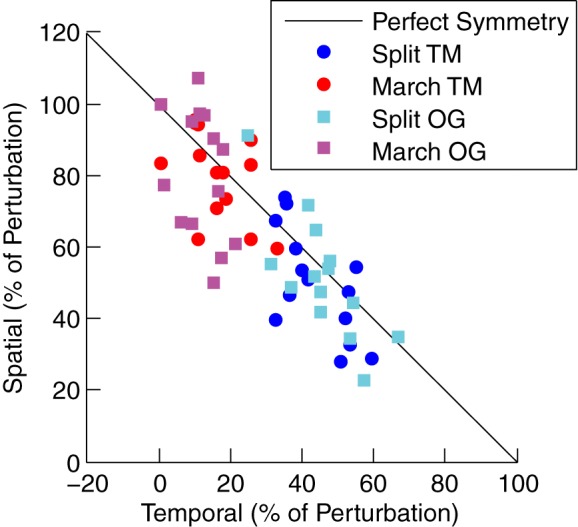
Model relative contribution in late adaptation (last 30 strides after 15 min of adaptation). The temporal and spatial components each cancel some percentage of the perturbation. Perfect symmetry is represented with a black line, meaning that anywhere along the line a subject is walking symmetrically. These data indicate that the marching-walking hybrid subjects utilize a strategy that is mostly spatial whereas the split-belt training subjects use a strategy that is a mixture of both temporal and spatial. Relative contributions are shown for groups from both experiment 1 and experiment 2.

Which components are stored when the belts return to tied speeds? Figure 4, A and B, right, show the components for postadaptation in experiment 1. Figure 4E shows that initial aftereffects in step length difference are largely due to the spatial component. The spatial component remains largely positive and is not significantly different between the two groups (P = 0.27). After adaptation, the belts are returned to the same speed so the perturbation term is near zero for both groups. There is a significant difference between the two groups in perturbation (P = 0.01) and in the temporal component (P = 0.004), but since these terms are relatively small their effects on the overall step length difference are minimal. Thus there is no significant difference between the two groups in the sum of the spatial and temporal terms (P = 0.52) or in the overall step length difference (P = 0.88). As a result, the positive aftereffect in step length difference was due almost exclusively to the spatial component, as can be seen in Fig. 4, A and B.

Over ground walking analysis.

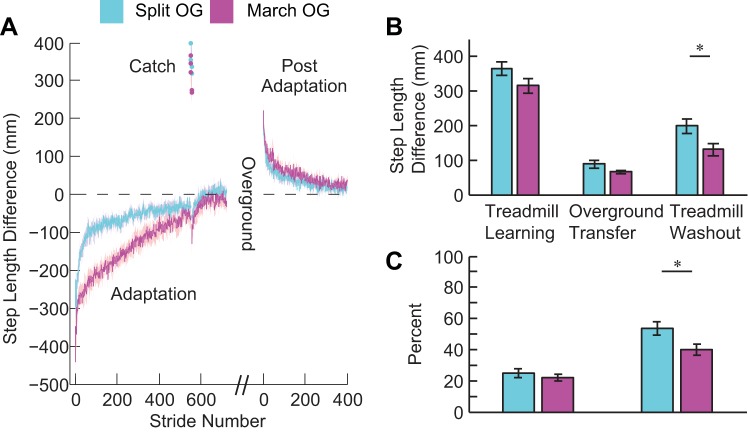
In experiment 2, we assessed both adaptation and over ground transfer for a new group of subjects. Figure 6A shows baseline-subtracted step length difference results for the treadmill segments. Both groups again have similar baseline tied-belt walking (P = 0.18), which was not different from 0 (P = 0.32). With these new groups of subjects, we confirmed the results of experiment 1 that the marching-walking hybrid had a larger initial adaptation step length difference (P = 0.03), adapted slower (P < 0.001), and deadapted slower (P = 0.07). We also observed again that the marching-walking hybrid utilized a strategy that was mostly spatial as shown by the relative contributions of the temporal and spatial components compared with the perturbation in Fig. 5.

Fig. 6.

Experiment 2 results. A: mean stride-by-stride step length difference for the treadmill portion of the split and march groups. B: step length difference for treadmill learning, over ground transfer, and treadmill washout for the 2 groups. C: over ground transfer and treadmill washout relative to the treadmill learning.

The main objective of experiment 2 was to compare the over ground transfer and treadmill washout between the two groups. We did not observe a difference in the amounts of treadmill learning between the groups (P = 0.11). There was significant over ground transfer in both groups relative to baseline (both P < 0.001). Furthermore, the amount and percentage of transfer to over ground walking were not significantly different between the groups (P = 0.09, P = 0.45, respectively) as shown in Fig. 6, B and C, respectively. On the other hand, the amount of treadmill washout was reduced in the marching-walking hybrid for both absolute (P = 0.03; see Fig. 6B) and percentage (P = 0.03; see Fig. 6C). In summary, the marching-walking hybrid group in experiment 2 transferred similarly to over ground walking compared with the split-belt walking group but washed out treadmill aftereffects less.

DISCUSSION

The objective of this study was to compare a marching-walking hybrid (in which one foot marches on a stationary surface and the other foot walks on a moving treadmill belt) to standard split-belt walking. In experiment 1, we demonstrated that the marching-walking hybrid induces adaptation and produces aftereffects in step length differences comparably to split-belt walking. In addition, we observed in this experiment that subjects in the marching-walking hybrid adapted slower and deadapted slower. In experiment 2, we observed that the marching-walking hybrid transferred to over ground walking to a similar extent as split-belt walking but washed out less. We also observed that the marching-walking hybrid groups utilize a spatial strategy whereas the split-belt walking groups utilize a spatial-temporal strategy to counter the perturbation induced by the belts moving at different speeds.

The marching-walking hybrid presented here is similar to a reduced gait used in previous locomotor studies. In a reduced gait, one limb is walking on a moving treadmill belt while the other limb is held “stiff” and steps in place (Faist et al. 1999; Van de Crommert et al. 1996). The marching-walking hybrid is slightly different in that the marching leg is not required to be stiff and allows flexion of the joints during the marching swing phase. In the work by Faist and colleagues, they demonstrated that the biceps femoris reflex as well as EMG signals of the lower limbs exhibited phase-dependent modulation (Faist et al. 1999; Van de Crommert et al. 1996). These signals were shown to be quite similar in the “stiff” leg to that of normal gait even though the stiff leg had little to no joint movement. Given the work in a reduced gait as well as the similarities in adaptation between the groups presented here, this suggests that there may be partial overlap in the neural circuits governing adaptation in the marching-walking hybrid and split-belt walking.

Sensory signals important for locomotion.

While these neural circuits may be similar between the groups studied here, the peripheral sensory signals experienced during the marching-walking hybrid are likely different from those of split-belt walking. Previous work in cats has demonstrated that extension of the hip and unloading of the stance leg are both important neural signals that influence the stance-to-swing transition (Anderson and Grillner 1981, 1983; Duysens et al. 2000; Duysens and Pearson 1976, 1980; Grillner and Rossignol 1978; McVea et al. 2005). This work has indicated that the stance leg needs to be extended and unloaded before flexion will begin. Additionally, these signals influence this transition even without input from the cerebral cortex, suggesting that some temporal elements of locomotion are controlled by subcortical circuits (possibly in the spinal cord) (Anderson and Grillner 1981, 1983; Grillner and Rossignol 1978). Similarly, it was shown in human infants that there is an inverse relationship between loading and limb extension that initiates this transition from stance to swing (Pang and Yang 2000). In our marching-walking hybrid, this unloading signal is still present in the transfer of weight to the moving limb, but there is little to no hip extension. This suggests that bilateral hip extension is not required to produce postadaptation effects in step length difference for healthy adults.

While most prior locomotion work has focused on sensory signals at the stance-to-swing transition, locomotor learning requires feedforward adjustments, and this type of learning has recently been shown to be related to variables associated with heel strike (Malone et al. 2012). However, little work has investigated the important neural signals at heel strike required for adaptation. While the neural signals are not recorded in this study, we can still make inferences based on the spatial-temporal balance of step length difference.

Spatial-temporal balance of step length difference.

Previous work from our lab has shown that split-belt walking adaptation contains a form of error-based learning and depends on the cerebellum (Morton and Bastian 2006). We have suggested that step length asymmetry, or the difference in step lengths, serves as an error signal driving learning (Reisman et al. 2005). Additionally, it has been shown that people adapt both spatially (“where to step”) and temporally (“when to step”) (Malone et al. 2012). Here we used a step length difference model that separates the treadmill perturbation (i.e., difference in treadmill belt speeds) from the spatial and temporal components involved in reestablishing step symmetry during adaptation. Importantly, the groups studied here received similar levels of perturbation to step length difference yet adjusted their spatial and temporal components differently in order to adapt. Here we refer to the perturbation as the size of the perturbation component and not the size of the initial step length difference. To cancel this perturbation, subjects in the marching-walking hybrid group used a strategy that was largely spatial, whereas the split-belt group used a strategy that was a mixture of both spatial and temporal components. Previous work has also shown that split-belt walking uses a spatial-temporal strategy (Finley et al. 2015). By comparing the marching-walking hybrid and split-belt walking paradigms presented here, this demonstrates that people are able to counter a perturbation of a particular size by varying their temporal and spatial strategies.

Fast-adapting temporal component.

While the size of the temporal component in late adaptation was different between the marching-walking hybrid and split-belt walking, the temporal component adapted quickly in both conditions. A fast-adapting temporal component is consistent with previous split-belt work in cats (Forssberg et al. 1980; Frigon et al. 2013), infants (Pang and Yang 2000), and adults (Dietz et al. 1994; Malone et al. 2012; Reisman et al. 2005). In both infants and decerebrate cats, there is a reduction or absence of strong descending input from the cerebral cortex. This suggests that the spinal cord may be selecting these temporal phase switches simply on the basis of the belt speed for each foot. This is further supported by recent work in decerebrate cats that demonstrates linear relationships between split-belt speeds and the times of stance and swing (Frigon et al. 2013). Given that each belt speed is different between the marching-walking hybrid and split-belt walking, it is possible that the observed differences in the size of the temporal component of our step length difference model may simply be a result of some relationship in the belt speed combinations and this relationship may be calculated in the spinal cord.

Slow-adapting spatial component.

In the work presented here, we observed that the spatial contribution to adaptation was larger in the marching-walking hybrid than in split-belt walking. Since the temporal component is established first, it is possible that the desired spatial component is then properly adjusted to result in symmetric walking. We predict that the cerebellum is involved in updating this spatial component based on evidence that 1) people with cerebellar damage do not show learning or aftereffects in step length symmetry (Morton and Bastian 2006) and 2) the aftereffect observed here is largely based on the spatial component. This is also supported with work by Jayaram and colleagues, who demonstrated that brain stimulation with transcranial direct current stimulation applied over the cerebellum could modulate the rates of spatial learning but not temporal learning (Jayaram et al. 2012).

Rates of step length adaptation and deadaptation.

In this work, we observed in both experiments that the marching-walking hybrid had larger (more negative) early step length differences. In postadaptation, we observed a significant early step length difference in experiment 1 and a near-significant early step length difference in experiment 2. These results suggest that subjects performing the marching-walking hybrid adapted slower and deadapted slower. It is possible that the rates of adaptation and deadaptation are a direct result of the locomotion behavior, but it is also possible that the belt speed ratio (infinite for the marching-walking hybrid vs. 3:1 for split-belt walking) may play a role even though we fixed the difference in belt speeds at 1.0 m/s for both groups. This is supported by previous work that showed that greater belt speed ratios resulted in slower adaptation rates (Reisman et al. 2005). Future work with different fast belt speeds for the marching-walking hybrid could be conducted to investigate this further.

Previous studies have indicated that the rate of adaptation can be heavily influenced by the degree to which the executive system is involved in the adaptive behavior (Taylor and Thoroughman 2008). Recently, it was shown in a split-belt experiment that conscious correction of step lengths increased adaptation rates whereas distraction in a dual task slowed adaptation rates (Malone and Bastian 2010). This work also demonstrated that distraction during adaptation resulted in a slower deadaptation rate. With this in mind, it is possible that requiring subjects to march on the stationary belt may distract from the locomotor adaptation process, increasing the early step length differences in adaptation and postadaptation of the marching-walking hybrid groups.

Comparison with unilateral stepping.

Recently, it was shown that unilateral stepping, in which one foot remains on a stationary surface and the other foot walks on a moving belt, has modest transfer to over ground walking for stroke survivors (Kahn and Hornby 2009) and is reduced in healthy control subjects compared with split-belt walking (Huynh et al. 2014). In light of the work in reduced gait (Faist et al. 1999; Van de Crommert et al. 1996), it is possible that the muscle activation patterns are similar across unilateral stepping, marching-walking hybrid, and split-belt walking; however, unilateral stepping does not have alternating single support periods, which is known to be an important sensory signal. Thus it is possible that the presence of this unloading signal in the marching-walking hybrid may result in a slight increase in over ground transfer as observed here in experiment 2. This is supported by previous work that shows that transfer can be improved if context cues that signal the differences between adaptation and the natural environment are reduced (Kluzik et al. 2008; Torres-Oviedo and Bastian 2010, 2012). While a direct comparison between our between-subject design and the unilateral stepping within-subject design by Huynh and colleagues cannot be conducted, it is important to know that both unilateral stepping and the marching-walking hybrid produce postlearning effects and potentially could be used for rehabilitation as an alternative to split-belt walking as done by Kahn and colleagues (Kahn and Hornby 2009).

Clinical implications.

Cerebral stroke survivors are known to walk with an asymmetric gait (Allen et al. 2011; Balasubramanian et al. 2007; Hall et al. 2012; Patterson et al. 2010). In our recent work, we observed that stroke survivors can have baseline asymmetries in the spatial, temporal, and perturbation contributions of our step length difference model (Finley et al. 2015). Additionally, some stroke survivors have gone through rehabilitation to walk symmetrically, but their new strategy typically is to compensate for the existing asymmetry in one term by modifying another term. For example, if they have a negative temporal term asymmetry, they might increase their spatial term to compensate instead of bringing the temporal term back to zero. This means that the individual will be walking with equal step lengths but using a strategy different from that of healthy control subjects. The work here supports the idea that different strategies can be utilized to walk with symmetric step lengths.

Previous work has shown that split-belt treadmill walking can improve step length asymmetry in stroke survivors (Reisman et al. 2007, 2009, 2013). However, split-belt treadmills are generally expensive and not easily accessible. In this study, we demonstrated that short-term training with a marching-walking hybrid induces adaptation and aftereffects similar to those of split-belt walking in healthy individuals. This suggests that a marching-walking hybrid rehabilitation strategy could possibly be used when split-belt treadmills are not available. In addition, since the marching-walking hybrid focuses on spatial adaptation, it is possible that patients with spatial asymmetries may benefit more from this type of training. Future work will be conducted to determine whether we see similar experiences in stroke survivors.

GRANTS

This work was supported by National Institute of Child Health and Human Development Grant HD-048741 and National Institute of Neurological Disorders and Stroke Grant NS-092241.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: A.W.L. and A.J.B. conception and design of research; A.W.L. performed experiments; A.W.L. analyzed data; A.W.L. and A.J.B. interpreted results of experiments; A.W.L. prepared figures; A.W.L. and A.J.B. drafted manuscript; A.W.L., J.M.F., and A.J.B. edited and revised manuscript; A.W.L., J.M.F., and A.J.B. approved final version of manuscript.

Appendix

In this appendix, we derive a model for step length difference that separates the contributions from spatial, temporal, and perturbation components. This derivation has been published elsewhere (Finley et al. 2015) but is provided here for clarity. We define step length as the anterior-posterior distance between the two ankle markers at heel strike. The fast step length occurs at heel strike on the fast treadmill belt, and the slow step length occurs at heel strike on the slow treadmill belt. We define the step length difference as

$$\text{Step}\hspace{0.17em}\text{Length}\hspace{0.17em}\text{Difference}=\text{Fast}\hspace{0.17em}\text{Step}\hspace{0.17em}\text{Length}-\hspace{0.17em}\text{Slow}\hspace{0.17em}\text{Step}\hspace{0.17em}\text{Length}$$

For a given stride, we define the first slow heel strike at time SHS1, the fast heel strike at time FHS, and the second slow heel strike at time SHS2. We then define the slow and fast step times (Malone et al. 2012), respectively, as

$${\text{t}}_{\text{s}}=\mathit{\text{FHS}}-\text{SHS1}\hspace{0.17em}\text{and}\hspace{0.17em}{\mathit{\text{t}}}_{\text{f}}=\mathit{\text{SHS2}}\mathit{-}\mathit{\text{FHS}}$$

For some time TIME, let x_f(TIME) and x_s(TIME) be the anterior-posterior position of the ankle markers for the fast and slow foot, respectively. These quantities are measured with respect to the average of the two hip markers to maintain a body-centered coordinate frame such that a positive value means the ankle is in front of the hip center (Finley et al. 2015). With these variables, the step lengths are defined as

$$\text{Fast}\hspace{0.17em}\text{Step}\hspace{0.17em}{\text{Length}=\mathit{\text{x}}}_{\text{f}}\left(\text{FHS}\right){-\mathit{\text{x}}}_{\text{s}}\left(\text{FHS}\right)\hspace{0.17em}\text{and}\hspace{0.17em}$$

$$\text{Slow}\hspace{0.17em}\text{Step}\hspace{0.17em}{\text{Length}=\mathit{\text{x}}}_{\text{s}}\left(\text{SHS2}\right){-\mathit{\text{x}}}_{\text{f}}\left(\text{SHS2}\right)$$

The approximate speed of each ankle (relative to the body) while on the moving belt can be written as v_s for the slow belt and v_f for the fast belt. We calculate these speeds with

$${\text{υ}}_{\text{s}}\text{=}\frac{{\mathit{\text{x}}}_{\text{s}}\left(\text{SHS}1\right){-\mathit{\text{x}}}_{\text{s}}\left(\text{FHS}\right)}{{\mathit{\text{t}}}_{\text{s}}}\hspace{0.17em}\text{and}\hspace{0.17em}{\text{υ}}_f\text{=}\frac{{\mathit{\text{x}}}_f\left(FHS\right){-\mathit{\text{x}}}_f\left(SHS\mathit{2}\right)}{{\mathit{\text{t}}}_f}\hspace{0.17em}$$

Given these definitions, we can rewrite the fast step length as

$$\text{Fast}\hspace{0.17em}\text{Step}\hspace{0.17em}{\text{Length}=\mathit{\text{x}}}_{\text{f}}\left(\text{FHS}\right)-\left({\mathit{\text{x}}}_{\text{s}}\left(\text{SHS}1\right){-\text{υ}}_{\text{s}}{\mathit{\text{t}}}_{\text{s}}\right){=\text{α}}_{\text{f}}{\text{+υ}}_{\text{s}}{\mathit{\text{t}}}_{\text{s}}\hspace{0.17em}\text{with}\hspace{0.17em}{\text{α}}_{\text{f}}{=\mathit{\text{x}}}_{\text{f}}\left(\text{FHS}\right){-\mathit{\text{x}}}_{\text{s}}\left(\text{SHS}1\right)$$

As shown in Fig. A1, the fast step length is now decomposed into a spatial term α_f and a temporal term v_st_s. The spatial variable only depends on where the two feet were placed relative to the body, and the temporal variable depends on how far the slow foot moved backwards during the step time. Similarly, we can rewrite the slow step length as

$$\text{Slow}\hspace{0.17em}\text{Step}\hspace{0.17em}{\text{Length}=\text{α}}_{\text{s}}{+\text{υ}}_{\text{f}}{\mathit{\text{t}}}_{\text{f}}\hspace{0.17em}\text{with}\hspace{0.17em}{\text{α}}_{\text{s}}{=\mathit{\text{x}}}_{\text{s}}\left(\text{SHS}2\right){-\mathit{\text{x}}}_{\text{f}}\left(\text{FHS}\right)$$

Note that in Fig. A1 the spatial term α_s is drawn as negative, indicating that the slow foot was placed behind the previous fast foot placement. We can now rewrite the step length difference equation as

$$\hspace{0.17em}\text{Step}\hspace{0.17em}\text{Length}\hspace{0.17em}\text{Difference}=\left({\text{α}}_{\text{f}}{-\text{α}}_{\text{s}}\right){\text{+υ}}_{\text{s}}{\mathit{\text{t}}}_{\text{s}}{-\text{υ}}_{\text{f}}{\mathit{\text{t}}}_{\text{f}}$$

Fig. A1.

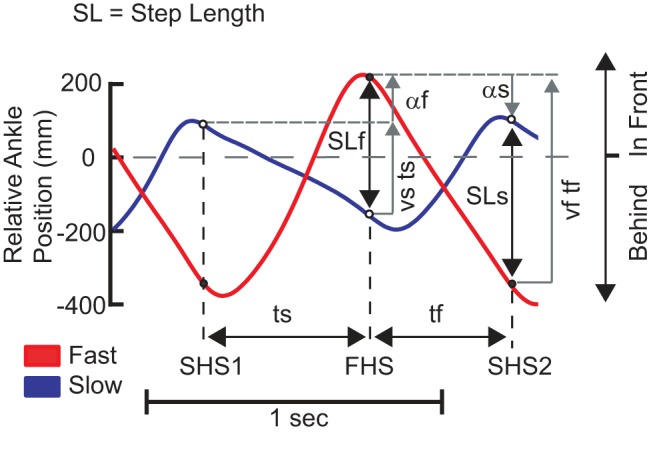
Model component derivation. The ankle position relative to the hip center for the fast and slow limbs is shown as a function of time. The step times t_s and t_f are the difference in times between heel strikes. Step length is defined as the distance between the 2 ankles as heel strike with the fast step length occurring with heel strike on the fast belt and the slow step length occurring with heel strike on the slow belt. The spatial variables α_f and α_s represent the position of the heel strike relative to the previous heel strike. Note that α_s is drawn as negative since the slow foot is placed behind the fast foot.

With some rearrangement, we can rewrite the step length difference as

$$\text{Step}\hspace{0.17em}\text{Length}\hspace{0.17em}\text{Difference}=({\alpha }_{\text{f}}-{\alpha }_{\text{s}})+\frac{{\nu }_{\text{s}}+{\nu }_{\text{f}}}{2}({\mathit{t}}_{\text{s}}-{\mathit{t}}_{\text{f}})+\frac{t_{\text{s}}+t_{\text{f}}}{2}({\nu }_{\text{s}}-{\nu }_{\text{f}})=\text{Spatial}+\text{Temporal}+\text{Peturbation}$$

This form of the step length difference equation is numerically equivalent to the difference in step lengths but breaks down the equation into spatial, temporal, and perturbation contributions.