Selecting causal genes from genome-wide association studies via functionally-coherent subnetworks

Abstract

While genome-wide association (GWA) studies have linked thousands of loci to human diseases, the causal genes and variants at these loci generally remain unknown. Although investigators typically focus on genes closest to the associated polymorphisms, the causal gene is often more distal. Relying on the literature to help prioritize additional candidate genes at associated loci can draw attention away from less-characterized causal genes. Here we describe a strategy that uses genome-scale ‘co-function’ networks to identify sets of mutually functionally related genes spanning multiple GWA loci. Using associations from ~100 GWA studies covering ten cancer types, this approach outperforms the common alternative strategy in ranking known cancer genes. The strategy’s power grows with more GWA loci, offering an increasing opportunity to elucidate causes of complex human disease.

Introduction

While simple (i.e. Mendelian) traits can be explained by only a few strong-effect loci, the modest effects at many complex trait loci complicate precise identification of causal variants ¹. Genome-wide association (GWA) studies in large cohorts help address this issue by being powered to detect modest associations at multiple loci simultaneously ². GWA studies have to date detected thousands of robust associations between genomic loci and disease-related traits. However, rather than identifying causal genes or variants directly, these associations generally identify “tag” single-nucleotide polymorphisms (or “tagSNPs”), each representing many linked variants. Moving from these genomic ‘landmarks’ to individual causal genes within these loci remains challenging, and precise understandings of the genotype-to-phenotype relationship for most traits remain elusive ³.

To address this gap, orthogonal genomic evidence can help prioritize candidate genes found at disease-associated loci ^3,4. Co-occurrences of gene names within PubMed abstracts, for example, have identified connections between candidate genes at different implicated loci ⁵. However, many genes are poorly characterized within the literature, and restricting analyses to ‘popular’ genes diminishes the opportunity for novelty. Likewise, protein-protein interactions (PPIs) have informed our mechanistic understandings of disease ^6–8, but interaction evidence alone is limited in scope, with much of the human proteome under-represented in high-quality databases ⁹ (Supplementary Fig. 1) and an even smaller fraction of the complete interactome having been mapped ¹⁰. Additionally, nearly half of all current human PPI knowledge comes from small-scale targeted studies which, like literature text-mining, limits the opportunity for novel discovery ¹¹.

‘Group-wise’ disease associations missed when testing SNPs in isolation can be found by testing sets of genes that share a common function ^7,12. Assigning SNPs to functional sets, however, requires (i) existing assignments of SNP effects to specific genes and (ii) complete knowledge of function, both of which remain problematic ¹³.

Co-function networks (CFNs) augment curated functional annotation by connecting pairs of genes that share --- or are likely to share --- biological function ¹⁴ (e.g. by sharing protein domain annotations). ‘Guilt-by-association’ ¹⁵ methods have used CFNs to assign function to uncharacterized genes for S. cerevisiae ¹⁴, A. thaliana ¹⁶, M. musculus ¹⁷, and H. sapiens ^18–20, amongst other species. CFNs have also contributed to fine-scale mapping of Mendelian disorder associations ²¹, and can prioritize genes not located at disease-associated loci (e.g. by connectivity to known “seed” causal genes ^8,22).

Here we use CFNs to prioritize groups of candidate genes from multiple disease-associated loci on the basis of mutual functional-relatedness. We frame the problem as a constrained optimization task, analogous to choosing mutually compatible items from a prix fixe restaurant menu, with one dish from each course (cocktail, appetizer, entree, dessert, etc.). Combinations of genes, with one gene from each locus, are evaluated for their collective extent of shared function within the CFN. We find that the “prix fixe” strategy improves upon the ubiquitous approach of ranking candidate causal genes by their genetic distance to trait-associated tagSNPs. Mutually-connected gene groups can reveal disease-relevant pathways and prioritize candidate disease genes. This method is freely available online and as a downloadable R package at http://llama.mshri.on.ca/~mtasan/GrandPrixFixe.

Results

Following a GWA scan for association, candidate genes within implicated loci may be selected for subsequent analysis. Often only genes overlapping or flanking the reported tagSNPs are considered, excluding other potentially-causal genes within the associated haplotype (see, for example, the “mapped genes” field in the NHGRI GWAS Catalog ²³). Moreover, these genes are typically examined in the context of existing literature, which may be subject to substantial confirmation bias. For example, the on-going rate of new publications is significantly higher for earlier-characterized genes when compared to those genes more recently ‘discovered’ within the literature (Supplementary Fig. 2). This ‘rich get richer’ phenomenon lures us from novel discoveries towards already well-characterized genes.

To prioritize candidate genes from disease-associated loci while minimizing bias towards well-studies genes, we integrated genome-scale data and analyzed published GWA studies spanning 23 diverse complex diseases and traits, including auto-immune disorders, cognition levels, and cardiovascular & metabolic traits, as well as 10 distinct cancer types (Table 1). We first describe the overall method (Fig. 1), then describe each step in greater detail below.

Table 1.

Traits and diseases analyzed in this work. “# Pubs” is number of distinct GWAS publications used in this study. “# Loci” gives the number of loci found after mapping the associated SNPs to non-redundant genomic windows. “# PF combinations” is the number of unique prix fixe subnetworks that can be derived from the associated loci and their constituent genes. “ALL” is acute lymphoblastic leukemia, “CLL” is chronic lymphocytic leukemia, “IBD” is irritable bowel disease. Full details of all GWA studies (including all associated SNPs) are available in the Supplementary Files.

Trait group	Trait	# Pubs	# Loci	# PF combinations
Cancers	ALL	7	44	2.4 × 108
	Breast cancer	1	58	7.5 × 1012
	CL	5	23	1.8 ×107
	Colorectal cancer	13	36	1.7 × 1010
	Gastric cancer	3	7	1.7 × 103
	Glioma	4	8	2.6 × 102
	Lung cancer	18	29	2.6 × 1012
	Ovarian cancer	4	11	8.7 × 104
	Pancreatic cancer	4	31	1.9 × 107
	Prostate cancer	19	73	7.8 × 1028
Auto-immune diseases	Type 1 diabetes	1	38	9.9 × 1019
	Multiple sclerosis	1	75	5.7 × 1035
	Crohn’s disease	1	70	6.7 × 1034
	Uncerative colitis	1	47	1.1 × 1021
	IBD	1	110	1.3 × 1053
Cardiovascular traits	Cholesterol, total	1	52	1.4 × 1024
	HDL cholesterol	1	47	7.3 × 1019
	LDL cholesterol	1	37	2.0 × 1018
	Triglycerides	1	32	6.1 × 1015
	QT interval	1	27	7.3 × 105
Metabolic traits	Height	1	183	1.7 × 1073
	Type 2 diabetes	1	26	2.2 × 108
Cognition	Cognitive performance (1)	1	57	5.7 × 1012
	Cognitive performance (2)	1	53	3.2 × 109

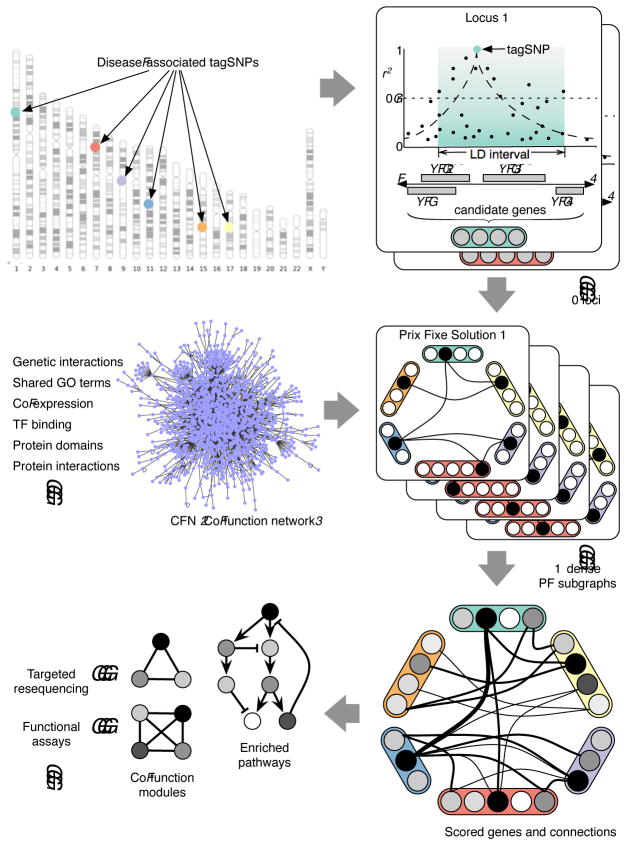
Figure 1.

Overview of prix fixe strategy. TagSNPs associated with disease are used to define linkage-disequilibrium “windows”. A co-function network (CFN) is then used to identify dense “prix fixe” (PF) subnetworks. Dense prix fixe subnetworks are aggregated and genes are scored to reflect their importance in the subnetworks. High-scoring genes are then used to find causal pathways, processes, and additional candidate genes.

After identifying tagSNPs associated with a trait, nearby genes (identified by linkage disequilibrium (LD)) are consolidated into disjoint gene sets. A stochastic optimization strategy then identifies “prix fixe menu selections”: sets of genes (with one gene per locus) that correspond to dense subnetworks of functional relationships. Finally, we measure each gene’s contribution to the top-scoring subnetworks. Top-scoring dense subnetworks yield sets of genes working in concert, highlighting particular processes that may contribute to disease etiology.

To illustrate the process, we use prostate cancer susceptibility as a case-study. Detailed results for all 23 diseases and traits analyzed (Table 1) are provided as Supplementary Files.

Identifying LD-ranges from associated SNPs

We systematically defined genomic boundaries for trait-associated loci using pairwise linkage-disequilibrium (LD) correlations (r²) between each associated tagSNP and nearby SNPs (Fig. 1). Genes (defined to capture cis-regulatory elements via up- and down-stream ‘padding’) within these boundaries were then identified for each trait-associated locus (Online Methods).

Inferring a human co-function network

To aggregate information about functional relationships between human genes, we constructed a CFN covering most of the human genome (Fig. 1 and Supplementary Fig. 3). For this, we used (i) a method based on gene-pair features (e.g. shared protein domain signatures) ¹⁹, and (ii) a graph-walking strategy to find pairs of genes that are likely to share function ²⁴ (Online Methods). The two networks cover nearly the full human genome, but are complementary (Supplementary Fig. 3), echoing earlier findings establishing that differing methods often each excel at inference for distinct functions ¹⁷. We merged these two networks into a single CFN, providing ~10⁷ ‘co-function’ links involving ~19,000 genes (covering 94% of the human genome).

Identifying mutually connected prix fixe subnetworks

To find common threads connecting trait-associated loci, we searched the CFN for groups of candidate genes appearing to work in concert (Fig. 1). More specifically, we sought densely-connected subnetworks such that each locus contributes a single gene to the subnetwork (i.e. with a ‘prix fixe’ constraint). In graph-theoretic terms, these are dense L-partite subgraphs for L loci, where density is a measure of mutual connectivity amongst the genes.

For most complex traits, the large number of associated loci and candidate genes make enumeration of all possible prix fixe subnetworks infeasible (Table 1, “PF combinations”). The 73 loci implicated in prostate cancer, for example, have ~10²⁹ potential prix fixe subnetworks, and for height this number exceeds 10⁷³. To tractably identify dense prix fixe subnetworks, we used a genetic algorithm ²⁵ seeded with a ‘population’ of random prix fixe gene sets (‘individuals’). Individuals are subjected to ‘mutation’ such that, with low probability, two genes at a given locus are swapped. Each subnetwork ‘individual’ is evaluated for its ‘fitness’ (here, edge density), and pairs of individuals are randomly mated (preferring fitter pairs) to create new subnetworks (Online Methods). After repeated ‘generations’ of selection, the population is enriched for dense prix fixe subnetworks (Fig. 1 and Supplementary Fig. 4). To measure significance, we compared the final population’s average edge density to the same measure from 1000 trials with random input sets matching the true input set in terms of number of genes and connectivity (Supplementary Fig. 2, Online Methods).

The importance of each gene at each locus was estimated by the difference in edge densities in subnetworks with and without that gene. For example, a gene with no connections yields the same density whether included or not, implying zero importance to that subnetwork. We averaged the importance measurements of each gene over the final ‘fittest’ population of prix fixe subnetworks, obtaining a “prix fixe score” (Fig. 1) for each candidate gene (Online Methods).

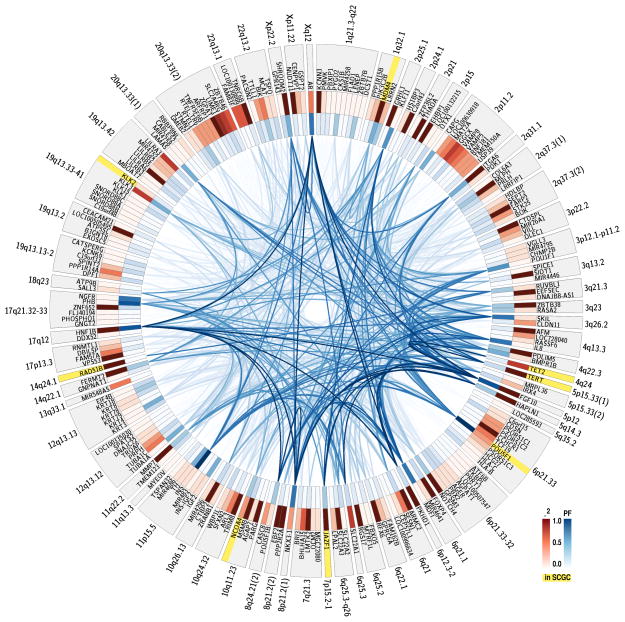
Both the gene scores and the frequencies with which edges appear in the subnetworks provide clues about how candidate genes work together. Amongst the 73 prostate cancer-associated loci, for example, at locus 6p21.33 the candidate gene POU5F1 (also known as OCT4) is highlighted, along with one of its frequent subnetwork partners, HNF1B (at locus 17q12; Fig. 2). Despite being previously linked to prostate cancer ²⁶, POU5F1 might have otherwise been overlooked given that four other genes are closer to the associated tagSNP. But both POU5F1 and HNF1B play important roles in embryonic development, and they boost each other’s importance. HNF1B has also recently been shown to modulate the effects of growth hormones and tumor progression ²⁷.

Figure 2.

Functional connectivity patterns in prostate cancer. Candidate genes are organized by locus in genomic order. Genes highlighted in yellow are members of the Sanger Cancer Gene Census. Red gene intensity indicates the LD (r²) value between the gene and tagSNP for that locus. Blue gene intensity reflects the prix fixe score. Edges represent presence in the final collection of dense subnetworks, with blue edge intensity reflecting the proportion of final dense subnetworks containing that edge.

Cancer-susceptibility gene prioritization

To broadly evaluate prix fixe-based gene prioritization, we explored GWA studies of multiple cancer types. We assembled 78 published GWA studies spanning ten types of cancer (Table 1). For nine types (all but chronic lymphocytic leukemia (CLL)), at least one associated multigenic locus contained a known cancer-linked gene, as defined by the Sanger Cancer Gene Census (SCGC) ²⁸.

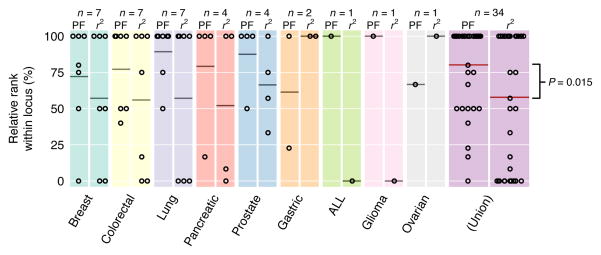
Prioritization success was measured at multigenic loci by ranking the SCGC gene by its prix fixe score within each locus, and rescaling this rank from 0 to 100% (Online Methods). The prix fixe score successfully identified the SCGC gene as the highest-ranked gene (100% relative rank) for 21 out of 34 loci, with an average relative rank of 80% for SCGC genes (Fig. 3), significantly higher than expected for non-informative random rankings (P = 4.9E-07, one-sided one-sample Student’s t-test). The prix fixe approach also out-performed the common alternative LD-based ‘closest gene’ strategy of ranking genes by tagSNP proximity (average relative rank 58%; P = 0.015, one-sided paired Wilcoxon signed-rank test, Fig. 3; Online Methods). Note that an ideal “gold standard” set of cancer genes would have included only genes for which germline susceptibility alleles have been observed, given that cancer susceptibility is the GWA trait under study. Although this more stringent reference standard yielded a similar effect size (average relative rank of 91%) but with only 8 qualifying loci had insufficient statistical power (P = 0.14). However, there is strong overlap between somatically-mutated cancer genes and cancer genes associated with germline susceptibility, with half (43/81) of SCGC genes showing evidence of disease-causing germline mutations also having somatic-mutation evidence. That cancer genes were significantly highly-ranked within the more complete set suggests that many of the cancer genes at these 34 loci that were previously known only through somatic mutations may also harbor germline predisposition alleles.

Figure 3.

Rank-based analysis of Sanger Cancer Gene Census (SCGC) prioritization. Genes are ranked within each cancer-associated locus and normalized ranks of SCGC genes are shown as dots for prix fixe-based (“PF”, left) and LD-based (“r²”, right) rankings (100% is highest ranked, 0% is lowest). Average relative rank of SCGC genes (for both methods) within each locus identified by horizontal bars; number of multigenic loci shown above as “n”. Right-most plot (“Union”) shows pooled results across all cancer-associated loci. PF SCGC ranks significantly outperform LD-based SCGC ranks (P = 0.015, one-sided paired Wilcoxon signed-rank test). CLL contained no SCGC-harboring loci in our primary analysis, and is thus not displayed here.

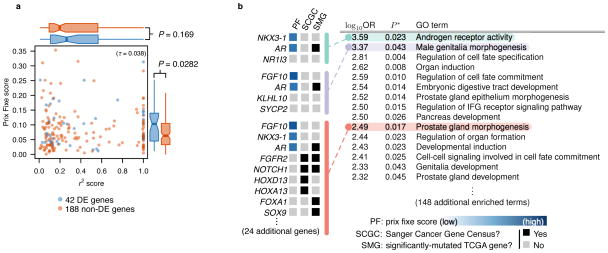
To further investigate our rankings, we used mRNA expression data from The Cancer Genome Atlas (TCGA) for both breast (BRCA) and prostate cancer (PRAD)¹. The prix fixe scoring method ranked differentially-expressed genes significantly higher than genes without a marked expression difference between matched tumor and healthy tissues for both cancers (P = 0.03 for PRAD and P = 0.01 for BRCA; Wilcoxon rank sum test; Fig. 4a and Supplementary Fig. 5; Online Methods). Closest-gene rankings did not show correlation with cancer-dependent expression (P = 0.17 and P = 0.59; Wilcoxon rank sum test; Fig. 4a and Supplementary Fig. 5).

Figure 4.

(a) Prix fixe scores are uncorrelated with LD (r²) values. Each scatter plot point is a candidate breast cancer gene. Correlation is computed using Kendall’s τ rank coefficient. Blue genes indicate significantly differentially-expressed mRNA levels in matched case-control TCGA prostate adenocarcinoma (PRAD) samples, while red genes indicate no evidence of cancer-dependent differential expression. Flanking boxplots indicate score distributions of differentially- and not-differentially-expressed genes. Boxplot whiskers extend to 1.5×IQR; outliers not shown. Boxplots compared by one-sided Wilcoxon rank sum tests. (b) Prix fixe rankings identify disease-relevant Gene Ontology (GO) terms for prostate cancer, with no a priori knowledge of disease etiology. Top-15 (by odds-ratio (OR)) GO terms shown using “ordered” functional enrichment analysis with significance (P*) corrected for multiple testing ²⁹. Three GO terms expanded to show constituent genes with (if available) “PF” score, “SCGC” (Sanger Cancer Gene Census) status, and “SMG” (significantly-mutated gene ³⁵) status. Full functional enrichment analysis for all traits provided in Supplementary File 3.

Identifying causal pathways

Commonalities amongst high-scoring candidate genes can provide insight into the processes contributing to disease (Fig. 1), and so for each trait, we searched for Gene Ontology (GO) terms that were over-represented amongst the highest-scoring genes ²⁹ (Online Methods). Prix fixe-ranked prostate cancer candidate genes yielded significant enrichment for 163 GO terms (Supplementary File 3). The maximal enrichment for most (75%) of these terms was found using just the top 23 genes, indicating a high concentration of shared function between these highest-scoring candidates. By contrast, functional enrichment analysis with the complete set of genes from prostate cancer-associated loci (i.e. an “unordered” search) yielded no enriched terms. More surprisingly, no terms were found in an ordered functional enrichment analysis of prostate cancer genes when ranked by the closest-gene approach. For all traits examined, prix fixe scoring provided more enriched terms than the closest-gene approach, with the latter method providing nearly the same amount of term enrichment as the unranked approach (Supplementary File 3).

Many enriched terms in our prostate cancer analysis have clear links to prostate function and development, including “androgen receptor activity”, “male genitalia morphogenesis”, and “prostate gland morphogenesis” (Fig. 4b). The high-scoring candidate genes AR (androgen receptor), FGF10 (fibroblast growth factor 10), and NKX3-1 (NK3 homeobox 1) --- found at Xq12, 5p12, and 8p21, respectively --- have all received considerable attention for their probable role in prostate cancer development, despite not yet being declared “causal” in the SCGC ^30–32. In particular, AR and receptors of the FGF family (i.e. FGFRs) are considered possible therapeutic targets for inhibiting prostate tumor progression ³³ and tumorigenesis more generally ³⁴. AR was among the few significantly-mutated genes (SMGs) detected by a recent “pan-cancer” whole-genome sequencing analysis of diverse tumor samples ³⁵ (Fig. 4b).

Enriched terms provide the opportunity to identify new candidate genes outside trait-associated loci. “Prostate gland morphogenesis”, for example, is associated with 30 genes not found within any prostate cancer-associated locus (Fig. 4b). Four of these genes are known to have causal roles in tumorigenesis (FGFR2, NOTCH1, HOXD13, and HOXA13), and four (in addition to AR) appear in the pan-cancer SMG list ³⁵ (Fig. 4b). Thus, the prix fixe method systematically prioritizes candidate genes which can then serve as “seeds” to find additional candidates (e.g. through guilt-by-association techniques).

For nearly every trait examined, we found enriched terms that were highly relevant to that trait (Supplementary Table 3), e.g. “learning or memory” for cognitive performance and “plasma lipoprotein particle assembly” for cholesterol levels. The processes highlighted by our candidate gene rankings also helped identify non-obvious or environmental factors contributing to complex traits. For example, top prix fixe-ranked lung cancer candidate genes are highly enriched for associations with “behavioral response to nicotine”, capturing the role of smoking in lung cancer and possible gene-environment interactions.

Finally, we found terms that were commonly-enriched across a subset of traits, indicating diseases with shared etiology. High-scoring genes in chronic lymphocytic leukemia (CLL), type 1 diabetes, Crohn’s disease, ulcerative colitis, inflammatory bowel disease, and multiple sclerosis, for example, were all associated with functions of immunity. More generally, “response to stress” was over-represented for nearly half of the traits examined in this work, underscoring commonalities of diverse diseases and disorders. Complete results for all traits can be found in Supplementary File 3.

Discussion

Genes contributing to the same trait often share functional relationships ³⁶. Here we have exploited this phenomenon to prioritize candidate causal genes without specifying a priori which functions contribute to the phenotype. We found limitations in the naïve (but commonly used) closest-gene approach, which provided almost no advantage over ranking genes within loci uniformly at random. The extensive haplotype block structures found in human populations limit the utility of the closest-gene strategy. Furthermore, the use of CFNs built from genome-scale data permits scoring for nearly all candidate genes in implicated loci, reducing the knowledge bias that is coupled with literature text-mining approaches.

The importance-scoring step of the prix fixe strategy provides flexibility when aggregating results across many dense prix fixe subnetworks. As not all loci are multigenic, this scoring method can measure the contributions of genes even at monogenic loci. Those genes with strong connections to other candidate genes achieve high scores (e.g. AR at Xq12 in Fig. 2), while the weakly-connected genes tend to score poorly (e.g. MYEOV at 11q13.3 in Fig. 2). The use of multiple top-scoring subnetworks followed by importance-scoring also allows for similarly-connected genes within a multigenic locus to obtain similar scores. For example, NGFR and PHB at 17q21.32–3 are both strong prostate cancer candidates (Fig. 2), and selecting one at the expense of the other by selecting only a single top-scoring subnetwork might have conferred false confidence in a single recommended gene. Individual SNP effect sizes may in the future be included to augment network-based prioritization methods (e.g. by placing prior probability ‘weights’ on candidate genes ³⁷), however, such analyses at large scale will require a (currently unavailable) catalog of annotated effect sizes for markers across all tested traits.

To better understand mechanisms underlying a given phenotype, candidate genes must be viewed in the context of biological processes and pathways ³. Ranking candidate gene sets by their level of collective cooperation within the cell is a principled way to simultaneously identify causal genes and explanatory causal pathways. In addition to those enriched functional annotations found for each trait, the enriched functions shared by different traits point to shared etiologies that might underlie co-morbidity patterns ³⁸ and may help in identifying therapies for one disease that might be repurposed for another.

Using CFNs and connectivity measures to prioritize large candidate lists can be extended beyond GWA studies. It could also be applied, for example, to candidate disease-related variants found by sequencing-based mutational burden studies. Incorporating prior functional knowledge about these candidates will help to prioritize subsets of genes, possibly even in mutually exclusive combinations ³⁹. Resulting gene sets can then be fed back to GWA prioritization results, tightening the net around the underlying causal pathways. The inclusion of large-effect rare variants may help solve the ‘missing heritability’ problem ⁴⁰.

Thus, the use of unbiased genomic datasets and a prix fixe-constrained optimization procedure can identify mutual functional similarity amongst genes in trait-associated loci to prioritize loci, genes, and trait-associated pathways.

Online Methods

Co-function network derivation

We derived a human co-function network (CFN) from two existing CFN resources and published methods. The first CFN was constructed as described in Tasan et al. (2012) ¹⁹, but with the exclusion of Online Mendelian Inheritance of Man (OMIM) ⁴¹ data. OMIM data was removed specifically for this study to limit any potential source of circular logic while evaluating our methods. The remaining predictive data types are briefly summarized below, each chosen with the intent of being as free of survey bias as possible such that combinations of their features retained low bias while providing increased power for discovery.

Protein domain signatures for all genes were downloaded from InterPro ⁴², represented as a binary matrix (i.e. presence or absence of each signature for each gene), and scores were computed for each gene-pair using the PhenoBlast method ⁴³. Transcription factor binding site (TFBS) information was acquired as UCSC Genome Browser ⁴⁴ hg19 tracks for TRANSFAC and ENCODE ChIP-Seq data. To assign TFBSs to genes, gene boundaries were defined by expanding RefSeq transcripts (also mapped to UCSC hg19 coordinates) upstream by 5000 bp and downstream by 500 bp, and any TFBS overlapping a gene was then assigned to that gene. A single binary matrix was created for all TFBS data and all genes, and similarity between gene-pairs was scored using the PhenoBlast method ⁴³. Similarity between phylogenetic profiles (downloaded from Inparanoid ⁴⁵) were also scored using the PhenoBlast method ⁴³. Normalized and summarized gene expression profiles covering normal human tissues were downloaded from BioGPS ⁴⁶. These expression data were then log-transformed and Kendall rank correlation coefficients were computed for each gene-pair. Finally, a catalog of literature-curated protein-protein interactions between human ORFs was separated into “binary” and “all” interactions, creating two features (where binary interactions must come from experiments specifically testing pairs of proteins, while the complete data set includes interactions derived from co-complex methods, such as affinity purification and mass spectrometry (AP-MS) experiments).

As positive training examples of gene-pairs sharing function, we used gene-pairs sharing Gene Ontology (GO) Biological Process (BP) terms. To ensure specificity in our definition of co-function, we limited the terms used to those with fewer than 300 non-electronic (i.e. excluding RCA and IEA GO evidence codes) gene associations. These data were then used to train a random forest ensemble classifier ⁴⁷, and the top 1% of scored gene-pairs were used as our predicted CFN. Note that gene pair scores were ‘out of bag’, in that the random forest used to score each gene pair excluded any tree that made use of that gene pair.

The second CFN we used was generated using a different prediction strategy also shown to produce high-quality inferences of shared function between genes using a label-propagation method ¹⁸. Pre-scored data were downloaded from GeneMANIA ²⁴, and as disease annotations were not included as a source dataset, we performed no additional pruning of these data.

Both strategies have been demonstrated to provide high-quality gene-function predictions for (amongst others) H. sapiens ^19,24, M. musculus ^17,48,49, D. rerio ⁵⁰, and S. cerevisiae ⁵¹. The union of these two CFNs were then taken as the single CFN used for this study, noting that while gene coverage overlap was high between the two networks, the gene-pair predictions were largely complementary (Supplementary Fig. 3).

Gene, SNP, and LD positional data

All gene definitions used in this study were acquired from the NCBI Gene database. Transcripts corresponding to these genes were mapped to UCSC hg19 coordinates ⁴⁴. Variation data from dbSNP 137 were also mapped to UCSC hg19 coordinates, and linkage-disequilibrium (LD) data for SNP-pairs within 500 kb of each other were downloaded from the International HapMap Project (Phase III, CEU population) ⁵².

GWA study data and gene-set construction

All GWA study data used in this work were acquired from the NHGRI GWAS Catalog ²³. As some publications report on associations to multiple distinct traits, we took each publication-trait pair and treated it as a distinct ‘study’. Studies were then ranked by their number of significantly-associated loci, and we chose to focus on complex and/or heterogeneous traits, generally with at least 20 reported loci per study. For our cancer analyses, we preferentially selected recent meta-analyses where available, but otherwise took the union of reported SNPs for studies addressing the same type of cancer. For our non-cancer traits, we treated each study independently. Many of the traits we analyzed were associated with more than 20 loci each, indicating substantial complexity in the underlying biology (Table 1). Prostate cancer, for example, has been associated with 73 loci, while height has been associated with nearly 200 loci ⁵³.

Each analyzed set of associated SNPs was then processed by first finding all other SNPs in LD with the associated markers. To this end, a genomic window was defined by taking the positions of the physically farthest upstream and downstream SNPs in LD, such that r² ≥ 0.5 between each boundary SNP and the associated SNP. Genes were defined by Refseq transcript boundaries, but extended 100 kbp upstream and 10 kbp downstream to include cis-regulatory regions. Overlapping windows (which may occur due to multiple SNPs in close proximity being reported for the same locus) were merged to create a set of disjoint genomic windows. The transcripts within these windows were mapped back to unique NCBI Gene IDs, creating a disjoint collection of gene sets. All PubMed IDs, dbSNP IDs, window coordinates, and candidate genes are available in Supplementary File 1.

LD-decay score

For each trait-associated locus, we derived a score for each candidate gene based solely on that locus’ local LD properties (the “r² score”). In cases where the locus was defined by a single tagSNP, we used that SNP for the procedure below. When a locus had been identified by multiple tagSNPs (leading to locus merging, as described above), the SNP with the strongest reported effect size was chosen as the representative SNP for that locus. (In cases where no effect size was available, the SNP with the smallest reported P-value was chosen.)

An LD-decay model for each locus was then learned using the r² correlations between the representative SNP and all other in-LD SNPs in the locus. The decay was modeled using beta regression ⁵⁴ with an inverse link function of $r^2=\frac{1}{1+x}$, where x is the distance (in bp) between the two SNPs. This follows the theoretical relationship between LD and genetic distance described as $r^2=\frac{1}{1+4N_{e}c}$ (where N_e is the effective population size and c is the recombination fraction between the two loci) ^55,56.

Each transcript in the locus was then given an r² “score” according to this model, where the r² decay value was computed for the point along the transcript closest to the representative SNP (i.e. the maximal predicted r² value along the length of the transcript). The transcripts were collapsed into unique genes, with the maximal score for these collapsed transcripts taken to represent the gene. Note that transcripts overlapping the representative SNP itself are assigned a score of 1, and the score monotonically decreases (towards 0) as the genes are farther in physical distance from the representative SNP, providing robustness to r² variability (seen here as “noise”) in local genomic regions. These r² scores are available for all candidate genes and all traits in Supplementary File 2.

Prix fixe subnetwork enrichment

For each collection of disjoint gene-sets, we searched through the CFN to find prix fixe subnetworks (i.e. where each locus was represented by a single gene). Because enumerating all possible such subnetworks is often computationally intractable, we used a genetic algorithm to enrich for dense prix fixe subnetworks, where density is defined as the number of edges within the subnetwork. An initial “population” of 5000 random prix fixe subnetworks was chosen (where the gene representing each locus was chosen uniformly at random). Each “generation” then consisted of a mutation step and a mating step. In the mutation step, genes representing each locus in the prix fixe subnetworks were swapped with other genes from the same locus. Each locus was mutated with a 5% probability, and the replacement gene was chosen from the remaining available genes in that locus uniformly at random. The mating procedure incorporates the notion of “fitness” by preferentially selecting denser prix fixe subnetworks for mating (and thus propagation to the next generation). The density d_i (edge-count) of each subnetwork i was computed and (cubically) transformed to a selection score $s_i=d_i^3$, which was then normalized to $s_i^{\ast }=\frac{s_i}{{\mathrm{\sum }}_{j=1}^{5000}{s}_j}$. Pairs of subnetworks were sampled (with replacement) where the probability of selecting a “parent” subnetwork i was equal to s^*_i. Each mating resulted in a new subnetwork, where the gene chosen for each associated locus was randomly selected from either parent (in a 50/50 coin-flip procedure). After 5000 such matings, each new population of subnetworks replaced the parental population and the procedure was repeated, starting again with the mutation step. The optimization cycle terminated when the newly-generated population’s average density failed to improve upon the previous generation’s average density by more than 0.5% (i.e. plateauing).

To measure the statistical significance of the final population of subnetworks, we used a randomization strategy intended to simulate the null case where non-informative collections of loci were provided in lieu of the true trait-associated loci. For a set of L loci with G_i genes in locus i, we generated L “matched” random and disjoint sets of genes, again with G_i genes per set i. To account for possible node-degree effects within the CFN, each random gene was selected such that its degree approximately matches the true candidate gene’s degree in the CFN. We chose approximate degree-matching over precise degree matching to prevent frequent selection of the actual true genes in the random trials, due to possible uniqueness in the true genes’ degree distribution. All genes in the CFN were distributed amongst 128 equal-sized bins based on the genes’ degrees (i.e. we used quantile-based binning of the degrees and associated nodes). Each original candidate gene was replaced with a random gene selected from the same bin, thus preserving approximate degree.

Each matched collection of random gene sets was then subjected to the genetic algorithm optimization method, and the average density of the final population in the random trial was used as a test statistic. The observed test statistic for the original loci was compared to test statistics for 1000 random trials (as described above), resulting in an empirical P-value representing the fraction of random trials producing final populations of subnetworks with higher average density than the average density seen with the true loci inputs (Supplementary Fig. 4).

Prix fixe gene-scoring

To score each candidate gene, we began with a single prix fixe subnetwork from the final population and modified this subnetwork one locus at at time, while keeping the subnetwork constant for all other loci. Consider a single prix fixe subnetwork and a locus i containing G_i genes (g₁,g₂,…,g_Gi), where g^* represents the gene “chosen” for that locus within the subnetwork. During the scoring procedure, g^* is “forgotten” and all G_i genes are considered, while the “chosen” genes for all other loci remain fixed. First, each gene g_i is iteratively used in place of g^* and the density (edge-count) for the subnetwork is recomputed. Then, the density of the subnetwork is recomputed in the absence of any gene for locus i (i.e. as if locus i were to be completely removed from the association study results): the “empty” locus case. The difference in densities for each gene g_i and this “empty” locus case indicate the contribution made by gene g_i to the cohesiveness of the rest of the subnetwork. Thus, if two genes are in locus i and have identical connectivity patterns to all other subnetwork loci (e.g. if the two genes are paralogs resulting from a localized duplication event), they will acquire the same score for this subnetwork, even if only one gene was chosen for this prix fixe subnetwork during the enrichment procedure described above. Genes with high connectivity to the other loci in the subnetwork will be assigned high scores, while genes with low connectivity are similar to the “empty” locus case and are given low scores. Each locus was similarly considered in turn, and thus all candidate genes were given a single score for each prix fixe subnetwork in the final population. These scores were then averaged over the full population of subnetworks leading to the aggregate score for each gene. Scores for all genes across all traits are available in Supplementary File 2. Genes at a locus but not found in our CFN were given “NA” scores, indicating the absence of information.

Rank-based prioritization evaluation

To evaluate gene scoring methods within a locus, we used a rank-based system seeking to identify the rank of a known “causal” gene (for those loci containing such a known gene). Genes were first ranked according to score, and to compare ranks between loci containing different numbers of genes, we used a relative rank that was rescaled to lie between 0% and 100%. For example, in a locus containing 5 genes with an SCGC gene ranked second, the normalized SCGC gene’s rank is 3/4 (with the bottom- and top-ranked genes having relative ranks of 0% and 100%, respectively).

In the GWA studies we analyzed, many of the candidate genes described in the source publications were selected based solely on their distance (either physical or genetic) from the associated tagSNP. Thus, we compared the prix fixe rankings to an alternative ‘closest gene’ strategy of ranking genes by tagSNP proximity (as defined by LD value). Genes were assigned scores based on the modeled r² decay between the tagSNP and SNPs proximal to the genes (as described above). SCGC genes were ranked as top candidates by this strategy in 16 out of the 34 loci (compared to the prix fixe approach’s 21/34), and the average relative rank was 58% (compared to the prix fixe approach’s 80%; Fig. 3). The 58% relative rank was only slightly better than the 50% expected from uniformly random gene rankings (P = 0.16, one-sided one-sample Student’s t-test). Across these 34 loci, the prix fixe approach significantly outperformed the closest gene strategy (P = 0.015, one-sided paired Wilcoxon signed-rank test; Fig. 3), arguing for the incorporation of orthogonal data when prioritizing genes in disease-implicated loci.

While the LD-based approach alone fared poorly, we wondered if enhanced SCGC rankings could be achieved using a combined strategy incorporating both LD and prix fixe scores. For these 34 loci, we found that linear combinations of these two scores showed almost no improvement over the prix fixe strategy alone (results not shown), suggesting that within haplotype blocks, local LD structure may be of little additional use in prioritizing candidate disease genes. We also note that while some GWA authors may use existing literature to identify top candidates for a locus, this risks falling into (and contributing to) the cycle of confirmation bias, thus limiting the ability to identify truly novel disease genes via GWA studies.

Replication & parameter variation

As the prix fixe subnetwork enrichment is a stochastic process, we repeated the prix fixe method for all traits to assess score reproducibility. For each trait, prix fixe scores were recomputed and we assessed correlation between the scores resulting from our primary analysis (presented above) and the replicate scores (using Kendall’s τ rank correlation coefficient). All such correlations were found to be very high (ranging between 0.97 and 1.0; Supplementary Fig. 6a), verifying that the stochastic search process robustly avoids finding only local optima.

To assess how parameter settings may affect results, we next repeated our analysis for all traits using two different r² thresholds: r² ≥ 0.25 and r² ≥ 0.75 (corresponding to ‘relaxed’ and ‘tightened’ genomic regions, respectively). Again we computed Kendall’s τ across gene scores for each trait with respect to the prix fixe scores for that trait’s initial analysis (where the LD threshold was r² ≥ 0.50). As varying the genomic regions often forces inclusion or exclusion of candidate genes, correlations were computed across only those candidate genes shared by both analyses. For both the relaxed and tightened genomic regions, these correlations were generally high (Supplementary Fig. 6b–c), indicating robustness of results to reasonable settings of LD. Despite resulting in varying numbers of candidate genes, alternative r² parameter settings also led to continued enriched prioritization of causal cancer genes (Supplementary Figs. 7 and 8), although in both cases with slightly weaker significance levels.

We further extended our repeat analyses to include alternative CFNs. For these trials, we kept the LD-threshold fixed at r² ≥ 0.50 (as it led to the best causal cancer gene prioritization, see above). Analyses were then repeated for all traits while using three different CFNs: HumanFunc (HF) only, GeneMANIA (GM) only, and the union of HumanFunc, GeneMANIA, and the high-confidence subset of STRING ⁵⁷. Each analysis was then compared to the primary (i.e. as presented in the main text) analysis for a given trait, again using score correlations. When using either the HF or GM CFN alone, score correlations with the initial combined HM ∪GM CFN remain high (Supplementary Fig. 9a–b), though generally lower than those seen while adjusting the LD-threshold parameter. This suggests that the prix fixe method exhibits greater sensitivity to the underlying network than to genomic region boundaries. For the addition of STRING data, we first re-computed STRING v9 scores (as described in Franceschini et al. (2013) ⁵⁷) to remove the text-mining contribution to the final STRING score, in an attempt to prevent literature-born confirmation bias. Prix fixe score correlations between the primary analyses and those scores obtained with this augmented CFN remain very high (Supplementary Fig. 9c), but we found no improvement in the ability to prioritize causal cancer genes with this larger CFN.

Functional enrichment

Functional enrichment analyses were performed using the FuncAssociate tool ²⁹. For each trait, we first ranked all candidate genes by their prix fixe score, independent of their genetic location. An “ordered” GO term enrichment analysis was then run, selecting for over-represented GO terms with a multiple-testing-corrected P-value threshold of 0.05, and terms themselves were ordered by decreasing effect size (odds ratio). All over-represented GO terms for each trait are available in Supplementary File 3.

We note that our CFNs were constructed using shared GO terms as examples of “gold-standard positive” co-functional links. For this reason, results should be interpreted primarily as answers to the question: “what types of co-function examples were useful in this classification process?”, and the interpretation of significance levels should account for this potential for circularity.

Independent replication of prix fixe results using T2D GWA

To examine the reproducibility of pathway identification across distinct GWA studies, we performed two type-II diabetes mellitus (T2D) analyses: one (as part of our primary set of analyses) with loci identified in a study from 2010 ⁵⁸, and one (for replication purposes) with loci found in two recent independent T2D GWA studies ^59,60. Our primary analysis of T2D was based on 26 loci, and a functional enrichment analysis revealed diabetes-related pathways such as “glucose homeostasis”, “pancreas development”, and “insulin secretion” (Supplementary File 3). We then performed a new prix fixe analysis using loci from the ‘new’ T2D GWA studies which identified 17 loci, 8 of which being unique to these newer recent studies.

Despite sharing only 9 loci (amongst 26 and 17 total in the two analyses, respectively), the separate analyses both identified genes involved in diabetes-related biological functions, including “glucose homeostasis”, “insulin secretion”, and “pancreas development” (Supplementary Files 3 and 5). Three of the top-11 scoring genes in our independent replication analysis have verified causal links to T2D, as annotated in the Online Mendelian Inheritance of Man (OMIM) ⁴¹. These include transcription factors TCF7L2 (a.k.a. TCF4), which has extensive evidence of being causal in T2D ^61,62, and HNF1B, which is a known cause of maturity onset diabetes of the young ⁶³. Other high-ranking candidate genes have been identified as therapeutic targets in T2D (e.g. CTBP1 ⁶⁴ and LEP ⁶⁵), and the high-scoring gene HHEX has recently been shown to play a key role in islet function ⁶⁶.

Cancer differential expression analysis

We used data from TCGA to estimate differential expression characteristics of genes within cancer-associated loci. TCGA projects using the RNASeqv2 pipeline were chosen, and we downloaded paired tumor-vs-normal samples. Only the breast invasive carcinoma (BRCA) and prostate adenocarcinoma (PRAD) projects had sufficient numbers of matched RNA samples processed by the RNASeqv2 pipeline, and so we downloaded “Level 3” data for both of these projects. All samples were paired using the TCGA participant and sample type barcodes (identifying patients and tissue types). Unpaired samples (i.e. normal tissue without tumor or vice versa) were not considered for this analysis.

The TCGA RNASeqv2 pipeline reports expected counts as produced by the RSEM ⁶⁷ program. We rounded “raw” counts to the nearest integer, and estimated differential expression with the edgeR R package ⁶⁸ using the GLM (general linear model) functions to force treatment of tumor and normal samples in paired fashion. Genes were declared to be significantly differentially-expressed if their mean estimated fold-change in tumor-vs-normal was greater than 2 (in either direction) and the associated FDR (false discovery rate) was less than 5% (using Benjamini-Hochberg FDR estimation ⁶⁹).

Publication rate analysis

To measure the rates of publications referencing genes in the human genome, we used the gene2pubmed data available from the NCBI Gene database ⁷⁰. For each gene x, the earliest associated publication was identified and the corresponding year t_0,x was used as the “first publication year”. Then, the total number of publications n_x associated with each gene x was found. The subsequent publication rate for gene x was then computed as $r(x)=\frac{n_x}{2013-t_{0,x}}$.

Each year from 1990 to 2012 (inclusive) was then used as a first publication year threshold t^*. Rates for all genes x with t_0,x≤t^* were averaged, giving the average rate of publications per year for all genes first described during or before year t^* (Supplementary Fig. 2).

Software availability

The methods described here are implemented and available as an R package from the authors and as a web application at http://dalai.mshri.on.ca/~mtasan/GranPrixFixe/html). Using the recommended (default) parameter settings described here, most analyses require only a few minutes on standard commodity computers, with minimal memory requirements.

Supplementary Material

Supplementary Figure 1. Supplementary Figure 1.

Much of the human proteome is unrepresented in protein-protein interaction databases. The proteome as defined here consists of all 20484 “protein-coding” genes in the NCBI GENE database. Interactions, both binary and co-complex, are taken from the HINT high-quality amortized protein-protein interaction database ⁹.

Supplementary Figure 2. Supplementary Figure 2.

Historical investigation bias in the literature. Genes characterized at earlier dates continue to appear in publications at higher rates than more-recently characterized genes. Circle positions indicate mean publication rate (y-axis) for genes first characterized during or before each year from 1990–2012 (x-axis). Circle sizes indicate the (cumulative) number of genes characterized during or before each year.

Supplementary Figure 3. Supplementary Figure 3.

Co-function network (CFN) coverage in terms of (a) genes and (b) gene-pairs. “HumanFunc” and “GeneMania” are computed as described in Online Methods. NCBI Gene data downloaded on 2013-07-17.

Supplementary Figure 4. Supplementary Figure 4.

Efficient enrichment for dense prix fixe subnetworks using prostate cancer case-study. Boxplot shows candidate prix fixe subnetwork fitness evolution over 20 generations, circles within boxes indicated mean fitness, whiskers extend cover the full range of observed fitnesses. Marginal histogram (on right) indicates distribution of final generations’ mean fitnesses for 1000 random trials (see Online Methods). Empirical P-value for final generation’s subnetwork enrichment is computed against this marginal distribution (dashed line).

Supplementary Figure 5. Supplementary Figure 5.

Prix fixe scores are uncorrelated with LD (r²) values. Each scatter plot point is a candidate breast cancer gene. Correlation is computed using Kendall’s τ rank coefficient. Blue genes indicate significantly differentially-expressed mRNA levels in matched case-control TCGA breast cancer (BRCA) samples, while red genes indicate no evidence of cancer-dependent differential expression. Flanking boxplots indicate score distributions of differentially- and not-differentially-expressed genes. Boxplot whiskers extend to 1.5×IQR; outliers not shown. Boxplots compared by one-sided Wilcoxon rank sum tests.

Supplementary Figure 6. Supplementary Figure 6.

Prix fixe score robustness with respect to varying LD (r²) thresholds. Each histogram represents a collection of Kendall’s τ rank correlation coefficients. Each single correlation coefficient represents a comparison of prix fixe rank orders for a single analyzed trait when the method is repeated using two different r² thresholds. (a) “Pure” replication (to measure stochastic variance) of the primary analyses using the identical r² ≥ 0.50 threshold. (b) Comparison of scores between primary analyses (r² ≥ 0.50) and a ‘permissive’ (r² ≥ 0.25) threshold. (c) Comparison of scores between primary analyses (r² ≥ 0.50) and a ‘restrictive’ (r² ≥ 0.75) threshold.

Supplementary Figure 7. Supplementary Figure 7.

Rank-based analysis of Sanger Cancer Gene Census (SCGC) prioritization when using a ‘permissive’ LD threshold of r² ≥ 0.25. Genes are ranked within each cancer-associated locus and normalized ranks of known cancer (i.e. SCGC) genes are shown as dots for prix fixe-based (“PF”, left) and LD-based (“r²”, right) rankings (100 is highest ranked, 0 is lowest). Average relative rank of SCGC genes (for both methods) within each locus identified by horizontal bars; number of multigenic loci shown above as “n”. Right-most plot (“Union”) shows pooled results across all cancer-associated loci. PF SCGC ranks significantly outperform LD-based SCGC ranks (P = 0.025, one-sided paired Wilcoxon signed-rank test).

Supplementary Figure 8. Supplementary Figure 8.

Rank-based analysis of Sanger Cancer Gene Census (SCGC) prioritization when using a ‘restrictive’ LD threshold of r² ≥ 0.75. Genes are ranked within each cancer-associated locus and normalized ranks of known cancer (i.e. SCGC) genes are shown as dots for prix fixe-based (“PF”, left) and LD-based (“r²”, right) rankings (100 is highest ranked, 0 is lowest). Average relative rank of SCGC genes (for both methods) within each locus identified by horizontal bars; number of multigenic loci shown above as “n”. Right-most plot (“Union”) shows pooled results across all cancer-associated loci. PF SCGC ranks significantly outperform LD-based SCGC ranks (P = 0.028, one-sided paired Wilcoxon signed-rank test).

Supplementary Figure 9. Supplementary Figure 9.

Prix fixe score robustness with respect to varying co-function networks (CFNs). Each histogram represents a collection of Kendall’s τ rank correlation coefficients. Each single correlation coefficient represents a comparison of prix fixe rank orders for a single analyzed trait when the method is repeated using two different CFNs. (a) Comparison of scores between primary analyses’ CFN (HF ∪GM) and the HF-alone CFN. (b) Comparison of scores between primary analyses’ CFN (HF ∪GM) and the GM-alone CFN. (c) Comparison of scores between primary analyses’ CFN (HF ∪GM) and a STRING-augmented CFN (HF ∪GM ∪STRING).