Abstract
The generalized hybrid orbital (GHO) method has previously been formulated for combining molecular mechanics with various levels of quantum mechanics, in particular semiempirical neglect of diatomic differential overlap theory, ab initio Hartree–Fock theory, and self-consistent charge density functional tight-binding theory. To include electron-correlation effects accurately and efficiently in GHO calculations, we extend the GHO method to density functional theory in the generalized-gradient approximation and hybrid density functional theory (denoted by GHO-DFT and GHO-HDFT, respectively) using Gaussian-type orbitals as basis functions. In the proposed GHO-(H)DFT formalism, charge densities in auxiliary hybrid orbitals are included to calculate the total electron density. The orthonormality constraints involving the auxiliary Kohn–Sham orbitals are satisfied by carrying out the hybridization in terms of a set of Löwdin symmetrically orthogonalized atomic basis functions. Analytical gradients are formulated for GHO-(H)DFT by incorporating additional forces associated with GHO basis transformations. Scaling parameters are introduced for some of the one-electron integrals and are optimized to obtain the correct charges and geometry near the QM/MM boundary region. The GHO-(H)DFT method based on the generalized gradient approach (GGA) (BLYP and mPWPW91) and HDFT methods (B3 LYP, mPW1PW91, and MPW1K) is tested—for geometries and atomic charges—against a set of small molecules. The following quantities are tested: 1) the C–C stretch potential in ethane, 2) the torsional barrier for internal rotation around the central C–C bond in n-butane, 3) proton affinities for a set of alcohols, amines, thiols, and acids, 4) the conformational energies of alanine dipeptide, and 5) the barrier height of the hydrogenatom transfer between n-C4H10 and n-C4H9, where the reaction center is described at the MPW1K/6–31G(d) level of theory.
Keywords: density functional calculations, molecular mechanics, molecular modeling, quantum mechanics, theoretical chemistry
1. Introduction
Combined quantum mechanical and molecular mechanical (QM/MM) methods have developed over the last decade into a standard tool in the repertoire of approaches available to study chemical reactivity in large systems. Many QM/MM formalisms have been proposed, primarily differing in their treatment of the QM/MM boundary.[1–36] A particularly appealing approach is the generalized hybrid-orbital (GHO) method,[31–35] which is similar to an earlier method based on strictly localized bond orbitals[5, 7, 24] and a later method based on frozen orbitals.[13, 20] The GHO method was initially[31–33] proposed for semiempirical calculations based on neglect of diatomic differential overlap (NDDO), and we have recently extended[34] it to the ab initio Hartree–Fock (GHO-AIHF) level. In the GHO-AIHF extension, we have shown how the GHO algorithm may be implemented without the NDDO approximation; this required explicit orthogonalization of the auxiliary GHO orbitals. A limitation of the GHO-AIHF theory is that it does not include electron-correlation effects in the QM part of the system. We also developed the GHO method to combine self-consistent charge density functional tight-binding (SCC-DFTB) theory with molecular mechanics (GHO-SCC-DFTB/MM).[35] Although the GHO-SCC-DFTB/MM method is very appealing in terms of its computational efficiency, electron correlation is approximated in a semiempirical fashion by fitting against density functional theory results. Furthermore overlap is included in SCC-DFTB. To provide more reliable results, it is desirable to employ GHO with a more accurate treatment of electron correlation. Among various possible QM choices for QM/MM calculations, the use of density functional theory[37] in the generalized gradient approximation[38] (denoted as GGA or simply as DFT) or hybrid density functional theory[38] (HDFT) for the QM part of the system has been shown to be particularly powerful and promising.[1, 14, 17, 18, 20, 22, 38–52] The aim herein is to use the GHO approach to provide a smooth connection between an MM subsystem and a QM subsystem that is described by (H)DFT.
QM/MM methods are useful for a wide variety of large- and multiscale applications, and they have been especially useful for molecular dynamics simulations of solvent effects,[21, 28, 53, 54] enzyme reactions,[19, 55–61] and solid-state catalysts.[15, 22, 61, 62]
This Article is arranged as follows: In Section 2, we give a brief review of theory and formulate the GHO-(H)DFT/MM method. Section 3 describes the software in which the GHO-(H)DFT/MM method is implemented. Validations of the proposed method and related discussion are presented in Section 4. Section 5 contains concluding remarks.
2. Theory
Our presentation of the GHO-(H)DFT method is organized in the following way: First, in Section 2.1, we sketch some general aspects of (H)DFT and introduce the particular density functionals used herein. Then, the modifications of the GHO method that are required for combining (H)DFT with molecular mechanics are described in Section 2.2. The GHO-(H)DFT analytical gradient expressions are derived in Section 2.3. In addition, we present a special self-consistent-field (SCF) convergence-acceleration procedure that is particularly useful for GHO-type wavefunctions in Section 2.4. Finally, Section 2.5 gives a prescription for parameterization of the method.
2.1. DFT and HDFT
Density functional theory[37, 63–69] has provided a powerful tool for calculating the structure and energetics of chemical systems. Density functional theory includes electron-correlation effects in a convenient way, and the method would be exact if the exact exchange-correlation functionals were known.[63]
Hybrid density functional theory (HDFT),[38, 70–76] also called the adiabatic connection method, replaces a certain fraction of the DFT exchange with the Hartree–Fock (HF) exchange. The mixing of HF exchange and DFT exchange is equivalent to integrating over a coupling parameter, which describes the extent of electron correlation in the system.[70] If one uses a two-point quadrature, the integration can be approximated by an average of two extreme cases, that is, 100% HF exchange without any correlation, and 100% DFT exchange correlation; the latter is called the generalized gradient approximation (GGA). It is well-known that GGA methods tend to underestimate reaction-barrier heights and overestimate binding energies.[73] Increasing the percentage of HF exchange provides a more realistic description of barrier heights.[73] Generally, the HDFT exchange (X) correlation (C) energy is written as [Eq. (1)]:
| (1) |
where x is the percentage of HF exchange (for GGA DFT, x = 0). In particular, for the three-parameter hybrid density functional B3LYP,[70, 71] the exchange-correlation energy is expressed as [Eq. (2)]:
| (2) |
where A, B, and C are empirical parameters. Although the VWN5[64] local correlation functional was used in the original three-parameter HDFT paper,[70] the popular electronic structure packages, such as Gaussian, implemented B3LYP with the VWN3[64] correlation functional.[71] To make our results comparable to most studies in the literature, we use the VWN3 correlation functional throughout our calculations. The other three DFT methods we are testing herein are based on the modified Perdew–Wang exchange[72] (mPW) and the Perdew–Wang correlation functional[67, 68] (PW91). Without including HF exchange, the GGA method combining mPW exchange and PW91 correlation is called mPWPW91.[72] The corresponding HDFT method with 20% HF exchange is called mPW1PW91.[72] Based on mPW1PW91, a method called MPW1K[73] has been developed for kinetics, in which the percentage of HF exchange was optimized to 42.8% to give accurate barrier heights for a set of hydrogen-transfer reactions in the gas phase.
2.2. GHO-(H)DFT/MM
Although the GHO-(H)DFT algorithm is similar in many aspects to what has been developed for GHO-AIHF, there are still a number of significant changes that need to be made to accommodate the GHO approach to (H)DFT. Therefore, we present the proposed GHO-(H)DFT method in a self-contained way. We will make the presentation for a QM/MM boundary that cuts only one bond, although the extension to more than one bond is straightforward.[34, 35]
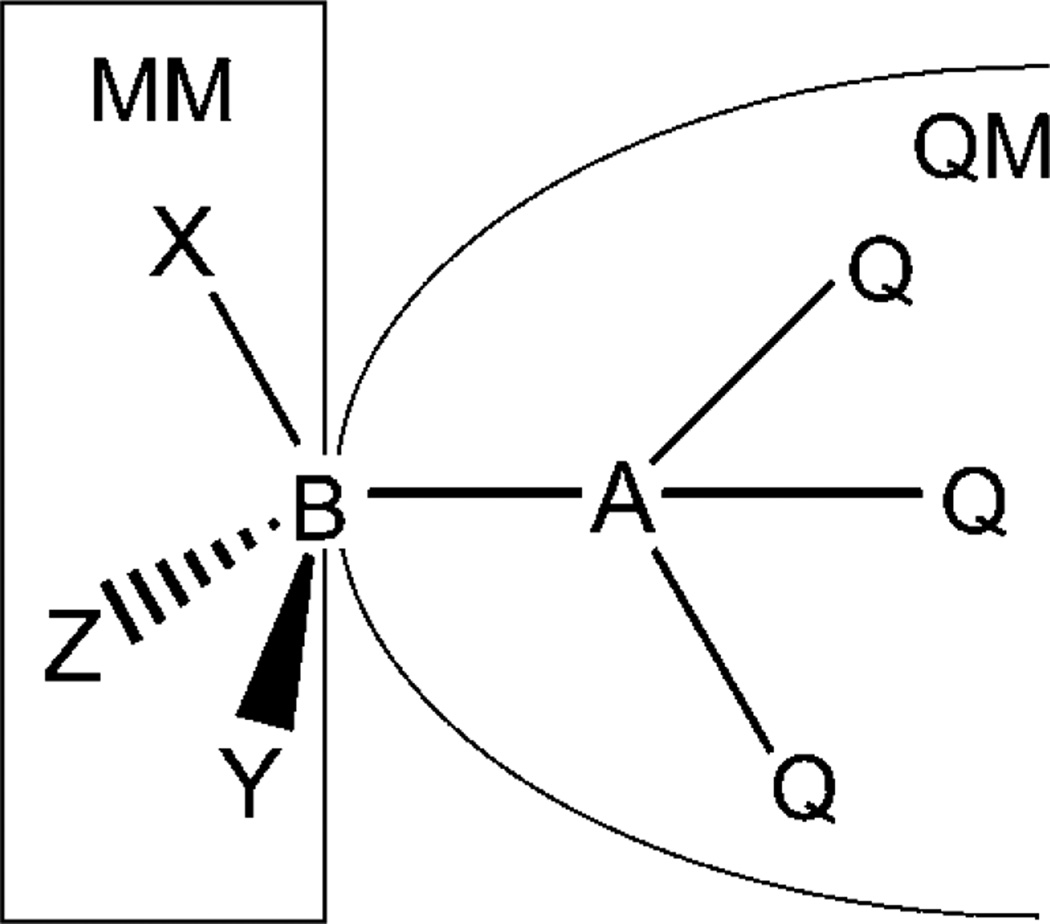
The bond cut by the QM/MM division is a covalent C–C bond between an sp3 carbon on the MM side and another carbon without restriction of its hybridization state on the QM side. The carbon on the MM side is called the GHO boundary atom and is denoted by the symbol B. The other carbon atom present in this QM/MM boundary bond is called the QM frontier atom and is denoted by the symbol A to distinguish it from other QM atoms that are not directly bonded to the GHO boundary atom B. The schematic QM/MM partition is shown in Figure 1, where the three MM atoms directly bonded to the GHO boundary atom B are labeled as X, Y, and Z, respectively. As we can see in Figure 1, the GHO boundary atom is placed at the connection point of the QM region and the MM region. The QM subsystem contains the GHO boundary atom B, the QM frontier atom A, and other fragments that are bonded to A, plus, optionally, some nonbonded solvent molecules. QM atoms other than B are called fully QM atoms since their electronic structure is treated fully by quantum mechanics. As a consequence, the MM subsystem consists of the remaining molecular fragments connected to the GHO boundary atom B on the other side of the A–B bond plus any solvent not included in the QM subsystem.
Figure 1.
Schematic representation of the QM/MM partition in the GHO method.
Following the GHO algorithm we developed for combining ab initio HF wavefunctions with molecular mechanics (GHO-AIHF/MM),[34] we use a minimal set of valence basis functions, denoted by STO-3Gv, to represent the GHO boundary carbon atom (the STO-3Gv basis is the valence subset of the standard[77, 78] STO-3G basis set). Based on these valence s and p atomic basis functions {s, px, py, pz}, a set of orthonormal hybrid basis functions {ηB, ηx, ηy, ηz} can be constructed via a 4 × 4 basis transformation matrix Tb [Eq. (3)] associated with a generalized hybridization procedure, which has been defined elsewhere:[32]
| (3) |
As a consequence of this hybridization, one of the resulting hybrid basis functions will approximately point towards the QM frontier atom A. This hybrid basis function therefore has a significant overlap with the orbitals on A to form the QM/MM boundary bond, and is called the active hybrid orbital, ηB. The other three hybrid orbitals {ηx, ηy, ηz} are called auxiliary hybrid orbitals and are orthogonal to ηB, as well as to each other:
| (4) |
For the fully QM atoms, we retain the flexibility of using various basis sets. If there are N basis functions, denoted by χu (u = 1, 2,…, N), on fully QM atoms, then the entire QM subsystem will be described by N + 4 basis functions. If we treat all these basis functions on an equal footing, the transformation from the atomic orbital (AO) basis to the hybrid (H) basis can be written as an (N + 4) × (N + 4) transformation matrix T [Eq. (5)]:
| (5) |
where IN is an N × N unit matrix, since the AO basis functions on fully QM atoms are not subjected to the hybridization.
In the Kohn–Sham formulation of DFT, as well as the HDFT generalizations, the total electron density ρ to evaluate the exchange-correlation energy is self-consistently represented by a set of one-electron orbitals called Kohn–Sham orbitals (KSOs)[37] and is determined by self-consistent-field (SCF) equations. The KSOs in GHO-(H)DFT fall into two categories: the active ones and the auxiliary ones. The active KSOs φi (i = 1, 2,…, N + 1) are expanded over an (N + 1)-dimensional active space consisting of the basis functions χu (u = 1, 2,…, N) on fully QM atoms plus the active hybrid basis function ηB [Eq. (6)]:
| (6) |
where we use χa (a = 1, 2,…, N + 1) to represent active basis functions and therefore χN + 1 = ηB. These N + 1 active KSOs (including both occupied and virtual ones) are determined by the SCF equations. The remaining three KSOs are called auxiliary KSOs since each of them is simply composed of an individual auxiliary hybrid basis function; these orbitals are frozen during the SCF process [Eq. (7)]:
| (7) |
Each frozen auxiliary KSO is provided with a frozen electron density to mimic the effective charge distribution in bonds formed by atom B and one of its MM neighbors X, Y, or Z. It is worthwhile to point out that these auxiliary densities in the auxiliary KSOs have to be consistently incorporated into the total GHO-(H)DFT electron density, ρ [Eq. (8)]:
| (8) |
where nocc is the electron occupation number for each Kohn–Sham orbital, and for a closed-shell QM subsystem [Eq. (9)]:
| (9) |
where qB denotes the MM point charge on B. This occupation corresponds to an even partition of the MM point charge of B over its three auxiliary orbitals. In the present Article, the CHARMM22 force field is used,[79] and two particular cases are involved in the test molecules, namely where B is a methyl carbon and where it is a methylene carbon, in which cases qB equals −0.27 or −0.18 atomic charge units, respectively, corresponding to occupation numbers of 1.09 and 1.06, respectively. Furthermore, when gradient-corrected functionals[65–76] are used, the gradient contributions due to GHO auxiliary densities should also be included in the density gradient.
In the rest of Section 2.2, as is common in the field, we will use DFT to denote both the GGA and HDFT. The QM/MM total energy is expressed as the sum of the DFT energy, the MM energy, and the DFT/MM interaction energy [Eq. (10)]:
| (10) |
Here EMM denotes the energy for the MM subsystem, and EDFT represents the DFT energy for the QM subsystem. In DFT based on the Kohn–Sham approach, the DFT energy is evaluated as [Eq. (11)]:
| (11) |
where the argument of EXC includes not only the density but also the orbitals because, in this Section, we include the possibility that some Hartree–Fock exchange is mixed into the density functional, as in Equations (1) and (2). In Equation (10), EDFT/MM is the DFT/MM interaction energy and is a sum of the electrostatic interactions and the van der Waals interactions, where the former takes the polarization effect of the MM point charges on the QM subsystem into account and the latter includes the van der Waals interactions between QM and MM atoms [Eq. (12)]:
| (12) |
where qM denotes the MM point charge on an MM atom M; Zα is the nuclear charge of a QM atom α; and VαM represents the van der Waals energy between α and M. Note that, as discussed in detail in previous articles,[31–35] the QM and MM subsystems also interact through stretching, bending, and torsion potentials, but the convention used in GHO is to consider that these are part of EMM, even when they involve QM atoms.
The SCF equations are solved, as usual, for a set of orthonormal orbitals. These orbitals, the KSOs, are eigenfunctions of the Fock–Kohn–Sham operator that contains the electronic kinetic energy and the SCF field of the nuclei and other electrons. Since only the active basis functions are used to expand the one-electron orbitals in the SCF equations, the orthonormality condition of the self-consistent orbitals is only satisfied for active Kohn–Sham orbitals. For the auxiliary hybrid orbitals that are frozen, special orthogonalization procedures need to be carried out to ensure the global orthonormality constraint for the orbitals that contribute to Equation (8). For this purpose, four orthogonalization schemes have been proposed and tested.[34] In the GHO-DFT method developed here, we adopt the global Löwdin orthogonalization (GLO) scheme.[34] In the GLO scheme, instead of directly mixing the s and p atomic valence basis to form the hybrid basis functions, one constructs the hybrid basis functions based on a set of pre-orthogonalized atomic orbital (OAOs) basis functions. In particular, we use the Löwdin[80] symmetric orthogonalization procedure to obtain OAOs. Because both the active one-electron QM orbitals and the auxiliary orbitals are now expanded in a single orthonormal set, the mutual orthogonality of these one-electron functions is satisfied. One of the distinguishing features of the Löwdin OAOs is that they maximally resemble the original AOs. Consequently, the resulting orthogonalized hybrid basis functions also maximally resemble the ones formed by a direct hybridization of the original AOs and, therefore, their physical characters are maximally retained after the orthogonalization.
In practice, one can combine the orthogonalization and hybridization into a total transformation matrix T that converts the non-orthogonalized atomic basis into the orthogonalized hybrid (OH) basis [Eqs. (13) and (14)]:
| (13) |
| (14) |
where the AO and OAO basis functions are related by the Löwdin orthogonalization (LO) transformation matrix TLO, and is the (N + 4)-dimensional overlap matrix expressed in the AO basis. Detailed descriptions of the orthogonalization procedure were presented previously.[34]
In the GHO-DFT implementation, the active KSOs are expanded over a reduced dimensional active space that consists of N + 1 active basis functions. The auxiliary hybrid KSOs are kept frozen, but they do contribute to the SCF field for the active KSOs. To accomplish this, we modified the SCF procedure in the following way:
Start with an initial guess of the total density matrix in the AO basis: .
Form the total Fock–Kohn–Sham matrix in the AO basis: .
- Transform the Fock–Kohn–Sham matrix from the AO basis to the orthogonalized hybrid (OH) basis [see Eq. (15)] by applying the total transformation matrix T, as defined in Equation (14):
(15) - Discard the columns and rows corresponding to auxiliary orbitals to form an active Fock matrix with reduced dimensionality [Eq. (16)]:
(16) - Solve the Kohn–Sham equation in the (N + 1)-dimensional active space to obtain a new set of active KSOs by diagonalizing the active Fock–Kohn–Sham matrix in the OH basis [Eq. (17)]:
(17) Form the active density matrix in the OH basis:
Expand the active density matrix, by appending the diagonal auxiliary density Pbb, to form the total density matrix in the OH basis: .
- Transform the density matrix from the OH basis to the AO basis [Eq. (18)]:
(18) Compute the total energy and test for SCF convergence. If not yet converged, go back to step 2.
2.3. GHO-(H)DFT Gradients
To compute the GHO-(H)DFT gradients analytically, a correction term due to the hybridization basis transformation must be incorporated. The final expression of the GHO-(H)DFT gradient is similar to those derived[34] for GHO-AIHF [Eq. (19)]:
| (19) |
where P and W represent the conventional density matrix and energy-weighted density matrix, respectively. The gradient due to the basis transformation on the density matrix and energy-weighted density matrix can be further expanded as [Eqs. (20) and (21)]:
| (20) |
| (21) |
where T is the total transformation matrix [Eq. (14)] carrying out the transformation from the AO basis to the orthogonalized hybrid (OH) basis. The detailed descriptions of the derivatives of the total transformation matrix T have been reported in a previous paper.[34]
2.4. DIIS for GHO-DFT SCF Convergence
It is well known that DFT converges slower than HF in the SCF procedure. We observed a similar trend for GHO-(H)DFT calculations compared to the GHO-AIHF variant. The use of SCF accelerators, such as damping, level shift, and extrapolation, are straightforward, since one can simply apply these techniques for GHO-type wavefunctions in the AO basis. Therefore, no modifications are required for these SCF convergers. However, for many cases, the usefulness of these simple techniques is limited, and one has to use more sophisticate SCF accelerators. The direct inversion of the iterative subspace (DIIS) procedure proposed by Pulay[81, 82] has been shown to be a very powerful way to improve SCF convergence at both the early and late stages of SCF iteration. The DIIS algorithm takes advantage of the fact that the density matrix commutes with the Fock matrix for a converged wavefunction. We note that this identity also holds for the GHO-type wavefunctions, but only for the subspace expanded by the N + 1 active orbitals. In the following, to explain our implementation, we use the closed-shell restricted Hartree–Fock (RHF) case as an example. For each SCF iteration, we form an error matrix by [Eq. (22)]:
| (22) |
where F, D, and S denote the Fock matrix, the density matrix, and the overlap matrix, respectively, represented in the (N + 1)-dimensional orthogonalized hybrid (OH) basis. For a converged GHO-type wavefunction, this error matrix [rather than the error matrix constructed in the (N + 4)-dimensional AO basis] should consist of zeros. The error matrices are used for calculating a set of linear coefficients[81] to extrapolate the Fock–Kohn–Sham matrix [Eq. (23)]:
| (23) |
where cj represents the weight of the Fock matrix of the jth SCF iteration in the extrapolation; denotes the (N + 1)-dimensional Fock matrix in the OH basis obtained at the jth SCF iteration; and is the extrapolated Fock matrix for the current iteration (the kth iteration). Although in Equation (23) the extrapolation is expressed in terms of the (N + 1)-dimensional Fock matrix in the OH basis, it is equivalent to extrapolating the (N + 4)-dimensional total Fock matrix in either the OH basis or the AO basis. Since the latter is more convenient for programming, we employ the extrapolation of the Fock matrix in the AO basis in our implementation [Eq. (24)]:
| (24) |
The performance of this DIIS accelerator is very satisfactory, and it provides significant efficiency improvement of the GHO-(H)DFT and GHO-AIHF methods in QM/MM calculations; for example, without the GHO-DIIS converger, SCF iterations in GHO-(H)DFT usually require more than 50 iterations for small organic systems such as ethane; with the aid of the GHO-DIIS converger, the SCF for these cases requires only about 12 iterations to converge.
2.5. Parameterization
Herein, the QM subsystem is described by the 6–31G(d)[78] valence double-zeta basis set. Without any parameters, the GHO-DFT method generally overestimated the A–B bond distances. This overestimation may be related to the frozen character of the GHO auxiliary orbitals during the optimization of the SCF-optimized wavefunctions, to the use of a minimal valence basis set on the GHO boundary atom, and/or to the unbalanced interaction across the QM/MM boundary. Furthermore, it is possible that the QM/MM geometry does not agree precisely with the QM geometry simply because of the disagreement between the MM and QM models, rather than because of the way in which the QM fragment is joined to the MM fragment. Although there are a variety of possible sources of these errors, we apply a simple scheme to adjust the interaction at the QM/MM boundary to obtain better agreement with the fully QM results. In particular, we apply a set of one-electron integral-scaling factors. These scaling parameters are applied only near the QM/MM boundary to minimize perturbation in the QM subsystem. In the AIHF parameterization[34] we also changed one of the MM terms near the boundary, but here we take a simpler approach of only adjusting one-electron integral-scaling factors.
The scaling is applied only to integrals involving the valence basis functions on the GHO boundary atom or the QM frontier atom (or both). Our experience[34] shows that scaling the kinetic energy integrals is more stable than scaling the potential energy part. We scale the integrals involving different combinations of s and p functions, separately, to add more flexibility. This is helpful because the bond angles may be more sensitive to p functions than to s functions. The final set of integral-scaling parameters consists of seven scaling factors that are optimized against a fitness function combining geometric features and charges. In particular, we use the same fitness function that we used for parameterizing GHO-AIHF/MIDI in our previous study.[34] Our present experience showed that the optimized parameters are largely determined by the basis set rather than by the specific exchange-correlation functionals. Therefore, in the present work, we optimized the scaling factors for GHO-B3LYP/6–31G(d) and applied this set of scaling parameters to other DFT and HDFT functionals as well. These optimized integral-scaling parameters are given in Table 1. The results discussed in Section 4 show that the transferability of this set of scaling parameters from one functional to another is quite satisfactory. We note that different scaling parameters will be required for different basis sets.
Table 1.
Optimized scaling factors for integrals involving boundary orbitals for GHO-B3LYP/6–31G(d) calculations.
| Parameters | Integral type | Optimized value[a] |
|---|---|---|
| c1 | (sA|T|sB) | 0.9976 |
| c2 | (sA|T|pB) | 0.9773 |
| c3 | (pA|T|sB) | 1.0084 |
| c4 | (pA|T|pB) | 0.9756 |
| c5 | (sB|T|sB) | 0.8650 |
| c6 | (pB|T|pB) | 0.9858 |
| c7 | (sB|T|pB) | 0.9543 |
Unlike ref. [34], the equilibrium angles for A–B–M bends are not modified in the present study.
3. Software
The GHO-(H)DFT/MM method for combined QM/MM calculations has been implemented in a modified version of GAMESSPLUS,[83, 84] where the molecular mechanics force field is provided by CHARMM.[85] The installation of the CHARMM/GAMESSPLUS combination as an integrated package[14] is supported by a separate utility package CGPLUS.[86] GAMESSPLUS also contains an implementation for GHO-AIHF. The DIIS SCF convergence accelerator is available in GAMESSPLUS for GHO-type wavefunctions at both the AIHF and (H)DFT levels.
4. Tests and Discussion
4.1. Geometry
The bond distance of the bond cut by the QM/MM boundary has been widely used as an indication of the performance of the QM/MM boundary treatment. The two-center integrals involving orbitals on A and B have a large influence on the predicted A–B bond characteristics and are scaled to make up for deficiencies in the raw GHO approximation. In Table 2, we show the A–B bond distances calculated by GHO-B3LYP/MM for a variety of molecules and ions with different QM functional groups near the boundary and compare them with the fully QM results. Without scaling, the median error in bond lengths is 0.14 Å, but with scaling this is reduced to 0.009 Å. Furthermore, the two largest errors are reduced from 0.21 and 0.18 Å to 0.06 and 0.04 Å, respectively.
Table 2.
Key A–B bond distances [Å] for unparameterized GHO-B3LYP/6–31G(d) and scaled GHO-B3LYP/6–31G(d) compared to the fully QM results.
| System[a] | GHO-B3LYP/6–31G(d) (unparameterized) |
GHO-B3LYP/6–31G(d) (with scaling) |
B3LYP/6–31G(d) |
|---|---|---|---|
| CH3BH2–AH3 | 1.638 | 1.538 | 1.529 |
| CH3BH2–AH2CH3 | 1.665 | 1.551 | 1.530 |
| CH3BH2AH2C(O)OH | 1.657 | 1.530 | 1.529 |
| CH3BH2–AH2NH2 | 1.661 | 1.531 | 1.525 |
| CH3BH2–AH2NH3+ | 1.665 | 1.529 | 1.523 |
| CH3BH2–AH2NH− | 1.677 | 1.566 | 1.536 |
| CH3BH2–AH2OH | 1.652 | 1.537 | 1.518 |
| CH3BH2–AH2O− | 1.703 | 1.597 | 1.557 |
| CH3BH2–AH2SH | 1.656 | 1.543 | 1.528 |
| CH3BH2–AH2S− | 1.662 | 1.551 | 1.532 |
| CH3BH2–AH=CH2 | 1.669 | 1.505 | 1.505 |
| CH3BH2–A(O)NH2 | 1.704 | 1.525 | 1.520 |
| CH3BH2–A(O)OH | 1.705 | 1.536 | 1.507 |
| CH3BH2–A(O)O− | 1.733 | 1.596 | 1.557 |
| CH3BH2–A(O)OCH3 | 1.679 | 1.507 | 1.508 |
| ethyl benzene | 1.716 | 1.461 | 1.504 |
| histidine[b] | 1.670 | 1.440 | 1.500 |
| alanine dipeptide[c] | 1.695 | 1.493 | 1.527 |
The training set molecules are in bold.
B is the methylene carbon and A is the ipso ring carbon.
B is Cα and A is a carbonyl carbon.
The mean unsigned errors (MUEs) of the GHO-B3LYP bond lengths and bond angles near the QM/MM boundary are given in Table 3 for both the unparameterized and parameterized methods. As shown in Table 3, in the method with scaling the MUE of the boundary A–B bond is reduced from 0.156 Å in the unparameterized scheme to 0.019 Å in the parameterized one. We note that scaling does not significantly alter the equilibrium bond lengths of bonds other than A–B near the boundary; for example, bonds of the QM frontier atom with its QM neighbors (Q–A) and bonds of the GHO boundary atom with its MM neighbors (B–M) retain small errors of about 0.01 Å. This is encouraging, since the integral-scaling factors we applied only involved the one- and two-center kinetic energy integral of the basis functions on A and B; therefore, the significantly affected interactions are expected to be those near the QM/MM boundary bond. The parameterized method also gives reasonably good bond angles over the whole test set; the MUEs for the Q–A–B and A–B–M angles are 2.8 and 2.2 °, respectively.
Table 3.
Mean unsigned errors in bond lengths [Å] and bond angles [°] with GHO-B3LYP/6–31G(d).
| System[a] | GHO-B3LYP/6–31G(d) (unparameterized) |
GHO-B3LYP/6–31G(d) (with scaling) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A–B[b] | Q–A[b] | B–M[b] | Q–A–B[c] | A–B–M[c] | A–B | Q–A | B–M | Q–A–B | A–B–M | |
| CH3BH2AH3 | 0.107 | 0.008 | 0.011 | 4.2 | 0.8 | 0.007 | 0.009 | 0.014 | 3.6 | 1.6 |
| CH3BH2AH2CH3 | 0.133 | 0.007 | 0.010 | 2.5 | 1.0 | 0.017 | 0.008 | 0.014 | 3.8 | 1.7 |
| CH3BH2AH2C(O)OH | 0.139 | 0.009 | 0.014 | 3.8 | 0.6 | 0.001 | 0.004 | 0.015 | 5.8 | 1.5 |
| CH3BH2AH2NH2 | 0.136 | 0.007 | 0.011 | 2.2 | 1.2 | 0.003 | 0.003 | 0.015 | 2.0 | 2.7 |
| CH3BH2AH2NH3+ | 0.144 | 0.006 | 0.017 | 2.0 | 0.8 | 0.007 | 0.006 | 0.015 | 2.2 | 3.0 |
| CH3BH2AH2NH− | 0.141 | 0.008 | 0.009 | 2.8 | 2.2 | 0.022 | 0.005 | 0.014 | 3.6 | 3.1 |
| CH3BH2AH2OH | 0.138 | 0.008 | 0.011 | 2.3 | 1.2 | 0.015 | 0.008 | 0.016 | 2.3 | 2.4 |
| CH3BH2AH2O− | 0.148 | 0.011 | 0.008 | 2.2 | 3.0 | 0.021 | 0.008 | 0.013 | 2.5 | 3.8 |
| CH3BH2AH2SH | 0.128 | 0.005 | 0.013 | 2.8 | 1.0 | 0.014 | 0.006 | 0.014 | 2.7 | 1.8 |
| CH3BH2AH2S− | 0.133 | 0.004 | 0.010 | 2.6 | 1.6 | 0.013 | 0.005 | 0.012 | 3.1 | 2.7 |
| CH3BH2AH=CH2 | 0.167 | 0.006 | 0.015 | 1.6 | 1.8 | 0.001 | 0.010 | 0.012 | 2.8 | 2.0 |
| CH3BH2A(O)NH2 | 0.192 | 0.011 | 0.015 | 0.6 | 2.0 | 0.003 | 0.012 | 0.015 | 1.0 | 3.0 |
| CH3BH2A(O)OH | 0.204 | 0.008 | 0.010 | 2.3 | 2.5 | 0.021 | 0.010 | 0.015 | 3.1 | 3.2 |
| CH3BH2A(O)O− | 0.178 | 0.009 | 0.008 | 0.8 | 2.7 | 0.020 | 0.007 | 0.013 | 0.7 | 3.6 |
| CH3BH2A(O)OCH3 | 0.175 | 0.017 | 0.019 | 1.5 | 2.0 | 0.008 | 0.018 | 0.018 | 1.6 | 3.1 |
| ethyl benzene | 0.204 | 0.003 | 0.019 | 0.5 | 2.0 | 0.053 | 0.014 | 0.013 | 1.4 | 2.2 |
| histidine | 0.171 | 0.002 | 0.022 | 1.9 | 2.0 | 0.060 | 0.009 | 0.024 | 6.0 | 3.8 |
| alanine dipeptide | 0.172 | 0.012 | 0.017 | 1.1 | 1.6 | 0.046 | 0.012 | 0.013 | 0.5 | 3.3 |
| training set | 0.150 | 0.008 | 0.012 | 2.6 | 1.5 | 0.012 | 0.009 | 0.014 | 3.1 | 2.2 |
| whole set | 0.156 | 0.008 | 0.013 | 2.1 | 1.7 | 0.019 | 0.009 | 0.014 | 2.8 | 2.2 |
The training set is in bold.
in Å/bond.
in degrees/angle.
In Tables 2 and 3, we have shown the usefulness of scaled integrals to improve the geometric description of the QM/MM boundary region. As mentioned above, we found that the optimal values of these scaling factors are largely basis-set-dependent but are not strongly dependent on the forms of the density functionals. To illustrate this, we carried out GHO calculations based on two other GGA methods, namely BLYP and mPWPW91, and two other HDFT methods, namely mPW1PW91 and MPW1K. Table 4 lists the errors in the GHO geometry for three representative systems calculated by BLYP, mPWPW91, mPW1PW91, and MPW1K, where the QM subsystem is still represented by the 6–31G(d) basis set, and where we use the same integral-scaling parameters (listed in Table 1). The results in Table 4 show that we consistently obtain small errors in the A–B bond distance, as well as reasonable bond angles, which suggests that the optimized scaling factors can be transferred from one functional to another.
Table 4.
Mean unsigned errors in bond lengths [Å] and bond angles [°] calculated by GHO based on BLYP, mPWPW91, mPW1PW91, and MPW1K.
| System | GHO-(H)DFT/6–31G(d)[a] | ||||
|---|---|---|---|---|---|
| A–B[b] | Q–A[b] | B–M[b] | Q–A–B[c] | A–B–M[c] | |
| BLYP | |||||
| CH3BH2AH2NH2 | 0.003 | 0.003 | 0.011 | 2.0 | 2.8 |
| CH3BH2AH2OH | 0.005 | 0.009 | 0.011 | 2.1 | 2.0 |
| CH3BH2A(O)OCH3 | 0.015 | 0.019 | 0.020 | 2.3 | 3.6 |
| mPWPW91 | |||||
| CH3BH2AH2NH2 | 0.013 | 0.005 | 0.012 | 2.3 | 2.1 |
| CH3BH2AH2OH | 0.011 | 0.009 | 0.012 | 1.9 | 2.8 |
| CH3BH2A(O)OCH3 | 0.015 | 0.032 | 0.017 | 1.3 | 3.5 |
| mPW1PW91 | |||||
| CH3BH2AH2NH2 | 0.015 | 0.005 | 0.019 | 2.8 | 2.5 |
| CH3BH2AH2OH | 0.014 | 0.008 | 0.019 | 2.3 | 2.6 |
| CH3BH2A(O)OCH3 | 0.005 | 0.018 | 0.017 | 1.5 | 3.2 |
| MPW1K | |||||
| CH3BH2AH2NH2 | 0.026 | 0.005 | 0.027 | 2.5 | 2.8 |
| CH3BH2AH2OH | 0.021 | 0.008 | 0.027 | 2.3 | 3.0 |
| CH3BH2A(O)OCH3 | 0.000 | 0.017 | 0.025 | 1.3 | 3.7 |
[a] Scaled by the scaling factors (listed in Table 1) optimized for GHO-B3LYP/6–31G(d).
in S/bond.
in degrees/angle.
4.2. Atomic Charges
As we described in Section 2, the GHO-(H)DFT method uses a minimal valence basis set, STO-3Gv, to represent the GHO boundary atom (to simplify the scheme). Section 4.1 showed that the imbalance of the basis set across the QM/MM boundary and the inconsistency of using QM on one side of the boundary and MM on the other are greatly alleviated by scaling of the integrals involving the boundary orbitals. In this Section we consider the quality of the atomic charges derived from population analysis based on the mixed basis set. The atomic charges provide a measure of the relative electronegativity across the A–B bond and of the ability of the GHO boundary atom to withdraw or donate electrons from the fully QM subsystem. We point out that the simple Mulliken population analysis scheme[87] may be inappropriate to reflect the physical charges near the boundary, since the equal partition assumption[87] of the electron density between two basis functions centered on the two atoms is inappropriate when the basis set is unbalanced. Löwdin charges[88] have been shown to be more stable with respect to the size of the basis set. Therefore, we prefer to use Löwdin atomic charges as an indication of the quality of the wavefunctions in the present work. In addition, the Löwdin charges were used in the parameterization of the method (as stated above, the fitting function is the same as in ref. [34]).
We compare the Löwdin atomic charges calculated from GHO-B3LYP with the fully QM results for propane and acetic acid in Tables 5 and 6, respectively. For propane (CH3BH2AH3), the GHO-HDFT method reproduces the QM charges well, and the QM methyl group is neutral within 0.04 charge units indicating that no significant polarization is introduced by the QM/MM boundary treatment. The results for acetic acid [BH3A(O)OH] also show that the GHO-HDFT method gives reasonable charges that are comparable to the fully QM results.
Table 5.
Löwdin atomic charges for propane determined at the GHO-B3LYP/6–31G(d) and the fully QM levels.
| Propane | GHO-B3 LYP (with scaling) |
B3LYP/6–31G(d) |
|---|---|---|
| A | −0.48 | 0.44 |
| H | 0.15 | 0.15 |
| H | 0.15 | 0.15 |
| H | 0.15 | 0.15 |
| B | −0.14 | −0.27 |
| AH3[a] | −0.04 | 0.00 |
[a] The sum of the charges on the quantum mechanical methyl group.
Table 6.
Löwdin atomic charges determined at GHO-B3LYP/6–31G(d) for acetic acid.
| Acetic acid | GHO-B3 LYP (with scaling) |
B3LYP/6–31G(d) |
|---|---|---|
| O(=A) | −0.34 | −0.36 |
| O(−A) | −0.25 | −0.26 |
| H(O) | 0.36 | 0.36 |
| A(=O) | 0.18 | 0.20 |
| B | −0.22 | −0.47 |
| BH3 | 0.05 | 0.06 |
4.3. Stretch Potential
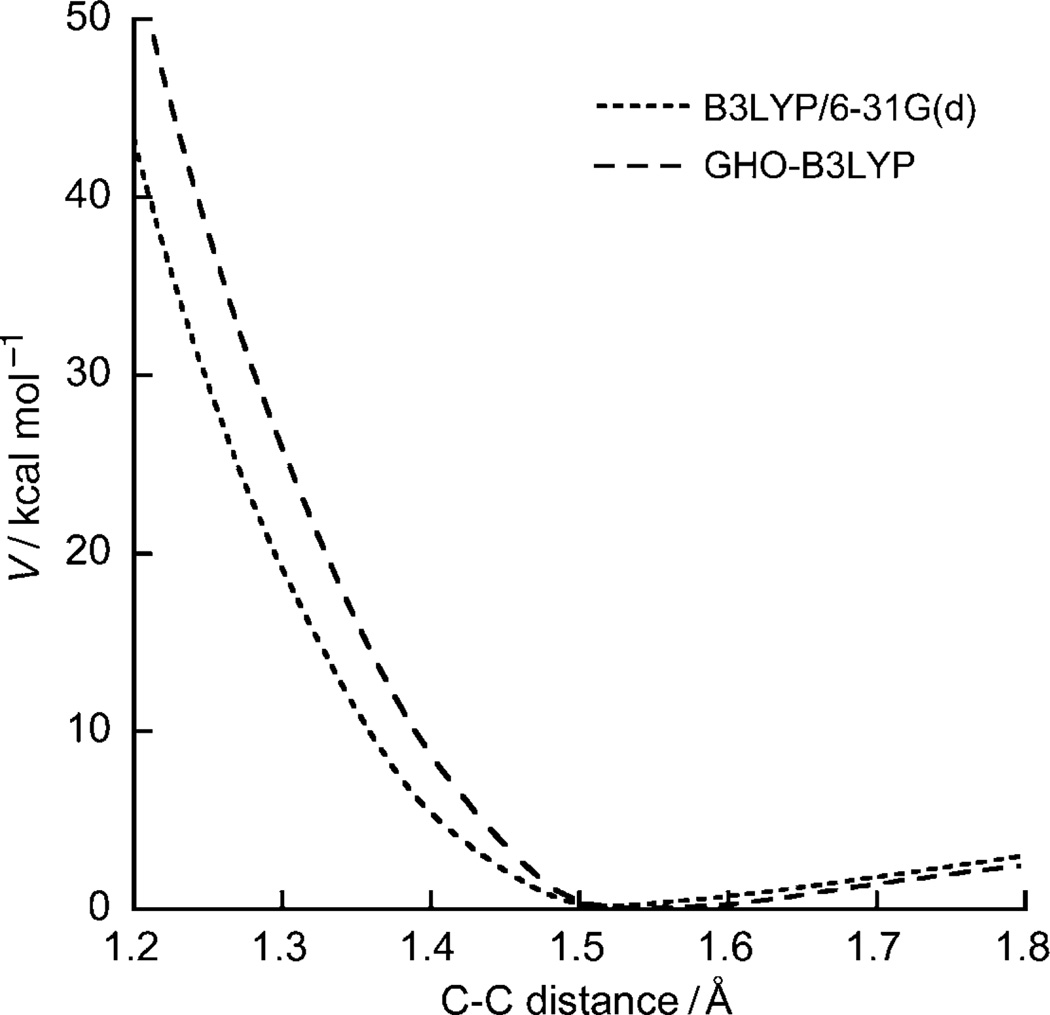
Figure 2 plots the C–C stretching potential curve in ethane, treated by fully QM [B3LYP/6–31G(d)] and QM/MM [GHO-B3LYP/6–31G(d)] methods. Encouragingly, GHO-B3LYP gives very good agreement with full QM over a wide range of C–C distances from 1.20 to 1.80 Å.
Figure 2.
C–C stretching potential in ethane, treated by fully QM [B3LYP/6–31G(d)] and QM/MM [GHO-B3LYP/6–31G(d)].
4.4. Internal Rotational Barrier
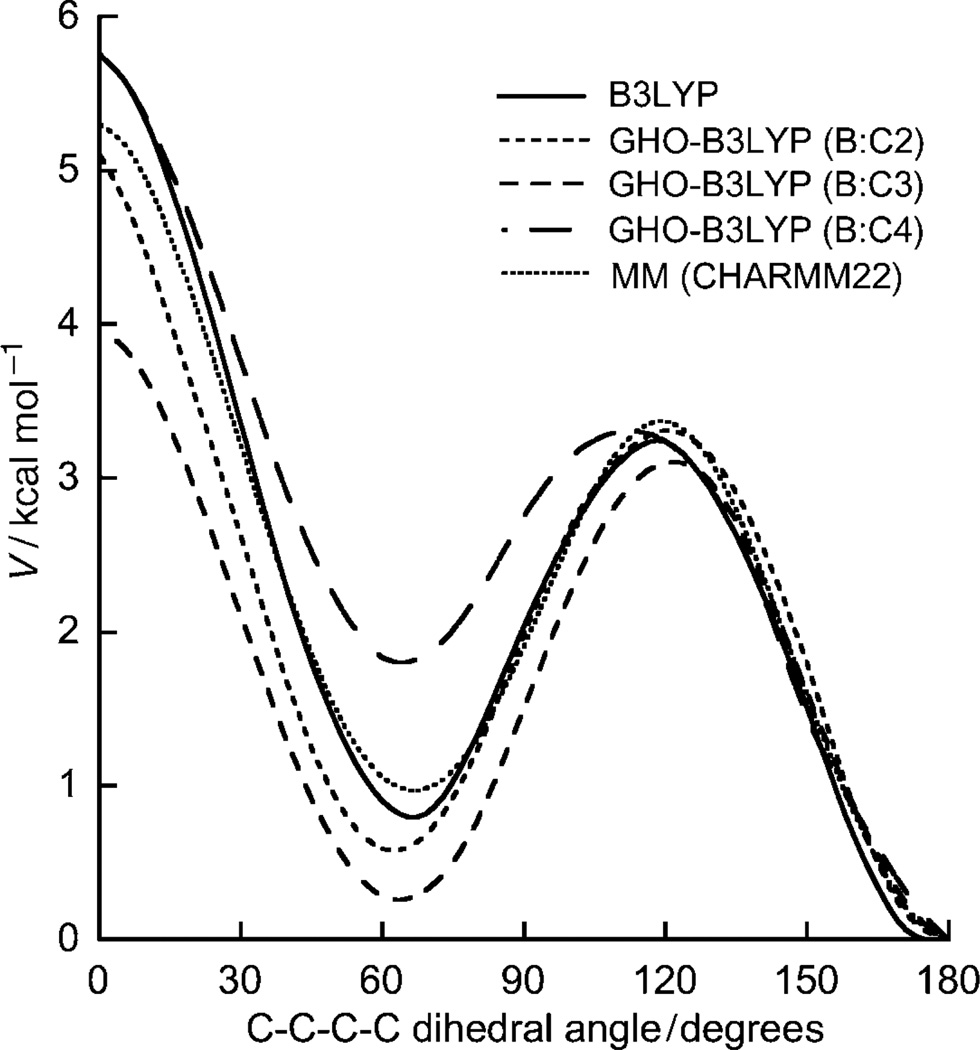
Figure 3 shows the internal rotational barrier around the central C–C bond in n-butane computed by GHO-B3LYP/6–31G(d). In separate calculations, the GHO boundary atom is placed successively at C2, C3, and C4, which corresponds to a change from a small to a large QM subsystem. The fully QM and MM potential curves are also given for comparison. In principle, for the case of the small QM subsystem (with C2 as the GHO boundary), the torsion potential around the central C–C bond (C2–C3) is largely determined by the MM contribution. Similarly, the results of using the large QM subsystem (with C4 as the GHO boundary) are expected to be consistent with the fully QM results. Since the MM rotational profile agrees very well with the fully QM results in this test, the C2 boundary case gives very good agreement with fully QM results. The energy of the second minimum around 60 ° is overestimated in the C4 case. For the intermediate case with C3 as a GHO boundary atom, where both the QM and MM contributions play approximately equal roles in determining the rotational profile in the QM/MM calculation, we obtained a slightly lower barrier height compared to the B3LYP/6–31G(d) calculation; nevertheless the overall shape of the torsion energy profile is still in good agreement with the fully QM results. Since the torsional energies about the frontier bond (A–B) have contributions from both QM and MM terms, the agreement between QM/MM and fully QM results could be further improved by adjusting the MM torsional parameters. However, we found this to be unnecessary in the present GHO-(H)DFT/MM method.
Figure 3.
Potential-energy curve for the internal rotation around the C2–C3 bond in n-butane using parameterized GHO-B3LYP/6–31G(d), pure QM [B3LYP/6–31G(d)], and MM (CHARMM22). For the GHO-B3LYP/6–31G(d) method, three cases are studied in which the GHO boundary atom is placed at C2, C3, and C4.
4.5. Proton Affinity
It is important that the QM/MM calculations faithfully reproduce the fully QM energetics. A stringent test to evaluate the performance of a QM/MM boundary treatment is to monitor the energy difference between systems with different protonation states. Herein, following the usual convention, we define the negative of the energy change from a species X or X− to its protonated state XH+ or XH as the proton affinity. Then, we calculate proton affinities for 15 alcohols, amines, thiols, and acids using GHO-B3LYP/6–31G(d). If parameters are not available for MM internal energy terms across the boundary, where both QM and MM atoms are involved, we consistently employ the parameters available for the corresponding neutral species. The resulting proton affinities are compared with the fully QM results in Table 7. The QM/MM boundary has been placed at various distances from the group, changing its protonation states, as indicated in the first column of Table 7. This test set has previously been used to test the GHO-AIHF[34] and GHO-SCC-DFTB[35] methods. The overall MUE for GHO-B3LYP/MM is 2.1 kcalmol−1 for all 30 cases, as compared to 2.6 kcalmol−1 for GHO-AIHF/MM and 1.7 kcalmol−1 for GHO-SCC-DFTB/MM. Examining the GHO-B3LYP/MM in more detail, we see that for cases where the QM/MM boundary is too close to the protonation center, an MUE as large as 3.1 kcalmol−1 is obtained. The MUE values are greatly reduced to 1.3 and 0.7 kcalmol−1 when the QM/MM boundary is moved two and three bonds away from the reaction center, respectively.
Table 7.
Proton affinities [kcal mol−1], determined by GHO-B3LYP/6–31G(d), compared with the B3LYP/6–31G(d) fully QM results.
| System | GHO-B3LYP/6–31G(d)[a] | B3LYP/6–31G(d) | QM/MM vs. QM |
|---|---|---|---|
| BH3–AH2O− | 401.1 | 399.3 | 2.0 |
| CH3BH2–AH2O− | 402.2 | 398.1 | 3.4 |
| BH3–AH2CH2O− | 399.0 | 398.1 | 1.4 |
| CH3CH2BH2–AH2O− | 401.2 | 397.5 | 3.5 |
| CH3BH2–AH2CH2O− | 399.2 | 397.5 | 2.0 |
| BH3–AH2CH2CH2O− | 397.7 | 397.5 | 0.7 |
| BH3–AH2NH2 | 224.4 | 230.5 | −3.9 |
| CH3BH2–AH2NH2 | 223.9 | 231.8 | −6.0 |
| BH3–AH2CH2NH2 | 228.8 | 231.8 | −1.2 |
| CH3CH2BH2–AH2NH2 | 223.9 | 232.6 | −7.0 |
| CH3BH2–AH2CH2NH2 | 229.1 | 232.6 | −2.2 |
| BH3–AH2CH2CH2NH2 | 231.1 | 232.6 | −0.7 |
| BH3–AH2NH− | 427.3 | 426.4 | 2.6 |
| CH3BH2–AH2NH− | 429.4 | 425.3 | 4.2 |
| BH3–AH2CH2NH− | 425.8 | 425.3 | 1.5 |
| CH3CH2BH2–AH2NH− | 428.1 | 424.8 | 4.2 |
| CH3BH2–AH2CH2NH− | 426.0 | 424.8 | 2.0 |
| BH3–AH2CH2CH2NH− | 425.4 | 424.8 | 0.8 |
| BH3–AH2S− | 366.6 | 367.3 | 1.0 |
| CH3BH2–AH2S− | 366.6 | 366.6 | 1.7 |
| BH3–AH2CH2S− | 367.1 | 366.6 | 0.6 |
| CH3CH2BH2–AH2S− | 366.7 | 366.4 | 1.8 |
| CH3BH2–AH2CH2S− | 367.3 | 366.4 | 0.9 |
| BH3–AH2CH2CH2S− | 366.8 | 366.4 | 0.4 |
| BH3–A(O)O− | 365.4 | 366.4 | −3.0 |
| CH3BH2–A(O)O− | 367.1 | 364.8 | −1.1 |
| BH3–AH2C(O)O− | 363.9 | 364.8 | 0.6 |
| CH3CH2BH2–A(O)O− | 366.1 | 364.2 | −1.2 |
| CH3BH2–AH2C(O)O− | 364.3 | 364.2 | 1.1 |
| BH3–AH2CH2C(O)O− | 365.0 | 364.2 | 1.0 |
Scaled by the scaling factors listed in Table 1.
To test the transferability of the scaling factors, we also performed the same test for GHO calculations with other functionals. Table 8 gives the proton affinities calculated using GHO-BLYP, GHO-mPWPW91, GHO-mPW1PW1, and GHO-MPW1K for three representative systems. In these calculations, the same scaling factors as those optimized for GHO-B3LYP/6–31G(d) are used. Again, the results indicate that the scaling factors are only weakly coupled to the specific form of the density functional.
Table 8.
Proton affinities [kcal mol−1] determined by GHO, based on BLYP, mPWPW91, mPW1PW91, and MPW1K, compared with the corresponding fully QM results.
| System | GHO-(H)DFT/6–31G(d)[a] | (H)DFT/6–31G(d) | QM/MM vs. QM |
|---|---|---|---|
| BLYP | |||
| CH3BH2–AH2CH2O− | 398.8 | 394.4 | 4.3 |
| CH3BH2–AH2CH2S− | 367.8 | 366.5 | 1.2 |
| CH3BH2–AH2C(O)O− | 364.4 | 363.6 | 0.8 |
| mPWPW91 | |||
| CH3BH2–AH2CH2O− | 396.7 | 394.6 | 2.2 |
| CH3BH2–AH2CH2S− | 367.2 | 366.1 | 1.1 |
| CH3BH2–AH2C(O)O− | 364.5 | 363.5 | 0.9 |
| mPW1PW91 | |||
| CH3BH2–AH2CH2O− | 399.3 | 397.7 | 1.6 |
| CH3BH2–AH2CH2S− | 366.9 | 366.0 | 0.8 |
| CH3BH2–AH2C(O)O− | 364.1 | 364.2 | −0.2 |
| MPW1K | |||
| CH3BH2–AH2CH2O− | 401.6 | 400.5 | 1.2 |
| CH3BH2–AH2CH2S− | 0.5 | ||
| CH3BH2–AH2C(O)O− | 364.7 | 364.9 | −0.3 |
Scaled by the scaling factors (listed in Table 1) optimized for GHO-B3LYP/6–31G(d).
4.6. Conformational Energies for Alanine Dipeptide
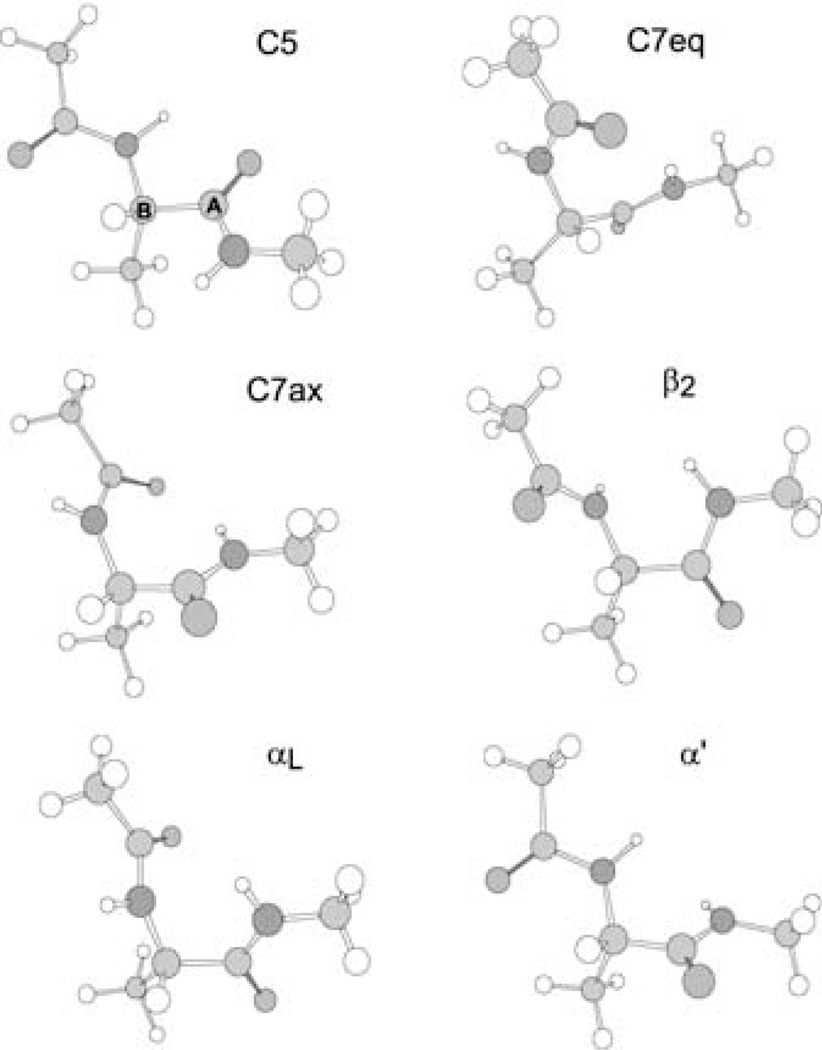
Conformational energies are sensitive to the detailed shape of the potential energy surface. The geometries and relative energies of the conformers of alanine dipeptide and alanine tetra-peptide have been widely used for testing the QM/MM boundary treatment.[12, 27] Herein, we use alanine dipeptide as a test case for the GHO-(H)DFT method. The QM/MM partition is between the Cα carbon and the carbonyl carbon (as illustrated in Figure 4). This partition has been used by Amara and Field[27] in testing their link-atom approach with delocalized Gaussians. It has been shown that this partition is a reasonable choice, although a somewhat larger QM fragment has been used by Philipp and Friesner,[13] where the QM/MM frontier bond is between the N and Cα carbon. Ferre and Olivucci,[89] in contrast, found that another possible boundary location, namely cutting an amide bond, poses great difficulty. The current QM/MM partition is also convenient for the GHO scheme (as we described above), where the Cα carbon (an sp3 hybridized carbon) is selected as the GHO boundary atom, and the QM frontier atom A is a carbonyl carbon atom. Table 9 gives the ϕ and ψ angles[90] for different conformers of alanine dipeptide, optimized by using GHO-B3LYP/6–31G(d), and compares them with the results obtained from fully QM and pure MM (CHARMM) calculations. As was the case at the HF level,[13] the fully quantal B3LYP/6–31G(d) calculation is able to locate six conformers for alanine dipeptide (shown in Figure 4). However, the pure MM CHARMM22 force field can only locate three of the six conformers, namely C5, C7eq, and C7ax. The QM/MM calculation gives an improved description of the torsion energy profile compared to the MM, and one more conformer (α′) can be found using GHO-B3LYP/6–31G(d). These results are consistent with tests carried out by Amara and Field.[27] With the same QM/MM partition, one of their recommended link-atom approaches gave four conformers, and the other located five conformers but failed by identifying C5 as the lowest-energy conformer. The relative energies for conformers of alanine dipeptide optimized by GHO-B3LYP/6–31G(d) are shown in Table 10.
Figure 4.
QM/MM partition of alanine dipeptide. The QM/MM division is placed along the covalent bond between Cα and the carbonyl carbon, where the Cα is selected as the GHO boundary atom (B), and the carbonyl carbon is selected as the QM frontier atom (A).
Table 9.
Torsion angles [°] in conformers of alanine dipeptide.
| GHO-B3LYP/6–31G(d)[a] | B3LYP/6–31G(d) | CHARMM | ||||
|---|---|---|---|---|---|---|
| Conf.[b] | φ | ψ | φ | ψ | φ | ψ |
| C5 | −150.6 | 167.1 | −157.4 | 161.2 | −151.1 | 169.9 |
| C7eq | −78.7 | 75.0 | −83.2 | 76.5 | −81.0 | 70.6 |
| C7ax | 70.2 | −67.3 | 73.4 | −57.4 | 69.4 | −67.5 |
| β2 | C7eq | C7eq | −131.1 | 23.4 | C7eq | C7eq |
| αL | C7ax | C7ax | 70.0 | 27.0 | C7ax | C7ax |
| α′ | −153.8 | −67.9 | −163.8 | −41.9 | C5 | C5 |
With scaling.
Starting conformation for the optimization. If the calculation converges to this conformation, φ and ψ are given. If the calculation converges to a different conformation, that conformation is given.
Table 10.
Conformational energy [kcal mol−1] of alanine dipeptide.[a]
| Conf.[c] | GHO-B3LYP/6–31G(d)[b] | B3LYP/6–31G(d) | CHARMM |
|---|---|---|---|
| C5 | 3.4 | 1.6 | 1.1 |
| C7eq | 0.0 | 0.0 | 0.0 |
| C7ax | 1.7 | 2.7 | 2.1 |
| β2 | C7eq | 3.2 | C7eq |
| αL | C7ax | 5.7 | C7ax |
| α′ | 7.7 | 6.8 | C5 |
Relative to C7eq.
With scaling.
Starting conformation for the optimization. If the calculation converges to this conformation, φ and ψ are given. If the calculation converges to a different conformation, that conformation is given.
4.7. Hydrogen-Transfer Barrier
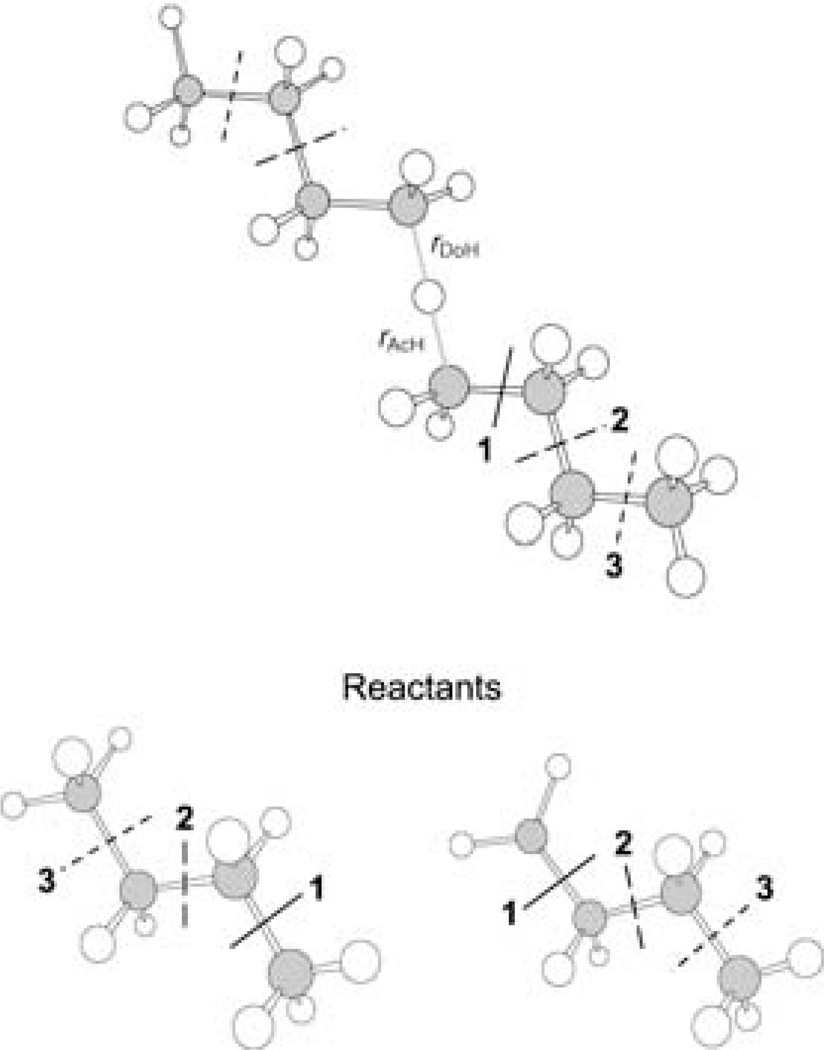
Hydrogen-atom transfer between two radicals is important in combustion,[91, 92] atmospheric chemistry,[93, 94] and enzymes.[95, 96] To validate GHO-DFT/MM, we applied it to the reaction of n-C4H10 with n-C4H9 to model the hydrogen-transfer process between two hydrocarbon radicals. Benchmark results for barrier heights, reaction energies, and transition-state geometries have been reported recently for the reactions CnH2n + 2 + CnH2n + 1 (n = 1–3) based on highly accurate ab initio, extrapolated, and hybrid density functional methods.[97] The target reaction studied here has more atoms and is too large for benchmark-quality quantum mechanical calculations, but it is well-suited for QM/MM studies. To obtain realistic barrier heights, we adopt the MPW1K level of DFT for treating the QM subsystem, and to use the parameterization presented above, we adopt the 6–31G(d) basis set. Three cases of QM/MM partitions are shown in Figure 5, corresponding to small, medium, and large QM subsystems. For each of these cases, two GHO boundary atoms are placed at equal distances from the reactive center in the transition state, and one GHO boundary atom is used in each of the two reactant molecules, as shown in Figure 5.
Figure 5.
The transition- and reactant-state configurations for hydrogen transfer between C4H10 and •C4H9. Three QM/MM division schemes are indicated, corresponding to small, medium, and large QM subsystems.
In the present test—for both reactants and the transition state—we compare zero-point-exclusive barrier heights from fully QM and QM/MM calculations, where, in each case, the transition-state geometry is optimized at the level tested. The symmetric transition-state configuration has the hydrogen atom being transferred between a donor (Do) and an acceptor (Ac) carbon atom, and the breaking and forming bond distances are equal to each other (rAcH = rDoH = 1.341 Å, in the full QM calculation). Transition states optimized at the GHO-MPW1K/6–31G(d) level yield distances for the breaking and forming bonds of 1.352, 1.339, and 1.345 Å, for three QM/MM partitions, which are in good agreement with the fully QM results. The energy difference between the transition state and the reactants was calculated both by MPW1K and GHO-MPW1K, and the results are given in Table 11. When the QM/MM boundary is twinned to the atom being transferred, the difference between the QM and QM/MM barriers is 1.1 kcalmol−1. Although this QM/MM partition is not recommended, this test gives an upper bound on the error of the method when it is pushed to its limit. With the QM/MM boundary shifted two or three bonds away from the reaction centers, the deviations of the GHO-MPW1K and fully QM results are reduced to less than 0.5 kcalmol−1, which is quite satisfactory. These results show that the GHO-DFT treatment can also be used for reaction barriers.
Table 11.
Hydrogen-atom-transfer barrier height for C4H10+•C4H9.
| QM/MM partition[a] | GHO-MPW1K/6–31G(d) | MPW1K/6–31G(d) |
|---|---|---|
| 2 | 17.7 | – |
| 4 | 17.0 | – |
| 6 | 16.4 | – |
| 8 | – | 16.6 |
The value given in the first column is the number of fully quantum-mechanical carbon atoms.
5. Concluding Remarks
We presented a generalized hybrid orbital (GHO) method for using density functional theory (DFT) and hybrid density functional theory (HDFT) in combined QM/MM calculations. The proposed GHO-(H)DFT method is able to provide a smooth connection between the QM and MM subsystems, and the use of (H)DFT for the QM region should be more accurate than using Hartree–Fock, AM1, PM3, or SCC-DFTB.
In our treatment, the GHO boundary atom is represented by a minimal set of valence basis functions. As in the GHO-AIHF algorithm developed previously,[34] orbital orthogonality is satisfied by forming hybrid orbitals from a set of Löwdin symmetrically orthogonalized atomic orbitals (OAOs). A DIIS SCF acceleration procedure is formulated to be compatible with GHO-type wavefunctions. Analytical first derivatives are available for molecular geometry optimizations or molecular dynamics. The method is parameterized by scaling integrals involving the boundary orbitals, and parameters are tested for five different functionals (B3 LYP, BLYP, mPWPW91, mPW1PW91, and MPW1K). The new method is tested for a variety of properties including molecular geometries, atomic charges, rotational barriers, protein affinities, conformational energies, and reaction barrier heights. We concluded that the proposed GHO-(H)DFT method provides an appealing and theoretically robust way to combine (H)DFT with molecular mechanics, and it gives satisfactory results for a variety of applications.
Acknowledgements
This work has been supported, in part, by grant no. CHE03–49 122 from the National Science Foundation and by a grant (GM46736) from the National Institutes of Health.
References
- 1.Gao J. Rev. Comp. Chem. 1996;7:119–185. [Google Scholar]
- 2.Gao J, Thompson M, editors. Combined Quantum Mechanical and Molecular Mechanical Methods: ACS Symp. Ser. Vol. 712. Washington DC: American Chemical Society; 1998. [Google Scholar]
- 3.Singh UC, Kollman PA. J Comput. Chem. 1986;7:718–730. [Google Scholar]
- 4.Field MJ, Bash PA, Karplus M. J Comput. Chem. 1990;11:700–733. [Google Scholar]
- 5.Ferenczy GG, Rivail J-L, Surjan PR, Naray-Szabo G. J Comput. Chem. 1992;13:830–837. [Google Scholar]
- 6.Aaqvist J, Warshel A. Chem. Rev. 1993;93:2523–2544. [Google Scholar]
- 7.Théry V, Rinaldi D, Rivail J-L, Maigret B, Ferenczy GG. J Comput. Chem. 1994;15:269–282. [Google Scholar]
- 8.Bakowies D, Thiel W. J Phys. Chem. 1996;100:10580–10594. [Google Scholar]
- 9.Svensson M, Humbel S, Froese RDJ, Matsubara T, Sieber S, Morokuma K. J Phys. Chem. 1996;100:19357–19363. [Google Scholar]
- 10.Eurenius KP, Chatfield DC, Brooks BR, Hodoscek M. Int. J. Quantum Chem. 1996;60:1189–1200. [Google Scholar]
- 11.Cummins PL, Gready JE. J Comput. Chem. 1997;18:1496–1512. [Google Scholar]
- 12.Zhang Y, Lee T-S, Yang W. J Chem. Phys. 1999;110:46–54. [Google Scholar]
- 13.Philipp DM, Friesner RA. J Comput. Chem. 1999;20:1468–1494. [Google Scholar]
- 14.Lyne PD, Hodoscek M, Karplus M. J Phys. Chem. A. 1999;103:3462–3471. [Google Scholar]
- 15.deVries AH, Sherwood P, Collins SJ, Rigby AM, Rigutto M, Kramer GJ. J Phys. Chem. B. 1999;103:6133–6141. [Google Scholar]
- 16.Antes I, Thiel W. J Phys. Chem. A. 1999;103:9290–9295. [Google Scholar]
- 17.Eichinger M, Tavan P, Hutter J, Parrinello M. J Chem. Phys. 1999;110:10452–10467. [Google Scholar]
- 18.Vreven T, Morokuma K. J Comput. Chem. 2000;21:1419–1432. [Google Scholar]
- 19.Hall RJ, Hindle SA, Burton NA, Hillier IH. J Comput. Chem. 2000;21:1433–1441. [Google Scholar]
- 20.Murphy RB, Philipp DM, Friesner RA. J Comput. Chem. 2000;21:1442–1457. [Google Scholar]
- 21.Mo Y, Gao J. J Comput. Chem. 2000;21:1458–1496. [Google Scholar]
- 22.Sauer J, Sierka M. J Comput. Chem. 2000;21:1470–1493. [Google Scholar]
- 23.Reuter N, Dejaegere A, Maigret B, Karplus M. J Phys. Chem. A. 2000;104:1720–1735. [Google Scholar]
- 24.Ferre N, Assfeld X, Rivail J-L. J Comput. Chem. 2002;23:610–624. doi: 10.1002/jcc.10058. [DOI] [PubMed] [Google Scholar]
- 25.Dilabio G, Hurley MM, Christiansen PA. J Chem. Phys. 2002;116:9578–9584. [Google Scholar]
- 26.Das D, Eurenius KP, Billings EM, Sherwood P, Chatfield DC, Hodoscek M, Brooks BR. J Chem. Phys. 2002;117:10 534–10 547. [Google Scholar]
- 27.Amara P, Field MJ. Theor. Chem. Acc. 2003;109:43–52. [Google Scholar]
- 28.Röhrig UF, Frank I, Hutter J, Laio A, VondeVondele J, Rothlisberger U. ChemPhysChem. 2003;4:1177–1182. doi: 10.1002/cphc.200300650. [DOI] [PubMed] [Google Scholar]
- 29.Kongsted J, Osted A, Mikkelsen KV, Christiansen O. J Phys. Chem. A. 2003;107:2578–2588. [Google Scholar]
- 30.Laio A, Gervasio FL, VondeVondele J, Sulpizi M, Rothlisberger U. J Phys. Chem. B. 2004;108:7963–7968. [Google Scholar]
- 31.Gao J, Amara P, Alhambra C, Field MJ. J Phys. Chem. A. 1998;102:4714–4721. [Google Scholar]
- 32.Amara P, Field MJ, Alhambra C, Gao J. Theor. Chem. Acc. 2000;104:336–343. [Google Scholar]
- 33.Garcia-Viloca M, Gao J. Theor. Chem. Acc. 2004;111:280–286. [Google Scholar]
- 34.Pu J, Gao J, Truhlar DG. J Phys. Chem. A. 2004;108:632–650. [Google Scholar]
- 35.Pu J, Gao J, Truhlar DG. J Phys. Chem. A. 2004;108:5454–5463. [Google Scholar]
- 36.Lin H, Truhlar DG. J Phys. Chem. A. 2005;109:3991–4004. doi: 10.1021/jp0446332. [DOI] [PubMed] [Google Scholar]
- 37.Kohn W, Sham LJ. Phys. Rev. A. 1965;140:1133–1138. [Google Scholar]
- 38.Kohn W, Becke AD, Parr RG. J Phys. Chem. 1996;100:12974–12980. [Google Scholar]
- 39.Stanton RV, Hartsough DS, Merz KM., Jr J Phys. Chem. 1993;97:11 868–11 870. [Google Scholar]
- 40.Wei D, Salahub DR. Chem. Phys. Lett. 1994;224:291–296. [Google Scholar]
- 41.Assfeld X, Rivail J-L. Chem. Phys. Lett. 1996;263:100–106. [Google Scholar]
- 42.Long XP, Nicholas JB, Guest MF, Ornstein RL. J Mol. Struct. 1997;412:121–133. [Google Scholar]
- 43.Eichler U, Kolmel CM, Sauer J. J Comput. Chem. 1997;18:463–477. [Google Scholar]
- 44.Tunon I, Martins-Costa MTC, Millot C, Ruiz-Lopez MF. J Chem. Phys. 1997;106:3633–3642. [Google Scholar]
- 45.Woo TK, Margl PM, Blochl PE, Ziegler T. J Phys. Chem. B. 1997;101:7877–7880. [Google Scholar]
- 46.Barone V, Bencini A, Cossi M, Matteo AD, Mattesini M, Totti F. J Am. Chem. Soc. 1998;120:7069–7078. [Google Scholar]
- 47.Cooper AC, Clot E, Huffman JC, Streib WE, Maseras F, Eisenstein O, Caulton KG. J Am. Chem. Soc. 1999;121:97–106. [Google Scholar]
- 48.Han W-G, Tajkhorshid E, Suhai S. J Biomol. Struct. Dyn. 1999;16:1019–1032. doi: 10.1080/07391102.1999.10508311. [DOI] [PubMed] [Google Scholar]
- 49.Nicoll RM, Hindle SA, MacKenzie G, Hillier IH, Burton NA. Theor. Chem. Acc. 2001;106:105–112. [Google Scholar]
- 50.Decker SA, Cundari TR. J Organomet. Chem. 2001;635:132–141. [Google Scholar]
- 51.Magistrato A, Pregosin PS, Albinati A, Rothlisberger U. Organometallics. 2001;20:4178–4184. [Google Scholar]
- 52.Carbo JJ, Maseras F, Bo C, van Leeuwen PWNM. J Am. Chem. Soc. 2001;123:7630–7637. doi: 10.1021/ja0101678. [DOI] [PubMed] [Google Scholar]
- 53.Gao J. Acc. Chem. Res. 1996;29:298–305. [Google Scholar]
- 54.Walewski L, Bala P, Elstner M, Frauenheim Th, Lesyng B. Chem. Phys. Lett. 2004;397:451–458. [Google Scholar]
- 55.Monard G, Merz KM., Jr Acc. Chem. Res. 1999;32:904–911. [Google Scholar]
- 56.Kollman PA, Kuhn B, Donini O, Perakyla M, Stanton R, Bakowies D. Acc. Chem. Res. 2001;34:72–79. doi: 10.1021/ar000032r. [DOI] [PubMed] [Google Scholar]
- 57.Warshel A. Acc. Chem. Res. 2002;35:385–395. doi: 10.1021/ar010033z. [DOI] [PubMed] [Google Scholar]
- 58.Truhlar DG, Gao J, Alhambra C, Garcia-Viloca M, Corchado J, Sanchez ML, Villa J. Acc. Chem. Res. 2002;35:341–349. doi: 10.1021/ar0100226. [DOI] [PubMed] [Google Scholar]
- 59.Carloni P, Rothlisberger U, Parrinello M. Acc. Chem. Res. 2002;35:455–464. doi: 10.1021/ar010018u. [DOI] [PubMed] [Google Scholar]
- 60.Lin H, Schoeneboom JC, Cohen S, Shaik SS, Thiel W. J Phys. Chem. B. 2004;108:10083–10088. [Google Scholar]
- 61.Sherwood P, de Vries AH, Guest MF, Schreckenbach G, Catlow CRA, French SA, Sokol AA, Bromley ST, Thiel W, Turner AJ, Billeter S, Terstegen F, Thiel S, Kendrick J, Rogers SC, Casci J, Watson M, King F, Karlsen E, Sjøvoll M, Fahim A, Schäfer A, Lennartz C. THEOCHEM. 2003;632:1–28. [Google Scholar]
- 62.Ferré N, Assfeld X. THEOCHEM. 2003;632:83–90. [Google Scholar]
- 63.Hohenberg P, Kohn W. Phys. Rev. B. 1964;136:864–871. [Google Scholar]
- 64.Vosko SH, Wilk L, Nusair M. Can. J. Phys. 1980;58:1200–1211. [Google Scholar]
- 65.Becke AD. J Chem. Phys. 1986;84:4524–4529. [Google Scholar]
- 66.Perdew JP, Wang Y. Phys. Rev. B. 1986;33:8800–8802. doi: 10.1103/physrevb.33.8800. [DOI] [PubMed] [Google Scholar]
- 67.Perdew JP. In: Electronic Structure of Solids ′91. Ziesche P, Eschrig H, editors. Berlin: Akademie Verlag; 1991. pp. 11–20. [Google Scholar]
- 68.Perdew JP, Chevary JA, Vosko SH, Jackson KA, Pederson MR, Singh DJ, Fiolhais C. Phys. Rev. B. 1992;46:6671–6687. doi: 10.1103/physrevb.46.6671. erratum: 1993, 48, 4978. [DOI] [PubMed] [Google Scholar]
- 69.Perdew JP, Burke K, Wang Y. Phys. Rev. B. 1996;54:16533–16539. doi: 10.1103/physrevb.54.16533. erratum: 1998, 57, 14 999. [DOI] [PubMed] [Google Scholar]
- 70.Becke AD. J Chem. Phys. 1993;98:5648–5652. [Google Scholar]
- 71.Stephens PJ, Devlin FJ, Chabalowski CF, Frisch MJ. J Phys. Chem. 1994;98:11623–11627. [Google Scholar]
- 72.Adamo C, Barone V. J Chem. Phys. 1998;108:664–675. [Google Scholar]
- 73.Lynch BJ, Fast PL, Harris M, Truhlar DG. J Phys. Chem. 2000;104:4811–4815. [Google Scholar]
- 74.Adamo C, Barone V. J Chem. Phys. 1999;110:6158–6170. [Google Scholar]
- 75.Zhao Y, Pu J, Lynch BJ, Truhlar DG. Phys. Chem. Chem. Phys. 2004;6:673–676. [Google Scholar]
- 76.Zhao Y, Lynch BJ, Truhlar DG. J Phys. Chem. A. 2004;108:2715–2719. [Google Scholar]
- 77.Hehre WJ, Stewart RF, Pople JA. J Chem. Phys. 1969;51:2657–2664. [Google Scholar]
- 78.Hehre WJ, Radom L, Schleyer PvR, Pople JA. Ab Initio Molecular Orbital Theory. New York: Wiley; 1986. [Google Scholar]
- 79.MacKerell AD, Jr, Bashford D, Bellott M, Dunbrack RL, Jr, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarty D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, III, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. J Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 80.Löwdin PO. Adv. Quantum Chem. 1970;5:185–199. [Google Scholar]
- 81.Pulay P. Chem. Phys. Lett. 1980;73:393–398. [Google Scholar]
- 82.Pulay P. J Comput. Chem. 1982;3:556–560. [Google Scholar]
- 83.Pu J, Thompson JD, Xidos JD, Li J, Zhu T, Hawkins GD, Chuang Y-Y, Fast PL, Rinaldi DL, Gao J, Cramer CJ, Truhlar DG. GAMESSPLUS version 4.4. Minneapolis: University of Minnesota; 2004. based on ref. [84]. [Google Scholar]
- 84.Schmidt MW, Baldridge KK, Boatz JA, Elbert ST, Gordon MS, Jensen JH, Koseki S, Matsunaga N, Nguyen KA, Su S, Windus TL, Dupuis M, Montgomery JA. J Comput. Chem. 1993;14:1347–1363. [Google Scholar]
- 85.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M, editors. Chemistry at Harvard Macromolecular Mechanics computer program, as described. J Comput. Chem. 1983;4:187–217. [Google Scholar]
- 86.Pu J, Gao J, Truhlar DG. CGPLUS version 1.1. Minneapolis: University of Minnesota; 2003. [Google Scholar]
- 87.Mulliken RS. J Chem. Phys. 1995;23:1833–1840. [Google Scholar]
- 88.Baker J. Theor. Chim. Acta. 1985;68:221–229. [Google Scholar]
- 89.Ferré N, Olivucci M. THEOCHEM. 2003;632:71–82. [Google Scholar]
- 90.Ramachandran GN, Ramakrishnan C, Sasisekharan V. J Mol. Biol. 1963;7:95–99. doi: 10.1016/s0022-2836(63)80023-6. [DOI] [PubMed] [Google Scholar]
- 91.Dixon-Lewis G, Williams DJ. Comprehensive Chem. Kinet. 1977;17:1–248. [Google Scholar]
- 92.Warnatz J. In: Combustion Chemistry. Gardiner WC Jr, editor. New York: Springer-Verlag; 1984. pp. 197–360. [Google Scholar]
- 93.Berntsen TK, Isaksen ISA, Fuglestvedt JS. Ber. Bunsenges. Phys. Chem. 1992;96:241–251. [Google Scholar]
- 94.Prinn RG, Weiss RF, Miller BR, Huang J, Alyea FN, Cunnold DM, Fraser PJ, Hartley DE, Simmonds PG. Science. 1995;269:187–192. doi: 10.1126/science.269.5221.187. [DOI] [PubMed] [Google Scholar]
- 95.Nesheim JC, Lipscomb JD. Biochemistry. 1996;35:10 240–10 247. doi: 10.1021/bi960596w. [DOI] [PubMed] [Google Scholar]
- 96.Banerjee R, Truhlar DG, Dybala-Defratyka A, Paneth P. In: Biological Aspects of Hydrogen Transfer. Schowen RL, editor. Weinheim: Wiley-VCH; 2005. in press. [Google Scholar]
- 97.Dybala-Defratyka A, Paneth P, Pu J, Truhlar DG. J Phys. Chem. A. 2004;108:2475–2486. [Google Scholar]