The LES is a global set of patterns that describes correlations between functional traits (e.g. carbon assimilation rate, lifespan) that determine terrestrial resource fluxes. Several classes of models have been proposed to explain the LES, but none have been extensively tested against each other with fine-scale data. Here we assemble a large set of genotypes of Arabidopsis thaliana that show variation in leaf functional traits. We show that no extant theory for the LES is supported, but that some leaf venation networks likely play a role in driving the pattern. Our study provides a roadmap for the measurements that could generate further insight into this fundamental ecological pattern.
Keywords: Arabidopsis, cytoplasm–cell wall partitioning, genotype, leaf economics spectrum, structural equation modelling, vein density, venation network
Abstract
The leaf economics spectrum (LES) describes strong relationships between multiple functional leaf traits that determine resource fluxes in vascular plants. Five models have been proposed to explain these patterns: two based on patterns of structural allocation, two on venation networks and one on resource allocation to cell walls and cell contents. Here we test these models using data for leaf and whole-plant functional traits. We use structural equation modelling applied to multiple ecotypes, recombinant inbred lines, near isogenic lines and vascular patterning mutants of Arabidopsis thaliana that express LES trait variation. We show that a wide variation in multiple functional traits recapitulates the LES at the whole-plant scale. The Wright et al. (2004) model and the Blonder et al. (2013) venation network model cannot be rejected by data, while two simple models and the Shipley et al. (2006) allocation model are rejected. Venation networks remain a key hypothesis for the origin of the LES, but simpler explanations also cannot be ruled out.
Introduction
The leaf economics spectrum (LES) describes correlations between multiple leaf traits, including carbon assimilation rate (Am), leaf lifespan (LL), leaf mass-per-area (LMA) and nitrogen content (Nm) (Wright et al. 2004). These patterns are found globally and across all vascular plant taxa (Reich et al. 1997; Wright et al. 2005). The trait correlations that define the LES describes a gradient of leaf and plant strategies between ‘live fast, die young’ and ‘live slow, die old’ (Wright et al. 2004; Reich 2014). The importance of the LES is clear: it describes an observed variation in plant strategies and highlights strong limitations on terrestrial nutrient fluxes. Moreover, the LES is found at multiple scales including between-species (Wright et al. 2004), within-species (Edwards 2006; Dunbar-Co et al. 2009; Vasseur et al. 2012; Niinemets 2015) and even within-individual plants (Blonder et al. 2013).
Recently, several physiological models for the mechanistic origin of the LES have been proposed. Each makes different predictions for the causal relationships and thus correlations between functional traits. However, these models have not been extensively tested against empirical data at the intraspecific scale, which would provide a test of underlying assumptions about physiological mechanisms. Additionally, these models have not been assessed in a genetic context, which can provide insights into the evolutionary mechanisms and genes [e.g. natural selection or genetic constraints (Donovan et al. 2011)] that generate the LES. We describe these models below.
Wright et al. (2004) model
In their original paper on the LES, Wright et al. (2004) proposed that patterns of trait covariation were due to several independent drivers. Following the interpretation of Shipley et al. (2006), high per-mass photosynthetic rates should be associated with large nitrogen investment or low carbon investment due to allocation trade-offs, resulting in Nm causing Am as well as an undetermined covariance between Nm and LMA. High photosynthetic rates may also be associated with low LL, because at the whole-plant scale, non-optimal resource use could arise if high-performance leaves lived long enough to experience self-shading from canopy growth: thus high Am should cause low LL (Ackerly and Bazzaz 1995). Additionally, long LL requires tougher construction that is associated with high LMA, resulting in LMA causing LL. This formulation of the Wright et al. model was rejected by Shipley et al. (2006), but it has not been tested at the intraspecific scale.
Meziane and Shipley (2001) model
An earlier model of Meziane and Shipley (2001) used similar logic to derive a slightly different set of predictions. Here, leaf mass is assumed to be primarily allocated to the cell wall, with a smaller allocation to the cytoplasm. Because most nitrogen is in the cytoplasm, higher LMA should displace cytoplasm volume and thus cause lower Nm. Additionally, higher LMA should be associated with thicker leaves and thus lower per-mass photosynthesis, resulting in LMA causing Am. As in the previous model, nitrogen is assumed to limit photosynthesis, such that Nm causes Am. Leaf lifespan can be added to the model in the same way as in the Wright et al. (2004) model.
Shipley et al. (2006) model
Shipley et al. (2006) applied exploratory methods of causal analysis to the original data of Wright et al. (2004) and found that the patterns of trait covariation could only be generated by an unmeasured (‘latent’) variable. They subsequently showed (their Fig. 3) that the patterns of covariation in the full LES data were consistent with a model in which each of Am, LL, LMA and Nm was caused by this single unmeasured variable, plus a direct effect from Am to LL, as implied by Kikuzawa's (1995) carbon gain optimization theory. Shipley et al. (2006) proposed a biological hypothesis that identified this unmeasured variable as the ratio of the volume of the leaf occupied by cytoplasm, Vc, to the volume occupied by cell walls, Vw. Metabolic activity (photosynthesis, respiration) and nitrogen (a key element in these metabolic activities) should scale with the volume of cytoplasm because these processes primarily occur in the cytoplasm. Leaf dry mass should scale with the volume occupied by cell walls, because dry mass occurs mostly in cell walls. Therefore, the mass-based metabolic processes involved in the LES should scale positively with the ratio of Vc to Vw (i.e. more metabolic activity per dry mass) while LMA and leaf construction costs (and thus leaf lifetime) should scale negatively with this ratio. While Vc/Vw is a difficult trait to measure, it should be negatively correlated with easily measured traits such as the ratio of leaf water to leaf dry mass or leaf dry matter content (LDMC), the ratio of leaf dry mass to fresh mass (dimensionless) (Shipley et al. 2006). Thus, the cell wall/cytoplasm allocation model predicts that higher values of a latent variable should be associated with lower LDMC, higher Am, lower LL, lower LMA and higher Nm, in addition to the negative relationship between Am and LL. Using 80 species for which LDMC and LES trait data were available, Shipley et al. (2006) found preliminary support for this latent variable model.
Blonder et al. (2011) model
Leaf functioning is closely linked to leaf hydraulics and the venation network (Brodribb et al. 2010; Sack and Scoffoni 2013). Leaf veins provide multiple functions (e.g. water transport, carbon transport, mechanical support and defense against herbivory). Blonder et al. (2011) emphasized a constrained spectrum of leaf trait combinations that are ultimately linked to the geometry of the leaf venation network. In their model, a key venation trait is vein density (VD; mm mm−2); i.e. the total length of veins per unit area of the leaf lamina. According to the Blonder et al. (2011) model, higher VD increases water transport capacity (i.e. transpiration rate) (Brodribb et al. 2007), leading to increased maximum stomatal conductance and increased maximum rate of carbon assimilation (Am); such high photosynthetic rates then may require higher Nm. Other assumptions about optimizing water flow imply that higher VD would then also decrease leaf thickness (Noblin et al. 2008; Brodribb et al. 2013). Lower leaf thickness can then lead to lower LMA and lower damage resistance (i.e. lower LL), assuming fixed tissue density. Thus, the original venation model predicts that higher VD should be associated with higher Am, lower LL, lower LMA and higher Nm. While empirical studies to test this model have been limited, these predictions were generally supported by empirical measurements across 25 species (Blonder et al. 2011).
Blonder et al. (2013) model
A recent elaboration of the Blonder et al. (2011) model further detailed additional couplings between VD and other leaf traits. Variation in leaf area and thickness, independent of VD, can modulate the LES correlations and, hence, the role of venation networks in the LES (Blonder et al. 2013). Depending on the intraspecific scaling relationships between these variables, the sign of other LES correlations can even change. This work leads us to hypothesize that the hydraulic path length (the characteristic distance for water transport from minor veins to stomata, dependent on both VD and mesophyll thickness) may play a more primary role than VD in shaping the LES because it more closely reflects water transport processes within the leaf (Brodribb et al. 2007; Boyce et al. 2009). Because the hydraulic path length's underlying two variables are relatively difficult to measure simultaneously, this model can be recast in structural equation modelling terms via two variables: an unmeasured (‘latent’) variable and VD. A revised venation-associated model thus predicts that higher values of a latent variable should cause higher VD, higher Am, lower LL, lower LMA and higher Nm.
Here we test each of these models for the LES by focusing on how well the physiological trade-offs predicted by each model apply across genotypes within the model species Arabidopsis thaliana. Our study uses phenotypic variation in A. thaliana, using multiple recombinant inbred lines (RILs), several wild-type accessions that span broad climatic gradients, as well as mutants at specific loci relevant to the LES. Previous studies have shown that a large fraction of the global variation in LES traits is expressed across these RILs (Vasseur et al. 2012). The set of mutants was chosen to evaluate the impact on the LES of a loss of function in the molecular pathway controlling a physiological process known, or hypothesized, to be associated with LES variation. Our experimental approach allows us to utilize the genomic resources available for this model species in order to assess the genotype–phenotype implications of each model as well as their predictions.
We test these models using two approaches. First, each of these models predicts specific (and differing) causal structures that are reflected in observed patterns of correlation and partial correlation between variables. We use structural equation modelling to determine whether each model could be rejected based on its causal structure and the observed data. Second, we can build on previous genetic studies to directly manipulate the genes hypothesized to underlie variation in the LES, and so determine whether such manipulations are consistent with hypotheses for leaf physiology. Because the LES implies strong limitations for leaf-level nutrient fluxes, it is also associated with important variations on whole-plant growth strategy (Freschet et al. 2010; Reich 2014). Recently, Vasseur et al. (2012) identified a small set of pleiotropic genes at two A. thaliana loci (EDI and FLG) that are involved in the variation of multiple functional traits related to the economy of carbon and nitrogen at the leaf and whole-plant level. These findings provide a set of mechanistic linkages between genes, physiology and trait correlations.
We apply both of the above approaches to assess the origin of the LES using multiple genotypes of the model plant A. thaliana. We assembled a dataset of 31 genotypes, including (i) five ecotypes with geographic ranges in the Northern hemisphere, (ii) 16 RILs generated by crossing two ecotypes from contrasting environments, (iii) five near isogenic lines (NILs) varying from wild-type only at loci previously identified to control LES variation and (iv) five knockout mutants, of which three have loss of function in candidate genes found within the above loci and two have reduced auxin sensitivity, causing vascular patterning defects. These genotypes have been extensively studied via molecular and phenotyping approaches (El-Assal et al. 2001; Doyle et al. 2005; Keurentjes et al. 2007; Fu et al. 2009; Vasseur et al. 2012) and now provide a wide range of phenotypes with known genetic causes. We grew replicates of each genotype under controlled environmental conditions and used a high-throughput phenotyping system (Granier et al. 2006) to study variations in functional traits (Am, measured at the rosette level; LL, measured at the rosette level by flowering time; LMA, measured at the rosette level; Nm; measured at the rosette level) as well as two possible predictor traits (VD, measured at the leaf level; and LDMC, measured at the rosette level). This study of functional covariation effectively extends the LES to the whole-plant scale (Vasseur et al. 2012).
Methods
Plant material
We selected five A. thaliana ecotypes originating in multiple environments (Col-0 and Col-4, originating in Germany; Cvi-0, originating in the Cape Verde Islands; Ler-0, Ler-2, from irradiated seeds originating in Poland). We also selected a subset of 16 contrasting RILs from a Ler × Cvi population (Alonso-Blanco et al. 1998). The phenotypes of these RILs cover the range of leaf trait values previously observed for a larger set of RILs from the same population (Vasseur et al. 2012). We also selected five NILs developed by introgressing Cvi regions into Ler background (Keurentjes et al. 2007) in order to assess the EDI and FLG loci, which are known to have multiple pleiotropic effects on the LES (Vasseur et al. 2012). Near isogenic lines 1–2.13, 1–2.5 and 1–3 carry introgressions of chromosome 1 associated with the EDI locus. Near isogenic lines 5–7 and 5–8 carry introgressions of chromosome 5 associated with the FLG locus. We also selected three knockout mutants for two candidates genes [CRY2, encoding a blue-light receptor involved in circadian regulation and reproductive transition (El-Assal et al. 2001), and HUA2, a repressor of floral transition (Doyle et al. 2005) known to be implicated in the EDI and FLG loci (Doyle et al. 2005)]. Mutants cry2-1 (Col-4 background) and fha-1 (Ler-0 background—http://arabidopsis.info/StockInfo?NASC_id=108) describe loss of function in CRY2, while mutant hua2-4 describe loss of function in HUA2 (Col-0 background). Finally, we also selected two knockout mutants for the AXR1 gene that confers resistance to auxin, a hormone involved in leaf vascular patterning (Alonso-Peral et al. 2006; Scarpella et al. 2010). Mutants axr1-3 and axr-12 (both Col-0 background—http://arabidopsis.info/StockInfo?NASC_id=3075, http://arabidopsis.info/StockInfo?NASC_id=3076) are associated with incomplete leaf vascular development and lower VD.
Growth conditions
We used the PHENOPSIS automated growth chamber facility (Granier et al. 2006; Fabre et al. 2011) to grow and phenotype the plants (Fig. 1A). This facility can maintain constant environmental conditions and take zenithal photographs of the plants. Briefly, plants were watered daily, with conditions standardized at 20 °C temperature and a 12 h light (200 µmol m−2 s−1)/12 h dark illumination cycle. For this study, we grew a total of 199 plants (n = 7.0 ± 2.2 s.d. per mutant, 6.4 ± 0.5 per NIL, 5.4 ± 0.7 per RIL and 9.0 ± 2.9 per ecotype). A full description of growth conditions can be found in Appendix 1 of Vasseur et al. (2012).
Figure 1.

(A) We use the PHENOPSIS automated phenotyping platform to grow many plants under tightly controlled conditions. Within these genotypes, venation network geometry is highly variable. Shown are two RILs from the Ler × Cvi cross: (B) with VD = 3.2 mm−1; (C) with VD = 1.9 mm−1. Full width for both images, 3 mm.
Trait measurements
All traits were collected at first flowering after removing flowering stems from the rosette. Leaf metabolism and hydraulic properties change dramatically during leaf development, leading to a transition from sink to source organ that varies between genotypes and among environmental conditions (Pantin et al. 2011). When possible, we measured leaf traits; otherwise, we measured whole-plant traits. Leaf traits were measured on fully expanded leaves to avoid trait variation due to source/sink differences among genotypes with different developmental trajectories. However, whole-plant traits may be influenced by source/sink differences among genotypes with different developmental trajectories (Pantin et al. 2011).
To measure whole-plant photosynthesis, we used a whole-plant chamber designed for A. thaliana and connected to an infrared gas analyzer (CIRAS 2; PP Systems, Amesbury, MA, USA). Before making measurements, we sealed the surface of the soil with plastic film to eliminate carbon fluxes from soil respiration. Am (nmol g−1 s−1) was determined at the time of flowering as the whole-plant rate divided by the total mass of leaf blades, under ambient light and CO2 levels. Our whole-plant metric of Am has several benefits. First, this metric is tractable to measure given the very small area of some genotypes’ leaves. Second, this metric is taken at a standardized developmental time-point for the whole plant, and leaf traits are often strongly correlated with whole-plant traits (Freschet et al. 2010), representing broader trade-offs at the whole-plant scale (Grime 1977).
Time to flowering is a key trait in annual species because longer flowering time is associated with bigger, thicker and older leaves. Senescence generally occurs shortly after flowering, so there are strong correlations between LL, whole-plant lifespan and age at flowering [see, for instance, the Supplemental Material of Vasseur et al. (2012)]. To estimate the whole-plant life-history cost of the variations in LES strategies, we measured LL (in day) using flowering time as a genetically determined proxy (Salomé et al. 2011). We also calculate LMA and other traits at the whole-plant level. We first harvested and weighed each rosette at flowering to get total leaf (blades + petioles) fresh mass. We then wrapped the rosette in moist paper and kept it at 4 °C overnight to fully rehydrate the leaves. The oldest non-senescing and fully expanded leaf was then stored in a vial at −80 °C to be later measured for VD. For all remaining leaves, the total leaf area was obtained by separating the blades from the petioles of all leaves, and digitally scanning each leaf. Blades and petioles were then dried at 65 °C for 72 h and weighed separately to determine total blade and total petiole dry mass. Leaf dry matter content (mg mg−1) was calculated as total leaf dry mass divided by total leaf fresh mass (blades + petioles). Leaf mass-per-area (g m−2) was then determined as the total blade dry mass divided by the total blade area. The range of LMA values we observed for individuals in this herbaceous species (14–69 g m−2) may seem high. However, our range of LMA values is similar to the range of values previously published for this species [e.g. 3.2–8.8 g m−2 (Bonser et al. 2010); 13–32 g m−2 (El-Lithy et al. 2010); 14–67 g m−2 (Des Marais et al. 2012; (Vasseur et al. 2012)]. The deviation in our range of LMA values with other studies (e.g. Li et al. 1998) is likely because of the differences in the growth conditions and developmental stage in which LMA was measured. Vein density was measured at leaf scale by a chemical clearing process and subsequent digital imaging and hand-tracing (Fig. 1B and C). Leaves were defrosted and cleared in a solution of 0.5 % safranin in ethanol for 7 days, then rinsed in a series of ethanol, 1 : 1 ethanol : toluene, and toluene before slide-mounting in the toluene-based Permount resin. After curing for 3 days, slides were back-illuminated and imaged using a dissecting microscope (SZX12, Olympus) and digital camera (T2i, Canon). Final image resolution was 195 pixels per millimetre. A contrast-limited adaptive histogram equalization was applied to the red channel of each image to enhance the image quality. Using an image-editing programme (GIMP, GNU), we hand-traced all veins within a section of each leaf. We then calculated leaf section area, and leaf section vein length using a custom programme (MATLAB, MathWorks). Vein density was then calculated as leaf section vein length divided by leaf section area. We hand-traced only a section of each leaf because some leaves did not completely clear or were mechanically torn during the slide-mounting process. We therefore identified one or more polygonal sections of each leaf that was fully cleared, as determined by high vein-lamina image contrast and/or clear evidence of minor veins or freely ending veinlets. We traced a mean sectional area of 52 mm2 (±30 s.d.) per sample, consistent with community guidelines (Pérez-Harguindeguy et al. 2013).
We obtained whole-plant estimates of Nm by measuring at least one individual for every genotype. Nm (g g−1) was determined on all dried leaves pooled together (without petioles) by mass spectrometry (EA20000, Eurovec; Isoprime, Elementar, Cheadle, UK). For some RILs, genotype-mean Nm values were obtained from measurements of the same genotypes grown under identical conditions in Experiment 1 of Vasseur et al. (2012).
Statistical analysis
All analyses were conducted in R (http://www.r-project.org). Standardized major axis regressions were made with the ‘smatr’ package. Power analyses were made with the ‘pwr’ package. Structural equation models were tested with the ‘lavaan’ package.
All structural equation models were built using genotype-mean values. Mean values were then log10-transformed to match the normality assumptions of structural equation modelling. We fit each candidate model using a Wishart likelihood (Wishart 1928), which can compensate for any remaining non-normality in the data. We report lack-of-fit P-values for each model that correspond to a maximum likelihood χ2 statistic.
Data availability
Datasheets and R code to replicate all analyses are available in Supporting Information. Pictures of leaf blades and petioles as well as raw biomass measurements are available at http://bioweb.supagro.inra.fr/phenopsis/ under experiment C3M13B (Fabre et al. 2011). Images of chemically cleared leaves (greyscale) and hand-traced subregions (annotated with yellow for fully cleared regions; with red for veins) are available at http://clearedleavesdb.org under the collection name ‘Arabidopsis thaliana genotypes’.
Results
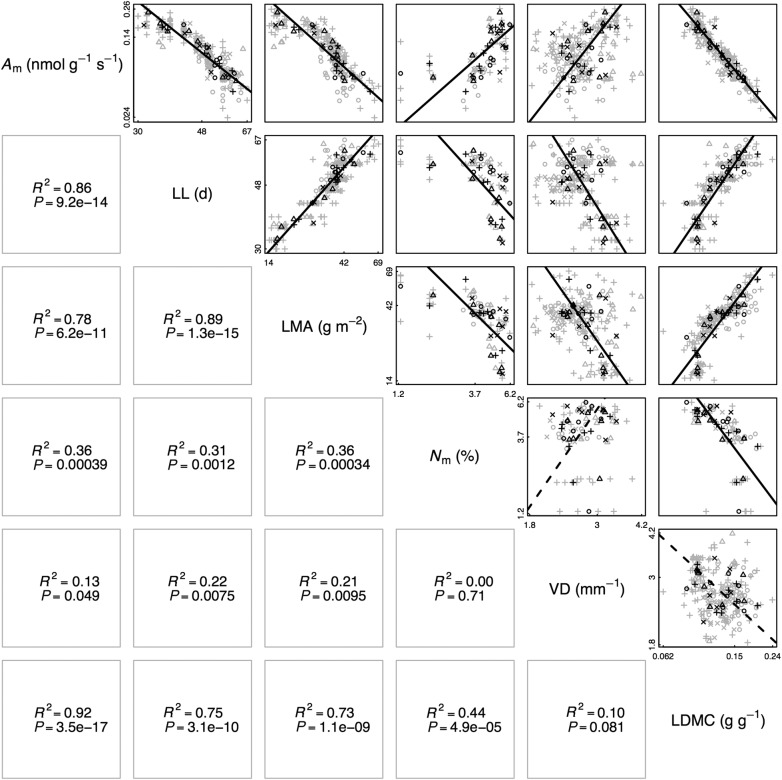
We first assessed correlations between LES traits. Consistent with a previous demonstration (Vasseur et al. 2012), LES correlations between Am, LL, LMA and Nm were found across genotypes (Fig. 2). All pairwise correlations between these genotype-mean values were significant (standard major axis regressions, all P < 0.05, R2 > 0.31), with signs the same as those described by the interspecific LES (Wright et al. 2004).
Figure 2.
Pairwise correlations between LES traits, VD and LDMC for multiple A. thaliana genotypes. Grey points indicate individual leaves; black points, genotype means. Symbols indicate genotype category: circles, mutants; triangles, NILs; pluses, RILs, crosses, ecotypes. Pairwise relationships between traits are shown, with lines indicating standard major axis regressions on genotype-mean log10-transformed data. Solid lines, P < 0.05; dashed lines, not significant. Regression statistics are shown in the lower panel for each pairwise relationship.
Leaf dry matter content and VD, the core traits of several of the models tested here, both showed wide ranges of variation. Vein density varied between 1.8 and 4.2 mm−1 and LDMC varied between 6.2 and 23.9 %. Both variables were significantly correlated with all LES traits (except for a non-significant correlation between VD and Nm). Correlations between LES traits with LDMC were generally higher than with VD.
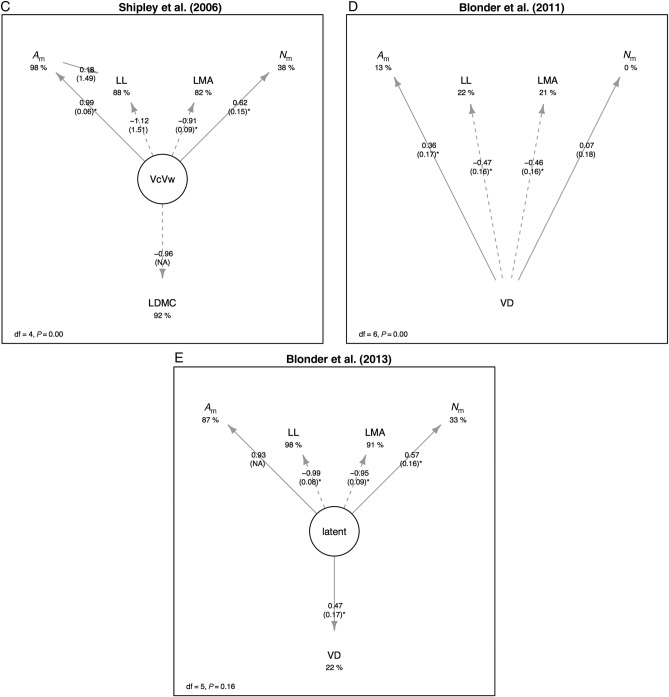
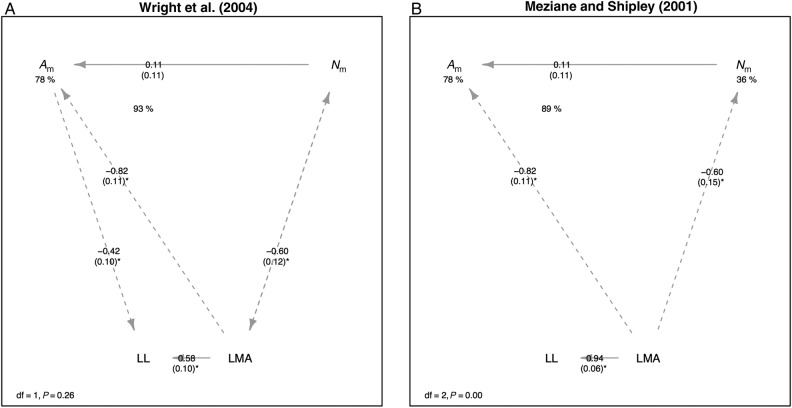
We next compared causal models for these LES correlations. The conceptual model of Wright et al. (2004) could not be rejected (χ2 = 1.28, df = 1, P = 0.26) and had coefficients with signs consistent with its original formulation. However, the conceptual model of Meziane and Shipley (2001) was strongly rejected (χ2 = 14.7, df = 2, P < 10−3). We then tested the Shipley et al. model that includes LDMC as an observed proxy of the latent variable Vc/Vw. The overall model was rejected (χ2 = 30.1, df = 4, P < 10−5) (Fig. 3A). We also found that the Blonder et al. (2013) model converged on coefficients with signs consistent with its original formulation (Fig. 3B), but the overall model was rejected (χ2 = 133.3, df = 6, P < 10−15). However, the revised venation-associated model was not rejected by data (χ2 = 7.8, df = 5, P = 0.16) and also converged on coefficients with signs consistent with predictions (Fig. 3C).
Figure 3.
Continued.
Figure 3.
Empirical evaluation of five possible models for the LES: (A) the model of Wright et al. (2004), (B) the model of Meziane and Shipley (2001), (C) the model of Shipley et al. (2006), (D) the venation model of Blonder et al. (2011) and (E) the revised venation-associated model of Blonder et al. (2013). Labels on arrows indicate standardized path coefficients, with standard errors in parentheses and an asterisk if significant at the α < 0.05 level. Paths are drawn with solid line if positive and dashed if negative. Values under dependent variables indicate R2 values. The overall model degrees of freedom and lack-of-fit P-value are shown in the legend; larger P-values indicate that the model is less likely to be rejected by observed data. Models are calculated using log10-transformed genotype-mean trait data.
We then compared relative support for the two models that could not be rejected by using AIC-based model selection. We found that the revised venation-associated model (Blonder et al. 2013) had less information loss (ΔAIC = 90) than the Wright et al. (2004) model. This result indicates that both models are plausible explanations of the data, but the revised venation-associated model is far more likely, even after correcting for differences in the number of free parameters in each model.
We also determined whether the genotypes known to show an LES trait variation also showed a variation in VD, a necessary condition for a venation network hypothesis to be supported. We found a significant variation in VD among ecotypes (ANOVA, F4,41 = 5.7, P = 0.0009) and among RILs (ANOVA, F15,70 = 7.0, P < 10−8) (Fig. 4). Using the NILs, we found that each line tied to the EDI locus (LCN 1–2.13, LCN 1–2.5 and LCN 1–3) had significantly different VD from the parent Ler-2 ecotype (t-tests, all P < 0.01). For the FLG locus, the LCN 5–7 line had significantly different VD than the parent (P = 0.003), but the LCN 5–8 line did not (P = 0.72). Using the mutants, we found that, for the CRY2 knockout, fha-1 had different VD values than its Ler-0 background (P = 0.01). In contrast, VD for cry2-1 was not different from VD in its Col-4 background (P = 0.18). For the HUA2 knockout, VD in hua2-4 was not different from VD in its Col-0 background (P = 0.39). We also tested two axr1 mutants directly affected in their venation network because of an impairment of auxin signalling. We found that the mutant with the more altered venation pattern, axr1-12, had different VD than its Col-0 background (P = 0.003) but did not find a difference relative to the mutant with the less altered venation pattern, axr1-3 (P = 0.21).
Figure 4.
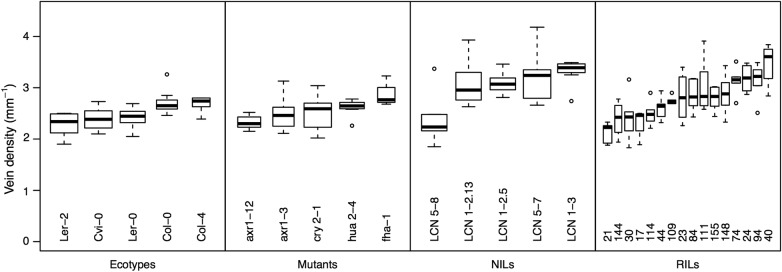
Vein density varies threefold between A. thaliana genotypes. This variation is found between ecotypes, mutants generated to target loci associated with the LES or vascular development, NILs or RILs generated from crosses between ecotypes.
Discussion
In the revised venation-associated model, we were not able to directly identify the latent variable controlling correlations between LES traits and VD. We hypothesize that it is linked to leaf hydraulics, based on theory and on the empirical result that the venation pattern-altered mutants also exhibited variations in LES traits. Nevertheless, the weak direct correlation between VD and other LES traits (all R2 < 0.13) suggests that the key trait is not VD but shows some relationship to it. Indeed, this latent variable may represent a combination of unknown but real physical variables.
Several other variables may also influence leaf economics via modulation of hydraulic conductance and total carbon cost. For example, variation in tissue density (Sack et al. 2013), mesophyll thickness (Brodribb et al. 2007), variation in vein size (Sack et al. 2012, 2013) or stomatal traits (Brodribb et al. 2013) may also influence the LES. For example, we note that a positive correlation between VD and LDMC was expected (Blonder et al. 2013) but not found here, suggesting that accounting for the variation in vein size would be useful.
We note that a ‘flux network theory’ was also recently proposed as an alternative model for venation models of the LES (Sack et al. 2013). In this framework, the LES emerges from interactions between a much wider suite of plant traits associated with resource fluxes and stocks. The validity of the many vs. few trait perspectives remains controversial (Blonder et al. 2014). This study was aimed at testing well-known specific few-trait models and was not able to assess this other class of hypotheses.
Our study also provides a roadmap for linking vascular patterning genes to the LES. Building on the work of Vasseur et al. (2012), we identified a role for the EDI and FLG loci, as well as for the AXR1 and CRY2 genes and potentially the HUA2 gene in leaf function and vascular development for A. thaliana. Further work may elucidate the molecular or developmental mechanisms coupling these genes to key functional traits, which—with the exception of AXR1 (Alonso-Peral et al. 2006)—remain unknown. Decades of study have yielded many more vascular patterning mutants in A. thaliana than were studied here (Pérez-Pérez et al. 2002; Scarpella et al. 2010). Generally, vascular development follows patterns of auxin concentration and is, therefore, sensitive to the presence of genes that modulate production and inhibition of auxin or sensitivity to it (Donner and Scarpella 2009). Determining whether the genes described above, as well as others at the EDI/FLG loci, are implicated in these pathways would further assess the hypotheses proposed here. With the progresses made in next-generation sequencing technologies, it is now possible to conduct genome-wide association studies (GWAS) on large panels of natural accessions in model species, as well as in many wild and cultivated species. Testing mechanistic models and causal relationships will be a powerful tool to investigate the mechanistic causes, the genetic determinism and the evolution of the LES.
Some caution should be taken when considering the generality of these results. We compared 31 genotypes of one species under a single set of environmental conditions. The processes generating the interspecific LES may differ from those generating the intraspecific LES. Moreover, a part of the variability in LES traits observed here may be explained by the functional variability associated with changes in flowering time, such as self-shading, reflecting more the whole-plant strategies for the economy of carbon and nutrients. If processes are scale- and species-dependent, then the global convergence in leaf functioning could be a common pattern arising from multiple processes. Many vascular plant species have vastly different life histories than A. thaliana, so it is plausible that multiple genetic pathways are responsible for the strong observed convergence in LES with and across taxa.
Data scale issues may also limit the generality of our conclusions. This study used a mixture of leaf-level measurements (VD) and whole-plant measurements (Am, Nm, LDMC and LMA and LL), which may conflate the LES (Wright et al. 2004) with the whole-plant economics spectrum (Reich 2014). This could reduce or bias correlations: for example, our measurements of Am and LMA include leaves of different ages, while VD is measured for a single leaf for each individual. There may also be a biased relationship between average LL and flowering time, because of the non-linear increase in leaf number with plant size. However, our whole-plant metrics are strongly correlated with leaf-level metrics in this system (Vasseur et al. 2012) and the small size and short lifespan of A. thaliana (i.e. no allocation to woody tissue) suggest that leaf and plant ecological strategies are probably tightly coordinated in this species. All models tested here were built to explain variations in the strategies of resource acquisition and use at the leaf level to, in turn, explain variations in whole-plant growth strategies and adaptation to variable environments. Our results indicate an important contribution of leaf-level functional variability to variations in plant economics. On the other hand, our study also pinpoints the role of an unknown variable on trait variation, which suggests that plant architecture and leaf geometry may also be part of strategies to optimize biomass allocation and nutrient-use efficiency.
Some of our null results (e.g. no significant difference in VD between a vascular patterning mutant and wild-type) may also be due to low statistical power. For an effect size of 0.5 (reasonable given the difference in means and error variances observed in these results) and a power of 0.9 (i.e. a 10 % chance of incorrectly deciding there is no difference in VD), a sample size of ∼70 would be required for these two-sided t-tests. Sample sizes for ecotypes, mutants and NILs were never larger than 12. However, the significant differences we did find are likely to represent true genetic effects on VD.
Lastly, these data and our analyses do indicate that the trait correlations seen in the LES are not just a statistical artefact of data normalization (Lloyd et al. 2013; Osnas et al. 2013). Correlations not reflective of physiological mechanism might be found when examining pairs of variables where one is a ratio of another and scale isometrically with each other (e.g. Am negatively correlated with LMA with a slope of −1.0). However, we found evidence that these correlations, as well as all others, are not driven simply by these statistical effects but rather by variations in a latent variable representing one or more physical quantities. Thus, our study supports the idea that LES trait correlations have a physiological basis and contribute strongly to variations in the whole-plant economic strategies.
Conclusions
Our data provide a starting point for assessing the functional basis of the LES in A. thaliana. Using structural equation modelling, we showed that the original conceptual model of Wright et al. (2004) could not be rejected by data. However, a revised venation-associated model (Blonder et al. 2013) is also consistent with the observed data for multiple genotypes whose phenotypes recapitulate the interspecific LES (Vasseur et al. 2012). We suggest that the latter model is more plausible, because (i) the Wright et al. model was rejected at the interspecific scale in a previous study (Shipley et al. 2006) and (ii) model-selection techniques indicated more relative support for the revised venation-associated model. Nevertheless, we emphasize that both models remain viable explanations for the LES given the extant data in A. thaliana.
Sources of Funding
B.B. was supported by an NSF pre-doctoral fellowship. F.V. was funded by a CIFRE grant (ANRT, French Ministry of Research) supported by BAYER Crop Science (contract 0398/2009 - 09 42 008). C.V. was supported by a Marie Curie International Outgoing Fellowship within the 7th European Community Framework Programme (DiversiTraits project, no. 221060) and by the European Research Council (ERC-2014-StG-CONSTRAINTS grant). B.S. was funded by the Natural Sciences and Engineering Research Council of Canada. B.J.E. was supported by a NSF Advancing Theory in Biology award. D.V. was supported by EIT Climate-KIC program AgWaterBreed.
Contributions by the Authors
B.B., C.V. and B.J.E. conceived the manuscript. B.B., F.V., C.V. and D.V. contributed to laboratory analyses. All authors contributed to statistical analyses and writing the manuscript.
Conflict of Interest Statement
None declared.
Supporting Information
The following additional information is available in the online version of this article –
File S1. CSV file. Trait measurements for all individual plants.
File S2. R code. Scripts to replicate analyses and figures.
Acknowledgements
The authors thank Nicolle Ioakem, John Lacson, Courtney Magness, Kyle Pendergrass, Lindsey Parker and Jessie Rebl for their careful laboratory work.
Literature Cited
- Ackerly DD, Bazzaz FA. 1995. Leaf dynamics, self-shading and carbon gain in seedlings of a tropical pioneer tree. Oecologia 101:289–298. 10.1007/BF00328814 [DOI] [PubMed] [Google Scholar]
- Alonso-Blanco C, Peeters AJM, Koornneef M, Lister C, Dean C, van den Bosch N, Pot J, Kuiper MTR. 1998. Development of an AFLP based linkage map of Ler, Col and Cvi Arabidopsis thaliana ecotypes and construction of a Ler/Cvi recombinant inbred line population. The Plant Journal 14:259–271. 10.1046/j.1365-313X.1998.00115.x [DOI] [PubMed] [Google Scholar]
- Alonso-Peral MM, Candela H, del Pozo JC, Martinez-Laborda A, Ponce MR, Micol JL. 2006. The HVE/CAND1 gene is required for the early patterning of leaf venation in Arabidopsis. Development 133:3755–3766. 10.1242/dev.02554 [DOI] [PubMed] [Google Scholar]
- Blonder B, Violle C, Bentley LP, Enquist BJ. 2011. Venation networks and the origin of the leaf economics spectrum. Ecology Letters 14:91–100. 10.1111/j.1461-0248.2010.01554.x [DOI] [PubMed] [Google Scholar]
- Blonder B, Violle C, Enquist BJ. 2013. Assessing the causes and scales of the leaf economics spectrum using venation networks in Populus tremuloides. Journal of Ecology 101:981–989. 10.1111/1365-2745.12102 [DOI] [Google Scholar]
- Blonder B, Violle C, Bentley LP, Enquist BJ. 2014. Inclusion of vein traits improves predictive power for the leaf economic spectrum: a response to Sack et al. (2013). Journal of Experimental Botany 65:5109–5114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonser SP, Ladd B, Monro K, Hall MD, Forster MA. 2010. The adaptive value of functional and life-history traits across fertility treatments in an annual plant. Annals of Botany 106:979–988. 10.1093/aob/mcq195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyce CK, Brodribb TJ, Feild TS, Zwieniecki MA. 2009. Angiosperm leaf vein evolution was physiologically and environmentally transformative. Proceedings of the Royal Society B: Biological Sciences 276:1771–1776. 10.1098/rspb.2008.1919 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodribb TJ, Feild TS, Jordan GJ. 2007. Leaf maximum photosynthetic rate and venation are linked by hydraulics. Plant Physiology 144:1890–1898. 10.1104/pp.107.101352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodribb TJ, Feild TS, Sack L. 2010. Viewing leaf structure and evolution from a hydraulic perspective. Functional Plant Biology 37:488–498. 10.1071/FP10010 [DOI] [Google Scholar]
- Brodribb TJ, Jordan GJ, Carpenter RJ. 2013. Unified changes in cell size permit coordinated leaf evolution. New Phytologist 199:559–570. 10.1111/nph.12300 [DOI] [PubMed] [Google Scholar]
- Des Marais DL, McKay JK, Richards JH, Sen S, Wayne T, Juenger TE. 2012. Physiological genomics of response to soil drying in diverse Arabidopsis accessions. The Plant Cell Online 24:893–914. 10.1105/tpc.112.096180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donner TJ, Scarpella E. 2009. Auxin-transport-dependent leaf vein formation. Botany 87:678–684. 10.1139/B09-002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donovan LA, Maherali H, Caruso CM, Huber H, de Kroon H. 2011. The evolution of the worldwide leaf economics spectrum. Trends in Ecology and Evolution 26:88–95. 10.1016/j.tree.2010.11.011 [DOI] [PubMed] [Google Scholar]
- Doyle MR, Bizzell CM, Keller MR, Michaels SD, Song J, Noh Y-S, Amasino RM. 2005. HUA2 is required for the expression of floral repressors in Arabidopsis thaliana. The Plant Journal 41:376–385. 10.1111/j.1365-313X.2004.02300.x [DOI] [PubMed] [Google Scholar]
- Dunbar-Co S, Sporck MJ, Sack L. 2009. Leaf trait diversification and design in seven rare taxa of the Hawaiian Plantago radiation. International Journal of Plant Sciences 170:61–75. 10.1086/593111 [DOI] [Google Scholar]
- Edwards EJ. 2006. Correlated evolution of stem and leaf hydraulic traits in Pereskia (Cactaceae). New Phytologist 172:479–789. 10.1111/j.1469-8137.2006.01850.x [DOI] [PubMed] [Google Scholar]
- El-Assal SED, Alonso-Blanco C, Peeters AJM, Raz V, Koornneef M. 2001. A QTL for flowering time in Arabidopsis reveals a novel allele of CRY2. Nature Genetics 29:435–440. 10.1038/ng767 [DOI] [PubMed] [Google Scholar]
- El-Lithy ME, Reymond M, Stich B, Koornneef M, Vreugdenhil D. 2010. Relation among plant growth, carbohydrates and flowering time in the Arabidopsis Landsberg erecta × Kondara recombinant inbred line population. Plant, Cell and Environment 33:1369–1382. [DOI] [PubMed] [Google Scholar]
- Fabre J, Dauzat M, Nègre V, Wuyts N, Tireau A, Gennari E, Neveu P, Tisné S, Massonnet C, Hummel I, Granier C. 2011. PHENOPSIS DB: an information system for Arabidopsis thaliana phenotypic data in an environmental context. BMC Plant Biology 11:77 10.1186/1471-2229-11-77 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freschet GT, Cornelissen JHC, Van Logtestijn RSP, Aerts R. 2010. Evidence of the ‘plant economics spectrum’ in a subarctic flora. Journal of Ecology 98:362–373. 10.1111/j.1365-2745.2009.01615.x [DOI] [Google Scholar]
- Fu J, Keurentjes JJB, Bouwmeester H, America T, Verstappen FWA, Ward JL, Beale MH, de Vos RCH, Dijkstra M, Scheltema RA, Johannes F, Koornneef M, Vreugdenhil D, Breitling R, Jansen RC. 2009. System-wide molecular evidence for phenotypic buffering in Arabidopsis. Nature Genetics 41:166–167. 10.1038/ng.308 [DOI] [PubMed] [Google Scholar]
- Granier C, Aguirrezabal L, Chenu K, Cookson SJ, Dauzat M, Hamard P, Thioux J-J, Rolland G, Bouchier-Combaud S, Lebaudy A, Muller B, Simonneau T, Tardieu F. 2006. PHENOPSIS, an automated platform for reproducible phenotyping of plant responses to soil water deficit in Arabidopsis thaliana permitted the identification of an accession with low sensitivity to soil water deficit. New Phytologist 169:623–635. 10.1111/j.1469-8137.2005.01609.x [DOI] [PubMed] [Google Scholar]
- Grime JP. 1977. Evidence for the existence of three primary strategies in plants and its relevance to ecological and evolutionary theory. The American Naturalist 111:1169–1194. 10.1086/283244 [DOI] [Google Scholar]
- Keurentjes JJB, Bentsink L, Alonso-Blanco C, Hanhart CJ, Vries HBD, Effgen S, Vreugdenhil D, Koornneef M. 2007. Development of a near-isogenic line population of Arabidopsis thaliana and comparison of mapping power with a recombinant inbred line population. Genetics 175:891–905. 10.1534/genetics.106.066423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kikuzawa K. 1995. Leaf phenology as an optimal strategy for carbon gain in plants. Canadian Journal of Botany 73:158–163. [Google Scholar]
- Li B, Suzuki J-I, Hara T. 1998. Latitudinal variation in plant size and relative growth rate in Arabidopsis thaliana. Oecologia 115:293–301. 10.1007/s004420050519 [DOI] [PubMed] [Google Scholar]
- Lloyd J, Bloomfield K, Domingues TF, Farquhar GD. 2013. Photosynthetically relevant foliar traits correlating better on a mass vs an area basis: of ecophysiological relevance or just a case of mathematical imperatives and statistical quicksand? New Phytologist 199:311–321. 10.1111/nph.12281 [DOI] [PubMed] [Google Scholar]
- Meziane D, Shipley B. 2001. Direct and indirect relationships between specific leaf area, leaf nitrogen and leaf gas exchange. Effects of irradiance and nutrient supply. Annals of Botany 88:915–927. 10.1006/anbo.2001.1536 [DOI] [Google Scholar]
- Niinemets Ü. 2015. Is there a species spectrum within the world-wide leaf economics spectrum? Major variations in leaf functional traits in the Mediterranean sclerophyll Quercus ilex. New Phytologist 205:79–96. [DOI] [PubMed] [Google Scholar]
- Noblin X, Mahadevan L, Coomaraswamy IA, Weitz DA, Holbrook NM, Zwieniecki MA. 2008. Optimal vein density in artificial and real leaves. Proceedings of the National Academy of Sciences of the USA 105:9140–9144. 10.1073/pnas.0709194105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osnas JLD, Lichstein JW, Reich PB, Pacala SW. 2013. Global leaf trait relationships: mass, area, and the leaf economics spectrum. Science 340:741–744. 10.1126/science.1231574 [DOI] [PubMed] [Google Scholar]
- Pantin F, Simonneau T, Rolland G, Dauzat M, Muller B. 2011. Control of leaf expansion: a developmental switch from metabolics to hydraulics. Plant Physiology 156:803–815. 10.1104/pp.111.176289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez-Harguindeguy N, Díaz S, Garnier E, Lavorel S, Poorter H, Jaureguiberry P, Bret-Harte MS, Cornwell WK, Craine JM, Gurvich DE, Urcelay C, Veneklaas EJ, Reich PB, Poorter L, Wright IJ, Ray P, Enrico L, Pausas JG, de Vos AC, Buchmann N, Funes G, Quétier F, Hodgson JG, Thompson K, Morgan HD, ter Steege H, Sack L, Blonder B, Poschlod P, Vaieretti MV, Conti G, Staver AC, Aquino S, Cornelissen JHC. 2013. New handbook for standardised measurement of plant functional traits worldwide. Australian Journal of Botany 61:167–234. 10.1071/BT12225 [DOI] [Google Scholar]
- Pérez-Pérez JM, Serrano-Cartagena J, Micol JL. 2002. Genetic analysis of natural variations in the architecture of Arabidopsis thaliana vegetative leaves. Genetics 162:893–915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich PB. 2014. The world-wide ‘fast-slow’ plant economics spectrum: a traits manifesto. Journal of Ecology 102:275–301. 10.1111/1365-2745.12211 [DOI] [Google Scholar]
- Reich PB, Walters MB, Ellsworth DS. 1997. From tropics to tundra: global convergence in plant functioning. Proceedings of the National Academy of Sciences of the USA 94:13730–13734. 10.1073/pnas.94.25.13730 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sack L, Scoffoni C. 2013. Leaf venation: structure, function, development, evolution, ecology and applications in the past, present and future. New Phytologist 198:983–1000. 10.1111/nph.12253 [DOI] [PubMed] [Google Scholar]
- Sack L, Scoffoni C, McKown AD, Frole K, Rawls M, Havran JC, Tran H, Tran T. 2012. Developmentally based scaling of leaf venation architecture explains global ecological patterns. Nature Communications 3:837 10.1038/ncomms1835 [DOI] [PubMed] [Google Scholar]
- Sack L, Scoffoni C, John GP, Poorter H, Mason CM, Mendez-Alonzo R, Donovan LA. 2013. How do leaf veins influence the worldwide leaf economic spectrum? Review and synthesis. Journal of Experimental Botany 64:4053–4080. 10.1093/jxb/ert316 [DOI] [PubMed] [Google Scholar]
- Salomé PA, Bomblies K, Laitinen RAE, Yant L, Mott R, Weigel D. 2011. Genetic architecture of flowering-time variation in Arabidopsis thaliana. Genetics 188:421–433. 10.1534/genetics.111.126607 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scarpella E, Barkoulas M, Tsiantis M. 2010. Control of leaf and vein development by auxin. Cold Spring Harbor Perspectives in Biology 2:a001511 10.1101/cshperspect.a001511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shipley B, Lechowicz MJ, Wright I, Reich PB. 2006. Fundamental trade-offs generating the worldwide leaf economics spectrum. Ecology 87:535–541. 10.1890/05-1051 [DOI] [PubMed] [Google Scholar]
- Vasseur F, Violle C, Enquist BJ, Granier C, Vile D. 2012. A common genetic basis to the origin of the leaf economics spectrum and metabolic scaling allometry. Ecology Letters 15:1149–1157. 10.1111/j.1461-0248.2012.01839.x [DOI] [PubMed] [Google Scholar]
- Wishart J. 1928. The generalised product moment distribution in samples from a normal multivariate population. Biometrika 20A:32–52. 10.1093/biomet/20A.1-2.32 [DOI] [Google Scholar]
- Wright IJ, Reich PB, Westoby M, Ackerly DD, Baruch Z, Bongers F, Cavender-Bares J, Chapin T, Cornelissen JHC, Diemer M, Flexas J, Garnier E, Groom PK, Gulias J, Hikosaka K, Lamont BB, Lee T, Lee W, Lusk C, Midgley JJ, Navas M-L, Niinemets Ü, Oleksyn J, Osada N, Poorter H, Poot P, Prior L, Pyankov VI, Roumet C, Thomas SC, Tjoelker MG, Veneklaas EJ, Villar R. 2004. The worldwide leaf economics spectrum. Nature 428:821–827. 10.1038/nature02403 [DOI] [PubMed] [Google Scholar]
- Wright IJ, Reich PB, Cornelissen JHC, Falster DS, Groom PK, Hikosaka K, Lee W, Lusk CH, Niinemets U, Oleksyn J, Osada N, Poorter H, Warton DI, Westoby M. 2005. Modulation of leaf economic traits and trait relationships by climate. Global Ecology and Biogeography 14:411–421. 10.1111/j.1466-822x.2005.00172.x [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Datasheets and R code to replicate all analyses are available in Supporting Information. Pictures of leaf blades and petioles as well as raw biomass measurements are available at http://bioweb.supagro.inra.fr/phenopsis/ under experiment C3M13B (Fabre et al. 2011). Images of chemically cleared leaves (greyscale) and hand-traced subregions (annotated with yellow for fully cleared regions; with red for veins) are available at http://clearedleavesdb.org under the collection name ‘Arabidopsis thaliana genotypes’.