Comparative study of the effectiveness and limitations of current methods for detecting sequence coevolution

Abstract

Motivation: With rapid accumulation of sequence data on several species, extracting rational and systematic information from multiple sequence alignments (MSAs) is becoming increasingly important. Currently, there is a plethora of computational methods for investigating coupled evolutionary changes in pairs of positions along the amino acid sequence, and making inferences on structure and function. Yet, the significance of coevolution signals remains to be established. Also, a large number of false positives (FPs) arise from insufficient MSA size, phylogenetic background and indirect couplings.

Results: Here, a set of 16 pairs of non-interacting proteins is thoroughly examined to assess the effectiveness and limitations of different methods. The analysis shows that recent computationally expensive methods designed to remove biases from indirect couplings outperform others in detecting tertiary structural contacts as well as eliminating intermolecular FPs; whereas traditional methods such as mutual information benefit from refinements such as shuffling, while being highly efficient. Computations repeated with 2,330 pairs of protein families from the Negatome database corroborated these results. Finally, using a training dataset of 162 families of proteins, we propose a combined method that outperforms existing individual methods. Overall, the study provides simple guidelines towards the choice of suitable methods and strategies based on available MSA size and computing resources.

Availability and implementation: Software is freely available through the Evol component of ProDy API.

Contact: bahar@pitt.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

With sequence data being generated at an ever increasing rate in the post-genomic era, it is becoming crucially important to develop efficient and accurate methods at the interface between evolutionary biology, computational biology and molecular biophysics to learn and make inferences from sequence data (Liberles et al., 2012). Structural and functional properties of proteins go hand-in-hand with their evolutionary properties. For instance, maintaining protein stability usually involves interactions between conserved residues at the core of the structure. Likewise, biochemical activities such as catalysis involve conserved residues. Recognition sites, on the other hand, may show correlated mutations that maintain the balance between specificity and adaptability (Tokuriki and Tawfik, 2009a, b). Recent studies also highlight how sequence evolution correlates with structural dynamics (Liu et al., 2010; Liu and Bahar, 2012). Coevolution patterns derived from multiple sequence alignments (MSAs) provide valuable constraints that assist in structure prediction (Marks et al., 2011, 2012; Morcos et al., 2011; Weigt et al., 2009). The idea of inferring inter-residue contacts for structure prediction, using sequence correlation data indeed goes back to the early 1990s (e.g. Göbel et al., 1994). Such applications may be particularly useful in the case of membrane proteins that can often be difficult to resolve (Hopf et al., 2012). Detection of correlated mutation sites could also assist in identifying hot spots, and provide guidance for protein design and engineering.

In line with increased sequence data and, thereby, increased opportunity for detecting and interpreting sequence correlations across the members of protein families, a broad range of theory and methods have been introduced for correlated mutations analysis (CMA) in the last decade. Mutual information (MI) (Gloor et al., 2005) from information theory was one of the first rigorous metrics adopted for quantifying the extent of cross-correlations between amino acid substitutions in proteins. A corrected version, MIp, where the background noise and phylogenetic effects were largely eliminated by subtracting an average product correction (APC) (Dunn et al., 2008) proved to enhance signals associated with amino acids that are proximal in the structure. Also, non-MI-based methods have been shown to help identify correlated mutations, such as the observed-minus-expected-squared (OMES) method (Kass and Horovitz, 2002) and the statistical coupling analysis (SCA) (Halabi et al., 2009; Lockless and Ranganathan, 1999). More recently, advanced approaches that require more expensive computations have been introduced, focused on removing indirect (or transitive) couplings that may obscure the detection of direct correlations between sequence positions. Such methods include direct coupling analysis (DCA or DI for direct information) (Morcos et al., 2011; Weigt et al., 2009), Protein Sparse Inverse COVariance (PSICOV) (Jones et al., 2012), a Bayesian network algorithm for disentangling direct from indirect dependencies between residues (Burger and van Nimwegen, 2010), the pseudolikelihood maximization DCA (plmDCA) method due to Ekeberg et al. (2013), Gremlin’s pseudo-likelihood method (Kamisetty et al., 2013) and a network deconvolution approach based on spectral decomposition of the correlation matrix (Feizi et al., 2013). These studies have shown success in detecting correlations that relate to contacts in the three-dimensional (3D) structure, and in reverse engineering the 3D structure from correlations.

In a control study, Horovitz and coworkers (Noivirt et al., 2005) demonstrated that CMA methods may erroneously yield coevolutionary signals even between non-interacting proteins. This study performed for a set of 16 non-interacting protein pairs (Supplementary Table S1) further showed that shuffling algorithms could be adopted to improve signal-to-noise ratio and reduce these false positives (FPs). Of interest is to see if methods developed for improving the detection of 3D contact-making residues are equally effective in eliminating intermolecular FPs. In a broader context, it is not often clear which method might be most suitable for a given set of data, or what are their limits of applicability. Which fraction of signals outputted by these methods can be reliably used for making structural or functional inferences? How does the size of the MSA affect the results? Can we estimate the minimum size of the MSA to achieve a certain level of accuracy? Can we design hybrid approaches, or combined methods, that take advantage of the strengths of different methods to outperform individual methods?

In the present study, we present a critical assessment of the performance of nine methods/approaches developed for predicting pairwise correlations from MSAs. Proteins in Supplementary Table S1 (see also Supplementary Information (SI), Supplementary Table S2) are adopted as a benchmark dataset for a detailed analysis, which is further consolidated by extending the analysis to a dataset of 2330 structurally resolved protein pairs extracted from Negatome 2.0 database (Blohm et al., 2014) of non-interacting proteins. Two basic performance criteria are considered: first, does the method correctly filter out intermolecular correlations (FPs) if the analyzed pairs of proteins are known to be non-interacting? Second, if one focuses on intramolecular signals, does the method detect the pairs that make tertiary contacts in the 3D structure (termed intramolecular true positives, TPs)? The study shows that the abilities of the existing methods to discriminate intermolecular FPs are comparable, but their abilities to identify intramolecular TPs vary, with DI and PSICOV outperforming others. We also analyse the relationship between the size of MSAs and the effectiveness of shuffling algorithm. We examine the similarities/dissimilarities, or the level of consistency, between the outputs from different methods, and provide simple guidelines for estimating how accuracy varies with coverage. Finally, using a naïve Bayesian approach with a training dataset of 162 families of proteins (SI, Supplementary Table S3), we propose a combined method of PSICOV and DI that provides the highest levels of accuracy. Overall, the study provides a clear understanding of the capabilities and deficiencies of existing methods to help users select optimal methods for their purposes.

2 Materials and methods

2.1 Dataset

We used two datasets for our computations: Dataset I, comprised of 16 pairs of non-interacting proteins (Supplementary Table S1) introduced by Horovitz and coworkers as a benchmarking set for CMA (Noivirt et al., 2005) and Dataset II derived from the Negatome 2.0 database of non-interacting proteins/domains (Blohm et al., 2014).

Dataset I contained 15 distinctive families of proteins, the properties of which are detailed in the SI, Supplementary Table S2. We present in Supplementary Table S1 the numbers of sequences/rows (m) as well as the number of columns (N) for each of the 16 MSAs generated for Dataset I. Supplementary Table S2 lists the corresponding Pfam (Punta et al., 2012) domain names, representative UNIPROT (UniProt Consortium, 2014) identifiers and Protein Data Bank (PDB) (Bernstein et al., 1977) structures, along with the MSA sizes (m and N) used for analyzing separately the intramolecular coevolutionary properties of the individual proteins. About half of the proteins in this set contained more than one Pfam domain (Supplementary Table S2). Only those domains that appeared in more than 80% of the sequences were considered for further analysis. For those domains, full MSAs (except for PF00005; see Supplementary Table S2) and representative structures were obtained from Pfam (Supplementary Table S2).

Dataset II comprised 2330 pairs (formed by 453 distinctive Pfam proteins/domains). These were selected from the Negatome 2.0 PDB-stringent dataset of 4161 pairs upon removing all pairs that involved multidomain proteins. The three panels in Supplementary Figure S1 display the histograms for (a) the number of columns, (b) the number of rows and (c) the average sequence identities between all pairs of rows, for the MSAs corresponding to Dataset II. Note that Dataset II contains two orders of magnitude larger data (2330 versus 16 pairs of proteins) compared with Dataset I, but the corresponding MSAs contained fewer sequences (rows) and smaller proteins (columns). The respective averages for the two sets were <N>_I = 495 and <N>_II = 230, and <m>_I = 1681 and <m>_II = 334. We used Dataset I for a detailed analysis and Dataset II for further validation of major results.

The following filters were applied in refining the MSAs: All sequences having less than 80% row occupancy (sequences having >20% gaps) were removed using ProDy (Bakan et al., 2014). The refined MSAs for individual proteins in Dataset I were concatenated whenever a protein was composed of more than one domain. Likewise, for each protein family pair, we concatenated the sequences from the same species to form a combined MSA. The sequence with the lowest average sequence identity with respect to all others in a given MSA was removed until the average sequence identity was above 25%. No upper sequence identity threshold was adopted for Dataset I, as the average sequence identities (last column in Supplementary Table S1) varied between 31% and 58%; and even in the case of the MSA containing the highest proportion of similar sequences, those pairs with more than 85% sequence identity were 3+ standard deviations apart from the mean. Dataset II showed a broader distribution, depicted in Supplementary Figure S1 (c). In this case, the pairs sharing more than or equal to 99% sequence identity amounted to 0.75% of the data, yielding on the average two to three such pairs per MSA. The effect of this small subset of highly similar paralogs can thus be expected to be negligible. We also confirmed the above by repeating calculations for Dataset II with 95% upper sequence identity cutoff (data not shown). The results showed that the effect of this small subset of highly similar paralogs was negligibly small. Finally, columns whose occupancy was lower than 90% (positions with >10% gaps) and those fully conserved were removed for coevolution analysis.

2.2 Methods for sequence coevolution analysis

The methods we used in our comparative study are MI (Gloor et al., 2005), MIp (Dunn et al., 2008), OMES (Kass and Horovitz, 2002), SCA (Halabi et al., 2009; Lockless and Ranganathan, 1999), PSICOV (Jones et Al., 2012) and DI (Morcos et al., 2011; Weigt et al., 2009). A summary of the methods included in our comparative study is presented in SI. Details may be found in the original studies. In each case, we evaluated the N × N sequence covariance matrix; the off-diagonal elements of which represent the degree of coevolution between pairs of amino acids. MI, MIp, OMES and SCA matrices were calculated using the Evol module of ProDy (Bakan et al., 2014), PSICOV by the code listed online (Jones et al., 2012) and DI by the code provided by Morcos et al. (2011).

2.3 Shuffling algorithm

The shuffling algorithm introduced earlier (Noivirt et al., 2005) was adopted here. Accordingly, for a given MSA of m sequences and N residues/columns, we shuffle the m elements within each column (e.g. column k) randomly while the other columns are kept unchanged. A new correlation matrix (MI, MIp or OMES) is calculated for each shuffling procedure. This process is repeated P = 10 000 times for each column (1 ≤ k ≤ N); and because each position is evaluated twice on either position shuffling, we obtain a total of 20 000 shuffled results for each pair. The new ‘random’ correlation value is compared with its original counterpart and we assign a P-value. For instance, if we observe a shuffled value more than or equal to original value in 200 times out of 20 000 iterations for a given pair, the P-value for the corresponding (original) covariance value is assigned as 200/20 000 = 0.01. We set the P-value significance threshold to 0.005, i.e. only those pairs with P-values < 0.005 were considered to be statistically significant. The newly generated covariance matrices are designated as MI^(S), MIp^(S) or OMES^(S). The shuffling algorithm can be practically implemented for these three methods among the six listed above. This is because DI and PSICOV require the inversion of the entire C at each iterative step, and repeating this task approximately 10⁴ times for each column is prohibitively expensive. Likewise, SCA does not lend itself to efficient iterative re-evaluation, and hence was not subjected to shuffling refinement.

3 Results

3.1 Rationale

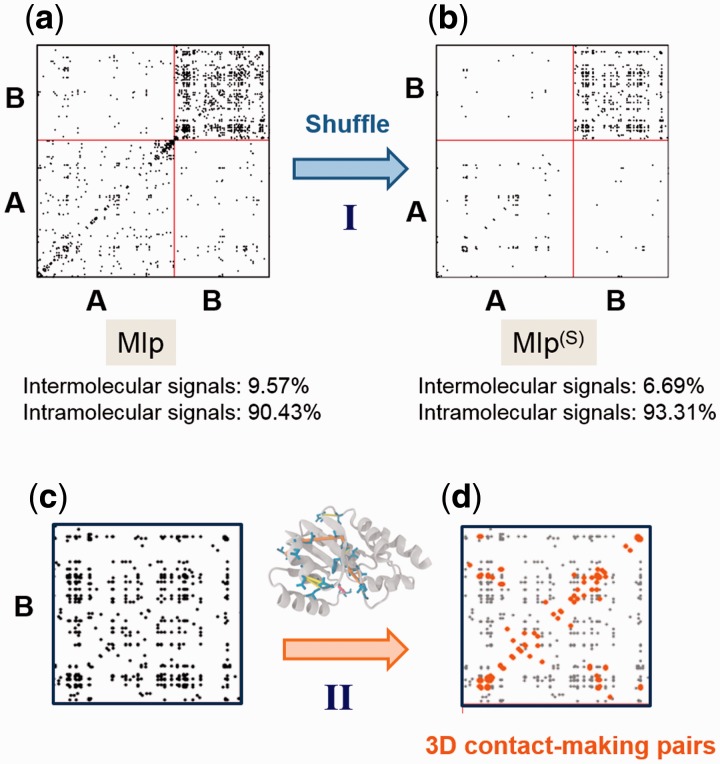
We assessed the performance of MI, MI^(S), MIp, MIp^(S), OMES, OMES^(S), SCA, PSICOV and DI based on two criteria: exclusion of intermolecular FPs, and ability to capture intramolecular contact-making pairs (TPs). The former criterion is assessed by examining the protein pairs that are known to be non-interacting (Datasets I and II; see Supplementary Table S1). We construct MSAs by juxtaposing the sequences of such pairs of proteins, e.g. A and B, each row corresponding to a given species/organism. The resulting covariance matrix is composed of four blocks/sub-matrices, two describing the intramolecular (A–A and B–B) correlations, and two, off-diagonal, associated with intermolecular (A–B or B–A) correlations (Fig. 1a). In principle, the latter two sub-matrices should not contain any signals as they are for non-interacting proteins, or the observed signals are FPs. The most accurate method is, therefore, the one where these FPs are negligible if not totally eliminated.

Fig. 1.

Two criteria for assessing the performance of different methods: (I) exclusion of intermolecular FPs and (II) detection of residue pairs that make intramolecular contacts. (a) and (b) The MIp and MIp^(S) matrices obtained for a pair of proteins [in this case, porphobilinogen deaminase (protein A) and ribosomal 50S L1 protein (protein B)] (Supplementary Table S1). Residue pairs yielding the top-ranking 1% signals are displayed by dots. Shuffling reduces the percentage of intermolecular signals (FPs) from 9.57 to 6.69%. (c) and (d) The individual proteins are separately analyzed and the physical distance between coevolving pairs is evaluated by examining the corresponding structure in the PDB

The second criterion, referred to as accurate detection of intramolecular contacts is assessed by examining if the coevolving pairs make inter-residue contacts in the 3D structure of the protein. Two residues are considered to make 3D contacts if at least one pair of atoms (belonging to the respective residues) is separated by a distance smaller than 8Å. Previous detailed examination of the coordination geometry of non-bonded residues in PDB structures has shown that this distance range includes all pairs within a first coordination shell (Bahar and Jernigan, 1996). A threshold of 8.0 Å (for C_α–C_α pairs) has been adopted in similar studies for defining inter-residue contacts (Burger and van Nimwegen, 2010; Kamisetty et al., 2013). The occurrence of a 3D contact is strong evidence for the biological or physical significance of the detected covariation. Methods that identify a larger number of such pairs (among the top-ranking coevolving pairs) are deemed to perform better.

3.2 Illustrations for selected pairs

Figure 1 illustrates the above two criteria for porphobilinogen deaminase and ribosomal 50S L1 protein (pair 11 in Supplementary Table S1), designated as proteins A and B, analyzed by MIp^(S). Panel (a) displays the MI map calculated after subtracting the APC, MIp. For clarity, only the strongest 1% signals are shown by dots. Among them, 90.43% lie in the lower-left and upper-right diagonal blocks, corresponding to the respective intramolecular signals within A and within B (A–A and B–B groups); and 9.57% lie in the other two blocks corresponding to intermolecular correlations (A–B or B–A; the matrix is symmetric). The latter subset constitutes the FPs in view of the lack of known physical interaction between these two proteins. Panel (b) shows that the application of shuffling algorithm to MIp to generate MIp^(S) reduces the percentage of FPs to 6.69%. Panels (c) and (d) illustrate the screening of the results for individual proteins against their PDB structures to identify the fraction of intramolecular signals that correspond to 3D contact-making pairs. In this example, 26.37% of residue pairs, shown by the orange dots, make physical (atom–atom) contacts.

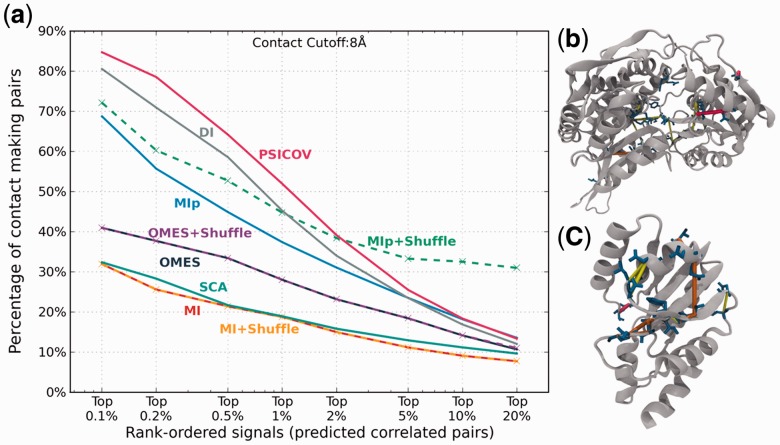
Figure 2 illustrates the analysis of the intramolecular signals obtained for γ-glutamyl phosphate reductase and pantetheine phosphate adenylyl transferase (pair 2 in Supplementary Table S1). Panel a compares the relative ability of the nine different methods to detect contact-making pairs of residues. Results are displayed for a range of signal strengths (or covariance scores), from top-ranking 0.1–20%. Clearly, the fraction of accurately predicted contacts drops as larger subsets are considered, but the results also show a strong dependency on the selected method. SCA and MI show the weakest performance: contact-making residue pairs amount to less than one-third of the identified pairs in either case, even when the strongest 0.1% signals are considered. On the other hand, at the same signal strength, a large majority (>85%) of residue pairs predicted by PSICOV make contacts in the 3D structures. PSICOV is closely followed by DI. Of note is the high performance of MIp^(S) in the range 5–20%, indicating little decrease with coverage compared with other methods. The improvement in MIp upon implementation of the shuffling algorithm is remarkable; whereas MI and OMES hardly change upon shuffling. Panels (b) and (c) display the locations of residue pairs that are accurately detected by at least seven methods within the respective proteins.

Fig. 2.

Comparison of the performance of different methods. The ability of the methods to detect residue pairs that make 3D contacts is illustrated for the pair 2 in Supplementary Table S1. Panel (a) displays the percentage of TPs among intramolecular predictions (based on subsets of different size, from top 0.1% to top 20%), TPs being defined as residue pairs that make contacts in the 3D structure. Panels (b) and (c) show the residue pairs (blue stick representation) within γ-glutamyl phosphate reductase (top) and pantetheine phosphate adenylyl transferase (bottom) predicted among the top 1% signals by all nine methods (red lines), or eight methods (orange lines) or seven methods (yellow lines)

3.3 Results for the complete Dataset I

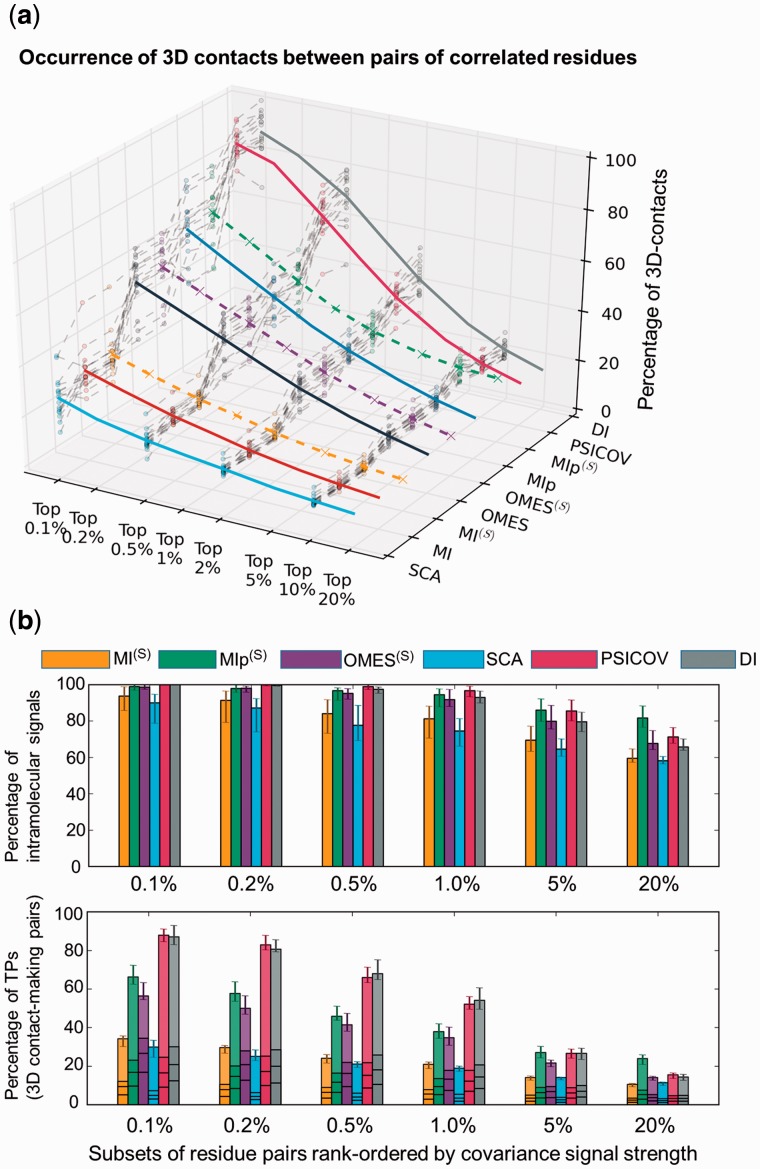
Results obtained for the complete Dataset I are presented in Figure 3 and SI, Supplementary Figure S2. First, we compare the ability of the nine methods [SCA, MI, OMES, MIp, PSICOV and DI (solid colored curves) and MI^(S)_, OMES^(S) and MIp^(S) (dashed colored curves)] to detect coevolving pairs that make intramolecular contacts (Fig. 3a and Supplementary Fig. S2b). To this aim, we examined the location of the top-ranking signals in the PDB structure of each investigated protein (Supplementary Table S2) and evaluated the percentage of 3D-contact-forming pairs (see Supplementary Fig. S3). The results are shown (z-axis) for increasingly larger subsets of predictions, starting from the strongest 0.1% coevolution signals, up to 20%. Results for individual proteins are displayed as a bundle of gray dashed curves. The averages over all proteins yielded the colored curves as a function of signal strength. A broad range of performance is observed. PSICOV and DI exhibit the highest performance; 87–88% of coevolving pairs predicted by these two methods that rank in the top 0.1% subset make 3D contacts. These are TPs whose coevolutionary behaviour may be rationalized by their physical interactions. The performance of these two methods drops with coverage, e.g. to 52–54% when the top 1% predictions are considered. In contrast, MI, MI^(S) and SCA exhibit the poorest performance; the corresponding fractions of TPs are 30–34% and 19–20% for the respective subsets. The lower panel in Figure 3b provides a clear comparison of these results obtained by DI, PSICOV, SCA and MI^(S), OMES^(S) and MIp^(S) averaged over all proteins and their standard deviations (see also Supplementary Fig. S2b). The two best performing methods, DI and PSICOV, are followed by MIp^(S), and then OMES, in the range less than 1%. Notably, MIp^(S) outperforms all others when a higher fraction of predictions (e.g. top 20%) is considered, as will be further discussed below.

Fig. 3.

Comparative analysis of the performance of different methods. (a) Ability to detect residue pairs that make contacts in the 3D structure. The fraction of contact-making pairs is plotted for increasingly larger subsets of pairs predicted to be coevolving (between the strongest 0.1% and 20% signals obtained by the indicated methods). DI and PSICOV outperform all other methods. (b) Results from two tests: elimination of intermolecular signals for non-interacting pairs (top) and detection of intramolecular contact-making pairs (bottom) displayed for six methods as a function of coverage. See more details in SI, Supplementary Figure S2. The bars in the lower plot are broken down into four pieces corresponding to contacts of various orders (1, 2, 3, and ≥4, starting from bottom) permitting us to distinguish between local (near-neighbours along the sequence) and non-local (spatially close but sequentially distant) contacts. Top-ranking predictions made by PSICOV contain the largest proportion of non-local contacts

Most methods were found to successfully eliminate intermolecular FPs. The upper panel in Figure 3b shows that the percentage of intermolecular signals (FPs) is approximately 5–30% (or that of intramolecular signals 70–95%) in general, with a small dependence on the method and overall decrease with increasing coverage (see also SI, Supplementary Fig. S2a). PSICOV and DI practically have no FPs among the top 0.5% coevolving pairs; and MIp, MIp^(S), OMES and OMES^(S) show equally good performance. In all these six cases, the fraction of FPs (intermolecular signals) remains smaller than 8% among the top-ranking 1% signals; whereas in the case of MI^(S) and SCA, the same fraction increases to 20–25%. Notably, the performance of MIp^(S) shows the least deterioration with increasing coverage, as already noted in the above illustrative case.

As an additional test, we examined the ability of these methods to predict not only contact-making pairs, but those pairs that are not nearest neighbours along the sequence. These will be termed non-local contacts (they are localized in space, but not along the sequence). The horizontal lines on the bars in Figure 3b (lower panel) indicate the proportions of contacts of different orders, starting from order 1 (bottom), then orders 2, 3 and finally more than or equal to 4 (top portion) which are viewed as non-local. A contact of order k means a contact made between residues i and i + k. In principle, it is conceivable that some of the neighbouring residues coevolve, compensating for some properties on a local scale. More interesting are the non-local couplings, which can serve as constraints for structure prediction. PSICOV yields the highest proportion of non-local contacts, followed by DI, again demonstrating the superior performance of these two methods.

3.4 Validation with Dataset II

As a further validation, we repeated the same analysis with Dataset II of 2330 protein pairs extracted from the Negatome database. Supplementary Figure S4 shows that the results obtained for Dataset II closely reproduced those obtained with Dataset I. The major difference was the larger variances in this case (shown by error bars), which resulted from the broader distribution of chain lengths (N) as well as the relatively small size of some of the MSAs included in Dataset II (see Supplementary Fig. S1). Note that the outputs here correspond to the MI, MIp and OMES in the absence of shuffling (which does not lend itself to high-throughput evaluation of thousands of MSAs). This mainly affects the performance of MIp at around 20% as can be seen in the figure. This further set of computations confirmed the robustness of the results presented in Figure 3, and firmly established the significantly higher ability of DI and PSICOV to detect residue pairs making 3D contacts.

3.5 Dependence on MSA size and efficacy of shuffling algorithm

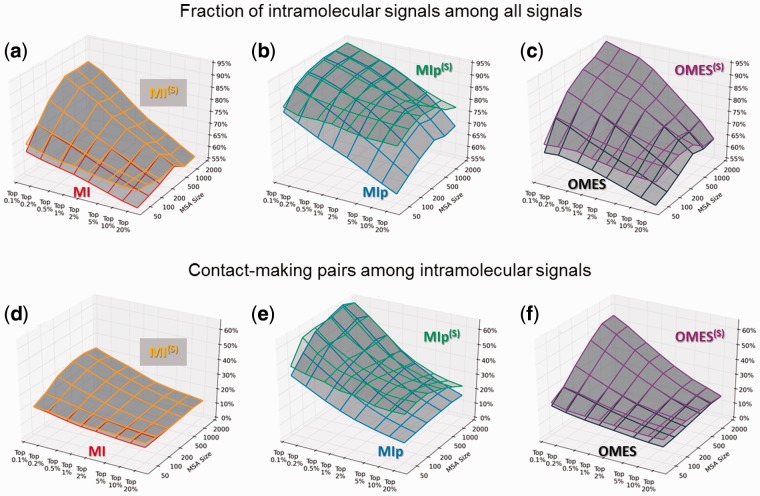
The above computations indicated an improved performance upon implementation of shuffling algorithms in the case of MIp, while the effects on MI and OMES were negligible on average. However, by looking closely at individual cases, we found that shuffling may be very effective for particular pairs (e.g. pairs 1 and 2) whose MSAs comprise fewer sequences. We speculated that the effectiveness of the shuffling algorithm correlates with the size of the MSA; those MSA containing fewer sequences benefiting more from this type of refinement. A systematic examination indeed showed that the level of improvement upon shuffling strongly depends on the size m of the MSAs. Figure 4 demonstrates the above observation. In order to obtain those results, we generated a series of MSAs with varying sizes in the range [50 ≤ m ≤ 2000] by choosing random subsets of concatenated sequences from the MSAs generated for Dataset I, as summarized in SI, Supplementary Table S4; and computations were performed for these test MSAs, using the three methods that lend themselves to shuffling, MI, MIp and OMES.

Fig. 4.

Effectiveness of shuffling algorithm as a function of MSA size and coverage. The performance of three methods before (lower surface) and after (upper surface) implementation of shuffling algorithm is compared, with respect to their ability to eliminate intermolecular FPs (a–c) and to identify evolutionarily correlated pairs that make direct contacts in the 3D structure (d–f). Shuffling algorithm partially compensates for the loss in accuracy that originates from the use of smaller size MSAs (containing for example a few hundreds of sequences) as well as that occurring with increasing coverage

As can be clearly seen in Figure 4, upon implementation of the shuffling algorithm, all methods exhibit some improvement in their ability to eliminate intermolecular FPs (panels a–c) and their ability to detect pairs supported by physical interactions in the 3D structures (panels d–f). The improvements are more pronounced when the input MSAs are smaller. Furthermore, shuffling helps when larger subsets of predictions (e.g. top 20%) are considered. In summary, shuffling emerges as a useful tool in the absence of a sufficiently large number of sequences that can be used in the MSA, and/or for alleviating the decrease in accuracy with increasing coverage.

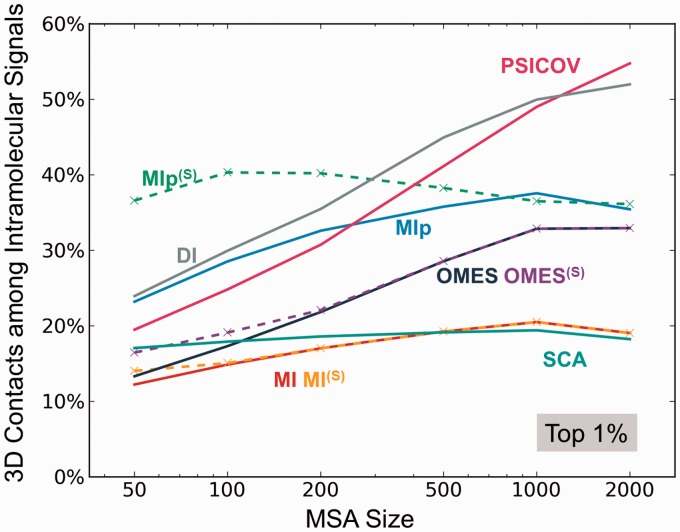
As a further assessment, we repeated the calculations for all nine methods and examined their ability to detect coevolving pairs that make contacts in the 3D structure as a function of MSA size. The results, based on the strongest 1% coevolution signals are presented in Figure 5. Their counterparts for the 0.1% and 10% subsets are presented in the respective panels a and b of Supplementary Figure S5. Notably, if the MSA size is of the order of a few hundreds of sequences (as opposed to a few thousands), MIp^(S) emerges as the method of choice: it allows for the detection of the highest proportion of contact-making pairs. This distinctive feature is particularly striking when the MSA contains 50–100 sequences (Figure 5), or when a larger coverage (of potentially contact-making residue) is of interest (see Supplementary Fig. S5b).

Fig. 5.

Dependence of the performance of different methods on the size of the MSA. The abscissa shows the number m of sequences included in the MSAs. The ordinate shows the percentage of 3D contact-making pairs among the most strongly coevolving (top 1%) pairs of residues predicted by different methods. PSICOV and DI show a strong dependence on m. MIp^(S) is distinguished by its superior performance when the number of sequences is as low as 50. See also the results for top 0.1% and 10% covarying residues in SI, Supplementary Figure S5. The latter case further exposes the distinctive effectiveness of MIp^(S) for identifying 3D contact-making pairs

3.6 Development and validation of a hybrid method

The above analysis exposes the different strengths of various methods in detecting of contact-making residue pairs, in discriminating intermolecular FPs and in dealing with small MSAs or providing more coverage at a relatively small loss in accuracy. Of interest is to examine the consistency of the predictions, i.e. to see whether the different methods are detecting different subsets of correlated pairs. Such an assessment of the overlap between predictions would also help in designing a hybrid method that takes advantage of the strengths of different methods. To this aim, we calculated the average correlation coefficients, s(a, b), between the top 20% predictions from each pair of methods (a, b).

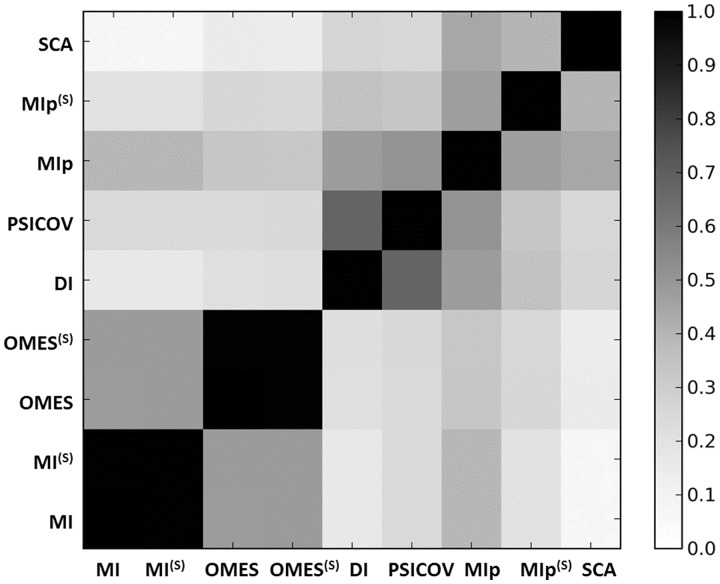
The results are shown in Figure 6. This analysis reveals that the DI and PSICOV yield consistent results with correlation coefficient s(DI, PSICOV) = 0.67, which may be attributed to the fact that both methods use a global optimization scheme that retrieves direct contacts. Likewise, MI and OMES (and their shuffled versions) show some overlap. MI and OMES are based on different formulations, but they both measure the observed departure from the expected results, which may explain their correlation of s(MI, OMES) = 0.48. MIp shows moderate correlations with all methods (except OMES), which vary between s(MIp, MI) = 0.39 and s(MIp, PSICOV) = 0.51. In contrast, SCA yields weak correlations (<0.26) with all methods, except with MIp (s = 0.44).

Fig. 6.

Correlation between the predictions of different methods. The entries represent the correlation coefficients calculated for the top 20% predictions made by the different methods, averaged over all proteins

The above analysis suggests that one might combine methods that exhibit different strengths to devise hybrid methods that may potentially outperform the individual methods. The construction of a model based on two methods has been successfully accomplished by Eloffson and coworkers (Skwark et al., 2013), by combining plmDCA and PSICOV to build the PconsC method. Recent application of PConsC (Michel et al., 2014) was found to improve protein models by improving contact predictions.

Towards this goal, we focused first on PSICOV and DI as they exhibit superior performance (see Fig. 3 and Supplementary Fig. S2). We designed a combined naïve Bayes classifier utilizing these two methods (Fig. 7). 162 Pfam families were utilized as training set, the properties of which are detailed in SI, Supplementary Table S3, along with the criteria for their selection from the entire dataset of Pfam families. PSICOV and DI matrices were calculated for all the 162 families, and each residue pair was classified as positive (+) (within interatomic distance range of 8Å in the 3D structure) or negative (−) (if otherwise). The density distributions of the positive and negative classes were modeled by kernel density estimation based on PSICOV and DI values (Fig. 7b). The kernel width was determined by Silverman’s rule (Silverman, 1986). For a given combination of DI and PSICOV scores, the combined method provides the posterior probability for positive as

$$P(+\text{|DI,PSICOV})=\frac{P(DI,PSICOV|+)P(+)}{P(DI,PSICOV|+)P(+)+P(DI,PSICOV|-)P(-)}$$ (1)

Fig. 7.

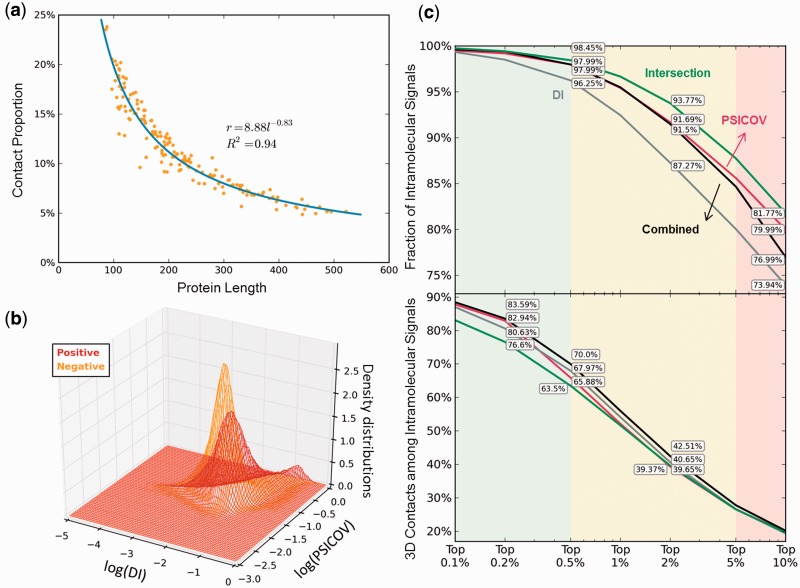
Development of hybrid methods. (a) Assessment of prior probability of 3D contact, P(+), by a regression analysis of a training set of 162 structurally known protein sequences. (b) Density distributions of positive and negative signals, P(DI, PSICOV∣+) and P(DI, PSICOV∣−) (see Equation 1), modelled by kernel density estimation. (c and d) Comparative performance of the individual methods DI (gray) and PSICOV (red), and the combined naïve Bayes classifier method (Equation 1) (black), based on the fraction of intramolecular signals (c) and fraction of 3D contact-making pairs (d). The predictions based on the intersection of MIp, DI and PSICOV are shown by the green curve

Application of this classifier to our dataset showed that an improvement, albeit incremental (e.g. 4.12% with respect to PSICOV for the subset of top 0.5% predictions), can be achieved over either method in so far as the prediction of contact-making pairs is concerned (Fig. 7d).

We note that for PconsC, on average nearly three quarters of the top N predictions seemed to be correct (Michel et al., 2014). This means, for a protein of 200 residues for example, the top 200 predictions, i.e. the top 1% (i.e. f = 0.1% using fN(N − 1)/2 = N for N = 200), and this fraction will be N-dependent. The performance of 75% of PconsC is thus achieved in our case if f < 0.4%, which would correspond to a protein length of N > 500. In the case of smaller proteins, e.g. N = 300, the fraction of contact-making residues drops to 65%. The hybrid method at that level of coverage shows an improvement of about 2–4% above either of the individual (DI and PSICOV) methods. We also checked whether the combined method can also eliminate intermolecular FPs as efficiently as PSICOV (which showed the best performance), and although the method was not trained on these properties, a performance comparable to that of PSICOV was obtained (Fig. 7c).

Finally, we examined whether one might obtain more accurate results upon selecting the intersection of the best methods. Examination of the intersection of PSICOV and DI did not provide an improvement over the individual methods when the same level of coverage was aimed, i.e. the top-ranking 1000 overlapping results from DI and PSICOV picked up entries ranking lower in the output list, which contained negative results. On the other hand, given the consistency of MIp with a broad range of methods, we examined the consensus predictions (or intersection) from MIp, DI and PSICOV. At the same level of coverage, the intersection led to a considerable improvement (e.g. 6.5% compared with DI, at top 2% signals) in eliminating intermolecular FPs, as depicted by the green curve in Figure 7c, but not in identifying 3D contact-making pairs (Fig. 7d).

4 Conclusion

The above comparative analysis led to the following conclusions summarized below in the context of three groups of outputs/regimes, colored light green, yellow and pink in Supplementary Figs. S2 and S7: strong coevolution signals (ranked in the top 0.5% subset), intermediate signals (0.5–5%) and relatively weak signals (5–20%).

First, among all studied methods, PSICOV and DI yielded the best performance in the strong signal regime. Both methods were successful in accurately detecting coevolving pairs of residues that make contacts in the 3D structure (Fig. 3a and b and Supplementary Figs. S2b and S4) including non-local contacts, or in eliminating the intermolecular FPs (Fig. 3b and Supplementary Fig. S2a). Their performance was particularly impressive when the strongest coevolutionary signals (top 0.1%) were considered. For a protein of N = 300 residues, 0.1% means 0.001 × N(N − 1)/2 ≈ 45 pairs. Thirty-nine of them predicted by these methods were, on average, observed to form inter-residue contacts in the structure; likewise, among the top 0.5% signals, 157 pairs (out of 224) would make contacts. The predictions thus help not only in elucidating evolutionarily relationships, but also in assisting in structure prediction. These methods are therefore uniquely useful in cases where no suitable template structures are available. DI indeed showed remarkable success in predicting the structures of membrane proteins (Hopf et al., 2012).

Second, in the intermediate regime, while the proportion of contacts among coevolving pairs predicted by PSICOV and DI remains high, we note that the discriminatory ability of OMES and MIp (and their shuffled versions) between intermolecular and intramolecular interactions start to pick up and outperform that of DI. Notably, MIp^(S) exhibits the highest performance in the relatively weak (but high coverage) regime, both in terms of elimination of FPs and identification of 3D contact-making TPs. This superior performance of MIp in situations where DI and PSICOV start to underperform is noteworthy. Two such situations are: (i) the search for a large number of predictions (or higher coverage) albeit at lower accuracy, and (ii) the search for coevolving pairs that potentially make 3D contacts, in the absence of a sufficient number of sequences (see Figs. 5 and Supplementary Fig. S5). MIp^(S) emerges as the method of choice in those situations. For example, if one is interested in exploring coevolutionary patterns within a small (sub)family of 50–200 sequences, one-third of predictions made by MIp^(S) would be, on the average, making contacts in the 3D structure among the top 10% signals; see Supplementary Fig. S5b). This subset of signals contains 4500 pairs for N = 300, of which 1500 would be physically interacting. This is a large majority of native contacts, based on inter-residue coordination number of z = 12 within 10 Å.

Third, the study highlights how the size m of MSA, a parameter known to be an important determinant of the statistical significance of results, affects different methods. It is well known that larger MSAs usually give better results, and some methods have specified lower bounds for m: 100 sequences for SCA, 250 for sensitive results from DI, and 1000 for full DI performance (Morcos et al., 2011). PSICOV doesn’t specify a lower bound, but there is a clear correlation between performance and MSA size (Jones et al., 2012). However, the present study further shows that the deficiency arising from small MSAs can be partially offset by the shuffling algorithm (Fig. 4). Shuffled MIp^(S) in particular emerges as a better choice than DI and PSICOV when dealing with small MSAs. Generally speaking, we need more than m = 250 sequences to justify the use of the computationally expensive DI and PSICOV methods; otherwise, MIp might be preferred together with a shuffling algorithm (Fig. 5 and Supplementary Fig. S5).

On a practical side, both PSICOV and DI involve the inversion of a covariance matrix and/or global optimization algorithms which may take hours, even days, depending on the size of the MSA. Specifically, PSICOV and DI need each about 2.5 GB memories to analyse a 400-residue MSA. The memory requirement increases quadratically with sequence size, and this O(N²) dependence may become prohibitively expensive for large proteins. The computing time for inverting the DI covariance matrix scales between N^2.373 (Williams, 2012) and N³ depending on the algorithm and parameters. MI, MIp and OMES, on the other hand, are very fast. As such, they lend themselves to high-throughput analysis, thus allowing for statistical inferences about sequence-structure-dynamics-function relations (see e.g. Liu and Bahar, 2012). Even though shuffling is time-consuming, it needs very small memory and we could speed up the calculation by adjusting the number k of shuffles because the computing time scales linearly with k, as O(kN²m). So, vis-à-vis the tradeoff between accuracy and efficiency, MIp^(S) could serve as an optimal approach, especially for MSAs of large proteins containing a small number of sequences.

Finally, our analysis permitted us to develop a hybrid method that takes advantage of the strengths of DI and PSICOV. The improvement in performance is incremental due to an already high overlap of 0.68 between the predictions of DI and PSICOV. Yet, one may advantageously adopt this hybrid method to maximize the fraction of contact-making predictions, especially in the intermediate coverage regime. Another useful recipe for case studies is to select the intersection of DI, PSICOV and MIp, which appears to be particularly useful for eliminating FPs. All methods are accessible via the Evol extension of ProDy (Bakan et al., 2014).

Funding

Funding from the National Institutes of Health grants (5P41 GM103712 and 5R01 GM099738 to I.B.) is gratefully acknowledged.

Conflict of Interest: none declared.