Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Jun 26;5:11793. doi: 10.1038/srep11793

Plasmonic Toroidal Dipolar Response under Radially Polarized Excitation

Yanjun Bao 1, Xing Zhu 1, Zheyu Fang 1,2,a
PMCID: PMC4481838  PMID: 26114966

Abstract

Plasmonic toroidal resonance has attracted growing interests because of its low loss electromagnetic properties and potential high sensitive nanophotonic applications. However, the realization in a metamaterial requires three-dimensional complicated structural design so far. In this paper, we design a simple metal-dielectric-metal (MIM) sandwich nanostructure, which exhibits a strong toroidal dipolar resonance under radially polarized excitation. The toroidal dipole moment as the dominant contribution for the scattering is demonstrated by the mirror-image method and further analyzed by Lagrangian hybridization model. The proposed toroidal configuration also shows a highly tolerant for misalignment between the structure center and the incident light focus. Our study proves the way for the toroidal plasmonic application with the cylindrical vector beams.

Toroidal dipole moment, characterized by currents flowing on the surface of a torus along its meridians, was first considered by Zel’dovich1 to explain parity violation in the weak interaction in nuclear physics. The static toroidal moment has been found in many natural materials, including ferroelectric2, ferromagnetic3 and magnetoelectric structures4,5, as well as biological materials6,7. Since the toroidal dipole moment violates both the space-inversion and time-reversal symmetries, many intrigue phenomena such as non-reciprocal refraction of light8, lasing spaser9 and dichroism10 have been predicted. Although the importance of static toroidal moment in solid state systems and particle physics has been recognized, the dynamic toroidal dipole moment in the classical electromagnetism is less known. Unlike the conventional dynamic multipoles, the toroidal dipole moment is not included in the standard multipole expansion11. With the intensity much weaker than the electric and magnetic resonance, the toroidal response is extremely hard to be observed in the experiment.

Metamaterial, an artificial sub-wavelength structure, that is engineered to have properties not available in natural materials, has become a subject of growing interest owing to a number of appealing applications such as artificial magnetic response12, cloaking13, negative refraction14,15 and perfect absorber16. Recently, by properly arranging four three-dimensional split rings in a unit cell, Kaelberer et al. demonstrated the existence of the toroidal dipolar resonance in the microwave frequency17 and Huang et al. further pushed its resonance to the optical frequency by scaling down the split-ring size18. Subsequently, various structures, such as asymmetric double-bars19, multifold double-rings20, oligomer nanocavities21, and other structures22,23,24,25,26,27 were proposed to support the dominant toroidal resonance. However, because the electromagnetic field distribution of linearly polarized light preserves space-inversion symmetry, geometric asymmetries are always introduced for the aim of space-inversion symmetry breaking17,18,19. This makes the structure complicated, which is quite a challenge for the modern nanofabrication especially at optical frequencies.

Cylindrical vector beam (CVB, such as radially and azimuthally polarized light) is a special light source with highly symmetric electromagnetic field distribution and ultra-small focal spot size (0.07λ2)28,29. Due to their unique polarization properties, the CVB is an excellent light source for the investigations of light-matter interaction in nano-optics, like high resolution imaging30,31, plasmonic focusing32,33, and other nanoplasmonic applications34,35,36,37,38. In this paper, we aim to eliminate the aforementioned challenge of the toroidal metamaterial design. Under the radially polarized light with inherently broken space inversion symmetry, the toroidal dipolar moment can be strongly excited in a metal-dielectric-metal (MIM) sandwich nanostructure. In addition, mirror-image method and Lagrangian hybridization model are used to understand and analyze the finite difference time domain (FDTD) simulation results.

Results

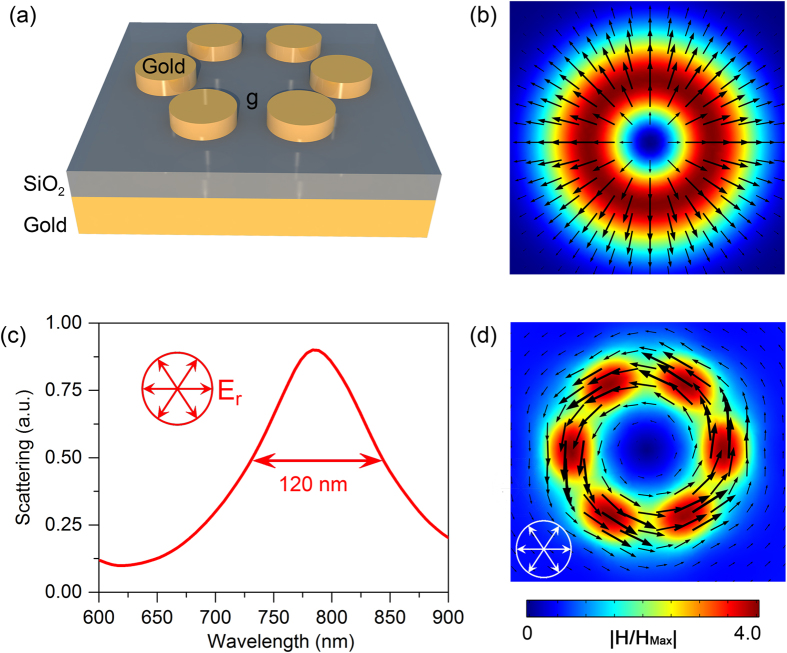
Figure 1a illustrates the geometry of the proposed toroidal structure, which is composed of a gold hexamer and a bottom gold mirror separated by a layer of silicon dioxide (SiO2). The numerical simulations were performed by using FDTD method. Radially polarized light with electric field parallel to the radius vector from the axis (Fig. 1b) was used to excite the structure. The refractive index of the SiO2 layer is chosen as 1.45 and the permittivity of gold is obtained by fitting the experimental data from the literature39. Figure 1c shows the calculated scattering spectra of the toroidal structure under radially polarized light (See Methods). A resonance peak appears at 785 nm in the scattering spectrum with a full-width at half-maximum (FWHM) of 120 nm. The optical response of the designed structure is also investigated under the excitation of linearly polarized light, where a resonance peak is observed at 750 nm with a FWHM of 150 nm (Figure S1a, Supporting Information). The different FWHMs under the two incident lights indicate the excitation of a lower loss mode under radially polarized light.

Figure 1. Structure of the toroidal structure and its optical response under radially polarized light.

Figure 1

Open in a new tab

(a) A schematic view of the toroidal structure composed of a gold hexamer and metallic mirror separated by a dielectric layer. The diameter and thickness of the gold disks are 120 nm and 30 nm, respectively. The thickness of the SiO2 spacer is 30 nm and the thickness of the gold mirror is 60 nm. The gap size between two neighbor gold disks is g = 50 nm. (b) The intensity and field profiles of radially polarized light. The black arrows indicate the vectors of the incident electric fields. (c) The FDTD calculated scattering spectra of the toroidal structure under radially polarized light. (d) The simulated magnetic field at the center of the dielectric layer at the resonance peak of 785 nm. The black arrows represent the vectors of the magnetic fields.

To understand the inside physics of the difference, the magnetic field distributions at the resonance peaks under the two optical excitations are calculated. It is known that, a gold disk and a bottom layer separated by a dielectric spacer can be regarded as a magnetic resonator (MR), in which antiparallel currents are excited in two gold layers, resulting in a strong magnetic dipole moment40,41. For the radially polarized light, a toroidal response characterized by a closed loops of the magnetic field is clearly observed (Fig. 1d). While for the linearly polarized light, the vectors of the magnetic field are split in two bundles at the left and right halves of the structure, leading to a net magnetic dipole along the y direction (Figure S1b, Supporting Information). The different FWHM values under the two optical excitations can be easily understood since the toroidal dipolar response has a higher quality factor as compared with that for a magnetic dipole mode17.

Although the toroidal dipolar response is observed, it should be made clear that if there are other multipoles, other than the toroidal moment, contributing significantly to the scattering spectrum. The conventional way is to calculate and compare the scattering powers of various multipolar moments by using the induced current in the metal. However, this method is difficult to deal with structure involving a metallic substrate. When a scatterer is placed above a planar metallic surface, the light is scattered into the out-of-plane propagating waves and surface plasmon-polariton (SPPs) waves propagating along the surface42,43. In this case, the currents in the metallic substrate include various components, such as the background field, the scatterer-induced field and the SPPs field, which cannot be used to calculate the multipolar moments. Nevertheless, for an in-plane current source j// placed above a lossy metallic ground (Fig. 2a), the field in the upper half-space can be considered as the superposition of contributions from the real source j// and its mirror image j’// = αj//. The correction factor α is given by44

Figure 2. Calculations of the scattering power from multipoles.

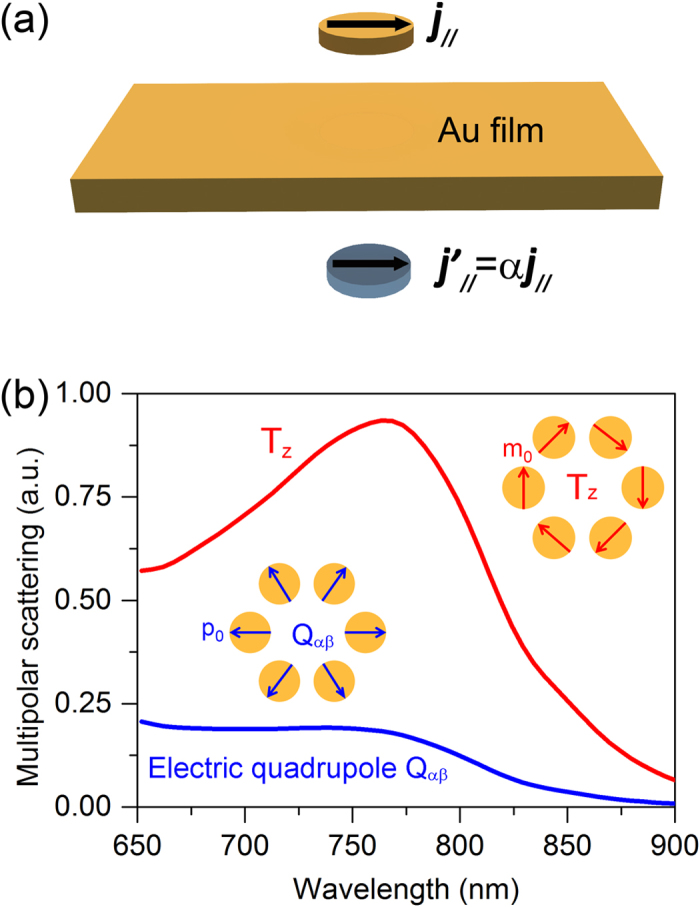
Figure 2

Open in a new tab

(a) Schematic of the mirror imagej’// for an in-plane current dipole source j// placed above a lossy metallic ground. (b) The arrangements of the residual electric dipoles and induced magnetic dipoles of the six MRs. (c) The calculated scattering powers for various multipole moments calculated from the currents in the upper gold hexamer and its image.

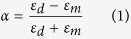graphic file with name srep11793-m1.jpg

where εd(m) is the relative permittivity of the dielectric in the upper half space (the metallic ground). For a perfect electrical conductor (PEC) ground with εm → + ∞i, the correction factor isα = −1. Since the mirror image j// cannot totally offset the real source current j// in the optical frequency, each MR possess a residual electric dipole p0 and a magnetic dipole m0.

Under the illumination of radially polarized light, the six magnetic (electric) dipoles are azimuthally (radially) oriented at the vertexes of a hexagon, resulting in non-zero multipolar moments of electric quadrupole and toroidal dipole, as shown in inset of Fig. 2b. Due to the symmetry of the six electric and magnetic dipoles, the multipoles of the net in-plane electric dipolesp//, magnetic dipoles and magnetic quadruples are all zero. The scattering powers of the multipolar moments are then calculated from the induced currents in the upper gold hexamer and its mirror image, as shown in Fig. 2b. As the figure shows, the z component of the toroidal moment Tz gives the dominant contribution in the entire considered frequency range and reaches its maximum at the resonance wavelength, demonstrating that the scattering power is mainly arisen from the toroidal dipole.

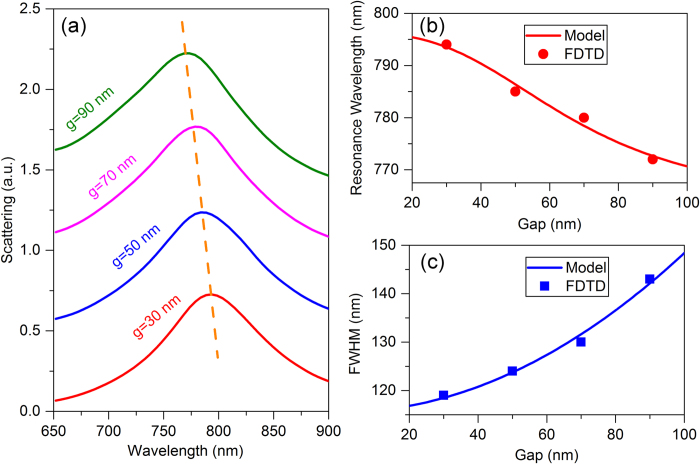
In Fig. 3a, we present the evolution of the calculated scattering spectra with the gap size g (defined in Fig. 1a) varying from 30 nm to 90 nm under radially polarized light. The resonance wavelength of the toroidal dipole mode is extracted and plotted in Fig. 3b (red filled circles), which shows a blue-shift with the increasing of the gap g. To understand the coupling of the six MRs, A Lagrangian hybridization model is adopted. The Lagrangian of the coupled system can be written as45

Figure 3. Optical responses of the toroidal structure with different gap size.

Figure 3

Open in a new tab

(a) The FDTD calculated scattering spectra for the gold hexamer with the gap size ranging from 30 nm to 90 nm under radially polarized light. The offset between curves in (a) is 0.5. Dashed lines are drawn to guide the eye of the resonance peaks. The resonance wavelength (b) and the FWHM (c) of the toroidal mode dependence on the gap size. The solid circles and squares are the FDTD simulated data and the solid lines are the fittings of the model.

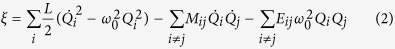graphic file with name srep11793-m2.jpg

where L and ω0 are the inductance and resonance frequency of a single MR, Qi(Qi) represents the charge (current) on the ith MR, Mij and Eij are the mutual inductances for the magnetic and electric interactions between the ith and jth MRs, respectively. Based on the orientations of the six electric and magnetic dipoles (inset of Fig. 2b), the resonance frequency of the coupled system can be obtained as (see details in the Supporting Information)

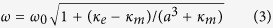graphic file with name srep11793-m3.jpg

where a is the size length of the hexagon (a = d + g, d is the diameter of the gold disk, 120 nm), κm and 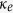Inline graphic represent the coupling coefficients of the overall magnetic and electric dipole-dipole interactions, respectively. It is obvious that the interaction between magnetic dipoles is attractive while the interaction between electric dipoles is repulsive. The blueshift with the increasing of the gap indicates that the magnetic dipole-dipole coupling strength κm exceeds the electric dipole-dipole coupling strength κe, showing that the overall coupling is attractive. Thus with increasing of the gap, the coupling is less attractive and the resonance wavelength blueshifts.

By fitting the data of the resonance wavelength (red solid line in Fig. 3b), the coupling strengths are easily to be calculated out as κm = 7.5 × 106 nm3 and κe = 6.3 × 106 nm3, which indeed shows κm>κe. To further demonstrate the correctness of this model, we consider a gold hexamer structure without the gold mirror, which is illuminated by radially polarized light. Since only the electric dipole-dipole interactions are involved in the system, the resonance wavelength is expected to exhibit a red-shift with increasing the gap, which is verified by the FDTD simulation (see details in Supporting Information).

The FWHM of the toroidal dipolar resonance as a function of the gap g is shown in Fig. 3c (blue filled squares). The FWHM Δf is associated with the Q factor and is defined as Δf = f/Q = fΔE/2πE46, where f is the frequency, E is the energy stored in the structure and ΔE is the dissipated energy. The dissipated energy ΔE is the sum of the Ohmic losses ΔEm in the metal and radiation losses ΔEr. For simplicity, we consider the Ohmic losses ΔEm and the stored energy E to be independent on the gap g. From the arrangement of the electric and magnetic dipoles of MRs, we can directly calculate the radiation losses as (see details in Supporting Information)

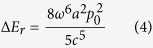graphic file with name srep11793-m5.jpg

for the electric quadruple and

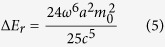graphic file with name srep11793-m6.jpg

for the z component of the toroidal dipole Tz. Thus the FWHM Δλ can be written as

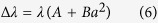graphic file with name srep11793-m7.jpg

where A and B are two parameters, λ is the resonance wavelength. By fitting the FDTD data with the analytical prediction of Eq. 6, we can estimate the parameters as A = 0.112 and B = 1.6 × 10−6 nm−2. The fitting curve in Fig. 3c (blue solid line) agrees well with the results of FDTD simulation (blue solid squares).

In the above analysis, we consider the beam center to overlap with that of the hexamer. However, at nanometer scale such alignment is difficult and some deviations may occur in practice. In order to investigate the optical response of the designed toroidal structure under such deviations, the scattering power from the multipoles as a function of the misalignment between the structure center and the incident light focus at the toroidal dipolar resonance is shown in Fig. 4. The contribution from the magnetic quadrupole Mαβis almost zero for different misalignments. For Tz, its scattering power almost maintains constant with the increasing of the misalignment. When the beam and the hexamer are not perfectly aligned, the scattering powers from the y component of the magnetic dipole My and the in-plane of the electric dipole p// emerge and increase with the increasing of the deviation, as well as the electric quadrupole Qαβ. The sharpest increase is observed for My, mainly as a consequence of the asymmetry breaking of the magnetic dipoles. Although the ratio of Tz in the total scattering power decreases as the misalignment is increased, it still gives the dominant contribution when the deviation is less than 50 nm, showing a robust, misalignment tolerant properties of the designed structure. The inset figure shows the magnetic field distributions when the beam center is misaligned of 50 nm, where a clear toroidal dipolar response can still be observed.

Figure 4. The misalignment tolerance property of the toroidal structure.

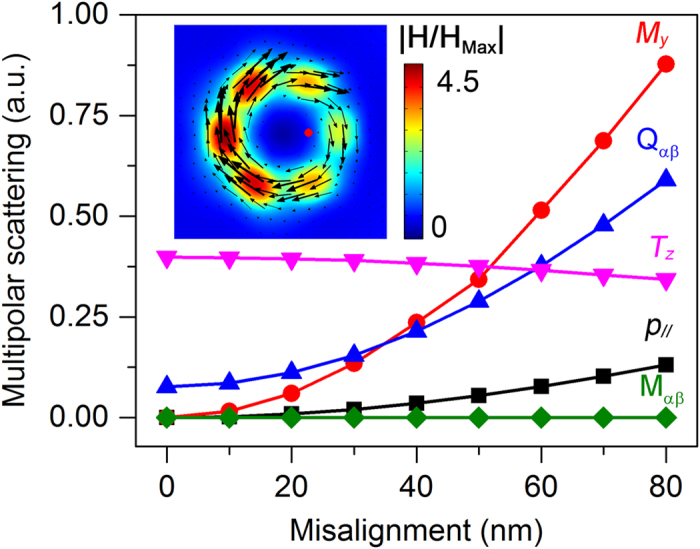
Figure 4

Open in a new tab

The scattering powers from the multipoles as a function of the misalignment between the structure center and the incident light focus. The inset figure shows the magnetic field distributions when the beam center is misaligned of 50 nm (red solid circle). The black arrows represent the vectors of the magnetic fields.

Discussion

We theoretically studied a novel MIM structure that exhibits resonant toroidal dipolar response in the optical frequency. Our configuration is based on the magnetic resonance of a gold disk placed on a gold mirror separated by a dielectric layer. By illuminating a radially polarized light, the designed structure is capable of suppressing the components of electric and magnetic dipole moments due to the symmetries of the incident light and structure. We show that the toroidal moment formed by a closed loop of the magnetic dipoles gives the dominant contribution in the scattering spectrum, which is much higher than that of the electric quadruple arising from the net electric dipoles due to the non-perfect mirror image of the gold disk. By investigating the frequency shift of the toroidal mode dependence on the gap of the gold hexamer, we further demonstrate that the magnetic dipole-dipole coupling exceeds the electric dipole-dipole coupling. Our study opens the way for the realization of unique resonance modes, combining complex plasmonic structures with the remarkable properties of cylindrical vector beam.

Methods

Simulation

The numerical computations were carried out by the software FDTD method. The radially polarized light has a doughnut-shape field distribution of E0·r·exp(−r2/σ2), where σ is the beam waist and is assumed to be 250 nm in the calculations. For the calculation of the scatter spectrum, we first computed a background fields from the radially polarized light incident on the substrate, and then calculated the total fields with the Au nanostructures present. The scattered fields were defined as the differences between the total fields and the background fields.

Additional Information

How to cite this article: Bao, Y. et al. Plasmonic Toroidal Dipolar Response under Radially Polarized Excitation. Sci. Rep. 5, 11793; doi: 10.1038/srep11793 (2015).

Supplementary Material

Supporting Information
srep11793-s1.doc (544.5KB, doc)

Acknowledgments

This work is supported by National Science Foundation of China (Grant No. 61422501 and 11374023), the National Basic Research Program of China (973 Program, Grant No. 2015CB932403), Beijing Natural Science Foundation (Grant No. L140007), and Foundation for the Author of National Excellent Doctoral Dissertation of PR China (Grant No.201420).

Footnotes

Author Contributions Y.B. conceived the idea, performed the numerical simulations and did the theoretical calculations. The manuscript was written by Y.B. and Z.F. in consultation with all other co-authors. Z.F. and X.Z. supervised the project.

References

  1. Zeldovich I. B. The Relation between Decay Asymmetry and Dipole Moment of Elementary Particles. Sov. Phys. JETP 6, 1148–1155 (1958). [Google Scholar]
  2. Wang J. & Zhang T. Y. Effect of long-range elastic interactions on the toroidal moment of polarization in a ferroelectric nanoparticle. Appl. Phys. Lett. 88, 182904 (2006). [Google Scholar]
  3. Klaui M., Vaz C. A. F., Lopez-Diaz L. & Bland J. A. C. Vortex formation in narrow ferromagnetic rings. J. Phys.: Condens. Matter 15, R985–R1023 (2003). [Google Scholar]
  4. Spaldin N. A., Fiebig M. & Mostovoy M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys.: Condens. Matter 20, 434203 (2008). [Google Scholar]
  5. Popov Y. F., Kadomtseva A. M., Belov D. V., Vorob’ev G. P. & Zvezdin A. K. Magnetic-field-induced toroidal moment in the magnetoelectric Cr2O3. JEPT Lett . 69, 330–335 (1999). [Google Scholar]
  6. Hingorani M. M. & O’Donnell M. A tale of toroids in DNA metabolism. Nat. Rev. Mol. Cell Biol. 1, 22–30 (2000). [DOI] [PubMed] [Google Scholar]
  7. Hud N. V. & Vilfan I. D. Toroidal DNA condensates: Unraveling the fine structure and the role of nucleation in determining size. Annu. Rev. Biophys. Biomol. Struct. 34, 295–318 (2005). [DOI] [PubMed] [Google Scholar]
  8. Sawada K. & Nagaosa N. Optical magnetoelectric effect in multiferroic materials: evidence for a Lorentz force acting on a ray of light. Phys. Rev. Lett. 95, 237402 (2005). [DOI] [PubMed] [Google Scholar]
  9. Huang Y. W. et al. Toroidal lasing spaser. Sci. Rep. 3, 1237 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Papasimakis N., Fedotov V. A., Marinov K. & Zheludev N. I. Gyrotropy of a metamolecule: wire on a torus. Phys. Rev. Lett. 103, 093901 (2009). [DOI] [PubMed] [Google Scholar]
  11. Dubovik V. & Tugushev V. Toroid moments in electrodynamics and solid-state physics. Phys. Rep. 187, 145–202 (1990). [Google Scholar]
  12. Pendry J. B., Holden A. J., Robbins D. J. & Stewart W. J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 47, 2075–2084 (1999). [Google Scholar]
  13. Schurig D. et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006). [DOI] [PubMed] [Google Scholar]
  14. Smith D. R., Pendry J. B. & Wiltshire M. C. Metamaterials and negative refractive index. Science 305, 788–792 (2004). [DOI] [PubMed] [Google Scholar]
  15. Shelby R. A., Smith D. R. & Schultz S. Experimental verification of a negative index of refraction. Science 292, 77–79 (2001). [DOI] [PubMed] [Google Scholar]
  16. Landy N. I., Sajuyigbe S., Mock J. J., Smith D. R. & Padilla W. J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 100, 207402 (2008). [DOI] [PubMed] [Google Scholar]
  17. Kaelberer T., Fedotov V. A., Papasimakis N., Tsai D. P. & Zheludev N. I. Toroidal dipolar response in a metamaterial. Science 330, 1510–1512 (2010). [DOI] [PubMed] [Google Scholar]
  18. Huang Y. W. et al. Design of plasmonic toroidal metamaterials at optical frequencies. Opt. Express 20, 1760–1768 (2012). [DOI] [PubMed] [Google Scholar]
  19. Dong Z. G. et al. Optical toroidal dipolar response by an asymmetric double-bar metamaterial. Appl. Phys. Lett. 101, 144105 (2012). [Google Scholar]
  20. Dong Z. G., Ni P. G., Zhu J., Yin X. B. & Zhang X. Toroidal dipole response in a multifold double-ring metamaterial. Opt. Express 20, 13065–13070 (2012). [DOI] [PubMed] [Google Scholar]
  21. Ogut B., Talebi N., Vogelgesang R., Sigle W. & van Aken P. A. Toroidal plasmonic eigenmodes in oligomer nanocavities for the visible. Nano Lett. 12, 5239–5244 (2012). [DOI] [PubMed] [Google Scholar]
  22. Miroshnichenko A. E. et al. Seeing the unseen: observation of an anapole with dielectric nanoparticles. arXiv : 1412.0299 (2014). [Google Scholar]
  23. Liu W., Zhang J., Lei B. & Hu H. Toroidal dipole induced transparency for core-shell nanoparticles. arXiv : 1412.4931 (2014). [Google Scholar]
  24. Liu W., Zhang J., Lei B., Hu H. & Miroshnichenko A. E. Invisible nanowires with interferencing electric and toroidal dipoles. arXiv : 1502. 02205 (2015). [DOI] [PubMed] [Google Scholar]
  25. Savinov V., Fedotov V. A. & Zheludev N. I. Toroidal dipolar excitation and macroscopic electromagnetic properties of metamaterials. Phys. Rev. B 89, 205112 (2014). [Google Scholar]
  26. Fedotov V. A., Rogacheva A. V., Savinov V., Tsai D. P. & Zheludev N. I. Resonant Transparency and Non-Trivial Non-Radiating Excitations in Toroidal Metamaterials. Sci. Rep. 3, 2967 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Basharin A. A. et al. Dielectric Metamaterials with Toroidal Dipolar Response. Phys. Rev. X 5, 011036 (2015). [Google Scholar]
  28. Dorn R., Quabis S. & Leuchs G. Sharper focus for a radially polarized light beam. Phys. Rev. Lett. 91, 233901 (2003). [DOI] [PubMed] [Google Scholar]
  29. Yang L. X., Xie X. S., Wang S. C. & Zhou J. Y. Minimized spot of annular radially polarized focusing beam. Opt. Lett. 38, 1331–1333 (2013). [DOI] [PubMed] [Google Scholar]
  30. Failla A. V., Qian H., Qian H., Hartschuh A. & Meixner A. J. Orientational imaging of subwavelength au particles with higher order laser modes. Nano Lett. 6, 1374–1378 (2006). [DOI] [PubMed] [Google Scholar]
  31. Mudry E. et al. Structured illumination microscopy using unknown speckle patterns. Nat. Photonics 6, 312–315 (2012). [Google Scholar]
  32. Chen W. B., Nelson R. L. & Zhan Q. W. Geometrical phase and surface plasmon focusing with azimuthal polarization. Opt. Lett. 37, 581–583 (2012). [DOI] [PubMed] [Google Scholar]
  33. Chen W. B., Abeysinghe D. C., Nelson R. L. & Zhan Q. W. Plasmonic Lens Made of Multiple Concentric Metallic Rings under Radially Polarized Illumination. Nano Lett. 9, 4320–4325 (2009). [DOI] [PubMed] [Google Scholar]
  34. Yanai A. et al. Near- and Far-Field Properties of Plasmonic Oligomers under Radially and Azimuthally Polarized Light Excitation. Acs Nano 8, 4969–4974 (2014). [DOI] [PubMed] [Google Scholar]
  35. Zhan Q. W. Trapping metallic Rayleigh particles with radial polarization. Opt. Express 12, 3377–3382 (2004). [DOI] [PubMed] [Google Scholar]
  36. Yang Y., Dai H. T. & Sun X. W. Split ring aperture for optical magnetic field enhancement by radially polarized beam. Opt. Express 21, 6845–6850 (2013). [DOI] [PubMed] [Google Scholar]
  37. Scheuer J. Ultra-high enhancement of the field concentration in Split Ring Resonators by azimuthally polarized excitation. Opt. Express 19, 25454–25464 (2011). [DOI] [PubMed] [Google Scholar]
  38. Hayazawa N., Saito Y. & Kawata S. Detection and characterization of longitudinal field for tip-enhanced Raman spectroscopy. Appl. Phys. Lett. 85, 6239 (2004). [Google Scholar]
  39. Johnson P. B. & Christy R. W., Optical Constants of the Noble Metals. Phys. Rev. B 6, 4370–4379 (1972). [Google Scholar]
  40. Liu N., Mesch M., Weiss T., Hentschel M. & Giessen H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 10, 2342–2348 (2010). [DOI] [PubMed] [Google Scholar]
  41. Leveque G. & Martin O. J. F. Tunable composite nanoparticle for plasmonics. Opt. Lett. 31, 2750–2752 (2006). [DOI] [PubMed] [Google Scholar]
  42. Jung J. & Søndergaard T. Green’s function surface integral equation method for theoretical analysis of scatterers close to a metal interface. Phys. Rev. B 77, 245310 (2008). [Google Scholar]
  43. Søndergaard T., Siahpoush V. & Jung J. Coupling light into and out from the surface plasmon polaritons of a nanometer-thin metal film with a metal nanostrip. Phys. Rev. B 86, 085455 (2012). [Google Scholar]
  44. Takashima T., Nakae T. & Ishibashi R. Calculation of Complex Fields in Conducting Media. IEEE Trans. Electr. Insul. 15, 1–7 (1980). [Google Scholar]
  45. Sersic I., Frimmer M., Verhagen E. & Koenderink A. F. Electric and Magnetic Dipole Coupling in Near-Infrared Split-Ring Metamaterial Arrays. Phys. Rev. Lett. 103, 213902 (2009). [DOI] [PubMed] [Google Scholar]
  46. Fedotov V. A. et al. Spectral Collapse in Ensembles of Metamolecules. Phys. Rev. Lett. 104, 223901 (2010). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
srep11793-s1.doc (544.5KB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES