Abstract
Motivation: Similarity search is the foundation of bioinformatics. It plays a key role in establishing structural, functional and evolutionary relationships between biological sequences. Although the power of the similarity search has increased steadily in recent years, a high percentage of sequences remain uncharacterized in the protein universe. Thus, new similarity search strategies are needed to efficiently and reliably infer the structure and function of new sequences. The existing paradigm for studying protein sequence, structure, function and evolution has been established based on the assumption that the protein universe is discrete and hierarchical. Cumulative evidence suggests that the protein universe is continuous. As a result, conventional sequence homology search methods may be not able to detect novel structural, functional and evolutionary relationships between proteins from weak and noisy sequence signals. To overcome the limitations in existing similarity search methods, we propose a new algorithmic framework—Enrichment of Network Topological Similarity (ENTS)—to improve the performance of large scale similarity searches in bioinformatics.
Results: We apply ENTS to a challenging unsolved problem: protein fold recognition. Our rigorous benchmark studies demonstrate that ENTS considerably outperforms state-of-the-art methods. As the concept of ENTS can be applied to any similarity metric, it may provide a general framework for similarity search on any set of biological entities, given their representation as a network.
Availability and implementation: Source code freely available upon request
Contact: lxie@iscb.org
1 Introduction
Recent advances in whole-genome sequencing and high-throughput techniques have generated a vast amount of sequence and omics data. One critical bottleneck in the post-genome era is the discernment of the biological meaning of uncharacterized sequences in the context of complex phenotypes. Similarity search, as the foundation of bioinformatics, plays a key role in establishing structural, functional and evolutionary relationships between biological sequences. In the case of protein function annotation and structure determination, although the power of the similarity search has increased steadily in recent years, the protein universe still contains a high percentage of ‘dark matter’, which consists of proteins that cannot be characterized by existing experimental or computational techniques (Levitt, 2009). Thus, new similarity search strategies are needed to identify homologs of new sequences efficiently and reliably and to infer their structures and functions in the context of biological systems via integrating heterogeneous omics data.
An increasing body of evidence suggests that protein space is continuous in general, although there exist discrete islands (Berezovsky and Trifonov, 2001; Efimov, 1997; Kolodny et al., 2006; Lupas et al., 2001; Nepomnyachiy et al., 2014; Pascual-Garcia et al., 2009, 2010; Petrey et al., 2009; Sadowski and Taylor, 2010; Sadreyev et al., 2009; Shindyalov and Bourne, 2000; Skolnick et al., 2009; Szustakowski et al., 2005; Taylor, 2002; Tendulkar et al., 2004; Tsai et al., 2000; Xie and Bourne, 2008; Zhang et al., 2010). It implies that two proteins could be related even if their pairwise similarity is undetectable. Thus, the protein universe is better represented as a graph, where each node is a protein. Two nodes are connected if there is a detectable relationship between them (Dokholyan et al., 2002). In this way, two remotely related proteins can be connected through a transitive path (Nepomnyachiy et al., 2014). However, widely used sequence similarity search methods such as PSI-BLAST (Altschul et al., 1997) and hidden Markov model (HMM, Eddy, 1998), and conventional protein sequence and structure classification schema such as Pfam (Finn et al., 2008), structural classification of proteins (SCOP, Murzin et al., 1995) and CATH (Orengo et al., 1997) are built on the assumption that protein space is discrete and hierarchical. As a result, novel structural and functional relationships can be missed if two sequences are very divergent. A network-based method, which connects all sequences into a graph model and exploits the global network structure of similarity relationships between proteins in a database, provides an alternative solution to explore the protein space in a continuous fashion (Chen et al., 2011a, b; Chipman and Singh, 2009; Melvin et al., 2009; Singh-Blom et al., 2013; Vanunu et al., 2010; Wang et al., 2013; Weston et al., 2004). Although it has demonstrated its potential in detecting novel relationships that could be missed by the pairwise-based method (Atkinson et al., 2009), the existing network-based method has two fundamental limitations. First, it provides the ranking of similarities but gives no information on their reliabilities. A model that can assess the statistical significance of similarity is one of the key components in both pairwise-based and profile-based methods and is critical in distinguishing true and false positives and enhancing the sensitivity of a similarity search. Second, few network-based methods can combine sequence and structural similarity. The incorporation of structural similarity into sequence profile has been successfully applied to detecting novel sequence–structure relationships, as the structure is more conserved than the sequence (Petrey et al., 2003; Tang et al., 2003).
In this article, we introduce a new similarity search method, Enrichment of Network Topological Similarity (ENTS), to address challenges in protein similarity search in terms of the continuous protein space. ENTS synthesizes several concepts: network inference to detect the global similarity of a protein, grouping of relevant proteins as a network profile, incorporation of structural information into the sequence search and an efficient statistics model to assess the reliability of the network topological similarity profile. We apply ENTS to a challenging unsolved problem: protein fold recognition. Our rigorous benchmark studies demonstrate that ENTS significantly outperforms state-of-the-art profile- and network-based methods for protein structure prediction. Moreover, ENTS can integrate different similarity measurements (e.g. sequence similarity and structure similarity) and biological classifications (e.g. SCOP) to infer novel protein structure and function. As the principal concept of ENTS can be applied to any similarity metric, ENTS provides a new general framework to boost the performance of the similarity search and may inspire novel methodologies in broad areas of bioinformatics, such as RNA structure prediction and disease gene identification.
2 Methods
2.1 Overview
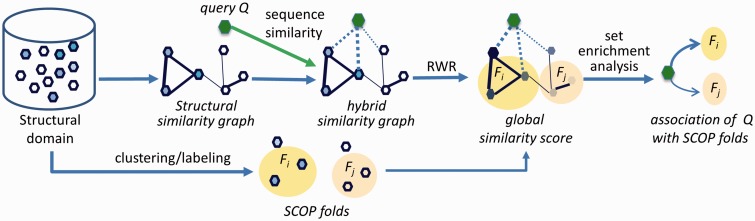
The rationale of ENTS is that when clusters of instances share common features, a cluster ranked closely together is more likely similar to the new instance than a cluster ranked randomly or spread out across the ranking. In addition, network topological similarity provides more robust and accurate global ranking across an entire hypothesis space than pairwise similarity does. Unlike conventional local ranking (e.g. k-nearest neighbors), global instance ranking can support statistical enrichment analysis because it draws valuable information on the ranking for all instances in a cluster from lower, non-randomly ranked cases. Figure 1 shows the scheme of ENTS.
Fig. 1.
Schema of ENTS-Struct, a special case of ENTS. ENTS-Struct connects protein structural domains (hexagons) into a graph whose edges are weighted by their structural similarity. Structure domains are grouped by their structural or functional classifications (e.g. SCOP). Each group is assigned with a label Fi (e.g. SCOP fold). A query sequence Q is linked to the graph using the sequence profile-profile similarity. RWR computes global similarity scores for the query to all structure domains in the graph. In the figure, darker nodes denote stronger similarities. Set enrichment analysis calculates statistically significant differences between observed distributions of similarity scores for each labeled group and a random one and ranks the labeled groups for the query with statistical significance (z-score)
2.2 A weighted graph representation of structural similarity
To initialize ENTS for structure prediction, ENTS builds a structural similarity graph of protein domains, which is essentially the same as the protein domain universe graph described by Dokholyan et al. (Dokholyan et al., 2002). The structural similarity graph is a weighted graph with one node for each structural domain and an edge between two nodes only if their pairwise similarity exceeds a certain threshold. In this article, the structural similarity score is determined by TM align (Zhang and Skolnick, 2005). The threshold is 0.4 of the TM align score. In other applications, the threshold depends on the features and the pairwise similarity metric. Any similarity metric (e.g. Euclidean distance, Jaccard index, HMM and kernel-based similarity) can be applied here.
2.3 Classification or clustering of protein structural domains
Next, some or all the structural domains in the database are labeled with SCOP (Murzin et al., 1995). If pre-classification is not used, clusters of structural domains can be assembled using structural similarity under unsupervised clustering techniques (Estivill-Castro, 2002) such as k-means (Hartigan and Wong, 1979), mean-shift (Comaniciu and Meer, 2002), affinity propagation (Frey and Dueck, 2007) or p-median model (Brusco and Kohn, 2008), etc. These domain clusters are applied to the next step. In general, the labeled clusters are not necessarily disjointed. They can overlap.
2.4 Network topological similarity
Given a query domain sequence and the goal to predict its structure, ENTS first links the query to all nodes in the structural similarity graph. The weights of these new edges are based only on the sequence profile-profile similarity derived from HHSearch (Soding, 2005). Then random walk with restart (RWR) is applied to perform a probabilistic traversal of the instance graph across all paths leading away from the query, where the probability of choosing an edge will be proportional to its weight. The algorithm will output a list of all instances in the graph, ranked by the probability tiq that a path from the query will reach the node i. In this way, RWR can capture global relationships that may be missed by pairwise similarity (Tong and Faloutsos, 2006).
We modified the RankProp algorithm (Melvin et al., 2009), a variant of RWR and implemented it using the boost library (http://www.boost.org). The graph is represented as an adjacency list to save memory and speed up the iterative algorithm. The current implementation is scalable to a graph with millions of nodes and hundreds of millions of edges.
2.5 Statistical significance of network topological similarity
A network topological search only ranks instances based on their similarity and gives no information on the reliability of the ranking. To assess the statistical significance of the ranking of a structural cluster Ci generated previously, ENTS compares the score distribution of the cluster Ci with that of a randomly drawn cluster of the same size. When the mean of global topological similarity scores in a cluster is used as the statistic, an efficient random-set method is used for the parametric approximation of the null distribution (Newton et al., 2007). The random-set method compares an enriched cluster of size m with all other distinct clusters of size m drawn randomly from a case graph on N nodes. The exact distribution of is intractable but can be approximated by the normal distribution with mean and variance as follows:
Where pj is the global topological similarity score of the structure j in the graph to the query.
The enrichment score of the cluster Ci is then normalized with
2.6 Benchmark
The SCOP database (Murzin et al., 1995) version 1.75B is used as a gold standard for benchmarking. SCOP manually classifies approximately 40% of protein structures in the RCSB Protein Data Bank (PDB, Deshpande et al., 2005) based on similarities in their three-dimensional shapes (i.e. folds) and amino acid sequences. If two proteins have a similar sequence, they are classified into a common ‘family’. If two proteins have dissimilar sequences but similar folds and common evolutionary origin, they belong to the same ‘superfamily’. Two proteins from different superfamilies may share the same fold. The benchmark in this study is to recognize the fold of a protein by searching for a database that does not include any protein that shares the same family and superfamily as that of the query protein. The SCOP 1.75B release includes 1195 folds and 1962 superfamilies. A list of 36 003 non-redundant protein structural domains with sequence identity less than 40% (termed the 36 003 set) and their pairwise structural similarity that is determined by FATCAT structural comparison software (Ye and Godzik, 2003) were downloaded from the RCSB PDB (August 2013) (Deshpande et al., 2005). These proteins and their similarities were used to build graph models for the structure prediction. It is noted that only 23.9% of the structure domains in the 36 003 set have the SCOP classification. If a structure domain does not have a SCOP assignment, it was assumed that the non-SCOP-assigned domain shares the same superfamily as that of the SCOP-assigned domain to which it is the most structurally similar. It is noted that temporary SCOP assignments were not used for the gold standard to evaluate the performance of algorithms but only for building a benchmark (details below). To reduce the bias in the existing fold coverage of the protein universe, one structural domain was randomly selected from each SCOP superfamily as a benchmark if its SCOP fold had more than one superfamily. A list of structural domains was compiled (the 885-set). Then a separated subset Bi of the 36 003 set was assigned to each structure Si in the 885 benchmark structures, such that all structures that have the same SCOP superfamilies (including the temporarily assigned SCOP superfamilies) as that of Si were removed from the original 36 003 set. Overall, the benchmark is designed to evaluate the performance of algorithms in detecting novel structural relationships when sequence similarity is weak and noisy.
2.7 Performance evaluation
For a given benchmark structure Si, a true positive is defined as a correctly recognized fold when searching Si against its corresponding Bi. The incorrectly assigned folds are false positives. In total, there were 885 searches and 1 057 575 combined fold hits, including 885 true positives and 1 056 690 false positives. To reflect the situation in the real application, the performance of the algorithms was evaluated by the ratio of true positives on the top-N ranked hits (N 2000).
2.8 Experimental design
2.8.1 HMM-HMM similarity of protein sequence
An HMM sequence profile model was built for the amino acid sequence of each structural domain in the 36 003-set and 885-set using the HH-Suite package (Soding, 2005). The UniProt20 sequence database (Apweiler et al., 2004) was used to generate multiple sequence alignment. The similarity between two HMM profiles was determined using HHSearch (Soding, 2005). All parameters to build and align HMMs used the default setting of the programs.
2.8.2 Fold recognition by HHSearch
Given a query sequence Si and its corresponding HMM profile, its HMM-HMM similarity to each HMM sequence profile of structural domains in the set of Bi was determined by HHBlits. HHBlits is a fast implementation of HHSearch, but the performance of each implementation is comparable (Remmert et al., 2012). For each SCOP fold Fj, its association score hij with the Si was assigned the best HMM-HMM probability score of the HMM hits that were classified as Fj. All hij were ranked. The top-ranked statistically significant Fj is the candidate fold assignment to Si. It is noted that the HHSearch probability score incorporates the similarity of secondary structures.
2.8.3 Fold recognition by CNFpred
Fold recognition of each query sequence Si was also done using CNFpred, another fold recognition program that correlates various sequence and structure features by using a conditional neural field’s model (Ma et al., 2012). The same procedure is applied as HHSearch.
2.8.4 Construction of homology models
The three-dimensional homology model is constructed using the sequence alignment derived from CNFpred by Modeller v9.14 (Sali and Blundell, 1993).
2.8.5. Construction of HMM-HMM similarity graph
An HMM-HMM similarity graph GHi was constructed for each Bi in which each structural domain was a node. Two nodes were connected if they had detectable HMM-HMM similarity according to HHSearch. Each edge was assigned with a weight whose value was the probability score of similarity determined by HHSearch (ranging from 0.0 to 1.0).
2.8.6 Construction of structural similarity graph
All-against-all pairwise structural comparisons of non-redundant structural domains were downloaded from the RCSB PDB (Deshpande et al., 2005). A structural similarity graph GSi was constructed for each Bi in which each structural domain was a node. Two nodes were connected if they had similar structure, which was determined by TM align (Zhang and Skolnick, 2005) (0.4 TM-align score < 1.0). Each edge was assigned a weight whose value was the TM-align structural similarity score.
2.8.7 Fold recognition by network topological similarity search
Given a query sequence Si, the RankProp algorithm was applied to rank all structures in GHi or GSi to Si based on their network topological similarity score. For each fold, the fold association score of Si was assigned using the same method as the fold recognition by HHSearch. The RankProp is called RankProp-HHSearch and RankProp-Struct, respectively, when applied to GHi or GS.
2.8.8 Fold recognition by ENTS
As shown in Figure 1, ENTS was determined as follows:
All structures that were classified as the same SCOP fold were put into a commonly labeled set.
A query sequence Si was connected to its corresponding similarity graph GHi or GSi. The edges and edge weights between Si and GHi (or GSi) were determined by HMM-HMM similarities.
The RankProp algorithm was applied to rank all structures in GHi or GSi to Si based on their network topological similarity score.
The distribution of the topological similarity score in each labeled SCOP set was determined. Set enrichment analysis was applied to each set in terms of its score distribution. A z-score Zij was calculated for each set that corresponds to a single fold Fj. Zij was the fold association score between Si and Fj.
For the purpose of benchmark comparison, all Zij from 885 experiments were combined and ranked.
When applied to GHi or GS, ENTS was called ENTS-HHSearch or ENTS-Struct, respectively.
3 Results
3.1 Overview of ENTS algorithm
We have developed a new algorithm, ENTS of Structure (ENTS-Struct), to infer protein structure based on the network topological similarity of a protein structure similarity network. As shown in Figure 1, ENTS-Struct consists of four key steps. First, we connect non-redundant protein structure domains found in the PDB into an all-against-all structure similarity network (referred to as StructWeb) based on a pairwise structural comparison. Second, if a structural domain has an existing annotation (e.g. SCOP), the structural domain is labeled with this annotation. Third, given a query protein, we connect the query to the StructWeb based on HMM-HMM similarity from HHSearch (Soding, 2005) and apply an RWR algorithm to define the network topological similarity between the query protein and other proteins in the StructWeb. Finally, to assess the statistical significance of the topological rank derived from the RWR, we apply random set theory to estimate the enrichment of a protein set that is associated with a structural or functional class (e.g. SCOP or GO) in terms of the distribution of its network topological similarity scores. The final output of ENTS-Struct is the statistical significance (z-score) of a list of inferred putative structures or functions for the query protein.
3.2 ENTS-Struct considerably improves the performance of fold recognition
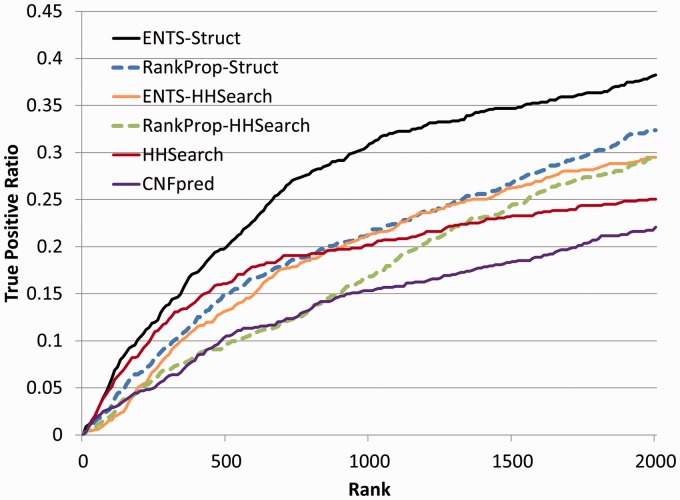
The performance of ENTS-Struct was evaluated using HHSearch and CNFpred as baselines. HHSearch is one of the most sensitive sequence profile-profile comparison methods developed so far, outperforming PSI-Blast and HMMER (Eddy, 1998). In addition, secondary structural similarity is incorporated into the probability score of HHSearch. CNFpred correlates various sequence and structure features by using a conditional neural field’s model (Ma et al., 2012). As shown in Figure 2, ENTS-Struct (black line) clearly outperforms the state-of-the-art algorithm HHSearch (red line) and CNFpred (purple line). With the same number of the highest ranked hits, ENTS-Struct consistently identifies more true positives than HHSearch. There are approximately 50% more true positives in the top 1000 ranked hits identified by ENTS-Struct than those identified by HHSearch. Although CNFpred improves the quality of sequence alignment, it does not perform as well as HHSearch in the fold recognition in our benchmark set.
Fig. 2.
True-positive ratio for all queries ranked with statistical significance by ENTS and three other algorithms HHSearch, CNFpred and RankProp for fold recognition
The improved performance of ENTS-Struct benefits from the use of the structural similarity network StructWeb. As a comparison, an all-against-all HMM-HMM profile similarity network of structural domains was constructed using HHSearch (referred to as ProfWeb). The ENTS procedure as shown in Figure 1 is applied to ProfWeb except that the StructWeb is replaced by the ProfWeb. The resulting algorithm is referred to ENTS-HHSearch. The performance of ENTS-HHSearch (orange line in Fig. 2) is much worse than ENTS-Struct. Although ENTS-HHSearch has the potential to identify more true hits than HHSearch, the false-positive rate is high in the top ranked regions. This is not surprising as the structural similarity detection is more accurate and less noisy (few false positives and false negatives) than the HMM-HMM similarity in terms of detecting remote relationships between proteins.
ENTS-Struct shares the RWR as a key component with RankProp, but ENTS-Struct is distinguished by its set enrichment analysis for statistical assessment of the ranking. Both ENTS-Struct and ENTS-HHSearch outperform their corresponding RankProp algorithm—RankProp-Struct (blue dashed line in the Fig. 2) and RankProp-HHSearch (green dashed line in the Fig. 2), respectively. It is noted that the sensitivity of RankProp is not as good as HHSearch for the top-ranked hits.
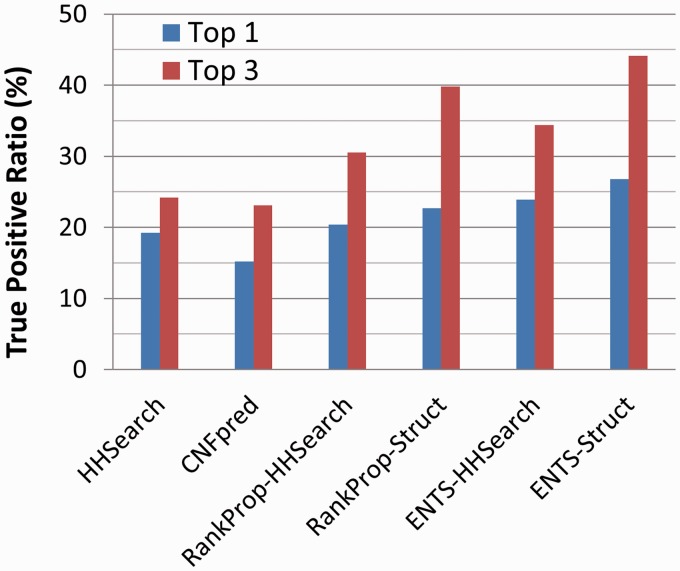
When only the top ranked hits are considered regardless of their statistical significance, the percentage of queries that can detect the correct fold at the top 1 and top 3 are shown in Fig. 3. The overall performance is ENTS-Struct > Rankprop-Struct ∼ ENTS-HHSearcn > Rankprop-HHSearch > HHSearch > CNFpred. ENTS-Struct ranks approximately 25% and 100% more true positives than the baseline HHSearch at top 1 and top 3, respectively.
Fig. 3.
True-positive ratio for each query ranked at the top 1 and top 3 regardless of statistical significance by ENTS and three other algorithms HHSearch, CNFpred and RankProp
A recent study suggests that the continuity of protein space is dependent on the structural class of the protein (Nepomnyachiy et al., 2014). The proteins belonging to SCOP α/β class can be linked with each other through an evolutionary path. However, other classes are relatively discrete (Nepomnyachiy et al., 2014). Consistent with this observation, Table 1 shows that the performance of ENTS varies when applied to different structural classes. ENTS improves the fold recognition in all classes. In regard to the ratio of true positives ranked at the top 3, the order of performance by both ENTS and HHSearch is α/β > all β > α+β > all α, as the α/β class is more evolutionarily related than the α, β and α+β classes, as observed by Nepomnyachiy et al. (2014). However, the improvements of ENTS relative to HHSearch vary by class, in the order of all β > α+β > all α > α/β. This implies that different network topological search parameters may be needed for different structural classes to balance the global and local perspective of structural similarity network.
Table 1.
The percentage of true positives at tops 1, 3 and 10, which are ranked by HHSearch and ENTS-Struct, for four SCOP classes
| All α |
All β |
α/β |
α+β |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Top 1 | Top 3 | Top 10 | Top 1 | Top 3 | Top 10 | Top 1 | Top 3 | Top 10 | Top 1 | Top 3 | Top 10 | |
| HHSearch | 15.1 | 19.1 | 20.4 | 28.3 | 34.6 | 37.1 | 38.7 | 42.4 | 45.3 | 15.2 | 23.9 | 26.6 |
| ENTS-Struct | 14.9 | 27.4 | 52.5 | 38.5 | 63.8 | 77.0 | 43.2 | 55.1 | 69.5 | 19.4 | 37.4 | 55.0 |
| ENST-Struct versus HHSearch | 0.99 | 1.43 | 2.57 | 1.36 | 1.84 | 2.08 | 1.12 | 1.30 | 1.53 | 1.28 | 1.56 | 2.07 |
3.3 Application of ENTS-Struct to hard targets of CASP11
To further test the performance of ENTS-Struct, we carried out a blind test of its performance on fold recognition for hard targets of CASP11. The hard targets are selected such that the highest HHSearch probability of profile–profile similarity between the CASP11 target and the PDB structural domain is <95.0% (e-value > 0.1). It is noted that all structural domains used in the benchmark were released by PDB prior to August 2013, 1 year earlier than that of CASP11. Table 2 lists nine hard targets that have released PDB structures, their most similar SCOP folds, the top 1 prediction from ENTS-Struct with medium and high confidences, their confidence levels, GDT-4.0 score (the percentage of residues in the model structure falling within 4.0 Å of their positions in the experimental structure) and root mean square deviation. Among these targets, ENTS-Struct correctly predicts the folds for the five domains of four targets (T0765, T0769, T0781 C-terminal, and T0808 N-terminal and C-terminal). Five structural domains of these targets (T0761, T0763, T0767, T0771 and the N-terminal domain of T781) do not have closely similar structures in the PDB. ENTS-Struct has four false-positive predictions and two true-negative predictions. Overall, the successful rate of ENTS-Struct is 63.5% (7 correct predictions over 11 cases) with a sensitivity of 83.3% and a specificity of 40.0%. It is noted that ENTS only assesses the statistical significance and re-ranks the hits of the structure prediction. The quality of homology models is dependent on the third party software for the alignment and model construction.
Table 2.
CASP11 hard targets
| Target | PDB Id | Similar SCOP fold(s) (FATCAT P value) | ENTS-Struct top 1 predicted SCOP folds | ENTS-Struct confidence | GDT-4.0 (%) | RMSD (Å) |
|---|---|---|---|---|---|---|
| T0761a | 4pw1 | — | d.304 | Medium | — | — |
| T0763a | 4q0y | — | k.17 | Medium | — | — |
| T0765 | 4pwu | d.58 (2.4e-8) | d.58 | High | 59.33 | 2.77 |
| T0767a | 4qpv | — | d.120 | High | — | |
| T0769 | 2mq8 | d.58 (2.4e-7) | d.58 | Medium | 64.12 | 1.87 |
| T0771a | 4qe0 | — | — | — | — | — |
| T0781 | 4qan | N: — | — | — | — | |
| C: d.17 (1.4e-2) | d.17 | High | 61.21 | 3.56 | ||
| T0800 | 4qrk | b.80 (1.0e-2) | d.131 | High | 18.16 | 9.24 |
| T0808 | 4qhw | N: b.18 (1.1e-3) | b.18 | High | 76.90 | 1.94 |
| C: b.29 (8.4e-4) | b.29 | Medium | 50.09 | 3.05 |
RMSD, root mean square deviation. GDT-4.0 score is defined as the percentage of residues in the model structure falling within 4.0 Å of their positions in the experimental structure.
aNo reliable homology models are built for targets due to poor alignments.
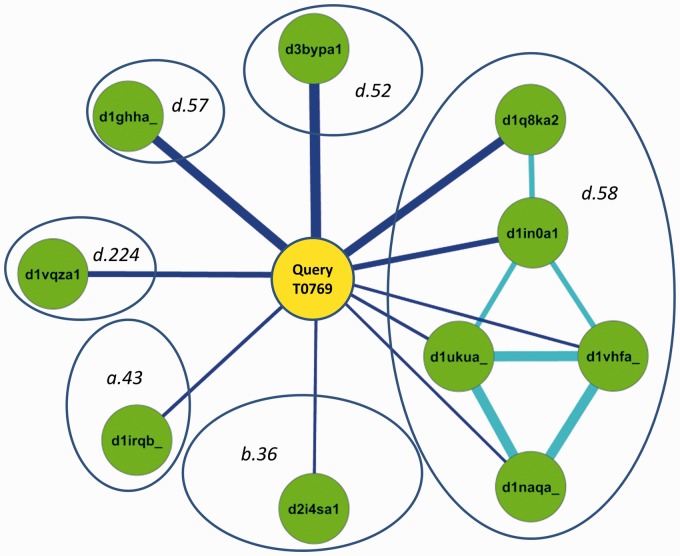
Using target T0769 as an example, Figure 4 and Table 3 demonstrate how ENTS-Struct improves the performance of fold recognition over HHSearch and RankProp-Struct. HHSearch only detects extremely weak similarity between T0769 and several structures that belong to SCOP fold d.58 (e-value ranges from 3.7 to 13). In addition, there are two false-positive hits d1ghha_ (SCOP fold d.57) and d3bypa1 (SCOP fold d.52). They rank above the correct hits. These highest ranked hits of HHSearch are corrected as a graph, as shown in Figure 4. There are multiple edges linking the target to structures that belong to SCOP fold d.58. As a result, RankProp-Struct improves the ranking of d.58 to rank 2. By applying the set enrichment analysis of the RankProp score distribution, ENTS-Struct correctly ranks d.58 as the top 1 hit. Moreover, ENTS-Struct provides reliability information on the ranking, which is missed by RankProp.
Fig. 4.
The graph representation of linkage of T0769 to StructWeb. For simplicity, only SCOP domains that are directly connected to T0769 are shown. The thickness of an edge is proportional to the edge weight. Domains are clustered by SCOP domains (open ovals). The size of the open oval is approximately proportional to the number of structural domains in the cluster
Table 3.
Ranking of similar fold to target T0769 by HHSearch, Rankprop-Struct and ENTS-Struct, respectively
| Fold | Ranking |
||
|---|---|---|---|
| HHSearch | Rankprop-Struct | ENTS-Struct (confidence) | |
| d.58 | 3 | 2 | 1 (medium) |
| d.57 | 1 | 3 | 2 (medium) |
| d.224 | 4 | 4 | 3 (low) |
| d.52 | 2 | 1 | 5 (low) |
| b.36 | 5 | 6 | 10 (low) |
| a.43 | 6 | 5 | 17 (low) |
In summary, the superior performance of ENTS-Struct comes from its addition of global set statistics of topology similarity scores as well as hybrid HMM-HMM and structural similarity onto the RWR topological similarity ranking of protein space. The RWR captures the global structure of protein space. However, conventional statistics models may fail when applied to global similarity problems, as it is not straightforward to normalize topological properties. Global set statistics is more powerful than the fitted parametric statistical model. However, it is less useful when only the nearest neighbors are considered, as the scores of most entities in the set are zeros, providing no information for hypothesis testing. When ENTS is applied to HHSearch directly, its performance is worse than selecting the hit that scored highest in a set of hits belonging to the same fold (data not shown). ENTS by integrating RWR and global set statistics provides a general framework to enhance similarity search and association detection. Although this article focuses on its application to protein structure prediction, it is expected that ENTS may improve the performance of other bioinformatics applications such as drug target identification, RNA structure prediction and disease gene identification.
4 Discussions
4.1 Potential broad applications of ENTS
In this article, we introduce the new computational framework ENTS to assess the reliability of network topological ranking and apply ENTS to the challenging problem of fold recognition. Network topological rankings have been widely applied in bioinformatics, such as in the cases of homology detection (Weston et al., 2004), gene-disease association (Chen et al., 2011a, b; Li and Patra, 2010; Singh-Blom et al., 2013; Vanunu et al., 2010), genetic interaction prediction (Chipman and Singh, 2009), drug target prediction (Wang et al., 2013), side effect prediction (Berger et al., 2010) and drug repurposing (Ng et al., 2014). However, they lack an efficient and generalized statistical model to normalize the ranking and to assess its reliability. As a result, it is not straightforward to determine a threshold for the selection of ranked hits in practice, especially when dealing with data on a large scale. In one application, the top first ranked hit could be a false positive. In another application, multiple top ranked hits can be true positives. The set statistical model introduced in ENTS is applicable to any similarity metric. Our benchmark studies clearly demonstrate that the application of ENTS to network topological rankings improves both the sensitivity and specificity of similarity search. Thus, it is expected that ENTS may have broad applications in bioinformatics and other domains.
Another unique feature of ENTS is that it can integrate heterogeneous similarity metrics. In the case of fold recognition, both reliable protein structural similarity and noisy sequence profile-profile similarity are used in the construction of the network. The integration of multiple omics data, which are often noisy, biased and incomplete, is one of the great challenges in the post-genome era. ENTS presents an alternative approach to integrate reliable and complementary relationships between biological entities with noisy data from heterogeneous data sources into a unified network model. As shown in our benchmark studies, the direct incorporation of structural similarity into sequence similarity search improves the performance of fold recognition. Similar strategies may be applicable to other bioinformatics problems.
4.2 Improvement of global topological similarity
ENTS can be improved in several aspects. The RWR step in the current iterative implementation of ENTS is computationally intensive. More efficient RWR implementation will make ENTS feasible for handling big data. Recent MapReduce-based graph querying and mining systems [e.g. GBase (Kang et al., 2011, 2012)] can support graphs with billions of nodes. They can be incorporated into ENTS. In principle, all steady-state probabilities of RWR are defined by the inversion of matrix Q = I − βW, where 1 − β is the restart probability and W is the edge weight matrix. If Q−1 is pre-computed, instant query response can be achieved. For graphs with specific block-linear structures that are common in biological and chemical networks, efficient linear system solvers that balance the pre-computational cost and on-line query response are available (Tong et al., 2006, 2008).
Other methods for computing global topological similarity may possess advantages over RWR. One of the disadvantages of RWR is that the convergence requires the normalization of edge weights. The normalization may result in the loss of similarity information between instances. For example, one instance has a similarity score of 1.0 with respect to its two neighbor instances. Another instance has the similarity score of 0.1 with respect to its two neighbor instances. After normalization in a graph representation, all edge weights may become 0.5. It has been suggested that diverse k-shortest paths analysis may overcome the shortcomings of RWR, thereby improving the detection of global topological relationships (Shih and Parthasarathy, 2012).
4.3 Improvement of set enrichment analysis
The mean set statistic calculation and the significance assessment using random set theory in the current implementation of ENTS are computationally efficient but may be suboptimal for performance, as the mean score distribution may not follow the normal distribution. Several other choices for the set statistic are available, for example, Kolmogorov–Smirnov statistics (Subramanian et al., 2005), maxmean statistics (Efron and Tibshirani, 2007), Wilcoxon rank sum test statistics and the conditional local false discovery rate (Efron, 2008). To assess significance, a non-parametric permutation test by shuffling labels may provide more accurate estimation when the underlying probability distribution is unknown. It is possible to adopt a two-step procedure for the significance assessment. The random-set method is first applied to filter out less significant hits, so only significant hits will be subject to the permutation test.
4.4 Integration with other methods for structure prediction
When ENTS is applied to protein structure prediction, it relies on a protein threading algorithm to link a query sequence to the structural similarity network and to align the sequence to the structure template. The threading method must detect structures similar to the query sequence, although confidence level does not need to be high. Indeed, the performance of ENTS is strongly dependent on the threading algorithms which are applied. The sequence similarity based on HHSearch outperforms that based on PSI-BLAST and the performance based on PSI-BLAST is better than that based on BLAST (data not shown). Thus, the incorporation of state-of-the-art protein threading algorithms such as MRFalign (Ma et al., 2014) into ENTS may further improve the performance of ENTS for structure prediction.
Although ENTS improves the performance of fold recognition over existing methods, the false-positive rate is still high. One possible solution is to build multiple conformational models for all top ranked hits. Then energy-based scoring functions can be used to distinguish true and false positives (Petrey et al., 2003). In addition, the nodes in the existing structural similarity network are structural domains. SCOP domain classification is used as the node label, mainly for the purpose of performance evaluation. If the query has a novel fold, the prediction is doomed to be a false positive. In principle, any structural classification, either automatic or manual, can be used to label the structure. Moreover, it is possible to use the recurrent structural fragment as a node to construct the structural similarity network. The query may have multiple statistically significant fragment hits. Many structure prediction methods [e.g. I-TASSER (Zhang, 2008)] then could be applied to assemble these fragments into a final structure.
5 Conclusion
Similarity is a fundamental concept in bioinformatics and the emerging discipline of data science, which seeks to harness big data to improve data-driven decision making. In this article, we propose a new method for computing statistically significant similarity via integrating similarity profiles, network topological similarity and set enrichment analysis. Because ENTS applies to any similarity metric, it is poised to make several contributions to bioinformatics. Individual predictive reliability is essential in risk-sensitive applications. ENTS is able to determine the statistical significance of any similarity metric and provides guidance for reliable discovery in large data sets. Robustness to noisy and incomplete data sets is important in bioinformatics applications. Many bioinformatics tasks need to handle data sets that are partially and/or positive-only labeled. ENTS provides a new approach to handling noisy and incomplete data. Thus, it is expected that ENTS has broad applications in bioinformatics.
Funding
This research was supported, in part, under National Institute of Health Grant LM011986, National Science Foundation Grants CNS-0958379 and CNS-0855217 and the City University of New York High Performance Computing Center at the College of Staten Island. R.H. and C.N. were supported by the John P. McNulty Scholars Program.
Conflict of Interest: none declared.
References
- Altschul S.F., et al. (1997) Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. , 25, 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Apweiler R., et al. (2004) UniProt: the universal protein knowledgebase. Nucleic Acids Res. , 32(Database issue), D115–D119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson H.J., et al. (2009) Using sequence similarity networks for visualization of relationships across diverse protein superfamilies. PLoS One , 4, e4345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berezovsky I.N., Trifonov E.N. (2001) Loop fold nature of globular proteins. Protein Eng. , 14, 403–407. [DOI] [PubMed] [Google Scholar]
- Berger S.I., et al. (2010) Systems pharmacology of arrhythmias. Sci. Signal , 3, ra30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusco M.J., Kohn H.F. (2008) Comment on “Clustering by passing messages between data points”. Science, 319, 726 author reply 726. [DOI] [PubMed] [Google Scholar]
- Chen Y., et al. (2011a) Uncover disease genes by maximizing information flow in the phenome-interactome network. Bioinformatics , 27, i167–i176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y., et al. (2011b) In silico gene prioritization by integrating multiple data sources. PLoS One ,6, e21137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chipman K.C., Singh A.K. (2009) Predicting genetic interactions with random walks on biological networks. BMC Bioinformatics , 10, 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comaniciu D., Meer P. (2002) Mean shift: a robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Machine Intell., 24, 603–619. [Google Scholar]
- Deshpande N., et al. (2005) The RCSB Protein Data Bank: a redesigned query system and relational database based on the mmCIF schema. Nucleic Acids Res. , 33(Database issue), D233–D237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dokholyan N.V., et al. (2002) Expanding protein universe and its origin from the biological Big Bang. Proc. Natl Acad. Sci. U S A , 99, 14132–14136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eddy S.R. (1998) Profile hidden Markov models. Bioinformatics , 14, 755–763. [DOI] [PubMed] [Google Scholar]
- Efimov A.V. (1997) Structural trees for protein superfamilies. Proteins , 28, 241–260. [DOI] [PubMed] [Google Scholar]
- Efron B. (2008) Simultaneous inference: when should hypothesis testing problems be combined? Ann . Appl. Stat. , 2, 197–223. [Google Scholar]
- Efron B., Tibshirani R. (2007) On testing the signifcance of sets of genes. Ann. Appl. Stat. , 1, 107–129. [Google Scholar]
- Estivill-Castro V. (2002) Why so many clustering algorithms—a position paper. ACM SIGKDD Explorations Newsl. , 4, 65–75. [Google Scholar]
- Finn R.D., et al. (2008) The Pfam protein families database. Nucleic Acids Res, 36(Database issue):D281–D288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frey B.J., Dueck D. (2007) Clustering by passing messages between data points. Science , 315, 972–976. [DOI] [PubMed] [Google Scholar]
- Hartigan J.A., Wong M.A. (1979) Algorithm AS 136: a K-means clustering algorithm. J. R. Stat. Soc. C , 28, 100–108. [Google Scholar]
- Kang U., et al. (2011) GBASE: a scalable and general graph management system. In KDD2011. ACM New York, NY, pp. 1091–1099. [Google Scholar]
- Kang U., et al. (2012) GBase: an efficient analysis platform for large graphs. VLDB J. , 21, 637–650. [Google Scholar]
- Kolodny R., et al. (2006) Protein structure comparison: implications for the nature of `fold space', and structure and function prediction. Curr. Opin. Struct. Biol. , 16, 393–398. [DOI] [PubMed] [Google Scholar]
- Levitt M. (2009) Nature of the protein universe. Proc. Natl Acad. Sci. U S A , 106, 11079–11084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y., Patra J.C. (2010) Genome-wide inferring gene-phenotype relationship by walking on the heterogeneous network. Bioinformatics , 26, 1219–1224. [DOI] [PubMed] [Google Scholar]
- Lupas A.N., et al. (2001) On the evolution of protein folds: are similar motifs in different protein folds the result of convergence, insertion, or relics of an ancient peptide world? J . Struct. Biol. , 134, 191–203. [DOI] [PubMed] [Google Scholar]
- Ma J., et al. (2012) A conditional neural fields model for protein threading. Bioinformatics , 28, i59–i66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J., et al. (2014) MRFalign: protein homology detection through alignment of Markov random fields. PLoS Comput. Biol. , 10, e1003500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melvin I., et al. (2009) RANKPROP: a web server for protein remote homology detection. Bioinformatics , 25, 121–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murzin A.G., et al. (1995) SCOP: a structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. , 247, 536–540. [DOI] [PubMed] [Google Scholar]
- Nepomnyachiy S., et al. (2014) Global view of the protein universe. Proc. Natl Acad. Sci. U S A , 111, 11691–11696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newton M.A., et al. (2007) Random-set methods identify distinct aspects of the enrichment signal in gene-set analysis. Ann. Appl. Stat. , 1, 85–106. [Google Scholar]
- Ng C., et al. (2014) Anti-infectious drug repurposing using an integrated chemical genomics and structural systems biology approach. Pac. Symp. Biocomput. , 19, 136–147. [PMC free article] [PubMed] [Google Scholar]
- Orengo C.A., et al. (1997) CATH—a hierarchical classification of protein domain structures. Structure , 5, 1093–1108. [DOI] [PubMed] [Google Scholar]
- Pascual-Garcia A., et al. (2010) Quantifying the evolutionary divergence of protein structures: the role of function change and function conservation. Proteins , 78, 181–196. [DOI] [PubMed] [Google Scholar]
- Pascual-Garcia A., et al. (2009) Cross-over between discrete and continuous protein structure space: insights into automatic classification and networks of protein structures. PLoS Comput. Biol. , 5, e1000331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrey D., et al. (2003) Using multiple structure alignments, fast model building, and energetic analysis in fold recognition and homology modeling. Proteins , 53(Suppl. 6), 430–435. [DOI] [PubMed] [Google Scholar]
- Petrey D., et al. (2009) Structural relationships among proteins with different global topologies and their implications for function annotation strategies. Proc. Natl Acad. Sci. U S A , 106, 17377–17382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remmert M., et al. (2012) HHblits: lightning-fast iterative protein sequence searching by HMM-HMM alignment. Nat. Methods , 9, 173–175. [DOI] [PubMed] [Google Scholar]
- Sadowski M.I., Taylor W.R. (2010) On the evolutionary origins of `Fold Space Continuity': a study of topological convergence and divergence in mixed alpha-beta domains. J. Struct. Biol. , 172, 244–252. [DOI] [PubMed] [Google Scholar]
- Sadreyev R.I., et al. (2009) Discrete-continuous duality of protein structure space. Curr. Opin. Struct. Biol. , 19, 321–328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sali A., Blundell T.L. (1993) Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol. , 234, 779–815. [DOI] [PubMed] [Google Scholar]
- Shih Y.K., Parthasarathy S. (2012) A single source k-shortest paths algorithm to infer regulatory pathways in a gene network. Bioinformatics , 28, i49–i58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shindyalov I.N., Bourne P.E. (2000) An alternative view of protein fold space. Proteins , 38, 247–260. [PubMed] [Google Scholar]
- Singh-Blom U.M., et al. (2013) Prediction and validation of gene-disease associations using methods inspired by social network analyses. PLoS One , 8, e58977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skolnick J., et al. (2009) The continuity of protein structure space is an intrinsic property of proteins. Proc. Natl Acad. Sci. U S A , 106, 15690–15695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soding J. (2005) Protein homology detection by HMM-HMM comparison. Bioinformatics , 21, 951–960. [DOI] [PubMed] [Google Scholar]
- Subramanian A., et al. (2005) Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl Acad. Sci. U S A , 102, 15545–15550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szustakowski J.D., et al. (2005) Less is more: towards an optimal universal description of protein folds. Bioinformatics , 21(Suppl. 2), ii66–ii71. [DOI] [PubMed] [Google Scholar]
- Tang C.L., et al. (2003) On the role of structural information in remote homology detection and sequence alignment: new methods using hybrid sequence profiles. J. Mol. Biol. , 334, 1043–1062. [DOI] [PubMed] [Google Scholar]
- Taylor W.R. (2002) A 'periodic table' for protein structures. Nature , 416, 657–660. [DOI] [PubMed] [Google Scholar]
- Tendulkar A.V., et al. (2004) Clustering of protein structural fragments reveals modular building block approach of nature. J. Mol. Biol. , 338, 611–629. [DOI] [PubMed] [Google Scholar]
- Tong H., Faloutsos C. (2006) Center-piece subgraphs: problem definition and fast solutions. In: SIGKDD2006. ACM New York, NY, pp. 404–413. [Google Scholar]
- Tong H., et al. (2006) Fast random walk with restart and its applications. In: ICDM2006. pp. 613–622. [Google Scholar]
- Tong H., et al. (2008) Random walk with restart: fast solutions and applications. Knowl. Inf. Syst. , 14, 327–346. [Google Scholar]
- Tsai C.J., et al. (2000) Anatomy of protein structures: visualizing how a one-dimensional protein chain folds into a three-dimensional shape. Proc. Natl Acad. Sci. U S A , 97, 12038–12043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanunu O., et al. (2010) Associating genes and protein complexes with disease via network propagation. PLoS Comput. Biol. , 6, e1000641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W., et al. (2013) Drug target predictions based on heterogeneous graph inference. Pac. Symp. Biocomput. , 18, 53–64. [PMC free article] [PubMed] [Google Scholar]
- Weston J., et al. (2004) Protein ranking: from local to global structure in the protein similarity network. Proc. Natl Acad. Sci. U S A , 101, 6559–6563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie L., Bourne P.E. (2008) Detecting evolutionary relationships across existing fold space, using sequence order-independent profile-profile alignments. Proc. Natl Acad. Sci. U S A , 105, 5441–5446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye Y., Godzik A. (2003) Flexible structure alignment by chaining aligned fragment pairs allowing twists. Bioinformatics , 19, ii246–ii255. [DOI] [PubMed] [Google Scholar]
- Zhang Q.C., et al. (2010) Protein interface conservation across structure space. Proc. Natl Acad. Sci. U S A , 107, 10896–10901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. (2008) I-TASSER server for protein 3D structure prediction. BMC Bioinformatics , 9, 40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Skolnick J. (2005) TM-align: a protein structure alignment algorithm based on the TM-score. Nucleic Acids Res. , 33, 2302–2309. [DOI] [PMC free article] [PubMed] [Google Scholar]