Likelihood approach for evaluating bioequivalence of highly variable drugs

Abstract

Bioequivalence (BE) is required for approving a generic drug. The Two-One-Sided-Test (TOST, or the 90% confidence interval approach) has been used as the mainstream methodology to test average BE (ABE) on pharmacokinetic parameters such as the area under the blood concentration-time curve and the peak concentration. However, for highly variable drugs (%CV > 30%), it is difficult to demonstrate ABE in a standard cross-over study with the typical number of subjects using the TOST due to lack of power. Recently, the US Food and Drug Administration and the European Medicines Agency recommended similar but not identical reference scaled average bioequivalence (RSABE) approaches to address this issue. Although the power is improved, the new approaches may not guarantee a high level of confidence for the true difference between two drugs at the ABE boundaries. It is also difficult for these approaches to address the issues of population BE (PBE) and individual BE (IBE). We advocate the use of a likelihood approach for representing and interpreting BE data as evidence. Using example data from a full replicate 2 × 4 cross-over study, we demonstrate how to present evidence using the profile likelihoods for the mean difference and standard deviation ratios of the two drugs for the pharmacokinetic parameters. With this approach, we present evidence for PBE and IBE as well as ABE within a unified framework. Our simulations show that the operating characteristics of the proposed likelihood approach are comparable with the RSABE approaches when the same criteria are applied.

1. Introduction

Bioavailability equivalence or bioequivalence (BE) is required by the US Food and Drug Administration (FDA) and regulatory authorities in other countries for approval and marketing of generic drugs or new formulations of an existing drug. A test drug (such as a new generic drug) is bioequivalent to a reference drug (such as an innovator drug) if the rate and extent of absorption of the test drug do not show significant differences from the reference drug when administered at the same molar dose of the therapeutic ingredient under similar experimental conditions [1]. As measures of the rate and extent of absorption, pharmacokinetic parameters such as the area under the blood/plasma concentration-time curve (AUC) and the peak concentration (C_max) have been used, obtained from pharmacokinetic studies with healthy adults [2, 3].

To test BE on these pharmocokinetic parameters, the following hypotheses (referred to as interval hypotheses) are used [4, 5, 6, 7]:

$$\begin{array}{ll}{H}_0:\hfill & {\mu }_T-{\mu }_R\le {\delta }_1\text{or}{\mu }_T-{\mu }_R\ge {\delta }_2;\hfill \\ H_1:\hfill & {\delta }_1<{\mu }_T-{\mu }_R<{\delta }_2,\hfill \end{array}$$ (1)

where μ_T and μ_R denote the population means of a pharmacokinetic parameter (typically logarithmically transformed AUC, or C_max) for the test (T) and reference (R) drugs, respectively, and δ₁ and δ₂ denote the specified equivalence limits; the current FDA guidance suggests δ₁ = log 0.8 and δ₂ = log 1.25 so that −δ₁ =δ₂ = 0.223.

Schuirmann’s Two-One-Sided-Tests (TOST) procedure [6], or the 90% confidence interval (CI) approach, has been used as the gold standard method for testing the above hypotheses since 1992 by the FDA and other countries [3]. According to the FDA, BE is demonstrated if the 90% CIs for μ_T − μ_R for both AUC and C_max fall completely within the suggested limit. In other words, the average bioequivalence (ABE) criteria are met if 90% CIs of the geometric mean ratios (GMR) of the test and the reference drugs for the pharmacokinetic measures fall completely within the limits (in %) of 80–125% [2].

Even though a review of more than a decade of BE data from the FDA supports the ABE criteria in approving high quality generic drugs [8], there are some concerns over some generic drugs that have a narrow therapeutic window such as some anti-epileptic and anti-coagulant drugs [9, 10, 11]. The one-size-fits-all criterion has been criticized by many authors because it does not consider the therapeutic window and variability of a drug, and thus does not address the issues of drug prescribability [related to a concept of population bioequivalence (PBE)] and switchability [related to a concept of individual bioequivalence (IBE)] [12]. Moreover, for highly variable drugs (HVDs), which are defined as drugs with within-subject coefficient of variation (CV) in one or more of the pharmacokinetic parameters being 30% or larger [13], the TOST has low power with a typical sample size of 24 or 36 [14, 15]. A highly variable reference drug may not be demonstrated to be bioequivalent even to itself in a typical cross-over study with a modest number of subjects [13]. A review of 1,010 BE studies of 180 generic drugs submitted to the FDA during 2003–2005 suggests that 31% (57/180) of those are highly variable [15]. Therefore, it is necessary to develop an alternative to the TOST for HVDs.

Berger et al. [14] and Brown et al. [16] have constructed uniformly more powerful tests than the TOST. But those tests are difficult to interpret due to polar coordinates, and the rejection region of those tests may have the undesirable property of being non-convex [17]. Recently, the FDA proposed a reference scaled average bioequivalence (RSABE) approach for HVDs, where the BE limits are scaled to the variability of the reference drug (i.e., the limits increase proportionally to the variance) [13, 18]. The RSABE approach requires either a partial replicate (three-way cross-over: e.g., RTR, RRT, or TRR) or full replicate (four-way cross-over: e.g., RTRT or TRTR) design, with a minimum subject number of 24. The European Medicines Agency (EMA) recently issued a guideline for BE assessment of HVDs [19], which is also a reference scaled approach. However, the EMA and the FDA RSABE approaches are not identical (see Methods).

Using the reference scaled approaches improves study power; however, the frequentist tests may not guarantee any level of confidence for the true difference between two drugs at the equivalence boundaries (for example, GMR = 0.8 and 1.25) [20, 21]. There has also been considerable debate on the practice of using the 100(1−2α)% rather than 100(1−α)% CI for the test at α-level [14, 22]. The root of these problems is the fundamental flaw in the frequentist framework, within which p-values are confused with the strength of evidence and the observed type I error rate [23, 24]. This motivated Choi et al. [24] to advocate the likelihood framework for representing and interpreting BE data as evidence.

Here we extend the likelihood approach for evaluating BE proposed by Choi et al. [24] to HVDs in full replicate 2 × 4 cross-over studies. We demonstrate how to present and interpret the evidence using the profile likelihood of the parameters of interest, including the mean difference and standard deviation ratios (both in log scale) of pharmacokinetic measures for two drugs. The profile likelihood approach can show the full spectrum of evidence for supporting one parameter value over another parameter value. We may even evaluate the mean and variance together in a unified framework as a way to address the PBE and IBE issues. Simulations are used to evaluate the operating characteristics of the likelihood approach when the FDA or EMA RSABE criteria are applied to the likelihood intervals (LI). All abbreviations are listed in Table A.1 in Appendices.

2. Background for the likelihood paradigm

The Law of Likelihood says [25, 26]:

If hypothesis A implies that the probability that a random variable X takes the value x is p_A(x), while hypothesis B implies that the probability is p_B(x), then the observation X = x is evidence supporting A over B if and only if p_A(x) > p_B(x), and the likelihood ratio, p_A(x)/p_B(x), measures the strength of that evidence.

Based on the Law of Likelihood, the likelihood paradigm has been developed and promoted by Royall, Blume and others [26, 27, 28, 29], providing an evidential framework for representing and interpreting statistical evidence. The paradigm focuses on understanding “what the data say”, and the sample space and prior information are irrelevant in this evidential framework. A tutorial of the likelihood paradigm can be found in Blume [27], and its application to practical problems have also been discussed (see [24, 29, 30, 31, 32]).

Nuisance parameters

When a likelihood function is indexed by a single parameter, it is straightforward to apply the Law of Likelihood to measure the strength of evidence for that parameter. However, when the likelihood function is indexed by several parameters (often one parameter of interest and several nuisance parameters that are not of interest), it is difficult to present the likelihood function as a function only of the parameter of interest. An example is the likelihood for a Gaussian model, where the mean, μ, is often the parameter of interest and the variance, σ², is a nuisance parameter. There are several ad hoc solutions to eliminate the nuisance parameters, including conditional, marginal, profile, and estimated likelihoods [26]. Among them, we suggest using the profile likelihood because it has asymptotically good properties in terms of the key performance of a true likelihood [33]. For the Gaussian example, the profile likelihood function for μ, denoted by L_p(μ), is defined as $L_p(\mu )=\underset{\sigma }{max}L(\mu ,\sigma )=L(\mu ,\widehat{\sigma }(\mu ))$, where the maximization of the likelihood function, L(·), is performed at a fixed value of μ, and σ is eliminated by replacing it with its partial maximum estimator, σ̂(μ), the maximum likelihood estimator of σ holding μ fixed (note that its dependence on the sample size is suppressed for simplicity). In the context of BE analysis, Choi et al. [24] demonstrated that the profile likelihood is a good alternative to the true likelihood.

Likelihood intervals

A plot of the standardized likelihood that is obtained by dividing the likelihood by its maximum has been suggested for representing the data as evidence [26]. This plot represents the likelihood ratio (as the strength of evidence) of any parameter value to the maximum likelihood estimate (MLE). A horizontal line of 1/k on the plot defines a set of parameter values, called the likelihood support interval (LI), for which the standardized likelihood values are ≥ 1/k, and hence are considered to be consistent with the data at k level. The k, k > 1, represents the strength of evidence, and any parameter values in LI are supported by the data at the kth level since the best supported value, MLE, is only better supported at most by a factor of k.

For normally distributed data with known variance, σ², the 1/k LI for the mean μ can be derived as $\widehat{\mu }\pm \sqrt{2logk}\sigma /\sqrt{n}$, while the 100(1 − α)% CI for μ can be written as $\widehat{\mu }\pm z_{\alpha /2}\sigma /\sqrt{n}$. As such, there is a one-to-one relationship between the LI and CI. Thus, for normally distributed data, the 100(1 − α)% CI can be a surrogate to an LI with $k=exp(z_{\alpha /2}^2/2)$; for example, the 1/4, 1/6.8 and 1/8 LIs approximately correspond to the 90%, 95% and 96% CIs, respectively. Note, however, that the LI does not have the long-run frequency interpretation of the CI.

Simple versus composite hypotheses

The Law of Likelihood is an axiom that explains how to use the likelihood function to measure evidence for one simple hypothesis over another simple hypothesis, for example, H₀: θ = θ₀ over H₁: θ = θ₁. However, in most of real problems, we often want evidence for composite hypotheses, H₀: θ ∈ Θ₀ over H₁: θ ∈ Θ₁. An example is H₀: θ ≥ 0 over H₁: θ < 0, where Θ₀ = [0,∞) and Θ₁ = (−∞, 0). The interval hypotheses (1) in BE trials also belong to composite hypotheses, where Θ₀ = (−∞, δ₁] ∪ [δ₂,∞) and Θ₁ = (−δ₁, δ₂). The use of the likelihood to measure the strength of evidence for composite hypotheses in the likelihood paradigm has not received much attention. Recently, Zhang et al. [30] proposed a generalized law of likelihood (GLL) using the generalized likelihood ratio (GLR) for the composite hypotheses in a clinical trial setting, supL(Θ₀)/supL(Θ₁) where the supreme (denoted by sup) is with respect to each hypothesized parameter space. As a consequence of GLL, a hypothesis is supported at least k compared to its complement if and only if the 1/k LI is contained in its hypothesized interval. Choi et al. [24] considered that the data present evidence at k strength in favor of BE if the entire 1/k LI for θ (i.e., θ = μ_T − μ_R; the mean difference) is contained within the ABE limit of [−0.223, 0.223], which is consistent with Zhang’s Theorem 3. The maximum of such k is essentially the $\text{GLR}=\underset{H_1}{sup}L(\theta )/\underset{H_0}{sup}L(\theta )$ for the interval hypotheses (1) when the MLE is contained within the limit. In this sense, the GLR (> 1) may be used for representing the maximum evidence for BE over bioinequivalence (BIE). Blume [27, 34] considered the GLL as a general rule that defines the best probability (i.e., the supreme) for less well-defined hypotheses such as composite hypotheses. In general, he argued against the summarization (a rule) of evidence for composite hypotheses to a single number such as the GLR.

Operating characteristics

As analogues of the type I and type II error rates in the frequentist framework, two important probabilities that are relevant in designing a study within the likelihood paradigm are the probabilities that a study generates misleading evidence (the likelihood ratio in favor of wrong hypothesis) or weak evidence (the likelihood ratio in favor of neither of the hypotheses). Suppose we wish to test two simple hypotheses H₀: θ = θ₀ versus H₁: θ = θ₁. When H₀ is true, the probabilities $P_0\left[\frac{L({\theta }_1)}{L({\theta }_0)}\ge k\right]$ and $P_0\left[\frac{1}{k}<\frac{L({\theta }_1)}{L({\theta }_0)}<k\right]$ are the probabilities of observing misleading evidence and observing weak evidence, respectively, where the subscript “0” of P denotes the corresponding hypothesis is true. Both of the probabilities are functions of sample size n (suppressed) and the threshold k. Although closely related, they are distinct from the type I and type II error rates in the sense that the type I error rate is fixed in hypothesis testing while these probabilities converge to zero as n → ∞ when H₀ is true (see [27] and [33]). It has been proven using Markov’s inequality that the probability of observing misleading evidence is no greater than 1/k, which is called the universal bound [26]. For most cases, the probability of observing misleading evidence is much smaller than the universal bound, for any choice of n.

3. Methods

3.1. The model

In order to demonstrate the likelihood approach and compare it with the RSABE approaches for evaluating HVDs, we consider a full replicate 2 × 4 cross-over design, where subjects are randomized to either RTRT or TRTR sequence. Each subject receives both drug formulations twice in the order of RTRT or TRTR to which the subject is randomized. Between the drug administrations, there is a “washout period” to avoid the possible effect of drugs administered in the previous period(s), called “carry-over” effect. We assume there is no “carry-over” effect, which is often reasonable in BE trials.

Suppose n₁ subjects are in sequence RTRT and n₂ subjects in sequence TRTR (total n = n₁ + n₂). Let Y_ijk be a random variable representing the logarithmically transformed response (i.e., Y = logAUC or log C_max) for subject i in period j of sequence k with i = 1, …, n_k, j = 1, 2, 3, 4, and k = 1, 2. The following model for Y_ijk is commonly assumed [14, 35]:

$$Y_{\mathit{ijk}}=\mu +P_j+F_{[j,k]}+S_k+{\gamma }_{i[j,k]}+e_{\mathit{ijk}},$$ (2)

where P_j is the fixed-effect of the jth period and ${\sum }_{j=1}^4{P}_j=0$; F_[j,k] is the fixed-effect of drug formulation administered in period j of sequence k, F_[1,1] = F_[3,1] = F_[2,2] = F_[4,2] = F_R, F_[2,1] = F_[4,1] = F_[1,2] = F_[3,2] = F_T, and F_R + F_T = 0; S_k denotes the fixed-effect of the kth sequence and S₁ + S₂ = 0 and μ is the overall mean. The γ_i[j,k] = γ_iR or γ_iT, is the random-effect of subject i on drug R or T. (γ_iR, γ_iT)′ are assumed to follow a bivariate normal distribution (N₂):

$${({\gamma }_{iR},{\gamma }_{iT})}^{\prime }~N_2\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{BR}^2& \rho {\sigma }_{BR}{\sigma }_{BT}\\ \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BT}^2\end{array}\right)\right],$$

where ${\sigma }_{BR}^2$ and ${\sigma }_{BT}^2$ are the between-subject variances for the reference and test drugs, and ρ is the correlation coefficient. The errors, e_ijk, are independent, and assumed to follow a normal distribution (N), $N(0,{\sigma }_{[j,k]}^2)$. We assume ${\sigma }_{[j,k]}^2={\sigma }_{WR}^2$ or ${\sigma }_{WT}^2$, the within-subject variance for the reference or test drug. The γ_i[j,k] and e_ijk are also independent of each other.

3.2. Estimation of the mean difference, and within-subject variance

To evaluate BE using the RSABE approaches, we derive the moment estimators for the mean difference, its standard error, and the within-subject variance of the reference drug. Table 1 displays the means and the observed data for a pharmacokinetic measure.

Table 1.

Mean and the observed logarithmically transformed response, y_ijk (in parentheses), in a 2 × 4 full replicate cross-over study.

	Period
Sequence	1	2	3	4
RTRT	μ + P1 + FR + S1 (yi11)	μ + P2 + FT + S1 (yi21)	μ + P3+ FR + S1 (yi31)	μ + P4 + FT + S1 (yi41)
TRTR	μ + P1 + FT + S2 (yi12)	μ + P2 + FR + S2 (yi22)	μ + P3+ FT + S2 (yi32)	μ + P4 + FR + S2 (yi42)

Let ϕ = F_T − F_R be the mean difference of the two drugs. Then, an unbiased estimate of ϕ is

$$\widehat{\varphi }=\frac{1}{2}\left[\frac{1}{n_1}\sum _{i=1}^{n_1}\left(\frac{y_{i21}+y_{i41}}{2}-\frac{y_{i11}+y_{i31}}{2}\right)+\frac{1}{n_2}\sum _{i=1}^{n_2}\left(\frac{y_{i12}+y_{i32}}{2}-\frac{y_{i22}+y_{i42}}{2}\right)\right],$$ (3)

and the standard error (SE) of ϕ̂ is

$$\text{SE}(\widehat{\varphi })=\frac{1}{2}s\sqrt{\frac{1}{n_1}+\frac{1}{n_2}},$$ (4)

where s² is the pooled sample variance of average difference within a subject,

$$\begin{array}{l}{s}^2=\frac{1}{n_1+n_2-2}\sum _{i=1}^{n_1}{\left[\left(\frac{y_{i21}+y_{i41}}{2}-\frac{y_{i11}+y_{i31}}{2}\right)-\left(\frac{{\overline{y}}_{·21}+{\overline{y}}_{·41}}{2}-\frac{{\overline{y}}_{·11}+{\overline{y}}_{·31}}{2}\right)\right]}^2+\\ \frac{1}{n_1+n_2-2}\sum _{i=1}^{n_2}{\left[\left(\frac{y_{i12}+y_{i32}}{2}-\frac{y_{i22}+y_{i42}}{2}\right)-\left(\frac{{\overline{y}}_{·12}+{\overline{y}}_{·32}}{2}-\frac{{\overline{y}}_{·22}+{\overline{y}}_{·42}}{2}\right)\right]}^2,\end{array}$$ (5)

where ȳ_·jk denotes the sample mean of j period of sequence k (each cell of Table 1).

In addition, the within-subject variance (Var) of the reference drug, ${\sigma }_{WR}^2=\frac{{\text{Var}}_{(Y_{i11}-Y_{i31})}}{2}=\frac{{\text{Var}}_{(Y_{i22}-Y_{i42})}}{2}$ can be estimated by $s_{WR}^2$:

$$s_{WR}^2=\frac{1}{2(n_1+n_2-2)}\left\{\sum _{i=1}^{n_1}{[(y_{i11}-y_{i31})-({\overline{y}}_{·11}-{\overline{y}}_{·31})]}^2+\sum _{i=1}^{n_2}{[(y_{i22}-y_{i42})-({\overline{y}}_{·22}-{\overline{y}}_{·42})]}^2\right\}.$$ (6)

3.3. The FDA and EMA RSABE approaches for HVDs

The FDA’s RSABE procedure for HVDs is summarized in [13, 36]. If the sample within-subject standard deviation of the reference drug, s_WR, for logAUC or log C_max is equal to or greater than 0.294 (corresponding to %CV being equal to 30%), the reference scaling method may be used. That is, if the upper 95% confidence bound for ${({\mu }_T-{\mu }_R)}^2-{\theta }_S{\sigma }_{WR}^2$ is less than or equal to 0 and the point estimate for μ_T − μ_R = ϕ falls within [−0.223, 0.223], then BE is concluded. Howe’s method [37] is suggested to determine the criterion bound for ${({\mu }_T-{\mu }_R)}^2-{\theta }_S{\sigma }_{WR}^2$ [36]. If s_WR is less than 0.294, the TOST should be used. Here, ${\theta }_S={(log1.25)}^2/{\sigma }_{W0}^2$ and σ_W0 = 0.25, yielding θ_S = 0.89².

On the other hand, EMA allows use of its RSABE approach only for log C_max. For logAUC, the unscaled ABE limit of [−0.223, 0.223] must be used. When s_WR is greater than or equal to 0.294 (i.e., %CV=30%) but less than 0.472 (i.e., %CV=50%), the 90% CI of ϕ for log C_max is required to fall completely within the limit of [−0.76s_WR, 0.76s_WR] to claim BE; when s_WR is greater than or equal to 0.472, a fixed limit of [−0.359, 0.359] (0.359 = 0.76 × 0.472) should be used. Therefore, the scaling factor, 0.76 for EMA approach (log 1.25/σ_W0, with σ_W0 = 0.294), is smaller than that of the FDA RSABE approach, 0.89. The EMA RSABE approach also requires the point estimate constraint.

3.4. Likelihood function and the likelihood approach

We reparameterize the model (2) so that the reparameterized model would specifically have ϕ as a parameter:

$$Y_{\mathit{ijk}}={\mu }^{\ast }+P_2^{\ast }I(j=2)+P_3^{\ast }I(j=3)+P_4^{\ast }I(j=4)+S^{\ast }I(k=2)+\varphi I(\text{drug}=\mathrm{T})+{\gamma }_{i[j,k]}+e_{\mathit{ijk}},$$ (7)

where I(·) is an indicator function, and μ^* is the population mean for the reference drug when there are no period or sequence effects.

In vector notation:

$${\mathbf{Y}}_{ik}={\mathbf{X}}_{ik}\mathit{\beta }+{\mathit{\gamma }}_{ik}+{\mathbf{e}}_{ik},$$ (8)

where Y_ik = (Y_i1k, Y_i2k, Y_i3k, Y_i4k)′, $\mathit{\beta }={({\mu }^{\ast },P_2^{\ast },P_3^{\ast },P_4^{\ast },S^{\ast },\varphi )}^{\prime }$, γ_i1 = (γ_iR, γ_iT, γ_iR, γ_iT)′, γ_i2 = (γ_iT, γ_iR, γ_iT, γ_iR)′, e_ik = (e_i1k, e_i2k, e_i3k, e_i4k)′, and

$${\mathbf{X}}_{i1}=\left(\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 1& 1& 0& 0& 0& 1\\ 1& 0& 1& 0& 0& 0\\ 1& 0& 0& 1& 0& 1\end{array}\right)\text{and}{\mathbf{X}}_{i2}=\left(\begin{array}{cccccc}1& 0& 0& 0& 1& 1\\ 1& 1& 0& 0& 1& 0\\ 1& 0& 1& 0& 1& 1\\ 1& 0& 0& 1& 1& 0\end{array}\right).$$

Again, γ_ik and e_ik are assumed to be independent and normally distributed with mean 0. Their variance and covariance matrices are:

$$\text{Cov}({\mathit{\gamma }}_{i1})=\left(\begin{array}{cccc}{\sigma }_{BR}^2& \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BR}^2& \rho {\sigma }_{BR}{\sigma }_{BT}\\ \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BT}^2& \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BT}^2\\ {\sigma }_{BR}^2& \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BR}^2& \rho {\sigma }_{BR}{\sigma }_{BT}\\ \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BT}^2& \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BT}^2\end{array}\right)\text{and}\text{Cov}({\mathbf{e}}_{i1})=\left(\begin{array}{cccc}{\sigma }_{WR}^2& 0& 0& 0\\ 0& {\sigma }_{WT}^2& 0& 0\\ 0& 0& {\sigma }_{WR}^2& 0\\ 0& 0& 0& {\sigma }_{WT}^2\end{array}\right),$$

respectively. For Cov(γ_i2) and Cov(eγ_i2), the subscripts R and T should be swapped.

Let ζ denote all the parameters. The likelihood function of the model (8) can be expressed as:

$$L(\mathit{\zeta };\mathbf{y})=\prod _{k=1}^2\prod _{i=1}^{n_k}\frac{1}{{(\sqrt{2\pi })}^4{\mid {\mathbf{V}}_{ik}\mid }^{1/2}}exp[-{({\mathbf{y}}_{ik}-{\mathbf{X}}_{ik}\mathit{\beta })}^{\prime }{\mathbf{V}}_{ik}^{-1}({\mathbf{y}}_{ik}-{\mathbf{X}}_{ik}\mathit{\beta })/2],$$ (9)

where ${\mathbf{V}}_{\mathbf{i}\mathbf{1}}=\left(\begin{array}{cccc}{\sigma }_{BR}^2+{\sigma }_{WR}^2& \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BR}^2& \rho {\sigma }_{BR}{\sigma }_{BT}\\ \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BT}^2+{\sigma }_{WT}^2& \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BT}^2\\ {\sigma }_{BR}^2& \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BR}^2+{\sigma }_{WR}^2& \rho {\sigma }_{BR}{\sigma }_{BT}\\ \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BT}^2& \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BT}^2+{\sigma }_{WT}^2\end{array}\right)$

and ${\mathbf{V}}_{\mathbf{i}\mathbf{2}}=\left(\begin{array}{cccc}{\sigma }_{BT}^2+{\sigma }_{WT}^2& \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BT}^2& \rho {\sigma }_{BR}{\sigma }_{BT}\\ \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BR}^2+{\sigma }_{WR}^2& \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BR}^2\\ {\sigma }_{BT}^2& \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BT}^2+{\sigma }_{WT}^2& \rho {\sigma }_{BR}{\sigma }_{BT}\\ \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BR}^2& \rho {\sigma }_{BR}{\sigma }_{BT}& {\sigma }_{BR}^2+{\sigma }_{WR}^2\end{array}\right)$.

Therefore, ζ includes β, and the variance terms and ρ in V_ik. We partition the parameters ζ= (θ, η), where θ is the parameter of interest and η are nuisance parameters, and we obtain the profile likelihood by profiling out η:

$$L_p(\theta ;\mathbf{y})=\underset{\mathit{\eta }}{max}L(\theta ,\mathit{\eta };\mathbf{y})=L(\theta ,\widehat{\mathit{\eta }}(\theta );\mathbf{y}),$$ (10)

where η̂(θ) denotes the maximum likelihood estimate of η for fixed θ. Obviously, the parameter of interest for ABE is θ = ϕ. We can present evidence for ABE using the profile likelihood of θ = ϕ. However, there is no consensus regarding what parameter(s) can be used to evaluate PBE and IBE. The core concept in PBE and IBE lies in our desire for the variability of the reference and test drugs to be “similar” while ensuring their means are equivalent. That is, in addition to the mean equivalence, we want the total variance of the reference $\text{drug}({\sigma }_{TR}^2={\sigma }_{BR}^2+{\sigma }_{WR}^2)$ to be equivalent to that of test $\text{drug}({\sigma }_{TT}^2={\sigma }_{BT}^2+{\sigma }_{WT}^2)$ for PBE, and similarly, the within-subject variance of reference $\text{drug}({\sigma }_{WR}^2)$ to be equivalent to that of test $\text{drug}({\sigma }_{WT}^2)$ for IBE. Thus, the ratio of the variance (or standard deviation) seems to be a natural choice for the parameter of interest. We suggest using the profile likelihoods for ϕ and σ_TT/σ_TR to present evidence for PBE. We reparameterize the likelihood (9) with these parameterizations and obtain the profile likelihood for σ_TT/σ_TR or σ_WT/σ_WR, respectively.

4. Example data analysis for a 2 × 4 cross-over bioequivalence study

We illustrate the likelihood approach for representing evidence for PBE and IBE as well as ABE using an example data. The ABE is also evaluated using FDA and EMA RSABE approaches for comparison.

4.1. Example data

The example data are obtained from a typical BE study with a full replicate 2 × 4 cross-over design with RTRT and TRTR for sequences 1 and 2, and twenty seven subjects for each sequence. The replicate design with RTRT and TRTR is recommended by the FDA [38]. The data are a modified version of Example 4.4 in Chapter 4 [38] such that the variance of AUC measurements for the test drug is inflated in order to emphasize the effect of different variance for the test and reference drugs. Figure 1 shows the logarithmically transformed AUC and Cmax from the data, presented by sequence, where the measurements for each subject are connected with lines.

Figure 1.

The plots of example data, with dots for drug R and triangles for drug T.

4.2. The likelihood approach

The profile likelihoods for the mean difference, ϕ, and the standard deviation ratios of the test and reference drugs, σ_TT/σ_TR and σ_WT/σ_WR, for logAUC and log C_max are displayed in Figures 2 and 3, respectively. The standardized profile likelihoods for each parameter can provide evidence of the data for that parameter.

Figure 2.

The standardized profile likelihoods for the mean difference, ϕ, the ratios of total and within-subject standard deviations of test/reference drugs, σ_TT/σ_TR and σ_WT/σ_WR, for log AUC. The dashed vertical lines represent the ABE limits of −0.223 and 0.223, and our suggested equivalence limits of 0.7 and 1.3 for the standard deviation ratios.

Figure 3.

The standardized profile likelihoods for the mean difference, ϕ, the ratios of total and within-subject standard deviations of test/reference drugs, σ_TT/σ_TR and σ_WT/σ_WR, for log Cmax. The dashed vertical lines represent the ABE limits of −0.223 and 0.223, and our suggested equivalence limits of 0.7 and 1.3 for the standard deviation ratios.

In Figure 2 for AUC, the best supported value (MLE) for ϕ is 0.149 (GMR=1.16), which is the same as the moment based estimate in (3) (also see Table 2). The 1/8 LI, [0.013, 0.287], is only partially contained within the ABE limit of [−0.223, 0.223]. The data fail to present evidence for ABE at k = 8 strength level according to Choi et al. [24]. We identify the largest k, at which the 1/k LI falls completely within the ABE limit, as 1.8, which equals to Zhang’s $\text{GLR}=\underset{H_1}{sup}L(\varphi )/\underset{H_0}{sup}L(\varphi )$. This means that at most the data support the ABE at k = 1.8 level, indicating very weak evidence for BE over BIE.

Table 2.

The analysis results for the example data using FDA and EMA RSABE approaches, compared with the likelihood approach.

	PK Parameter	GMR (90% CI)	sWR	BE limits	criterion bound	BE result
FDA	AUC (exp ϕ)	1.16 (1.04, 1.30)	0.337	[0.74, 1.35]	−0.016	passed
	Cmax (exp ϕ)	1.49 (1.31, 1.70)	0.546	[0.61, 1.63]	0.061	failed
EMA	AUC (exp ϕ)	1.16 (1.04, 1.30)	0.337	[0.80, 1.25]		failed
	Cmax (exp ϕ)	1.49 (1.31, 1.70)	0.546	[0.70, 1.43]		failed
Likelihood	AUC (exp ϕ)	1.16 (1.04, 1.30)*	NA	NA	NA	see Sec.4.2 for interpretations
	AUC (σTT/σTR)	1.12 (0.97, 1.31)*	NA	NA	NA
	AUC (σWT/σWR)	1.31 (1.04, 1.66)*	NA	NA	NA
	Cmax (exp ϕ)	1.49 (1.31, 1.70)*	NA	NA	NA
	Cmax (σTT/σTR)	1.08 (0.93, 1.25)*	NA	NA	NA
	Cmax (σWT/σWR)	0.94 (0.75, 1.18)*	NA	NA	NA

^*MLE and 1/4 LI in the parentheses.

NA, not applicable.

The evidence for equivalence of the variances of the two drugs is represented in the standardized profile likelihoods for σ_TT/σ_TR and σ_WT/σ_WR, which could be used to evaluate PBE and IBE. Since there are no regulatory criteria for σ_TT/σ_TR and σ_WT/σ_WR available, we suggest using an equivalence limit of [0.7, 1.3], assuming that the test drug standard deviation in log scale (CV in the original scale approximately) within 30% of the reference drug would be reasonably close. The best supported value for σ_TT/σ_TR is 1.129, and the 1/8 LI is slightly out of the suggested equivalence limit of [0.7, 1.3]. For the within-subject standard deviation ratio, σ_WT/σ_WR, the best supported value is 1.312, almost at the upper bound of 1.3. The strongest evidence for equivalence (i.e., the largest k or GLR) for the total variance and the within-subject variance are about 3.4 and 1.0, respectively, suggesting only weak or little evidence for BE over BIE in terms of interval hypotheses according to Choi et al. [24] and Zhang et al.[30].

In Figure 3 for C_max, the best supported value for ϕ, 0.401, is totally out of the ABE limit of [−0.223, 0.223], indicating evidence for BIE, while those for σ_TT/σ_TR and σ_WT/σ_WR are close to 1, indicating evidence for equivalence. None of the 1/k LIs for ϕ are completely contained within the ABE limit, demonstrating little evidence for ABE. Zhang’s GLR in this case is 0.08, suggesting moderate evidence for supporting BIE (1/0.08=12.5) over BE. The strongest evidence for equivalence on σ_TT/σ_TR and σ_WT/σ_WR is 8.6 and 9.5, respectively, with our suggested limit of [0.7, 1.3], suggesting moderate evidence for BE over BIE by Choi et al.[24] and Zhang et al.[30].

4.3. The FDA and EMA RSABE approaches

Table 2 presents the analysis results for the example data using the FDA and EMA RSABE approaches, as well as the results from the likelihood approach with 1/4 LI that corresponds to the 90% CI for comparison. If the conventional BE test method (i.e., TOST), is to be used, we would fail to conclude ABE for AUC and C_max since neither of the 90% CIs for GMR fall completely within the [0.8, 1.25] limit. The reference drug is indeed highly variable for both AUC and C_max with s_WR being equal to 0.337 and 0.546 (both higher than 0.294), respectively.

According to the FDA RSABE criteria, we would conclude BE for AUC since the 95% criterion is less than 0 and the GMR point estimate, 1.16, is within the range of [0.8, 1.25]. But for C_max, we fail to demonstrate BE since the criterion bound is larger than 0 and the GMR point estimate, 1.49, is out of the range of [0.8, 1.25].

For the EMA approach, the BE limit for GMR for AUC is always [0.8, 1.25] regardless of s_WR. Thus, we fail to demonstrate BE for AUC since the 90% CI does not fall completely within the limit. For C_max, the scaled limit is expanded to [exp(−0.359), exp(0.359)], or [0.70, 1.43], since s_WR is larger than 0.472 (%CV=50%). Neither the 90% CI nor the GMR point estimate of C_max is completely contained within their corresponding limits, failing to conclude BE for C_max as well.

For purpose of comparison with the FDA RSABE for AUC, if we had applied the EMA scaled limits to AUC, which are exp(−0.76 × 0.337) = 0.77 and exp(0.76 × 0.337) = 1.29, we would still not conclude BE since the 90% CI for GMR would not fall completely within these limits. Thus, BE is concluded for AUC according to FDA RSABE criteria, but we would fail to conclude BE according to EMA RSABE criteria. This is because the FDA RSABE is more permissive due to the larger scaling factor.

5. Simulation studies

We conduct simulation studies to compare the operating characteristics of the likelihood approach for evaluating ABE with those of the FDA and the EMA RSABE approaches. The simulated data are generated from the random-effects model (7) with a full replicate 2 × 4 cross-over design, assuming equal number of subjects in each sequence (RTRT or TRTR) and no period and sequence fixed-effects. We also assume that μ^* = 5, the between-subject variances ${\sigma }_{BR}^2={\sigma }_{BT}^2=0.04$, and the random-effects γ_iR = γ_iT (i.e., ρ= 1). The following scenarios as combinations of several factors are considered to evaluate their effects on the operating characteristics:

1. The total sample size, n = n₁ + n₂ = 24, 36, and 72;

2. The within-subject standard deviation of reference drug, σ_WR = 0.198, 0.294, 0.385, 0.472, 0.631 corresponding to %CV= 20, 30, 40, 50, 70%, respectively;

3. The within-subject standard-deviation ratio, σ_WT/σ_WR = 0.7, 1.0 and 1.3;

4. The GMR of test and reference drugs = 1.0, 1.1, 1.15, 1.2, 1.25, 1.3, 1.4 and 1.6.

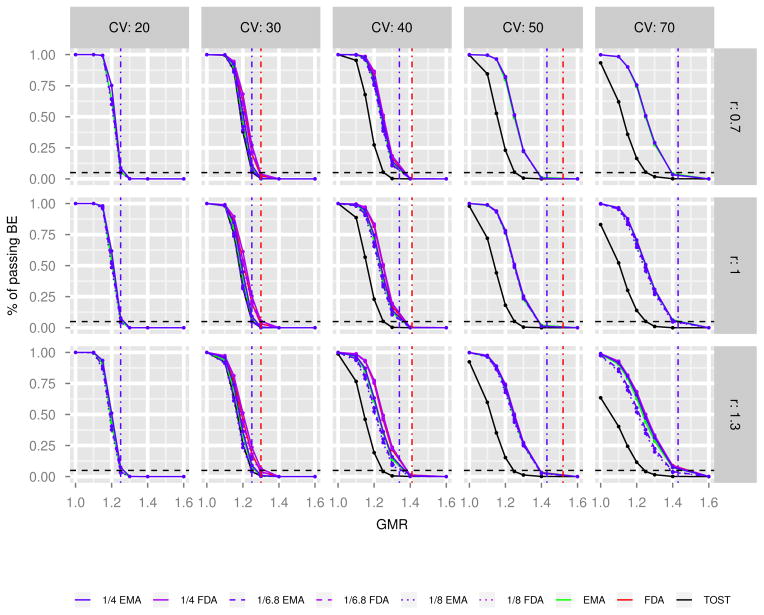
Examples of simulated dataset with various parameters are plotted in Figures A.1 to A.3 in Appendices. For each simulated data, we apply four approaches to evaluate ABE: TOST, FDA RSABE, EMA RSABE, and the likelihood approach. For the likelihood approach, we calculate the 1/4, 1/6.8 and 1/8 profile LIs for the mean difference, ϕ, and examine whether these intervals fall within the FDA or EMA RSABE limits that depend on s_WR. The data are considered to present evidence for BE if the 1/k profile LI for the mean difference falls completely within the RSABE (FDA or EMA) limit and the point estimate constraint is satisfied. The percentage of simulations that present evidence for BE from 1000 simulations for each scenario is calculated, and those under different scenarios for different approaches are plotted in Figures 4 to 6 with increasing sample size. The layout of figures is as follows. Each curve represents a power (y-axis) as a function of true GMR (x-axis) for a specified approach at a combination of σ_WR (i.e., %CV = 20,30,40,50,70) and σ_WT/σ_WR (i.e., r = 0.7, 1, 1.3): the black, green and red solid lines are power curves for TOST, EMA RSABE, FDA RSABE approaches, respectively. The blue solid, dashed, and dotted lines are those for the 1/k LI approach using EMA RSABE limits, while the purple lines are those using FDA RSABE limits. The red and blue dot-dash vertical lines represent the FDA and EMA RSABE limits for the corresponding %CV. The FDA RSABE limit for %CV=70%, 1.76, is out of the range of the x-axis, and hence is not shown. The black-dashed horizontal line is drawn at 0.05 in each plot to show the desired type I error rate.

Figure 4.

The power curves for n = 24. The black, green and red solid lines are those for TOST, EMA RSABE, FDA RSABE approaches, respectively. The blue solid, dashed, and dotted lines are those for the 1/k LI approach using EMA RSABE limits, while the purple lines are those using FDA RSABE limits. The red and blue dot-dash vertical lines represent the FDA and EMA RSABE limits for the corresponding %CV. The FDA RSABE limit for %CV=70%, 1.76, is out of the range of the x-axis, and hence is not shown. The black-dashed horizontal line at 0.05 in each plot shows the desired type I error rate. r is defined as σ_WT/σ_WR.

Figure 6.

The power curves for n = 72. The black, green and red solid lines are those for TOST, EMA RSABE, FDA RSABE approaches, respectively. The blue solid, dashed, and dotted lines are those for the 1/k LI approach using EMA RSABE limits, while the purple lines are those using FDA RSABE limits. The red and blue dot-dash vertical lines represent the FDA and EMA RSABE limits for the corresponding %CV. The FDA RSABE limit for %CV=70%, 1.76, is out of the range of the x-axis, and hence is not shown. The black-dashed horizontal line at 0.05 in each plot shows the desired type I error rate. r is defined as σ_WT/σ_WR.

When the within-subject variability of the reference drug is small (i.e., 20% CV), the powers of TOST, FDA RSABE, EMA RSABE, and the LI methods are close to each other, especially when the sample size is large. These results are reasonable since when %CV is less than 30%, RSABE approaches are basically the TOST, and under the normal model the LIs for k = 4, 6.8 and 8 approximately correspond to the frequentist 90, 95 and 96% CIs, respectively.

When the sample size is small (n = 24 and 36), the larger the %CV of the reference drug and the ratio of σ_WT/σ_WR, the larger the differences between the methods using FDA RSABE limits and those using EMA RSABE limits (red and purple lines versus green and blue lines). When the sample size is large (n = 72) and %CV is large (50–70%), these differences disappear. These results reflect the basic difference between FDA RSABE and EMA RSABE methods as shown by Karalis et al. [39].

The comparison between the FDA RSABE approach and the LI methods using the FDA RSABE limits shows that, when the sample size is small (n = 24) and %CV is between 30–50%, the powers of 1/4 LI method are slightly higher than the FDA RSABE (purple versus red lines). This difference becomes smaller with the increase of the sample size and %CV, and even disappears at %CV=70 for n = 24. The power of FDA RSABE approach is about the same as the 1/6.8 and 1/8 LI methods. We use the 95% criterion bound along with the point estimate constraint to determine BE for the FDA RSABE approach here. This may make the power of the FDA RSABE approach closer to the 1/6.8 LI (corresponding to 95% CI) than to the 1/4 LI (about 90% CI) method with an intermediate range of %CV and a small sample size. For higher %CV (i.e., 70%), the point estimate constraint in the FDA RSABE approach and the LI methods using FDA RSABE criteria is very important in determining the power, which can be seen by comparing these results with those without the point estimate constraint (data not shown). Therefore, the FDA RSABE approach and the LI methods using the FDA RSABE criteria have very similar power regardless of the k, the sample size and σ_WT/σ_WR when %CV is high.

Indeed, the comparison between the EMA RSABE approach and the LI methods using EMA RSABE limits shows that the power of the 1/4 LI method is closer to the EMA RSABE approach (which uses the 90% CI), and it is almost the same as the EMA RSABE when the sample size is ≥ 36, regardless of the σ_WR and σ_WT/σ_WR.

As expected, the larger k is for the LI method, the smaller the power is. In addition, we observe that the σ_WT/σ_WR affects the power of all approaches, especially when the %CV of the reference drug is large. Notice that the current FDA and EMA RSABE approaches do not consider the variability of the test drug, which could be problematic.

In summary, if the same RSABE limit criteria are applied, the power of the LI approach is comparable with the FDA RSABE or EMA RSABE approaches.

6. Discussions

The FDA working group developed and recommended the RSABE approach for HVDs. Haidar et al. [40] demonstrated improved power of RSABE as the within-subject variability increases, compared with the conventional ABE test method (i.e., TOST) using a 3 × 3 partial replicate design. Karalis et al. [39] compared the performance of FDA RSABE with the EMA RSABE for the partial replicate study design. They found that: 1) FDA RSABE and EMA RSABE are basically the same for %CV < 30%; 2) FDA RSABE is more permissive when %CV > 30%; 3) The major difference was found for %CV > 50%, where the point estimate constraint is necessary for FDA RSABE, but less important for EMA approach. Their findings are consistent with our simulation results with a full replicate 2 × 4 cross-over design. We found that the FDA RSABE is more permissive than EMA RSABE, especially for small sample size (n = 24) and large %CV (50–70%), with the largest difference at 70%. Patterson et al. [41] argued against the FDA RSABE for the following reason: when the point estimate constraint in FDA RSABE drives the inference for large sample size and large within-subject variability, this method may not protect the public from the potential large changes in exposure when patients switch between generic drugs. They are also concerned that the scaled approach relies on the observed s_WR so heavily that it may make it easier for a “bad” study to show BE.

A related issue is that the FDA and EMA RSABE approaches do not consider the variability of the test drug. Haidar et al.[40] and our simulations show that not only the within-subject variability of the reference drug (σ_WR), but also σ_WT/σ_WR affects the power, especially when the within-subject variability of the reference drug is large; the higher the ratio, the smaller the power.

An interesting result is the trade-off between the power and the type I error rate. Our simulations, along with studies of [39] and [40], all show that, if we still consider the upper limit for BE for GMR to be 1.25, then when the power is improved over the BE range (1 ≤ GMR < 1.25), the type I error rate (i.e., power at GMR =1.25) also increases. However, we may argue that the type I error rate should be the power at the expanded limit boundaries, such as GMR = 1.30, 1.41, 1.52 and 1.76 for %CV= 30, 40, 50 and 70% if the FDA RSABE limits are applied. If this is the case, it appears that the type I error rate is preserved for the FDA RSABE approach, thanks to the point estimate constraint at larger %CV. Then, we are left with two questions: “Are the two drugs really bioequivalent when their GMR is ‘1.76’?” and “Is the type I error rate really a type I error rate with this point estimate constraint?”. Clearly, these frequentist approaches for BE may not guarantee any level of confidence for the GMR at the ABE boundaries of 0.8 and 1.25, even when BE is concluded. Thus, alternatively, we advocate the evidential likelihood framework for BE trials, which can show evidence for all hypotheses through the likelihood function so that we may identify the better supported hypotheses. This approach does show what the data say regarding the strength of evidence for BE over BIE, even though it does not make any conclusions of BE or BIE. It is impossible to show evidence for BIE using frequentist approaches such as the FDA or EMA RSABE since failing to reject the null does not imply that the null (BIE) is likely. The likelihood approach does not conflict between the evidence and the type I & II error rates. Therefore, there is no controversy about which CI should be used, 100(1−2α)% or 100(1−α)%, for an α level test, which has been a confusing issue to the scientists working in BE trials. Moreover, the probability of observing misleading evidence is small [26].

Another advantage of the likelihood approach is that it is easy to address the PBE issue (linked to prescribability) by considering the evidence for the mean and the total variability together. The current FDA position on prescribability is that the ABE criterion ensures the safety and efficacy of the generic drug and thus its prescribability [12]. For the IBE issue (linked to switchability), the likelihood approach can provide evidence for the closeness of the within-subject variances between the two drugs using the profile likelihood for the within-subject standard deviation ratio. In the FDA 2001 guidance, the IBE criteria based on Schall and Luus [42] was recommended. The main idea was that within-subject differences between the reference and test drugs (i.e., Y_T − Y_R) should not be much different from within-subject differences between two measurements for the reference drug (i.e., $Y_R-Y_R^{\prime }$) to ensure switchability. This led to three components in the aggregated criteria: the squared mean difference (ϕ²), the within-subject variance difference ( ${\sigma }_{WT}^2-{\sigma }_{WR}^2$) and the variance of subject random effects difference between the two drugs (i.e., $\text{Var}({\gamma }_{iT}-{\gamma }_{iR})={\sigma }_{BT}^2+{\sigma }_{BR}^2-2\rho {\sigma }_{BT}{\sigma }_{BR}$), denoted by ${\sigma }_D^2$. The last component, ${\sigma }_D^2$, called the subject-by-formulation interaction variance is the key component of the criteria, but sometimes behaves unreasonably as discussed in Zariffa et al. [43]. In addition, the evaluation of the aggregated criteria is statistically challenging. At present, the FDA does not consider the IBE as an applicable approach, perhaps due to the difficulty in its implementation [12]. However, these issues are often the targets of criticism concerning the current ABE method. Instead of taking the aggregate approach, we propose to evaluate evidence for BE for each component separately within a unified approach. If the correlation between the subject random effects, ρ, is moderate to high, which we conjecture to be true for most cases, we can ensure IBE as long as the likelihood supports the closeness of the means as well as the between and within-subject variances of the two drugs since ${\sigma }_D^2\approx 0$ for these cases. However, if the correlation is low, the subject-by-formulation interaction variance could be large, and hence the proposed method alone may not ensure the IBE. It would be interesting to see how the subject-by-formulation interaction variance could be evaluated in the likelihood approach. We leave this as future research.

Not only may we evaluate the mean and the variance for one pharmacokinetic parameter together within the same paradigm, we can also consider multiple pharmacokinetic measures (AUC and C_max) simultaneously using their joint likelihood function [24]. Furthermore, it is straightforward to combine the existing data with the newly obtained data together to evaluate the evidence without the adjustment of type I error rate within the likelihood paradigm. This is important, especially because, since 2009 the FDA requires all the previous repeated and failed BE study data when applications for generic drug approval are submitted.

We use simulations to demonstrate that, if we applied the same FDA’s or EMA’s limit criteria to the LIs, the operating characteristics of the likelihood approach at fixed k would be comparable with the FDA RSABE or EMA approach. Note that we do not, however, recommend using the likelihood approach for evaluating BE in this way. The simulations are for the purpose of comparison with the frequentist method to evaluate the operating characteristics. Instead, we advocate employing the likelihood approach to present evidence for BE in the manner that we have illustrated using the example data.

We extend the likelihood approach applied to conventional BE data proposed by Choi et al. [24] to HVDs. The likelihood approach proposed here can be used for any BE evaluations, regardless of variability. For HVDs, such as the drug in the example data, we recommend comparing the variances of the drugs directly, along with the mean.

We might desire to use one summary number, such as Zhang’s GLR, as the strength of evidence for BE over BIE for the interval hypotheses (1). However, since GLR depends on the rule of $L(\theta \in H_1)=\underset{H_1}{sup}L(\theta )$, we expect that it would not behave like the likelihood ratio for simple hypotheses, thus the Law of Likelihood may not apply (see discussions about this topic in [27, 30, 34, 44]). Our simulations (data not shown) show that, indeed, the probability of observing misleading evidence using the GLR would not converge to 0 at the boundary between the two hypotheses being compared, as the sample size increases. Therefore, we recommend presenting the evidence using the profile likelihoods, not just the summary number.

We suggest that the evaluation of evidence for BE should be decoupled from the decision making for approval of generic drugs. According to the evidence and the extent to which the consumer risk and producer risk are minimized, regulatory authorities can work with scientists to decide how strong the evidence should be required to be to conclude BE or BIE.

Figure 5.

The power curves for n = 36. The black, green and red solid lines are those for TOST, EMA RSABE, FDA RSABE approaches, respectively. The blue solid, dashed, and dotted lines are those for the 1/k LI approach using EMA RSABE limits, while the purple lines are those using FDA RSABE limits. The red and blue dot-dash vertical lines represent the FDA and EMA RSABE limits for the corresponding %CV. The FDA RSABE limit for %CV=70%, 1.76, is out of the range of the x-axis, and hence is not shown. The black-dashed horizontal line at 0.05 in each plot shows the desired type I error rate. r is defined as σ_WT/σ_WR.

Appendices

A. Abbreviations used in the text

Table A.1.

Abbreviations used in the text.

Abbreviation	Full text
ABE	average bioequivalence
AUC	area under the blood concentration-time curve
BE	bioequivalence
BIE	bioinequivalence
Cmax	peak concentration
CI	confidence interval
CV	coefficient of variation
EMA	European Medicines Agency
FDA	The United States Food and Drug Administration
GLL	generalized law of likelihood
GLR	generalized likelihood ratio
GMR	geometric mean ratio
HVD	highly variable drug
IBE	individual bioequivalence
LI	likelihood interval
MLE	maximum likelihood estimate
PBE	population bioequivalence
RSABE	reference scaled average bioequivalence
TOST	Two-One-Sided-Tests

B. Simulated data examples

See Figures A.1 to A.3.

Figure A.1.

Simulated data with GMR=1, CV=20% (σ_WR = 0.198), and σ_WT/σ_WR = 1.

Figure A.2.

Simulated data with GMR=1, CV=40% (σ _WR = 0.385), and σ_WT/σ_WR = 1.

Figure A.3.

Simulated data with GMR=1.25, CV=40% (σ _WR = 0.385), and σ_WT/σ_WR = 1.

C. Software

All the analysis and simulations were performed using the programming language R version 3.1.0 [45]. The code is available upon request. A package based on the code is under construction.