CONSPECTUS
Enzymatic transition states have lifetimes of a few femtoseconds (fs). Computational analysis of enzyme motions leading to transition state formation suggests that local catalytic site motions on the fs time scale provide the mechanism to locate transition states. An experimental test of protein fs motion and its relation to transition state formation can be provided by isotopically heavy proteins. Heavy enzymes have predictable mass-altered bond vibration states without altered electrostatic properties, according to the Born–Oppenheimer approximation. On-enzyme chemistry is slowed in most heavy proteins, consistent with altered protein bond frequencies slowing the search for the transition state. In other heavy enzymes, structural changes involved in reactant binding and release are also influenced. Slow protein motions associated with substrate binding and catalytic site preorganization are essential to allow the subsequent fs motions to locate the transition state and to facilitate the efficient release of products. In the catalytically competent geometry, local groups move in stochastic atomic motion on the fs time scale, within transition state-accessible conformations created by slower protein motions. The fs time scale for the transition state motions does not permit thermodynamic equilibrium between the transition state and stable enzyme states. Isotopically heavy enzymes provide a diagnostic tool for fast coupled protein motions to transition state formation and mass-dependent conformational changes. The binding of transition state analogue inhibitors is the opposite in catalytic time scale to formation of the transition state but is related by similar geometries of the enzyme-transition state and enzyme–inhibitor interactions. While enzymatic transition states have lifetimes as short as 10−15 s, transition state analogues can bind tightly to enzymes with release rates greater than 103 s. Tight-binding transition state analogues stabilize the rare but evolved enzymatic geometry to form the transition state. Evolution to efficient catalysis optimized this geometry and its stabilization by a transition state mimic results in tight binding. Release rates of transition state analogues are orders of magnitude slower than product release in normal catalytic function. During catalysis, product release is facilitated by altered chemistry. Compared to the weak associations found in Michaelis complexes, transition state analogues involve strong interactions related to those in the transition state. Optimum binding of transition state analogues occurs when the complex retains the system motions intrinsic to transition state formation. Conserved dynamic motion retains the entropic components of inhibitor complexes, improving the thermodynamics of analogue binding.
Graphical Abstract
I. TEMPORAL DISCONNECT IN TRANSITION STATE AND STEADY-STATE ENZYMATIC CATALYSIS
Events defining the steady-state rates of enzymatic catalysis include, at minimum, diffusional collisions causing reactant binding, formation of the Michaelis complex, protein structural changes that bring the Michaelis complex to a reactive configuration, transition state formation to achieve the on-enzyme chemical step, and protein structural changes, mostly a reverse of those forming the Michaelis complex, to enable the release of products from the catalytic site. The slowest step in the enzymatic reaction sequence is often the release of products from the catalytic site, but can also be the rate of on-enzyme chemistry. The slowest step defines the maximum observed rates of catalysis during steady-state action of the enzyme. In rare enzyme examples, all steps are very fast, creating an unusual but much discussed protein catalyst, the “perfect” enzyme.1 Perfect enzymes are limited only by the solvent-limited diffusion of reactants to the enzyme and products away from the catalytic site. Perfect enzymes with small substrates like catalase (H2O2 → H2O and O2) or carbonic anhydrase (CO2 + H2O → H2CO3) can have rates as high as 106 s−1. However, group and local catalytic site motions in proteins are much faster and can occur many times before the transition states are formed. Fast protein motion has been implicated in on-enzyme chemistry.2–4 The kinds of protein conformational steps involved in reactant binding, and protein changes leading to chemical bond changes at the transition state can be expressed in a log10 time expansion plot (Figure 1).
Figure 1.
Time scales for motions related to enzyme catalysis arranged in orders of magnitude. The top line represents 1000 s, and the bottom line represents 0.000000000000001 s.
Time scales for protein and atomic motion can be exemplified with purine nucleoside phosphorylase (PNP), lactate dehydrogenase (LDH), and dihydrofolate reductase (DHFR).2–4 The transition state lifetimes for these enzymes have been characterized by computationally unbiased transition path sampling methods.5 Identifiable kinetic steps in enzymatic catalysis vary in time scale by at least 1014. Transition state lifetimes are a few femtoseconds (fs; 10−15 s for LDH or DHFR, and 10−14 s for PNP) while the steady-state turnover lifetime for an enzymatic catalytic cycle is typically in the several milliseconds (ms) scale (around 10−2 s for DHFR, 10−3 s for LDH, and 10−1 s for PNP). The slow ms events that govern enzymatic function are related to relatively large scale motions of domains, loops, or flaps that cover the catalytic site or close for catalysis and open for project release. In perfect enzymes, these motions are minimized or are at least faster than the diffusion rate of reactants and products, but are many orders of magnitude slower than transition state lifetime.
II. A 10 fs TRANSITION STATE FOR HUMAN PURINE NUCLEOSIDE PHOSPHORYLASE
Human PNP is a modest catalyst on the scale of the most proficient enzymes, some of which are reported to enforce catalysis rates up to 1021 of that without enzyme.6 Extrapolating from the acid- and base-catalyzed solvolysis of purine nucleosides, PNP increases the reaction rate by approximately 1013.7 Steady-state, pre-steady-state, and T-jump studies of PNPs together with structural and computational studies give a detailed picture of what happens in catalysis.
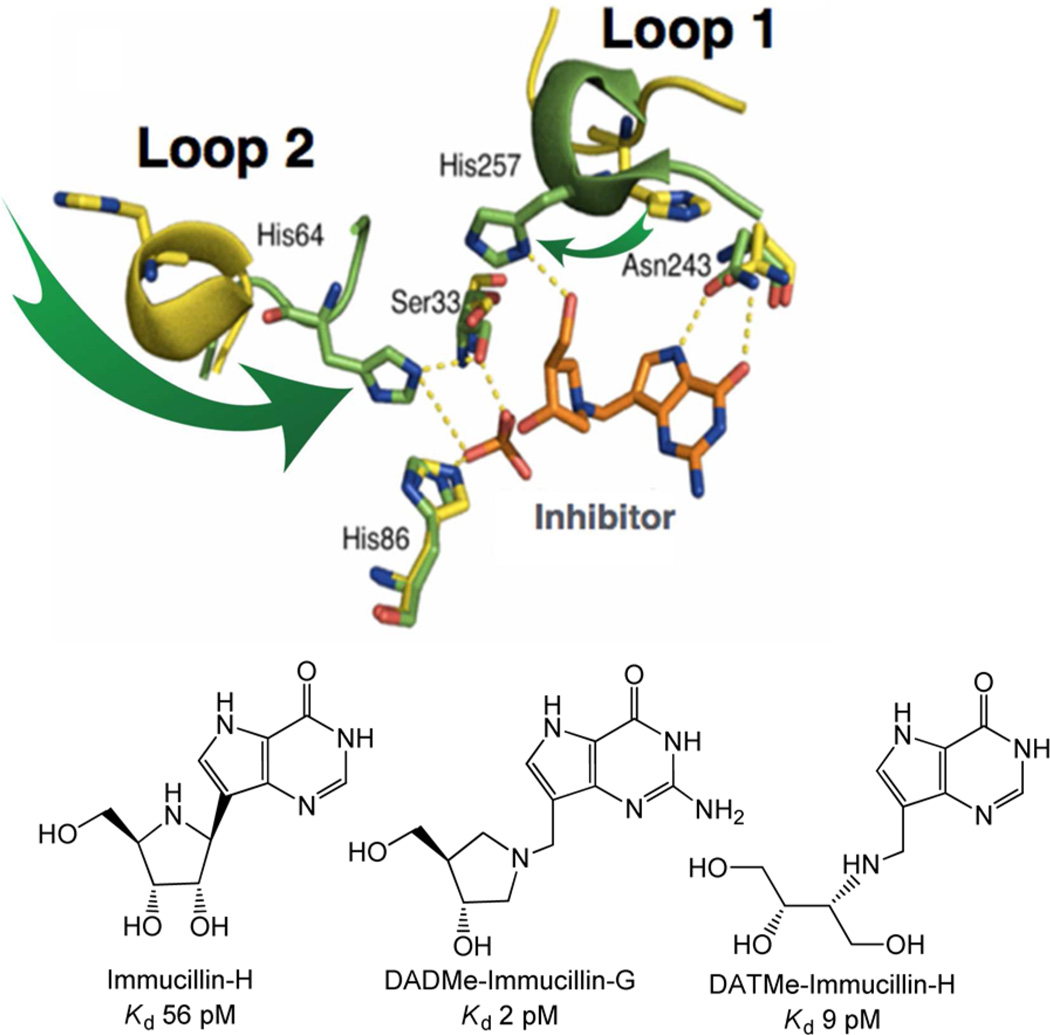
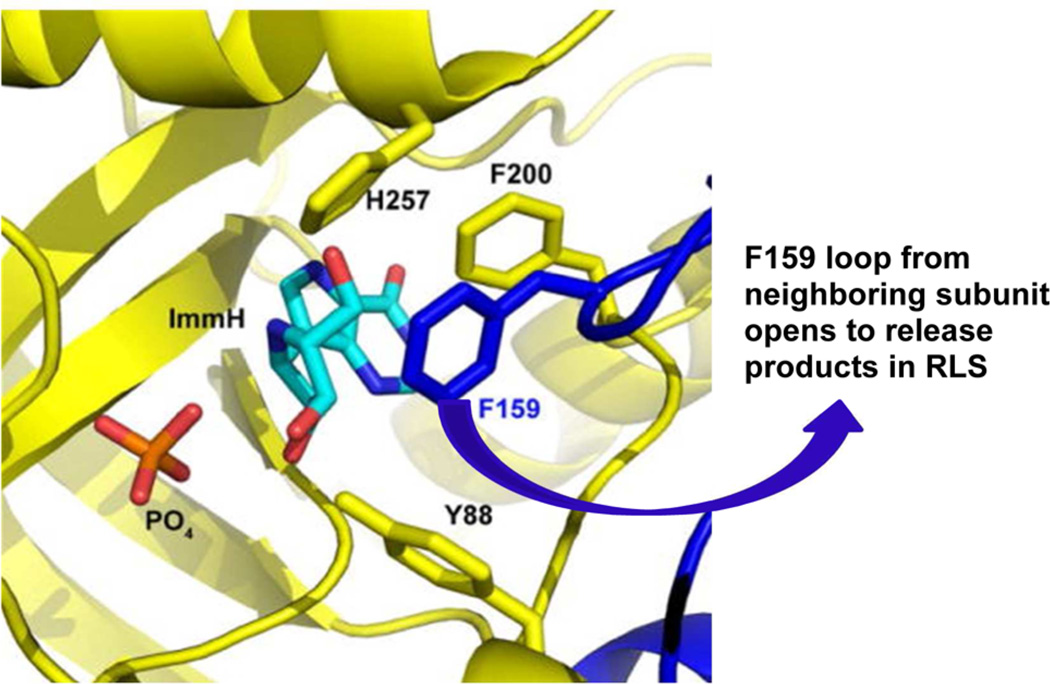
After inosine or guanosine nucleosides and phosphate bind to an open catalytic site, two mobile loops surrounding the catalytic site make large protein structural changes to position groups for transient interactions with the bound reactants in the Michaelis complex. His257 is on a flexible loop in the unliganded enzyme, and this region is converted to an α-helical segment to move the His257 imidazole ring by approximately 15 Å to form contact with the 5′-hydroxyl group of bound nucleoside (Figures 2 and 3).8–10 His257 contact provides part of the electrostatic interaction involved in forming the fully developed ribocation known to exist at the transition state (Figure 2). Another large conformational change occurs with His64, one of the polarizing interactions to the bound phosphate nucleophile. Unliganded PNP has the His64 loop in an α-helical segment that reorganizes to a loop with His64 in contact to the nucleophilic phosphate when ligands are bound. Other regions of the catalytic site undergo only small conformational changes upon catalytic site filling. Interactions at the purine base, Asn243 and Phe200, and the interaction of His86 with phosphate undergo relatively small changes in geometry on substrate binding. Phe159 from the adjacent subunit, together with His257, Phe200, and Tyr88 are involved in forming a hydrophobic cover for the bound nucleoside in the catalytic site. Catalytic site motions involving these loop-to-helix transitions occur on the 10−4–10−5 s time scale, as established by changes in fluorescent Trp probes by T-jump experiments with Phe159Trp.11 Slower conformational changes are associated with product release from the catalytic site and limit the overall reaction rate of the enzymatic reaction (Figure 3).
Figure 2.
Human PNP catalytic site filled with phosphate and DADMe Immucillin-G (upper panel). The phosphate and DADMe Immucillin-G ligands are in orange. The PNP-phosphate structure (yellow shading) shows His64 (loop 2) and His257 (loop 1) turned out of the catalytic site. The PNP structure with the catalytic site filled with phosphate and DADMe Immucillin-G, a 2 pM transition state analogue inhibitor (green shading), shows His64 and His257 turned in to make hydrogen bond contacts. The green arrows indicate the His relocation motions. Only six of more than a dozen interactions are shown. Ribbons represent α-helical segments, and tubes represent loop structures. The lower panel shows transition state analogues of human PNP.
Figure 3.
Catalytic site of human PNP with Immucillin-H (ImmH) and inorganic phosphate (PO4) at the catalytic site. The PO4 is buried in the protein. Side chains from Y88, F159, F200, and H257 form a layer between the catalytic site and solvent. F159 is from the adjacent subunit (dark blue). It must relocate to permit product release (blue arrow), the rate-limiting step (RLS) of catalysis.
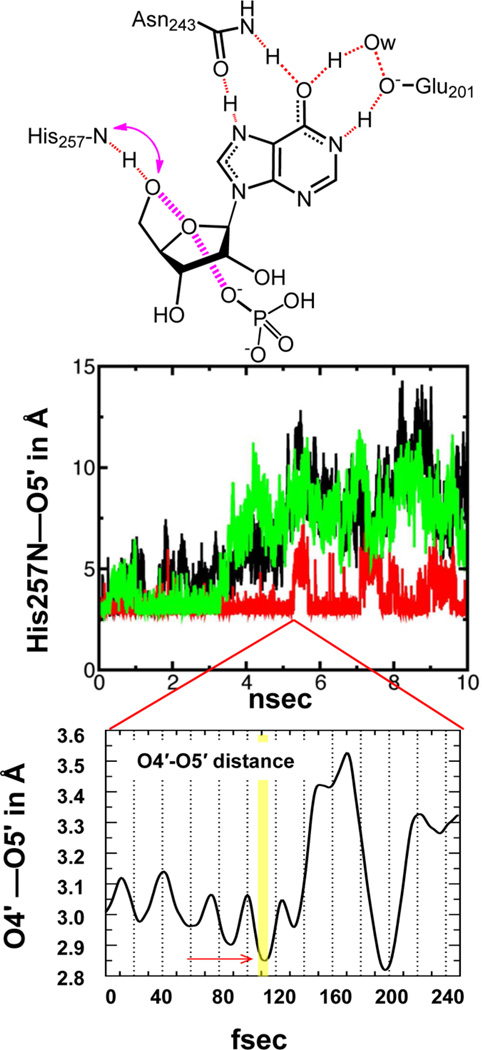
PNP molecular dynamics (ns time scale) show the interaction of His257 with the 5′-hydroxyl of inosine to be stable about 50% of the time (Figure 4).12 This interaction participates in the formation of the transition state. An unbiased QM/MM transition path sampling computational approach identified motions associated with transition state formation and provided estimates of the reaction coordinate and transition state lifetimes. Transition path sampling was pioneered for solution organic chemistry by the Chandler group,5 and expanded by the Schwartz group for application to enzymes.13 During close contacts between His257 and the O5′ reactant hydroxyl group in PNP, dynamic motion from the His257 interacts with the O5′ group to compress the O4′—O5′ distance (Figure 4 bottom panel). Oscillations of a few tenths of an angstrom create altered electrostatic potentials varying on the fs time scale, and these fast motions are candidates for transition state formation. Minimizing the O4′—O5′ distance is a common feature of transition state formation, sampled over many transition state excursions (Figure 4). The His257 interaction contributes to, but is not sufficient for catalysis, as the purine leaving group interactions to Asn243 and Glu201 must be optimized at the same time to form the transition state. When compressed, the O4′—O5′ interactions destabilize ribosyl electrons into the purine leaving group where they are stabilized by the H-bonds with Asn243, Glu201, and a bridging structural water molecule. When these interactions are optimized at the same time, the barrier to the transition state is minimized, the transition state forms, the barrier is crossed, and enzyme-bound products are formed. The reaction coordinate motion is formed by migration of the C1′ anomeric carbon of the ribosyl group from the purine leaving group to the enzyme bound and polarized phosphate group. The reaction coordinate motion is approximately 70 fs and the fully developed ribocation transition state has a lifetime of 10 fs.2
Figure 4.
Motion of His257 with inosine at the catalytic site of in human PNP and transition state formation. The upper panel shows three of the amino acid contacts to reactants in the Michaelis complex. His257 forms a hydrogen bond to the O5′ hydroxyl group and orients the 5′ oxygen toward the 4′-ribose ring oxygen. The interaction (pink curved arrow) is transient, on the ns time scale, as indicated in molecular mechanics calculation (middle panel). (Reprinted with permission from ref 12. Copyright 2010 American Chemical Society.) The three dynamic traces show the interactions in each of the three catalytic subunits of PNP (green, red, and black) on the ns time scale. The His257 interaction causes compression of the O4′–O5′ distance, destabilizing the N-ribosidic bond. Minimization of the O4′–O5′ distance is associated with transition state formation (lower panel; copyright 2008, Proceedings of the National Academy of Sciences, U.S.A.). The transition state has a lifetime of 10 fs (yellow bar, lower panel) as determined by unbiased quantum chemical transition path sampling.2 The local dynamic search for the transition state for this interaction has a oscillation period of approximately 30 fs. In the 5 ns period where the His257N–O5′ hydroxyl interaction is maintained, the 30 fs search can occur 167 000 times. Time scales in the middle and lower panels differ by 40 000.
Alignment of all catalytic site groups required for turnover requires 15–40 ms, depending on the PNP substrate. Most local motions (ps–fs) involved in the TS search are off the reaction coordinate. Catalytic site motions associated with transition state formation and a period of 30 fs can occur more than 1012 times to engage the interactions needed for the ms catalytic rate. The simultaneous optimization of multiple fast interactions gives the observed on-enzyme chemistry rate. In this dynamic mechanism of catalysis, the transition state is reached by the stochastic search of local fs vibrational modes that occur within the slower motions, like those occurring on the ns to ms time scales (Figure 4). Computational evidence for fast dynamic motions linked to transition state formation came from the application of computational transition path sampling to enzymes from the Schwartz group.2,14 Computational predictions are often difficult to test, but in the case of protein vibrations on the atomic bond scale, perturbations can be introduced by isotope substitution.15,16
III. TESTING THE HYPOTHESIS THAT FEMTOSECOND MOTIONS ARE COUPLED TO TRANSITION STATE FORMATION
Protein motions observed by NMR, fluorescent label methods, or T-jump methods can often be correlated with the rate of steady-state catalysis.17–19 Steady-state rates for the overall catalytic cycle involve the slow conformational changes involved in catalytic site alignment to permit the transition state search and also those associated with the release of products. Transition states are the loss of a restoring mode in breaking bonds, and thus have lifetimes on the time scale of individual bond vibrational frequencies. Coupling of fs bond vibrations to conformational motions on the ms time scale is unlikely. If fs motions (e.g., Figure 4) are coupled to transition state formation, changing the frequency of the fast fs modes would be expected to alter the probability of finding the transition state.
Expression of enzymes in medium containing all amino acid precursors labeled with heavy isotopes of hydrogen (2H), carbon (13C), and nitrogen (15N) increases the mass of proteins by approximately 10% (heavy protein). Each of the amino acids involved in contacts to reactants will experience altered bond vibrational frequencies, and these will alter the fs dynamic search interactions with the reactants. Slow motions of loops or backbone structural changes that are limited by diffusional motion or solvent viscosity will not be significantly altered by the mass change. For isotopically labeled PNP, it is also possible that the distribution of reactive substates might be altered, since it is known that isotope labels in lactate dehydrogenase alter these states.20 Experiments with heavy labels in specific amino acids should be able to resolve the issue of substate distributions.
When human PNP was expressed as a heavy protein (all nonexchangeable 2H, 13C, and 15N), its mass increased by 9.9%. The steady state kinetics of kcat and Km were not changed. Likewise, the transition state structure (from intrinsic kinetic isotope effects) was also unchanged. Thus, the slow protein motions regulating steady-state turnover were unchanged. The transition state structure, defined by the position of all atoms participating in the reaction coordinate when the transition state is reached, was unaltered. However, the on-enzyme chemical step, measured by single-turnover rate constants for bound reagents, was slowed for heavy PNP. The slowed enzyme bond vibrational frequency caused by heavy amino acids reduced the probability of finding the transition state. Heavy enzyme isotope effects for on-enzyme chemistry were 1.25 and 1.37 for inosine and guanosine as substrates, respectively, where the isotope effects are expressed as [kchem normal PNP/kchem heavy PNP].15
A challenge in heavy enzyme experiments is to distinguish small kinetic differences in distinct proteins (heavy and light) from mass differences. On-enzyme presteady state kinetics where the enzyme is present in large excess to reactants gives pseudo-first-order kinetics, and thus kinetic constants independent of enzyme concentration. A second method, independent of enzyme concentration, involves forward commitment measurements. Forward commitment is the partition of reactants in the Michaelis complex to cross the transition state barrier to products relative to the probability to dissociate to unbound reactants. In cases like PNP, where Km is unchanged by enzyme mass, the commitment factor reports on the probability of barrier crossing, and is also independent of enzyme concentration. Heavy PNP exhibited decreased forward commitment factors with heavy enzyme isotope effect values within experimental errors of those for on-enzyme chemistry.15 It was concluded that increased atomic mass in human PNP alters bond vibrational modes on the femtosecond time scale, reduces on-enzyme chemical barrier crossing, and demonstrates coupling of enzymatic bond vibrations on the femtosecond time scale to transition state barrier crossing.
IV. HEAVY ENZYME EFFECTS IN OTHER SYSTEMS
Following the original report of heavy PNP, other reports of heavy enzymes have included HIV protease, pentaerythritol tetranitrate reductase, alanine racemase, and dihydrofolate reductase. For HIV protease, the on-enzyme chemistry step was 37% slower for heavy enzyme.16 HIV protease differed from PNP, because in addition to the reduced on-enzyme chemistry, it also exhibited altered Km values, associated with mass-dependent local motion of the small loops covering the catalytic site.16 With pentaerythritol tetranitrate reductase, the nature of the transition state, as determined by kinetic isotope effects was altered by heavy enzyme. The on-enzyme chemistry rate was not quantified.21 Alanine racemace showed 23% slower on-enzyme chemistry for the heavy enzyme.22 Heavy dihydrofolate reductase showed small mass effects that were attributed to altered barrier recrossing because of a slowed ability of fast motions in the protein needed to complete barrier crossing or to altered fast conformation steps.23 The sum of heavy atom enzyme studies has been the subject of a recent review.24 In most cases, increased enzyme mass altered the central function of the enzyme in forming the transition state, supporting a proposal that mass-altered vibrational coupling to the transition state is common. However, a transition path sampling analysis of dihydrofolate reductase from Escherichia coli reported that there was no direct (fs or ps) coupling between the protein and transition state formation, thus the vibrational coupling comes from the near-geometry of the reactants themselves, and the role of the protein is to create a favorable reactant geometry.25
V. AN EXCEPTION: HEAVY DIHYDROFOLATE REDUCTASE (DHFR) FROM E. coli HAS NO PROMOTING VIBRATIONS
As one of the most studied enzymes, DHFR was selected as a subject for transition path sampling.25 The Schwartz group found that DHFR differed from other enzymes by lacking correlated fs to psec motions between the catalytic site amino acids and the dihydrofolate and NADPH reactants. Rather, the catalytic site provides reactant alignment and electrostatic facilitation. The fast dynamic motion of the bound reactants provides the reaction coordinate. Stark spectroscopy studies, coupled to QM/MM analysis exploring the electrostatic environment near the DHFR catalytic site, using modified amino acid probes, predicted that the ground-state electrostatic environment near the catalytic site is sufficient to accelerate the reaction without dynamic coupling of motion to the protein.26
The computational prediction that DHFR lacks fast promoting vibrations provided a test of the heavy enzyme approach. A mechanistic comparison of heavy and light DHFRs including steady-state kinetics, intrinsic kinetic isotope effects, dissociation constants, and rate constants for complexes along the reactions path, indicated no change in barrier crossing efficiency at physiological temperature.27 The results were in agreement with the transition path sampling results.25 On-enzyme chemistry rate, transition state structure (from intrinsic KIEs) were unchanged in heavy and light DHFRs at physiological temperatures. Small changes in protein–ligand binding rate constants were observed. Mass-altered binding constants support mass-dependent rates related to substrate binding and product release in DHFR, a finding similar to that for HIV protease.16 Thus, some enzymes will have mass-sensitive reactant binding and release, without changing the rate of on-enzyme chemistry. Transition state structure (from KIEs) is unlikely to be altered in heavy enzymes.15
The predictions for mass-sensitive barrier crossing based on transition path sampling have been validated by heavy enzyme studies in both PNP and DHFR, two intrinsically different chemical mechanisms. A computational transition path sampling study on isotopically heavy human heart LDH predicts a slower reaction coordinate (on enzyme chemistry) and also a decreased coordination of the normally concerted movement of the hydride ion and the proton.28 Transition path sampling with isotopically heavy PNP indicated that the fs catalytic site motions required to form the transition state are less well coordinated in the heavy enzyme.29 Evolution of protein dynamic motion to find transition states occurred with natural abundance proteins, and it is hypothesized that mass-altered protein vibrational frequencies moves the dynamic protein architecture away from that optimized by evolution.
VI. DISTINGUISHING AN ENZYMATIC TRANSITION STATE FROM AN INTERMEDIATE
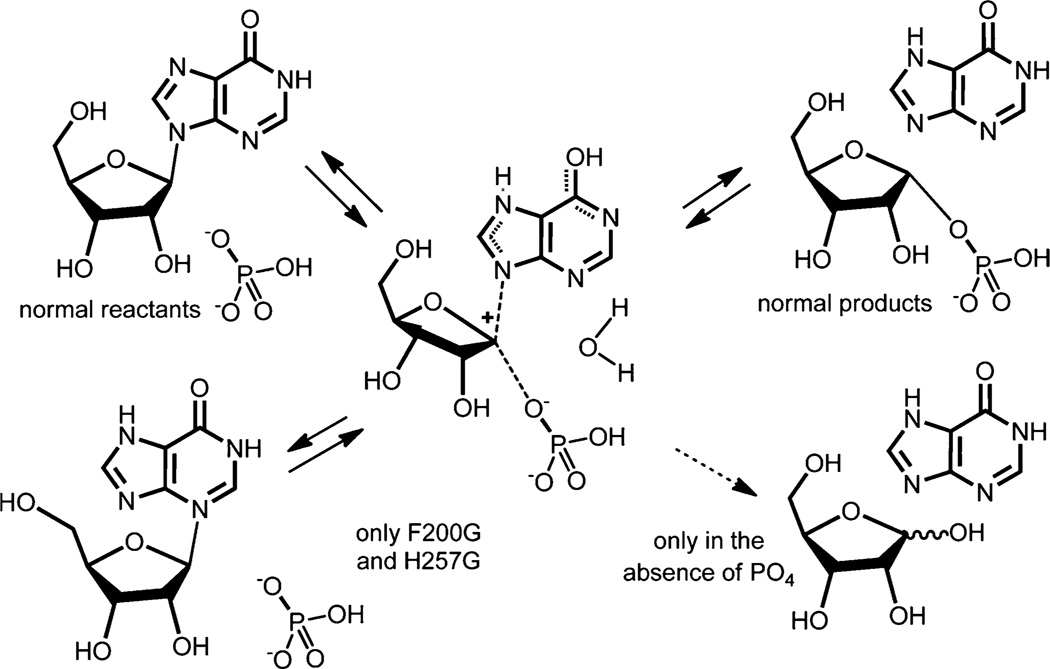
William P. Jencks considered chemical cases of intermediate lifetimes in his 1980 Accounts of Chemical Research article: “When is an intermediate not an intermediate? Enforced mechanisms of general acid–base catalyzed, carbocation, carbanion and ligand exchange reactions.”30 Jencks considered that when an intermediate decomposes faster than a vibrational frequency, the barrier for breakdown is insignificant, it will cease to exist, and the reaction will be concerted. He also considered glycoside cations to be in this class although he indicated that they were “…widely believed to proceed through an intermediate oxocarbonium ion…” As enzymes are often considered to act by stabilizing the transition state species, we explored the nature of the ribocation formed at the transition state of human PNP in chemical trapping experiments, to test the 10 fs computed transition state lifetime. If PNP forms a stabilized ribocation transition state (a lifetime of many bond vibrations), nucleophiles introduced to compete with phosphate at the catalytic site should react with the enzyme-stabilized ribocation. We introduced water into the catalytic site by removing amino acids from catalytic site loops that occlude reactants in the catalytic site from solvent. The amino acid side chains of Tyr88, Phe159, His257 and Phe200 are involved in this waterproofing (Figure 3).31 Each was mutated to glycine to permit water access to the catalytic site. Molecular dynamics confirmed that solvent water has diffusional access to the catalytic site.12 If the ribocation has a lifetime to permit water to diffuse (at its rate of ~1 Å ps−1), it will capture a fraction of the ribocation, causing part of the ribosyl product to be d-ribose instead of α-d-ribose 1-phosphate (Figure 5). Reactants and products were equilibrated through the transition state for 2 × 107 catalytic turnovers with NMR monitoring to quantitate α-d-ribose 1-phosphate and d-ribose. No ribose was formed in native PNP or any “open site” mutant in the presence of phosphate. In the absence of phosphate, when the phosphate site is filled with water, ribose is formed. Thus, the ribocation transition state lifetime is too short to permit water to diffuse and capture the ribocation. Jencks calls these systems preassociation mechanisms with no barrier, no intermediate, and therefore fully concerted reactions. The experimental absence of a ribocation intermediate is consistent with the 10 fs transition state lifetime predicted from transition path sampling, although the same result would be obtained with transition state lifetimes up to 100 fs based on the diffusion rate of water.2
Figure 5.
Chemical consequences of introducing solvent access to the catalytic sites of PNP. Refer to Figure 3 for the location of these amino acids. The normal reaction and transition state are shown in the upper reaction path. Catalytic site mutations do not permit formation of ribose (lower right), but it does form if phosphate is absent. Mutations F200G and H257G permit misalignment of the transition state reactants and N3-isoinosine forms (lower left).
Although no α-d-ribose 1-phosphate was diverted to d-ribose in PNP or its catalytic site mutants, N3-isoinosine appears as a novel product in the equilibrating reaction [inosine + phosphate ↔ hypoxanthine + α-d-ribose 1-phosphate] with H257G and F200G. This instructive side reaction teaches us that amino acids covering the catalytic site are not needed to protect the catalytic site from water, but are needed to keep the purine in alignment with the ribocation and thereby ensure nucleophilic fidelity to N9 and inosine formation. Loss of the alignment permits N3 to become the nucleophile and the misaligned ribocation rebound gives N3-isoinosine (Figure 5).31
VII. COMPARING THE TRANSITION STATE TO TRANSITION STATE ANALOGUES
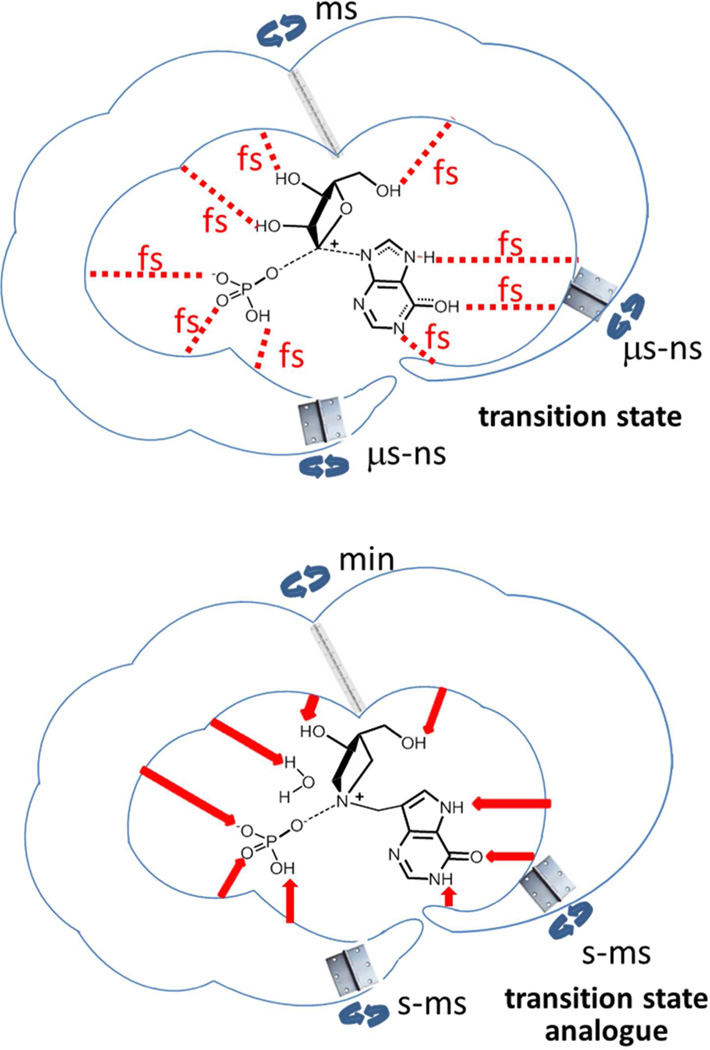
Enzymes evolved to accelerate chemistry (i.e., form the transition state).6 Efficient catalysis also includes slower motions of reactant binding and preorganization to permit the local dynamic search for the transition state, as chemistry is rarely rate-limiting. Catalytic site motion on the fs time scale is mass-coupled to the transition state but is too fast to permit conformational changes involving significant backbone adjustments or structural rearrangements that are commonly seen in reactant binding and release (cartoon Figure 6). Crossing the transition state barrier causes chemical changes in the reactants, and the altered chemistry facilitates catalytic site opening and release of the products to regenerate reactive enzyme. The transition state is formed by coincident fs dynamic excursions of catalytic site atoms along the reaction coordinate. This motion is local and does not constitute tight binding or compression of the extended protein architecture. The transition state lifetime is too short to thermally equilibrate with slow conformational changes.
Figure 6.
Cartoons of the distinct time scales for PNP catalysis and transition state analogue binding. Substrate and the pretransition state conformational changes are on the ms to ns time scale (upper panel). Within these times, the local catalytic site contacts (red dashed lines) vary their distance on the fs time scale. Optimized fs interactions locate the transition state which exists only for 10 fs. The fs excursions are from a relaxed form of the enzyme. When a transition state analogue is bound (bottom panel), each of the interactions is stabilized (red arrows), the protein condenses around the analogue, and the motions for release become orders of magnitude slower than in the normal catalytic cycle.
Transition state analogues enter the catalytic site in the same way as substrate, by diffusional collision and catalytic site closing to form the pretransition state complex. However, the slow conformation and fast stochastic searches that have evolved to locate the transition state with reactants differ with transition state analogues, to locate a structure closely related to the transition state, but one that is chemically stable. In normal enzyme chemistry, fs dynamic motions find a simultaneous set of electrostatic interactions that permit transition state formation. With transition state analogues, the dynamic generation of favorable electrostatic contacts does not lead to chemistry but to an ensemble of stable enzyme–analogue interactions. In enzyme chemistry, the transition state occurs from a rare protein geometry coupled to barrier crossing, and the reaction facilitates an efficient release of products. Transition state analogs induce a time-dependent reorganization of the enzyme to cause slow-onset inhibition, a state that can include large changes to the protein structure (see below). Stable interactions with transition state analogues result in slow inhibitor release and therefore in tight-binding interactions. Key to understanding tight-binding interactions is that protein catalytic site motions are dynamic during catalysis, but less dynamic when transition state analogues are bound (Figure 6). Protein architecture remote from the catalytic site can become more or less dynamic when transition state analogues are bound, resulting in favorable or unfavorable entropic contributions to binding.
The Wolfenden equilibrium approximation for binding of transition state analogues indicates binding proportional to the chemical rate enhancement imposed by the enzyme.32 Exact mimics of the transition state are not possible because of their nonequilibrium bond lengths, and the theoretical affinities have not been achieved. The dynamic mechanism of ligand binding introduces the paradox that tight-binding analogues tend to stabilize their cognate protein structures and by doing so, reduce the dynamic motion of the complex, thereby imposing substantial entropic penalties on the system. Examples in the N-ribosyltransferases demonstrate these changes.
VIII. DYNAMIC SIGNIFICANCE OF THERMODYNAMICS IN TRANSITION STATE ANALOGUE BINDING
Human PNP has a ribocation transition state with a 3 Å distance between the ribocation and the purine leaving group (the C1′-N9 reaction coordinate parameter; Figure 6).33 A family of transition state analogues with varying similarity to the transition state have been characterized for their thermodynamics of binding (Figure 2).34 An analogue with a C1′-N9 reaction coordinate parameter too short to match the 3 Å distance of the transition state has profound effects on the protein structure. Immucillin-H is a 56 pM Kd transition state analogue with a 1.5 Å reaction coordinate distance. It binds to human PNP, to cause structural compaction of the protein sufficient to increase its sedimentation rate by 3%.35 This more ordered protein structure creates a large entropic penalty on Immucillin-H binding to human PNP, with ΔH being large and favorable by −21.2 kcal/mol and TΔS being unfavorable by 7.1 kcal/mol to give a ΔG of −14.1 kcal/mol.34 DATMe-Immucillin-H is a structurally flexible transition state analogue for human PNP, and is more similar to the transition state (2.5 Å in the reaction coordinate parameter). Although DATMe-Immucillin-H also causes the enzyme to become more compact, it increases the sedimentation coefficient only by 0.95%, and induces a smaller entropic (TΔS) penalty of only 2.3 kcal/mol and thus binds more tightly, with a ΔG of −15.2 kcal/mol. Why is this? Molecular dynamics investigation demonstrates that when the inherent flexibility of the bound inhibitor is similar to the inherent flexibility of the groups in the catalytic site, the system retains more of the dynamic motion of the prebound state, and pays a reduced entropic penalty.12 This matched flexibility demonstrates that the best inhibitors are those that coordinate to the normal dynamic motions of the enzyme to minimize the entropic penalty.
The fit of the analogue to the transition state has also been explored in the distortion forces placed on transition state analogues by the enzyme when bound to PNP. The “too short” Immucillin-H experiences a 0.1 Å elongation of the C–C bond that defines the reaction coordinate parameter when bound to PNP, a distortional force of approximately 10 kcal/mol. In contrast, DADMe-Immucillin-H, with a distance of 2.5 Å in the reaction coordinate parameter, shows no significant distortion in this parameter when bound to human PNP, and binds more tightly.36
Another example of enhanced binding by retaining system dynamic motion is provided by the bacterial 5′-methylthioadenosine nucleosidases (MTANs), enzymes involved in quorum sensing in Gram-negative bacteria, and in menaquinone synthesis in helical bacteria.37,38 MTANs from E. coli and Vibrio cholera are closely related in catalytic properties and catalytic site structure. Yet, transition state analogues bind several orders of magnitude more tightly to the enzyme from E. coli.39 Molecular dynamic simulations of these enzymes bound to common inhibitors revealed a greater flexibility in the E. coli enzyme around the catalytic site. Consequently, the atoms of bound transition state analogues are more dynamic in the catalytic site of the E. coli enzyme than in the V. cholera enzyme.40 The most powerful transition state analogues for the MTANs have the unusual property of favorable entropic and enthalpic characteristics. They contain a hydrophobic group that replaces waters in the hydrophobic area of the protein and also engage the methylthioribosyl cation in contact with an activated water molecule as mimics of the transition state. The complex of MTAN and transition state analogue together with the single nucleophilic water molecule are sufficiently stable to enter the vacuum phase together in the nanoelectrospray quadrupole time-of-flight mass spectrometer.41 A similar property has been reported for transition state analogues bound to cytidine deaminase.42,43
IX. SUMMARY AND CONCLUSIONS
Chemistry at catalytic sites occurs by vibrational coupling of stochastic fs atomic motions to the protein or to nearby reactant groups. The slower chemistry observed at catalytic sites reflects the low probability of synchronizing all required participating groups. Heavy-enzyme experiments support this mechanism. Transition state analogues stabilize the favored transition state geometry evolved in enzymes for catalysis. Stable analogues form strong interactions to the protein and can cause conformational condensation of the protein with slow release of the analogue.
Biography
Vern L. Schramm studied chemistry and bacteriology at the South Dakota State University for the B.S. degree and biochemistry and nutrition at Harvard for the M.S. degree. He received a Ph.D. degree in biochemistry with John Morrison at the Australian National University, John Curtin School of Medical Research. His research using kinetic isotope effects to understand enzymatic transition state structure began at the Temple University School of Medicine. The application of transition state knowledge to drug development and protein dynamic contributions to catalysis was developed at the Albert Einstein College of Medicine where Schramm is the Ruth Merns Chair and Professor of Biochemistry.
Footnotes
The authors declare no competing financial interest.
REFERENCES
- 1.Knowles JR. Enzyme Catalysis: Not Different, Just Better. Nature. 1991;350:121–124. doi: 10.1038/350121a0. [DOI] [PubMed] [Google Scholar]
- 2.Saen-Oon S, Quaytman-Machleder S, Schramm VL, Schwartz SD. Atomic Detail of Chemical Transformation at the Transition State of an Enzymatic Reaction. Proc. Natl. Acad. Sci. U. S. A. 2008;105:16543–16548. doi: 10.1073/pnas.0808413105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Basner JE, Schwartz SD. How Enzyme Dynamics Helps Catalyze a Reaction in Atomic Detail: A Transition Path Sampling Study. J. Am. Chem. Soc. 2005;127:13822–13831. doi: 10.1021/ja043320h. [DOI] [PubMed] [Google Scholar]
- 4.Schwartz SD. Protein Dynamics and the Enzymatic Reaction Coordinate. Top. Curr. Chem. 2013;337:189–208. doi: 10.1007/128_2012_412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bolhuis PG, Chandler D, Dellago C, Geissler PL. Transition Path Sampling: Throwing Ropes over Rough Mountain Passes, in the Dark. Annu. Rev. Phys. Chem. 2002;53:291–318. doi: 10.1146/annurev.physchem.53.082301.113146. [DOI] [PubMed] [Google Scholar]
- 6.Wolfenden R. Massive Thermal Acceleration of the Emergence of Primordial Chemistry, the Evolution of Enzymes, and the Tempo of Spontaneous Mutation. J. Biol. Chem. 2014;289:30198–30204. doi: 10.1074/jbc.R114.567081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.DeWolf WE, Jr, Emig FA, Schramm VL. AMP Nucleosidase: Kinetic Mechanism and Thermodynamics. Biochemistry. 1986;25:4132–4140. doi: 10.1021/bi00362a022. [DOI] [PubMed] [Google Scholar]
- 8.Pugmire MJ, Ealick SE. Structural Analyses Reveal Two Distinct Families of Nucleoside Phosphorylases. Biochem. J. 2002;361:1–25. doi: 10.1042/0264-6021:3610001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ho MC, Shi W, Rinaldo-Matthis A, Tyler PC, Evans GB, Clinch K, Almo SC, Schramm VL. Four Generations of Transition-State Analogues for Human Purine Nucleoside Phosphorylase. Proc. Natl. Acad. Sci. U. S. A. 2010;107:4805–4812. doi: 10.1073/pnas.0913439107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Suarez J, Haapalainen AM, Cahill SM, Ho MC, Yan F, Almo SC, Schramm VL. Catalytic Site Conformations in Human PNP by 19F-NMR and Crystallography. Chem. Biol. 2013;20:212–222. doi: 10.1016/j.chembiol.2013.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ghanem M, Zhadin N, Callender R, Schramm VL. Loop-Tryptophan Human Purine Nucleoside Phosphorylase Reveals Submillisecond Protein Dynamics. Biochemistry. 2009;48:3658–3668. doi: 10.1021/bi802339c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hirschi JS, Arora K, Brooks CL, 3rd, Schramm VL. Conformational Dynamics in Human Purine Nucleoside Phosphorylase with Reactants and Transition-State Analogues. J. Phys. Chem. B. 2010;114:16263–16272. doi: 10.1021/jp108056s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Antoniou D, Abolfath MR, Schwartz SD. Transition Path Sampling Study of Classical Rate-Promoting Vibrations. J. Chem. Phys. 2004;121:6442–6447. doi: 10.1063/1.1782813. [DOI] [PubMed] [Google Scholar]
- 14.Núñez S, Wing C, Antoniou D, Schramm VL, Schwartz SD. Insight into Catalytically Relevant Correlated Motions in Human Purine Nucleoside Phosphorylase. J. Phys.s Chem. A. 2006;110:463–472. doi: 10.1021/jp051277u. [DOI] [PubMed] [Google Scholar]
- 15.Silva RG, Murkin AS, Schramm VL. Femtosecond Dynamics Coupled to Chemical Barrier Crossing in a Born-Oppenheimer Enzyme. Proc. Natl. Acad. Sci. U. S. A. 2011;108:18661–18665. doi: 10.1073/pnas.1114900108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kipp DR, Silva RG, Schramm VL. Mass-Dependent Bond Vibrational Dynamics Influence Catalysis by HIV-1 Protease. J. Am. Chem. Soc. 2011;133:19358–19361. doi: 10.1021/ja209391n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Villali J, Kern D. Choreographing an Enzyme’s Dance. Curr. Opin. Chem. Biol. 2010;14:636–643. doi: 10.1016/j.cbpa.2010.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hammes-Schiffer S. Catalytic Efficiency of Enzymes: A Theoretical Analysis. Biochemistry. 2013;52:2012–2020. doi: 10.1021/bi301515j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Henzler-Wildman K, Kern D. Dynamic Personalities of Proteins. Nature. 2007;450:964–972. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- 20.Peng HL, Deng H, Dyer RB, Callender R. Energy Landscape of the Michaelis Complex of Lactate Dehydrogenase: Relationship to the Catalytic Mechanism. Biochemistry. 2014;53:1849–1857. doi: 10.1021/bi500215a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pudney CR, Guerriero A, Baxter NJ, Johannissen LO, Waltho JP, Hay S, Scrutton NS. Fast Protein Motions Are Coupled to Enzyme H-Transfer Reactions. J. Am. Chem. Soc. 2013;135:2512–2517. doi: 10.1021/ja311277k. [DOI] [PubMed] [Google Scholar]
- 22.Toney MD, Castro JN, Addington TA. Heavy-Enzyme Kinetic Isotope Effects on Proton Transfer in Alanine Racemase. J. Am. Chem. Soc. 2013;135:2509–2511. doi: 10.1021/ja3101243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Luk LY, Javier Ruiz-Pernía J, Dawson WM, Roca M, Loveridge EJ, Glowacki DR, Harvey JN, Mulholland AJ, Tuñón I, Moliner V, Allemann RK. Unraveling the Role of Protein Dynamics in Dihydrofolate Reductase Catalysis. Proc. Natl. Acad. Sci. U. S. A. 2013;110:16344–16349. doi: 10.1073/pnas.1312437110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Swiderek K, Javier Ruiz-Pernía J, Moliner V, Tuñón I. Heavy Enzymes-Experimental and Computational Insights in Enzyme Dynamics. Curr. Opin. Chem. Biol. 2014;21C:11–18. doi: 10.1016/j.cbpa.2014.03.005. [DOI] [PubMed] [Google Scholar]
- 25.Dametto M, Antoniou D, Schwartz SD. Barrier Crossing in Dihydrofolate Reductase Does Not Involve a Rate-Promoting Vibration. Mol. Phys. 2012;110:531–536. doi: 10.1080/00268976.2012.655337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Liu CT, Layfield JP, Stewart RJ, 3rd, French JB, Hanoian P, Asbury JB, Hammes-Schiffer S, Benkovic SJ. Probing the Electrostatics of Active Site Microenvironments along the Catalytic Cycle for Escherichia coli Dihydrofolate Reductase. J. Am. Chem. Soc. 2014;136:10349–10360. doi: 10.1021/ja5038947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wang Z, Singh P, Czekster CM, Kohen A, Schramm VL. Protein Mass-Modulated Effects in the Catalytic Mechanism of Dihydrofolate Reductase: Beyond Promoting Vibrations. J. Am. Chem. Soc. 2014;136:8333–8341. doi: 10.1021/ja501936d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Masterson JE, Schwartz SD. Changes in Protein Architecture and Subpicosecond Protein Dynamics Impact the Reaction Catalyzed by Lactate Dehydrogenase. J. Phys. Chem. A. 2013;117:7107–7113. doi: 10.1021/jp400376h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Antoniou D, Ge X, Schramm VL, Schwartz SD. Mass Modulation of Protein Dynamics Associated with Barrier Crossing in Purine Nucleoside Phosphorylase. J. Phys. Chem. Lett. 2012;3:3538–3544. doi: 10.1021/jz301670s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jencks WP. When Is an Intermediate Not an Intermediate? Enforced Mechanisms of General Acid-Base Catalyzed, Carbocation, Carbanion, and Ligand Exchange Reactions. Acc. Chem. Res. 1980;13:161–169. [Google Scholar]
- 31.Ghanem M, Murkin AS, Schramm VL. Ribocation Transition State Capture and Rebound in Human Purine Nucleoside Phosphorylase. Chem. Biol. 2009;16:971–979. doi: 10.1016/j.chembiol.2009.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wolfenden R. Transition State Analogues for Enzyme Catalysis. Nature. 1969;223:704–705. doi: 10.1038/223704a0. [DOI] [PubMed] [Google Scholar]
- 33.Lewandowicz A, Schramm VL. Transition State Analysis for Human and Plasmodium Falciparum Purine Nucleoside Phosphorylases. Biochemistry. 2004;43:1458–1468. doi: 10.1021/bi0359123. [DOI] [PubMed] [Google Scholar]
- 34.Edwards AA, Mason JM, Clinch K, Tyler PC, Evans GB, Schramm VL. Altered Enthalpy-Entropy Compensation in Picomolar Transition State Analogues of Human Purine Nucleoside Phosphorylase. Biochemistry. 2009;48:5226–5238. doi: 10.1021/bi9005896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Edwards AA, Tipton JD, Brenowitz MD, Emmett MR, Marshall AG, Evans GB, Tyler PC, Schramm VL. Conformational States of Human Purine Nucleoside Phosphorylase at Rest, At Work, And with Transition State Analogues. Biochemistry. 2010;49:2058–2067. doi: 10.1021/bi902041j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Vetticatt MJ, Itin B, Evans GB, Schramm VL. Distortional Binding of Transition State Analogues to Human Purine Nucleoside Phosphorylase Probed by Magic Angle Spinning Solid-State NMR. Proc. Natl. Acad. Sci. U. S. A. 2013;110:15991–15996. doi: 10.1073/pnas.1313657110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Parveen N, Cornell KA. Methylthioadenosine/S-Adenosylhomocysteine Nucleosidase, a Critical Enzyme for Bacterial Metabolism. Mol. Microbiol. 2011;79:7–20. doi: 10.1111/j.1365-2958.2010.07455.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Li X, Apel D, Gaynor EC, Tanner ME. 5′-Methylthioadenosine Nucleosidase Is Implicated in Playing a Key Role in a Modified Futalosine Pathway for Menaquinone Biosynthesis in Campylobacter jejuni. J. Biol. Chem. 2011;286:19392–19398. doi: 10.1074/jbc.M111.229781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gutierrez JA, Crowder T, Rinaldo-Matthis A, Ho MC, Almo SC, Schramm VL. Transition State Analogues of 5′-Methylthioadenosine Nucleosidase Disrupt Quorum Sensing. Nat. Chem. Biol. 2009;5:251–257. doi: 10.1038/nchembio.153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Motley MW, Schramm VL, Schwartz SD. Conformational Freedom in Tight Binding Enzymatic Transition-State Analogues. J. Phys. Chem. B. 2013;117:9591–9597. doi: 10.1021/jp4030443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wang S, Lim J, Thomas K, Yan F, Angeletti RH, Schramm VLA. Complex of Methylthioadenosine/S-Adenosylhomocysteine Nucleosidase, Transition State Analogue, And Nucleophilic Water Identified by Mass Spectrometry. J. Am. Chem. Soc. 2012;134:1468–1470. doi: 10.1021/ja211176q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Schroeder GK, Zhou L, Snider MJ, Chen X, Wolfenden R. Flight of a Cytidine Deaminase Complex with an Imperfect Transition State Analogue Inhibitor: Mass Spectrometric Evidence for the Presence of a Trapped Water Molecule. Biochemistry. 2012;51:6476–6486. doi: 10.1021/bi300516u. [DOI] [PubMed] [Google Scholar]
- 43.Borchers CH, Marquez VE, Schroeder GK, Short SA, Snider MJ, Speir JP, Wolfenden R. Fourier Transform Ion Cyclotron Resonance MS Reveals the Presence of a Water Molecule in an Enzyme Transition-State Analogue Complex. Proc. Natl. Acad. Sci. U. S. A. 2004;101:15341–15345. doi: 10.1073/pnas.0406781101. [DOI] [PMC free article] [PubMed] [Google Scholar]