Mechanisms of Gait Asymmetry Due to Push-off Deficiency in Unilateral Amputees

Abstract

Unilateral lower-limb amputees exhibit asymmetry in many gait features, such as ground force, step time, step length, and joint mechanics. Although these asymmetries result from weak prosthetic-side push-off, there is no proven mechanistic explanation of how that impairment propagates to the rest of the body. We used a simple dynamic walking model to explore possible consequences of a unilateral impairment similar to that of a transtibial amputee. The model compensates for reduced push-off work from one leg by performing more work elsewhere, for example during the middle of stance by either or both legs. The model predicts several gait abnormalities, including slower forward velocity of the body center-of-mass (COM) during intact-side stance, greater energy dissipation in the intact side, and more positive work overall. We tested these predictions with data from unilateral transtibial amputees (N = 11) and non-amputee control subjects (N = 10) walking on an instrumented treadmill. We observed several predicted asymmetries, including forward velocity during stance phases and energy dissipation from the two limbs, as well as greater work overall. Secondary adaptations, such as to reduce discomfort, may exacerbate asymmetry, but these simple principles suggest that some asymmetry may be unavoidable in cases of unilateral limb loss.

I. INTRODUCTION

INDIVIDUALS with unilateral transtibial limb loss typically exhibit asymmetrical gait patterns. Asymme-tries observed in the literature include bilateral differences in timing or distance parameters, such as swing and stance times and step lengths [1]–[6]. These differences may arise as a result of a substantial mechanical difference between the prosthetic and intact sides, most notably the inability to actively produce ankle power. As a result, gait analysis shows asymmetric ground reaction forces and altered joint kinematics and kinetics throughout the rest of the body [7]–[10]. Despite considerable evidence for these and other asymmetries, there is no established explanation why loss of the ankle and foot should lead to the particular effects observed in other joints in the body, or how these should lead to general asymmetries in timing and speed. Nor is it clear what biomechanical compensations might be most economical for amputees [11]–[15]. A mechanistic study of the fundamental effects of unilateral limb loss and strategies for compensating for this loss might yield insights regarding asymmetric gait.

One of the primary effects of transtibial limb loss is a reduction of ankle power in that limb. In contrast to ankle moment trajectories that do not appear drastically different from the unimpaired case [10], [16], the ankle power is greatly reduced during the push-off phase, which begins about 2 – 3% before the beginning of a stride (defined by successive heel contacts on intact side), and continues to about 12% of that stride. This also results in considerably reduced positive work on the overall body center of mass (COM), which leads to greater dissipation of mechanical energy in the nearly simultaneous collision (about 0 – 15% of stride) of the intact leg with ground [13], which should then be restored through more positive work elsewhere in the body [11]. The greater amount of work could potentially explain greater metabolic energy expenditure for walking in amputees [11]–[15].

That loss of power could have a causal link to asymmetries observed elsewhere in the body. For example, it could mean that other joints must compensate for the reduced push-off by performing a greater amount of work. The distribution and amount of joint work could change in both timing and location, and thus lead to asymmetries in other timing and distance metrics. An example is the greater collision loss on the intact side [12], [17], which should cause the ensuing stance phase to be slower compared to prosthetic side stance (which benefits from a preceding unimpaired push-off). This suggests that asymmetric stance times could be associated with asymmetric power production. But such explanations presumably depend on how and when the compensatory work is performed. It is therefore helpful to consider what compensations, of a nearly limitless possible variety, might be most economical.

We propose to address this question with a simple modeling approach. Here we employ a dynamic walking model to predict how weak push-off on one leg should affect COM mechanics. We model unilateral impairment as a reduction in push-off work from a single leg, and examine several possible compensations to maintain the same overall walking speed. The model shows that some asymmetries, such as the increased intact-side stance time discussed above, are a nearly unavoidable consequence of reduced prosthetic-side push-off. These and other predicted asymmetries are then compared with experimental data from unilateral transtibial amputees and non-amputees. This allows us to test whether reduced push-off causes a cascade of asymmetries that are not prevented by simple adaptations.

II. METHODS

We devised a dynamic walking model to predict the effects of unilateral impaired push-off on bipedal gait. The model has several possible ways for the model to compensate for reduced push-off. These compensations then lead to several gait pattern asymmetries, which are then compared with experimental data from human subjects with unilateral transtibial amputation. We compared model and human results to assess whether asymmetries commonly observed in amputees are likely caused by weak push-off, or are instead the byproduct of secondary compensations. Here we briefly summarize how the model compensates for impaired push-off, followed by details of the experimental measurements.

A. Model

Our model (Fig. 1) is a variation on previous dynamic walking models for bipedal gait. It has two pendulum-like legs that can swing freely about the hips, restricted to sagittal plane motion only. It has rigid curved feet and a pelvis, with mass distribution roughly similar to human. Placed on a descending slope, the model produces a passive dynamic walking gait [18]. On level ground, it uses impulsive push-off from the trailing leg just before heel strike to power a dynamic walking gait (“Anthropomorphic model” of [19]–[21]). It may also be powered through a hip extension torque on the stance leg, as might result from leaning the torso forward. McGeer [18] showed that such powering is nearly identical to setting a ground slope, which we therefore use to model a virtual trunk for hip power. In the present study, the main difference with previous models [19]–[21] is that we weaken push-off from one of the legs, as a model of the prosthetic side in unilateral transtibial limb loss, and then compensate by adding hip power. All compensations are restricted to produce the same nominal walking speed and stride length, equivalent to about 1.25 m/s and 1.4 m in humans (or dimensionless values of 0.4 and 1.39, respectively, using body mass, leg length, and gravitational acceleration as base units).

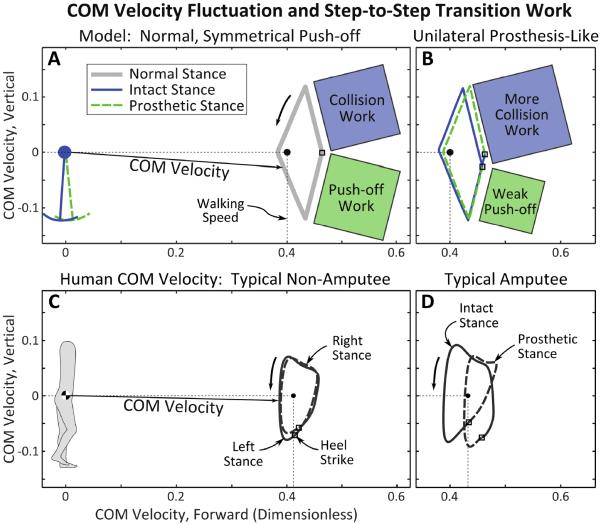
Fig. 1.

Conceptual model of walking and compensations for push-off asymmetry. (A) A symmetrical model experiences sharp changes in COM (body center-of-mass) velocity (small arrows) in the step-to-step transition. Impulsive push-off (PO) from the trailing leg and impulsive collision (CO) of the leading leg redirect the COM velocity from forward-and-down to forward-and-up (dotted lines), performing positive and negative work, respectively, on the COM. (B) In the asymmetric model, weak push-off from one leg (Prosthetic, lighter shading) results in greater collision and lower speed during the ensuing (Intact) stance phase. The model can compensate by adding work through the stance hip to accelerate. Despite this acceleration, speed during middle-stance is slower on average during Intact stance than during Prosthetic stance. (C) In humans, step-to-step transition is not perfectly impulsive but COM velocity experiences similar fluctuations. (D) Unilateral amputees have weak push-off, which is expected to lead to greater collision, slower middle-stance speed, and greater compensatory work on the intact leg. Step length asymmetry is also possible, defined here between contact points for the model (B) and between ankles for humans (D).

The model for unilateral transtibial limb loss is to reduce push-off work performed by one leg. Rather than eliminate push-off entirely, we reduce it to 63% of normal, in line with observations from amputee subjects [13], [16] showing that the residual limb and other joints do perform some push-off work on the COM. In our model of both the normal symmetric and unilaterally impaired cases, push-off occurs as an impulse immediately before the other leg's collision, which accounts for the only energy dissipation in the model. The push-off reduces the collision velocity and dissipated energy, the latter amount being proportional to the square of the collision velocity and the square of step length [19], [22]. That relationship makes asymmetric collisions less economical than symmetric, because one leg's higher collision dissipates more energy than is saved by the other leg's smaller collision. A primary prediction of the model is that reduced prosthetic-side push-off should result in greater collision of the intact leg with ground.

Possible compensations may be divided into two broad categories. The first involves performing more positive work to speed the prosthetic-side stance phase, either from greater intact-side push-off, or from prosthetic-side hip work. Greater intact push-off should reduce the prosthetic side collision, but it should also speed the ensuing prosthetic side stance phase, resulting in an even greater loss from the next intact side collision. It thus accentuates the collision asymmetry, making it quite uneconomical. Positive prosthetic-side hip work should similarly speed that stance phase and increase the collision asymmetry, although with somewhat different effects on the swing phase. Both of the approaches that speed prosthetic-side stance are possible ways to compensate for weak push-off, but would not be regarded as optimal.

The other compensation is to perform positive work to speed the intact-side stance phase. This is achieved by performing positive hip work during intact-side stance. It restores the speed lost from reduced prosthetic-side push-off, and thus makes the collisions more symmetrical. This may also be accompanied by additional hip work during prosthetic-side stance, which does less to improve economy, but distributes the work across both legs. In either case, intact-side hip work should be more economical than speeding prosthetic-side stance, and thus the most sensible strategy for the model to compensate for unilaterally reduced push-off.

Regardless of compensation, there are four main predicted consequences of impairment. The first is that reduced prosthetic-side push-off should result in greater intact-side collision work, and greater positive work overall, as stated previously. Second, there will be an asymmetry in forward speed of the COM at mid-stance. This is because the greater intact-side collision causes the inverted-pendulum-like stance phase to begin with a relatively low speed. Stance phase hip powering can gradually speed the pendulum throughout stance, but the mid-stance speed will still be slower than the corresponding speed for the prosthetic side, for a fixed overall walking speed. A third and related prediction is that uni-lateral impairment should cause an asymmetry in stance durations. Again, despite hip work, the intact-side stance phase will be slower and take relatively more time than the prosthetic-side stance phase. Fourth, the same effect is expected to cause an overall reduction in COM velocity symmetry throughout the two stance phases. This may be visualized in a “COM hodograph” plot of the vertical and forward components of COM velocity against each other [19], [22], [23]. Each stance phase yields a counter-clockwise loop for the hodograph (Fig. 2). We expect the intact-side loop should be slower overall than the prosthetic side, and to have differently-shaped extremes due to the dynamics of collision and rebound [22].

Fig. 2.

Velocity trajectories for the body center of mass for model and human. Plot of vertical vs. forward COM velocity, termed a COM hodograph, traces a counter-clockwise path; it is the path traced by the tip of the COM velocity vector (A,C). Heel strike is marked with a square in each diagram. (A) In the normal symmetric model, push-off and collision impulses perform positive and negative work, respectively (relative amounts denoted by shaded boxes), to redirect the COM velocity. The stance phase acts like an inverted pendulum and completes the path with no energy change. (B) An asymmetric model produces less push-off from the prosthetic side, resulting in a larger collision loss on the intact side. The loss requires more work elsewhere in the stride, and more total work overall, to maintain the same walking speed. The asymmetric collision also causes COM speed to be slower during intact-side stance phase than prosthetic-side stance. For human (C) non-amputees and (D) amputees, COM hodographs also trace a counter clockwise path, but with a more rounded profile due to forces being less impulsive. In amputees, the forward velocities of the two stance phases are different, with the intact side stance occurring at lower speed than prosthetic side stance.

We use an example case of our model to demonstrate these consequences (Fig. 3). Here we have used positive hip work on the intact side as the compensation, and quantify the effects on work, mid-stance speed, stance phase duration, step length, and in COM hodographs. In this demonstration case, intact-side collision work increased by 43% compared to normal, and the model performs 26% more work overall to maintain the same speed. As a result, the mid-stance speed is slower on the intact-side than prosthetic-side, and time spent in intact stance is greater. Step length in this example (defined as forward distance from the trailing, contralateral foot's “toe” contact point to the measured foot's “heel” contact point, at heel strike) is very slightly less on the prosthetic side than on the intact side.

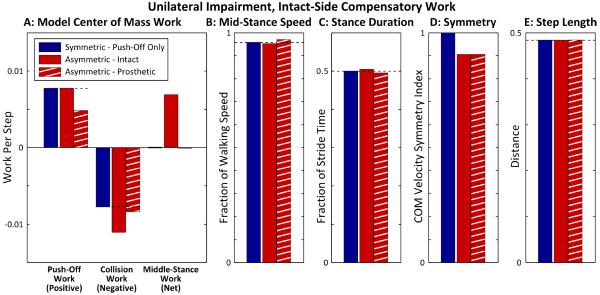
Fig. 3.

Model predictions for COM work and gait parameters. Two models are compared: A normal, symmetric model powered by push-off (left-most bars, in blue for either leg); and an asymmetric model with weak push-off in one (prosthetic-side) leg, powered by intact-side hip work (middle bars in red for strong leg, right-most bars in hatched red for prosthetic leg). (A) Positive push-off work, negative collision work, and net middle-stance work are shown for the symmetric model, and for the asymmetric model with unilaterally reduced push-off. Reduced push-off results in greater intact-side collision work, compensated for here by positive hip work during intact-side stance. (B) Greater collision produces slower forward speed at mid-stance during intact-side stance, and compensatory work produces faster speed during prosthetic-side stance. (C) Similarly, stance duration is longer on the intact side than the prosthetic side. (D) A symmetry index that quantifies the degree of match between COM velocities on the two sides (Fig. 2) summarizes the greater asymmetry due to reduced push-off. (E) Step length has very slight asymmetry, which depends on compensation strategy. With intact-side hip work, steps are slightly longer with the model's prosthetic leg; with prosthetic-side or bilateral hip work, prosthetic-side steps are shorter (see Supplementary Material).

To remove these asymmetries entirely, a highly non-smooth (and very physiologically demanding) means of performing work would be required, to speed the early intact-side stance phase.. These predictions are therefore largely independent of which of the possible compensation strategies are employed. In the Supplementary Material, we also summarize results from alternate compensation strategies using middle-stance work on the prosthetic side or both sides. These yield somewhat different quantitative effects, but they are qualitatively similar to the predictions shown here (Fig. 3). The exception is step length: using prosthetic-side or bilateral work to compensate leads to slightly longer steps on the intact leg.

B. Experimental Measurements

We compared walking in unilateral transtibial amputees against predictions from the model. We tested a range of speeds, to determine whether amputees increase push-off at higher speed as non-amputees do [24], and whether the impact of the impairment increases. Subjects walked at speeds from 0.7 to 1.6 m·s⁻¹ on an instrumented treadmill [25], wearing their prescribed prostheses (all commercially available passive devices) and their customary shoes (athletic shoes for most subjects). We measured ground reaction forces and estimated center of mass mechanics, and compared the results against the predicted asymmetries in collision work, total work, mid-stance COM velocity, stance time, step length, and COM velocity symmetry. We also measured step length by recording motion capture trajectories of markers on the lateral malleolus of each leg (estimated for the prosthetic side). Amputee subjects (N = 11; mass 84.1 kg ranging 68.6 – 99.2 kg; leg length 0.893 ranging 0.827 – 0.984 m) walked at speeds of 0.7, 1.0, 1.3 and 1.6 m·s⁻¹. Four amputee subjects were uncomfortable with walking on a treadmill at 1.3 m·s⁻¹, and five with 1.6 m·s⁻¹, resulting in missing data points. As a basis for comparison, we also measured non-amputee subjects (N = 10, mass 77.5 kg, ranging 57.8 – 98.9 kg), leg length 0.934 m, ranging 0.864 -1.040 m) walking at speeds of 0.7, 0.9, 1.1, 1.25, 1.4 and 1.6 m·s⁻¹, the greater number of speeds owing to higher tolerance for extended walking. All subjects gave their written informed consent to these procedures as approved by the University of Michigan Institutional Review Board.

We estimated work performed on the COM from recorded ground reaction forces (GRF) from each leg. The forces were integrated to estimate COM velocity [22], whose dot product with force yielded the rate of work performed by each leg on the COM [26]. We assumed that strides (beginning with intact side for amputees, left leg for non-amputees) were periodic, but allowed for asymmetric steps. We integrated COM work rate to determine COM work performed by each leg during the push-off and collision phases of gait [12], [13], [16], [26], and total work during the stride. The push-off and collision phases of the step-to-step transition were delineated by the downward and upward extremes of COM velocity direction surrounding double-support [22].

We computed a series of metrics to quantify gait asymmetries. For comparison with model predictions (Fig. 2), work metrics for each leg included COM work performed in push-off and collision, and total positive COM work (integral of positive intervals of COM work rate) over the stride. We also quantified the net work performed during the middle of stance, in the period following collision and prior to push-off. Termed middle-stance work, this quantity combines two phases we have previously referred to separately as rebound and preload e.g., [27], [28]; the present model only performs hip work analogous to the net middle-stance work of that combination. We also computed COM velocity at midstance (defined by zero vertical velocity), and stance time for each leg. As a measure of differences in COM velocity trajectories between the two legs, we further defined an overall symmetry index, as the maximum value of the mean (across forward and vertical components) autocorrelation coefficients of the COM velocity signal, with lag no greater than 75% of a stride. This symmetry metric captures asymmetries in both magnitude and timing along each component; it can range from 1 (perfect symmetry) to −1. Finally, we used motion capture data to measure the step length on each side, defining the leading leg's step length as the forward distance from the trailing to the leading lateral malleolus markers at the time of equal force on the two legs (about halfway through double support).

These metrics were applied to data from each experimental condition. For each subject, we identified the first seven clean strides per condition, then computed and averaged the resulting metrics across these strides. We classified each value according to the “leg type” that produced it: an amputee's prosthetic (P) or intact (I) leg, or a non-amputee (N) subject's leg. Quantities were nondimensionalized according to each subject's body mass M, standing leg length L (floor to greater trochanter), and the gravitational acceleration, g. For example, work was normalized by MgL (value using subject mean parameters: 723.9 J); power by Mg(gl)^0.5 (2373.2 W); velocity by (gL)^0.5 (2.99 m · s⁻¹); frequency by gL^−0.5 (3.28 Hz); and step length by L (0.913 m).

Statistical tests were performed to identify significant asymmetries. Because amputee and non-amputee groups exhibited different speed capabilities, their data were compared across all speeds using sample-wide analysis of covariance (ANOCOVA). Metrics were compared pairwise across the three leg types (prosthetic, intact, and non-amputee). Significant differences were determined by comparing the population marginal means of each leg type, subject to a Dunn-Sidak significance adjustment [29]. The population marginal means (PMM) analysis compares the linear regressions and confidence intervals of overlapping but unmatched samples, evaluated at point in the middle of the range of the independent variable (dimensionless speed). Differences in each output metric between any two leg types were considered sig nificant if the 95% confidence interval of their difference did not include zero, corresponding to α = 0.05. Confidence intervals and standard deviations reported in the text and figures were estimated from the standard error of the PMM.

III. RESULTS

We observed several of the hypothesized gait asymmetries in individuals with unilateral lower limb loss. These included reduced COM work from prosthetic-side push-off, increased intact-side collision work, and increased work overall, across walking speeds (see Fig. 4 for representative data from an amputee and a non-amputee). Qualitative differences include greater initial peaks in vertical ground reaction forces on the intact side (Fig. 4A), greater COM work rate magnitudes during collision (Fig. 4B), and highly asymmetric COM hodo-graphs (Fig. 4C), suggesting a large asymmetry in forward speed during mid-stance. The main observations were also tested quantitatively in comparison with model predictions. Statistical tests were evaluated for walking at a dimensionless speed of 0.376 (1.12 m·s⁻¹), which is a typical walking speed for unilateral amputees [12]. Results are reported as PMM ± 95% confidence interval (CI), and all stated differences are statistically significant unless otherwise indicated.

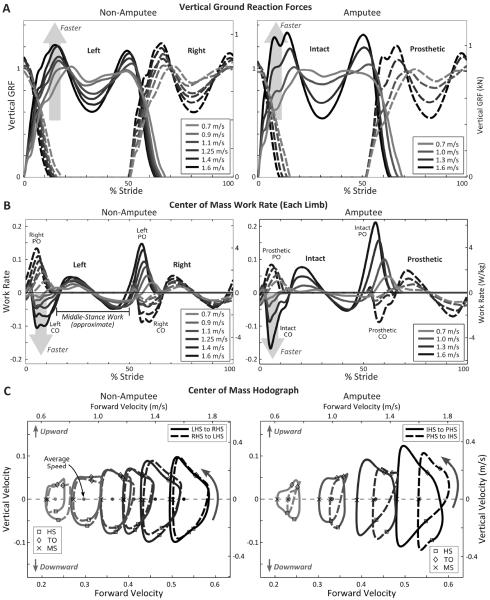
Fig. 4.

Examples of ground reaction forces, center of mass (COM) work rate, and COM hodographs for non amputee and amputee (left and right columns, respectively). Data shown are from a representative subject from each group. (A) Vertical ground reaction forces (GRF) show asymmetries between groups. Higher speeds increase peak forces in both amputees and non amputees, but the peaks are higher on the intact side of amputees. (B) COM work rate, defined as the dot product of GRF and COM velocity, shows negative collision (CO) work at beginning of stance and positive push-off (PO) work at end of stance. Push-off and collision intervals are separated by an interval of middle-stance work. Total work over a stride is the sum of all three intervals. At all speeds, push-off was lower on the prosthetic side of amputees, and collision was much greater on the intact side compared to non amputees. (C) COM hodographs show symmetry of COM velocities in non-amputees, and asymmetry in amputees. Asymmetry is especially pronounced in forward speed during prosthetic-side vs. intact-side stance. HS: Heel-strike; TO: Toe-off; MS: Mid-stance; L: Left; R: Right; P: Prosthetic; I: Intact.

Amputees performed only 53% as much positive push-off work with their prosthetic-side leg as with their intact leg (Fig. 5A). The average prosthetic-side push-off work was about 0.113 J·kg⁻¹ per stride, or in dimensionless terms, 0.0126 ± 0.0008. This was significantly less than intact-side push-off of 0.211 J·kg⁻¹, or 0.0236 ± 0.0008, which was not significantly different from non-amputees (0.217 J·kg⁻¹, or 0.0243 ± 0.0004).

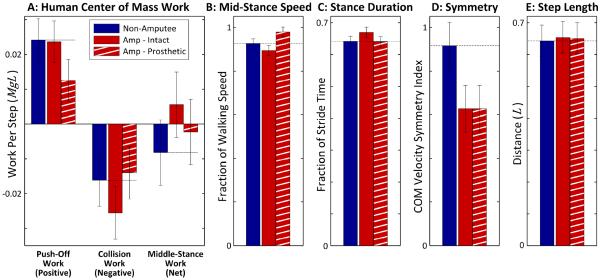
Fig. 5.

Experimental measurements of COM work and gait parameters in non-amputees and amputees (PMM ± SD, dimensionless). Non-amputee results are shown for one leg (left most bars, in blue), whereas amputee results are shown for both the intact and prosthetic side (middle bars in red and right-most bars in hatched red, respectively). (A) Positive push-off work, negative collision work, and net middle-stance work are shown. Amputees exhibited reduced prosthetic-side push-off work, increased intact-side collision work, and greater (more positive) total work during the middle-stance period. (B) In terms of mid stance speed, amputees also exhibited slower forward speed at mid-stance on the intact side, and faster speed on the prosthetic side. (C) Stance duration was longer on the intact side than the prosthetic side. (D) The COM velocity symmetry index showed lower symmetry in amputees than in non-amputees. (E) Step length was not statistically different among leg types, though absolute step length asymmetry was frequently higher in amputees (see supplementary material).

Push-off was followed by about 83% greater magnitude of negative collision work on the intact side, compared to the prosthetic-side collision, or about 58% higher than in non-amputees. The collision work quantities were −0.228 J·kg⁻¹ on the intact side (−0.0255 ± 0.0010 dimensionless, PMM ± 95% CI) vs. −0.125 J·kg⁻¹ (−0.0140 ± 0.0010) on the prosthetic side for amputees. Prosthetic-side negative collision work was about 16% less than in non-amputees, who performed −0.144 J·kg⁻¹ (−0.0161 ± 0.0005) per stride.

Total positive COM work rate was 15% higher in amputees than in non-amputees. This quantity incorporates separate periods of “rebound” and “preload” work (Fig. 4; [22]), as distinct from the predicted middle-stance work that allows these phases to cancel each other (Fig. 5). The total positive work rate for amputees was 0.614 W·kg⁻¹ (0.0209 ± 0.0003), compared with 0.533 W·kg⁻¹ (0.0182 ± 0.0002) for non-amputees. The difference was associated with roughly 12% higher work per stride (0.0756 ± 0.0013 vs. 0.0676 ± 0.0007 dimensionless) and 2% higher stride rate (0.88 vs. 0.86 Hz; 0.268 ± 0.003 vs. 0.261 ± 0.001 dimensionless).

Net middle-stance COM work, performed between the collision and push-off phases, was also asymmetric in amputees. This work was greater on the intact side (0.050 J·kg⁻¹; 0.0056 ± 0.0012) than the prosthetic side (−0.020 J·kg⁻¹; −0.0023 ± 0.0011). Both were significantly greater (more positive) than the non-amputee's −0.073 J·kg⁻¹ (−0.0082 ± 0.0006). Non-amputees actually performed substantial negative net middle-stance work, as they perform more push-off work than is dissipated in the collision.

Asymmetries were also observed in mid-stance forward speed, stance duration, and the symmetry index (Fig. 5). At mid-stance, the forward speed of the COM was significantly lower on the intact side compared to the prosthetic side. As a percentage of overall walking speed, the mid-stance speeds were about 89.3% ± 0.3% for the intact side and 97.9% ± 0.3% for the prosthetic side. For comparison, non-amputees produced a midstance speed about 92.5% ± 0.2% of their overall walking speed. Stance duration was greater on the intact limb of amputees (67.0% ± 0.2% of stride) than on the prosthetic side (64.0% ± 0.2%) or in non-amputees (64.2% ± 0.1%). In terms of the defined symmetry index, sagittal plane COM velocity fluctuations were less symmetric (Fig. 5) in amputees (symmetry index 0.627 ± 0.013) than in non-amputees (0.915 ± 0.007).

Step length was not statistically different between prosthetic and intact sides or compared to non-amputees. Prosthetic-side step length was 0.594 m (0.651 ± 0.017), which was not different from the intact-side (0.597 m; 0.654 ± 0.017) or non-amputees (0.587 m; 0.644 ± 0.009). However, step length asymmetry (intact step length minus prosthetic step length; see supplementary material) was highly variable in amputees (standard deviation across all subjects and conditions: 0.058 m; 0.063 dimensionless) in comparison to non-amputees (left-right asymmetry S.D.: 0.019 m; 0.021 dimensionless).

The above statistical results are reported from the population marginal means analysis at a single, moderate speed. Most of these outcome metrics exhibit similar relationships across the entire range of speeds tested, 0.7 to 1.6 m·s⁻¹. Specific quantitative results for all speeds are presented in the supplementary material.

IV. DISCUSSION

We used a simple modeling approach to examine the mechanics of asymmetry in amputee gait. Based only on a reduction in push-off work on one leg, the model predicted several asymmetries. These include an increase in intact-side collision work and in overall work performed on the COM. The model also predicted several effects on the intact stance phase: a slower mid-stance speed, greater stance phase duration, and an overall slower COM velocity compared to the prosthetic side. Similar effects were observed in amputees, in contrast to the efficient, symmetrical gait of non-amputees. We also found the model to exhibit qualitatively similar asymmetries regardless of the compensatory power produced to offset the unilateral reduction of push-off. This suggests that the observed asymmetries may be nearly unavoidable for individuals with unilateral reduced push-off.

Perhaps the most consequential effect observed from weak prosthetic-side push-off was an 83% greater collision on the intact leg. This result corroborates Houdijk et al.'s [13] previous report of greater intact-side collision losses. Increased collision is further suggested by observed increases in the initial ground reaction force peaks from amputees (e.g., Fig. 5; [30], [31], [8], [9]). In our model, this collision is caused by two compounding factors that increase the velocity of the COM at heel-strike: reduced push-off work from the prosthetic-side leg, and the need to add work by other means to maintain the same overall walking speed. To maintain speed, more positive work must be performed elsewhere in the body, likely amplifying the collision velocity. A further contributor in amputees may be late push-off from the prosthetic leg. Passive prostheses return energy only as the force applied to them decreases. This unloading relies mostly on shifting of body weight to the intact limb, which may delay both ankle and COM push-off until after heel strike (Fig. 4B). Delayed push-off may increase intact-side collisions even further [23]. As predicted by the model, we also observed greater total COM work in amputees. This is expected because push-off is hypothesized to differ from other methods of performing work, in that it actually reduces the ensuing collision [24], [27], [32]. All compensations for reduced push-off therefore require more work overall, observed to be about 15% more in amputees. This increase could also explain the greater metabolic energy expended by amputees, by 20% or more [14], [15], [33]. Indeed, devices that increase prosthetic push-off also tend to reduce the collision, and in some cases metabolic energy expenditure [11], [17], [12], [14]. The compounding effects of weak push-off underscore the importance of increasing work output from the prosthetic ankle during push-off [11], [14], [34], which could potentially reduce the metabolic energy penalty for amputee gait.

Reduced push-off also appears linked to kinematic asymmetries. In amputees, forward COM speed at midstance was roughly 9% lower in intact side than prosthetic side. This effect is actually considerably greater than the model predicts. Part of the difference may be due to the different mass of the prosthetic foot and pylon, which are typically lighter than the corresponding intact side. Estimating reduced mass of up to 1.5% body weight (Mattes, 2000) and a mid-swing ankle speed about three times walking speed, prosthetic-side swing (during intact-side stance) could account for as much as 4.5% asymmetry in mid-stance speed, even if the legs moved with identical kinematics. Even so, there remains a substantial asymmetry, about 4 – 5% walking speed that is also corroborated by a 3% longer duration observed for prosthetic-side stance. This longer duration has been reported previously for both transtibial [5] and transfemoral [35] amputees; the latter have also been found to have asymmetric forward trunk velocity [36], similar to our findings for the COM. These observations all suggest that weak prosthetic-side push-off could indeed result in a slower intact-side stance phase.

Others have previously interpreted asymmetric stance durations as a result of early toe-off, surmising that the lack of prosthetic plantarflexion causes the toe to leave the ground earlier than a natural toe [10], [37]. Although we do not disagree with this possibility, we find it an insufficient explanation, because it suggests that prosthetic stance should be shorter than non-amputee stance, which we did not observe (64.0% vs. 64.1% of stride, respectively; see Fig. 5). It also does not explain why intact-side stance should be longer (67.0% of stride), as our model predicted and has been observed in past studies, e.g. [2], [5], [30], [38], [39]. Our interpretation is that reduced push-off and increased collision both lead to less kinetic energy for intact-side stance, and hence less speed for the inverted pendulum-like motion. Even if the hip or other joints were to add energy with positive work, it would be challenging to restore speed sufficiently to match the prosthetic side by the time of mid-stance. Our present results support this proposed chain of causality.

Our data also suggest possible compensation mechanisms performed by amputees. The increased total work, required as a consequence of reduced push-off, appears to be performed by both legs in the form of middle-stance work. In amputees, middle-stance work was greater on the intact side than prosthetic side (Fig. 7), and both were greater than in non-amputees. Our model is most economical when restoring power through the intact-side hip work alone. Practically speaking, this additional work places a large burden on a single leg, which already experiences a greater collision loss and performs more positive work during push-off. The data suggest that amputees do perform such compensation, but not exclusively; they also appear to perform more work during the prosthetic side stance phase, as observed at the hip by Winter and Sienko [10]. In addition, some of the negative middle-stance work may be due to elastic loading of the ankle [40], [41], which appears to be reduced on the prosthetic side [11], and therefore may skew the prosthetic middle-stance work toward the positive. We caution, however, that these are preliminary interpretations in the present study, because our COM work measurements cannot verify that the work was indeed performed at the hip as opposed to other joints. A more comprehensive inverse dynamics analysis would be required to test this proposed mechanism. We therefore tentatively propose that amputees perform compensatory work primarily with the intact side, but distribute some of the work to the prosthetic side as well.

Step length was not statistically different between prosthetic and intact sides across our sample of amputees. This result is consistent with the model, in which step length asymmetry was very small, and switched sign depending on the compensation method – which we interpret as no clear prediction of step length asymmetry. It is also compatible with prior literature, which includes cases of longer [3], [30], [42]–[44] and shorter [39], [45] steps on the prosthetic side. While step length did not favor a particular leg in this group of amputees, many did show significant asymmetry overall. The high standard deviation of asymmetry in amputees suggests that step length asymmetry is common, but the relationship between the two sides may be subject-dependent.

While we did not observe systematic step length asymmetry in this subject pool, incorporating such asymmetry could influence the biomechanical costs of gait. For example, taking a shorter step with the intact leg may reduce the COM redirection needed after intact heel strike, and the consequent intact-side collision. This approach could be attempted as a way of attenuating the increased intact-side collision that results from weak prosthetic push-off. Experimentally inducing step length asymmetry in future work could elucidate this effect.

One unexpected finding was that prosthetic-side collision dissipated 13% less energy than the collision of non-amputees. The model predicted that the prosthetic side would experience an equal or slightly greater collision, due to the faster collision velocity from intact-side stance-phase hip work. A possible explanation is that there was actually greater dissipation that was not reflected in collision work, due to simultaneous positive work in the same leg, for example at the hip [10], [46]. This is a limitation of our COM work metric, which is intended as a simple indicator of COM mechanics, and does not resolve simultaneous work by separate joints within one leg. This explanation is also beyond the capabilities of our model, which performs push-off and collision impulsively and does not consider simultaneous hip work. The same mechanism could also potentially explain an unexpectedly low increase in total work estimated in Houdijk et al.'s [13] study of amputees (a non-significant 5%). This limitation suggests that our estimation of collision work could underestimate actual dissipative work, as well as simultaneous positive work from other joints. Fortunately, the potential underestimate is conservative, making statistical tests less likely to detect significant differences. Similar effects could contribute to discrepancies between net middle-stance work and work evaluated from the rebound and preload periods separately.

There are a number of other limitations to this study. We devised a very simple model that cannot capture the many complexities of actual gait. The model does not consider all possible compensations for reduced push-off. For example, it is theoretically possible to pitch the trunk forward and backward such that there is no collision and no need for push-off [47]. We presume that most such alternatives would require unrealistic features such as extremely high hip compliance, but cannot rule out these possibilities entirely. We also focused only on the mechanistic consequences of reduced push-off, whereas some asymmetries could be due to other aspects of amputee gait. For example, the effective shape and length of the foot have been shown to affect contralateral limb loading [20], [31], [48], [49], and may vary among prostheses [50], [51]. Additionally, socket fit, altered collision mechanics of a prosthetic foot, and gait adaptations due to pain, fatigue, or poor prosthesis alignment may contribute. Although many such characteristics surely contribute to amputee gait, they also do not eliminate the possible contribution of the causal effects proposed here.

Our findings may have clinical implications for amputees. We found that the intact leg experiences greater collisions and performs more work during stance, while also performing similar push-off work as non-amputees. The intact leg may therefore be at increased risk of overuse injury, of which the high incidence of knee osteoarthritis [17], [52] may be one symptom. We also found that some aspects of asymmetric gait in amputees may be unavoidable, because no compensation can completely substitute for the lost prosthetic-side push-off. Although amputees may be encouraged to adopt a symmetric gait, in part for the sake of appearance, it is also possible that true symmetry is unachievable, and attempts to achieve it may have their own disadvantages [7], [31].

There may also be implications for gait conditions other than amputation. Our simple model of reduced push-off could potentially apply to other conditions that affect plantarflexion. For example, unilateral plantarflexor paralysis due to nerve blocks or surgery can cause shorter step lengths and/or increased loading on the unaffected limb [53]–[55]. Unilateral ankle arthrodesis can also cause reduced push-off [56] and asymmetry in step length and time [57], [58]. The mechanistic effects explored here might apply to these and other conditions where push-off is impaired unilaterally.

V. CONCLUSIONS

Push-off impairment and its compensations may explain some asymmetries observed in the gait of unilateral transtibial amputees. Weak prosthetic-side push-off leads to a greater loss of energy in the collision of the intact leg with the ground. This results in a slower stance phase for the intact side, with reduced speed and higher stance duration. To compensate for reduced push-off, simple model suggests that positive work should be performed at the hip during stance, most economically during intact-side stance. Experimental measurements suggest that amputees may indeed adopt such a compensation, and may also add some positive hip work during prosthetic-side stance. Both the impairment and associated compensation lead to overall decreases in the symmetry of COM work and motion. These asymmetries result either directly from the limited push-off of the prosthetic limb, or from compensatory work performed elsewhere in the body to offset that limitation. As explained by our simple model, the observed asymmetries may be difficult to avoid despite a variety of compensation methods. We suggest that some degree of asymmetry may be expected in cases of unilateral leg impairment, and perhaps even preferable, in terms of economy, to making gait more symmetric.