Computational prediction of manually gated rare cells in flow cytometry data

Abstract

Rare cell identification is an interesting and challenging question in flow cytometry data analysis. In the literature, manual gating is a popular approach to distill flow cytometry data and drill down to the rare cells of interest, based on prior knowledge of measured protein markers and visual inspection of the data. Several computational algorithms have been proposed for rare cell identification. To compare existing algorithms and promote new developments, FlowCAP-III put forward one computational challenge that focused on this question. The challenge provided flow cytometry data for 202 training samples and two manually gated rare cell types for each training sample, roughly 0.02% and 0.04% of the cells, respectively. In addition, flow cytometry data for 203 testing samples were provided, and participants were invited to computationally identify the rare cells in the testing samples. Accuracy of the identification results was evaluated by comparing to manual gating of the testing samples. We participated in the challenge, and developed a method that combined the Hellinger divergence, a downsampling trick and the ensemble SVM. Our method achieved the highest accuracy in the challenge.

1 Introduction

Flow cytometry is a powerful technology that is able to simultaneously measure multiple proteins for individual cells, and process a large number of cells quickly [1, 2]. The flow cytometry data of a given biological sample is typically in the form of a tall thin matrix, where the rows correspond to individual cells (∼ 10⁶) and the columns correspond to measured protein markers (up to 27) [3]. Such single-cell data reflects the cellular heterogeneity of biological systems, and enables identification of rare cell subpopulations, which are often of great biological interests, such as stem cells [4], cancer [5, 6] and immunology [7,8].

The traditional and most widely-used approach for flow cytometry data analysis is manual gating, which identifies cell types by user-defined regions-of-interest on a user-defined sequence of nested bivariate projections [9,10]. Manual gating relies on prior knowledge of the protein markers and visual inspection of the data, which is subjective, labor-intensive and difficult to reproduce [11]. These drawbacks motivated development of automated clustering algorithms for objective and reproducible analysis of flow cytometry data. Examples include variations of K-means [12–14], mixture models [15–18], density-based clustering [19–24], spectral analysis [25] and hierarchical Bayesian [26]. In addition, efforts have been spent on the FlowCAP challenge [27], which provided well-annotated flow cytometry datasets for comparing the performance of automated cluster algorithms. In the FlowCAP-I challenge, participating algorithms were applied to cluster cells into distinct subgroups, and the clustering results were evaluated against manual gating using the F-measure (the harmonic mean of precision and recall). The F-measures of the top-performing algorithms exceeded 0.9 [27]. Since the evaluation was based on the clustering of all cells, the encouraging F-measures indicated that the top-performers recapitulated the abundant cell types defined by manual gating, but did not reflect whether rare cell types were accurately clustered.

Identification of rare cell types is a challenging problem. When a clustering algorithm is directly applied to data containing both abundant and rare cell types, its optimization objective is typically dominated by the abundant cell types, whereas the rare cell types have little influence on the clustering result. Therefore, special consideration is needed to identify rare cell types. One existing approach is to downsample the abundant cell types, which effectively enhances the presence of rare cells [25, 28]. Another approach is to perform iterative partitioning to hone in on the rare cell types gradually [23,24]. When analyzing multiple samples jointly, Baysian approach has been proposed to borrow strength and identify rare cell types that commonly exist in those samples [26]. To compare existing algorithms and promote new developments for rare cell identification, FlowCAP-III included a computational challenge that focused on this question. The challenge provided flow cytometry data for training samples, in which two rare cell types were manually defined. In addition, flow cytometry data for testing samples were provided, and the research community were invited to predict which cells in each testing sample belong to the two rare cell types. Predictions were evaluated against manual gating using the F-measures of the two rare cell types. This paper describes our participation which achieved the highest F-measure in the challenge. Briefly, we implemented an approximation of the Hellinger divergence [29] to identify batch effect in the data, applied a downsampling trick to reduce the number of abundant cells, and used ensemble SVM (support vector machine) for learning and prediction [30, 31]. In the following, details of our method are described.

2 Materials and Methods

2.1 Data and Challenge Setup

In the rare cell identification challenge of FlowCAP-III, the dataset was produced by multiple labs participating in the External Quality Assurance Program Oversight Laboratory (EQAPOL) project. The dataset consisted of flow cytometry data for 405 samples (405 FCS files [32]). The samples corresponded to multiple biological replica under several experimental conditions, and were processed by different labs. All samples shared an identical set of 6 markers. The number of cells varied from sample to sample, and the average was 280,079. Therefore, the dataset was a collection of 405 matrices, with 6 columns and varying numbers of rows. Half of the samples (202) formed the training set, in which manual gating results for two rare cell types were given. Therefore, for each training sample, participants knew which cells belonged to the two rare cell types. In the training set, the average abundance of the two rare cell types were 0.019% and 0.044% of the total number of cells, respectively. Participants were invited to predict which cells in the testing samples belong to each of the two rare cell types.

The challenge was organized in two phases. In phase one, although participants knew that experimental conditions and processing labs were potential sources of variabilities in the data, the metadata relating samples to those factors was not provided, and participants were requested to make predictions without metadata of the samples. After participants’ phase-one predictions were submitted, the challenge organizers stared phase two of the challenge by releasing the metadata. Phase two aimed to test whether participants were able to improve their predictions by incorporating knowledge of biological and technical variabilities among the samples.

2.2 Hellinger divergence

Flow cytometry data of a given biological sample can be viewed as a point cloud of cells living in the high-dimensional space defined by the measured protein markers [28], or a probability distribution in that space [18,23]. When comparing multiple samples, the traditional manual gating approach generates histograms (univariate marginal distributions in Figure 1) and contour plots (bivariate marginal distributions in Figure 2), so that we can visually appreciate the similarities and differences among the samples in terms of their cellular distributions. In an automated analysis, we would like to compute a distance metric that can quantify similarities among those distributions.

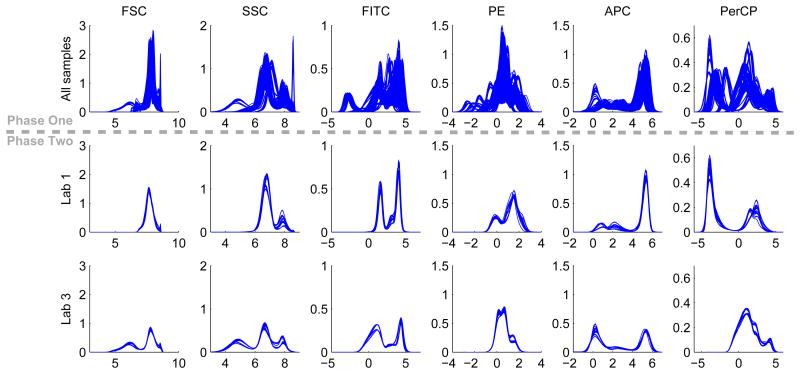
Figure 1.

Histograms of the 6 measured markers in individual samples. The top row contain histograms for all 405 samples, showing considerable variability. The middle and bottom rows contain histograms of samples processed by lab 1 and lab 3 (27 samples for each lab).

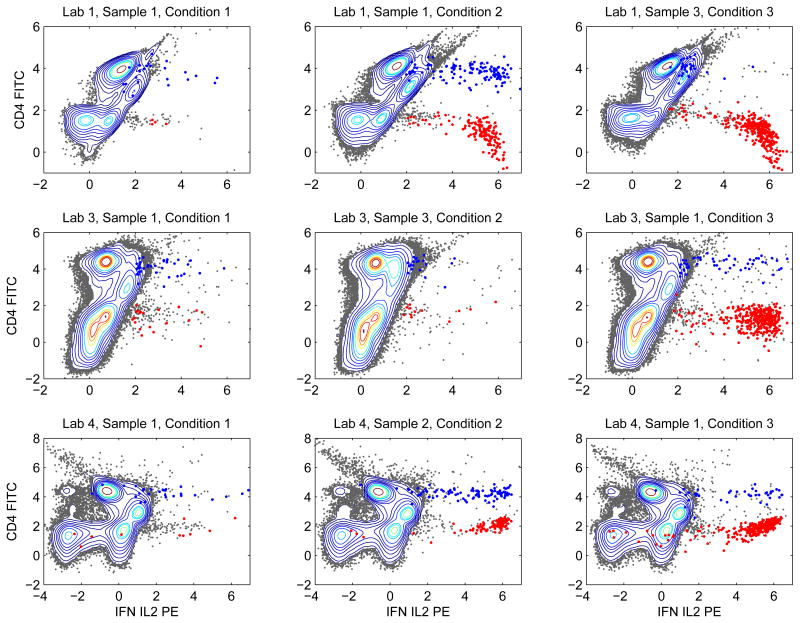
Figure 2.

Contour plots of bivariate projections of nine training samples to the subspace defined by FITC and PE. These nine samples were subjected to different stimulations and processed by different labs.

In probability and information theory [33], the Kullback-Leibler (KL) divergence is a well-known metric for comparing probability distributions. Given two probability distributions P and Q over the multivariate space defined by the protein markers, their KL divergence, denoted as D_KL(P∥Q), is a non-symmetric measure of how well Q is able to approximate P. The KL divergence can be computed with the following formula:

$$D_{\mathit{\text{KL}}}\left(P\parallel Q\right)=\int log\left(\frac{p\left(x\right)}{p\left(x\right)}\right)p\left(x\right)\mathit{\text{dx}}$$ (1)

One problem of computing the KL divergence is the q(x) in the denominator. When the supports of P and Q are different, there exists x such that q(x) = 0 and p(x) ≠ 0, and the integrant in (1) is not defined. This can be a practical issue. When comparing two flow cytometry samples, we use kernel-based density estimation to approximate P and Q, and their supports can be different depending on the choice of the kernel and the data itself. Therefore, a distance metric without such singularity is more desirable.

KL divergence is a special case of a broader class called f-divergence [34]. A relatively less well-known member of this class is called the Hellinger divergence [29]. It is a symmetric distance metric that quantifies the similarity between two probability distributions, and is well-defined as long as p(x) and q(x) are continuous functions with respect to x. Therefore, we chose to use the Hellinger divergence in our analysis. The squared Hellinger divergence is defined as follows.

$$D_H^2\left(P\parallel Q\right)=\frac{1}{2}\int {\left(\sqrt{p\left(x\right)}-\sqrt{q\left(x\right)}\right)}^2\mathit{\text{dx}}$$ (2)

Computing the Hellinger divergence between flow cytometry samples is a nontrivial task. When the number of cells in each sample is large, evaluation of the kernel-based density estimates of p(x) and q(x) is computationally expensive. To reduce the computational cost for density estimation, we apply faithful downsampling [25] to reduce the number of cells. Faithful downsampling obtains a representative subset of cells, such that all cells in the original data fall into a σ–radius of at least one of the representative cells. Each representative cell is weighted by the percentage of original cells belonging to its σ–radius neighborhood. Assume we would like to compute the Hellinger divergence of two flow cytometry samples. Denote the downsampled cells and weights of the first sample as (x_p,i, w_p,i), i = 1, 2, …, K_p; the downsampled cells and weights of the second sample as (x_q,j, w_q,j),j = 1, 2, …, K_q; and the dimension of the data as d. The kernel-based density estimates can be calculated using equations (3) and (4). To compute the squared Hellinger distance, the integral in equation (2) was approximately proportional to the Monte Carlo sum of the downsampled points with corresponding weights, as shown in equation (5). In this study, for each sample, we chose σ such that faithful downsampling generated 1000 representative cells for the sample, and used the same σ in the kernel-based density estimates.

$$\widehat{p}\left(x\right)=\sum _{i=1}^{K_p}\frac{w_{p,i}}{{\sqrt{2\pi {\sigma }^2}}^d}{e}^{-\frac{\parallel x-x_{p,i}{\parallel }^2}{2{\sigma }^2}}$$ (3)

$$\widehat{q}\left(x\right)=\sum _{j=1}^{K_q}\frac{w_{q,j}}{{\sqrt{2\pi {\sigma }^2}}^d}{e}^{-\frac{\parallel x-x_{q,j}{\parallel }^2}{2{\sigma }^2}}$$ (4)

$${\widehat{D}}_H^2\left(P\parallel Q\right)\propto \sum _{i=1}^{K_p}{(w_{p,i}(\sqrt{\widehat{p}\left(x_{p,i}\right)}-\sqrt{\widehat{q}\left(x_{p,i}\right)})}^2+\sum _{j=1}^{K_q}{w}_{q,j}{(\sqrt{\widehat{p}\left(x_{q,j}\right)}-\sqrt{\widehat{q}\left(x_{q,j}\right)})}^2$$ (5)

2.3 Ensemble SVM

Support vector machine (SVM) is a commonly used supervised machine learning algorithm, which can be applied in classification analysis. Given a set of training data points and labels that categorize them into two classes, the linear SVM training algorithm is able to find a hyperplane that maximizes the separation between the two classes of data points. The hyperplane can be used as a decision boundary that predicts the class labels of testing data points [30]. SVM can be combined with nonlinear kernels (e.g. polynomial, gaussian, etc) to create nonlinear decision boundaries [35]. In this analysis, data points are the cells, and class labels distinguish cells in a rare cell type form all other cells. We used the linear form of SVM implemented in the libsvm package [36].

In this rare cell identification challenge, there are two general strategies of applying SVM. One strategy is to learn an overall SVM classifier based on all the training samples together, and apply the overall SVM classifier to predict the rare cells in the testing samples. The other strategy is to learn multiple classifiers from the training samples, apply all of them to the testing samples, and make predictions based on the ensemble consensus of the classifiers. The ensemble classification strategy has been successfully applied in many studies [31, 37, 38]. Given the variabilities we observed in the data, we expected that one single overall classifier would perform poorly, and chose to use the ensemble classification strategy.

3 Results

3.1 Sources of variabilities in the data

In phase one of the challenge, participants were informed that the 405 samples corresponded to replica of several biological samples under three experimental conditions, and the samples were processed by different labs. Those factors were potential sources of variabilities in the data. However, metadata linking the samples to those factors was not released in phase one. In our analysis, before attempting to build any prediction models, we first examined the variabilities in the data.

We transformed the raw flow cytometry data using the inverse hyperbolic sine transformation, with cofactor being 100 [39]. For each of the 6 measured markers, we computed its histogram in each of the 405 samples and overlaid the histograms in the top row of Figure 1, where we observed considerable variation across the samples. The thick bands showed that the samples were organized in groups, suggesting possible batch effect. After the metadata of the samples was released in phase two of the challenge, we were able to stratify the samples according to the labs that processed them. When we overlaid histograms from samples processed by the same lab, we observed that the within-lab variation was small for every lab. For example, the second and third rows of Figure 1 showed the histograms from samples processed by lab 1 and lab 3, respectively. The small within-lab variation and large overall variation together suggested that the main source of variability in the data was due to the labs that processed the samples.

We also visualized bivariate projections of the data using contour plots. In Figure 2, we showed nine training samples projected to the bivariate subspace defined by markers CD4-FITC and IFN-IL2-PE. Each row of Figure 2 contained samples processed by one lab, and each column corresponded to one experimental condition. The contours within each row were similar to each other, but the contours in different rows exhibited quite different shapes. Such an observation suggested that distributions of the abundant cell types were similar for samples processed by the same lab regardless of the experimental conditions, but significantly different across labs. The blue and red dots highlighted cells belonging to the two rare cell types defined by manual gating. By comparing the columns of Figure 2, we observed that the two rare cell types were affected by the experimental conditions. Under experimental condition 1, counts of both rare cell types were small. Under experimental condition 2, counts of the two rare cell types either both stayed small or both increased. Experimental condition 3 increased counts of the “red” cells but did not affect the “blue” cells.

In summary, variabilities in the distributions of abundant cell types were mainly due to the labs that processed the samples, whereas the counts for the two rare cell types were affected by the experimental conditions. These insights were made in phase two of the challenge when the metadata was available. In phase one of the challenge, we only observed the variabilities in both abundant and rare cell types across the samples, but did not know the interpretations in terms of labs and experimental conditions.

3.2 Similarity among the samples

The observed variabilities suggested that samples might be organized into groups. In phase one of the challenge, we hypothesized that, in order to effectively predict the rare cells in a given testing sample, we should use training samples similar to that testing sample, rather than using all training samples. By “similar”, we meant similar in term of the distribution of the abundant cell types, because it is difficult to evaluate the similarity of the rare cell types between a training sample and a testing sample.

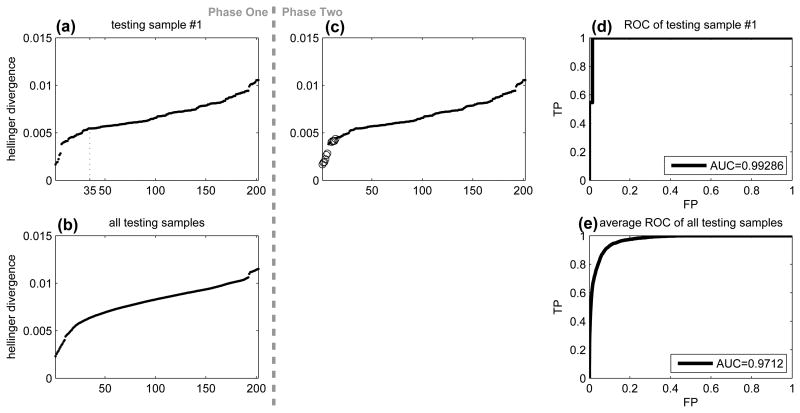
To identify training samples similar to a given testing sample, we used the Hellinger divergence. Taking testing sample #1 as an example, we computed its Hellinger divergence to all the 202 training samples, rank-ordered the training samples according to the Hellinger divergence, and showed the result in Figure 3(a). We observed that six training samples were quite similar to testing sample #1, with small Hellinger divergence. After a gap, there seemed to be a reflection point around the 35th training sample, and the Hellinger divergence increased at a slightly larger slope before the reflection point. Although the reflection point was not clear, it suggested that the training samples before the reflection point might also be considered as similar to testing sample #1. We performed the same analysis for all the 203 testing samples, and computed the average of the sorted Hellinger divergence as shown in Figure 3(b). Although Figure 3(b) did not contain any visually appreciable reflection point, it appeared that the average sorted Hellinger divergence increased at a constant slope after the 50th training sample. Therefore, for each testing sample, we chose the 50 training samples with smallest helligner divergence, and used those 50 training samples to learn predictive models for identification of the rare cell types in the testing sample. The number 50 was an arbitrary choice based on visual inspection of Figures 3(a) and 3(b).

Figure 3.

Hellinger divergence for predicting samples processed by the same lab. (a) Sorted Hellinger divergence between testing sample #1 and the training samples. (b) Average of panel (a) for all testing samples. (c) Duplicate of panel (a) with training samples from the same lab of testing sample #1 highlighted as circles. (d) ROC of Hellinger divergence to identify training samples from the same lab as testing sample #1. (e) Average ROC for all testing samples.

After the metadata of the sample information was released in phase two of the challenge, we were able to examine the performance of the similarity measure based on the Hellinger divergence. Figure 3(c) showed the same result as 3(a). The only difference was that training samples from the same lab of testing sample #1 were highlighted, most of which had small Hellinger divergence. If we treated the Hellinger divergence as a predictor for training samples from the same lab as testing sample #1, we would obtain the receiver operating curve (ROC) in Figure 3(d) with an area-under-curve of 0.99. The average ROC for all testing samples was shown in Figure 3(e) with an area-under-curve of 0.97. Therefore, the Hellinger divergence was highly predictive of the processing labs.

We noted in retrospect that 50 was not the best threshold for selecting training samples from the same lab as a given testing sample. As shown in Figure 3(c), only 11 of the top 50 training samples were processed by the same lab as testing sample #1, which translated to 22%. In fact, the total number of training samples processed by each lab varied from 10 to 19. For each testing sample, we computed the percentage of how many of the top 50 training samples were correctly selected (i.e., processed by the same lab as the testing sample), and the average was 25%. However, since we did not have the metadata in phase one of the challenge, we proceeded with the choice of 50.

3.3 Downsample abundant cell types

As mentioned above, due to the variabilities in the data, we decided to select training samples similar to a given testing sample, build one linear SVM classifier from each selected training sample, apply all the classifiers to the testing sample, and use their consensus to predict the rare cells. When we tried this strategy to perform leave-one-sample-out cross-validation in the training samples, we observed that the prediction performance was poor. The classifier learned from one training sample could not generalize to another training sample processed by the same lab. The reason might be two-fold: (1) the extremely unbalanced numbers of data points for SVM to separate, i.e. classification of rare cells (∼ 0.01%) against the rest (∼ 99.99%); (2) outlier data points that were far away from the rare cells but might overwhelm the SVM. Therefore, we came up with a trick to downsample the abundant cells far away from the rare cells:

• Before learning an SVM classifier for a rare cell type in a given training sample, we first constructed a kernel-based probability density estimate based on the rare cells only, and evaluated the probability density at all the cells in the training data. We then picked 20,000 cells with highest probability, which typically included all the rare cells, as well as the abundant cells that are close to the rare cells. After that, an SVM was trained on the 20,000 selected cells.

• When the SVM classifier was applied to a testing sample, the same trick was applied. We took the probability density estimate of the rare cells in the training sample, evaluated the probability density at all the cells in the testing sample, and picked the top 20,000 cells. Then, we applied the SVM classifier to predict which cells in the top 20,000 belong to the rare cell type.

The number of 20,000 was an arbitrary choice. After such downsampling, the abundant cells that are far away from the rare cells were filtered out, and the rare cells increased from ∼ 0.01% to ∼ 0.1%. Although the sizes of abundant and rare cell types were still unbalanced, the prediction performance of leave-one-sample-out cross-validation in the training samples improved significantly.

3.4 Prediction of the rare cells

The analysis and prediction pipeline we developed in phase one of the challenge is as follows:

1. for each of the 405 samples do

2. perform arcsinh transformation with (cofactor=100) [39],

3. faithful downsampling to reduce number of cells to roughly 1000 [25],

4. kernel-based density estimate using downsampled points,

5. end for

6. for each testing sample do

7. compute Hellinger divergence to all training samples,

8. rank order training samples by the Hellinger divergence,

9. pick the most similar 50 training samples,

10. for each selected training sample do

11. build two SVM's for the two rare cell types,

12. apply the SVM's to predict the two rare cell types in the testing sample,

13. end for

14. Derive prediction by majority vote.

15. end for

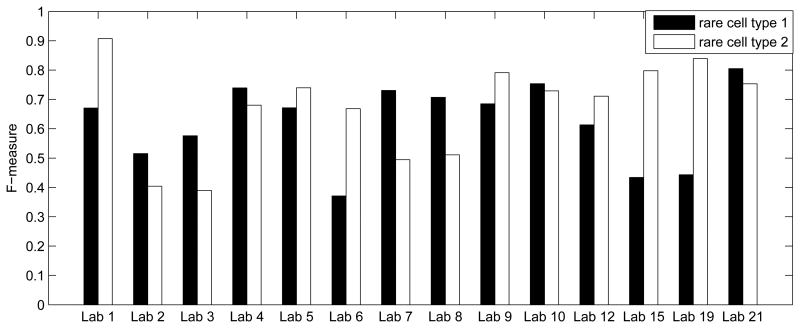
This pipeline was also able to make predictions for the training samples in a leave-one-sample-out-cross-validation fashion. In each iteration of the for-loop between steps 6 and 15, we worked on one training sample, computed its Hellinger divergence to all other training samples, picked the 50 most similar samples to construct SVM's, and derived predictions of the two rare cell types by the consensus of the SVM's. The prediction performance was quantified by the F-measure, the harmonic mean of precision (pr) and recall re), F = (2 pr × re)/(pr + re). In this leave-one-sample-out cross-validation analysis of the training samples, the average F-measures for the two rare cell types were 0.6208 and 0.6866, respectively. By averaging these two numbers, we obtained an overall F-measure of 0.6537 in cross-validation. In Figure 4, we used the lab information in phase two to visualize the average cross-validation F-measures for each lab, showing that the prediction accuracy varied across different labs.

Figure 4.

Average F-measure of leave-one-sample-out cross-validation analysis of the training samples.

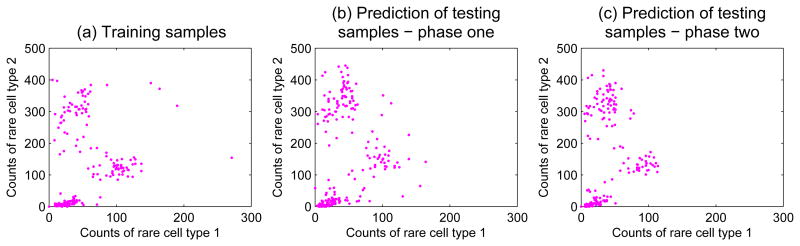
In phase one, we applied the above pipeline to predict the two rare cell types in the testing samples. Since the ground truth of the rare cells in the testing samples was not available in phase one, we were not able to directly evaluate the prediction performance. Instead, we used the counts of the two rare cell types to summarize and compare the training and testing samples. Figure 5(a) showed 202 dots corresponding to the 202 training samples, and the two axes indicated the number of cells in the two manually gated rare cell types. Figure 5(a) visualized the joint distribution of the counts of the two rare cell types in the training samples, where we observed that the training samples can be roughly divided into three clusters. Figure 5(b) visualized the counts of the two predicted rare cell types in our phase-one analysis of the 203 testing samples, which also formed three clusters with a similar distribution as the training samples. This result provided side-evidence that our phase-one prediction had decent accuracy.

Figure 5.

Distributions of counts of the two rare cell types. (a) Each point corresponds to one training sample. The two axes represent the counts of the two rare cell types defined by manual gating of the training samples. (b) Each point corresponds to one testing sample. The two axes represent the counts of the two rare cell types in the testing samples predicted by our phase-one analysis. (c) Counts of rare cells predicted by our phase-two analysis of the testing samples.

In phase two of the challenge, we realized that the variabilities captured by the Hellinger divergence were primarily manifestations of differences among the processing labs. Therefore, we slightly adjusted our analysis pipeline to obtain our phase-two prediction. For each testing sample, instead of making prediction based on the 50 training samples that were most similar to the testing sample, we simply picked the training samples from the same lab as the testing sample, and the rest of the analysis pipeline remained the same. Figure 5(c) summarized the cell counts in our phase-two prediction. The counts distribution was tighter than our phase-one result, and more similar to the distribution of the training samples. We expected the accuracy of our phase-two prediction to be better than phase one, which was indeed the case when the final result of the challenge was released.

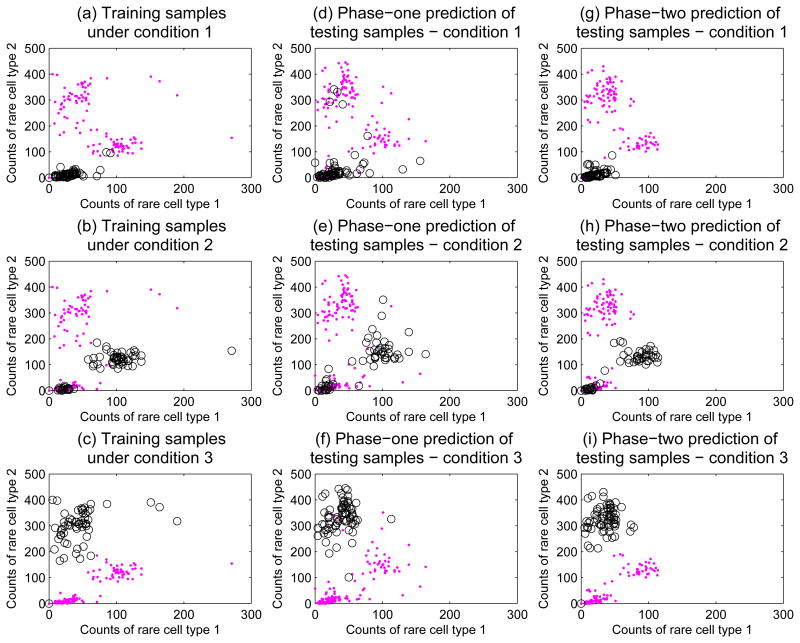
During phase two of the challenge, we were able to further examine the distributions in Figure 5 by stratifying samples according to processing labs and experimental conditions. In Figures 6(a-c), we visualized counts of the two rare cell types in the training samples same as Figure 5(a), and highlighted samples under the three experimental conditions separately. Figure 6(a) highlighted training samples under condition 1, which appeared to be an unstimulated baseline condition where counts of both rare cell types were small. Training samples under experimental condition 2 were highlighted in Figure 6(b). Condition 2 seemed to be a stimulation that increased both rare cell types, but roughly $\frac{1}{4}$ of the samples did not respond to the stimulation. Figure 6(c) showed training samples under condition 3, another stimulation condition that significantly increased one rare cell type, but did not affect the other one. In Figures 6(d-f), our phase-one predictions of rare cell counts in the testing samples were stratified according to the experimental conditions, and showed a similar pattern as the training samples. Figures 6(g-i) showed our phase-two prediction results stratified by the experimental conditions. The cell counts pattern of our phase-two predictions was more similar to the training samples than our phase-one predictions.

Figure 6.

Distributions of counts of the two rare cell types stratified by experimental conditions. (a) Distribution of counts in the training samples, with training samples under condition 1 highlighted in circles. (b) Distribution of counts in the training samples with training samples under condition 2 highlighted. (c) Distribution of counts in the training samples with training samples under condition 3 highlighted. (d-f) Phase-one predictions of rare cell counts in the testing samples stratified according to the three experimental conditions. (g-i) Phase-two prediction results stratified by the experimental conditions.

After the challenge concluded, the FlowCAP organizers evaluated the predictions submitted by the participants. For each participant, the prediction performance was assessed by the F-measure, and a confidence interval was derived using bootstrap. Among all phase-one participants, our prediction achieved the highest F-measure of 0.64. The F-measure of the second place was 0.47, and the ensemble prediction from all phase-one participants achieved F-measure 0.55. Our confidence interval did not overlap with the confidence intervals of the 2nd place and the ensemble prediction, indicating that our prediction was significantly better. The F-measure of our phase-two prediction was improved to 0.69, also significantly better than predictions from other phase-two participants. In addition, our F-measures in the testing samples were comparable to those in our cross-validation analysis of the training samples, indicating that our method did not over-fit.

4 Discussion

Our prediction achieved high accuracy mainly because of three ingredients in the analysis pipeline: recognizing the batch effect, downsampling the abundant cell types, and applying the ensemble strategy. In phase one of the challenge, we applied the Hellinger divergence to evaluate pairwise similarity among the samples, which accurately revealed batch effect in the data (i.e., batch by labs that processed the samples). Recognizing such batch effect led to the idea of working on different batches separately, which was probably the biggest contributing factor of the accuracy of our phase-one prediction. When attempting to learn SVM classifiers to separate the abundant and rare cells in the training samples, we observed that the prediction accuracy on the training samples themselves was poor, probably due to the extremely unbalanced size of the rare and abundant cell types. Our trick for downsamping the abundant cells improved the accuracy of the SVM classifiers. Finally, because the downsampling trick operated on each training sample separately, the ensemble prediction strategy was a natural choice. In phase two when the batch information was available, we noticed that our phase-one analysis already identified the batch information with high accuracy. Therefore, the batch information provided in phase two only brought small improvement on our prediction performance.

The prediction performance in this challenge was evaluated by comparing to manually gated rare cells as ground truth. Since it has been shown that manual gating can be inconsistent [24], one may ask whether manually gated rare cells should serve as the ground truth. We believe that the answer is yes in this dataset. The F-measure of our prediction suggested that our automated analysis pipeline matched well with the manually gated cells in the testing samples. The fact that an automated algorithm can match manual gating provided side-evidence that the manual gating analysis of this dataset was of decent quality and consistency.

The batch effect according to labs was clearly visible in 1D histograms and 2D contour plots as shown in Figures 1 and 2. From our analysis using the Hellinger divergence, we knew that the batch effect was accurately predicted in higher dimensional space. We hypothesize that the batch effect is probably more pronounced in higher dimensional space, but we do not have a visualization algorithm to validate this hypothesis. Here, an interesting research question is how to develop visualization algorithms to enable us to visually appreciate differences between two multivariate distributions. Two existing algorithms toward this direction are SPADE [28] and viSNE [40], but more effective visualization algorithms can be appreciated.