Understanding spatial organizations of chromosomes via statistical analysis of Hi-C data

Abstract

Understanding how chromosomes fold provides insights into the transcription regulation, hence, the functional state of the cell. Using the next generation sequencing technology, the recently developed Hi-C approach enables a global view of spatial chromatin organization in the nucleus, which substantially expands our knowledge about genome organization and function. However, due to multiple layers of biases, noises and uncertainties buried in the protocol of Hi-C experiments, analyzing and interpreting Hi-C data poses great challenges, and requires novel statistical methods to be developed. This article provides an overview of recent Hi-C studies and their impacts on biomedical research, describes major challenges in statistical analysis of Hi-C data, and discusses some perspectives for future research.

Introduction

How a genome is organized in three-dimensional (3D) space inside the nucleus (Figure 1) is of long and great interest to biologists [1,2]. Such an organization plays important roles in gene regulation, DNA replication and maintenance of genome stability [3–8]. Many diseases, including cancer, are characterized by alternations in the spatial organizatn of the genome [9,10]. However, the high complexity of the genome 3D structure makes understanding chromatin spatial organization extremely challenging. For instance, human genome consists of about 3.2 billion base pairs of nucleotides, which form an approximately two-meter long polymer when stretched out, and fit into a nucleus with roughly ten-micrometer in diameter in vivo. Despite revealing the entire sequence of the genome, very little has been understood about the principles of high level compression of chromatin in 3D space.

Figure 1. The major structures in DNA compaction; DNA, the nucleosome, the 10 nm “beads-on-a-string” fiber, the 30 nm fiber and the metaphase chromosome.

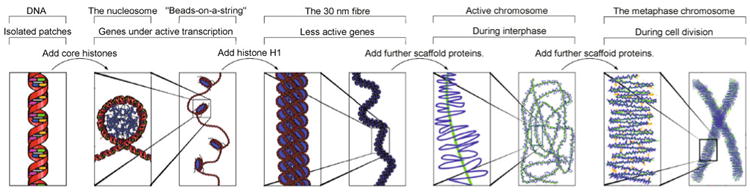
Source: http://en.wikipedia.org/wiki/File:Chromatin_Structures.png.

The 3D organization of chromosomes has traditionally been studied by microscopic and cytogenic methods such as florescent in situ hybridization (FISH). FISH uses florescent probes to bind to the genomic regions of interest, and then measures the spatial distances between pairs of florescent probes within a few hundred cells under microscope. Several key insights of chromosome organizations have been obtained by FISH studies [11]. For example, although still open to debate, it is generally accepted that interphase chromosomes at low resolution level occupy distinct regions in the cell nucleus, termed as chromosome territories [12,13]. Within chromosome territories, chromosomes form highly compact, non-random conformations to facilitate the communication between genes and their regulatory elements [14,15]. Moreover, the compactness of chromatin folding at the high resolution level is not uniform, which is in general negatively associated with gene density but not associated with gene activity [16].

Although having been widely used, microscopic and cytogenic methods are limited by low throughput, low resolution and probe sequence specificity. The several hundreds of cells measured by a FISH experiment usually cannot fully represent millions of cells within a cell population. In addition, the florescent probes used in FISH experiments are typically around a few kilobases in size, which often cannot capture the detailed chromatin structure at the regulatory element scale. More importantly, florescent probes, which are designed based on specific DNA sequences, can only bind to a few selected genomic loci, and thus cannot provide an unbiased view of the genome-wide spatial organizations.

Complementary to the individual cell based microscopic and cytogenic methods, biological and molecular methods have been recently proposed to measure genome-wide chromatin interactions within the whole cell population (reviewed by Refs. [11,17,18]). In a seminal study, Dekker et al. [19] developed the chromosome conformation capture (3C) technology to detect the chromatin interactions between any two genomic loci. 3C provides a population-based quantification at high resolution level but with limited throughput. Later on, several 3C-based approaches have been proposed to generate higher throughput chromatin interactome data. Combining 3C with microarray, chromosome conformation capture-on-chip (4C) [20,21] technology is able to assess chromatin interactions between one genomic locus of interest with any genomic loci represented by microarray. 4C data can be interpreted as a one-dimensional genome-wide chromatin interaction profile of a specific genomic locus. Another variant of 3C, carbon-copy chromosome conformation capture (5C) [22,23] allows the detection of chromatin interactions among multiple genomic loci, providing a two-dimensional chromatin interaction map of several pre-specified genomic regions. Adding chromatin immuno-precipitation (ChIP) to 3C protocol, ChIP-combined loop (ChIP-loop) [24–27] assay can detect chromatin interactions bound by specific proteins. Chromatin interaction analysis by paired-end tag sequencing (ChIA-PET) [28] further improves ChIP-loop to yield the transcription factor dependent chromatin interaction map at base-pair resolution [29]. All these 3C based methods have been successfully applied to study long-range looping or chromosomal interactions between genomic loci [28,30– 33].

More recently, by harnessing the power of next generation sequencing technologies, Dekker and his colleagues developed a genome-wide version of 3C-based approach named Hi-C [34,35]. Hi-C technology captures chromatin interactions by a process of experimental steps, including formaldehyde cross-linking in solution, restriction enzyme digestion, biotinylated junctions pull-down and high throughput paired-end sequencing. Compared to the microscopic and cytogenic methods and other existing 3C based methods, Hi-C technology provides high resolution, high throughput genome-wide chromatin interaction maps for the whole cell population, enabling the complete 3D views of the genome [36]. Later on, similar approaches have also been proposed and applied to mammalian genome [37] and yeast genome [38].

As a revolutionary technology, Hi-C enables studying genome-wide chromosome organizations at an unprecedented resolution. Hi-C data facilitate inferring consensus 3D chromosomal structures and characterizing chromatin structural variations in the mammalian genomes [33,37,39] and the yeast genome [38,40], leading to a deeper understanding of genome function [41]. In the original Hi-C study [34], researchers have shown that the Hi-C data support a fractal globule model for chromosomes at the megabyte scale, suggesting that chromatin is in a compact and unentangled conformation, allowing for both dense compressing and easy folding and unfolding at each genomic locus. Several alternative polymer models, including random loop model [42], dynamic loop model [43] and strings and binders switch model [44], have been proposed as the underlying biophysical principles governing chromatin packing revealed by Hi-C data.

Hi-C data provides a novel measurement of chromatin properties via genome-wide 3D interactome map, which is intractable by any existing 1D genome profiling techniques. Analyzing these 3D interactome maps, several recent studies [45–48] have shown that genome consists of topological domains with strong intra-domain chromatin interactions and weak inter-domain chromatin interaction. These topological domains appear to serve as units of genome structure and perhaps function. More importantly, an analysis of Hi-C data together with other genomic and epigenetic data reveals lots of insights of 3D genome architecture (reviewed by Refs. [1,49]), which have a significant impact on functional genomics research [50–54], DNA replication mechanism study [55–57], cancer research [58–66] and evolutionary biology [67].

While the Hi-C technology shares many similarities in overall flavor and objectives with the microscopic and cytogenic methods and the 3C-based methods, Hi-C data are quite different from other types of massively parallel sequencing data (e.g., ChIP-Seq data and RNA-Seq data) in terms of data generating mechanism, data format and data interpretation. These unique features of Hi-C data therefore require delicate preprocessing procedure. Moreover, multiple layers of biases, noises and uncertainties buried in the Hi-C experimental protocol need to be explicitly taken into consideration, requiring the development of novel statistical tools. Lack of careful statistical analysis of Hi-C data may result in potentially misleading biological conclusions. For instance, two recent Hi-C studies [38,68] used the hypergenometric test to access the statistical significance of three dimensional co-localization of genomic loci of interest. However, Witten and Noble [69] pointed out that the hypergenometric test is invalid in the Hi-C data analysis since chromatin interactions between genomic loci pairs are not independent. They re-analyzed the data in Refs. [38,68] and obtained different p-values and different biological conclusions via a non-parametric resampling approach based on the bootstrap technique. Recently, Paulsen et al. [70] proposed a similar resampling approach to test 3D co-location of regions containing somatic mutations in leukemia cells, which also emphasizes the importance of rigorous statistical modeling in Hi-C data analysis.

This article provides a comprehensive review of recent Hi-C studies and their impacts on biomedical research, describes some major challenges in statistical analyses of Hi-C data, and discusses some perspectives for future research. We start with a brief overview of the Hi-C experimental protocol and the Hi-C data preprocessing procedure in Section 2. We then review a few key topics in Hi-C data analysis, including bias reduction, genome partition, studying biophysical principles governing chromatin folding, inferring consensus 3D chromosomal structure, and evaluating structural variations of chromatin, in Section 3–7, respectively (Table 1). We conclude by a description of several future directions of high priority in this field.

Table 1. A summary of existing methods for Hi-C analysis.

Topics	Methods	Features	Pros	Cons	References
Bias reduction	Yaffe and Tanay	Non-parametric bias correction	Effective bias reduction	Computationally intensive, difficult interpretation	[73]
	HiCNorm	Parametric bias correction	Computationally efficient, easy interpretation	Rely on parametric assumption	[87]
	ICE	Normalization method	No assumption on any specific systemic biases	Limited for equal-sized genome partition	[74]
	SCN	Normalization method	Effective removal of DNA circularization bias	Limited for equal-sized genome partition	[86]
Genome partition	PCA	Chromosome-wide variance decomposition	Discovery of two compartments based on spatial proximity	Low resolution (several MBs) genome partition	[34]
	Dixon et al.	Hidden Markov model	Discovery of topological domain based on local chromatin interactions	Two-step procedure of bias reduction and genome partition	[45]
	Sexton el al.	Local distance-scaling model	Combining Yaffe and Tanay's bias correction model [73] with genome partition	Computationally intensive	[47]
	Hou et al.	Poisson mixture model	Model intra-domain and inter-domain interactions via two Poisson distributions	Two-step procedure of bias reduction and genome partition	[48]
	GeSICA	Markov clustering algorithm	Exploration of hierarchical sub-domain structures	Lack of bias reduction	[93]
Polymer model	Fractal globule model	Model chromatin as a knot-free configuration	NA*	NA*	[98,99]
	Equilibrium globule model	Model chromatin as a highly knotted configuration	NA*	NA*	[100]
	Random loop model	Looping is formed by random interaction between monomers	NA*	NA*	[42]
	Dynamic loop	Looping is formed by diffusional motion of monomers	NA*	NA*	[43]
	Strings and binds switch	Looping is affected by concentrations of binding molecules	NA*	NA*	[44]
Inferring consensus 3D chromosomal structure	Optimization-based methods	Optimize a target function to measure the fitting of a 3D model	Use biophysical constraints in 3D model reconstruction	Local modes, fail to model experimental uncertainties	[33,38,40]
	MCMC5C	Gaussian model	First statistical model for Hi-C experimental uncertainties	No bias removal, Gaussian variance estimate is ad hoc	[39]
	BACH	Poisson model	Combing bias removal with 3D model reconstruction	Lack of biophysical constraints, computational intensive	[103]
Evaluating structural variation of chromatin via statistical model	Optimization-based methods	Use multiple parallel runs to measure chromatin structural variation	Explore all possible 3D models optimizing the target function	Computationally intensive, sensitive to initialization	[33,38,40]
	Kalhor et al.	Population-based approach	Direct link Hi-C data to presence or absence of chromatin interaction	Fail to model experimental uncertainties	[37]
	BACH-MIX	Poisson mixture model	Combing bias removal with evaluating chromatin structural variation	Limited for studying local chromatin structural variation	[103]

^*A comprehensive comparison of pros and cons of each polymer model, which can be found in Ref. [94], is beyond the scope of this paper.

Overview of Hi-C Experiment and Hi-C Data Preprocessing Procedure

The detailed protocol of a Hi-C experiment can be found in two original Hi-C papers [34,35] and one recent review paper [71]. A few variant experimental protocols have also been proposed [37,38,72]. Here we focus on the original Hi-C protocol [34,35] since other alternatives share similar essence.

Figure 2, which is a direct copy of Figure 1A in Ref. [34], briefly illustrates the procedure of a Hi-C experiment. In the original Hi-C protocol [34], cells are first cross-linked with formaldehyde to maintain DNA-protein and protein-protein interactions. The spatial distance between two genomic loci (red curve and blue curve in Figure 2A) with close spatial proximity is preserved although these two loci could be far away from each other in 1D genomic distance. Chromatin is then isolated and digested with a restriction enzyme of choice (Figure 2B). The two ends of a restriction enzyme cutting site, marked with biotin (purple dots in Figure 2C), are ligated together to form ring-shaped chimeric molecules (Figure 2D). These chimeric molecules are then purified and sheared into DNA fragments. The DNA fragments without biotin are washed out; while the biotinylated junctions are pulled down (Figure 2E) and form the Hi-C library after size selection. Each biotinylated junction in the Hi-C library represents two genomic loci not only with close spatial proximity but also near the corresponding restriction enzyme cutting sites. Subsequently, the Hi-C library is subject to deep paired-end sequencing using one of the next generation sequencing platforms, resulting in millions of paired-end reads (black arrows in Figure 2F).

Figure 2. The procedure of Hi-C experiment.

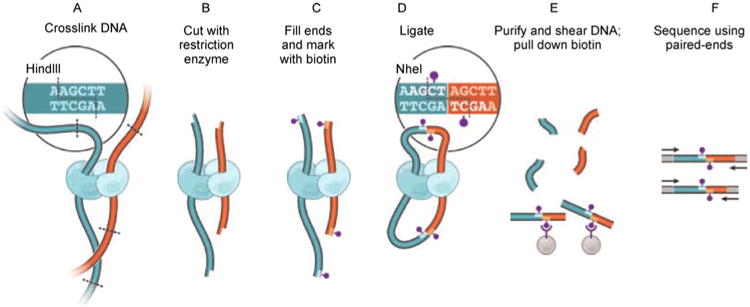
(direct copy of Ref. [34], Figure 1A).

The very first step in Hi-C data analysis is the preprocessing of millions of paired-end reads in order to remove experimental artifacts. Several recent papers [45,48,61,73,74] proposed similar Hi-C data preprocessing procedures, which in general consist of four steps: mapping paired-end reads to the reference genome, read-level filtering, fragment-level filtering and pooling reads into a Hi-C contact matrix at a lower resolution level (reviewed by Ref. [71]). We briefly summarize the four steps below. A more detailed flowchart of the Hi-C data preprocessing procedure is displayed in Figure 3A.

Figure 3. The Hi-C data preprocessing procedure.

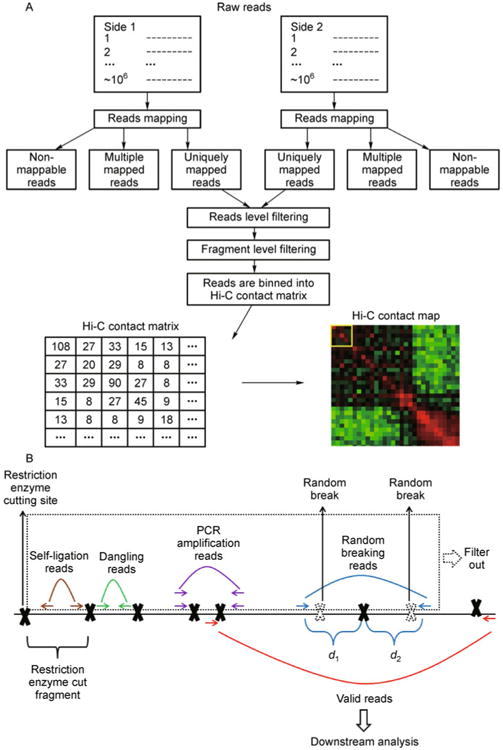
(A) Flowchart of the Hi-C data preprocessing procedure; (B) An illustration of reads level filtering. The solid black line represents a genomic region of interest. Solid black crosses represent the restriction enzyme cutting site. The genomic region between any two adjacent restriction enzyme cutting sites is the restriction enzyme cut fragment (fragment in short). The paired-end reads in which both sides can be uniquely mapped to the reference genome can be divided into the following groups. If both sides of a paired-end reads are mapped within the same fragment, according to the directions of two sides, they are either self-ligation reads (brown arrows) or dangling reads (green arrows). Multiple paired-end reads may be mapped to the exactly same genomic location (purple arrows), possibly due to the PCR amplification artifact. If the sum of two reads to the nearest restriction enzyme cutting site (d₁+ d₂) is larger than the Hi-C library maximum (usually 500 bp), they (blue arrows) are probably due to random breaking (dashed black crosses) in the middle of a fragment. After filtering out self-ligation reads, dangling reads, PCR amplification reads and random breaking reads (the reads in the dashed box), the remainder (red arrows) are defined as the valid reads for the downstream analysis.

In the read mapping step, two sides of each paired-end reads are mapped to the reference genome separately by commonly-used read mapping tools, such as BWA [75], MAQ [76], Bowtie [77] or Novoalign [78]. According to the mismatch threshold, each side of a paired-end read can be classified into one of the following three categories: the uniquely mapped reads, the multiple mapped reads, and the non-mappable reads. In most studies, the read length is fixed (50 bp used in Ref. [73]) to control the quality of base calling (although longer reads tend to reduce the probability of multiple mapping), and only the paired-end reads containing both uniquely mapped sides are kept for the downstream analysis. In a recent work, Imakaev et al. [74] pointed out that the paired-end reads containing one uniquely mapped side also contribute to the total coverage of pericentromeric regions, and need to be included in the analysis as well. Imakaev et al. [74] also proposed an iterative read mapping strategy that supports different lengths for different reads, resulting in a larger proportion of uniquely mapped reads.

Next, uniquely mapped paired-end reads are subject to read-level filtering (Figure 3B) in order to remove several artifacts due to the technical limitations of the Hi-C protocol. In Hi-C experiments, restriction enzyme digests the genome into restriction enzyme cut fragments (fragments in short). Ideally, chromatin ligation is aimed to capture interactions between two different fragments. However, some paired-end reads may be mapped to the same fragment. According to the directions to two reads, they represent either self-circulation ligation products (brown arrows in Figure 3B) or unligated dangling products (green arrows in Figure 3B). In another scenario, multiple paired-end reads (purple arrows in Figure 3B) may be mapped to exactly the same genomic location. The redundant reads are mainly due to the side effect of PCR amplification, and need to be removed from the analysis. Picard tools [79] can be used to remove the redundant reads. In addition, the size selection step in Hi-C library preparation implies that both ends of a paired-end read should be close to the nearest restriction enzyme cut site. However, it has been observed that for some paired-end reads, one (sometimes both) of the two sides is far away from the nearest restriction enzyme cut site (blue arrows in Figure 3B). This phenomenon is mainly due to the random breaking of the genome (dashed black crosses in Figure 3B), i.e., the genome is randomly broken down at fragile locations without a restriction enzyme cut site. Let d₁ and d₂ represent the genomic distances between each side of a paired-end read to the nearest restriction enzyme cut site, respectively (Figure 3B). In practice, if the summation of d₁ and d₂ is larger than the certain threshold (500 bp suggested by Ref. [73]), this paired-end read will be filtered out. After filtering out the self-ligation reads, the dangling reads, the PCR amplification reads and the random breaking reads (which are highlighted by the dashed box in Figure 3B), the remaining reads are treated as valid reads, and subjected to the next step of fragment-level filtering.

The primary goal of fragment-level filtering is to remove fragments whose mappability score is too low. Usually, a fragment near centromere or telomere regions tends to contain a large proportion of repetitive sequence and leads to a low mappability score. This type of fragments contains little information, while tending to disturb the downstream analysis because their properties are quite different from other normal fragments. In practice, Yaffe and Tanay [73] suggested to filter out fragments with mappability score less than 0.5. In addition to filtering fragments with low mappability score, Imakaev et al. [74] suggested to further remove fragments with length shorter than 100 bp or longer than 100 KB, and remove the top 0.5% fragments with the greatest number of reads, which are prone to PCR amplification artifacts.

At the end, the preprocessed paired-end reads can be summarized into a Hi-C contact matrix at the fragment level. The Hi-C contact matrix is a symmetric count matrix, in which each off-diagonal entry represents the number of paired-end reads spanning two different fragments. One key challenge is that the fragment level Hi-C contact matrix is extremely sparse. For example, the human genome contains around 10¹² fragment pairs with 6 bp restriction enzyme, but a typical Hi-C experiment only generates around 10⁸ paired-end reads. Distributing 10⁸ paired-end reads into a matrix with 10¹² entries results in an extremely sparse matrix. In practice, such a high-dimensional sparse matrix is neither stable nor feasible for downstream analysis. Therefore, it is necessary to partition the genome into large scale bins, and pool the reads falling into each pair of bins to generate a Hi-C contact matrix at a lower resolution level, in which each off-diagonal entry represents the number of paired-end reads spanning two different bins. In the exploratory data analysis, the Hi-C contact matrix, which is the input of all the downstream Hi-C analysis, can be visualized as a heat map using software HiTC [80], CytoHiC [81] and the WashU Epigenome Brower [82].

Bias Reduction

Although Hi-C technology provides an efficient way for genome-wide chromatin interaction discovery, multiple systematic biases buried in the complicated process of Hi-C experiments make the analysis and interpretation of Hi-C data extremely challenging. A delicate analysis by Yaffe and Tanay [73] demonstrated that the Hi-C data obtained from the original Hi-C experiment [34] exhibit three major sources of biases: restriction enzyme cutting, GC content and sequence uniqueness. The restriction enzyme bias is due to the fact that the restriction enzyme cutting sites are not uniformly distributed along the genome (Figure 4A). Within the Hi-C contact matrix, bins with more restriction enzyme cutting sites tend to show a higher level of chromatin interactions (Figure 4A). The GC content bias (Figure 4B) [83,84] and the mappability bias (Figure 4C) are similar to the biases commonly observed in other types of next generation sequencing data (e.g., ChIP-Seq data and RNA-Seq data). In addition, Yaffe and Tanay [73] also pointed out that fragments with different lengths exhibit variable ligation efficiency, which is directly related to the observed chromatin interactions (Figure 4D). Related to Yaffe and Tanay's work [73], Gascoigne et al. [85] found that the reported Hi-C results [34] are also confounded by chromatin state. Furthermore, by a careful analysis of the yeast Hi-C data [38], Cournac et al. [86] identified an additional bias due to the circularization of DNA molecules, which does not apply to the original Hi-C study [34], suggesting that the systematic biases could be specific to the genome of interest.

Figure 4. Multiple sources of systematic biases buried in Hi-C experiments.

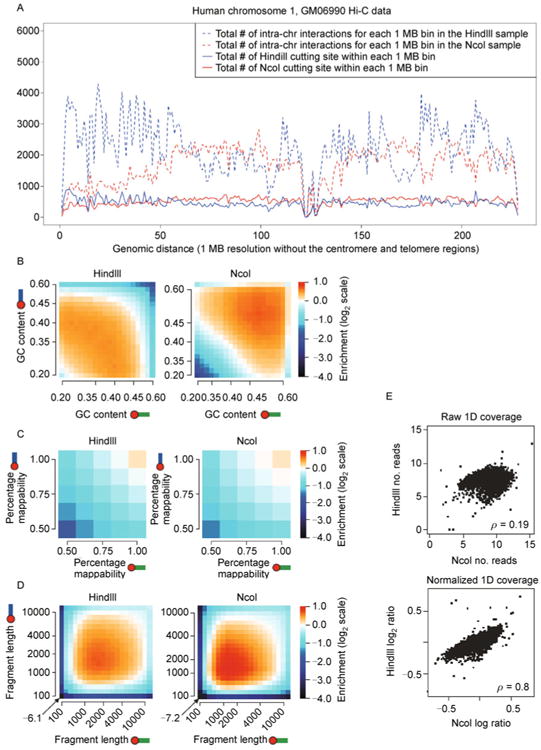
(A) The restriction enzyme bias. We use the Hi-C data on human GM06990 cells [34] as an example. The red solid curve and the blue solid curve represent the total number of restriction enzyme cutting site within each 1 MB bin in the human chromosome 1 for the restriction enzyme HindIII and the restriction enzyme NcoI, respectively. The restriction enzyme cutting sites are not uniformly distributed along the human chromosome 1. The cutting site distributions of HindIII and NcoI (the red solid curve and the blue solid curve) are weakly correlated (Pearson correlation coefficient = 0.1496). The red dashed curve and the blue dashed curve represent the total number of intra-chromosomal interactions for each 1 MB (row sum in the Hi-C contact matrix) in the human chromosome 1 for the HindIII sample and the NcoI sample, respectively. The row sums in the HindIII sample and the NcoI sample (the red dashed curve and the blue dashed curve) are poorly correlated (Pearson correlation coefficient = −0.0283). Chromosome regions with more restriction enzyme cutting sites tend to show a higher level of chromatin interactions. Row sum in the Hi-C contact matrix and the restriction enzyme cutting site distribution are highly correlated (Pearson correlation coefficient = 0.9268 in the HindIII sample, 0.9321 in the NcoI sample). Noticeably, the restriction enzyme bias is specific to the enzyme used in Hi-C experiments, since different enzymes have different cutting site densities. (B) The GC content bias (direct copy of Ref. [73], Figure 1f). Lighter color represents enriched chromatin interactions, while darker color represents depleted chromatin interactions. Noticeably, the GC content is specific to the enzyme used in Hi-C experiments, since different enzyme cutting sites have different GC contents. (C) The mappability bias (direct copy of Ref. [73], Figure 1h). Lighter color represents enriched chromatin interactions, while darker color represents depleted chromatin interactions. Noticeably, the mappability bias is similar for Hi-C experiments with different restriction enzymes. (D) The fragment length bias (direct copy of Ref. [73], Figure 1d). Lighter color represents enriched chromatin interactions, while darker color represents depleted chromatin interactions. Noticeably, the fragment length bias is similar for Hi-C experiments with different restriction enzymes. (E) Effectiveness of the Yaffe and Tanay's method [73] in Hi-C bias reduction (direct copy of Ref. [73], Figure 2d). 1D coverage profile is defined as the total number of inter-chromosome interactions involving each of the 1 MB chromosomal bins. The raw 1D coverage profiles between the HindIII sample and the NcoI sample are weakly correlated (Spearman correlation coefficient = 0.19). The normalized 1D coverage profiles between the HindIII sample and the NcoI sample are highly correlated (Spearman correlation coefficient = 0.8).

Recently, several approaches have been proposed to remove systematic biases from the Hi-C contact matrix, which in general can be categorized into two groups: the “correction” methods and the “normalization” methods (Table 1). The correction methods explicitly model and remove the impact of each bias source on the Hi-C data. As the first Hi-C bias reduction method, Yaffe and Tanay [73] used a non-parametric step function with 420 unknown parameters to approximate the joint effect of restriction enzyme cutting, GC content and sequence uniqueness, and went through all possible fragment pairs (in order of 10¹²) to obtain the corrected Hi-C data. Yaffe and Tanay's method is able to effectively remove systematic biases, and significantly increase the reproducibility between biological replicates (Figure 4E). Using a similar idea, Hu et al. [87] directly modeled the effects of different bias sources in the low resolution Hi-C contact matrix by a Poisson regression model, achieving better correction results with a computing time of several magnitudes shorter.

Normalization methods normalize the experimental visibility of each equal sized genomic locus, without assuming any specific systemic biases. Based on the equal visibility assumption, Imakaev et al. [74] proposed the iterative correction and eigenvector decomposition (ICE) technique, and showed that ICE substantially outperforms the Yaffe and Tanay's approach [73] in terms of the reproducibility between two biological replicates with different restriction enzymes. A similar method, sequential component normalization (SCN) [86], has also been developed to study the Hi-C contact matrix in the yeast genome.

Compared with correction methods, which require a pre-specification of known systematic biases, normalization methods can remove any type of known or unknown systematic biases. However, a major limitation of the normalization methods is that they can be used only to equal sized genomic loci. A generalization of the equal visibility assumption is needed to apply normalization methods to the Hi-C contact matrix with unequal genome partition.

Although many bias reduction methods have been proposed, how to assess performances of these methods still requires further investigation. A commonly used criterion is the reproducibility between the corrected/normalized Hi-C contact matrices from two biological replicates [34]. However, a high reproducibility is a necessary but not sufficient condition for an effective bias reduction procedure. A potentially better criterion is the consistency between the corrected/normalized chromatin interactions and the corresponding spatial distances measured by FISH experiments, which have been widely accepted as the gold standard for spatial proximity quantification.

Genome Partition

After the bias reduction procedure, the corrected/normalized Hi-C contact matrix can be used to explore chromatin interactions. It has been discovered that the magnitude of chromatin interactions varies across the genome [34]. In the original Hi-C study [34], Lieberman-Aiden et al. applied principle component analysis (PCA) to partition the human genome into two compartments A and B based on the spatial proximity between two genomic loci. They found enriched chromatin interactions between genomic regions with the same compartment label, and depleted interactions between those with different compartment labels. Furthermore, compartment A is associated with gene rich, actively transcribed regions and compartment B is associated with gene poor, repressively transcribed regions (Figure 5A). Partitioning the genome into several compartments with enriched or depleted chromatin interactions provides a novel perspective to study genome function [1].

Figure 5. Genome partition.

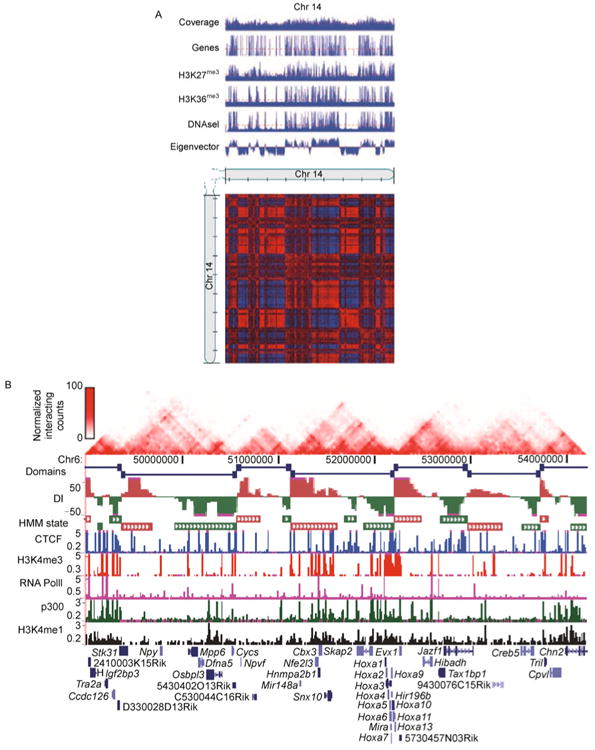
(A) Compartment labels are associated with different genetic and epigenetic markers (direct copy of Ref. [34], Figure 3G). We use chromosome 14 in human GM06990 Hi-C dataset [34] as an example. The Hi-C contact map and genetic and epigenetic markers are at 100 KB resolution. A PCA based approach was applied to the normalized Hi-C contact map to obtain eigenvectors. The compartment A is defined as those 100 KB bins with positive eigenvectors, and the compartment B is defined as those 100 KB bins with negative eigenvectors. Compartment A is associated with gene rich, actively transcribed regions and compartment B is associated with gene poor, repressively transcribed regions. (B) Topological domains appear to serve as units of genomic organization and perhaps function (direct copy of Ref. [45], Figure 1a). We use chromosome 6 in mouse embryonic stem cell Hi-C dataset [45] as an example. The Hi-C contact map and genetic and epigenetic markers are at 40 KB resolution. A hidden Markov model based approach was applied to the normalized Hi-C contact map to identify topological domain boundaries. Overlap of topological domains and other genetic and epigenetic features revealed that the domain boundary regions are enriched for the insulator binding protein CTCF and house-keeping genes.

A recent study [45] on a high resolution human and mouse Hi-C dataset has discovered that compartments A and B can be further divided into megabase-long and evolutionarily conserved topological domains, with high frequencies of intra-domain chromatin interactions but infrequent inter-domain chromatin interactions. Integrative analysis [45] of topological domains and other genetic and epigenetic features revealed that domain boundary regions constrain the spread of heterochromatin, and are enriched with the insulator binding protein CTCF and house-keeping genes, suggesting that these topological domains may serve as units of genomic organization and perhaps function (Figure 5B). Similar results have also been reported in the mouse chromosome X [46] and the drosophila genome [47,48]. The topological domain organization of interphase chromosomes and its relation to genome functions have been intensively reviewed recently [88–92].

Partitioning the genome into topological domains reveals more detailed knowledge about genome organization and function. However, a direct visualization [45] of the Hi-C contact map reveals that most transitions between two adjacent domains are not sharp, and large domains appear to contain complex hierarchal sub-domain structures. Together with aforementioned systematic biases, identifying domain boundary regions poses a great challenge. Several methods have been proposed to address this challenge (Table 1). Dixon et al. [45] evaluated differences between upstream and downstream chromatin interactions and developed a hidden Markov model to identify domain boundary regions. Sexton et al. [47] extended the Yaffe and Tanay's bias correction model [73] by including a local distance-scaling factor, and demarcated domains using the topmost 5th percentile of inferred distance-scaling factors. Hou et al. [48] developed a Poisson mixture model to characterize the difference between intra-domain and inter-domain chromatin interactions. Liu et al. [93] proposed Genome Segmentation from Intra-Chromosomal Associations (GeSICA) to first dichotomize the human genome into two genomic states, and then explore detailed hierarchical sub-domain structures using a Markov clustering algorithm. Most of these available methods take the corrected/normalized Hi-C contact matrix as input data, and thus, treat the bias reduction and genome partition as two separate steps. Since a two-step strategy is almost always sub-optimal, it would be desirable to develop an integrative approach combining bias reduction and domain calling together.

Polymer Models for Studying Biophysical Principles Governing Chromatin Folding

It is widely accepted that genome structure affects genome function [49]. A reliable model of 3D chromosomal structure has the potential to improve our understanding of chromosome organization and function. Over the past few decades, biophysicists have proposed various polymer models to study biophysical principles governing chromatin folding and their mechanistic implications. Here we briefly summarize the recent development of polymer models using information obtained from Hi-C data (Table 1). A comprehensive review, which is beyond the scope of this paper, can be found in Ref. [94].

In polymer physics, the spatial organization of chromosome is modeled as a polymer folding in the three dimensional space. The probability of observing a specific conformation of polymer folding is determined by the interaction energy among chromosome regions. The distribution of all possible conformations of polymer folding, termed as Boltzmann distribution or Gibbs distribution, provides an ensemble view of chromatin folding. Understanding statistical properties of such ensemble is critical for explaining high spatial and temporal variability of 3D chromosomal structures [49,95–97], and revealing biophysical principles governing chromatin folding.

As early attempts to explore 3D chromosomal structures via polymer model, the fractal globule model [98,99] and the equilibrium globule model [42,100] have been proposed and debated for a long time. The fractal globule model assumes that chromatin is in a knot-free configuration, while the equilibrium globule model assumes that chromatin is in highly knotted configuration. The Hi-C technology provides us experimental evidences to check these models at unprecedented resolution and throughput. The read count data from Hi-C experiments allow us to evaluate the average frequency of chromatin interactions for any given genomic distance (i.e., the contact probability introduced in Ref. [34]). Based on the theoretical analysis, the fractal globule model and equilibrium globule model lead to different predictions of contact probability as the function of genomic distance, therefore a comparison between the theoretical predictions and the contact probability estimated from the Hi-C data can be used to access the fit of these two models. Following this reasoning, Lieberman-Aiden et al. [34] showed that the fractal globule model achieved better fitting to the Hi-C data than the equilibrium globule model, and thus represents better the spatial organizations of chromosomes. Detailed biophysical properties of the fractal globule model and its functional implications have been reviewed in a recent paper [101].

Different from the fractal globule model and the equilibrium globule model, which focus on the configuration of chromatin looping, a few alternative polymer models have been proposed recently to study the biophysical principles governing chromatin looping. Mateos-Langerak et al. [42] described the random loop model, which assumes that each pair of monomers has certainty probability to interact and form a loop. Later on, Bohn and Heermann [43] introduced the dynamic loop model to explain chromatin looping by diffusional motion of monomers. Most recently, Barbieri et al. [44] explored the strings and binders switch model, in which the concentration of binding molecules affects the equilibrium state of chromatin looping. Noticeably, the strings and binders switch model is consistent not only with individual chromosome contact probabilities measured by Hi-C experiments, but also achieves high consistency with the FISH data. All of these polymer models have significantly improved our understanding of the mechanism of chromatin spatial organization.

The development of polymer models is driven by biophysical principles governing chromatin folding. Although polymer models provide a lot of insights into the general mechanism of chromosome spatial organizations, they usually use the Hi-C data indirectly. Most polymer models are linked to the Hi-C data via the contact probability, which is the conditional expectation of the contact frequency given the genomic distance. The logic is that, if the theoretical contact probability predicted by a polymer model is consistent with the observed contact probability in Hi-C experiments, the polymer model will be supported by the Hi-C data. From the statistical perspective, this criterion corresponds to the moment estimation based on the first order moment. It is possible that multiple polymer models can match the first order moment equally well. An extension of moment matching from the first order moment to higher order moments will enable a deeper exploration of the Hi-C data and a better comparison among different polymer models.

Data-driven statistical models, which directly model stochastic uncertainties in the Hi-C data and employ rigorous statistical analysis, are necessary complements of the principle-driven polymer models. In the following two sections, we describe two important topics in statistical analysis of the Hi-C data: inferring consensus 3D chromosomal structure and evaluating structural variation of chromatin.

Statistical Models for Inferring Potential Consensus 3D Structure of Chromosomes

Measuring genome-wide chromatin interactions simultaneously, Hi-C technology provides an unprecedented opportunity to generate 3D models for chromosomes. However, different from protein structures, chromosomal structures exhibit high spatial and temporal variability [49,95–97]. Therefore, chromatin interactions captured by Hi-C experiments, in which millions of cells are measured simultaneously, can only be interpreted as an “average structure” of the whole cell population (Figure 6). In the study of mammalian genomes, the interpretation of Hi-C data is further complicated by the fact that two homologous chromosomes may exhibit distinct 3D chromosomal structures. These facts pose great challenges in inferring 3D chromosomal structures from Hi-C data, and make DNA structural modeling an active research area.

Figure 6. An illustration of the mixture cell population.

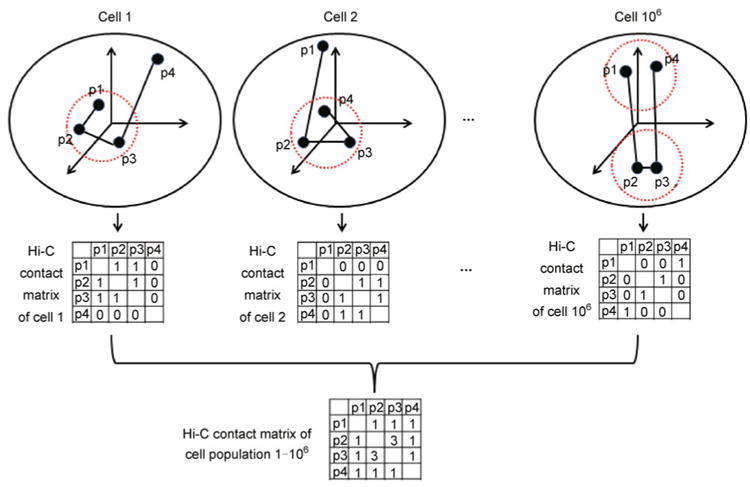
Assume that a cell population contains 10⁶ cells. We use beads-on-a-string model to represent the spatial organization of four loci (p1, p2, p3 and p4) in each cell. Assume that chromatin interaction between two loci can be measured by the Hi-C experiment only if the spatial distance between them is less than certain threshold (diameter of the dashed red circles). We further assume that the Hi-C experiment can be conducted on each single cell, and no chromatin interactions among p1, p2, p3 and p4 are observed except for the selected three cells (cell 1, cell 2 and cell 10⁶). Within each cell, only one paired-end reads can be produced from two interacting loci pair. The observed Hi-C contact matrix is a population summation of cell specific Hi-C contact matrices, which correspond to multiple distinct 3D chromosomal structures.

Lots of efforts have been made to address these challenges, which in general assume that there exists a dominant consensus 3D chromosomal structure among the cell population, and the two homologous chromosomes of each diploid individual share the same 3D chromosomal structure. Although these assumptions are generally thought to be impractical at the whole chromosome level, the recent discovery of topological domains [45–48] suggests that they might be acceptable for some local genomic regions. The 3D chromosomal structure of each topological domain likely exhibits low structural variability across the cell population, while the spatial arrangement of multiple topological domains could be flexible resulting in a high structural variability within the cell population. Based on the assumption of global or local consensus 3D chromosomal structures, several approaches have been proposed to build up 3D model from Hi-C data. In this section, we provide a comprehensive review of existing statistical approaches to infer both global and local consensus 3D chromosomal structures (Table 1). Statistical methods to verify the assumption of global or local consensus 3D chromosomal structures will be reviewed in the next section.

Although the fractal globule model and other polymer models have provided new insights on biophysical principles of chromatin folding, it has two limitations. First, Lieberman-Aiden et al. [34] confirmed that the fractal globule model matches well with the Hi-C data at the megabase scale (in terms of a few representative “features” such as the first moment). However, it is not clear whether the consistency still holds at a higher resolution scale and how such models can help predict detailed properties of biological relevance. More importantly, it is the 1D genomic distance instead of the 3D spatial distance that directly involves the theoretical analysis of the fractal globule model, resulting in an insufficient usage of the information in the Hi-C data. It is necessary to develop novel 3D models to predict the spatial distance between two genomic loci of interest (e.g., between genes and their regulatory elements) based on all available experimental evidences, which is more biologically relevant.

For this purpose, the beads-on-a-string model (Figure 7), which is widely used in chemistry, was proposed for modeling consensus 3D chromosomal structures. In the beads-on-a-string model, the genomic region of interest is partitioned into consecutive, disjoint loci represented by beads. Given a consensus 3D chromosomal structure, represented by the Euclidian coordinates of the beads, the population average spatial distance between any two genomic loci can be calculated by the Euclidian distance between them. Several studies [34,45] have demonstrated a negative association between the number of paired-end reads spanning two genomic loci and the spatial distance between them. Based on such negative association, a translation from the read counts to spatial distance can be built up computationally. Therefore, the Hi-C contact matrix can be interpreted as a surrogate of the pair-wised spatial distance matrix of the genomic loci of interest. Our goal is to infer the consensus 3D chromosomal structure of the genomic region of interest from the indirect observation of the pair-wised spatial distance matrix, i.e., the Hi-C contact matrix.

Figure 7. An illustration of the Hi-C data generation mechanism and the consensus 3D chromosomal structure inferring procedure under the beads-on-a-string model.

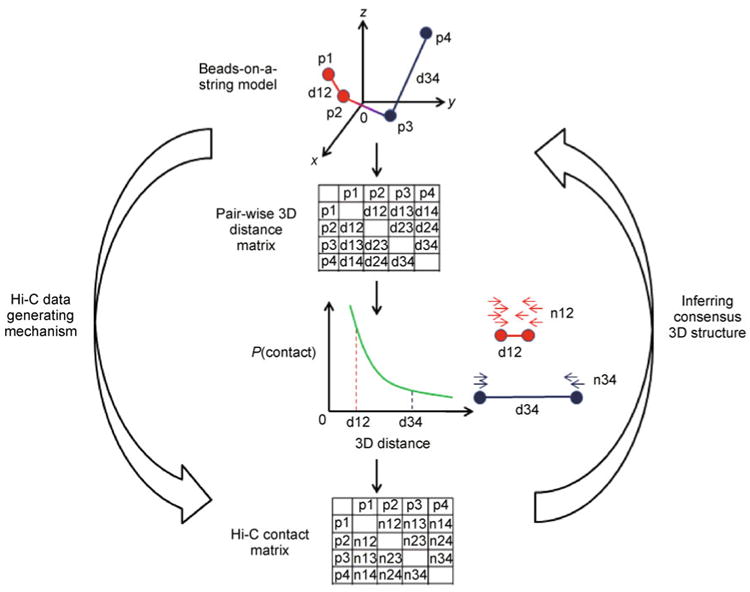
The genomic region of interest is divided into four regions (p1, p2, p3 and p4), each represented by a bead in 3D space. Given the Euclidian coordinates of each bead, it is straightforward to calculate the pair-wise 3D distance matrix. The Hi-C contact matrix is generated according to the pair-wise 3D distance matrix, with the assumption that the probability of observing a chromatin contact between two genomic loci is negatively associated with the 3D distance between them. For example, loci pair p1 and p2 (red beads) are closer to each other than loci pair p3 and p4 (blue beads), therefore the chromatin contact between loci pair p1 and p2 (n12 in the Hi-C contact matrix) is higher than the chromatin contact between loci pair p3 and p4 (n34 in the Hi-C contact matrix). The problem of inferring consensus 3D structure is defined as identifying a beads-on-a-string model which best fits the observed Hi-C contact matrix.

Given a consensus 3D chromosomal structure, it is straightforward to get the corresponding pair-wised distance matrix. However, the inverse problem, inferring consensus 3D chromosomal structure from the distance matrix, is challenging, especially when the distance matrix is complicated by various experimental noises and biases. Figure 7 gives an illustration of the Hi-C data generating mechanism and the consensus 3D chromosomal structure inferring procedure under the beads-on-a-string model.

Several optimization-based approaches [33,38,43] have been proposed to infer consensus 3D chromosomal structures based on the beads-on-a-string model (reviewed by Ref. [102]) (Table 1). These methods design a target function to measure the goodness-of-fit of a 3D model with respect to the Hi-C data, and search the model space to optimize the target function with some pre-specified constraints (e.g., the spatial distance between two loci must fall into a certain range). The main limitations of these optimization-based approaches are 1) they are easy to be trapped in local modes; 2) the target functions involved are usually ad hoc and cannot take the experimental uncertainties of the Hi-C data into consideration; and 3) they cannot explicitly quantify estimation uncertainties.

To overcome limitations of optimization-based approaches, model-based approaches were developed later, which explicitly model the uncertainties in the Hi-C data via statistical models (Table 1). The MCMC5C proposed by Rousseau et al. [39] models the Hi-C data by Gaussian distribution, and designs Markov-chain Monte Carlo-based methods to infer the consensus 3D chromosomal structures. Recently, Hu et al. [103] proposed a more efficient Bayesian approach named BACH. Different from MCMC5C, BACH uses the Poisson distribution to model the count data in the Hi-C contact matrix, and incorporates advance Markov-chain Monte Carlo techniques (sequential Monte Carlo [104] and hybrid Monte Carlo [105,106]) to improve the efficiency in exploring the model space. Moreover, BACH is the only available algorithm that incorporates bias correction into the inference of chromosomal structures. Applying BACH to a high resolution Hi-C data set generated from mouse ES cells, Hu et al. [103] discovered that the 3D structure, especially the shape, of a topological domain is highly correlated with several genomic and epigenetic features of the domain. In addition, Hu et al. [103] constructed a whole chromosome 3D model, which reveals the spatial separation of euchromatic and heterochromatic regions (Figure 8).

Figure 8. Spatial organization of compartment A and B.

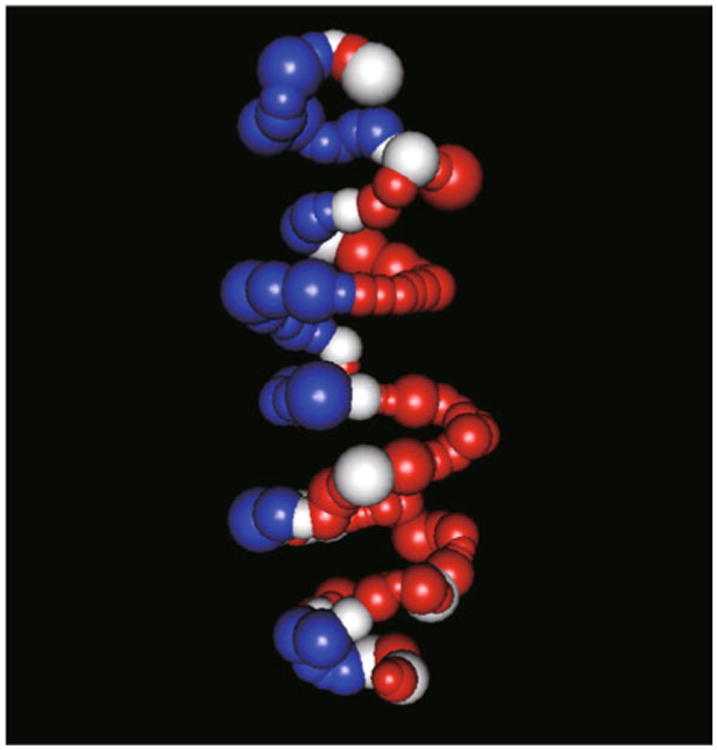
We use the 3D chromosomal structure BACH [103] predicted for the mouse chromosome 6 in the mouse embryonic stem cell Hi-C dataset with restriction enzyme HindIII [45] as an illustrative example. Each sphere represents a topological domain. The volume of each sphere is proportional to the genomic size of the corresponding topological domain. The red, white and blue colors represent topological domains belonging to compartment A, straddle region and compartment B, respectively. Compartment A contains gene rich, actively transcribed, accessible and early replicated chromatin. Compartment B contains gene poor, lowly transcribed, inaccessible and late replicated chromatin. In this 3D model, topological domains with the same compartment label tend to locate on the same side of the structure. The spatial organization of compartment A and B is consistent with their interaction frequencies and the observation that compartment B tends to be associated with nuclear membrane.

Statistical Models for Evaluating Structural Variation of Chromatin

The structural variation of chromatin can be modeled in two different ways: First, the magnitude of structural variation is uniform along the genome; second, the magnitude of structural variation is relatively low within each topological domain but much higher between adjacent topological domains, leading to a train-like structure. Each compartment of the train has a homogeneous local structure, while the global structure of the train can be very flexible depending on the spatial arrangement of the different compartments. A recent study by Hu et al. [103] suggests that the second model could be acceptable for mammalian genomes.

Several optimization-based approaches [33,38,40] have been developed to quantify structural variation of chromatin (Table 1). These optimization-based approaches in general contains two steps: First, apply the method to the Hi-C data multiple times in parallel runs with different initial configurations, each resulting in a 3D structure; and then, measure the chromatin structural variation by comparing structures obtained from these multiple runs. In this way, for example, Bau et al. [33] found that the cancer cells exhibit higher chromatin structural variations than the normal cells. However, their limitations are also obvious. First, such parallel computing approaches are computationally intensive and difficult to interpret if not impossible. Second, the clustering results are sensitive to the initial state of each parallel run, since any finite number of parallel runs cannot guarantee to fully characterize the huge space of possible 3D structures. Third, parallel runs maybe trapped in individual local modes, which may not correspond to biologically meaningful sub-populations. Finally, these multiple structures are not equally weighted; therefore the group sizes obtained from the clustering procedure cannot accurately reflect the size of each sub-population. More importantly, none of these methods models the possible existence of sub-populations within the cell population, which requires a mixture-component model.

Recently, Kalhor et al. [37] proposed the first population-based modeling approach, which directly links the Hi-C data to the presence or absence of chromatin interactions instead of the population average spatial distances. Compared to the previous proposed consensus 3D chromosomal structure models, this population-based analysis provides a more realistic representation of global genome landscape [107]. However, Kalhor et al.'s approach [37] involves the optimization of a population-based target function, which fails to incorporate experimental uncertainties in the Hi-C data.

In order to study chromatin structural variations in a principled way, Hu et al. [103] proposed the BACH-MIX approach under the assumption that the genome is organized as the train-like structure. The BACH-MIX approach assumes that each topological domain exhibits a consensus 3D structure (thus, can be reconstructed by BACH), and modeled the spatial arrangement of two adjacent topological domains via a mixture component model. Each mixture component corresponds to a specific spatial arrangement of two adjacent topological domains, and the weight of each mixture component represents the proportion of corresponding sub-population in the cell population. Note that BACH is a special case of BACH-MIX where the number of mixture components is one.

In practice, we can apply BACH-MIX with different strategies. For example, we can either treat each topological domain as a compartment (called domain-level BACH-MIX), or further divide each topological domain into two sub-domains and treat each sub-domain as a compartment (called sub-domain-level BACH-MIX). If the genome of interest does follow the train-like structure with topological domains as compartments, we will expect that domain-level BACH-MIX fits the data significantly better than BACH (in terms of model selection criteria such as AIC [108]), while sub-domain-level BACH-MIX does not. Applying domain-level BACH-MIX as well as sub-domain-level BACH-MIX to a high resolution Hi-C dataset on mouse embryonic stem cells [45], Hu et al. [103] found that most topological domains tend to have a homogeneous 3D chromosomal structures, while the spatial arrangement of two adjacent domains tends to be heterogeneous among the cell population. Moreover, the structural variations of chromatin are closely related to several genomic and epigenetic features: Gene rich, accessible and early replicated chromatins are more likely to exhibit multiple structural configurations than gene poor, inaccessible and late replicated chromatins.

Although available tools for inferring chromatin structural variations provide many insights on spatial organizations of chromosomes, most evidences for validation are indirect. Without a systematic comparison between spatial distances predicted by these tools and spatial distances measured by FISH experiments, it remains unclear how to evaluate the biological significance of these 3D models. More experimental data are needed to fully access and further refine 3D modeling approaches.

Conclusion and Perspective

As a powerful approach to measure genome-wide chromatin interactions, Hi-C technology has substantially strengthened our understanding on genome architecture. However, the development of statistical and bioinformatics tools for analyzing Hi-C data is lagging behind because of two major obstacles: First, the underlying biology and the experiment assay are quite complicated for non-biologists to grasp; second, the data generated from Hi-C experiments, which measures the average chromatin interactions among millions of cells in a cell population, compounded by multiple layers of biases accumulated during the long experimental protocol, require delicate analysis and careful interpretation. Although great efforts have been made in this field, many important questions still remain unsolved. Here we describe a few topics of high priority for future researches.

As the very first step in Hi-C data analysis, bias reduction is critical for all the downstream analysis. Non-parametric model [73] is able to effectively capture and remove systematic biases. However, it is limited by the extremely intensive computation. The parametric model in Ref. [87] is computationally efficient, but is highly dependent on the assumption of parametric functional form of bias effects. Borrowing strengths from both non-parametric and parametric models, the semi-parametric model is appealing to achieve a balance between effective bias reduction and efficient computation.

After applying effective bias reduction methods, reproducibility between Hi-C biological replicates cannot be perfect. Several technical variations, including restriction enzyme cutting efficiency, PCR amplification and the total number of paired-end reads cannot be fully controlled. Moreover, biological variations due to spatial and temporal chromatin interaction dynamics are still not fully understood. To address all these challenges, rigorous statistical analyses are of urgent need to quantify multiple levels of technical variations and biological variations raised from Hi-C experiments.

Another topic of great interest is to identify topological domain boundaries from the Hi-C data. It is widely accepted that mammalian chromosomes can be partitioned into topological domains. However, methods for quantifying the variability of topological domain boundaries still lag behind. Most currently available domain boundary callers [45,47,48,93] are designed for analyzing a single Hi-C dataset, or pooled Hi-C dataset. Novel domain boundary callers for analyzing multiple Hi-C datasets simultaneously have the potential to accurately identify domain boundaries and precisely quantify their biological variability.

Identifying long-range chromosomal interactions is a fundamental question in Hi-C data analysis. This is analogous to the peak calling problem in ChIP-Seq data analysis, except that the problem is now on a two dimensional Hi-C contact matrix. The key challenge is to propose a proper background model for characterizing random chromosomal interactions between two loci, which can take full consideration of all factors that may affect the contact frequency among genomic loci. In addition, under the limited sequencing depth in Hi-C experiments, Hi-C count data corresponding to long-range chromosomal interactions between two loci are usually very sparse. Pooling information in the neighborhood genomic regions will improve the statistical power of identifying biologically meaningful chromosomal interaction hot spots.

Principle-driven polymer models and data-driven statistical models are two major directions in 3D modeling using the Hi-C data. Polymer models are able to unveil underlying biophysical principles, but usually cannot fully explore information in the Hi-C data. Statistical models are capable of explicitly modeling stochastic variability in the Hi-C data, but usually fall short in yielding mechanistic insights. We speculate that a joint effort between biophysicists and statisticians will enable borrowing strengths from both polymer models and statistical models, and result in more biologically meaningful results in Hi-C data analysis.

One common challenge in both polymer models and statistical models is to efficiently explore the high dimensional solution space according to the corresponding probability distribution, which is defined by the biophysical energy function or the statistical likelihood function. To solve the high dimensional optimization or sampling problems, multiple parallel runs are routinely used to avoid local modes. However, as dimensionality increases rapidly, even a very large number of parallel runs cannot guarantee to converge to the global optimum. Furthermore, strong correlation among unknown parameters, such as Euclidian coordinates of each genomic locus, typically results in extremely slow convergence. Advanced MCMC techniques have been shown to achieve high computational efficiency in solving complex statistical inference problem [103]. We speculate that MCMC methods will generate a broader interest in Hi-C data analysis in the near future.

It is widely accepted that chromosome spatial organizations exhibit substantial spatial and temporal dynamics. However, capturing such dynamics using statistical models is extremely challenging. To achieve a balance between the complexity in real life and the computational cost, mixture models [103] are of particular interest, but have not been fully explored in Hi-C data analysis. Under the assumption that there are a limited number of mixture components within the cell population, mixture models could be effective tools for characterizing chromatin structural dynamics.

Last but not least, it is of great interest to link Hi-C data with other genomic profiling data and conduct joint analysis of multiple high throughput genomic datasets. The Bayesian statistical modeling framework is extremely promising to achieve this goal, since it is able to naturally incorporate the knowledge from other genomic studies as informative prior.