Prediction of in-hospital mortality after ruptured abdominal aortic aneurysm repair using an artificial neural network

Abstract

Objective

Ruptured abdominal aortic aneurysm (rAAA) carries a high mortality rate, even with prompt transfer to a medical center. An artificial neural network (ANN) is a computational model which improves predictive ability via pattern recognition, while continually adapting to new input data. The goal of this study was to effectively use ANN modeling to provide vascular surgeons a discriminant adjunct to assess the likelihood of in-hospital mortality on a pending rAAA admission using easily obtainable patient information from the field.

Methods

One-hundred and twenty-five of 332 total patients from a single-institution from 1998–2013 who had attempted rAAA repair were reviewed for preoperative factors associated with in-hospital mortality. One-hundred and eight patients received an open operation, and 17 patients received endovascular repair. Five variables were found significant upon multivariate analysis (P < .05), and four of these five: preoperative shock, loss of consciousness, cardiac arrest and age were modeled via multiple logistic regression and an ANN. These predictive models were compared against the Glasgow Aneurysm Score (GAS). All models were assessed by generation of receiver operating characteristic curves and Actual vs. Predicted outcomes plots, with area under the curve (AUC) and Pearson r² value as the primary measures of discriminant ability.

Results

Of the 125 patients, 53 (42%) did not survive to discharge. Five preoperative factors were significant (P < .05) independent predictors of in-hospital mortality in multivariate analysis: advanced age, renal disease, loss of consciousness, cardiac arrest and shock, though renal disease was excluded from the models. The sequential accumulation of zero to four of these risk factors progressively increased overall mortality rate, from 11% to 16% to 44% to 76% to 89% (Age ≥ 70 considered a risk factor). Algorithms derived from multiple logistic regression, ANN and GAS models generated AUC values of .85 ± .04, .88 ± .04 (training-set) and .77 ± .06, and Pearson r² values of .36, .52 and .17, respectively. The ANN model represented the most discriminant of the three.

Conclusions

An ANN-based predictive model may represent a simple, useful and highly discriminant adjunct to the vascular surgeon in accurately identifying those patients who may carry a high mortality risk from attempted repair of rAAA, using only easily definable preoperative variables. Though still requiring external validation, our model is available for demonstration at https://redcap.vanderbilt.edu/surveys/?s=NN97NM7DTK.

INTRODUCTION

Ruptured abdominal aortic aneurysm (rAAA) is a vascular surgical emergency, in which 50% of patients die before reaching the hospital, and may carry overall mortality rate of 80–90%.¹ While predictive models have been developed using multiple logistic regression analysis, their clinical use has been hindered due to lack of availability of all variables necessary to calculate a score, difficulty in interpretation, development in an age prior to endovascular repair (EVAR), as well as lack of consistent validation.^1–4

The first reported predictive scoring system for survival after repair of rAAA is the Glasgow Aneurysm Score (GAS), first described in 1994.³ This model retrospectively examined 500 patients who underwent open repair for rAAA from 1980–1990 for risk factors associated with postoperative death, and found that age, preoperative shock, myocardial disease (MCD), cerebrovascular disease (CVD) and renal disease (RD) were independent predictors of mortality upon multivariate analysis.^{3, 5} Using variable weights suggested by multiple logistic regression coefficients, the GAS algorithm was reported as: GAS = age (yrs) + 17 (if shock) + 7 (if myocardial disease) + 10 (if cerebrovascular disease) + 14 (if renal disease).^{1, 3} Scores over 95 corresponded to mortality over 80%. In 1996, the Hardman Index was reported after a retrospective analysis of 154 patients who underwent open rAAA repair from 1985–1993, in Australia.^{1, 2, 5–8} One point was awarded for each of five factors present on presentation: age > 76, loss of consciousness after presentation (LOC), creatinine > 2.1 mg/dL, hemoglobin level < 9 g/dL and indicators of ischemia on electrocardiogram (ECG).⁸ While simple to calculate and interpret, Tambyraja et al., in 2008, showed that the Hardman Index was not specific in predicting death in patients with 3 or more variables, the initially reported score cut-off for uniform mortality.⁵

Through the 2000s, additional predictive models emerged that represented U.S. cohorts. The Vascular Study Group of New England (VSGNE) recently reported and internally validated a risk score for in-hospital mortality after open rAAA repair using age, preoperative cardiac arrest (CPR), LOC and suprarenal aortic clamping as significant predictors of postoperative in-hospital mortality, via analysis of 242 patients at 10 U.S. centers from 2003–2009.¹ The development of a risk score that incorporates patients who underwent either EVAR or open AAA repair remains elusive. The endovascular approach may lead to improved survival in tertiary care centers where it is readily accessible,⁹ although prospective data currently does not support this in the case of emergent rAAA repair.¹⁰

The artificial neural network (ANN) is an emerging tool for outcomes modeling, in which a series of interconnecting parallel nonlinear processing elements (nodes) is “taught” to model a dataset, accounting for the complex relationships among the variables. The ANN is trained with selected patient data, and provides an output layer with a prediction of endpoint(s) based on factors that were input.^11–14 As with any model, the input variables can be categorical or continuous, and can be rationally selected or determined via significance or trend in statistical analysis.

Since current prognostic models are rarely used for preoperative guidance, the purpose of this study was to utilize an ANN to develop a model applicable to surgeons at a tertiary care center with open and endovascular capability, in which readily available preoperative factors can provide accurate prognostic guidance, and help determine appropriate candidates for rAAA repair. Furthermore, we aim to propose methods to conveniently facilitate the use of an ANN-derived model in the clinical setting such that a complex algorithm may provide easily interpretable data for the surgeon. To assess our algorithm’s discriminant ability, our four-variable ANN model was compared to its analog derived via multiple logistic regression, and to GAS, as a representative current scoring system.

METHODS

Patients who underwent repair for rAAA were determined using the Vanderbilt University Synthetic Derivative, a de-identified mirror of the institutional electronic medical record, StarPanel.¹⁵ As no identifying information was available, this study was approved by the Vanderbilt University Institutional Review Board, and patient consent was waived. In Synthetic Derivative, a search for the ICD-9 code of either 441.3 (abdominal aortic aneurysm, ruptured) or 441.5 (aortic aneurysm of unspecified site, ruptured) was performed, yielding 332 patients with the diagnosis from between 1998–2013. Patients were included if they underwent emergent operation for rAAA; operation was defined as the administration of anesthetic with the intent to operate.⁵ Exclusion criteria included patients who had thoracic pathology, isolated iliac pathology, ruptured viscus (non-aorta), aortoenteric fistula, aortic dissection or pseudoaneurysm, as well as those with non-operative management, death prior to operation, or lack of sufficient information in the medical record. Ultimately, 125 patients were included for analysis.

Prognostic variables were initially examined to determine those preoperative factors associated with postoperative in-hospital mortality. The screened variables were chosen based on inclusion in at least one of five previously validated rAAA models for prediction of postoperative mortality, with sufficient reliable information retrospectively available in the Synthetic Derivative.^{1, 3, 5, 8, 16} The initial set of rationally selected variables included gender, age at rupture, loss of consciousness after presentation (LOC; defined as loss of consciousness, GCS < 15, or altered mental status necessitating protective intubation)^{2, 8}, signs of shock (SBP < 90, HR > 120, pallor, diaphoresis)³, preoperative cardiac arrest/cardiopulmonary resuscitation (CPR), and history of: MCD (myocardial infarction or angina)³, CVD (stroke or transient ischemic attack, CVD)³ and RD (any of chronic renal failure, acute kidney injury, urea level > 20 mmol/L, or creatinine level > 1.7 mg/dL on presentation, RD).^{3, 5, 8} Documentation in the medical record was sufficient for attribution of a variable. ECGs and laboratory values were not sufficiently available to surgeons prior to operation and were falsely altered due to blood transfusions, thus, were not considered. Measures necessitating preoperative imaging or pertaining to intraoperative decision making (such as need for suprarenal clamp) were excluded. Open or endovascular operation was noted, as 13.6% of patients received EVAR; there was no distinguishing between the two in the subsequent analysis. The primary outcome of this study was in-hospital mortality.

Bivariate analysis of the eight initial variables was performed on all 125 patients to screen for those risk factors associated with in-hospital mortality. Variables with P < .05 via Fisher’s exact test were considered for standard least squares multivariate analysis.¹⁷ The five variables with P < .05 on multivariate analysis were age, LOC, shock, CPR and RD. While significant, RD was not felt to help the clinician preoperatively, as ascertaining its presence may be difficult, thus, it was not included in the two subsequent models.

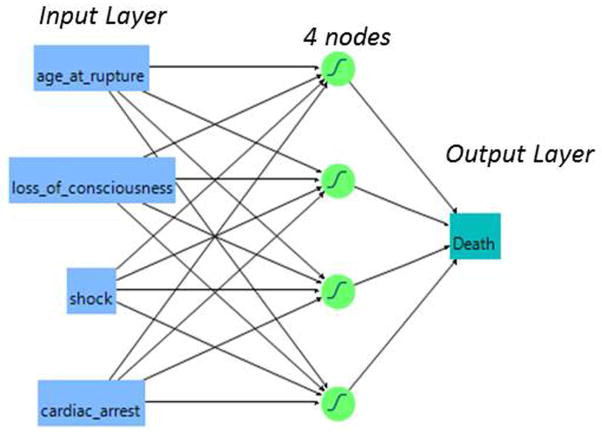
For the four-variable ANN, 107 patients with all variables known were considered for analysis. The data was converted into comma-delimited files suitable for interfacing with JMP Software, and input in the ANN. A back-propagation ANN with k-fold validation, with 4 nodes each assigned a learning value of 0.333 was used, and the model was trained with 3 iterations. The model was internally validated using the k-fold method to mitigate over-fitting the data.^{18, 19} A full mathematical description of the ANN methodology has been reviewed previously.^{20, 21} Briefly, all variables are input into an ANN program, and a “training” set of 80% of patients is randomly selected. The software uses a series of equations based on the hyperbolic tangential function to develop a complex model of which factors or combinations thereof lead to survival or in-hospital mortality, and outputs a value between 0 (survival) and 1 (in-hospital mortality). While no minimum sample size or parameters are needed for the model, the 20% validation set and k-fold validation method was required as a precaution against overfitting the data, ensuring internal validity. A schematic of the ANN showing input and output layers, and four processing layers (nodes) is diagrammed in Figure 1. The input layer represents the factors chosen for use in modeling the outcome (death), and the order of imputation of these factors is not important.

Fig. 1.

Schematic representation of the four-variable artificial neural network, ANN-4. The four variables on the left comprise the input layer. The four processing elements (nodes) represent the ANN’s hidden layer; a training value of 0.333 was used. The output layer is a predicted likelihood of death, transformed from 0 (survival to discharge) to 1 (in-hospital mortality).

Eighty-three patients with all GAS criteria known had their risk scores calculated and correlated with in-hospital mortality. All models had receiver operating characteristic (ROC) curves generated and quantified by the area under the curve (AUC, c-statistic), expressed as area ± standard error.^{22, 23} Actual vs. Predicted outcomes plots were also generated for all models, with Pearson r² value of the simple linear regression line as the primary measure of goodness of fit. Bivariate data analysis was done using GraphPad Prism (La Jolla, CA); all higher-level analysis and ANN modeling was performed using JMP statistical software (Cary, NC). P < .05 was used to denote statistical significance.

RESULTS

One-hundred and twenty-five patients were included for analysis in this study using the Synthetic Derivative database. Of this group, 105 were male (84%), and the average age at rupture was 70.3 years. One-hundred and six patients were Caucasian, 4 were African-American and 15 were of unknown race. One-hundred and eight patients (86%) received an open operation, and 17 patients (14%) received EVAR, at the surgeon’s discretion. The mortality rate between open and EVAR patients was similar (χ² = 0.01; P = .91). Seventy-two of 125 patients (58%) survived to discharge and 53/125 (42%) did not. The mean (± standard deviation) age was 69±8 years for survivors and 73±8 years in-hospital mortalities. A summary of patient characteristics and mortality rates is seen in Table I.

Table I.

Patient characteristics and mortality rates stratified by potential risk factors

Risk Factor	# of Patients	Mortality Rate (w/RF)	Mortality Rate (w/o RF)
Female	16% (20/125)	50% (10/20)	42% (44/105)
Age ≥ 70	54% (68/125)	53% (36/68)	30% (17/57)
LOC	38% (42/112)	71% (30/42)	19% (13/70)
Shock	70% (76/117)	54% (41/76)	18% (7/40)
CPR	13% (15/113)	87% (13/15)	33% (32/98)
MCD	33% (34/102)	50% (17/34)	24% (16/68)
CVD	12% (12/99)	33% (4/12)	30% (26/87)
RD	53% (53/100)	47% (25/53)	19% (9/47)

RF, risk factor; CI, confidence interval; LOC, loss of consciousness; MCD, myocardial disease; CVD, cerebrovascular disease; RD, renal disease.

^*Age expressed as binary in bivariate assessment; used as a continuous variable in prediction models.

Bold indicates variable was considered in multivariate analysis to determine independent association with in-hospital mortality.

Bivariate analysis identified those variables that were associated (P < .05) with postoperative inhospital mortality. The variables age at rupture, LOC, shock, CPR, MCD and RD were found to be significant. Standard least squares multivariate analysis was performed on the variables identified from bivariate analysis, using the 81 patients for whom all six variables were known. The results of the bivariate and multivariate analysis are outlined in Table II. Independent predictors of in-hospital mortality were found to be increased age (P = .03), LOC (P < .001), shock (P = .02), CPR (P = .004) and RD (P = .006); MCD was not significant (P > .05). The four variables age, LOC, shock and CPR were chosen for inclusion in the two models; presence of RD was thought not to be sufficiently available preoperatively, and not considered. Table III illustrates the mortality rates based on how many of the four risk factors were present (age ≥ 70 was used as a risk factor), for the 107 patients for whom all four variables were known. The multiple logistic regression function was then derived, with the corresponding ROC curve and Actual vs. Predicted outcomes plot (Figure 2). AUC of the ROC curve was 0.85 ± 0.04, and the Pearson r² of the simple linear regression line of the Actual vs. Predicted outcome plot was .36.

Table II.

Bivariate and multivariate assessment for risk factors for in-hospital mortality after rAAA repair

	Bivariate Analysis		Multivariate analysis
Risk Factor	Odds Ratio (95% CI)	P value	Spearman ρ correlation coefficient (95% CI)	P value
Female	0.7 (0.3,1.9)	.62	-	-
Age ≥ 70a	2.6 (1.3,5.6)	.01	.27 (.05,.46)	.03
LOC	11 (4.5,27)	<.001	.36 (.16,.54)	<.001
Shock	5.4 (2.1,14)	<.001	.27 (.05,.46)	.02
CPR	13 (2.9,63)	<.001	.32 (.11,.50)	.004
MCD	3.3 (1.4,7.8)	.01	.17 (−.05,.38)	.12
CVD	1.1 (0.3,4.0)	1.0	-	-
RDb	3.8 (1.5,9.3)	.006	.30 (.09,.49)b	.006b

^aconsidered as a continuous variable in multivariate analysis;

^bnot included in the ANN or multiple logistic regression model despite P < .05.

Bold- Included in multivariate analysis (P < .05). Bold Italics- included in multiple logistic regression and ANN models, as P < .05; LOC, loss of consciousness; MCD, myocardial disease; CVD, cerebrovascular disease; RD, renal disease

Table III.

Mortality rate based on number of risk factors

Number of Risk Factors	Mortality Rate (n = 107 patients)
0	11% (2/19)
1	16% (5/31)
2	44% (12/27)
3	76% (16/21)
4	89% (8/9)

Risk Factors include age ≥ 70, loss of consciousness, shock and CPR

Fig. 2.

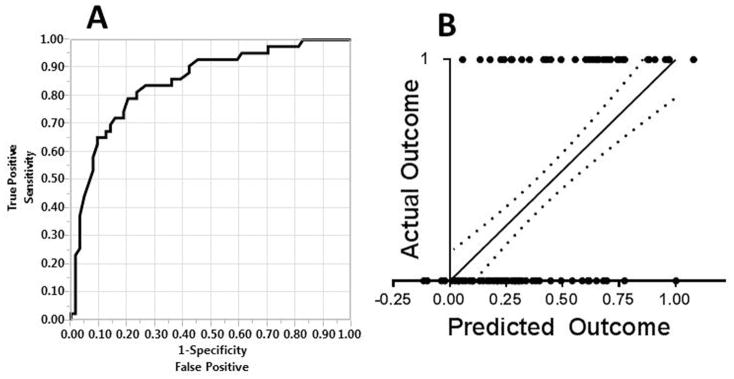
Four-Variable Multiple Logistic Regression Model. A- Receiver operating characteristic (ROC) curve for the multiple logistic regression analysis with the four significant variables considered in the algorithm (n = 107 patients). The AUC was 0.85 ± 0.04. B- Actual vs. Predicted outcomes plot; the correlation between actual and predicted death via simple linear regression was r² = .36. Root mean square error (RMSE) = 0.40. Dotted lines represent the 95% confidence band. Axes: 0- survival (predicted or actual); 1- in-hospital mortality (predicted or actual)

The same 107 patients were input into an ANN, with 86 patients (80%) for training and 21 for validation (20%). The ROC curve generated by the training and validation sets, and Actual vs. Predicted outcomes plot for all 107 patients using the training set algorithm are shown in Figure 3. The AUC values for the training and validation set were 0.88 ± 0.04 and 0.95 ± 0.06, respectively; Pearson r² value of the simple linear regression line of the Actual vs. Predicted outcome plot was .52.

Fig. 3.

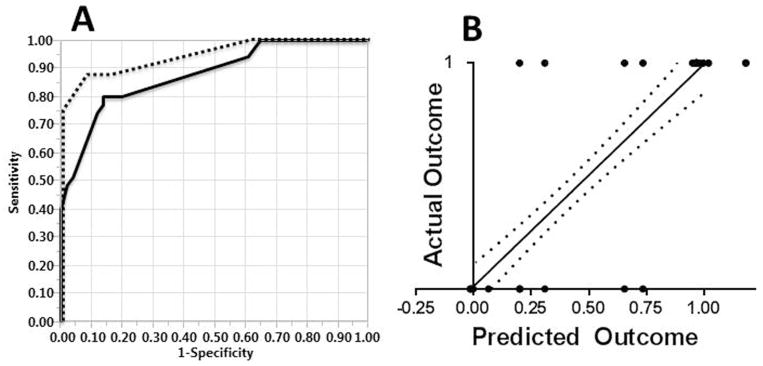
Four-Variable Artificial Neural Network Model. A- ROC Curve for the simplified ANN-4 training cohort (solid line, n = 86 patients, AUC was 0.88 ± 0.04) and ANN-4 validation cohort (dashed line, n = 21 patients, AUC = 0.95 ± 0.06) B- Actual vs. Predicted outcomes plot; the correlation between actual and predicted death via simple linear regression on all 107 patients, using the training set-derived algorithm, was r² = .52. RMSE = 0.34. Dotted lines represent the 95% confidence band. Axes: 0- survival (predicted or actual); 1- in-hospital mortality (predicted or actual)

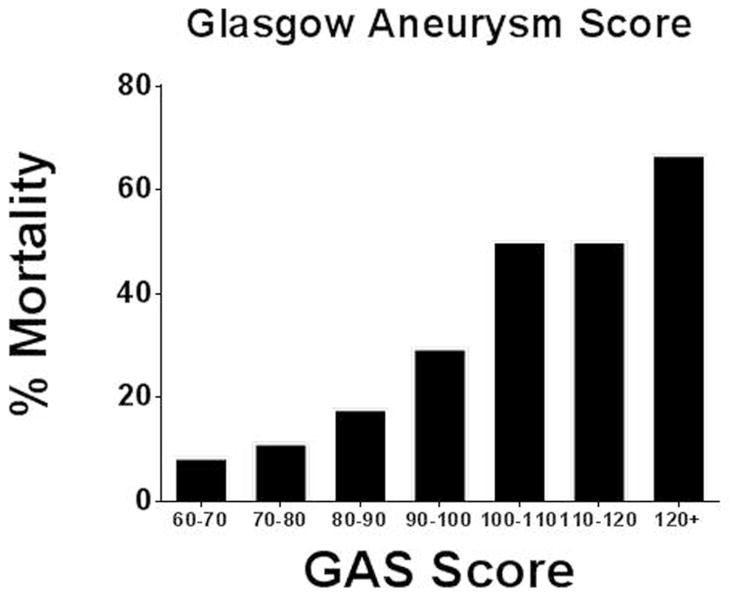
The 83 patients who had all GAS variables available had their risk score calculated and correlated to outcome. Stratification of mortality by GAS score is shown in Figure 4. The ROC curve and Actual vs. Predicted outcomes plot derived from GAS-prediction of in-hospital mortality are seen in Figure 5. The AUC and Pearson r² values were 0.77 ± 0.06 and .17, respectively.

Fig. 4.

Patient in-hospital mortality expressed by GAS score stratum (n = 83 patients)

Fig. 5.

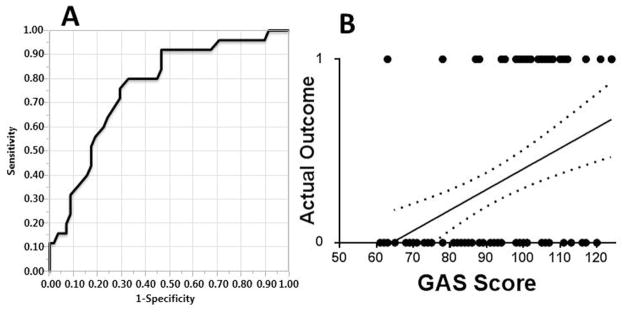
In-hospital mortality was correlated to the Glasgow Aneurysm Score (GAS, n = 83 patients). A- The ROC curve is shown; AUC is 0.77 ± 0.06. B- Actual vs. Predicted outcomes plot; the correlation between actual and predicted death via simple linear regression was r² = .17. RMSE (GAS scores normalized to 0–1 scale) = 0.46. Dotted lines represent the 95% confidence band. Axes: 0- survival (predicted or actual); 1- in-hospital mortality (predicted or actual)

In summary, the rAAA cohort was modeled in three ways: ANN (86 patients in the training set), multiple logistic regression (107 patients) and GAS score (83 patients). Statistics derived from each of the models are summarized Table IV. The ANN had the highest AUC and Pearson r² square value of all models, with the best accuracy (98%), sensitivity (94%), specificity (100%), positive predictive value (100%) and negative predictive value (97%).

Table IV.

Summary of descriptive statistics of models

Model	n	AUC	SE	r2	RMSE	Cutoffb	Acc. (%)	Sens. (%)	Spec. (%)	PPV (%)	NPV (%)
MLR	107	.85	.04	.36	.40	0.5	78	67	84	74	79
ANN	107	.88a	.04	.52	.34	0.5	84	79	88	81	86
GAS	83	.77	.06	.17	.46	101.5	74	52	83	57	80

^avalue derived from ROC curve of training set only;

^bvalue used to predict presence or absence of inhospital mortality, chosen to optimize accuracy;

n, number of patients used in analysis; AUC, area under curve; SE, standard error; r², Pearson r² value of simple linear regression line of Actual vs. Predicted outcomes plot; RMSE, root mean square error of simple linear regression; Sens, sensitivity; Spec, specificity; Acc., accuracy; PPV, positive predictive value; NPV, negative predictive value; MLR, seven-variable multiple logistic regression analysis; ANN, four-variable artificial neural network model; ANN-4, four-variable artificial neural network model; GAS, Glasgow Aneurysm Score

DISCUSSION

The goal of our study was to utilize an ANN model to accurately determine which patients are prone to in-hospital mortality after rAAA repair, using easily obtainable preoperative variables. In 2008, Tambyraja et al. reviewed over fifty case series worldwide from 1985–2005, identifying preoperative variables predictive of death after rAAA repair.² Among these studies, over 25 variables were found to be significant independent predictors, albeit many of them required laboratory measurements, detailed past medical history or imaging.² It presented a challenge to identify those variables that had the highest pre-test probability of significance in this study, one which looks at a U.S. cohort at a tertiary medical center, in the age of EVAR. The Glasgow Aneurysm Score, Hardman Index, Edinburgh Ruptured Aneurysm Score, Vancouver score and VSGNE were identified as models that are most clinically practical for the surgeon in the critical preoperative period.^{1, 3, 5, 8, 16} As such, preoperative variables contained within these models were chosen a priori as the most likely candidates for association with in-hospital mortality in our cohort.

Our general findings show a mortality rate directly proportional to the number of risk factors present, including advanced age, LOC, shock and CPR (Table III). The data from our ANN allow prediction of in-hospital mortality for surgical rAAA patients with greater discriminant ability than a multiple logistic regression model or the established GAS score. While the latter two models give each variable a specific weight, the ANN excels at identifying those combinations of age and categorical risk factors that may in fact portend the worst prognosis with the added benefit of a continually evolving algorithm based on newly derived continually input data, if desired. In the ANN analysis, RD was excluded as its presence may not be reliably known or deducible. This adjustment necessarily sacrificed predictive ability at the expense of enhanced simplicity and usefulness, especially since the four variables are all readily available under emergent conditions and easy to quantify or estimate. Practically, these four variables can be relayed to the surgeon by either the first responder attending to a patient with suspected rAAA in the field, or by the staff from an outside medical facility from where the patient is expected to transfer. Using the ANN-4 training algorithm, postoperative in-hospital mortality was predicted with a high degree of accuracy (84%), and with 79% sensitivity and 88% specificity using an arbitrary output score of 0.5 as a cutoff for death.

The advantage of an ANN lies in its ability to predict non-linear relationships between variables and outcomes, while adapting to data as it is continuously added. ANNs allow discovery and modeling of complex interactions of variables within data sets, culminating in the generation of an easily understood output layer. However, derivation of a simple predictive score from a higher order predictive equation that may continue to evolve is not practical. Therefore, its use to the surgeon must necessarily be facilitated. The ANN algorithm can be incorporated as a platform, perhaps within an electronic medical record or smart phone application, in which a health care provider can input relevant patient data and receive an output prognostic score. As an example, a simple estimator of in-hospital mortality based on our ANN algorithm is available for demonstration at https://redcap.vanderbilt.edu/surveys/?s=NN97NM7DTK. Furthermore, ANN outputs tend to be less ambiguous, generally predicting either survival or mortality. While no model can predict 100% correctly, this information may provide a more useful estimate to the surgeon and family who is unsure whether to proceed with an operation, presenting a more helpful alternative to current models.

This study is predicated upon two previous neural network-based analyses of patients with AAA. In 2000, Turton et al. identified 102 patients who underwent open rAAA repair from 1990–1997.²⁴ This study identified hypotension, intraperitoneal rupture, cardiac arrest and coagulopathy as independent preoperative predictors of mortality; subsequent ANN analysis predicted survival with a sensitivity of 86.4% and specificity of 79.3%.²⁴ Subsequently, in 2006, in-hospital mortality was assessed on both elective and emergent AAA repairs in a British cohort by Hadjianastassiou et al.²⁵ The variables identified were age, acute physiology score, emergency operation, and chronic health evaluation.²⁵ Both of these studies demonstrated a statistically rigorous application of an ANN with potentially useful predictive models. ANNs with improved diagnostic or prognostic abilities have been successfully developed in all medical fields; prediction of post-subarachnoid hemorrhage vasospasm, diagnosis of myocardial infarction and prognosis after ischemic stroke are a few notable examples relevant to the vascular surgeon.^{20, 26, 27} Though these models remain largely academic, ANN-based decision-making has been successfully translated to clinical practice, to a limited extent. As an example, PAPNET is an FDA-approved, commercially available automated microscopy program which uses a neural network algorithm to identify findings concerning for cervical dysplasia or cancer on Papaniclaou smears.^28–30 For improved practicality and potential application, our investigation sought to ultimately only include variables which are readily available, with a model derived from an American-based tertiary center cohort with EVAR capability.

An advantage of an ANN model is the removal of ambiguity in its prediction. Often times, the patients with rAAA present in extremis, with a high risk of mortality by any assessment or risk score. The ANN can thus predict, with confidence, that an operation may be futile. Nonetheless, no model can say with certainty that mortality is imminent, as a small percent chance of survival may still be acceptable to the patient and patient’s family, particularly if the patient had recently been transferred from another medical center for the purpose of an operation being offered. To this effect, surgical futility presents an ethical issue common to the vascular surgeon. End-of-life care and determination of medical futility has been extensively reviewed, and guidelines for determining futility of care and approaching this issue with families has been extensively reviewed, in the intensive care setting.^{31, 32} In an acute vascular surgical emergency, however, the clinician must make the assessment and appropriate articulate it to the patient and his family in a prompt manner. Adjuncts to the vascular surgeon’s judgment in these scenarios include suggestions of proposing the most likely non-death outcomes from surgical intervention (i.e. prolonged ventilation or hospitalization, loss of meaningful functional capacity), as well as emergent engagement of the hospital ethics committee, should the surgeon not feel comfortable with performing the procedure.³³ A fully informed patient and family, however, may still elect to proceed with an unwarranted operation; our risk score is best suited for use as an evidence-based adjunct to the surgeon, as support that an operation may be futile.³⁴ This study has limitations including the lack of external validation, use of a single-center cohort and the drawbacks inherent in the accuracy and bias of data collected retrospectively rather than prospectively. Introduction of prospectively acquired data into an ANN would yield an improved predictive model. Next, there is the necessity for exclusion of patients in the various models. While sample sizes in many rAAA outcome analyses are often restricted, it nonetheless represents a limitation in our study with respect to the strength of evidence of association between preoperative variables and in-hospital mortality, particularly in multivariate analysis. Though no difference in mortality rate was observed, we also had a relatively small EVAR cohort. Finally, the ANN model uses a complex algorithm which does not output a relative weight given to a specific variable, as opposed to a multiple logistic regression. Therefore, the ANN algorithm represents a “black box” that does not provide the user with insight into its prognostication.³⁵ It is not recommended that clinical judgment be substituted for an ANN-based risk score, rather, it is demonstrated that ANN models may function as a discriminant adjunct to the vascular surgeon in making the determination as to the suitability of an operative candidate in the context of rAAA.

CONCLUSIONS

For this study, we used our institutional database to determine those factors associated with in-hospital mortality in rAAA patients. An emerging paradigm in outcomes research, the ANN was used to model the complex relationships among age, CPR, LOC and shock. This allowed the development of an internally validated, user-friendly aid for risk assessment. As this ANN model reliably predicted the presence of in-hospital mortality, it may function as an evidence-based adjunct to the vascular surgeon’s clinical judgment in estimation of mortality of a rAAA patient, on the basis of easily obtained preoperative factors.