Endpoint comparison for bone mineral density measurements in North Central Cancer Treatment Group cancer clinical trials N02C1 and N03CC (Alliance)

Abstract

Summary

Bone mineral density (BMD) measurement can vary depending upon anatomical site, machine, and normative values used. This analysis compared different BMD endpoints in two clinical trials. Trial results differed across endpoints. Future clinical trials should consider inclusion of multiple endpoints in sensitivity analysis to ensure sound overall study conclusions.

Introduction

Methodological issues hamper efficacy assessment of osteoporosis prevention agents in cancer survivors. Osteoporosis diagnosis can vary depending upon which bone mineral density (BMD) anatomical site and machine is used and which set of normative values are applied. This analysis compared different endpoints for osteoporosis treatment efficacy assessment in two clinical studies.

Methods

Data from North Central Cancer Treatment Group phase III clinical trials N02C1 and N03CC (Alliance) were employed involving 774 patients each comparing two treatments for osteoporosis prevention. Endpoints for three anatomical sites included raw BMD score (RawBMD); raw machine-based, sample-standardized, and reference population-standardized T scores (RawT, TSamp, TRef); and standard normal percentile corresponding to the reference population-standardized T score (TPerc). For each, treatment arm comparison was carried out using three statistical tests using change and percentage change from baseline (CB, %CB) at 1 year.

Results

Baseline correlations among endpoints ranged from 0.79 to 1.00. RawBMD and TPerc produced more statistically significant results (14 and 19 each out of 36 tests) compared to RawT (11/36), TSamp (8/36), and TRef (7/36). Spine produced the most statistically significant results (26/60) relative to femoral neck (20/60) and total hip (13/60). Lastly, CB resulted in 44 statistically significant results out of 90 tests, whereas %CB resulted in only 15 significant results.

Conclusions

Treatment comparisons and interpretations were different across endpoints and anatomical sites. Transforming via sample statistics provided similar results as transforming via reference or machine-based norms. However, RawBMD and TPerc may be more sensitive to change as clinical trial endpoints.

Introduction

Osteoporosis is a significant public health problem due to its impact on morbidity and mortality in the elderly [1–3]. In recent years, there have been numerous attempts to discover and validate treatments for the prevention and amelioration of osteoporosis [4]. Most recently, a concern was raised about the potential increase in fractures resulting from antiosteoporosis treatments in breast cancer patients that turned out to be untrue based on a large meta-analysis [5]. The North Central Cancer Treatment Group (NCCTG) completed clinical trials N02C1 and N03CC (Alliance) intended to assess interventions to prevent and/or treat osteoporosis in cancer patients.

Alongside these clinical investigations, there have been challenges and advances in defining and optimizing ways to assess the presence and severity of osteoporosis. Little foundational work has been performed to assess the relative merit of alternative measures for osteoporosis. This spurred the present investigation regarding how to best approach the analysis of these studies in a consistent manner. This manuscript reports results of a comparison of alternative computational approaches for bone mineral density (BMD) endpoints using data from N02C1 and N03CC. We propose a new computational method that may have some advantages over existing methods for assessing BMD in clinical trials.

The present gold standard for diagnosing osteoporosis is based on the World Health Organization (WHO) and International Society for Clinical Densitometry (ISCD) criteria [6]. In an attempt to attain some consistency across populations and sites, the identification of osteoporosis is based on whether an individual’s BMD is sufficiently low relative to what it would be for a young healthy individual [7]. There is consensus that a T score below −2.5 (i.e., a person whose BMD is 2.5 standard deviations below mean BMD for a healthy individual) indicates osteoporosis [8]. AT score below −1 but not below −2.5 is indicative of osteopenia [9].

There are numerous sources of measurement error and considerable inconsistency in the way that BMD data are presented and analyzed in the literature [10]. The diagnosis of osteoporosis for an individual can vary depending upon which BMD site is used [11–16], which machine is used for the assessment, and which set of normative values are applied [17].

The T score is an often-used value intended to standardize BMD scores across population variability. One problem in the application of this value is defining which population should be used as the reference for calculation of the T scores. Table 1 presents a variety of reference data for BMD achieved through a local reference population or the machine manufacturers’ values. The variety, both across machine and anatomical site, is considerable. The reference values hence can be different depending upon the anchor distribution used. This is consistent with other aspects of measurement such as assessing clinical significance of patient-reported outcomes [18]. Using WHO data versus other normative data can produce widely discrepant estimates for the prevalence of osteoporosis (a T score below −2.5) [19]. Studies assessing wide variety of endpoints for BMD measures in premenopausal and postmenopausal women show marked variability depending upon the endpoint itself and even within the same endpoint for different reference populations [20]. Hence, there is a need for examination of the relative impact of alternative BMD endpoints on the results of clinical studies. The present study was intended to address this knowledge gap by carrying out a statistical comparison of alternative post hoc computational approaches to BMD measurement.

Table 1.

Mean (standard deviation) for bone mineral density parameters from different machines used for the calculation of T scores

Bone mineral density parameter	Local reference population	Manufacturers’ values
Hologic Sahara speed of sound (m/s)	1560.7 (25.1)	not available
Hologic UBA575+ speed of sound (m/s)	1507.5 (6.6)	not available
Osteometer DTUone speed of sound (m/s)	1553.5 (8.4)	not available
Hologic Sahara heel (g/m2)	0.561 (0.10)	0.537 (0.08)
Dual x-ray absorptiometry lumbar spine (g/m2)	1.068 (0.12)	1.047 (0.11)
Dual x-ray absorptiometry femoral hip (g/m2)	0.892 (0.10)	0.895 (0.10)
Dual x-ray absorptiometry total hip (g/m2)	0.988 (0.10)	0.975 (0.12)

From [10]

Methods

Patient population

We used data from two NCCTG (Alliance) clinical trials, namely N02C1 [21] and N03CC [22]. N02C1 was a phase III randomized, placebo-controlled, double-blind trial of risedronate for prevention of bone loss in premenopausal women undergoing chemotherapy for primary breast carcinoma. N03CC was a randomized, controlled, open-label trial of empiric prophylactic versus delayed use of zoledronic acid for prevention of bone loss in post-menopausal women with breast cancer initiating therapy with letrozole after tamoxifen. Study design, monitoring, treatment, and eligibility criteria for each clinical trial are presented elsewhere [21, 22]. Each participant across studies signed an IRB-approved, protocol-specific informed consent in accordance with federal and institutional guidelines.

Bone mineral density measurements

For these studies, the total lumbar spine was used as the anatomical site for the primary BMD endpoint; however, both protocols specified multiple other anatomical sites within secondary endpoints. The primary endpoint in N02C1 was change from baseline at 1 year post-randomization in spine BMD, whereas N03CC employed percentage change from baseline. Both protocols employed a comparison between arms using a two-sample t test.

In these studies, the amount of data acquired per subject varied, ranging from a single value to a series of BMD measures for various anatomical sites. There were numerous possible endpoints that could be used per anatomical site as the basis for analysis:

1. The observed raw BMD values (RawBMD)

2. The observed T scores (using a machine-based reference sample; RawT)

3. The transformed T scores using the sample mean and sample standard deviation (TSamp)

4. The transformed T scores using the mean and standard deviation from a reference population such as the National Health and Nutrition Examination Survey (NHANES) data [23], the WHO [24], or from the UK local reference population [10, 17] (TRef)

5. The standard normal percentile corresponding to the reference population-standardized [10] T score (TPerc)

RawBMD and RawT are bone mineral density values as reported on the case report forms, which are presumably the values reported via the bone mineral density measurement clinical findings report. To compute TSamp, we must first compute the sample mean and sample standard deviation of the baseline RawBMD values. Then, TSamp is computed by subtracting the baseline sample mean from each RawBMD value and dividing by the baseline sample standard deviation. For example, for N02C1, the sample mean and sample standard deviation of the baseline spine RawBMD values was 1.21 and 0.16 (Table 2), respectively. So, the spine TSamp value would be computed for a patient with a spine RawBMD score of 1.13 at a given time point as (1.13–1.21)/0.16 or −0.50. TRef is similarly computed; however, a mean and standard deviation from a reference population is used instead of the baseline RawBMD sample mean and baseline RawBMD sample standard deviation. For example, using a reference population spine mean and standard deviation of 1.047 and 0.11 (Table 1), respectively, the spine TRef value would be computed for a patient with a spine RawBMD score of 1.13 at a given time point as (1.13–1.047)/0.11 or 0.75. Finally, TPerc is computed as the probability that an observation from the standard normal distribution is less than or equal to TRef. For the example in which a patient’s TRef value was 0.75 at a given time point, TPerc is computed as P(Z≤0.75)=0.77.

Table 2.

Mean and standard deviation (SD) for five spine bone mineral density endpoints at baseline in two North Central Cancer Treatment Group studies (N02C1 and N03CC)

Endpoint	N02C1 N=204		N03CC N=505
	Mean	SD	Mean	SD
RawBMD	1.21	0.16	1.10	0.16
RawT	0.46	1.19	−0.17	1.18
TSamp	0.00	1.00	0.00	1.00
TRef	1.51	1.44	0.50	1.49
TPerc	0.80	0.26	0.59	0.32

All of the above endpoints, except for the percentile, which is a new idea, have been used in previous studies [8–10, 17, 20, 25–27]. However, there has been no discussion in the literature regarding the relative clinical significance of these various endpoints other than to indicate that one might make mistaken clinical conclusions depending upon which endpoint is used. It is unclear what each of these endpoints really means in terms of impact on data interpretation. All five endpoints have substantial inherent variability and measurement error. Note that TSamp and TRef are monotonic or order-preserving transformations in addition to being linear transformations of RawBMD, resulting in identical results when comparing absolute (but not percentage) change from baseline between groups using a Wilcoxon rank-sum test, a two-sample t test, or analysis of covariance (ANCOVA) for these three endpoints. These analyses are described in the following section. Data collection and statistical analyses were conducted by the Alliance Statistics and Data Center. All analyses were based on the frozen study databases reported in the primary manuscripts [21, 22].

Statistical analysis

Studies to date have been powered to detect various effect sizes, most often based on a percentage change using a Wilcoxon rank-sum test [23], two-sample t test [8], or ANCOVA procedure [26] comparing groups. The ANCOVA would typically include the corresponding baseline BMD endpoint value as a covariate.

For each of the five endpoints, change from baseline (CB) and percentage change from baseline (%CB) were calculated using all available data for eligible patients for three anatomical sites: spine (LTotal), femoral neck (femur neck), and total hip (femur total). Student’s two-sample t test [28], Wilcoxon rank-sum test [29], and ANCOVA (corresponding baseline BMD endpoint value used as a covariate) [30] were used to compare treatment arms for each endpoint. Each clinical trial was analyzed separately. P values<0.05 were considered statistically significant throughout (i.e., as if the given analysis represented the primary comparison for the study).

To compare and contrast the various measures of BMD, we also calculated summary statistics and Pearson correlations [28] among the five endpoints at baseline.

Results

Details of the study populations are presented elsewhere [21, 22] but are summarized here. In total, 204 and 505 patients provided data for this analysis from N02C1 and N03CC, respectively. Patients ranged in age from 36 to 88 with a median age of 59 years. Ninety-seven percent of the patients were Caucasians.

Correlations among the five alternative osteoporosis endpoints at baseline ranged from 0.79 to 1.00 for each anatomical site within each study. RawBMD, TSamp, and TRef are perfectly correlated (i.e., are linear transformations of each other). Hence, all five endpoints are strongly correlated and some are pseudo-redundant psychometrically in terms of correlation. Table 2 provides descriptive statistics at baseline for each endpoint for spine bone mineral density.

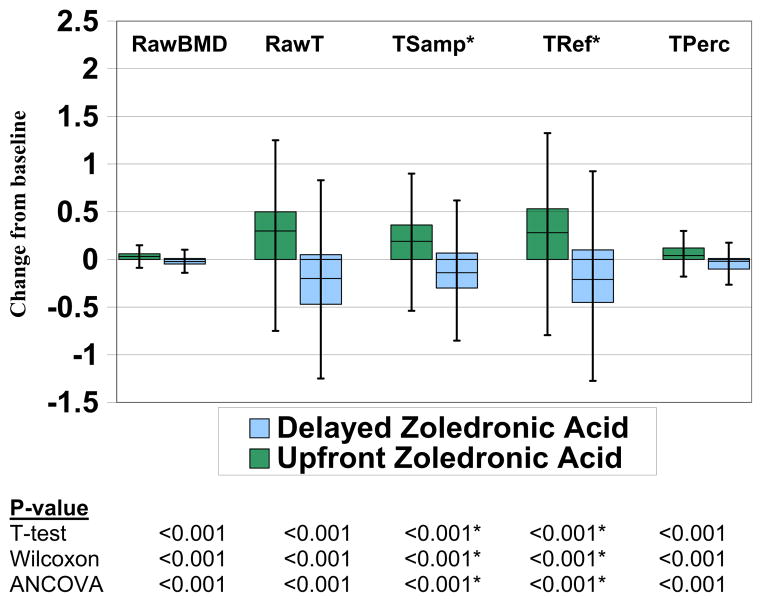
The primary goal of this analysis was to see if the choice of endpoint would change the study outcome. Figures 1 and 2 present side-by-side boxplots of the five different endpoints based on change from baseline using spine measurements by treatment arm for each of the two studies. The statistical significance of this comparison differed depending upon the endpoint and test used within N02C1, but results were highly statistically significant for all endpoints and tests in N03CC.

Fig. 1.

Boxplots showing the distribution of spine bone mineral density change from baseline endpoints by treatment arm for N02C1

* TSamp and TRef are linear transformations of RawBMD, resulting in identical results when comparing absolute (but not percentage) change from baseline between groups using a Wilcoxon rank-sum test, a two-sample t-test, or analysis of covariance (ANCOVA).

Fig. 2.

Boxplots showing the distribution of spine bone mineral density change from baseline endpoints by treatment arm for N03CC

* TSamp and TRef are linear transformations of RawBMD, resulting in identical results when comparing absolute (but not percentage) change from baseline between groups using a Wilcoxon rank-sum test, a two-sample t-test, or analysis of covariance (ANCOVA).

We then compared the BMD analysis results when using different anatomical sites for generation of the BMD data (Table 3). We performed three statistical tests for each cell in the table comparing treatment arms (two-sample t test, Wilcoxon, ANCOVA). Among the five endpoints, RawT, TSamp, and TRef had 11, 8, and 7 statistically significant results out of 36 tests, respectively. RawBMD and TPerc produced the most statistically significant results, 14 and 19, respectively. Across the three anatomical sites, spine, femoral neck, and total hip had 26, 20, and 13 statistically significant results out of 60 tests, respectively. Lastly, in comparing CB to %CB, use of CB resulted in 44 statistically significant results out of 90 tests, whereas %CB results in only 15 significant results.

Table 3.

Number of significant statistical tests obtained from three different statistical procedures for each combination of anatomical site, endpoint, and clinical trial (N02C1 and N03CC)

Endpoint	N02C1							N03CC							Total
	Change from Baseline			% Change from Baseline			Total	Change from Baseline			% Change from Baseline			Total
	Spine	Fem. neck	Total hip	Spine	Fem. neck	Total hip		Spine	Fem. neck	Total hip	Spine	Fem. neck	Total hip
RawBMD	0	0	0	0	0	0	0	3	3	1	3	3	1	14	14
RawT	1	0	0	0	0	0	1	3	3	3	1	0	0	10	11
TSamp	0*	0*	0*	0	0	0	0	3*	3*	1*	1	0	0	8	8
TRef	0*	0*	0*	0	0	0	0	3*	3*	1*	0	0	0	7	7
TPerc	3	1	0	1	0	0	5	3	3	3	1	1	3	14	19
Total	4/15	1/15	0/15	1/15	0/15	0/15	6/90	15/15	15/15	9/15	6/15	4/15	4/15	53/90	59/180

^*TSamp and TRef are linear transformations of RawBMD, resulting in identical results when comparing absolute (but not percentage) change from baseline between groups using a Wilcoxon rank-sum test, a two-sample t test, or analysis of covariance (ANCOVA)

For N02C1 (reported as a negative study), we observed six statistically significant results overall out of 90 tests, with statistically significant results being limited to TPerc (5/18 tests) and RawT (1/18 tests). All other statistical results were non-significant. These statistically significant results were also limited to spine (5/30 tests) and femoral neck (1/30 tests) sites, with no differences observed for the total hip site regardless of endpoint or method. Percentage change from baseline resulted in only one statistically significant result (out of 45 tests).

For N03CC, despite reporting overwhelmingly positive results in the primary report, not all approaches produced a significant result. Considering only change from baseline, non-significant results for three of the five endpoints were noted when the total hip values were used, whereas the BMD results for spine and femoral neck were all significant. Percentage change from baseline indicated fewer statistically significant differences than for raw change from baseline (14 versus 39 each out of 45 tests). Consistent with N02C1, RawBMD, and TPerc provided the most statistically significant results (14/18 tests each).

Discussion

In this study, we examined the impact of five methods for calculating BMD endpoints on the likelihood of finding statistically significant differences between randomized treatment groups in patients with cancer. One of the main findings was that among the five endpoints, machine-based T score (RawT), sample-adjusted T score (TSamp), and reference population-adjusted T score (TRef) had 11, 8, and 7 statistically significant results out of 36 tests, respectively, whereas RawBMD and percentile T score (TPerc) produced 14 and 19 statistically significant results, respectively. Thus, in this case, the treatment comparisons had different conclusions depending upon the endpoint selected. Reference-based endpoints (RawT, TSamp, and TRef) aid in interpretation within the given study because values are reported in terms of standard deviations above or below a population mean. Transforming via sample statistics provided similar results as transforming via reference or machine-based norms. However, TSamp lacks the ability to be interpreted relative to an external reference population (or across trials). Specifically, baseline values appear similarly distributed between the two clinical trials in this report based on TSamp, whereas RawT and TRef properly show that patients on N03CC had lower baseline BMD relative to patients on N02C1. The new approach (TPerc) may be more sensitive to change and has the added benefit of being readily interpretable as a percentile.

In terms of anatomical site, spine, femoral neck, and total hip had 26, 20, and 13 statistically significant results across the two trials. The variability in results highlights that study conclusions could differ depending on the chosen anatomical site, consistent with recent studies that indicated using various measures of osteoporosis could cause different conclusions to be drawn [23].

Statistical testing based on change from baseline resulted in more statistically significant results relative to percentage change from baseline (39 versus 14). Percentage change from baseline endpoints generally suffer from lower statistical power relative to their respective change from baseline endpoint assuming normally distributed baseline and post-baseline scores with a range of correlations, do not protect from bias in the presence of baseline imbalances in the endpoint, and potentially violate normality assumptions of parametric statistical tests (e.g., t tests and ANCOVA) [31]. Percentage change from baseline endpoints is often employed nonetheless as endpoints likely due to the ease in interpretation of point estimates. While possible to construct non-normal data scenarios (i.e., data scenarios not investigated via simulation in the work of Vickers [31]) in which power may be similar or slightly improved by using percent change from baseline relative to change from baseline, results from the current report using observed clinical trial data revealed that statistical analysis based on change from baseline endpoints led to a greater number of statistically significant results compared to percent change from baseline. As suggested by Vickers [31], statistical testing based on change from baseline endpoints can be supplemented with percentage change point estimates (computed from mean baseline and follow-up scores) if percentage type endpoints are desired for reporting purposes.

We have focused our findings on selecting among endpoints, and less so on selecting among statistical tests (in this case between the non-parametric Wilcoxon rank-sum test and a parametric two-sample t test or ANCOVA approach). The parametric two-sample t test will provide better power than the Wilcoxon rank-sum test under the assumption that data are normally distributed. An ANCOVA approach provides an additional gain in power over the two-sample t test if the selected covariate is correlated with the endpoint being compared. However, despite the loss of information in reducing data to their ranks, the Wilcoxon rank-sum test is only marginally less powerful than the two-sample t test under the assumption of normality, but often more powerful than the two-sample t test when the normality assumption fails [32] perhaps making the Wilcoxon rank-sum test the recommended choice to accommodate a wider range of possible data scenarios. All in all, selection of an appropriate test among the tests employed here as well as many other possible hypothesis testing procedures should always be based on the study design, expected distributional properties of the data, and ideally, on previous data exploration.

While we have identified that TPerc and analysis based on change from baseline are the most sensitive approaches, further study is needed to determine if this is desirable. We have provided direct empirical evidence that different answers regarding treatment efficacy are possible from different measurement approaches so caution in interpretation of study results is indicated. Researchers should consider calculating these measures in future trials as sensitivity analyses. Caution in conclusions based on the primary endpoint is indicated when sensitivity analyses show lack of consistency across endpoints. Researchers should also clearly report how endpoints were calculated in all publications due to the possible variability of results across endpoints.

This study also uncovered logistical hurdles that became lessons learned for future research. Analysis of data from BMD scanners at clinics without careful planning and forethought may lead to errors. In theory, it would be optimal to have the same scanner, same operator, same reference population, and the same site for providing BMD assessment for a given clinical trial, though this approach is impractical for most clinical studies, particularly multi-center studies such as the two clinical trials used in the current analysis. However, technical specification of the BMD assessment (e.g., clear definition of the anatomical sites to be assessed) in the protocol and well-defined data fields on case report forms can contribute to improved standardization. Multiple post hoc statistical techniques cannot overcome the inherent variability of the measurement process due to a lack of standardization.

Our study has limitations. First, as previously mentioned, our criterion for comparing endpoints and anatomical sites was based on the number of statistically significant results (i.e., sensitivity). This may not be an ideal strategy. However, our purpose in this analysis was to highlight that the choice of endpoint can impact study conclusions. A second limitation is that the endpoint and analyses in this report did not take into account variability by center, scanner, or other sources of known variation in BMD assessment. As these were both multi-center trials, it became apparent over the courses of these trials that BMD was not measured uniformly across sites. Possible sources of variation among centers included different machines, reference values, clinical report formats, and definitions of anatomical sites. Careful consideration of the data processes is vital to the science of the study. Standardization across centers may produce less variability across the endpoints examined in this report.

In conclusion, the five osteoporosis endpoint measures examined in this study are not necessarily the same and results differ across the anatomical sites tested. TPerc seems to be the most sensitive among the alternative statistical approaches. This new measure might be more practical than others because it is easily interpretable. Whether or not the seeming superior sensitivity is merely due to an increased type I error rate, however, is an open question in need of further study. Our ultimate recommendation is for future clinical trials to use multiple endpoints by way of a sensitivity analysis to ensure the credibility and veracity of overall study conclusions.