Abstract
Neural decoding has played a key role in recent advances in brain–machine interfaces (BMIs) by converting brain signals into control commands to drive external devices such as robotic limbs or computer cursors. A number of practical algorithms including the well-known linear regression and Kalman filter models have been used to predict continuous movement in a real-time online context using recordings from a chronically implanted multielectrode microarray in the motor cortex. Though effective, those models were often based on a strong assumption that the neural signal sequence is a stationary process. Recent work, however, indicates that the motor system significantly varies over time. To characterize the dynamic relationship between neural signals and hand kinematics, here we develop an adaptive approach for each of the linear regression and Kalman filter methods. Experimental results show that the new adaptive algorithms generate more accurate decoding than the nonadaptive algorithms. To make the new algorithms feasible in an online situation, we further develop a recursive update approach and theoretically demonstrate its superior efficiency. In particular, the adaptive Kalman filter is shown to be more accurate and efficient. We also test the new methods in a simulated BMI experiment where the true hand motion is not known. The successful performance suggests these methods could be useful decoding algorithms for practical applications.
Keywords: Adaptive models, brain–machine interfaces (BMIs), motor cortex, nonstationarity, real-time neural decoding
I. INTRODUCTION
EMERGING as a highly interdisciplinary field in less than a decade, a great deal of progress has been made in cortically controlled brain–machine interfaces (BMIs). The primary goal of this field is to restore motor function in the severely disabled by building direct interfaces between brain and external devices such as robotic limbs or computer displays [1]–[3]. Recent advances on developing BMIs have demonstrated the feasibility of direct neural control using implanted electrodes in non-human primates [4]–[7] as well as in humans [8]. These results are based on a variety of linear and nonlinear decoding methods that predict motor parameters, such as hand movement direction or hand position, from population neuronal activity in the motor cortex and other brain areas. These methods can be categorized into two groups. The first group decodes discrete parameters such as movement direction and it includes maximum likelihood [9], [10] and maximum a posteriori [11] methods. The second group decodes continuous parameters such as position and velocity. There are significantly more methods in this group which include population vectors [6], [12], multiple linear regression [4], [5], the Kalman filter and it variants [13]–[15], particle filters [16], [17], and nonlinear neural network models [7], [18]. Except for particle filters, these continuous decoding methods perform in real-time and can be directly used in an online BMI environment. In particular, both the linear regression and Kalman filter models are preferred due to their simplicity, efficiency, and accuracy [4], [5], [13], [15], [19].
All those methods, however, are often based on a strong assumption that the neural signal sequence is a stationary process, and the prediction is performed under a common cross-validation framework; that is, a certain initial period of recording is taken as training data, the parameters of the model are learned, and then a prediction is made on test data that was recorded in a later period. However, as we observed during the experiments, the research subjects may be engaged in the task with a variable degree of attention. They often have a strong motivation to behave in the initial stage, but then gradually lose interest and become reluctant to move in the later period of the experiment. A recent study by Kim et al. [20] addressed this issue by showing that overall neural activity in motor cortex significantly varies over time and therefore should not be regarded as a stationary process. For example, the mean firing rates of some neurons keep increasing over time whereas the kinematic parameters are fairly consistent. This indicates that as time evolves, the model fitted by the fixed training data in the initial period will become more and more inappropriate in describing the dynamic relationship between neuronal activity in the brain and the movement parameters. To better characterize the relationship between motor behavior and the neural signals in motor cortex, it is critical to find an adaptive model which could appropriately characterize such variability over time.
Several recent studies addressed the nonstationarity of neural signals in various frameworks. Helms Tillery et al. added a supervised learning method which modified the parameters in the population vector [21]. They found the new method significantly improved brain-controlled cursor movement. Gage et al. examined naive coadaptive cortical control in rat subjects using a Kalman filter where parameters in the model were adaptively updated over time [22]. Kim et al. proposed an estimation approach under multiinput multioutput (MIMO) neural network systems [23]. The method successfully tracked the linear relationship between neural activity and hand kinematics. Eden et al. provided an adaptive point process filtering method using a state-space model [24]. They simulated a neuronal ensemble to examine the dynamic representation of movement information and found that the algorithm was able to accurately estimate the hand direction [25].
Focusing on accuracy and efficiency, here we propose an adaptive approach to address the nonstationarity by updating the model when new observations are available. In contrast to Eden et al. where they built the model on the spike trains, we use a rate code to represent the dynamic relationship between neural activity and hand kinematics. We develop the adaptive methods based on commonly used linear regression and Kalman filter models as they have been preferred in the latest online human neural prosthetic work [8], [13]. To demonstrate the effectiveness of the new approach, we need to answer two questions. 1) Can this adaptive approach improve the decoding accuracy? 2) Is this approach computationally efficient? Here, we update the training data over time and fit the parameters in the new model by the least squares [9] and the maximum likelihood estimate [15]. In particular, the procedure for the adaptive Kalman filter is similar to that by Gage et al. [22], while the parameters are updated in a more efficient way. The decoding accuracy of each adaptive approach (linear regression or Kalman filter) is compared to its static version using experimental recordings from two macaque monkeys. To address the second question, we further develop a recursive approach which makes the estimation more efficient for each adaptive method. Both theoretical and practical costs of the recursive approaches are also compared to the nonrecursive methods.
II. METHODS
A. Experimental Method
Electrophysiological Recording
The neural data used here were previously recorded and have been described elsewhere [26]. Briefly, silicon microelectrode arrays containing 100 platinized-tip electrodes (1.0 mm electrode length; 400 microns interelectrode separation; Cyberkinetics Inc., Salt Lake City, UT) were implanted in the arm area of primary motor cortex (MI) in two juvenile male macaque monkeys (Macaca mulatta). Signals were filtered, amplified (gain, 5000) and recorded digitally (14-bit) at 30 kHz per channel using a Cerebus acquisition system (Cyberkinetics Neurotechnology Systems, Inc., Foxborough, MA). Only waveforms (1.6 ms in duration) that crossed a threshold were stored and spike-sorted using Offline Sorter (Plexon Inc., Dallas, TX). Single units were manually extracted by the contours and templates methods. Interspike interval histograms were computed to verify single-unit isolation by ensuring that less than 0.05% of waveforms possessed an inter-spike interval less than 1.6 ms. The number of units in each electrode varied from one to five. One data set was collected and analyzed for each monkey where the number of distinct units was 124 for the first monkey, and 125 for the second one.
Task
The monkeys were operantly trained to perform a random target pursuit (RTP) task by moving a cursor to targets via contralateral arm movements. The cursor and a sequence of seven targets (target size: 1 cm × 1 cm) appeared on a horizontal projection surface. At any one time, a single target appeared at a random location in the workspace, and the monkey was required to reach it within 2 s. As soon as the cursor reached the target, the target disappeared and a new target appeared in a new, pseudo-random location. After reaching the seventh target, the monkey was rewarded with a drop of water or juice. A new set of seven random targets was presented on each trial. The majority of trials were approximately 4–5 s in duration. In data set one, the first monkey successfully completed 550 trials, and in data set two, the second monkey completed 400 trials. We deliberately arranged more targets in the boundary area of the rectangle workspace so that sufficient hand position data over the full working space were collected. The monkey’s arm rested on cushioned arm troughs secured to links of a two-joint robotic arm (KINARM system, see [27]) underneath the projection surface. The shoulder joint was abducted 90° such that shoulder and elbow flexion and extension movements were made in the horizontal plane. The robotic arm contained two motor encoders that directly measured the shoulder and elbow joint angles of the monkey’s arm at a sampling rate of 500 Hz. The monkey’s hand positions were calculated and recorded using the forward kinematics equations [27]. All of the surgical and behavioral procedures were approved by the University of Chicago’s Institutional Animal Care and Use Committee (IACUC) and conform to the principles outlined in the Guide for the Care and Use of Laboratory Animals (NIH publication no. 86-23, revised 1985).
Analysis
The firing rates of single cells were computed by counting the number of spikes within the previous 50-ms time window. To match time scales, the hand position were down-sampled every 50 ms and from this we computed velocity and acceleration using simple differencing. Recent studies, including ours, indicated that the averaged optimal latency between firing activity in MI and hand movement is around 100 ms [15], [26], [28], [29]. Therefore, in all our analysis we compared the neural activity in a 50-ms bin with the instantaneous kinematics (position, velocity, and acceleration) of the arm measured 100 ms later (i.e., a 2 time bin delay). Note that the hand motions in this task were richer than those in the more common stereotyped tasks (e.g. “center-out” task in [6]) in that the motions spanned a full range of directions, positions, and speeds (see [29] for details).
For neural coding in motor cortex, we examined the relations between firing activity and hand kinematics. We found that the averaged hand positions (averaged within each trial) were very consistent from trial to trial, whereas the averaged firing rates of a subpopulation (around 50%) of neurons significantly varied over time (see Fig. 1 for two example neurons). This suggests it would be inappropriate to describe the neural signals as a stationary process. In this paper, we address this dynamic relation by developing adaptive models based on the linear regression and Kalman filter.
Fig. 1.
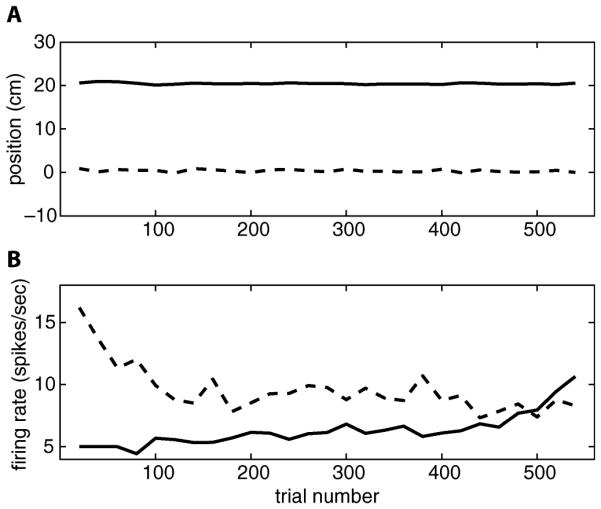
Averaged hand positions and firing rates of two example neurons in dataset 1.(a) Smoothed averaged x-positions (dashed line) and y-positions (solid line) over all trials. (b) Smoothed averaged firing rates of neuron 17 (dashed line) and neuron 41 (solid line) over all trials.
B. Statistical Methods
Both linear regression and Kalman filter are well-known estimation methods and their implementations are standard. They have been successfully used in decoding neural signals for both offline and online experiments. Our focus here is on the development of a real-time adaptive version of these methods where the model is updated when new observations are available and the decoding is performed using each updated model. Note that in practice it is not necessary to update the model at each time step as that typically has little effect on the model. The effect would be more significant if we update the model with every new trial.
1) Adaptive Linear Regression
The linear regression method has been used in the decoding of neural signals in motor cortex, and particularly in closed-loop neural control tasks [4], [5], [7], [8]. It reconstructs hand position as a linear combination of the firing rates over some fixed time period; that is
where xk,i is the x-position (or, equivalently, the y-position) in the ith trial at time tk = kΔt(Δt = 50 ms), i = 1, 2, …, T, k = N, N + 1, …. a is a constant offset, is the firing rate of neuron c in the ith trial at time tk–j, and are the filter coefficients. C denotes the number of neurons in the data, and T denotes the number of trials. In our experiments, we take N = 20 which means the hand position is determined from firing data over 1 s which is an appropriate history period [15].
The coefficients are the parameters in the linear model and can be learned from training data using a simple least squares technique [30]. To simplify the notation, we denote the coefficients as a matrix , where the 1 + CN rows correspond to coefficients in the linear equation and the two columns correspond to x- and y-positions. Let K1, K2, …, KT represent the numbers of time bins in the T trials, respectively. For i = M, M + 1,…, T, we use the most recent M trials as the training data. That is, the training data are from trial i − M + 1 to i. fi can be estimated by minimizing the cost function
| (1) |
whose solution is
| (2) |
where
in which and rj and pj (j = i − M + 1, …, i)are defined as
and
Calculating the computational cost of each matrix operation, we have that the total cost of (2) is O(Σj(Kj − N + 1)(1 + CN)2)+O((1 + CN)3)+O(Σj(Kj − N + 1)(1 + CN)) + O((1 + CN)2). In general, the number of time bins in the data, ΣjKj, should have larger magnitude than the number of neurons C, the history steps N, and their product CN. Therefore the cost can be simplified to O(ΣjKj(1 + CN)2). In many practical situations such as the two datasets in this study, all trials have similar time length. That is, Kj’s are approximately equal to a constant, K. Therefore, the cost can be further simplified to O(MK(1 + CN)2).
In practical neural data, the number of recorded neurons varies from tens to over a hundred, and the filter length N is often chosen from 10 to 30 (0.5–1.5 s). In the two collected datasets, the number of bins in each trial is around 100 (5 s). We take M = 80 (in dataset 1) and 110 (in dataset 2) to make sure there is enough training data to fit the parameters in the model. To facilitate the comparison of computational cost, we list the typical order of each parameter in Table I.
TABLE I.
Typical Order of Each Parameter
| Parameter | Order |
|---|---|
| K: Number of bins in each trial | 102 |
| M: Number of trials in the training data | 10 – 102 |
| C: Number of neurons | 10 – 102 |
| N: Number of history trials in the linear regression | 10 |
Update From Trial i to Trial i + 1
To appropriately represent the temporal variability of neural activity we update the encoding model when new observations are available. Such update can properly describe the dynamic relationship between neural activity and kinematics. The procedure above uses a training set of the M latest trials to estimate fi. Here, we study the update at the new trial i + 1. To make the new model describe the current firing pattern of neural signals, we keep using the latest measurements of trials to estimate the linear model.
If we update the model directly using (2), the computational cost could be expensive. In order to make the adaptive method more favorable in neural decoding, we would desire the update to be conducted in a more efficient way. In this paper, we propose the following recursive approach to update the linear model, where we assume that the old encoding model is already obtained using training data from trial i − M + 1 to trial i. Let . Then the parameters fi+1 can be computed by
| (3) |
Equation (3) (assuming Ei+1 and Fi+1 are known) only involves inversion and multiplication of two matrices with order (1 + CN), and therefore its computational cost is O((1 + CN)3).
As we have shown in the computation of above, the cost of computing Ei+1 and Fi+1 is O(MK(1 + CN)2) if they are directly calculated by Ri+1 and Pi+1. However, based on the definition of Ei+1 and Fi+1, they can be estimated by a recursive scheme; that is
| (4) |
and
| (5) |
Equations (4) and (5) involve elementary operations of a few matrices with order (1 + CN), and therefore the computational cost is . As the cost in (3) is only O((1 + CN3), the total cost to compute the filter coefficients is O((1 + CN)3). This is often more efficient than the nonrecursive computing cost, O(MK(1 + CN)2) (see Table I).
Recursive Least Squares
Note that the solution in (3) needs to calculate the inverse of a large matrix, Ei+1. Such a calculation is inefficient and often ill-conditioned. In adaptive filter theory, many stochastic-gradient methods, such as the least mean squares (LMS) and recursive least squares (RLS), were introduced to avoid this inverse calculation by various recursive techniques [31]. Here, we examine the performance of the RLS method as it also obtains the exact solution to (1) (we do not examine the LMS algorithm as it only finds an approximation).
The standard RLS algorithm recursively updates the linear model using a new sample point at each time step [32]. However, the stepwise update shows very slow variation over time. In the current framework, the model is updated by adding a new observed trial and removing the trial in the most distant past. Here, we slightly modify the RLS to a trial-wise update as follows.
Applying the matrix inversion formula, (A + BCD)−1 = A−1 −A−1B(C−1 + DA−1B)−1D−1, to (4), the inverse of Ei+1 can be recursively estimated as
| (6) |
Computing the cost of all matrix calculations in (3), (5), and (6), we find the total is . As CN is often larger than K (see Table I), this cost is more efficient than that in the simple recursive method, where the cost is O((1 + CN)3). However, we note that the improvement is only marginal. As the RLS method involves more matrix calculations, its efficiency in practical data may not always be superior.
2) Adaptive Kalman Filter
The Kalman filter is another efficient decoding system in motor cortex, with recent applications to human neural prosthetics [13]. In general, decoding involves estimating the state of the hand at the current instant in time; i.e. representing x-position, y-position, x-velocity, y-velocity, x-acceleration, and y-acceleration in trial i at time tk. The Kalman filter model assumes the state is linearly related to the observations which here represents a C × 1 vector containing the firing rates in trial i at time tk for C observed neurons; the state is linearly related to itself over time as well. Such assumptions can be described in the following two equations:
| (7) |
| (8) |
where , are the linear coefficient matrices. The noise terms qk,i, wk,i are assumed zero mean and normally distributed, i.e. . These equations define a linear Gaussian model from which the state and its uncertainty can be estimated recursively using the Kalman filter algorithm [15].
The parameters Ai, Hi, Wi, Qi in the Kalman filter equations can be estimated from training data using the maximum likelihood estimation. As in the linear regression method, the training data are chosen from trial i − M + 1 to trial i. Let Zi and Xi denote all firing rates and hand kinematics (position, velocity, acceleration) in the training data, respectively. We seek the coefficient matrices that maximize the joint distribution p(Zi, Xi), that is
The above maximization has closed-form solutions
where , and all sums on j are from i − M + 1 to i.
The above equations involve inversions and a few elementary operations such as addition, multiplication, and transpose of matrices with size up to Kj × C. Consequently, their computational cost is
Update from Trial i to Trial i + 1
Similar to the adaptive linear regression method, here we show how we update the Kalman filter model in a more efficient way. We study the update at each new trial i +1, i = M, M + 1, …, T − 1. To make the new model describe the current firing pattern of neural signals, we keep using the measurements of latest M trials to estimate the parameters Ai+1, Hi+1, Wi+1, Qi+1. That is, the training data is updated by adding trial i + 1, and removing trial i = M, … , T, let
where all sums on j are from i − M + 1 to i. Assume {U,V,R,S,T,L}i are obtained in the old model, the matrices {U,V,R,S,T,L}i+1 can be recursively computed as follows:
These equations only involve elementary operations of a few matrices with size up to Ki+1 × C or Ki−M+1 × C. Their computational cost therefore is 0((Ki−M+1 × C2) ≈ O(KC2). Given that (U, V, R, S, T, L)i+1 are known, the parameters {A, W, H, Q}i+1 can be identified as follows:
Likewise, the above equations involve inversions and a few elementary operations of matrices with size up to C×C. Therefore, their computational cost is also O(C2). Taking the sum of these computations, the overall cost of the adaptive Kalman filter for the model updating at each trial is O(KC2).
Note that the above calculations include two matrix inverses, and . As the sizes of these two matrices are both 6 × 6, the computational cost of the inverses is negligible. This indicates that the RLS technique in the adaptive linear regression does not benefit the computation here. Actually, O(KC2) is the most efficient cost to recursively identify the adaptive model. This can be observed by examining one of the coefficient matrices, , which has size C × C. It is estimated by algebraic operations of a few matrices which include the new firing rate matrix, , whose size is K × C. The operations must include the product of K × C a matrix and a C × K matrix, and we know its cost is KC2. This shows that O(KC2) is the optimal efficiency.
In summary, the efficiency of each adaptive model is stated in Table II.
TABLE II.
Computational Cost of Each Update Method
| Method | Adaptive LR | Adaptive KF |
|---|---|---|
|
| ||
| Non-recursive update | O(MK(1 + CN)2) | O(MKC2) |
| Recursive update | O((1 + CN)3) | O(KC2) |
| RLS | O(K(1 + CN)2) | |
We have shown that for each i, the linear regression and Kalman filter models are recursively estimated with training data from trial to i − M + 1 to i. The kinematics at trial then can be estimated by the linear model and Kalman filter algorithm with observed firing rates at trial [15]. As the adaptive models can capture the variability in the neural signals, we expect they would result in improvement in the decoding accuracy.
III. RESULTS
A. Adaptive Modeling and Decoding
We performed modeling and decoding in the two datasets that we collected from two monkey subjects. As we have shown before, several minutes of training data are typically sufficient to identify the parameters in the model using firing activity of 42 neurons [15]. Taking into account more neurons in the current datasets (124 and 125, respectively), we used the first 80 trials as the training data in dataset 1, and 110 trials in dataset 2, where the total durations are around 7–9 min. More detailed study on the number of trials in the training data is given below. For non-adaptive linear regression and Kalman filter, we identified each model using the first M trials, and then reconstructed trajectories on the remaining trials. In contrast, for adaptive models we recursively updated each of them using trial to trial i − M + 1, and then reconstructed the trajectory for trial i + 1, where i = M, M + 1, … , T − 1.
We have shown that both linear regression and Kalman filter models possess accurate decoding performance [15]. Here we conducted the decoding on the two datasets using both non-adaptive methods and their adaptive counterparts. The results are summarized in Table III, where the mean squared error (MSE) is used to quantitatively measure the averaged decoding accuracy over all testing trials. We can see that on average, the MSE using the adaptive linear regression is approximately 14% lower than that using the nonadaptive one. Likewise, the adaptive Kalman filter performs better than the nonadaptive Kalman filter (MSE is approximately 11% lower in the adaptive method). Note that consistent with the results in [15], the Kalman filters generate more accurate decoding than the linear regression methods. Overall the adaptive Kalman filter has the optimal decoding performance in the comparison (see Fig. 2 for two example trials).
TABLE III.
Comparison of MSE(cm2) in the Testing Trials of the Two Datasets Using Each Method
| Decoding Method | Dataset 1 | Dataset 2 |
|---|---|---|
| Non-adaptive linear regression | 10.7 | 10.1 |
| Adaptive linear regression | 8.8 | 9.0 |
| Non-adaptive Kalman filter | 7.9 | 8.2 |
| Adaptive Kalman filter | 6.8 | 7.5 |
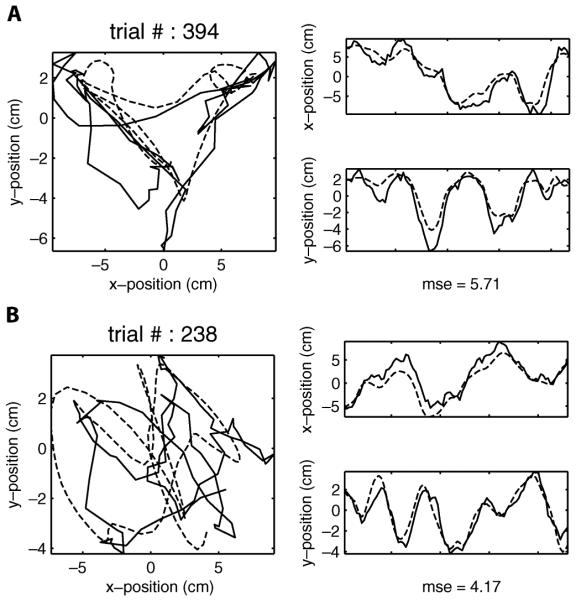
Fig. 2.
Reconstruction on two test trials. (a) True hand trajectory (dashed) and reconstruction using the adaptive Kalman filter of an example trial from dataset 1. Left column: Trajectories in the 2-D working space. Right column: Trajectories by their x and y components. MSE denotes the reconstruction accuracy. (b) Same as (a) except for an example trial from dataset 2.
Effect of Number of Trials in Training Data
We have used 80 and 110 trials as the training data to fit the model in the two datasets, respectively. We here examined the appropriateness of those values under the adaptive Kalman filter framework on account of its accuracy and efficiency. We varied M from 20 to 160, and measured the stability of the identified parameters using the first trials in the model. In particular, the parameters of matrix are of interest in that they describe the dynamic correlation between neural activity and hand motion. In a stationary system, these parameters would converge to a constant when M gets large. However, as the neural activity does not hold a stationary pattern, the parameters will not become stable over time.
To summarize the variation of hundreds of parameters in , we focused on the variation of the L2-Norm (the largest singular value) of the matrix ; that is, . It was found that varied following different patterns before and after around 80 trials in dataset 1 and around 110 trials in dataset 2 [Fig. 3(a) and (b)]. We regard the variation in the former period results from insufficiency of the training data and that in the latter period results from the nonstationary neural activity.
Fig. 3.
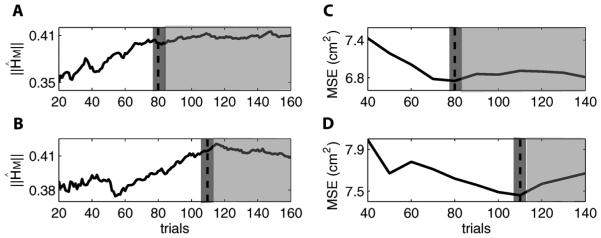
(a) Solid line is the estimated in the Kalman filter model as a function of number of training trials in dataset 1. White area denotes the first varying period when more data are needed to fit the parameters in the model. Light gray area denotes the second varying period when training data are sufficient yet nonstationary over time. Dashed line and dark gray area denote the transition region. (b) Same as (a) except for dataset 2. (c) Solid line is MSE in the adaptive Kalman filter decoding as a function of number of training trials in dataset 1. This function approximately decreases in the white area and then levels off around the dashed line and dark gray area. (d) Same as (c) except for dataset 2.
Alternatively, we examined the decoding performance in the two datasets when M varies from 40 to 140. It was found that in dataset 1 MSE approximately decreases when M varies from 40 to 80, and then levels off when gets larger [Fig. 3(c)]. A similar pattern was observed in dataset 2 except that the leveling off occurs at 110 [Fig. 3(d)]. These decoding results further support our selection of the number of training trials (80 and 110) in the two datasets.
Improvement Over Time
We have described that the adaptive decoding approaches are motivated by the nonstationarity of neural signals. We update the encoding model using firing rates in each new trial and then predict the trajectory in the next. As compared to the adaptive methods, the fixed nonadaptive models should be less appropriate over time in characterizing the relationship between neural signals and hand kinematics. This suggests that the improvement in decoding accuracy of the adaptive methods would be more significant in the later part of the data.
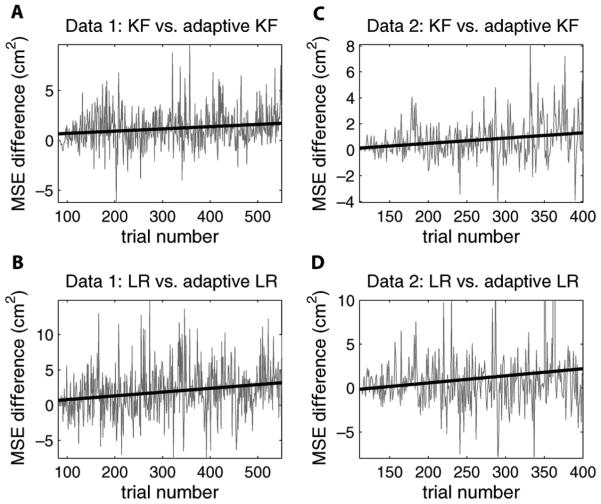
To test this hypothesis, we compared the decoding accuracy over all testing trials by calculating the MSE difference between a nonadaptive (Kalman filter and linear regression) method and its adaptive version in both datasets (see Fig. 4). To measure the improvement over time, we fit the difference with a linear function in each comparison. The slope of the fitted line is 0.0022 when comparing the MSE between the nonadaptive and adaptive Kalman filters in dataset 1. This indicates that on average, the adaptive method improves the MSE accuracy by 0.0022 (cm2) per trial. This result seems insignificant. However, there are 470 testing trials in dataset 1. The improvement at the end of the data would be approximately 470 × 0.0022 = 1.03 (cm2), This is about 13% improvement over the averaged MSE and should not be overlooked. The slopes in the other three comparisons are 0.0041, 0.0053, and 0.0081, respectively. They are considerably larger than the slope in the first comparison and therefore would imply more significant improvements. Statistically, the significance of these improvements can be justified using a t-test. Under the null hypothesis that the slope = 0 (alternative hypothesis: the slope > 0), we can reject the null with significance level α = 0.05 for each of the 4 comparisons.
Fig. 4.
Comparison of MSE between nonadaptive decoding methods and the corresponding adaptive methods in the testing trials of the two datasets. (a) Gray line is the MSE difference between the nonadaptive Kalman filter and the adaptive Kalman filter in 470 testing trials in dataset 1. Black straight line is the optimal linear fit with a positive slope. (b) Same as (a) except for the comparison between the nonadaptive and adaptive linear regressions. (c) and (d) Same as (a) and (b) except in 290 testing trials in dataset 2.
B. Real-Time Performance
The system identification and decoding software was written in Matlab (The Mathworks Inc., Natick, MA) and the experiments were run on a computer with an Intel CPU 2.00-GHz processor. We examined the practical time cost of each method. Here, we only compared the cost in the updating part as the decoding part of the nonrecursive and recursive methods are identical.
The result is summarized in Table IV. For example, in dataset 1 the recursive, adaptive Kalman filter on average (over all test trials) takes around 5 ms to update the model in each trial. This cost is extremely small, almost an order of magnitude less than the 50 ms of the time bin size. Note that if we directly estimate the parameters from the data without the recursive approach, the cost would be 230 ms. Taking into account the decoding accuracy in Table III, the recursive, adaptive Kalman filter is optimal (in terms of accuracy and efficiency) among these decoding methods.
TABLE IV.
Practical Cost of Each Method in the Two Datasets
| Decoding Method | Dataset 1 | Dataset 2 |
|---|---|---|
| Non-recursive, adaptive linear regression | 49s | 68s |
| Recursive, adaptive linear regression | 21s | 22s |
| RLS adaptive linear regression | 42s | 44s |
| Non-recursive, adaptive Kalman filter | 230ms | 390ms |
| Recursive, adaptive Kalman filter | 5ms | 6ms |
The improvement on efficiency can also be observed in the adaptive linear regression method. In dataset 1, a nonrecursive, adaptive linear regression takes 49 s to learn the parameters in the model. Using the proposed recursive approach or RLS, the time can be shortened to 21 s or 42 s. Note that although the RLS method is theoretically more efficient than the proposed recursive method, its practical expense is actually higher here. This can also be observed in dataset 2.
C. Applications
We have shown that the proposed adaptive methods better capture the nonstationary neural activity and possess more accurate decoding. More importantly, the adaptive Kalman filter can perform efficiently in real-time and the method could be exploited in many neural control experiments [13], [19]. However, in practical prosthetic applications, the disabled subjects often do not have the ability to move and therefore there would be no “actual” hand motion to train the proposed model. This indicates that the adaptive Kalman filter can not be directly used for a BMI as it relies on the actual hand position to fit the model.
To make the method applicable, here we use a simple yet reasonable scheme to generate the “actual hand positions.” In Section II, we have described that the behavioral task is a goaldriven movement. That is, at each time instant, the monkey’s hand movement is to control the cursor to reach a target. In a typical human BMI experiment, the target is often known and the patient is trained to imagine using his hand to track a cursor to reach the target. The “training data” would be the simultaneously recorded neural activity and imaginary hand movement (actually cursor motion) [8]. In our experiment, there are seven targets in each movement trial. Motivated by the imaginary movement, we propose to use a straight line linking adjacent targets (see one example trial in Fig. 5). The time length of the line is assumed to equal the actual time length between the two targets in the recording, and the “hand positions” are distributed over the line with a bell-shaped speed profile between adjacent targets; that is, the speed is around zero at both ends, while reaches maximum in the middle point. We regard these straight lines as the “true” hand trajectories and use them in the proposed adaptive models.
Fig. 5.
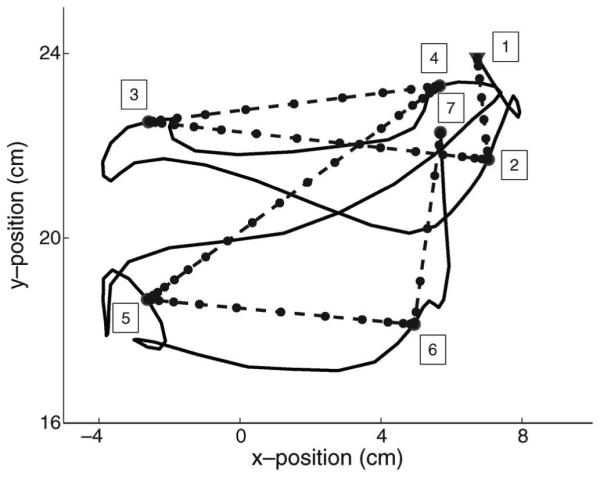
A sample movement trial (solid line) and its “straight line” version (dashed line). Hand started at the first target (triangle point), and then moved to reach each target sequentially. Trial was complete when the seventh target was reached. The “straight line” trajectory is constructed by linearly connecting the adjacent targets with a bell-shaped speed profile. The dots denote the “straight line” hand positions with 50-ms time step.
Using the same decoding process as described above where the kinematics are known, here we conducted the decoding on the “straight-line” datasets using the adaptive Kalman filter. As simulated kinematics only describe the main trend of the movement, the correlation coefficient (CC) is a more appropriate criterion than the MSE to measure the decoding performance. Here, CC is calculated between the estimated and simulated position in x- and y-coordinate, respectively [15]. We found that the averaged CC equals (0.82, 0.75) in dataset 1, and (0.81, 0.64) in dataset 2. These high CCs imply the possibility that the method could be utilized when actual hand movement is not available in BMI paradigms such as in Hochberg et al. [8]. However, we note that the simulated movement is based on the target information, while the target can only be known in a training process. In practical interfaces, only neural activity should be used to control external devices.
IV. DISCUSSION
Recent studies indicate that the neuronal firing activity in motor cortex over time is not a stationary process. To appropriately describe the dynamic relation between neural activity and kinematics, we present an adaptive approach by updating the encoding model when the new observations are available. Our work focuses on the development of an adaptive real-time decoding algorithm. Real-time efficiency is needed to allow the new approaches to be feasible for neural prosthetic applications. In this paper, we build our adaptive approaches based on the linear regression and Kalman filter methods. Both methods are classical estimation systems and are preferred in decoding neural activity in motor cortex for their simplicity, accuracy, and successful performance in closed-loop neural control experiments [4], [5], [7], [13], [22]. They approximate the relationship between firing activity and hand kinematics using linear models. More powerful nonlinear, and non-Gaussian, likelihood models can be constructed and used for decoding [14], [16], [17], [33]; the decoding task, however, becomes more complex and inefficient, and hence, are not yet appropriate for neural prosthetic applications.
Our approaches follow an online estimation framework. In each recording session, we take the first part of data as training data to fit the linear regression or Kalman filter model. The model is updated with new observations at each trial, and then is used to decode the neural signals in the next trial. We tested the new methods on two datasets and found that they are more accurate than the nonadaptive methods. We have further developed a recursive update approach and demonstrated its efficiency using theoretical estimation as well as practical comparison in the two datasets. In particular, we compared the proposed recursive, adaptive linear regression with an RLS method, and found that the RLS method is theoretically marginally superior. However, the practical cost in the two datasets show that the proposed recursive method is actually more efficient.
Several previous BMI studies have addressed the nonstationarity of neural activity from various perspectives. As it is known, population vector, linear regression, and Kalman filter are three preferred methods in current BMI applications [2], [4]–[8], [13], [19]. Helms Tillery et al. [21] added a supervised learning method which modified the parameters in the population vector during a 3-D reaching movement. They found the new method significantly improved brain-controlled cursor movement. In contrast, our study focused on applications of the other two methods. Gage et al. [22] examined naive coadaptive cortical control in rat subjects using a Kalman filter. Our study is similar to this work though there are a few important differences. First, Gage’s work directly addressed the online neural control, while our study focused on the methods and we theoretically compared the efficiency of all models. An online test of the models would be our next step. Second, Gage’s work updated the model in a nonrecursive form, while we were very concerned with the efficiency and proposed a recursive way to update the model. Third, there are only 16 electrodes and 1-D “out frequency” in Gage’s work, while we examined over 100 neurons and multidimensional hand kinematics. This also indicates why the efficiency is a very important factor in our study.
State-space models follow an elegant Bayesian framework and are preferred in current neural modeling work [34], [35]. Eden et al. proposed an adaptive point process filtering approach to study the plasticity of receptive fields [24]. The method successfully tracked the system parameters and state in two simulated data examples. The authors further applied the method to motor cortical neurons to track changes in the firing activity of neural ensemble. They found the adaptive algorithm was able to accurately estimate the hand direction, but not the velocity [25]. Furthermore, Srinivasan et al. developed a general-purposed filter design which generalizes commonly used state-space models for various neural signals. The investigation on simulated data demonstrates that the unified framework outperforms previous approaches [36]. Other neural decoding studies also addressed the nonstationarity of neural signals. Kim et al. proposed an adaptive MIMO neural network and demonstrated that the method can successfully track the relationship between neural activity and hand kinematics [23]. In contrast, our goal has been to build efficient and accurate tools for potential BMI applications, and our approach is different from these studies in the following sense. First, both linear regression and Kalman filter have been successfully exploited in BMIs. Further study on these methods would result in more useful applications. In contrast, nonlinear methods generally are more accurate while more complex and difficult to use. Second, our methods directly investigate real neural data instead of simulations, which is more relevant in the study of neural coding. Third, recent studies indicate that although nonlinear models are theoretically important, they do not significantly outperform linear methods in practical motor cortical decoding [4], [33].
From the results, we conclude that the adaptive Kalman filter would be our optimal selection for an online decoding method. It only takes a few milliseconds to update the model and has the best decoding accuracy. A nonadaptive Kalman filter has been successfully used in a neural control experiment [19], and recently be applied to a human neural prosthetic study [13]. These studies strongly suggest the adaptive Kalman method could be exploited in BMI applications. In contrast, although the adaptive linear regression also improves the decoding accuracy, it takes about half a minute for each update. This makes the method difficult to be useful in practical interfaces. Note that by comparing the decoding accuracy, we see a fixed Kalman filter performs even better than an adaptive linear regression method. This further supports the superiority of Kalman filters over linear filters in neural decoding in motor cortex [15].
We have shown the adaptive models have better offline decoding than their nonadaptive counterparts. However, we should note that the improvement of the decoding accuracy may not be essential to the subject’s behavior. The neural modulation in the brain could accommodate all these errors, and the improvement of the algorithms could be outweighed by adaptive improvements by the brain to control the device. Note that the offline study in this paper would not be able to address this issue. In the future, we will test the hypothesis by comparing the online neural control performance between nonadaptive and adaptive Kalman filters.
V. CONCLUSION
In this paper, we have presented an adaptive version for the commonly used linear regression and Kalman filter methods. Analysis of the new methods was performed using two datasets involving complex, continuous, hand motions. Neural recordings from two monkeys were obtained from chronically implanted microelectrode arrays. Our focus has been to provide a more appropriate description of the data and more accurate, efficient performance for the neural control of 2-D cursor motion. We have shown that the adaptive methods estimated trajectories from firing rates of a population of cells in primary motor cortex more accurately than those produced by the static methods. In particular, the adaptive Kalman filter has real-time efficiency using a recursive approach.
Our future work will focus on evaluating the performance of the adaptive Kalman filter for closed-loop neural control of cursor motion in the continuous movement task. To make the method applicable to human trials, we will test the performance when there is no true hand motion in the training data. Furthermore, we will explore adaptive versions for more complicated nonlinear methods [16], [33]. Such investigations could help better understand the nonlinear dynamic relations between the neural activity and kinematics and further improve decoding performance.
ACKNOWLEDGMENT
The authors would like to thank S. Francis, D. Paulsen, and J. Reimer for training the monkeys and collecting the data.
The work of W. Wu was supported by Florida State University First Year Assistant Professor Award and Planning grant. The work of N. G. Hatsopoulos was supported by the National Institutes of Health-National Institute of Neurological Disorders and Stroke under Grant R01 NS45853.
Biographies

Wei Wu received the B.S. degree in applied mathematics from the University of Science and Technology of China, Hefei, China, in 1998, and the M.S. in computer science and Ph.D. in applied mathematics from Brown University, Providence, RI, in 2003 and 2004, respectively.
He joined the faculty at Florida State University, Tallahassee, in 2006, where he is an Assistant Professor in the Department of Statistics. His research interests are in statistical models of neural systems and their applications to brain–machine interfaces.

Nicholas G. Hatsopoulos received the B.A. degree in physics from Williams College, Williamstown, MA, in 1984, and the M.S. degree in psychology and the Ph.D. degree in cognitive science from Brown University, Providence, RI, in 1991 and 1992, respectively.
He joined the faculty at the University of Chicago, Chicago, IL, in 2002 and is currently an Associate Professor in the Department of Organismal Biology and Anatomy and is a member of the Committees on Computational Neuroscience and Neurobiology. His research focuses on the neural coding of motor behavior in large cortical ensembles and on the development of brain–machine interfaces (BMIs). In 2001, he cofounded a company, Cyberkinetics Neurotechnology Systems, Inc., Foxborough, MA, which is developing BMI technology to assist people with severe motor disabilities.
Contributor Information
Wei Wu, Department of Statistics, Florida State University, Tallahassee, FL 32306 USA.
Nicholas G. Hatsopoulos, Department of Organismal Biology and Anatomy, Committees on Computational Neuroscience and Neurobiology, University of Chicago, Chicago, IL 60637 USA
REFERENCES
- [1].Donoghue JP. Connecting cortex to machines: Recent advances in brain interfaces. Nat. Neurosci. 2002 Nov;5:1085–1088. doi: 10.1038/nn947. [DOI] [PubMed] [Google Scholar]
- [2].Lebedev MA, Nicolelis MA. Brain-machine interfaces: Past, present and future. Trends Neurosci. 2006;29(9):536–546. doi: 10.1016/j.tins.2006.07.004. [DOI] [PubMed] [Google Scholar]
- [3].Schwartz A, Cui XT, Weber D, Moran D. Brain-controlled interfaces: Movement restoration with neural prosthetics. Neuron. 2006;56:205–220. doi: 10.1016/j.neuron.2006.09.019. [DOI] [PubMed] [Google Scholar]
- [4].Carmena JM, Lebedev MA, Crist RE, O’Doherty JE, Santucci DM, Dimitrov DF, Patil PG, Henriquez CS, Nicolelis MAL. Learning to control a brain–machine interface for reaching and grasping by primates. PLoS Biol. 2003;1(2):193–016. doi: 10.1371/journal.pbio.0000042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Serruya MD, Hatsopoulos NG, Paninski L, Fellows MR, Donoghue JP. Brain-machine interface: Instant neural control of a movement signal. Nature. 2002;416:141–142. doi: 10.1038/416141a. [DOI] [PubMed] [Google Scholar]
- [6].Taylor DM, Tillery SI, Schwartz AB. Direct cortical control of 3D neuroprosthetic devices. Science. 2002;296:1829–1832. doi: 10.1126/science.1070291. [DOI] [PubMed] [Google Scholar]
- [7].Wessberg J, Stambaugh C, Kralik J, Beck LM, Chapin PJ, Kim J, Biggs S, Srinivasan M, Nicolelis M. Real-time prediction of hand trajectory by ensembles of cortical neurons in primates. Nature. 2000;408:361–365. doi: 10.1038/35042582. [DOI] [PubMed] [Google Scholar]
- [8].Hochberg LR, Serruya MD, Friehs GM, Mukand JA, Saleh M, Caplan AH, Branner A, Chen D, Penn RD, Donoghue JP. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature. 2006;442:164–171. doi: 10.1038/nature04970. [DOI] [PubMed] [Google Scholar]
- [9].Serruya MD, Hatsopoulos NG, Fellows MR, Paninski L, Donoghue JP. Robustness of neuroprosthetic decoding algorithms. Biol. Cybern. 2003 Mar;88(3):219–228. doi: 10.1007/s00422-002-0374-6. [DOI] [PubMed] [Google Scholar]
- [10].Shenoy KV, Meeker D, Cao S, Kureshi SA, Pesaran B, Buneo CA, Batista AP, Mitra PP, Burdick JW, Andersen RA. Neural prosthetic control signals from plan activity. NeuroReport. 2003 Mar;14(4):591–596. doi: 10.1097/00001756-200303240-00013. [DOI] [PubMed] [Google Scholar]
- [11].Hu J, Si J, Olson BP, He J. Feature detection in motor cortical spikes by principal component analysis. IEEE Trans. Neural Syst. Rehabil. Eng. 2005 Sep;13(3):256–262. doi: 10.1109/TNSRE.2005.847389. [DOI] [PubMed] [Google Scholar]
- [12].Georgopoulos A, Schwartz A, Kettner R. Neuronal population coding of movement direction. Science. 1986;233(4771):1416–1419. doi: 10.1126/science.3749885. [DOI] [PubMed] [Google Scholar]
- [13].Kim SP, Simeral J, Hochberg L, Donoghue JP, Friehs G, Black MJ. Multi-state decoding of point-and-click control signals from motor cortical activity in a human with tetraplegia; 3rd IEEE EMBS Conf. Neural Eng..May, 2007. pp. 486–489. [Google Scholar]
- [14].Wu W, Black MJ, Mumford D, Gao Y, Bienenstock E, Donoghue JP. Modeling and decoding motor cortical activity using a switching kalman filter. IEEE Trans. Biomed. Eng. 2004 Jun;51(6):933–942. doi: 10.1109/TBME.2004.826666. [DOI] [PubMed] [Google Scholar]
- [15].Wu W, Gao Y, Bienenstock E, Donoghue JP, Black MJ. Bayesian population decoding of motor cortical activity using a kalman filter. Neural Comput. 2006;18(1):80–118. doi: 10.1162/089976606774841585. [DOI] [PubMed] [Google Scholar]
- [16].Brockwell AE, Rojas AL, Kass RE. Recursive bayesian decoding of motor cortical signals by particle filtering. J. Neurophysiol. 2004;91:1899–1907. doi: 10.1152/jn.00438.2003. [DOI] [PubMed] [Google Scholar]
- [17].Gao Y, Black MJ, Bienenstock E, Shoham S, Donoghue JP. Probabilistic inference of hand motion from neural activity in motor cortex. In: Dietterich TG, Becker S, Ghahramani Z, editors. Advances in Neural Information Processing Systems 14. MIT Press; Cambridge, MA: 2002. pp. 213–220. [Google Scholar]
- [18].Sanchez JC, Erdogmus D, Principe JC, Wessberg J, Nicolelis MAL. Interpreting spatial and temporal neural activity through a recurrent neural network brain machine interface. IEEE Trans. Neural Syst. Rehabil. Eng. 2005 Jun;13(2):213–219. doi: 10.1109/TNSRE.2005.847382. [DOI] [PubMed] [Google Scholar]
- [19].Wu W, Shaikhouni A, Donoghue JP, Black MJ. Closed-loop neural control of cursor motion using a kalman filter. Proc. IEEE Eng. Med. Biol. Soc. 2004 Sep;:4126–4129. doi: 10.1109/IEMBS.2004.1404151. [DOI] [PubMed] [Google Scholar]
- [20].Kim SP, Wood F, Fellows M, Donoghue JP, Black MJ. Statistical analysis of the non-stationarity of neural population codes; 1st IEEE/RAS-EMBS Int. Conf. Biomed. Robotics Biomechatronics.Feb, 2006. pp. 295–299. [Google Scholar]
- [21].Tillery SIH, Taylor DM, Schwartz AB. Training in cortical control of neuroprosthetic devices improves signal extraction from small neuronal ensembles. Rev. Neurosci. 2003;14:107–119. doi: 10.1515/revneuro.2003.14.1-2.107. [DOI] [PubMed] [Google Scholar]
- [22].Gage G, Ludwig K, Otto K, Ionides E, Kipke D. Naive coadaptive cortical control. J. Neural Eng. 2005;2:52–63. doi: 10.1088/1741-2560/2/2/006. [DOI] [PubMed] [Google Scholar]
- [23].Kim SP, Sanchez JC, Principe JC. Real time input subset selection for linear time-variant MIMO systems. Optimization Methods Software. 2007;22(1):83–98. [Google Scholar]
- [24].Eden UT, Frank LM, Barbieri R, Solo V, Brown EN. Dynamic analyses of neural encoding by point process adaptive filtering. Neural Comp. 2004;16(5):971–998. doi: 10.1162/089976604773135069. [DOI] [PubMed] [Google Scholar]
- [25].Eden UT, Truccolo W, Fellows MR, Donoghue JP, Brown EN. Reconstruction of hand movement trajectories from a dynamic ensemble of spiking motor cortical neurons; Proc. IEEE EMBS; Sep, 2004. pp. 4017–4020. [DOI] [PubMed] [Google Scholar]
- [26].Wu W, Hatsopoulos N. Evidence against a single coordinate system representation in the motor cortex. Exp. Brain Res. 2006;175(2):197–210. doi: 10.1007/s00221-006-0556-x. [DOI] [PubMed] [Google Scholar]
- [27].Scott SH. Apparatus for measuring and perturbing shoulder and elbow joint positions and torques during reaching. J. Neurosci. Methods. 1999;89(2):119–127. doi: 10.1016/s0165-0270(99)00053-9. [DOI] [PubMed] [Google Scholar]
- [28].Moran D, Schwartz A. Motor cortical representation of speed and direction during reaching. J. Neurophysiol. 1999;82(5):2676–2692. doi: 10.1152/jn.1999.82.5.2676. [DOI] [PubMed] [Google Scholar]
- [29].Paninski L, Fellows M, Hatsopoulos N, Donoghue JP. Spatiotemporal tuning of motor cortical neurons for hand position and velocity. J. Neurophysiol. 2004;91:515–532. doi: 10.1152/jn.00587.2002. [DOI] [PubMed] [Google Scholar]
- [30].Warland D, Reinagel P, Meister M. Decoding visual information from a population of retinal ganglion cells. J. Neurophys. 1997;78(5):2336–2350. doi: 10.1152/jn.1997.78.5.2336. [DOI] [PubMed] [Google Scholar]
- [31].Haykin S. Adaptive Filter Theory. 4 Prentice Hall; Englewood Cliffs, NJ: 2001. [Google Scholar]
- [32].Sayed AH. Fundamentals of Adaptive Filtering. Wiley; New York: 2003. [Google Scholar]
- [33].Gao Y, Black MJ, Bienenstock E, Wu W, Donoghue JP. A quantitative comparison of linear and non-linear models of motor cortical activity for the encoding and decoding of arm motions; Proc. 1st Int. IEEE/EMBS Conf. Neural Eng.; Capri, Italy. Mar, 2003. pp. 189–192. [Google Scholar]
- [34].Srinivasan L, Eden UT, Willsky AS, Brown EN. A statespace analysis for reconstruction of goal-directed movements using neural signals. Neural Comput. 2006;18:2465–2494. doi: 10.1162/neco.2006.18.10.2465. [DOI] [PubMed] [Google Scholar]
- [35].Yu BM, Kemere C, Santhanam G, Afshar A, Ryu SI, Meng TH, Sahani M, Shenoy KV. Mixture of trajectory models for neural decoding of goal-directed movements. J. Neurophysiol. 2007;97:3763–3780. doi: 10.1152/jn.00482.2006. [DOI] [PubMed] [Google Scholar]
- [36].Srinivasan L, Eden UT, Mitter SK, Brown EN. General-purpose filter design for neural prosthetic devices. J. Neurophysiol. 2007;98:2456–2475. doi: 10.1152/jn.01118.2006. [DOI] [PubMed] [Google Scholar]