Computational neuroimaging and population receptive fields

Abstract

Functional magnetic resonance imaging (fMRI) noninvasively measures human brain activity at millimeter resolution. Scientists use very different approaches to take advantage of the remarkable opportunities presented by fMRI. We describe progress using the computational neuroimaging approach in human visual cortex, which aims to build models that predict the neural responses from the stimulus and task. We focus on a particularly active area of research, the use of population receptive field (pRF) models to characterize human visual cortex responses to a range of stimuli, in a variety of tasks, and in different subject populations.

Understanding sensory circuits

A mark of understanding a sensory system is the ability to predict how it will respond to stimulation. In the case of human visual cortex, we would like to accurately predict how each part of the system responds to any visual input. Such predictions are beyond current capabilities, but progress has been made: There are well-defined models that predict how certain parts of the system respond to many stimuli.

Receptive field modeling is an important sensory science tool that is used to predict responses and clarify brain computations. Over the last few decades, many investigators applied receptive field models to characterize responses in human visual cortex. Human neuroscience instruments often measure the pooled responses of many neurons, so that these models are commonly called population receptive field (pRF) models. PRF models have become a cornerstone of computational neuroimaging, the effort to build quantitative models that predict the fMRI time series from the visual stimulus [1].

Receptive field models have two valuable properties. First, the key pRF parameters (receptive field position and size) have interpretable units that are specified in the stimulus frame; this enables us to directly compare model parameters that are estimated using different instruments [2]. Second, receptive fields can be estimated in individual subjects. Thus, it is possible to meaningfully compare model parameters between two subjects, the same subject across different conditions, or the same subject measured with different instruments. These two properties provide a solid scientific foundation and support clinical applications.

Receptive field models

For more than 75 years, visual neuroscientists have relied on the receptive field concept to make progress in the face of limited knowledge of the neural circuitry [3]. Sherrington [4] coined the phrase ‘receptive field’ to describe the region of skin from which a scratch reflex could be elicited: “The ‘receptive field’ may be conveniently applied to designate the total assemblage of receptive points whence by suitable stimuli a particular reflex movement can be evoked (Sherrington, 1910, p. 32).” Hartline applied the concept to visual neurons [5]. Hartline’s initial definition, like Sherrington’s, emphasized the spatial extent of the receptive field: “No description of the optic responses in single fibers would be complete without a description of the region of the retina which must be illuminated in order to obtain a response in any given fiber. This region will be termed the receptive field of the fiber (Hartline, 1938, p. 410).” Over the years, the receptive field concept has expanded to include stimulus features (e.g., orientation, motion, contrast) and to be based on explicit and quantitative models [3]. In modern usage, particularly in applications to awake-behaving animals, the receptive field model has been further generalized to accept both the stimulus and task as inputs. The receptive field and pRF model can be applied equally to measurements obtained from different instruments, including fMRI, electroencephalography (EEG), microelectrodes, and electrocorticography (ECoG). The model uses the same logical foundation when applied to data from any of these instruments [6, 7].

It is important to distinguish the scale measured by the instrument from the scale of the object under study. The microelectrode measures voltages at a micron scale, and therefore some authors write as if single-unit recordings measure receptive fields at the micron scale. But, single-unit recordings measure the processing performed by a large network of neurons, not just the recorded neuron. That the receptive field does not represent the processing of the single neuron is evident from considering that the neuron’s computation is clearly a function of its inputs; the specific inputs to the neuron are usually unknown and thus the portion of the computation attributable to that neuron is also unknown.

In the primate brain the receptive field of a single-unit informs us about the computations of millions of neurons, including feed forward projections from the sensory surface, lateral interactions with nearby neurons and glial cells, feedback projections from neurons elsewhere in the brain, and neuromodulation from subcortical nuclei [3, 8–11]. Hence, even when we measure the electrical activity of a single neuron, the object under study is a distributed network of millions of neurons that span many centimeters, includes a variety of signaling mechanisms, and whose components change with the stimulus and task. Visual neuroscientists do not yet have the ability to model such distributed and complex circuits; instead, we rely on systematic measurements and computational models to characterize the network that produces the single-unit recordings [12].

The receptive field of a single voxel in an fMRI data set also informs us about the computations of a large network of neurons, but the measurement differs in many ways from electrophysiology. First, the neurons in a voxel are likely to participate in a larger collection of networks than any single neuron. Second, the fMRI signal depends on the blood oxygenation and flow, which is an indirect measure of metabolism, itself an indirect measure of multiple types of neural activity including restoring membrane potentials, action potentials, and other neural functions [13, 14]. These complexities suggest that the fMRI signal too needs to be characterized using systematic measurements and computational models.

The pRF model for neuroimaging

FMRI measures human brain activity at a coarser scale than a microelectrode, but it is possible to analyze fMRI signals in terms of similar response properties to those ascribed to cells. For example, in an early fMRI study, response differences in various visual field maps were explained by invoking receptive field properties [15]. Such response differences could be converted into tuning functions [16], allowing for a comparison of spatial sensitivity of the fMRI signal as a function of visual field map and eccentricity. These results showed two patterns consistent with single unit measurements in animals: broader spatial tuning in more peripheral eccentricities and in visual field maps further from V1 in the visual hierarchy.

The pRF approach builds on these earlier studies and adds an explicit computational model of the fMRI response [7]. The pRF model implemented for fMRI [7] had three components: a representation of the stimulus, a representation of the receptive field, and a computation combining the two representations to predict the fMRI response. The model accounted for the stimulus location but not the stimulus pattern. This was accomplished by representing the stimulus as a contrast mask, a binary image with a value of 1 in the region of the contrast pattern and a 0 in the uniform region. The receptive field shape was modeled as a circularly symmetric (isotropic) Gaussian in the visual field. This shape can be described by three parameters (field position, (x,y) and spread (s), both in visual degrees). The Gaussian parameters can be estimated from fMRI responses to many different types of stimuli, including expanding ring, rotating wedge, a series of bar patterns that sweep through the visual field in different directions, or a series of stimuli placed at different visual field positions. The computation combining the stimulus representation with the receptive field was multiplication, the point-by-point product of the binarized stimulus images and the Gaussian receptive field. At each voxel, the pRF parameters are adjusted to bring the predicted and measured fMRI time series into agreement. Because these pRF parameters are specified in image space, they have meaningful physical units.

There are aspects of the pRF modeling approach which distinguish it from earlier models of the fMRI signal. The pRF approach is an explicit model, and it is expressed in terms of input-referred parameters such as locations in the visual field rather than in terms of a statistic of the fMRI time series. The explicit computational model with input-referred parameters provides a helpful path for generalizing to new stimuli and comparing measurements from other instruments.

PRF models, and computational neuroimaging generally, is not centered on statistical hypothesis testing and null models. Rather, the strategy follows the constructivist philosophy of creating models to account for an increasingly large range of stimuli in many visual areas. This strategy accepts the engineering maxim that all models are wrong, but some are useful [17]. The payoff is that the parameters of a model that accounts for a broad range of measurements will represent valuable information about the circuit - even if the model is incomplete. A useful model accurately predicts responses over some range of conditions and yields parameters for that range that are of scientific or clinical value.

For example, the linear model applies well to only a restricted range of stimuli [18, 19]. Yet, its parameters efficiently identify many visual field maps and capture important features of brain organization, such as the variation in receptive field size with eccentricity. There are now models that account for a much wider stimulus range (see Box 1), but more experimental time is required to obtain the data necessary to fit these models, and for some applications the simple linear model is adequate. Computational neuroimaging is not unique in this constructivist approach; the use of an adequate rather than an optimal tool is common in many areas of engineering, science and life. We need not account for the earth’s curvature when measuring the distance to the grocery store.

Box 1. Extending the pRF models and the stimulus range.

A goal of computational neuroimaging is to predict the responses to any input. The linear pRF model [7] predicts responses in visual cortex based on one stimulus property: the image locations that contain contrast. The spatial sensitivity in the model is a symmetric, two-dimensional Gaussian.

To accurately capture the pattern of cortical responses to a wide variety of stimuli, more complex models are needed. The greater complexity of newer models has primarily come in two forms: a greater variety of pRF shapes and additional computations on the visual image. An example of more flexibility in pRF shape is the extension from one to two Gaussians [71]. The second Gaussian is a negative surround and picks up systematic deviations in which the fMRI time series falls below the baseline level set by the uniform field. Moreover, one need not assume a Gaussian pRF at all. Several groups have described methods to estimate pRF patterns from a much broader class of allowable shapes [33, 72–74].

A second type of improvement concerns the calculations. Extending the linear pRF model to include a compressive spatial summation substantially increases the range of stimuli the model accurately predicts [18]. Other recent models have been constructed to operate on (band limited) image data containing significant amounts of second order contrast (spatial variation in the contrast), rather than the binary representation of image contrast [75]. These models predict responses that depend on stimulus pattern, rather than only stimulus location. Further extensions of pRF models have been developed to account for spatiotemporal images [76, 77]. These models have been used both to predict the BOLD signal given a stimulus and to reconstruct the stimulus (a naturalistic movie) given the pattern of voxel responses.

The newer generation of models brings the field closer to a quantitative characterization of visual cortex responses to a wide range of stimuli, spanning space, pattern and motion.

PRFs across the visual field

Beginning in the retina, the visual system implements a relationship between eccentricity and receptive field size [20]. The relationship can also be observed in single-unit measurements in non-human primates [21]. Using fMRI and pRF modeling it is possible to measure this relationship across many visual field maps in cortex.

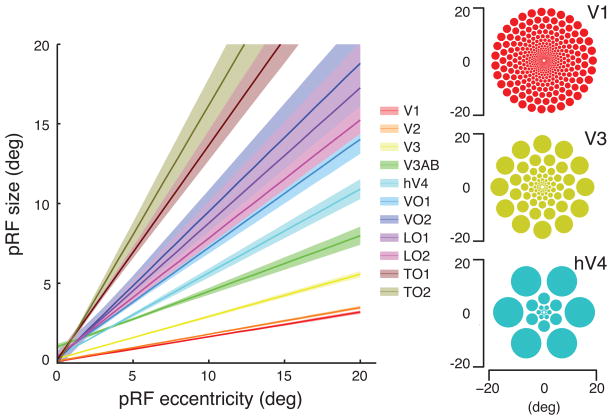
Within each cortical map the pRF size and eccentricity increase together [7, 16]. The rate of pRF size increase differs between visual field maps (Figure 1); this observation has now been repeated many times [18, 22–25]. FMRI enables us to measure this fundamental relationship noninvasively in an individual human subject during a half-hour long experiment.

Figure 1.

Regularities in human population receptive field properties measured with functional MRI. Left: Population receptive field size as a function of eccentricity in several human retinotopic maps. Two clear trends are evident. First, the population receptive field size increases with eccentricity within each map. Second, the population receptive field size differs between maps, with the smallest pRFs in V1, and much larger pRFs in ventral (hV4, VO-1/2) and lateral (LO-1/2, TO-1/2) maps. Replotted from [18]. Right: The spatial array of pRFs using the parameters in the left panel. The radius of each circle is the apparent receptive field size at the appropriate eccentricity. Reproduced with permission of J Winawer and H Horiguchi (https://archive.nyu.edu/handle/2451/33887).

Cortical point spreads

The stimulus-referred pRF parameters vary significantly across the visual field and between subjects. For example, the pRF stimulus-referred size, V1 surface area, and the cortical magnification factor (cortical separation between positions representing points separated by 1 deg of visual angle) all vary substantially. Analysis using pRF methods revealed a feature of the cortical circuitry that unifies these measures [24]. The cortical surface area that responds to a point image is approximately constant (3.5mm). This constant spread holds for a series of visual field locations from the fovea to the near eccentricity (though there is a slight decline). Thus, the fundamental unit of processing appears to be the cortical surface area. The variations in other parameters arise because of the (a) non-uniform mapping of the visual field into the cortical map, and (b) differences in the cortical surface area size between subjects.

Comparable results have been obtained from animal models using voltage sensitive dyes [26] and in previous human fMRI analyses [27]. Both methods provide a summary measure of population activity, and capture the uniform spatial spread in V1 from a point image. Single-unit recordings are not well suited to characterize population activity over several millimeter distances.

Coverage maps

The pRF model is computed one voxel at a time, but it can be informative to summarize the results across a collection of voxels. The visual field map is one example [28, 29], and the coverage map is a second example [22, 23, 30]. The coverage map summarizes how effectively different parts of the visual field evoke responses from an extended region of cortex, not just a single voxel. The visual field map specifies the visual field location that is most effective at evoking a response from each voxel in a region. The coverage map complements the visual field map by indicating the visual field locations that evoke a response from a collection of voxels.

The coverage can be large even when the span of pRF center positions is small. For example, the most effective visual field positions for voxels in V1 span much of the hemifield, while in TO-2 they are relatively confined (Figure 2, left). But the coverage in TO-2 has much greater extent, spanning both hemifields, because the pRF sizes in TO-2 are very large.

Figure 2.

PRF centers and coverage maps. The images show pRF center distributions (left) and pRF coverage maps (right) within two visual field maps, V1 (top) and left temporal-occipital-2 (TO-2, bottom). Data are averaged across several observers and hemispheres. Data from the right hemispheres are flipped across vertical mid-line to combine with data from the left hemispheres. On the left, the color maps indicate the proportion of voxels with pRF centers at a given field position. For both V1 and TO-2, the majority of pRF centers are in the right visual field, with the densest representation near the fovea and the horizontal meridian. The sparser representation of the vertical meridian may be due to sampling limits of the fMRI measurements. On the right, the color map accounts for the spread of each pRF in addition to the center position. The TO-2 pRF sizes are much larger than those in V1; consequently the TO-2 coverage plot extends much further into the ipsilateral hemifield. The maximum stimulus eccentricity was 15 deg, which is why the coverage ends at that eccentricity. Reproduced from [22] with permission from American Physiological Society.

Comparing data from different instruments

Direct comparison of the signals from different types of instruments can be very awkward because the signals do not have common units. For example, fMRI data measure the blood oxygenation change over time, while electrodes measure a voltage. There is no immediate or obvious relationship between the instrumental signals themselves.

Input-referred modeling is a valuable tool for comparing data from different instruments [2]. For example, pRF methods have been used to compare the local field potentials (LFPs) arising from electrodes implanted in human subjects with fMRI measurements in the same regions of cortex [31, 32]. By fitting pRF models to both types of measurements, one can compare the parameters (location and pRF size) although the instrumental signals are very different.

The human LFP response to flickering stimuli can be separated into two components [32]. One component is closely locked to the flicker rate of the stimulus (stimulus-locked). The second component is a general increase in the LFP variance (asynchronous broadband). When a compressive summation pRF model is fit to the two response components separately, the two compressive parameters differ substantially [32]. The asynchronous broadband signal parameter matched those of the fMRI signal, while the stimulus-locked parameter did not. PRF analysis of fMRI and ECoG signals also shed light on the circuitry associated with excitatory and suppressive neural signals. The asynchronous broadband ECoG signal increases when a stimulus enters the electrode’s receptive field; in contrast, low frequency (alpha) oscillations were associated with surround suppression [31].

The ability to use pRF models to relate measurements at different spatial and temporal scales is valuable because the direct comparison of the measures - LFP voltage, spike rate, and fMRI response contrast - has no logical foundation. Input-referred parameters of the pRF model enable us to rigorously compare measurements from very different instruments.

Applying pRF models

PRF parameters can be used for quantifying how clinical conditions and cognitive task demands influence responses in visual cortex.

Attention

A number of labs have assessed the impact of spatial attention and visual load on neural circuitry using pRF parameters [33–37]. The estimated pRF centers vary systematically as subjects change their spatial attention, with the center shifting towards the attended location [34]. The size of the shift increases systematically across visual field maps; the effect is small in V1/V2 and larger at increasing levels of the visual hierarchy (e.g., hV4, LO, and IPS maps). The effect of attention can be modeled as a multiplicative field, which is centered on the attended location but spread widely across the visual field. Multiplying each pRF by this field shifts the centers systematically towards the focus of attention. According to this model, the larger shifts in pRF centers at higher levels of the visual hierarchy are explained by larger pRF sizes, even when a single-sized attention-field is assumed for all visual areas.

Linear pRF models measure how spatial attention influences fMRI responses [33, 35, 36]. In extrastriate maps, the pRF sizes increase when subjects attend to the stimulus (compared to the pRF size in passive fixation). Likewise, attention to face stimuli systematically modulates responses in ventro-temporal cortex and these effects change the position, gain, and size of the pRFs [37].

Attention also influences the center and size of single-units’ receptive fields [38, 39] in area MT in a way that depends on the nature of the task. There is a good opportunity to make quantitative comparisons of these measurements.

Stability and plasticity in adult visual cortex

Under some conditions, adult brain circuits change in response to sensory experience or disease. Clarifying the mixture of brain plasticity and stability is important as we design systems - from electronics to optogenetics - that interface with brain tissue. There are various general reviews of stability and plasticity in human visual cortex (e.g., [40, 41]). Here we describe measurements that use pRF modeling to characterize plasticity and stability.

In adults with lesions in the central (macular) retina, pRF measurements provide no substantial evidence of large-scale remapping of the cortical responses [42]. PRF measurements in a macaque with acquired macular degeneration and their results matched these findings [43]. There are alternative interpretations about adult cortical plasticity [44–46]. For example, pRF sizes near the lesion projection zone (occipital pole) are larger, both in patients and controls who were presented stimuli that simulated a foveal lesion. Quantitative modeling using the pRF method suggests that feedback from extrastriate cortex may explain the increase in pRF size with artificial scotomas and in patients with real lesions [47–50].

Adult cortical plasticity was also studied with pRF methods in patients blinded in a quarter of the visual field by cortical lesions [51]. The pRF model parameters in these subjects can be compared with measurements from control subjects presented stimuli with a simulated quarterfield scotoma. No large-scale changes in the spared-V1 topography were found. The pRF coverage maps showed responses in portions of the spared-V1 at visual field locations where the subjects reported no conscious vision (dense scotomas). These visual field locations, which can be found in individual subjects, provide a patient-specific target for visual restoration therapies.

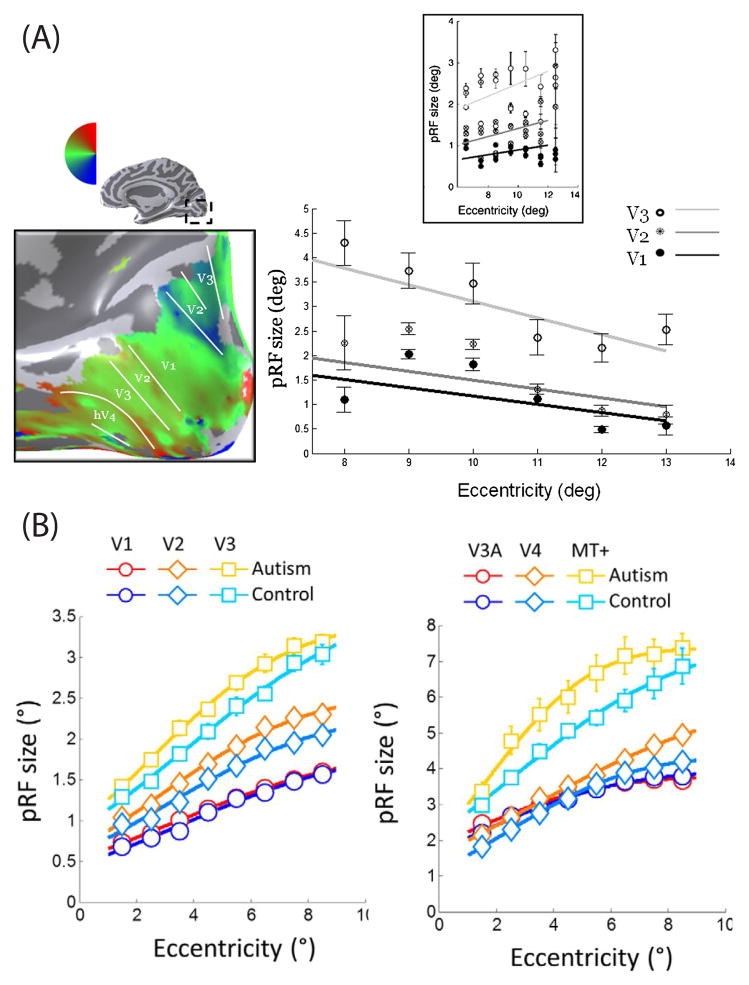
PRF modeling can be a useful tool for studying sight restoration. A remarkable subject, MM, lost one eye at three years of age. The spared eye had severely damaged optics that deprived him of contrast vision [52, 53], but after 43 years, the optics was repaired. MM has not regained normal vision more than a decade after the optical restoration [53]. PRF measurements have been used to understand why MM has a limited ability to see [54]. The measurements reveal that MM has an organized eccentricity map in calcarine cortex that differs from controls in several ways. First, the most effective eccentricities are beyond 3 deg, while control subjects have a large portion of the occipital lobe devoted to the central few degrees. The pRF sizes are somewhat larger than the pRF sizes of controls at the same eccentricity, and the size of the pRF decreases with eccentricity while in controls the size increases. MM’s unusual pRF properties may be explained by the loss of neurons with small receptive fields (Figure 3a).

Figure 3.

Clinical use of pRFs. Upper: PRFs in a subject with abnormal visual inputs. Subject MM’s right hemisphere angle map is shown on the smoothed cortical surface (left, magnified posterior, medial view). The scatterplot shows MM’s pRF size in visual areas V1, V2 and V3, as a function of eccentricity (right). The pattern differs from measurements in control subjects (inset). In control subjects, the pRF sizes increase with eccentricity; in MM they do not. Reprinted from [58]. Lower: PRF sizes in subjects with autism and in controls. In both populations, pRF size increases with eccentricity in all visual areas. PRF size also increases across the visual hierarchy, with the smallest pRF sizes in V1 and the largest in MT+. In most visual areas, the pRF sizes are larger in subjects with autism than in controls.

PRF modeling provides a quantitative framework that tests hypotheses about why the fMRI response changes as a consequence of retinal and cortical dysfunction. These papers advance the study of adult cortical plasticity beyond the question of whether adult cortex is plastic, and the methods can be used to study individual subjects.

Developmental plasticity

The pRF computational models are also being applied to new measurements in extraordinary developmental cases. One example is a subject who had a complete removal of the left hemisphere (hemispherectomy) at the three years of age [40]. Despite having only a right hemisphere, the patient is bilingual and has a partially recovered right-sided hemiplegia, suggesting extensive developmental plasticity in these systems. But the subject’s vision shows the expected adult pattern: complete, right hemifield blindness. In the spared right hemisphere, the pRF parameters in early visual field maps (V1–V3) are close to the normal range, but the pRF size in extrastriate maps (LO-1) are smaller than normal.

The case of a hemispherectomy at three years of age contrasts sharply with a congenital case of a subject whose right hemisphere failed to develop in utero, prior to the 7th week of embryonic gestation [55]. The congenital subject has vision in both the contralateral and ipsilateral visual fields and some abnormalities in the organization of the early visual field maps. Hence, the timing of the disruption is of great significance and 3 years of age may be a critical period for LO development [40]. This is the same age when subject MM’s damage occurred, and responses in his LO and ventral regions are abnormal; but the disruption in MM’s case is quite different (loss of contrast vision vs. epileptic activity and hemispherectomy). These outcome differences emphasize the importance of studying individual patients.

Albinism and achiasma are developmental disorders that affect the optic nerve crossing at the chiasm. The case of achiasma is particularly extreme. The optic nerves arising from the nasal retina do not cross the chiasm; instead, the entire retina projects to the ipsilateral lateral geniculate nucleus and then V1. Hence the pattern of inputs to the brain is very different from typical subjects. Both conditions have been studied using visual field mapping [56–59]. Responses in the cortex of achiasmic subjects are explained by an unusual model in which the pRF comprises two distinct Gaussian regions centered at positions mirrored around the vertical meridian [58]. The sizes of each of these regions are similar to the sizes measured in control subjects at comparable eccentricities, though perhaps slightly larger. This unusual two-component pRF is also present in extrastriate ventral stream areas [59].

Psychiatric and neurological disorders

Important neurological and psychiatric disorders arise from failures in developmental plasticity [60, 61] or attention networks [62]. The success of pRF methods in assessing developmental plasticity and attention suggests that these methods may have value in diagnosing and understanding the biological basis of these disorders. For example, pRF measurements have been made in individual patients with mild Alzheimers’ disease [63]. One subject had disordered visual field maps (V1, V2, V3 and hV4), while the second had typical map organization. In both cases, the pattern of pRF size as a function of eccentricity differed from the control distribution. The differences may be the source of visual symptoms reported early in the disease [64].

PRF measurements also document differences between autistic and control populations. While the visual field maps in autistic and control subjects are comparable [65, 66], the pRF sizes in certain extrastriate maps are larger in the autism group than in controls (Figure 3b). There are no pRF size differences in V1 or V3A. The visual cortical function in the autism group may be characterized by extrastriate cortical hyperexcitability or differential attentional deployment [66].

Functional labels and computational neuroimaging

Computational neuroimaging is but one of several fMRI strategies, and the differences between strategies are significant. Perhaps the most common strategy is to design experiments that compare different populations that are grouped based on a behavioral measure (good readers vs. poor readers; depressed vs. healthy; blind vs. sighted; cognitive impairment or not). FMRI measurements between the groups are compared and reliable differences are labeled and interpreted. This group-comparison strategy is used widely in medical research beyond neuroimaging; for example, it is used to identify genetic factors. This approach removes the signals that are common between the groups, even though these signals may be part of the computational processing. For this reason group comparison designs are not well suited for computational neuroimaging. The strategy is most useful for identifying biomarkers.

Many psychologists and electrophysiologists use stimulus selectivity to interpret function. In this strategy, experiments are designed to compare responses to stimulus groups (faces vs. houses; words vs. pseudowords; moving vs. static; colorful vs. achromatic), and a functional label is assigned to locations with some stimulus-selectivity (e.g., face area, word area, motion area, color area). The approach is used in both neuroimaging and single-unit electrophysiology, and there are advocates for this approach in human neuroimaging [67]. But the stimulus-selectivity approach has limited value for computational neuroimaging where it is accepted that the absence of a response is useful information (zero is a number, too). Consider the simple example of localizing a stimulus in space from the V1 response. We identify a foveal point stimulus because there is a positive response in the foveal representation and a zero response in the peripheral representation.

Concluding remarks

PRF models significantly extend the traveling wave method that has been widely used to characterize human visual field maps [27, 68–70]. The pRF models extract information from the fMRI time series that is not captured by conventional mapping. The pRF computational analyses, but not the experiments, are more complex than the traveling wave analyses.

PRF models are being applied to a range of phenomena. These models provide a quantitative description of brain activity that is beyond assigning a functional label (color area, motion area, face area, word area). The pRF modeling methods are providing an accurate description of the data based on reliable parameter estimates, and the methods themselves continue to develop. As input-referred models, they can be helpful in coordinating information between different measurement methods. The pRF models provide quantitative baseline measures for different subject populations that can be used to understand clinical conditions in personalized medicine applications. The pRF models are a promising computational neuroimaging method that is contributing to both science and medicine.

BOX 2. Cortical-referred mapping (Connective fields).

Single-unit electrophysiological measurements typically acquire data from a region that is very small compared to the size of the cortical circuit, and there is no opportunity to measure most of the network of inputs and outputs. The field of view in fMRI is much wider, and in many cases it is the data contain measurements from a significant portion of the neural circuitry that determines the voxel’s activity. Consequently, there has been a great deal of interest in using fMRI data to identify and measure large-scale cortical circuits. The most common approach is to use correlations to identify the circuit and causal analyses to separate inputs and outputs [78].

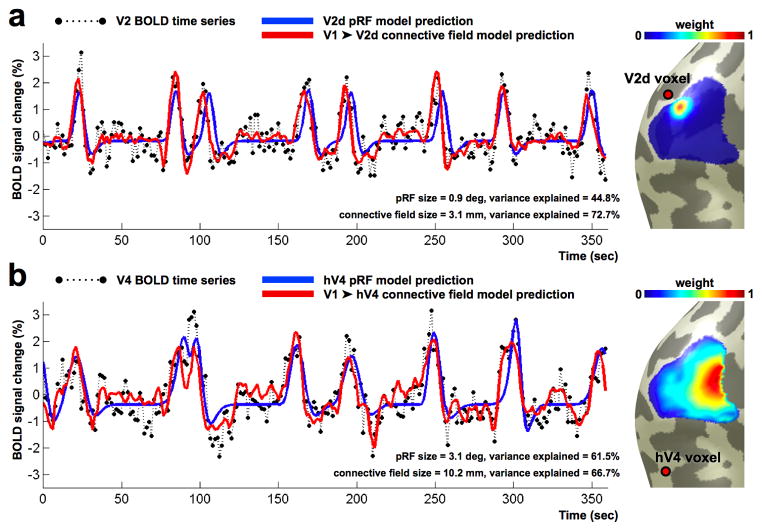
Computational neuroimaging and pRF models are an alternative to the correlational-causal analysis. The computational model can be framed as modeling the fMRI signal in a response region (e.g., V2) as arising from the weighted sum of signals in a source region (e.g., V1). In this formulation, the input to the pRF model is cortex-referred rather than stimulus-referred. There has been progress in developing cortex-referred models that express our current understanding of the functional relationship as a model: compact regions of V1 project to compact regions in V2. We can then solve for the shape and strengths of the connections between the two cortical regions [79, 80] (See Figure I).

This method has mainly been applied to visual cortex, but the approach can be used at other sites. There is significant value in stating an explicit cortex-referred model, fitting its parameters, and testing the accuracy of its predictions. Quantification of the model parameters and accuracy offers an approach that improves on correlational-causal methodology that relies mainly on smoothing, hypothesis testing, and arbitrary correlation thresholds.

Figure I.

Cortically referred pRFs. (a) Two models are used to predict the response in a V2 voxel. The position of the V2 voxel is indicated by the red dot on the brain mesh. V1 is the adjacent region labeled in blue. One model prediction is derived from the stimulus (stimulus-referred, blue line). A second model prediction is derived from a weighted sum of responses in V1, rather than from the stimulus (V1-referred, red line). In this case, the V1 weights are constrained to be a 2D-Gaussian on the cortical surface. The color map on the brain shows the V1-referred model weights. Both models predict the BOLD time series (black) accurately. Unlike the stimulus model, the V1-referred model can predict fluctuations in the V2 response when no stimulus is present. (b) A cortex-referred analysis for a voxel in hV4. The V1- referred receptive field is much larger for the hV4 voxel compared to the V2 voxel. From [79].

BOX 3. Outstanding questions.

1. How to coordinate computational imaging findings and methods? The development of new computational models raises the challenge of developing standards and scientific norms for sharing and validating new approaches. Simplifying sharing and making such behavior a scientific norm will be necessary for computational neuroimaging to succeed.

2. How do visual cortex response properties change across the lifespan? To date, there is a small literature developing in elderly subjects [63, 81, 82] but no population receptive field studies in children. Characterization of maps and pRF properties in development and normal aging will provide useful benchmarks for clinical and scientific questions.

3. How to integrate measurements across species and technologies? The number of tools used to measure brain function continues to grow. There are challenges in measuring any particular circuit or function with just a single technology or experimental paradigm. Additional computational models will be needed to make quantitative comparisons in experiments carried out with different instruments in different species.

Highlights.

• Functional MRI responses to visual stimuli can be predicted accurately using population receptive field (pRF) models

• Input-referred pRF parameters have meaningful units that permit comparisons across labs and measurement modalities

• PRF applications have been extended from basic visual analyses to clarify the effects of attention, developmental plasticity, and neurological and psychiatric disorders