Fundamental limits on the accuracy of demographic inference based on the sample frequency spectrum

Significance

Numerous empirical studies in population genetics have used a summary statistic called the sample frequency spectrum (SFS), which summarizes the information in a sample of DNA sequences. Despite their popularity, the accuracy of inference methods based on the SFS is difficult to characterize theoretically, and it is currently unknown how the estimation accuracy improves as more sites in the genome are used. Here, we establish information theoretic limits on the accuracy of all estimators that use the SFS to infer population size histories. We study the rate of convergence to the true answer as the amount of data increases, and obtain the surprising result that it is exponentially worse than known convergence rates for many classical estimation problems in statistics.

Abstract

The sample frequency spectrum (SFS) of DNA sequences from a collection of individuals is a summary statistic that is commonly used for parametric inference in population genetics. Despite the popularity of SFS-based inference methods, little is currently known about the information theoretic limit on the estimation accuracy as a function of sample size. Here, we show that using the SFS to estimate the size history of a population has a minimax error of at least O(1/log s), where s is the number of independent segregating sites used in the analysis. This rate is exponentially worse than known convergence rates for many classical estimation problems in statistics. Another surprising aspect of our theoretical bound is that it does not depend on the dimension of the SFS, which is related to the number of sampled individuals. This means that, for a fixed number s of segregating sites considered, using more individuals does not help to reduce the minimax error bound. Our result pertains to populations that have experienced a bottleneck, and we argue that it can be expected to apply to many populations in nature.

The past decade has seen a revolution in our ability to interrogate the genome at the molecular level. Fueled by technological advances in DNA sequencing, studies now routinely query thousands or tens of thousands of individuals [refs. 1–4 and UK10K Project (www.uk10k.org) and Exome Aggregation Consortium (exac.broadinstitute.org)] to better understand disease susceptibility, heritability, population history, and other phenomena. In most cases, the conclusions of these studies come in the form of statistical estimates obtained from models that relate the effect of interest to mutation patterns arising in sampled DNA sequences. As genetic sample sizes explode, it is natural to wonder how additional data improve the quality of these estimates. While this general question has received intense focus in theoretical statistics, certain aspects of the genetics setting (for example, non-Gaussianity and lack of independence among samples) complicate efforts to study such models using classical techniques. New methods are needed to theoretically characterize some common models in statistical genetics.

Here, we address this need for a specific estimation problem in population genetics known as demographic inference. As we explain in further detail below, the aim of this problem is to reconstruct the sequence of historical events—including population size changes, migration, and admixture—that gave rise to present-day populations, using DNA samples obtained from those populations. We focus on the simplest problem of estimating the size history of a single population backward in time.

A summary statistic known as the (SFS; defined below) is often used in empirical studies (2, 5–11), but there have been fewer attempts to understand SFS-based estimation from a theoretical perspective. The main result of this paper is to show that, for a common class of estimators that analyze the SFS, there is a fundamental limit on their accuracy as a function of the sample size. More precisely, we show that, under a standard statistical error metric known as minimax error, the rate at which these estimators converge to the truth for certain populations is at best inversely logarithmic in the number of independent segregating sites analyzed, and does not depend at all on the number of individuals sampled. Compared with other types of statistical estimation problems (for example, linear regression), this is an extremely slow rate of convergence. Our proof is information theoretic in nature and applies to any estimator that operates solely on the SFS. This is the first result we are aware of that characterizes the convergence rate of demographic history estimates as a function of sample size.

The remainder of this paper is organized as follows. In Preliminaries, we formally define our notation and model. In Main Results, we state our main theoretical results, followed by a discussion of their practical implications in Discussion. To streamline our exposition, all mathematical proofs are deferred until Proofs.

Preliminaries

The stochastic process underlying the inference procedure we consider is Kingman’s coalescent (12–14), which evolves backward in time and describes the genealogy of a collection of chromosomes randomly sampled from a population. The population size is assumed to change deterministically over time and is described by a function $\eta :\left[0,\infty \right)\mathrm{\to }\left(0,\infty \right)\mathrm{,}$ with $\eta \left(t\right)$ being the population size at time t in the past. The instantaneous rate of coalescence between any pair of lineages at time t is $1/\eta \left(t\right)$.

As in the standard infinite sites model of mutation (15), we assume that every dimorphic site (i.e., a site with exactly two observed allelic types) has experienced mutation exactly once in the evolutionary history of the sample. Further, for each such site, we assume that it is known which allele is the ancestral type versus the mutant type. In what follows, we use the terms “dimorphic” and “segregating” interchangeably.

A population size function $\eta \left(t\right)$ induces a probability distribution on the number of derived alleles found at a particular segregating site. Specifically, for a sample of $n\ge 2$ randomly sampled individuals, let ${\xi }_{n,b}^{\left(\eta \right)}$, for $1\le b\le n-1$, denote the probability that a segregating site contains b mutant alleles in a sample of n individuals under model η. The vector ${\mathbf{\xi }}_n^{\left(\eta \right)}\stackrel{\text{def}}{=}\left({\xi }_{n,1}^{\left(\eta \right)},\dots ,{\xi }_{n,n-1}^{\left(\eta \right)}\right)$ is called the expected SFS. In the coalescent setting, a general expression for ${\xi }_{n,b}^{\left(\eta \right)}$ is given by (16)

$${\xi }_{n,b}^{\left(\eta \right)}\propto {\displaystyle \sum _{k=2}^{n-b+1}\frac{\left(\begin{array}{c}n-b-1\\ k-2\end{array}\right)}{\left(\begin{array}{c}n-1\\ k-1\end{array}\right)}\cdot k\cdot \mathbb{E}{T}_{n,k}^{\left(\eta \right)}},$$

where $\mathbb{E}{T}_{n,k}^{\left(\eta \right)}$ denotes the amount of time (in coalescent units) during which the genealogy of the sample contained k lineages under model η. The expected waiting time $\mathbb{E}{T}_{m,m}^{\left(\eta \right)}$ to the first coalescence in a sample of m individuals is given by

$$c_m^{\left(\eta \right)}\stackrel{\text{def}}{=}\mathbb{E}{T}_{m,m}^{\left(\eta \right)}={\displaystyle \underset{0}{\overset{\infty }{\int }}t\frac{a_m}{\eta \left(t\right)}\exp \left\{-a_m{R}_{\eta }\left(t\right)\right\}\text{d}t},$$ [1]

where $a_m\stackrel{\text{def}}{=}\left(\begin{array}{c}m\\ 2\end{array}\right)$ and $R_{\eta }\left(t\right)\stackrel{\text{def}}{=}{\displaystyle {\int }_0^t\frac{1}{\eta \left(s\right)}\text{d}s}$ is the cumulative rate of coalescence up to time t. It turns out (17) that there is an invertible linear transformation that relates $\left(\mathbb{E}{T}_{n,2}^{\left(\eta \right)},\mathbb{E}{T}_{n,3}^{\left(\eta \right)},\dots ,\mathbb{E}{T}_{n,n}^{\left(\eta \right)}\right)$ to ${\mathbf{c}}^{\left(\eta \right)}\stackrel{\text{def}}{=}\left(c_2^{\left(\eta \right)},c_3^{\left(\eta \right)},\dots ,c_n^{\left(\eta \right)}\right)$. Using this relation, the quantity ${\xi }_{n,b}^{\left(\eta \right)}$ can be written as (18)

$${\xi }_{n,b}^{\left(\eta \right)}=\frac{\langle {\mathbf{c}}^{\left(\eta \right)},{\mathbf{W}}_{n,b}\rangle }{\langle {\mathbf{c}}^{\left(\eta \right)},{\mathbf{V}}_n\rangle },$$ [2]

where ${\mathbf{W}}_{n,b}=\left(W_{n,b,2},\dots ,W_{n,b,n}\right)$ and ${\mathbf{V}}_n=\left(V_{n,2},\dots ,V_{n,n}\right)$ are vectors of universal constants that do not depend on the population size function η, and $\langle \cdot ,\cdot \rangle$ denotes the $l_2$ inner product. Under model η, the quantity $\langle {\mathbf{c}}^{\left(\eta \right)},{\mathbf{W}}_{n,b}\rangle$ is the total expected length of edges subtending b out of n individuals sampled at time 0, while the quantity $\langle {\mathbf{c}}^{\left(\eta \right)},{\mathbf{V}}_n\rangle$ is the total expected tree length for a sample of size n. Both quantities are positive for all population size functions η. For an arbitrary population size function η, we have ${\displaystyle {\sum }_{b=1}^{n-1}{W}_{n,b,m}}=V_{n,m}$ for all $2\le m\le n$, which implies

$${\displaystyle \sum _{b=1}^{n-1}\langle {\mathbf{c}}^{\left(\eta \right)},{\mathbf{W}}_{n,b}\rangle }=\langle {\mathbf{c}}^{\left(\eta \right)},{\mathbf{V}}_n\rangle .$$ [3]

For a constant function $\eta \left(t\right)\equiv N$,

$$c_m^{\left(\eta \right)}=\frac{N}{a_m},$$

$$\langle {\mathbf{c}}^{\left(\eta \right)},{\mathbf{W}}_{n,b}\rangle =\frac{2}{b}N,$$ [4]

$$\langle {\mathbf{c}}^{\left(\eta \right)},{\mathbf{V}}_n\rangle =2N\hspace{0.17em}{H}_{n-1},$$ [5]

where $H_{n-1}\stackrel{\text{def}}{=}{\displaystyle {\sum }_{b=1}^{n-1}\frac{1}{b}}$.

To formulate the problem, we use the following notation. We suppose that a sample of $n\ge 2$ randomly sampled individuals has been typed at s independent segregating sites. These data are used to form the empirical sample frequency spectrum, which is an $\left(n-1\right)$-tuple $\left({\widehat{\xi }}_{n,1},\dots ,{\widehat{\xi }}_{n,n-1}\right)$, where ${\widehat{\xi }}_{n,b}$ denotes the proportion of segregating sites with b copies of the mutant allele and $n-b$ copies of the ancestral allele. A frequency-based estimator is any statistic $\widehat{\eta }$ that maps an empirical SFS to a population size history.

Main Results

Here, we establish a minimax lower bound on the ability of any estimator $\widehat{\eta }$ to accurately reconstruct population size functions.

A General Bound on the Kullback−Leibler Divergence Between Two SFS Distributions.

Abusing notation, we use $D\left(\eta \Vert {\eta }^{\prime }\right)$ to denote the Kullback−Leibler (KL) divergence between the probability distributions ${\mathbf{\xi }}_n^{\left(\eta \right)}$ and ${\mathbf{\xi }}_n^{\left({\eta }^{\prime }\right)}$. In Proofs, we prove the following general upper bound on the KL divergence between two SFS distributions:

Theorem 1.

Let $\mathrm{ℳ}$ denote a general space of population size functions and suppose $\eta ,{\eta }^{\prime }\in \mathrm{ℳ}$ satisfy $\eta \left(t\right)={\eta }^{\prime }\left(t\right)$ for all $0\le t\le t_c$ and ${\text{max}}_{t>t_c}\eta \left(t\right)\le {\text{min}}_{t>t_c}{\eta }^{\prime }\left(t\right)$. Then,

$$D\left(\eta \Vert {\eta }^{\prime }\right)\le \frac{\langle {\mathbf{c}}^{\left({\eta }^{\prime }\right)}-{\mathbf{c}}^{\left(\eta \right)},{\mathbf{V}}_n\rangle }{\langle {\mathbf{c}}^{\left(\eta \right)},{\mathbf{V}}_n\rangle }.$$ [6]

Bounds for a Family of Piecewise Constant Models.

We now focus on a particular class of population size functions that are easier to analyze and are popular in the literature (11, 19, 20). For a fixed positive integer $K>1$, let ${\mathrm{ℳ}}_K\subset \mathrm{ℳ}$ denote the space of piecewise constant size functions with exactly K pieces. A population size function η is a member of ${\mathrm{ℳ}}_K$ if and only if there exist positive real numbers $t_1<\dots <t_{K-1}$ and $N_1,N_2,\dots ,N_K$ such that

$$\eta \left(t\right)={\displaystyle \sum _{k=1}^K{N}_k\mathbf{1}\left\{t_{k-1}\le t<t_k\right\}},$$ [7]

where, by convention, we define $t_0=0$ and $t_K=\infty$. For such an η, define

$$S_k^{\left(\eta \right)}\stackrel{\text{def}}{=}{\displaystyle \sum _{j=1}^k\frac{t_j-t_{j-1}}{N_j}}.$$ [8]

For $\eta \in {\mathrm{ℳ}}_K$, the expected waiting time $c_m^{\left(\eta \right)}$ defined in Eq. 1 is given by

$$c_m^{\left(\eta \right)}=\frac{1}{a_m}{\displaystyle \sum _{k=1}^K{N}_k\left(e^{-a_m{S}_{k-1}^{\left(\eta \right)}}-e^{-a_m{S}_k^{\left(\eta \right)}}\right)}.$$ [9]

Note that since $t_K=\infty$,

$$e^{-a_m{S}_K^{\left(\eta \right)}}\equiv 0,\hspace{0.17em}\text{for}\hspace{0.17em}\text{all}\hspace{0.17em}\eta \in {\mathrm{ℳ}}_K.$$ [10]

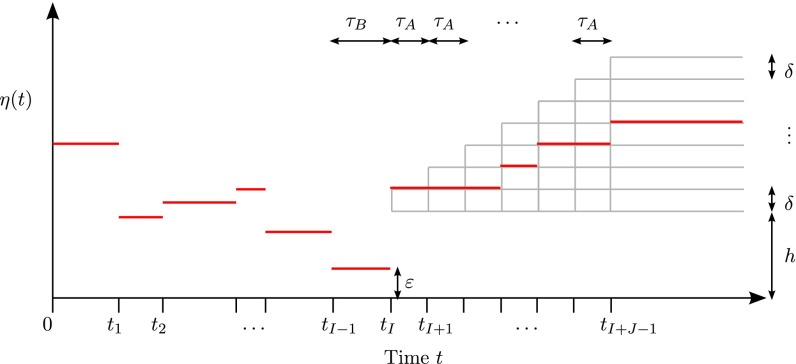
To formulate our result, we let $I,J$ denote positive integers that satisfy $I+J=K$, and introduce a subfamily ${\mathrm{ℱ}}_{I,J}\subset {\mathrm{ℳ}}_K$ of piecewise constant functions defined as follows. See Fig. 1 for illustration. We assume that all change points $t_1<\dots <t_{I+J-1}$ are fixed and that the sizes $N_1,\dots ,N_I$ of the first I epochs are also fixed, with $N_I$ being the smallest size. So, all functions in ${\mathrm{ℱ}}_{I,J}$ are identical to each other for the first I epochs, and there is a population bottleneck in the last epoch. Then, for $t\ge t_I$, every function $\eta \in {\mathrm{ℱ}}_{I,J}$ undergoes jumps according to the following rules:

• 1.For the interval $t_I\le t<t_{I+1}$, $\eta \left(t\right)$ takes a constant value of either h or $h+\delta$, where $h>N_I$ and $\delta >0$.
• 2.At later change points $\left\{t_{I+1},\dots ,t_{I+J-1}\right\}$, η either stays the same or jumps upward by δ.

Fig. 1.

A family ${\mathrm{ℱ}}_{I,J}$ of piecewise-constant population size models with $K=I+J$ epochs.

Hence, ${\mathrm{ℱ}}_{I,J}$ consists of $2^J$ distinct piecewise constant functions that are nondecreasing functions of t for $t\ge t_I$. Note that ${\text{min}}_t\eta \left(t\right)=N_I$ for all $\eta \in {\mathrm{ℱ}}_{I,J}$. For ease of notation, we use $\epsilon \stackrel{\text{def}}{=}{N}_I$ to denote the bottleneck size and ${\tau }_B\stackrel{\text{def}}{=}{t}_I-t_{I-1}$ to denote the bottleneck duration. To facilitate analysis later, we fix $t_{I+j}-t_{I+j-1}$ to some positive constant ${\tau }_A$ for all $j=1,\dots ,J-1$.

For any two models in ${\mathrm{ℱ}}_{I,J}$, we obtain the following bound on the difference of their waiting times to the first coalescence:

Lemma 2.

For all $\eta ,{\eta }^{\prime }\in {\mathrm{ℱ}}_{I,J}$,

$$\left|c_m^{\left(\eta \right)}-c_m^{\left({\eta }^{\prime }\right)}\right|\le J\frac{\delta }{a_m}{e}^{-a_m{\tau }_B/\epsilon }.$$ [11]

Together with Theorem 1, this lemma can be used to show

Theorem 3.

Let $\eta ,{\eta }^{\prime }\in {\mathrm{ℱ}}_{I,J}$ that satisfy ${\text{max}}_{t\ge t_I}\eta \left(t\right)\le {\text{min}}_{t\ge t_I}{\eta }^{\prime }\left(t\right).$ Then,

$$D\left(\eta \Vert {\eta }^{\prime }\right)\le J\frac{\delta }{\epsilon }{e}^{-{\tau }_B/\epsilon }.$$ [12]

Proofs of these results are deferred to Proofs. It is interesting that the above bound does not depend on the number n of sampled individuals.

Minimax Lower Bounds.

Before using the above results to obtain a minimax lower bound, we first note a subtle fact. Given any population size function η, consider a function ζ that satisfies $\zeta \left(t\right)=\kappa \cdot \eta \left(t/\kappa \right)$ for all $t\in \left[0,\infty \right)$, where κ is some positive constant. Such functions are equivalent, as it turns out that ${\xi }_{n,b}^{\left(\zeta \right)}={\xi }_{n,b}^{\left(\eta \right)}$ for all $n\ge 2$ and $1\le b\le n-1$. To mod out by this equivalence, we assume that every $\eta \in \mathrm{ℳ}$ satisfies $\eta \left(0\right)=N_{\hspace{0.17em}\text{fix}}$, where $N_{\hspace{0.17em}\text{fix}}$ is some fixed positive constant.

Let ${\Vert \cdot \Vert }_{*}$ denote a generic norm (specific examples will be given later) and let ${\mathbb{E}}_{\eta }(\cdot )$ denote expectation with respect to the SFS distribution ${\mathbf{\xi }}_n^{\left(\eta \right)}=\left({\xi }_{n,1}^{\left(\eta \right)},\dots ,{\xi }_{n,n-1}^{\left(\eta \right)}\right)$ induced by population size function η. Then, note that

$$\underset{\widehat{\eta }}{\text{inf}}\underset{\eta \in \mathrm{ℳ}}{\text{sup}}{\mathbb{E}}_{\eta }{\left|\left|\widehat{\eta }-\eta \right|\right|}_{*}\ge \underset{\widehat{\eta }}{\text{inf}}\underset{\eta \in {\mathrm{ℳ}}_K}{\text{sup}}{\mathbb{E}}_{\eta }{\left|\left|\widehat{\eta }-\eta \right|\right|}_{*}\ge \underset{\widehat{\eta }}{\text{inf}}\underset{\eta \in {\mathrm{ℱ}}_{I,J}}{\text{sup}}{\mathbb{E}}_{\eta }{\left|\left|\widehat{\eta }-\eta \right|\right|}_{*}.$$

In what follows, we will put a lower bound on the last quantity. We first fix a sensible distance metric on $\mathrm{ℳ}$. An intuitive way to measure distance between two population size functions is their $L_1$ distance, ${\left|\left|{\eta }_a-{\eta }_b\right|\right|}_1={\displaystyle {\int }_0^{\infty }\left|{\eta }_a\left(t\right)-{\eta }_b\left(t\right)\right|\text{d}t}$, but this is unreasonably stringent in that ${\left|\left|{\eta }_a-{\eta }_b\right|\right|}_1=\infty$ if ${\eta }_a$ and ${\eta }_b$ do not agree infinitely far back into the past. Instead we will focus on the following truncated $L_1$ distance: ${\left|\left|{\eta }_a-{\eta }_b\right|\right|}_{1,T}\stackrel{\text{def}}{=}{\displaystyle {\int }_0^T\left|{\eta }_a\left(t\right)-{\eta }_b\left(t\right)\right|\text{d}t}$, which measures the discrepancy between ${\eta }_a$ and ${\eta }_b$ back to some fixed time T in the past.

Henceforth, let $\widehat{\eta }$ be any estimator of the population size function that operates on a sample of s independent segregating sites obtained from a sample of n randomly sampled individuals. In Proofs, we prove the following main results of our paper:

Theorem 4.

Consider the subfamily ${\mathrm{ℱ}}_{I,J}$ of models described above, and suppose $J>8$ and $T\ge t_{I+J-1}+{\tau }_A$. Then,

$$\underset{\widehat{\eta }}{\text{inf}}\underset{\eta \in {\mathrm{ℱ}}_{I,J}}{\text{sup}}{\mathbb{E}}_{\eta }{\left|\left|\widehat{\eta }-\eta \right|\right|}_{1,T}\ge C{\tau }_A\frac{{\left(J-8\right)}^2}{J}\frac{\epsilon }{s}{e}^{{\tau }_B/\epsilon },$$ [13]

where C is a positive constant.

The above theorem applies to all models in ${\mathrm{ℱ}}_{I,J}$. We now consider the subset ${\mathrm{ℱ}}_{I,J}^M=\left\{\eta \in {\mathrm{ℱ}}_{I,J}:{\Vert \eta \Vert }_{\infty }<M\right\}$, which is the set of all models in ${\mathrm{ℱ}}_{I,J}$ that are bounded by some constant M. For this family of bounded population size functions, a sharper asymptotic lower bound can be obtained as follows.

Theorem 5.

Suppose $J>8$ and $T\ge t_{I+J-1}+{\tau }_A$. Then,

$$\underset{\widehat{\eta }}{\text{inf}}\underset{\eta \in {\mathrm{ℱ}}_{I,J}^M}{\text{sup}}{\mathbb{E}}_{\eta }{\left|\left|\widehat{\eta }-\eta \right|\right|}_{1,T}\ge C^{\prime }\frac{{\left(J-8\right)}^2}{J}\frac{{\tau }_B{\tau }_A}{\log s},$$ [14]

where $C^{\prime }$ is a positive constant.

By specializing ${\mathrm{ℱ}}_{I,J}^M$, a simplified version of Theorem 5 can be obtained:

Corollary 6.

Suppose $T\ge t_{I+J-1}+{\tau }_A$ and let ${\mathrm{ℱ}}_{I,\mathrm{\star }}^M={\mathrm{\cup }}_{J\ge 1}{\mathrm{ℱ}}_{I,J}^M$. Then,

$$\underset{\widehat{\eta }}{\text{inf}}\underset{\eta \in {\mathrm{ℱ}}_{I,\mathrm{\star }}^M}{\text{sup}}{\mathbb{E}}_{\eta }{\left|\left|\widehat{\eta }-\eta \right|\right|}_{1,T}\ge C^{″}\left(T-t_I\right)\frac{{\tau }_B}{\log s},$$ [15]

where $C^{″}$ is a positive constant.

Note that the above lower bounds do not depend on the dimension of the SFS (which is equal to $n-1$). Hence, for a fixed number s of segregating sites considered, using more individuals does not diminish the error bounds.

Bottleneck Followed by Exponential Growth.

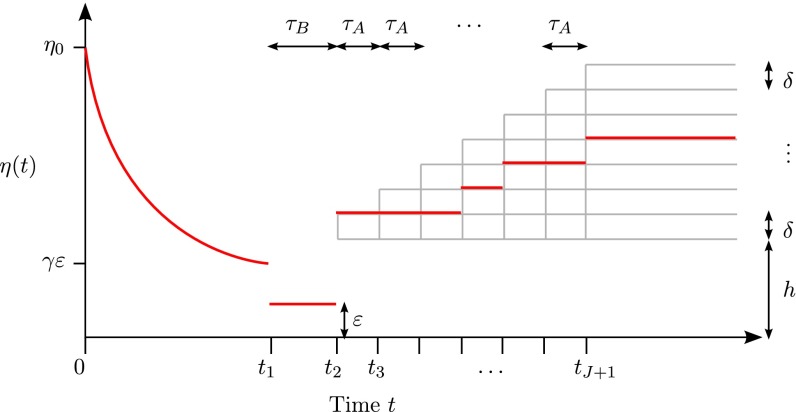
In the results presented above, we dropped smaller terms to obtain the dominant contribution to our lower bound. Here, we provide a more detailed analysis to study how the model in the recent past (i.e., the period $0\le t\le t_{I-1}$) affects the lower bound. A slight modification of the above results permits us to analyze the following model class, which is of interest in, for example, human genetics (2, 3, 7): Let ${\mathcal{G}}_J$ be the family of models illustrated in Fig. 2 with exponential growth in the recent past. Specifically, $\eta \left(t\right)={\eta }_0{e}^{-\beta \left({\eta }_0\right)t}$ for the period $0\le t\le t_1$. The rate of growth $\beta \left({\eta }_0\right)=\text{log}\left({\eta }_0/\gamma \epsilon \right)/t_1$ is defined so that $\eta \left(t_1\right)=\gamma \epsilon$ for all $\eta \in {\mathcal{G}}_J$, where $\gamma \ge 1$. The part for $t>t_1$ is the same as that for $t>t_{I-1}$ in ${\mathrm{ℱ}}_{I,J}$ (Fig. 1). We obtain the following result for the subfamily ${\mathcal{G}}_J$:

Fig. 2.

A family ${\mathcal{G}}_J$ of population size models with exponential growth in the recent past. This family consists of size histories that are piecewise constant before the bottleneck, and then jump to some level $\gamma \epsilon$ and undergo (identical) exponential growth from time $t_1$ to present.

Theorem 7.

Consider the subfamily ${\mathcal{G}}_J$ of models described above, and suppose $J>8$ and $T\ge t_J+{\tau }_A$. Then,

$$\underset{\widehat{\eta }}{\text{inf}}\underset{\eta \in {\mathcal{G}}_J}{\text{sup}}{\mathbb{E}}_{\eta }{\left|\left|\widehat{\eta }-\eta \right|\right|}_{1,T}\ge C{\tau }_A\frac{{\left(J-8\right)}^2}{J}\frac{\epsilon }{s}\exp \left[\frac{{\tau }_B}{\epsilon }+t_1\frac{\frac{1}{\gamma \epsilon }-\frac{1}{{\eta }_0}}{\text{log}\left({\eta }_0\right)-\text{log}\left(\gamma \epsilon \right)}\right].$$ [16]

Theorem 4 is a measure of how (a lower bound on) estimation error depends on growth following a bottleneck. The two extremes ${\eta }_0\to \mathrm{\infty }$ and ${\eta }_0\to \gamma \epsilon$ have intuitive interpretations. For large ${\eta }_0$, the bound in Eq. 16 tends to the corresponding bound given by Theorem 4, as expected since coalescences become increasingly less likely in the first time period. Small ${\eta }_0$ has the effect of ‘‘prolonging’’ the bottleneck, thus increasing the minimax lower bound. In particular, if $\gamma =1$ then $t_1\left[\left(1/\gamma \epsilon \right)-\left(1/{\eta }_0\right)\right]/\left[\text{log}\left({\eta }_0\right)-\text{log}\left(\gamma \epsilon \right)\right]\to \left(t_1/\epsilon \right)$ as ${\eta }_0\to \gamma \epsilon$, so that the effect of low population growth on the minimax lower bound is to simply prolong the bottleneck effect by an additional $t_1$ time periods.

Discussion

In this paper, we have theoretically characterized fundamental limits on the accuracy of demographic inference from data. We have shown that the minimax error rate for estimating the piecewise-constant demography of a single population is at least $O\left(1/\log s\right)$, where s is the number of independent segregating sites analyzed. In contrast, the minimax error for many classical estimation problems in statistics (for example, nonparametric regression or density estimation) decays inverse polynomially in the sample size (21). Compared with these problems, exponentially more samples would be required to estimate a population size history function to within a similar magnitude of error. The paper that most closely relates to the present work is by Kim et al. (22), who obtain lower bounds on the amount of exact coalescence time data necessary to distinguish between size histories in a hypothesis testing framework. Since coalescence times are never observed and must be estimated from data, these bounds place a limit on the accuracy with which a population size function can be inferred. The authors also describe an estimator that uses coalescence times (again observed without noise) to accurately recover the underlying population size function with high probability, at a rate that roughly matches the lower bound.

Another line of work centers around the identifiability of the parameter $\eta \left(t\right)$ using the SFS. Roughly speaking, a family of statistical models ${\left\{P_{\theta }\right\}}_{\theta \in \mathrm{\Theta }}$ defined over a parameter space $\mathrm{\Theta }$ is identifiable if, for any ${\theta }_1,{\theta }_2\in \mathrm{\Theta }$ with ${\theta }_1\ne {\theta }_2$, the sampling distributions induced by $P_{{\theta }_1}$ and $P_{{\theta }_2}$ are different. In our context, this simply says that, for all n, ${\mathbf{\xi }}_n^{\left({\eta }_1\right)}\ne {\mathbf{\xi }}_n^{\left({\eta }_2\right)}$ unless ${\eta }_1={\eta }_2$ almost everywhere. Standard desiderata for statistical estimators (e.g., consistency or unbiasedness) are impossible without identifiability, so it is the weakest possible regularity condition one can impose on a useful family of models.

Perhaps surprisingly, it turns out that, in general, a population size function is not identifiable from the SFS (23). Indeed, for any given $\eta \left(t\right)$, it has been shown that an infinite number of smooth functions $F\left(t\right)$ exist such that ${\mathbf{\xi }}_n^{\left(\eta \right)}={\mathbf{\xi }}_n^{\left(\eta +F\right)}$. Moreover, explicit examples can be constructed that demonstrate this phenomenon (23). On the other hand, these counterexamples consist of functions that exhibit an unbounded frequency of oscillatory behavior near the present time, which is perhaps unrealistic when modeling naturally occurring populations. More recently, it has been shown (19) that identifiability holds for many classes of population size functions used by practitioners (including piecewise constant, piecewise exponential, and piecewise generalized exponential). Furthermore, the number n of sampled individuals sufficient for identifiability can be explicitly given and is a function of the complexity of the underlying class of models being studied (19).

Identifiability asserts that, given an infinite amount of data (specifically, taking the number of segregating sites $s\to \infty$), the model parameter $\eta \left(t\right)$ can be uniquely recovered. In practice, s is finite, and only a perturbed version of the expected frequency spectrum, say ${\widehat{\mathbf{\xi }}}_n^{\left(\eta \right)}$, is observed. From a practical standpoint, it is important to understand how these perturbations ultimately affect the parameter estimate $\widehat{\eta }\left(t\right)$. It is this question that forms the starting point for the present work.

A single population evolving under a piecewise-constant demography is a special case of many richer classes of demographic models. For example, it is a (limiting) member of the family of exponential growth models, seen by taking each exponential growth parameter to zero. In the multispecies coalescent setting (10, 24), multiple population size histories must be estimated, and the error of that estimate must necessarily be lower bounded by that of estimating a single such history. Thus, our result can be expected to apply to a broader class of models than the one we have studied here.

As detailed in Proofs, the result in Theorem 5 follows from setting $\epsilon ={\tau }_B/\log s$ and $\delta \propto \frac{\epsilon }{s}\exp \left({\tau }_B/\epsilon \right)$ in the subfamily ${\mathrm{ℱ}}_{I,J}^M$. The size ${\tau }_B/\log s$ is in coalescent units. In terms of the number of individuals, it is proportional to $g_B/\log s$, where $g_B$ is the number of generations corresponding to duration ${\tau }_B$ in the coalescent limit. Intuitively, as the severity of the bottleneck increases, the population is increasingly likely to find its most recent common ancestor (MRCA) during that time; farther back in time than the MRCA, no information is conveyed concerning the demographic events experienced by the population.

One might object to considering models with a bottleneck size that scales inversely with the number s of segregating sites in the data, and it is indeed possible that a better convergence rate may be achievable for populations that are known not to contain a bottleneck. On the other hand, we note that $1/\log s$ decreases sufficiently slowly with s that our result can be expected to apply to many real-world examples. For example, for $s\approx {10}^8$, which is a conservative upper bound for most organisms, $g_B/\log s\approx 0.054g_B$. This implies that for populations that have experienced roughly an order-of-magnitude increase in effective population size during their history, accurate estimation of demographic events that occurred before this expansion is difficult using SFS-based methods. Additionally, an interesting aspect of our work is that our minimax lower bounds do not depend on the number n of sampled individuals; increasing n is not enough to overcome the information barrier imposed by the presence of a bottleneck. This is intuitively plausible since, as n increases, the $\left(n+1\right)$ th sampled lineage becomes more likely to coalesce early on.

An interesting question that we have not attempted to analyze is whether the $O\left(1/\log s\right)$ rate is optimal, i.e., whether there exists some estimator $\widehat{\eta }\left(t\right)$ that achieves the minimax lower bound established here. In practice, from Eqs. 2, 8, and 9, it can be seen that naively maximizing the likelihood of the observed SFS with respect to $\eta \left(t\right)$ requires solving a nonconvex optimization problem, so that convergence to the global maximum is not even guaranteed. Computational issues aside, finding such an estimator remains an open theoretical challenge.

In closing, we stress that our result is specific to SFS-based estimators, which analyze only independent sites. The main allure of these estimators is their mathematical tractability, rather than their realism. In fact, a rich source of additional information exists in the correlation structure found among linked sites in the genome. Methods that seek to exploit this structure by modeling the action of recombination pose greater mathematical and computational difficulties, but there has been recent progress in this area (20, 25–29). Our result serves to underscore the importance of pursuing more realistic models of genomic evolution, challenging though they may be.

Proofs

Proof of Theorem 1. To simplify the notation, we write $\mathbf{c}={\mathbf{c}}^{\left(\eta \right)}$ and ${\mathbf{c}}^{\prime }={\mathbf{c}}^{\left({\eta }^{\prime }\right)}$. Then, using Eq. 2, we can write

$$D\left(\eta \Vert {\eta }^{\prime }\right)={\displaystyle \sum _{b=1}^{n-1}{\xi }_{n,b}^{\left(\eta \right)}}\log \frac{{\xi }_{n,b}^{\left(\eta \right)}}{{\xi }_{n,b}^{\left({\eta }^{\prime }\right)}}={\displaystyle \sum _{b=1}^{n-1}{\xi }_{n,b}^{\left(\eta \right)}\left[\log \left(\frac{\langle \mathbf{c},{\mathbf{W}}_{n,b}\rangle }{\langle {\mathbf{c}}^{\prime },{\mathbf{W}}_{n,b}\rangle }\right)+\log \left(\frac{\langle {\mathbf{c}}^{\prime },{\mathbf{V}}_n\rangle }{\langle \mathbf{c},{\mathbf{V}}_n\rangle }\right)\right]}.$$

The assumption ${\text{min}}_{t>t_c}{\eta }^{\prime }\left(t\right)\ge {\text{max}}_{t>t_c}\eta \left(t\right)$ implies that, for all times $t,t^{\prime }>t_c$, the instantaneous rate of coalescence at time t in model η is greater than or equal to $\ge$ the instantaneous rate of coalescence at time $t^{\prime }$ in model ${\eta }^{\prime }$. Hence, this assumption together with $\eta \left(t\right)={\eta }^{\prime }\left(t\right)$ for all $0\le t\le t_c$ implies $\langle \mathbf{c}-{\mathbf{c}}^{\prime },{\mathbf{W}}_{n,b}\rangle \le 0$ for all $1\le b\le n-1$; equivalently, $\text{log}\left(\langle \mathbf{c},{\mathbf{W}}_{n,b}\rangle /\langle {\mathbf{c}}^{\prime },{\mathbf{W}}_{n,b}\rangle \right)<0$. Additionally, $\left(\langle {\mathbf{c}}^{\prime }-\mathbf{c},{\mathbf{V}}_n\rangle /\langle \mathbf{c},{\mathbf{V}}_n\rangle \right)>-1$ and $\text{log}\left(1+x\right)\le x$ for all $x\ge -1$. Combining these facts, we obtain

$$D\left(\eta \Vert {\eta }^{\prime }\right)\le {\displaystyle \sum _{b=1}^{n-1}{\xi }_{n,b}^{\left(\eta \right)}}\log \left(\frac{\langle {\mathbf{c}}^{\prime },{\mathbf{V}}_n\rangle }{\langle \mathbf{c},{\mathbf{V}}_n\rangle }\right)\le {\displaystyle \sum _{b=1}^{n-1}{\xi }_{n,b}^{\left(\eta \right)}}\frac{\langle {\mathbf{c}}^{\prime }-\mathbf{c},{\mathbf{V}}_n\rangle }{\langle \mathbf{c},{\mathbf{V}}_n\rangle }=\frac{\langle {\mathbf{c}}^{\prime }-\mathbf{c},{\mathbf{V}}_n\rangle }{\langle \mathbf{c},{\mathbf{V}}_n\rangle },$$

where we have used ${\displaystyle {\sum }_{b=1}^{n-1}{\xi }_{n,b}^{\left(\eta \right)}}=1$ in the final equality.

Proof of Lemma 2. We distinguish two particular models, ${\eta }_{\ell },{\eta }_u\in {\mathrm{ℱ}}_{I,J}$, which are the lower and the upper envelopes of ${\mathrm{ℱ}}_{I,J}$. The function ${\eta }_{\ell }$ stays constant at h for all $t\ge t_I$, while ${\eta }_u$ jumps upward by δ at every change point $t_I,\dots ,t_{I+J-1}$. Hence, ${\eta }_{\ell }\le \eta \le {\eta }_u$ pointwise for all $\eta \in {\mathrm{ℱ}}_{I,J}$. The two enveloping functions will form the basis of subsequent analysis.

Fix $\eta ,{\eta }^{\prime }\in {\mathrm{ℱ}}_{I,J}$ and note that, by the definition of ${\mathrm{ℱ}}_{I,J}$, one of these functions must pointwise dominate the other. Therefore, assume without loss of generality that $\eta \left(t\right)\le {\eta }^{\prime }\left(t\right)$ for all t. Then, for all t,

$${\eta }_{\ell }\left(t\right)\le \eta \left(t\right)\le {\eta }^{\prime }\left(t\right)\le {\eta }_u\left(t\right),$$

which implies

$$c_m^{\left({\eta }_{\ell }\right)}\le c_m^{\left(\eta \right)}\le c_m^{\left({\eta }^{\prime }\right)}\le c_m^{\left({\eta }_u\right)},$$

for all $m=2,\dots ,n$. Using these inequalities, we conclude

$$c_m^{\left({\eta }^{\prime }\right)}-c_m^{\left(\eta \right)}\le c_m^{\left({\eta }_u\right)}-c_m^{\left({\eta }_{\ell }\right)},$$

so it suffices to demonstrate Eq. 11 for $c_m^{\left({\eta }_u\right)}-c_m^{\left({\eta }_{\ell }\right)}$. Now, by Eq. 9 and the definition of ${\eta }_{\ell }$,

$$a_m{c}_m^{\left({\eta }_{\ell }\right)}={\displaystyle \sum _{i=1}^I{N}_i\left[e^{-a_m{S}_{i-1}^{\left({\eta }_{\ell }\right)}}-e^{-a_m{S}_i^{\left({\eta }_{\ell }\right)}}\right]}+{\displaystyle \sum _{j=1}^{J}h\left[e^{-a_m{S}_{I+j-1}^{\left({\eta }_{\ell }\right)}}-e^{-a_m{S}_{I+j}^{\left({\eta }_{\ell }\right)}}\right]}={\displaystyle \sum _{i=1}^I{N}_i\left[e^{-a_m{S}_{i-1}^{\left({\eta }_{\ell }\right)}}-e^{-a_m{S}_i^{\left({\eta }_{\ell }\right)}}\right]}+h{e}^{-a_m{S}_I^{\left({\eta }_{\ell }\right)}},$$

where we have used Eq. 10. Similarly,

$$a_m{c}_m^{\left({\eta }_u\right)}={\displaystyle \sum _{i=1}^I{N}_i\left[e^{-a_m{S}_{i-1}^{\left({\eta }_u\right)}}-e^{-a_m{S}_i^{\left({\eta }_u\right)}}\right]}+{\displaystyle \sum _{j=1}^J\left(h+j\delta \right)\left[e^{-a_m{S}_{I+j-1}^{\left({\eta }_u\right)}}-e^{-a_m{S}_{I+j}^{\left({\eta }_u\right)}}\right]}={\displaystyle \sum _{i=1}^I{N}_i\left[e^{-a_m{S}_{i-1}^{\left({\eta }_u\right)}}-e^{-a_m{S}_i^{\left({\eta }_u\right)}}\right]}+h{e}^{-a_m{S}_I^{\left({\eta }_u\right)}}+{\displaystyle \sum _{j=1}^{J}j\delta \left[e^{-a_m{S}_{I+j-1}^{\left({\eta }_u\right)}}-e^{-a_m{S}_{I+j}^{\left({\eta }_u\right)}}\right]}.$$

Now, using the fact that ${\eta }_{\ell }$ and ${\eta }_u$ agree on the first I epochs, we obtain

$$a_m\left[c_m^{\left({\eta }_u\right)}-c_m^{\left({\eta }_{\ell }\right)}\right]={\displaystyle \sum _{j=1}^{J}j\delta \left[e^{-a_m{S}_{I+j-1}^{\left({\eta }_u\right)}}-e^{-a_m{S}_{I+j}^{\left({\eta }_u\right)}}\right]}=\delta {\displaystyle \sum _{j=1}^J{e}^{-a_m{S}_{I+j-1}^{\left({\eta }_u\right)}}}\le J\delta e^{-a_m{\tau }_B/\epsilon },$$ [17]

where the second line follows from telescoping and the fact that $S_{I+J}^{\left({\eta }_u\right)}=\infty$, while the last line follows from the fact that $\frac{{\tau }_B}{\epsilon }\le S_{I+j-1}^{\left({\eta }_u\right)}$ for all $j=1,\dots ,J$.

Proof of Theorem 3. For ease of notation, define $\mathbf{c}={\mathbf{c}}^{\left(\eta \right)}$ and ${\mathbf{c}}^{\prime }={\mathbf{c}}^{\left({\eta }^{\prime }\right)}$. By Lemma 2,

$$\langle {\mathbf{c}}^{\prime }-\mathbf{c},{\mathbf{V}}_n\rangle ={\displaystyle \sum _{m=2}^n\left(c_m\prime -c_m\right)}{V}_{n,m}\le J\delta {\displaystyle \sum _{m=2}^n\frac{V_{n,m}}{a_m}{e}^{-a_m{\tau }_B/\epsilon }}\le J\delta e^{-{\tau }_B/\epsilon }{\displaystyle \sum _{m=2}^n\frac{V_{n,m}}{a_m}},$$

where the second inequality follows from $e^{-a_m{\tau }_B/\epsilon }\le e^{-{\tau }_B/\epsilon }$ for all $m=2,\dots ,n$. Now, noting that ${\displaystyle {\sum }_{m=2}^n\left(V_{n,m}/a_m\right)}$ corresponds to the total tree length for the constant population size function $\eta \equiv 1$ and using Eq. 5, we obtain

$$\langle {\mathbf{c}}^{\prime }-\mathbf{c},{\mathbf{V}}_n\rangle \le J\delta e^{-{\tau }_B/\epsilon }2H_{n-1}.$$ [18]

To finish the proof, recall that $\langle \mathbf{c},{\mathbf{V}}_n\rangle$ is the total expected branch length of the coalescent tree under model η. Since ${\min }_t\eta \left(t\right)=\epsilon ,$ we have that $\langle \mathbf{c},{\mathbf{V}}_n\rangle$ is at least as large as the corresponding quantity under a model with constant population size ε. By Eq. 5, the total expected tree length under the latter model equals $2\epsilon H_{n-1}$. Thus, $\langle \mathbf{c},{\mathbf{V}}_n\rangle \ge 2\epsilon H_{n-1}$, and combining this result with Eq. 18 gives

$$\frac{\langle {\mathbf{c}}^{\prime }-\mathbf{c},{\mathbf{V}}_n\rangle }{\langle \mathbf{c},{\mathbf{V}}_n\rangle }\le J\frac{\delta }{\epsilon }{e}^{-{\tau }_B/\epsilon }.$$

Finally, Eq. 12 follows from this inequality and Theorem 1.

Proof of Theorem 4. Our proof uses a generalized form of Fano’s inequality (30). Adapted to our setting and notation, the method reads as follows.

Theorem 8 (Fano’s method). Consider a space $\mathrm{ℳ}$ of population size models. Let $r\ge 2$ be an integer, and let $S_n^r=\left\{{\eta }_1,{\eta }_2,\dots ,{\eta }_r\right\}\subset \mathrm{ℳ}$ contain r population size functions such that for all $a\ne b$, ${\left|\left|{\eta }_a-{\eta }_b\right|\right|}_{*}\ge {\alpha }_r$ and $D\left({\xi }_n^{\left({\eta }_a\right)}\Vert {\xi }_n^{\left({\eta }_b\right)}\right)\le {\beta }_r$. Let ${\widehat{\eta }}^{\left(n,s\right)}={\widehat{\eta }}^{\left(n,s\right)}\left(X_1,\dots ,X_s\right)$ be an estimator of η based on the SFS data $X_1,\dots ,X_s$ sampled independently from ${\xi }_n^{\left(\eta \right)}$; i.e., $X_1,\dots ,X_s$ are SFS data for n individuals at s independent segregating sites. Then,

$$\underset{\widehat{\eta }}{\text{inf}}\underset{\eta \in \mathrm{ℳ}}{\text{sup}}{\mathbb{E}}_{\eta }{\left|\left|{\widehat{\eta }}^{\left(n,s\right)}-\eta \right|\right|}_{*}\ge \frac{{\alpha }_r}{2}\left(1-\frac{s\cdot {\beta }_r+\log 2}{\log r}\right).$$ [19]

This theorem places a lower bound on the minimax rate of convergence of a population size history estimator based on the SFS.

For $\eta \in {\mathrm{ℱ}}_{I,J}$, let $w_j$ denote the variable $\in \left\{\mathrm{0,1}\right\}$ indicating whether η jumps by δ at change point $t_{I+j}$. Let $\mathcal{Y}=\left\{\mathbf{w}=\left(w_0,\dots ,w_{J-1}\right)|w_i\in \left\{\mathrm{0,1}\right\}\right\}$, where $J\ge 8$. By the Varshamov−Gilbert lemma (see ref. 31, Lemma 4.7), there exist $\mathcal{X}=\left\{{\mathbf{w}}^0,\dots ,{\mathbf{w}}^M\right\}\subset \mathcal{Y}$ such that (i) ${\mathbf{w}}^0=\left(0,\dots ,0\right)$, (ii) $M\ge 2^{J/8}$, and (iii) $H\left({\mathbf{w}}^i,{\mathbf{w}}^j\right)\ge J/8$, where $H(\cdot ,\cdot )$ denotes the Hamming distance.

Let ${\mathrm{ℱ}}_{I,J}^{\mathcal{X}}$ denote the subset of $2^{J/8}+1$ functions in ${\mathrm{ℱ}}_{I,J}$ with the indicator variable for δ jumps at $t_I,\dots ,t_{I+J-1}$ given by $\mathbf{w}\in \mathcal{X}$. Then, for any two ${\eta }_a\ne {\eta }_b\in {\mathrm{ℱ}}_{I,J}^{\mathcal{X}}$, we have

$${\left|\left|{\eta }_a-{\eta }_b\right|\right|}_{1,T}\ge \frac{J}{8}\cdot {\tau }_A\cdot \delta .$$ [20]

Using Theorem 8 via Eq. 20 and Theorem 3, we obtain

$$\underset{\widehat{\eta }}{\text{inf}}\underset{\eta \in {\mathrm{ℱ}}_{I,J}}{\text{sup}}{\mathbb{E}}_{\eta }{\left|\left|{\widehat{\eta }}^{\left(n,s\right)}-\eta \right|\right|}_{1,T}\ge \frac{J\cdot {\tau }_A\cdot \delta }{16}\left[1-\frac{sJ\frac{\delta }{\epsilon }{e}^{-{\tau }_B/\epsilon }+\log 2}{\log \left(2^{J/8}+1\right)}\right]\ge \frac{J\cdot {\tau }_A\cdot \delta }{16}\left[1-\frac{sJ\frac{\delta }{\epsilon }{e}^{-{\tau }_B/\epsilon }+\log 2}{\frac{J}{8}\log 2}\right].$$ [21]

We now optimize the bound with respect to δ. A straightforward calculation shows that the maximum is attained at

$${\delta }^{*}=\frac{\left(J-8\right)\log 2}{16J}\left(\frac{\epsilon }{s}\right)e^{{\tau }_B/\epsilon },$$ [22]

and setting $\delta ={\delta }^{*}$ in Eq. 21 yields the result.

Proof of Theorem 5. The result is obtained by scaling ε with the number of segregating sites s. Denote this scaling by $\epsilon \left(s\right)$; we will determine $\epsilon \left(s\right)$ that produces the largest possible lower bound. Starting from Eq. 22 in the proof of Theorem 4, note that ${\delta }^{*}$ scales as $\left(\epsilon /s\right)e^{{\tau }_B/\epsilon }=:f\left(\epsilon \right)$. To satisfy the constraint that ${\left|\left|\eta \right|\right|}_{\infty }<M$ for all $\eta \in {\mathrm{ℱ}}_{I,J}^M$ and s, the condition

$$\underset{s\to \infty }{\text{lim}\hspace{0.17em}\text{sup}}\max \left\{\frac{\epsilon \left(s\right)}{s}{e}^{{\tau }_B/\epsilon \left(s\right)},\epsilon \left(s\right)\right\}<\infty$$ [23]

must therefore hold. This implies that $\epsilon \left(s\right)s^p\to \mathrm{\infty }$ as $s\to \infty$ for all $p>0$. Suppose that $q\stackrel{\text{def}}{=}{\text{lim}\hspace{0.17em}\text{inf}}_{s\to \infty }\left[\left(\epsilon \left(s\right)\log s\right)/{\tau }_B\right]<1$; note that $\epsilon \left(s\right)>0$ implies $q>0$. Then there exists a diverging sequence $s_1,s_2,\dots \to \mathrm{\infty }$ with $\log \left(s_i\right)<\left[\left(1+q\right)/2\right]\left[{\tau }_B/\left(\epsilon \left(s_i\right)\right)\right]$ for all i, whence

$$\underset{s\to \infty }{\text{lim}\hspace{0.17em}\text{sup}}\frac{\epsilon \left(s\right)}{s}{e}^{{\tau }_B/\epsilon \left(s\right)}\ge \underset{i\to \infty }{\text{lim}\hspace{0.17em}\text{sup}}\frac{\epsilon \left(s_i\right)}{s_i}{e}^{\frac{2}{1+q}\log \left(s_i\right)}=\underset{i\to \infty }{\text{lim}\hspace{0.17em}\text{sup}}\epsilon \left(s_i\right)s_i^{\frac{1-q}{1+q}}=\infty .$$

From this, it follows that $\epsilon \left(s\right)\ge {\tau }_B/\log s$ for sufficiently large s. Now, on the interval $\left(0,\infty \right)$, the function $f\left(\epsilon \right)$ is convex with a unique minimum at $\epsilon ={\tau }_B$. Let ${\epsilon }^{\prime }$ be a point where $f\left({\epsilon }^{\prime }\right)>f\left({\tau }_B/\log s\right)={\tau }_B/\log s$. Then ${\epsilon }^{\prime }\notin \left[{\tau }_B/\log s,{\tau }_B\right]$. If ${\epsilon }^{\prime }>{\tau }_B$, then $f\left({\epsilon }^{\prime }\right)<\left({\epsilon }^{\prime }/s\right)e^1$. Since $\frac{{\tau }_B}{\log s}<f\left({\epsilon }^{\prime }\right)$, we then conclude ${\epsilon }^{\prime }>s{\tau }_B/\left(e^1\log s\right)$, which is not bounded as $s\to \infty$.

In summary, we see that the largest possible lower bound that obeys Eq. 23 must have $f\left(\epsilon \right)$ asymptotically $\le {\tau }_B/\log s$, and that this bound is achieved by setting $\epsilon \left(s\right)={\tau }_B/\log s$. Plugging this in to Eq. 19 yields the claim.

Proof of Corollary 6. For $c\in \left(0,\hspace{0.17em}1\right)$, choose J large enough so that $\left(J-8\right)/J>c$, and fix ${\tau }_A$ so that $T=t_I+J{\tau }_A$. Then $\left(J-8\right){\tau }_A\ge cJ{\tau }_A=c\left(T-t_I\right)$. Substituting the above inequalities into Eq. 14 and letting $C^{″}=C^{\prime }{c}^2$ yields the desired result.

Proof of Theorem 7. The theorem is obtained by suitably modifying the preceding results to account for the effect of exponential growth in the first period. Let ${\eta }_u,{\eta }_{\ell }$ be the analogously defined upper and lower envelope functions for ${\mathcal{G}}_J$. Then

$${\displaystyle \underset{0}{\overset{t_{j+1}}{\int }}\frac{ds}{{\eta }_u\left(s\right)}}=\frac{e^{\beta \left({\eta }_0\right)t_1}-1}{{\eta }_0\beta \left({\eta }_0\right)}+\frac{{\tau }_B}{\epsilon }+{\displaystyle \sum _{i=3}^{j+1}\frac{t_i-t_{i-1}}{N_i}}=t_1\frac{\frac{1}{\gamma \epsilon }-\frac{1}{{\eta }_0}}{\log \left({\eta }_0\right)-\log \left(\gamma \epsilon \right)}+\frac{{\tau }_B}{\epsilon }+{\displaystyle \sum _{i=3}^{j+1}\frac{t_i-t_{i-1}}{N_i}},$$

where we have used the definition of $\beta \left({\eta }_0\right)$ in the second equality. Since all size histories in ${\mathcal{G}}_J$ are equal up to period $t_2$, the steps of Lemma 2 all go through unchanged. Starting from Eq. 17, we obtain the modified bound

$$a_m\left[c_m^{\left({\eta }_u\right)}-c_m^{\left({\eta }_{\ell }\right)}\right]\le J\delta \exp \left\{-a_m{t}_1\frac{\frac{1}{\gamma \epsilon }-\frac{1}{{\eta }_0}}{\log \left({\eta }_0\right)-\log \left(\gamma \epsilon \right)}\right\}{e}^{-a_m{\tau }_B/\epsilon }.$$ [24]

Propagating the modified bound (Eq. 24) through Theorems 3 and 4 ultimately yields the claim.