Significance
An ongoing challenge in modern materials science is to create artificial structures, termed metamaterials, with an unconventional response that can be programmed by suitable design of their geometry or topology. We demonstrate a novel metamaterial in which small structural variations single out regions that buckle selectively under external stresses. Surprisingly, these regions are at first glance indistinguishable from the rest of the structure. Our samples are examples of topological metamaterials that are the mechanical analogues of topologically protected electronic systems. As a result, the buckling response is robust against structural perturbations yet tunable without affecting secondary physical properties in the buckling region. This feature is desirable for optomechanical or thermomechanical metamaterials in which multiple characteristics need to be tuned simultaneously.
Keywords: isostatic lattices, topological modes, topological mechanics, tunable failure
Abstract
States of self-stress—tensions and compressions of structural elements that result in zero net forces—play an important role in determining the load-bearing ability of structures ranging from bridges to metamaterials with tunable mechanical properties. We exploit a class of recently introduced states of self-stress analogous to topological quantum states to sculpt localized buckling regions in the interior of periodic cellular metamaterials. Although the topological states of self-stress arise in the linear response of an idealized mechanical frame of harmonic springs connected by freely hinged joints, they leave a distinct signature in the nonlinear buckling behavior of a cellular material built out of elastic beams with rigid joints. The salient feature of these localized buckling regions is that they are indistinguishable from their surroundings as far as material parameters or connectivity of their constituent elements are concerned. Furthermore, they are robust against a wide range of structural perturbations. We demonstrate the effectiveness of this topological design through analytical and numerical calculations as well as buckling experiments performed on two- and three-dimensional metamaterials built out of stacked kagome lattices.
Mechanical metamaterials are artificial structures with unusual properties that originate in the geometry of their constituents, rather than the specific material they are made of. Such structures can be designed to achieve a specific linear elastic response, like auxetic (negative Poisson ratio) (1) or pentamode (zero-shear modulus) (2) elasticity. However, it is often their nonlinear behavior that is exploited to engineer highly responsive materials, the properties of which change drastically under applied stress or confinement (3–7). Coordinated buckling of the building blocks of a metamaterial is a classic example of nonlinear behavior that can be used to drive the auxetic response (4, 8), modify the phononic properties (5), or generate 3D micro/nanomaterials from 2D templates (9).
Buckling-like shape transitions in porous and cellular metamaterials involve large deformations from the initial shape, typically studied through finite element simulations. However, many aspects of the buckling behavior can be successfully captured in an approximate description of the structure that is easier to analyze (5, 6, 10, 11). Here, we connect the mechanics of a cellular metamaterial, a foamlike structure made out of slender flexible elements (12, 13), to that of a frame—a simpler, idealized assembly of rigid beams connected by free hinges—with the same beam geometry. We exploit the linear response of a recently introduced class of periodic frames (14), inspired by topologically protected quantum materials, to induce a robust nonlinear buckling response in selected regions of two- and three-dimensional cellular metamaterials.
Frames, also known as trusses, are ubiquitous minimal models of mechanical structures in civil engineering and materials science. Their static response to an external load is obtained by balancing the forces exerted on the freely hinged nodes against internal stresses (tensions or compressions) of the beams. However, a unique set of equilibrium stresses may not always be found for any load (15). First, the structure may have loads that cannot be carried because they excite hinge motions called zero modes that leave all beams unstressed. Second, the structure may support states of self-stress—combinations of tensions and compressions on the beams that result in zero net forces on each hinge. An arbitrary linear combination of states of self-stress can be added to an internal stress configuration without disrupting static equilibrium, implying that degenerate stress solutions exist for any load that can be carried. The respective counts and of zero modes and states of self-stress in a d-dimensional frame with nodes and beams are related to each other by the generalized Maxwell relation (16, 17):
| [1] |
As Eq. 1 shows, states of self-stress count the excess constraints imposed by the beams on the degrees of freedom provided by the hinge positions.
States of self-stress play a special role in the mechanical response of repetitive frames analyzed under periodic boundary conditions (18). Macroscopic stresses in such systems correspond to boundary loads, which can only be balanced by states of self-stress involving beams that cross the boundaries. If these states span the entire system, boundary loads are borne by tensions and compressions of beams throughout the structure. Conversely, by localizing states of self-stress to a small portion of a frame, load-bearing ability is conferred only to that region. Our approach consists of piling up states of self-stress in a specific region of a repetitive frame so that the beams participating in these states of self-stress are singled out to be compressed under a uniform load at the boundary. In a cellular material with the same beam geometry, these beams buckle when the compression exceeds their buckling threshold.
Although our strategy is of general applicability, it is particularly suited to isostatic lattices (19, 20), with and no zero modes other than the d rigid body motions under periodic boundary conditions. According to Eq. 1, these lattices only have d states of self-stress, insufficient to bear the possible independent macroscopic stresses (18, 21). Additional states of self-stress can significantly modify the load-bearing ability of these structures at the cusp of elastic stability. Trivial states of self-stress can be created by locally adding extra beams between hinges. However, some isostatic periodic lattices can harbor topological states of self-stress that owe their existence to the global structure of the frame. These frames, introduced by Kane and Lubensky (14), are characterized by a polarization and its origin can be traced to topological invariants calculated from the geometry of the unit cell. Domain walls between different topological polarizations, as in Fig. 1A (14, 22), and lattice defects (23) can harbor localized states of self-stress, which can be used to drive localized buckling. Unlike their trivial counterparts, the existence of these topological states of self-stress cannot be discerned from a local count of the degrees of freedom or constraints in the region. An attractive feature for potential applications is their topological protection from perturbations of the lattice or changes in material parameters that do not close the acoustic gap of the structure (14, 24–27).
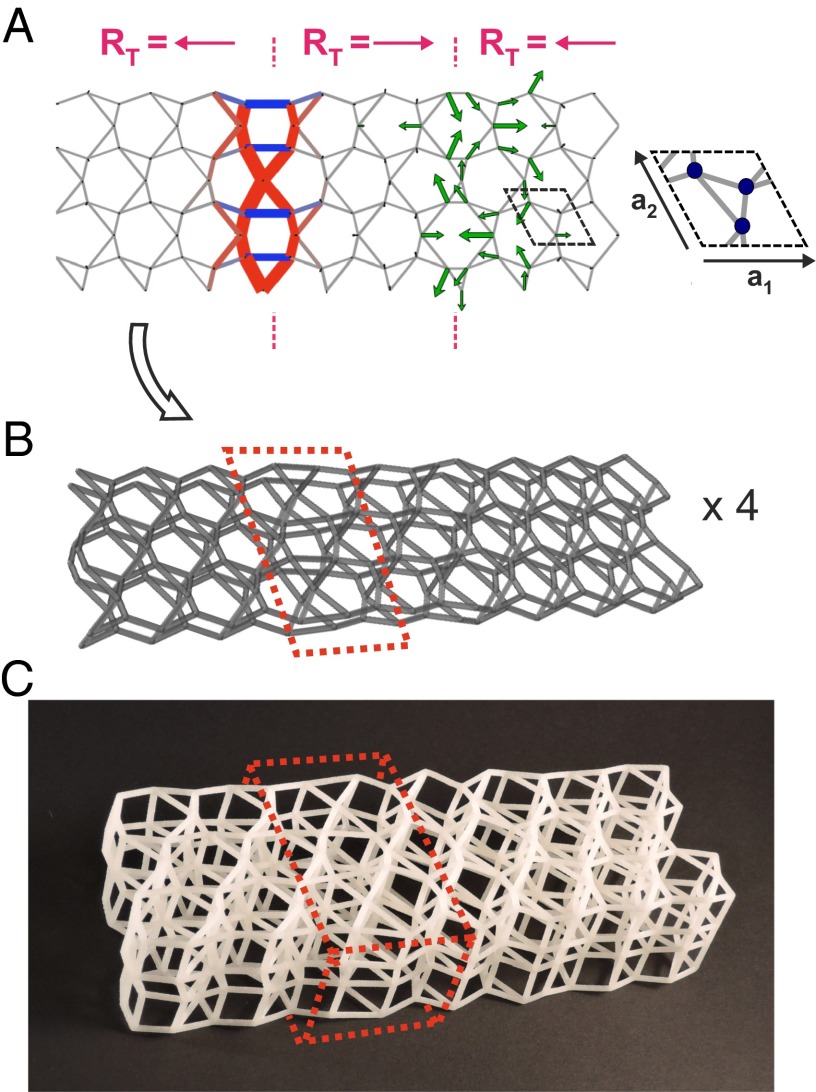
Fig. 1.
Topological buckling zone in a cellular metamaterial. (A) Isostatic frame containing two domain walls that separate regions built out of opposite orientations of the same repeating unit (boxed; the zoom shows the three unique hinges in the unit cell as disks). This unit cell carries a polarization (solid arrow), and the periodic frame displays topological edge modes (14). The left domain wall harbors topological states of self-stress, one of which is visualized by thickened beams identifying equilibrium-maintaining tensions (red) and compressions (blue) with magnitudes proportional to the thickness. The right domain wall harbors zero modes, one of which is visualized by green arrows showing relative displacements that do not stretch or compress the beams. Modes were calculated using periodic boundary conditions. (B) A 3D cellular metamaterial is obtained by stacking four copies of the beam geometry in A, and connecting equivalent points with vertical beams to obtain a structure with each interior point connecting six beams. The beams are rigidly connected to each other at the nodes and have a finite thickness. Points are perturbed by random amounts in the transverse direction and a small offset is applied to each layer to break up straight lines of beams. A 3D-printed realization of the design made of flexible plastic (Materials and Methods) is shown in C. The sample has a unit cell size of 25 mm and beams with circular cross-section of 2 mm diameter. The stacking creates a pile-up of states of self-stress in a quasi-2D region, highlighted by dotted lines.
In the remainder of this article, we use robust states of self-stress to design buckling regions in topological metamaterials composed of flexible beams rigidly connected to each other at junctions. As shown in Fig. 1, the states of self-stress are localized to a quasi-2D domain wall obtained by stacking multiple layers of a pattern based on a deformed kagome lattice (14). The domain wall separates regions with different orientations of the same repeating unit (and hence of the topological polarization of the underlying frame). When the material is compressed uniaxially, beams participating in the topological states of self-stress will buckle out of their layers in the portion of the lattice highlighted in red, see Movie S1. The region primed for buckling is indistinguishable from the remainder of the structure in terms of the density of beams per site and the characteristic beam slenderness. We verify using numerical calculations that the states of self-stress in the idealized frame influence the beam compressions of the cellular structure in response to in-plane compressions along the edges. The phenomenon survives even when the patterns on either side of the domain wall are nearly identical, reflecting the robustness of the topological design.
Linear Response of the Frame
The distinguishing feature of the isostatic periodic frame used in our design is the existence of a topological characterization of the underlying phonon band structure (14). If the only zero modes available to the structure are the d rigid-body translations, its phonon spectrum has an acoustic gap; i.e., all phonon modes have nonzero frequencies except for the translational modes at zero wavevector. A gapped isostatic spectrum is characterized by d topological indices , one for each primitive lattice vector ( for the 2D lattice used in our design). Although the phonon spectrum can be changed by smoothly deforming the unit cell geometry, the indices themselves are integer valued and thus invariant to smooth perturbations. Their value can only be changed by a deformation that closes the acoustic gap. Analogous to topological electronic systems such as quantum Hall layers and topological insulators that harbor protected edge states (28), the existence of these invariants guarantees the presence of zero modes or states of self-stress localized to lattice edges or domain walls where the change value.
The count of topological mechanical states at an edge or domain wall is obtained via an electrostatic analogy. The lattice vector (Fig. 1A) can be interpreted as a polarization of net degrees of freedom in the unit cell. Just as Gauss’s law yields the net charge enclosed in a region from the flux of the electric polarization through its boundary, the net number of states of self-stress (minus the zero modes) in an arbitrary portion of an isostatic lattice is given by the flux of the topological polarization through its boundary (14). In Fig. 1A, the left domain wall has a net outflux of polarization and harbors topological states of self-stress (the right domain wall, with a polarization influx, harbors zero modes). Although only one of each mechanical state is shown, the number of states of self-stress and zero modes is proportional to the length of the domain wall. Similar results can be obtained by using other isostatic lattices with an acoustic gap and a topological polarization, such as the deformed square lattice in ref. 23.
The linear response of a frame can be calculated from its equilibrium matrix , a linear operator that relates the beam tensions (a vector with as many elements as the number of beams ) to the resultant forces on the nodes (a vector with one element for each of the degrees of freedom of the nodes) via . States of self-stress are vectors that satisfy , i.e., they are beam stresses that do not result in net forces on any nodes (the index q identifies independent normalized states of self-stress that span the null space of ). The same null vectors are also an orthogonal set of incompatible strains of the structure, i.e., beam extensions that cannot be realized through any set of point displacements (15).
Because we are interested in triggering buckling through uniform loads that do not pick out any specific region of the lattice, we focus on the response to affine strains, where affine beam extensions are imposed geometrically by some uniform strain across the sample via
| [2] |
Here, α indexes the beams and is the end-to-end vector of beam α. To attain equilibrium, the beams take on additional nonaffine extensions . Under periodic boundary conditions, affine strains are balanced by loads across the system boundary rather than loads on specific nodes, which implies that the resultant beam tensions must be constructed solely out of states of self-stress (18, 29) (we assume for simplicity that all beams have identical spring constant k). Therefore, where and the are the weights of the states of self-stress. These weights are determined by requiring that the nonaffine strains have zero overlap with the set of incompatible strains (15) (the affine strains are automatically compatible with the affine node displacements):
| [3] |
which gives the solution
| [4] |
| [5] |
Therefore, the beam tensions under an affine deformation are obtained by projecting the affine strains onto the space of states of self-stress.
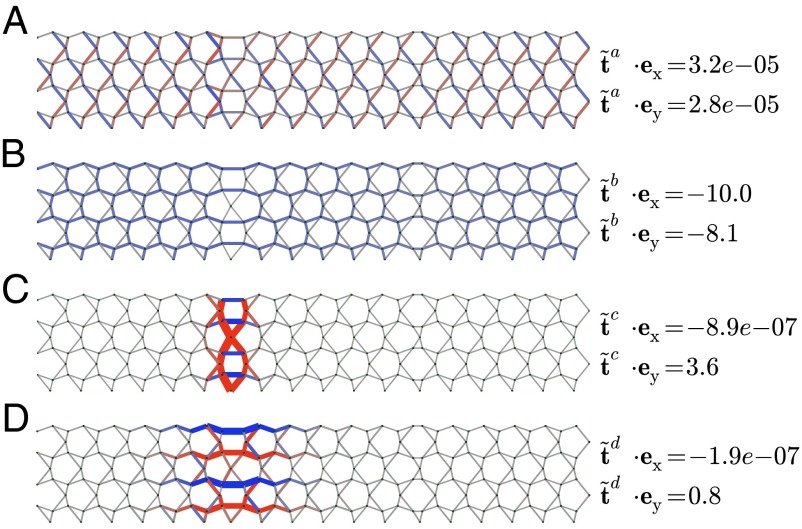
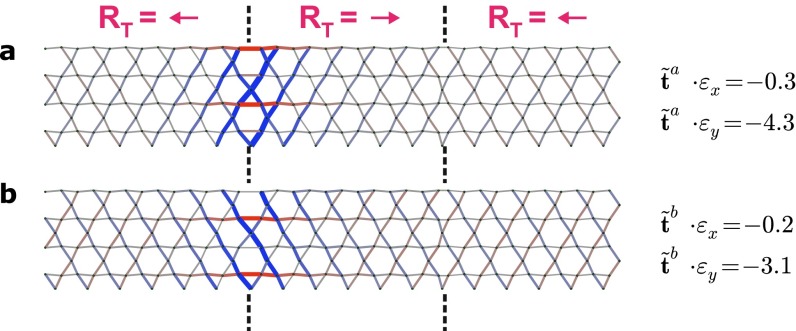
Eq. 5 shows that the loading of beams under affine strains is completely determined by the states of self-stress. In a frame consisting of a single repeating unit cell, loads are borne uniformly across the structure. However, if the structure also has additional states of self-stress with nonzero entries in confined to a small region of the frame, it would locally enhance tensions and compressions in response to affine strains, provided the have a nonzero overlap with the affine bond extensions imposed by the strain. Fig. 2 shows the approximate states of self-stress for the domain wall geometry of Fig. 1A, which has a nonzero overlap with affine extensions and due to uniaxial strains and , respectively. (These approximate states of self-stress become exact when the separation between the two domain walls becomes large.) The system-spanning states of self-stress and in Fig. 2 A and B, respectively, do not single out any particular region. Although they have a nonzero overlap with both and , they do not provide significant stiffness to a uniaxial loading because a combined affine strain exists with such that the overlaps of the corresponding affine extensions with and are small (less than ). Upon compression along one direction, say y, the frame can expand in the perpendicular direction to keep the tensions and compressions low in the majority of the sample. In contrast, the localized states of self-stress shown in Fig. 2 C and D have a significant overlap with but not . Therefore, according to Eq. 5, a uniform compression applied to the lattice along the vertical direction, with the horizontal direction free to respond by expanding, will significantly stretch or compress only the beams participating in the localized states of self-stress.
Fig. 2.
Extended and localized states of self-stress of the frame. (A–D) States of self-stress in the infinite periodic frame obtained by tiling the design of Fig. 1A in both directions. The states A and B are largely uniform over the structure, whereas C and D are localized to the left domain wall. The overlaps of each state of self-stress with the affine strains and (main text) are also shown. Only states of self-stress with significant overlaps are shown; all other states of self-stress in the structure have .
Whereas the topological polarization guarantees the presence of states of self-stress localized to the left domain wall, their overlap with one of the three independent affine strains is determined by the specific geometry of the hinges and bars. For the frame in Fig. 2, the states of self-stress visualized in Fig. 2 C and D are crucial in triggering buckling response, which may be predicted to occur under compression along the y direction (or extension along the x direction, which would also lead to y compression because the lattice has a positive Poisson ratio set by β). In other domain wall geometries, or other orientations of the domain wall relative to the lattice, the localized states of self-stress could have small overlap with affine strains, which would make them inconsequential to the buckling behavior. Alternatively, states of self-stress that overlap significantly with shear deformations could also be realized that would enable buckling to be triggered via shear.
Buckling in Topological Cellular Metamaterials
The cellular metamaterial differs from the ideal frame in two important ways. First, real structures terminate at a boundary, and loads on the boundary are no longer equilibrated by states of self-stress, but rather by tension configurations that are in equilibrium with forces on the boundary nodes (15). However, these tension states are closely related to system-traversing states of self-stress in the periodic case, with the forces on the boundary nodes in the finite system playing the role of the tensions exerted by the boundary-crossing beams in the periodic system. Therefore, the states of self-stress also provide information about the load-bearing regions in the finite structure away from the boundary.
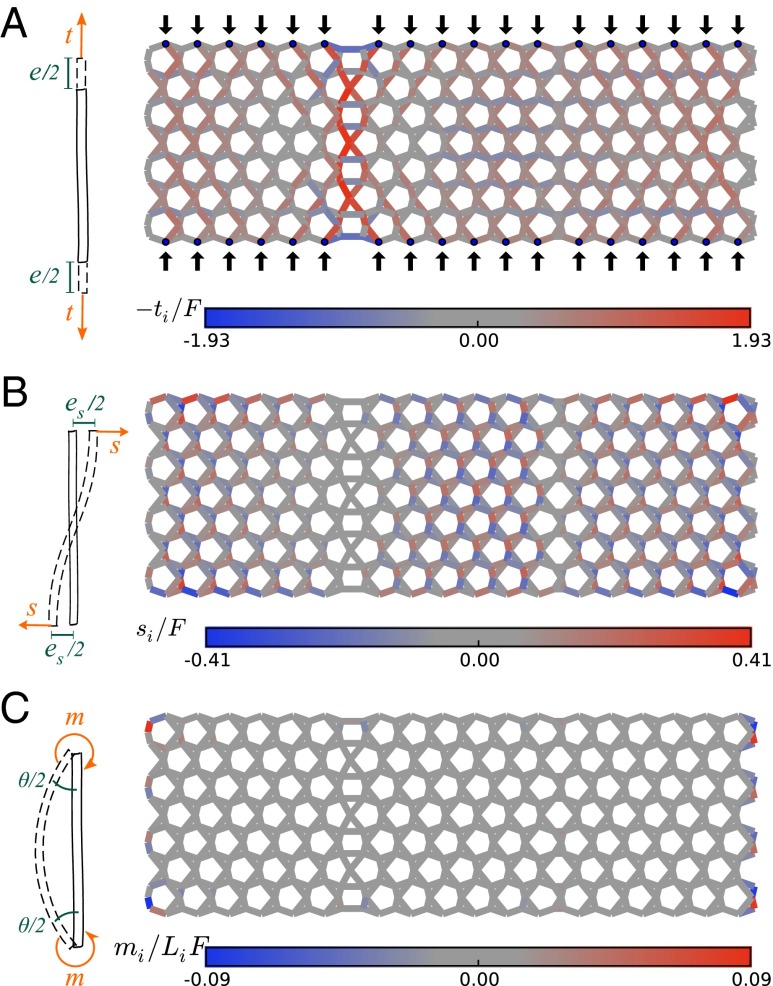
In addition to having boundaries, the cellular block probed in Fig. 1 also departs from the limit of an ideal frame, as it is made of flexible beams rigidly connected at the nodes and can support external loads through shear and bending of the beams in addition to axial stretching or compression. Nevertheless, the states of self-stress and tension states of the corresponding frame (with the same beam geometry) determine the relative importance of bending to stretching in the load-bearing ability of the cellular structure (21). To verify that the localized states of self-stress in the underlying frame influence the response of the finite cellular structure, we numerically calculate the in-plane response of each layer treated as an independent 2D cellular structure with loading confined to the 2D plane. Each beam provides not just axial tension/compression resistance but also resistance to shear and bending. A beam of length L, cross-sectional area A, and area moment of inertia I resists (i) axial extensions e with a tension , (ii) transverse deformations with a restoring shear force , and (iii) angular deflections of the end nodes θ with restoring moment (Fig. 3). Because and for a beam of width w, the relative contribution of the bending, shear and torsional components to the total stiffness is set by the aspect ratio of each beam; the frame limit with no bending or shear stiffness is recovered when . The physical sample has beams with aspect ratios in the range , indicating a small but appreciable contribution of shear and torsion to the response.
Fig. 3.
Stretching, shear, and bending contributions to the linear in-plane response of the cellular metamaterial. Response of a planar cellular structure, related to the lattice in Fig. 2 but with free edges, subject to a vertical compressive force F (solid arrows) at each point highlighted along the top and bottom edges. The structure is modeled as a network of flexible beams connected by rigid joints at the nodes, and with each beam providing torsional stiffness in addition to axial stiffness. The beams are colored according to (A) axial compression; (B) shear load; and (C) bending moment.
The 2D linear response of such a structure is calculated by augmenting the equilibrium matrix to include an additional degree of freedom (a rigid rotation angle) at each node, and two additional restoring forces (shear and torsion) for each beam, see Materials and Methods. The resulting equilibrium matrix is of size , which implies that cellular solids based on isostatic frames with are severely overconstrained for , and structurally stable even with free boundaries. In particular, they can support any loads exerted on the boundary nodes as long as the net forces and torques about the center of mass are zero. Once the equilibrium matrix is constructed, its singular value decomposition can be used to completely determine all stresses and torques experienced by the beams in response to forces specified on the boundary nodes (15). Fig. 3 shows the linear response of each plane of the cellular pattern corresponding to the domain wall geometry of Fig. 2 under uniform compressive force applied to the nodes on the top and bottom edges. The beams participating in the states of self-stress at the left domain wall are singled out by their high compression; in contrast, the rest of the structure primarily supports the boundary load through shear rather than compression or bending. Remarkably, the unique compression-dominated response of the left domain wall (originating from the topological invariant in the idealized isostatic frame with freely hinged joints) survives in cellular structures away from the isostatic condition.
We expect a similar localized compression-dominated response in each layer of the stacked structure (Fig. 1 B and C). The enhanced compressions along the left domain wall trigger buckling when the compression exceeds the Euler beam buckling threshold, , where c is a positive numerical factor determined by the clamping conditions as well as cooperative buckling effects. Buckling is signified by a loss of ability to bear axial loads, as the beam releases its compression by bending out of plane. Upon compressing the 3D sample between two plates as shown in Fig. 4A, we see a significant out-of-plane deflection for beams along the left domain wall (Fig. 4 B and C), consistent with buckling of the maximally stressed beams in Fig. 3A. The deflection in different layers is coordinated by the vertical beams connecting equivalent points, so that beams within the same column buckle either upwards (column 1) or downward (column 2) to produce a distinctive visual signature when viewed along the compression axis. Beams connecting different planes in the stacked pattern create additional states of self-stress that traverse the sample vertically, but these do not single out any region of the material, and do not couple to the specific in-plane loading of Fig. 4A.
Fig. 4.
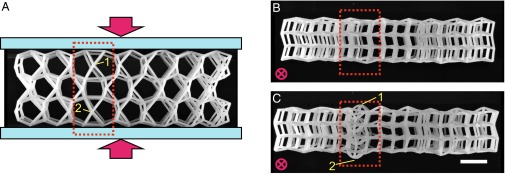
Buckling in the 3D topological cellular metamaterial. (A) Top view of the 3D sample (constructed as outlined in Fig. 1) showing the compression applied by confining the sample between transparent plates in contact with the front and back surfaces. The buckling zone is highlighted in red as in Fig. 1. Two vertical columns within this zone are labeled in yellow. Magenta arrows show the compression direction. (B and C) View along the compression axis at compressions of 0 and 20%, respectively. The beams in the region with states of self-stress have buckled in the vertical direction, whereas other beams have largely deformed within their stacking planes. (Scale bar, 25 mm.)
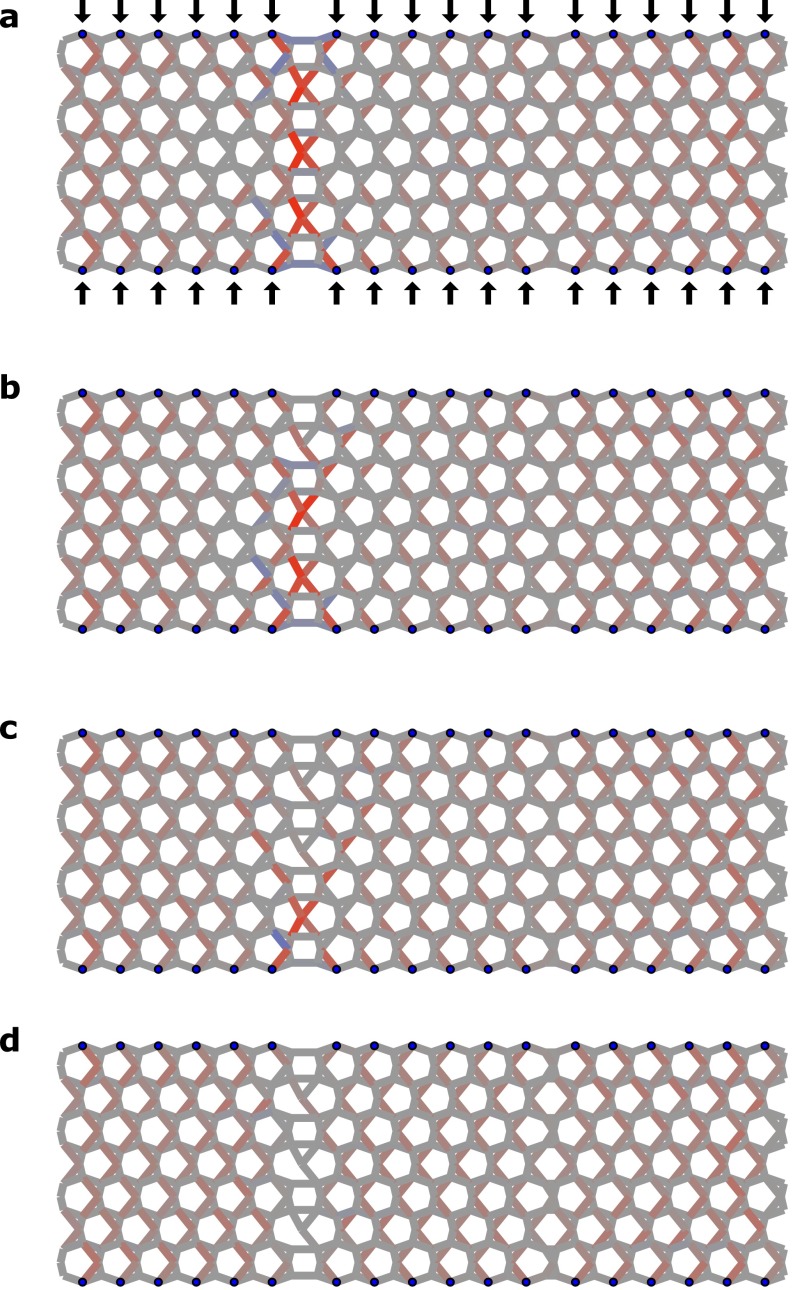
We emphasize that having as many states of self-stress as there are unit cells along the domain wall is crucial for the buckling to occur throughout the domain wall. When a beam buckles, its contribution to the constraints of distances between nodes essentially disappears, reducing the number of load-bearing configurations by one. If there were only a single localized state of self-stress in the system, the buckling of a single beam would eliminate this state, and the compressions on the other beams would be relaxed, preventing further buckling events. However, the presence of multiple states of self-stress, guaranteed in this case by the topological origin of the states, allows many buckling events along the domain wall. In the SI Text, we use an adaptive simulation that sequentially removes highly compressed beams to show that each repeating unit along the y direction experiences a unique buckling event even when the loss of constraints due to other buckling events is taken into account (Fig. S1).
Fig. S1.
Sequential removal of beams to recreate the effect of buckling in the linear response. (A) Axial compression of the cellular material shown in Fig. 3A under identical loading, but with beams colored by the propensity for buckling, . The beam with the highest value of this quantity will be the first to buckle as the force F on the boundary points is ramped up. (B–D) Result of sequentially removing the beam with the highest propensity for buckling and recalculating the compressions in the remaining beams under the same axial loading.
Robustness of the Buckling Region
Finally, we show that the robustness of the topological states of self-stress predicted within linear elastic theory carries over to the buckling response in the nonlinear regime. There is a wide range of distortions of the deformed kagome unit cell which do not close the acoustic gap, leaving the topological invariants and hence the polarization unchanged (14). These distortions may bring the unit cell arbitrarily close to the regular kagome lattice with equilateral triangles of beams (for which the gap is closed and the polarization is undefined). The unit cell of the 2D lattice shown in Fig. 5A is minimally distorted away from the regular kagome lattice, but this barely noticeable distortion (Fig. 5A, Inset) is sufficient to induce the same topological polarization in the underlying frame as before. As a result, the domain wall on the left (characterized by a net outflux of polarization) localizes states of self-stress (shown in Fig. S2), even though the unit cells are nearly identical on either side.
Fig. 5.
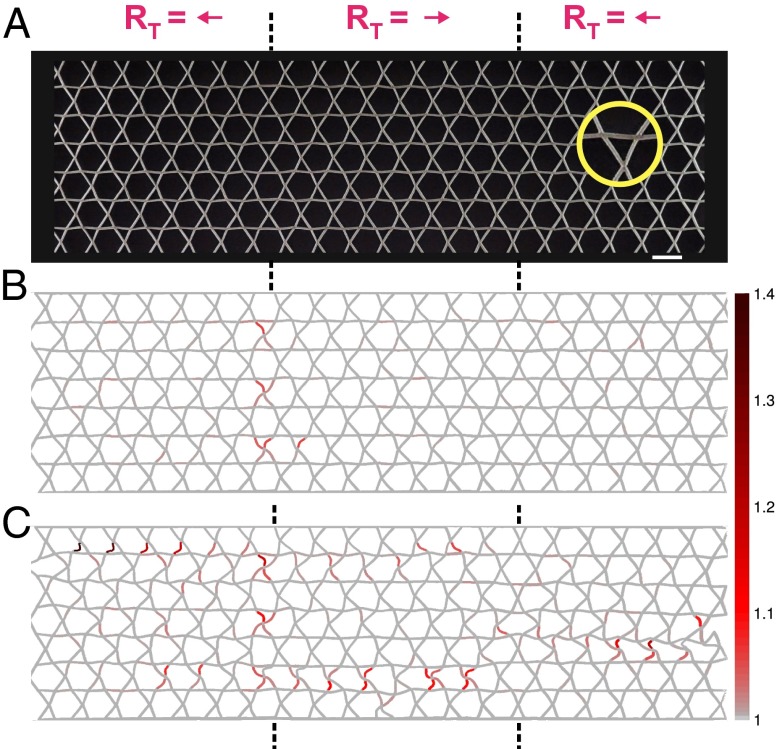
Buckling is robust under polarization-preserving changes of the unit cell. (A) A 2D foam cellular prototype, whose unit cell maintains the topological polarization even though its distortion away from the regular kagome lattice is small (a zoom of the constituent triangles is shown within the yellow circle). The domain wall geometry is identical to that of the 3D sample, with the left domain wall localizing states of self-stress. (Scale bar, 2 cm.) (B) Response of the structure under a vertical compression of 4% with free left and right edges. The beams are colored by the tortuosity, the ratio of the initial length of the beam to the end-to-end distance of the deformed segment (color bar). (C) Response of the structure under 7% compression, with beams colored by tortuosity using the same color scale as in B.
Fig. S2.
Localized states of self-stress for frame corresponding to design of Fig. 5A. The numerically obtained states of self-stress for a frame with the same domain wall geometry as in Fig. 2, but with the unit cell parameterized by which has a smaller distortion away from the regular kagome lattice and is used in Fig. 5A. The left domain wall still has a net outflux of the topological polarization and localizes states of self-stress, which have a significant overlap with the affine bond extensions and associated with uniform strains along x and y, respectively. Two independent states of self-stress exist with a significant overlap, shown in A and B.
For ease of visualization, we tested this design in a 2D prototype cellular metamaterial, obtained by laser-cutting voids in a 1.5-cm-thick slab of polyethylene foam (Materials and Methods), leaving behind beams 1–2 mm wide and 10–12 mm long (Fig. 5A). The aspect ratio of the beams is comparable to that of the 3D sample. Because the slab thickness is much larger than the beam width, deformations are essentially planar and uniform through the sample thickness, and can be captured by an overhead image of the selectively illuminated top surface. The sample was confined between rigid acrylic plates in free contact with the top and bottom edges, and subjected to a uniaxial in-plane compression along the vertical direction by reducing the distance between the plates. Using image analysis (Materials and Methods) we computed the beams’ tortuosity, defined as the ratio of the contour length of each beam to its end-to-end distance. Buckled beams have a tortuosity significantly above 1. Under a vertical compression of 4%, only beams along the left domain wall show a tortuosity above 1.05, consistent with a localized buckling response (Fig. 5B). However, under higher strains, the response of the lattice qualitatively changes. When beams have buckled along the entire domain wall, its response to further loading is no longer compression dominated (Fig. S1). Future buckling events, which are triggered by coupling between torsional and compressional forces on beams due to the stiff hinges, no longer single out the left domain wall and happen uniformly throughout the sample (Fig. 5C and Movie S2).
We have demonstrated that piling up localized states of self-stress in a small portion of an otherwise bending-dominated cellular metamaterial can induce a local propensity for buckling. Whereas this principle is of general applicability, our buckling regions exploit topological states of self-stress (14), which provide two advantages. First, they are indistinguishable from the rest of the structure in terms of node connectivity and material parameters, allowing mechanical response to be locally modified without changing the thermal, electromagnetic, or optical properties. This feature could be useful for optomechanical (30) or thermomechanical (31) metamaterial design. Second, the buckling regions are robust against structural perturbations, as long as the acoustic bulk gap of the underlying frame is maintained. This gap is a property of the unit cell geometry. Large deformations that close the gap could be induced through external actuation (32) or confinement, potentially allowing a tunable response from localized to extended buckling in the same sample, reminiscent of electrically tunable band gaps in topological insulators (33).
Materials and Methods
Deformed Kagome Lattice Unit Cell.
The deformed kagome lattices are obtained by decorating a regular hexagonal lattice, built from the primitive lattice vectors , where a is the lattice constant, with a three-point unit cell that results in triangles with equal sizes. The unit cells are described by a parameterization introduced in ref. 14, which uses three numbers to quantify the distortion of lines of bonds away from a regular kagome lattice (). The unit cell in Fig. 1A, which forms the basis for the 3D cellular structure, is reproduced by for which the topological polarization is (14). The unit cell for the design in Fig. 5A parameterized by has the same polarization. In all cases we describe the unit cell and polarization in the outer region; the inner region between the domain walls rotates this unit cell by π, which flips the polarization direction.
Construction of the Equilibrium/Compatibility Matrix.
Analysis of the linear response of a frame or a cellular material begins with the construction of the equilibrium matrix . Because it is more natural to relate node displacements to beam length changes, we describe how to build the compatibility matrix , relating point displacements to extensions via . We construct the compatibility matrix from the contributions of individual beams. Consider a single beam aligned to the x axis connecting hinge 1 at to hinge 2 at . There are six degrees of freedom potentially constrained by the beam: the positions at each node i and the torsion angle . Within Euler–Bernoulli beam theory, these values are sufficient to determine the shape of the beam along its length as well as the forces and torques at each end needed to maintain equilibrium (34). Three independent combinations of forces and torques can be identified and which are proportional to generalized strains experienced by the beam: pure tension , pure shear , and pure bending torque , as illustrated schematically in Fig. 3. In matrix form, this gives
| [6] |
The forces and torque (generalized stresses) are obtained from the generalized strains through the stiffness matrix , which depends on the Young’s modulus E, the cross-sectional area A, the area moment of inertia I, and the beam length L:
| [7] |
The compatibility matrix for a beam with arbitrary orientation is obtained by projecting the displacement vectors at the end of each beam onto the axial and transverse directions using the appropriate rotation matrix, which depends on the angle made by the beam with the x axis. Each beam in an assembly provides three rows to the compatibility matrix, with additional columns set to zero for the degrees of freedom unassociated with that beam. In the simpler frame limit, each beam only resists axial extensions, and contributes one row (the first row of the matrix in Eq. 6) to the compatibility matrix.
Once the equilibrium matrix is constructed, the approximate states of self-stress of the periodic frame (Fig. 2) as well as the linear response of the cellular material under loads (Fig. 3) are obtained from its singular value decomposition following the methods of ref. 15. More details of the computation are provided in the SI Text.
Construction and Characterization of 2D and 3D Prototypes.
The 3D structures were printed by Materialise N.V. through laser sintering of their proprietary thermoplastic polyurethane TPU 92A-1 (tensile strength 27 MPa, density 1.2 g/cm3, Young’s modulus 27 MPa).
The 2D structures were cut using a VersaLaser 3.5 laser cutter (Laser & Sign Technology) from 1.5 cm thick sheets of closed-cell cross-linked polyethylene foam EKI-1306 (EKI B.V.; tensile strength 176 kPa, density 0.03 g/cm3, Young’s modulus 1.7 MPa). A characteristic load-compression curve of a 2D sample is shown in Fig. S3.
Fig. S3.
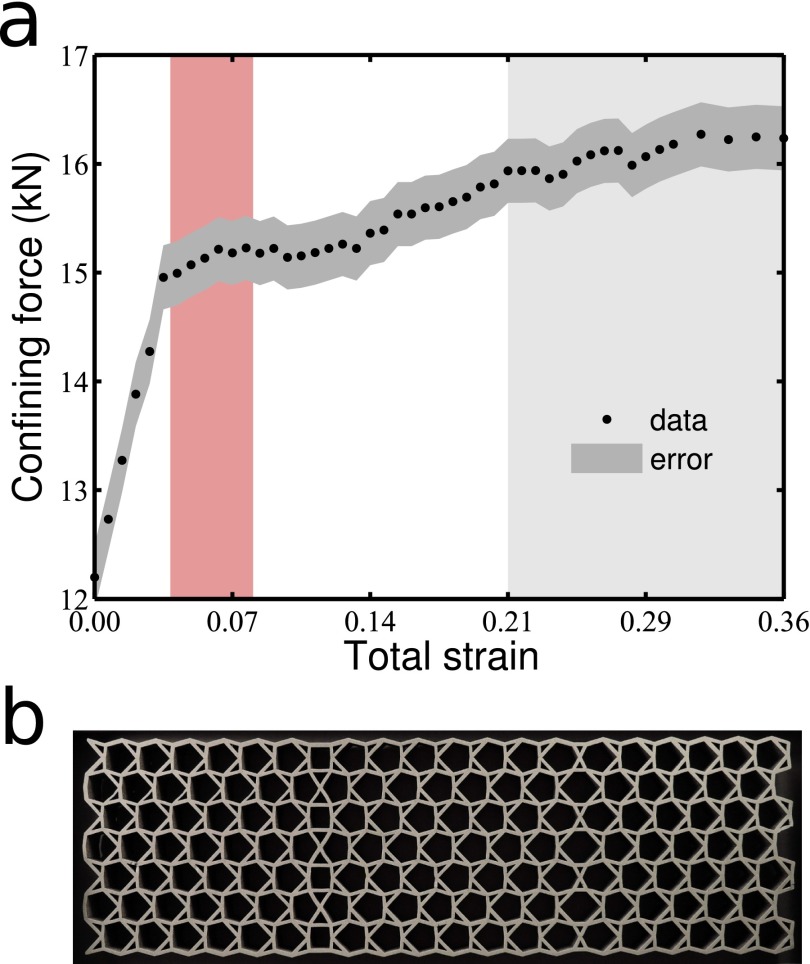
Measurement of the total confining force as a function of imposed strain for a 2D cellular prototype sample (Fig. 5). (A) The measured data (black circles) and an estimate of the measurement error (dark gray contour) are shown. The red region indicates the strain regime in which the beams within the topologically rigid domain wall buckle. In the light gray region, the sample response is dominated by out-of-plane buckling of the entire sample rather than by in-plane deformations of the cellular structure. The error was estimated at 0.2 kN based on uncertainties in the compression and force due to the rudimentary measurement apparatus; (B) the 2D cellular prototype for which the load-compression curve was measured. Its unit cell in the outer region is parameterized by .
Image Analysis of 2D Experiment.
Images of the 2D cellular prototype (Fig. 5) were obtained using a Nikon CoolPix P340 camera and stored as 3,000 × 4,000 px 24-bit JPEG images. To quantitatively identify the buckled beams in the 2D prototype under confinement, we extracted the tortuosity τ of each beam, defined as the ratio of the length of the beam to the distance between its endpoints. Tortuosity was estimated from the sample images through a series of morphological operations, as detailed in SI Text and Fig. S4. Straight beams have , whereas beams that buckle under axial compression have . Unlike other measures of curvature, tortuosity distinguishes buckled beams from sheared beams (schematic, Fig. 3B), which have .
Fig. S4.
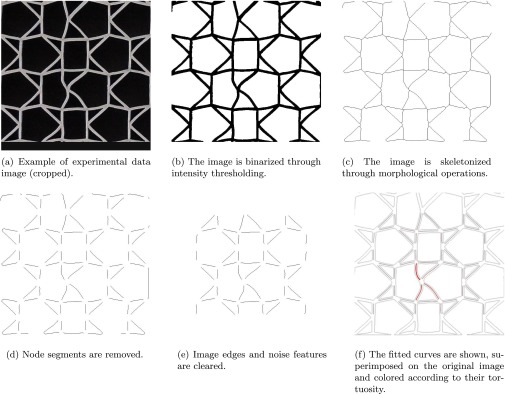
Demonstration of steps in the image analysis process.
SI Text
SVD Analysis of Equilibrium Matrix.
The linear response of the frame as well as the cellular metamaterial are obtained using the singular value decomposition (SVD) of the equilibrium matrix, as detailed in ref. 15 and summarized below. The SVD analysis simultaneously handles the spaces of node forces as well as beam stresses, and properly takes into account states of self-stress in the structure.
The SVD of the equilibrium matrix with rows and columns expresses it as the product of three matrices:
| [S1] |
where is a square matrix composed of independent column vectors , is a square matrix of independent column vectors , and is a matrix with r nonnegative values on the leading diagonal and all other values zero, r being the rank of .
The first r columns of provide the finite-energy displacement modes of the structure, whereas the remaining column vectors are the zero modes. Similarly, the first r and remaining column vectors of provide the finite-energy bond tension configurations and the states of self-stress, respectively.
For the frame in Fig. 2 under periodic boundary conditions, the count of topological states of self-stress predicts eight localized states of self-stress if the left domain wall were isolated, in addition to the two extended states of self-stress expected under periodic boundary conditions. However, because the separation between the left and right domain walls is finite, the SVD produces only two actual states of self-stress, and six approximate states of self-stress with large . The corresponding tension configurations are the last eight column vectors of . For of these (, , , and ) have a significant overlap with or . These are displayed in Fig. 2 A–D, respectively.
The response of the cellular network in Fig. 3 is calculated for the finite block with free edges. Unlike the frame, this is highly overconstrained and has many generalized states of self-stress (now corresponding to mixtures of tensions, shears, and torques that maintain equilibrium). An external load , corresponding to a force specification on each point, is supportable by the structure provided its overlap with the space of zero-energy motions is zero; i.e.,
| [S2] |
Because the cellular block only has three zero motions corresponding to the two translations and one rotation, any set of forces with no net force or torque on the structure, such as the force configuration shown in Fig. 3A, satisfies this condition. The generalized stresses (three per beam) are then given by
| [S3] |
where the second term is an arbitrary combination of the states of self-stress given by the last columns of . The weights are determined by requiring zero overlap of the generalized strains with the incompatible strains (states of self-stress), which leads to the equation
| [S4] |
which can be solved for to get the complete generalized stresses (three per beam, plotted separately in Fig. 3 A–C).
Sequential Removal of Beams.
Fig. 3 showed that the axial compressions in the cellular material under uniaxial loading were concentrated along the left domain wall, matching the expectation from the analysis of the frame with similar beam geometry. However, every time a beam buckles, its axial load-bearing ability is lost. This fundamentally changes the load-bearing states of the underlying frame, and there is no guarantee that the beams with the highest compression continue to be along the left domain wall. However, the number of topological states of self-stress localized to the left domain wall in the underlying periodic frame grows linearly with the length of the domain wall (14), suggesting that the load-bearing ability of the left domain wall may not vanish completely with just a single buckling event. Here, we numerically show using a sequential analysis of the finite cellular frame that the left domain wall can support as many buckling events as there are repeating units along the y direction.
To recap, Fig. 3A shows the compressions in a finite cellular block, obtained by tiling the same pattern 3 times along the y direction, under forces applied to undercoordinated points at the top and bottom edge. Because the threshold for buckling under compression scales as for beam i of length , we expect that the beam with the largest value of will buckle first as the compressive force F is increased. We examine the influence of the buckling event on the compression response by removing this beam from the cellular structure and recalculating the axial tensions without changing the forces on the boundary points. This process can be repeated, sequentially removing the beam with the largest value of after the linear response of the cellular structure has been recalculated. The result is show in Fig. S1, in which beams are colored by , i.e., the beam with the highest intensity in each iteration is removed in the next. For the first three iterations of the sequential process, the beam chosen for removal lies along the left domain wall (Fig. S1 A–C), showing that the multiplicity of load-bearing states localized to the left domain wall is sufficient for at least one buckling event to occur for each repeating unit of the domain wall.
Furthermore, after each repeating unit along the y direction has experienced buckling, the beams in the rest of the lattice experience much lower compressions relative to the initial compressions along the left domain wall (Fig. S1D), signifying that the lattice remains entirely bending/shear dominated away from the domain wall.
By performing simulations on different system sizes, we confirmed that upon increasing the sample size along the y direction, the number of buckling events localized to the left domain wall increases proportionally.
Load-Compression Curve of a 2D Sample.
A rudimentary measurement (Fig. S3) of the load-compression curve of a 2D cellular prototype has been performed to assess the effect of the localized buckling events on the mechanical response. The prototype, shown in Fig. S3B, uses a unit cell characterized by in the parameterization of ref. 14. This is geometrically similar to the unit cell used for the 3D sample in the main text and has the same polarization. However, we use more unit cells in the 2D sample to reduce edge effects on the measurement. The overall geometry is similar to that of the finite 2D lattice used in the linear response calculations of Fig. 3.
The 2D cellular foam sample (460 mm × 150 mm × 15 mm; beam widths 1.5–2.5 mm; see Materials and Methods for more details) was positioned with its narrow edge against a supporting acrylic plate and scale (Kern PCB 10000–1). The sample was confined from above by a second acrylic plate. No lateral confinement was provided. The distance between top and bottom plates was incrementally decreased from 140 to 90 mm using a laboratory jack. At each confinement step the system was allowed to relax and the equilibrium force on the sample edge was recorded from the scale, resulting in a quasistatic measurement of the sample’s load-compression curve. A small upward drift of ca. 0.5 kN was recorded in the scale’s force response due to long relaxation times. This drift (assumed to be linear in the confinement) has been subtracted from the recorded data. The complete measurement is shown in Fig. S3A. Buckling of the beams along the domain wall leaves a clear signature in the form of a sudden softening of the response (region highlighted in red). Before buckling, the main resistance to confinement was provided by the compressed beams along the domain wall because the rest of the beams could easily bend to accommodate the confinement. Buckling effectively removes the compressional stiffness of the beams along the domain wall. Further confinement is only resisted by additional bending of all beams, which leads to a significantly softer response.
A linear load compression followed by a plateau is typical of elastomeric cellular materials (12). Such materials also tend to have a secondary stiffening regime due to densification when adjacent beams contact each other along their lengths. In our measurement, however, the entire sample buckled in the lateral direction before this regime could be reached.
Details of 2D Image Analysis.
In Materials and Methods, we outlined the quantitative analysis of the 2D experimental data in Fig. 5. Here, we provide more details of the image processing required to measure the tortuosity of each beam in a cellular sample under compression. The tortuosity is defined as the ratio of the length of each beam to its end-to-end distance.
The analysis starts with a raw image such as in Fig. 5A, a top–down view of the sample whose top surface is selectively illuminated so that the beams making up the cellular material sample are visible against a dark background. Fig. S4A shows a subset of a different sample with similar beam lengths and widths, on which we illustrate the image processing steps.
Isolating beam sections.
To quantify the tortuosity of the lattice beams, the neutral axis (center line) of each beam must be isolated. The image is first binarized through intensity thresholding (Fig. S4B): pixels with an intensity value above/below a certain threshold are set to 1/0. This separates the structure (1) from the background (0).
The finite-width beams are then reduced to 1-pixel-wide center lines by finding the morphological skeleton of the binarized image. To do this, we perform a repeated sequence of binary morphological operations: skeletonizing and spur removal. The former consists of removing edge “1” pixels without breaking up contiguously connected regions. The latter is a pruning method that removes protrusions under a certain threshold length; it reduces spurious features due to uneven lighting and resolution limitations. The resulting skeleton is shown in Fig. S4C.
Next, we break up the skeleton into the neutral axes of individual beams. Note that the topology of the frame, with four beams coming together at each joint, is not reproduced in the skeleton, due to the finite size of the beam joints. Instead, the skeleton has short segments connecting junctions of pairs of beams. To remove these segments, we identify the branch points of the skeleton (pixels with more than two neighbors) and clear a circular area around them. The size of the segments and of the cleared disk is of the same order as the original beam width. The resulting image, consisting of the beams’ approximate neutral axes, is shown in Fig. S4.
Once the beam axes have been separated, two steps are implemented to improve the signal-to-noise ratio. First of all, beams near the edges of the sample are ignored. They are not always separated correctly from their neighboring beams, because they have lower connectivity than beams in the bulk of the lattice; this can lead to overestimation of the tortuosity. Second, because our lattices are fairly regular, the beams have a restricted size. Beam elements above and below these length thresholds are artifacts, and we ignore them. Fig. S4E illustrates the processed image data after these final steps.
Computing the tortuosity of each neutral axis.
After the beam axes have been isolated, connected components (sets of contiguous “1” pixels) are found and labeled. Each connected component corresponds to an individual beam axis. Numerical data can be extracted from it by analyzing its pixels’ coordinates, . These coordinates are fitted with polynomials parameterized by the normalized path length along the beam, :
| [S5] |
Cubic polynomials in l successfully capture the shape of the neutral axis of each beam, and smooth out pixel noise, which leads to small-wavelength features in the binary skeleton. Fig. S4F displays the smoothed contours superimposed on the original image, showing that the shapes of the individual beam sections are faithfully reproduced by the parametric form of Eq. S5.
The tortuosity τ of the beam axes is the arc length A along the line divided by the distance D between the endpoints. Both quantities can be extracted from the fitted model of the beam axes, :
| [S6] |
| [S7] |
Once the tortuosities of the beam segments have been computed, pixels in each segment of the binary image (Fig. S4B) are colored according to the corresponding tortuosity to obtain images such as Fig. 5 B and C.
Supplementary Material
Acknowledgments
We thank Denis Bartolo, Bryan Chen, Martin van Hecke, Charlie Kane, and Tom Lubensky for useful discussions, and Jeroen Mesman at the Leiden University Fine Mechanics Department for designing and building the compression stage. This work was funded by the Foundation for Fundamental Research on Matter and by the Delta Institute for Theoretical Physics, a program of The Netherlands Organization for Scientific Research, which is funded by the Dutch Ministry of Education, Culture, and Science.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1502939112/-/DCSupplemental.
References
- 1.Lakes R. Foam structures with a negative Poisson’s ratio. Science. 1987;235(4792):1038–1040. doi: 10.1126/science.235.4792.1038. [DOI] [PubMed] [Google Scholar]
- 2.Kadic M, Buckmann T, Stenger N, Thiel M, Wegener M. On the practicability of pentamode mechanical metamaterials. Appl Phys Lett. 2012;100:191901. [Google Scholar]
- 3.Shim J, et al. Harnessing instabilities for design of soft reconfigurable auxetic/chiral materials. Soft Matter. 2013;9:8198–8202. [Google Scholar]
- 4.Babaee S, et al. 2013. 3D soft metamaterials with negative Poisson’s ratio. Adv Mater 25(36):5044–5049.
- 5.Shan S, et al. Harnessing multiple folding mechanisms in soft periodic structures for tunable control of elastic waves. Adv Funct Mater. 2014;24(31):4935–4942. [Google Scholar]
- 6.Florijn B, Coulais C, van Hecke M. Programmable mechanical metamaterials. Phys Rev Lett. 2014;113(17):175503. doi: 10.1103/PhysRevLett.113.175503. [DOI] [PubMed] [Google Scholar]
- 7.Driscoll MM, Chen BG-g, Beuman TH, Ulrich S, Nagel SR, Vitelli V. 2015. Tunable failure in marginally rigid matter. arXiv 1501.04227v1. [DOI] [PMC free article] [PubMed]
- 8.Bertoldi K, Reis PM, Willshaw S, Mullin T. Negative Poisson’s ratio behavior induced by an elastic instability. Adv Mater. 2010;22(3):361–366. doi: 10.1002/adma.200901956. [DOI] [PubMed] [Google Scholar]
- 9.Xu S, et al. Materials science. Assembly of micro/nanomaterials into complex, three-dimensional architectures by compressive buckling. Science. 2015;347(6218):154–159. doi: 10.1126/science.1260960. [DOI] [PubMed] [Google Scholar]
- 10.Matsumoto EA, Kamien RD. Elastic-instability triggered pattern formation. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;80(2 Pt 1):021604. doi: 10.1103/PhysRevE.80.021604. [DOI] [PubMed] [Google Scholar]
- 11.Kang SH, et al. Complex ordered patterns in mechanical instability induced geometrically frustrated triangular cellular structures. Phys Rev Lett. 2014;112(9):098701. doi: 10.1103/PhysRevLett.112.098701. [DOI] [PubMed] [Google Scholar]
- 12.Gibson L. Modelling the mechanical behavior of cellular materials. Mater Sci Eng A. 1989;110:1–36. [Google Scholar]
- 13.Jang D, Meza LR, Greer F, Greer JR. Fabrication and deformation of three-dimensional hollow ceramic nanostructures. Nat Mater. 2013;12(10):893–898. doi: 10.1038/nmat3738. [DOI] [PubMed] [Google Scholar]
- 14.Kane CL, Lubensky TC. Topological boundary modes in isostatic lattices. Nat Phys. 2014;10:39–45. [Google Scholar]
- 15.Pellegrino S. Structural computations with the singular value decomposition of the equilibrium matrix. Int J Solids Struct. 1993;30:3025–3035. [Google Scholar]
- 16.Maxwell JC. On the calculation of the equilibrium and stiffness of frames. Philos Mag. 1864;27:294–299. [Google Scholar]
- 17.Calladine C. Buckminster Fuller’s tensegrity structures and Clerk Maxwell’s rules for the construction of stiff frames. Int J Solids Struct. 1978;14:161–172. [Google Scholar]
- 18.Guest S, Hutchinson J. On the determinacy of repetitive structures. J Mech Phys Solids. 2003;51:383–391. [Google Scholar]
- 19.Liu AJ, Nagel SR. The jamming transition and the marginally jammed solid. Annu Rev Condens Matter Phys. 2010;1:347–369. [Google Scholar]
- 20. Lubensky TC, Kane CL, Mao X, Souslov A, Sun, K (2015) Phonons and elasticity in critically coordinated lattices. arXiv 1503.01324. [DOI] [PubMed]
- 21.Deshpande VS, Ashby MF, Fleck NA. Foam topology: Bending versus stretching dominated architectures. Acta Mater. 2001;49:1035–1040. [Google Scholar]
- 22.Chen BG, Upadhyaya N, Vitelli V. Nonlinear conduction via solitons in a topological mechanical insulator. Proc Natl Acad Sci USA. 2014;111(36):13004–13009. doi: 10.1073/pnas.1405969111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Paulose J, Chen BG-g, Vitelli V. Topological modes bound to dislocations in mechanical metamaterials. Nat Phys. 2015;11:153–156. [Google Scholar]
- 24.Prodan E, Prodan C. Topological phonon modes and their role in dynamic instability of microtubules. Phys Rev Lett. 2009;103(24):248101. doi: 10.1103/PhysRevLett.103.248101. [DOI] [PubMed] [Google Scholar]
- 25.Vitelli V. Topological soft matter: Kagome lattices with a twist. Proc Natl Acad Sci USA. 2012;109(31):12266–12267. doi: 10.1073/pnas.1209950109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sun K, Souslov A, Mao X, Lubensky TC. Surface phonons, elastic response, and conformal invariance in twisted kagome lattices. Proc Natl Acad Sci USA. 2012;109(31):12369–12374. doi: 10.1073/pnas.1119941109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vitelli V, Upadhyaya N, Chen BG-g. 2014. Topological mechanisms as classical spinor fields. arXiv 1407.2890.
- 28.Franz M, Molenkamp L. Topological Insulators. Contemporary Concepts of Condensed Matter Science. Elsevier, Oxford; 2013. [Google Scholar]
- 29.Stenull O, Lubensky TC. Penrose tilings as jammed solids. Phys Rev Lett. 2014;113(15):158301. doi: 10.1103/PhysRevLett.113.158301. [DOI] [PubMed] [Google Scholar]
- 30.Eichenfield M, Chan J, Camacho RM, Vahala KJ, Painter O. Optomechanical crystals. Nature. 2009;462(7269):78–82. doi: 10.1038/nature08524. [DOI] [PubMed] [Google Scholar]
- 31.Guda Vishnu K, Strachan A. Shape memory metamaterials with tunable thermo-mechanical response via hetero-epitaxial integration: A molecular dynamics study. J Appl Phys. 2013;113:103503. [Google Scholar]
- 32.Leung A, Guest S. Single member actuation of kagome lattice structures. J Mech Mat Struct. 2007;2:303–317. [Google Scholar]
- 33.Drummond ND, Zlyomi V, Fal’ko VI. Electrically tunable band gap in silicene. Phys Rev B. 2012;85:075423. [Google Scholar]
- 34.Logan DL. A First Course in the Finite Element Method. Thomson; Ontario: 2007. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.