Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Jun 30;5:10792. doi: 10.1038/srep10792

Self-organized iron-oxide cementation geometry as an indicator of paleo-flows

Yifeng Wang 1,a, Marjorie A Chan 2, Enrique Merino 3
PMCID: PMC4485175  PMID: 26123788

Abstract

Widespread iron oxide precipitation from groundwater in fine-grained red beds displays various patterns, including nodulation, banding and scallops and fingers. Hematite nodules have been reported also from the Meridiani Planum site on Mars and interpreted as evidence for the ancient presence of water on the red planet. Here we show that such patterns can autonomously emerge from a previously unrecognized Ostwald ripening mechanism and they capture rich information regarding ancient chemical and hydrologic environments. A linear instability analysis of the reaction-transport equations suggests that a pattern transition from nodules to bands may result from a symmetry breaking of mineral dissolution and precipitation triggered by groundwater advection. Round nodules tend to develop under nearly stagnant hydrologic conditions, while repetitive bands form in the presence of persistent water flows. Since water circulation is a prerequisite for a sustainable subsurface life, a Martian site with iron oxide precipitation bands, if one were found, may offer a better chance for detecting extraterrestrial biosignatures on Mars than would sites with nodules.

Fine-grained sandstone in Mesozoic red beds of the Colorado Plateau in the southwestern United States contains iron oxide cements (mainly hematite and goethite). Some are early diagenetic grain coats and films that impart an overall red-bed appearance and others are late diagenetic features that display spectacular repetitive patterns, including evenly spaced nodules and repetitive bands with nested scales spanning two to three orders of magnitude (Fig. 1; Supplementary Figure S1). These nodules are commonly referred to as concretions, which are cemented mineral masses. The size of concretions typically ranges from millimeters to centimeters (Fig. 1A), while the spacing of bands ranges from millimeters to sub-meters (Fig. 1B). Spatial transition of one pattern to another (Fig. 1C) or one pattern superimposed on another (Fig. 1A) is also observed (Fig. 1A, C, D). These patterns may embed important information about paleo-diagenetic environments, especially regarding paleo-fluid migration and reactions1,2. Field evidence indicates that the formation of iron oxide precipitation bands in sandstone may be closely related to groundwater flows1,2. Concretions formed in Jurassic Navajo Sandstone have been proposed as a terrestrial analogue to hematite spherules detected by the rover Opportunity at the Meridiani Planum site on Mars3,4.

Figure 1. Formation of iron oxide concretion nodules, bands and scallops in Navajo eolian sandstone.

Figure 1

Open in a new tab

(A) Iron oxide concretions (several cm in diameter) in cross-bedded host rock at Snow Canyon, southwestern Utah. Nodule formation is superimposed on eolian laminae and has periodic banding (insert). (B) Very fine (~mm-thick) diagenetic iron oxide bands cut across the original eolian laminae (approximately horizontal) at Coyote Buttes, northern Arizona. Image width ~20 cm. (C) To the right of center note the spatial transition from bands (above) to small concretions at Coyote Buttes, northern Arizona. (D) Multiple “scallop” iron oxide bands at Calf Creek, Grand Staircase Escalante National Monument, Utah. Image width ~25 cm.

Repetitive iron oxide precipitation bands in rocks have generally been lumped as “Liesegang bands” without further elaboration of underlying mechanisms. Typical Liesegang bands are thought to form by counter-diffusion of two reactants via a nucleation-growth-depletion mechanism5,6 or post-nucleation Ostwald ripening7,8. These theories, however, are unable to account for key features of iron oxide precipitation bands observed in sandstone. First, it seems that the nucleation-growth-depletion mechanism is unlikely, simply because iron oxide precipitation in red-bed sandstone is usually pervasive, suggesting that nucleation was not a limiting factor for the initiation of individual bands (Fig. 1B, C). Furthermore, the spacing between two neighboring bands in a specific packet of bands is observed to be more or less constant (Fig. 1B), contrary to the exponentially increasing banding spacing predicted from the counter-diffusion Liesegang banding theory9. Also, the spacing of the bands in some cases can reach sub-meters, which apparently exceed a typical scale of Liesegang bandings that can be produced in a diffusion-dominated system. In addition, it is hard to imagine that a counter diffusion process alone would be able to generate iron oxide bands over significant volumes of sandstone (up to tens of meters vertically and kilometers laterally). We postulate that these large volumes of banded sandstone must have involved regional groundwater flows, as suggested by field observations1,2. Other mechanisms have also been proposed to explain the iron oxide patterning. For example, the formation of iron oxide nodules has been attributed to microbial oxidation, which could be induced when an Fe(II)-containing fluid is mixed with an oxidizing fluid10,11. But how this reaction becomes periodically localized in space remains unexplained. In addition, the environment for red bed deposition and diagenesis is generally poor in organic matter and microbial activity may be limited12. Importantly, no existing theory can explain a geometrical transition from one pattern to another, for example, from nodulation to bandings or vice versa.

The field evidence seems to indicate a self-organizational origin of iron oxide precipitation patterns13,14, whereby patterns arise from the internal dynamics of the water-rock system, without external periodic forces or preexisting templates. This assertion is supported by the observation that iron oxide nodules or bands cut cross the original eolian laminae (Fig. 1B and Figure S1). In this paper, we show that iron oxide precipitation patterns in fine-grained sandstone can autonomously emerge from a previously unrecognized Ostwald ripening mechanism. We further show that a geometric transition from one pattern to another can be triggered by a change in groundwater flow velocity. Thus, these patterns can potentially capture important information regarding paleo-flows. This work provides a new perspective for interpreting geochemical and hydrological signatures of widespread iron oxide cementation patterns including those detected on Mars.

Results

Ostwald ripening in confined pore space

Self-organization requires a positive feedback among physical and chemical processes involved in a system15. We here propose a new mechanism for the pattern formation of iron oxide precipitation in fine-grained sandstone by considering Ostwald ripening confined in small pore space and coupled with groundwater advection. In Ostwald ripening, larger particles grow even larger at expense of smaller particles because of the size dependence of particle solubility16:

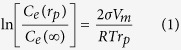graphic file with name srep10792-m1.jpg

where Ce(rp) is the solubility of a particle with a radius rp; Ce(∞) is the solubility of the bulk solid phase; σ is the surface energy between iron oxide and water; Vm is the molar volume of the solid; R is the gas constant; and T is the absolute temperature. Ostwald ripening is effective only for small particles, less than 50 micrometers in size, so that a slight variation in size would result in a significant solubility difference between two nearby particles (Fig. 2). Once the particle size of iron oxides becomes sufficiently large, Ostwald ripening ceases, and a pattern formed would become arrested. However, the size of iron oxide precipitate particles is limited by the sandstone pore size, which is typically smaller than tens of microns17,18. Note that a typical particle size of iron oxide in Navajo Sandstone is ~10 mcrometers3. Thus, iron oxide precipitates confined in these pores remain effective almost forever for Ostwald ripening. Also, because of their high surface energies19, according to Equation (1), iron oxides (or hydroxides) are expected to have a higher tendency than other authigenic minerals for Ostwald ripening. All these combined lead to widespread iron oxide pattern formation in eolian sandstone, as observed (Fig. 1)3,4. The proposed Ostwald ripening mechanism is consistent with iron isotopic measurements from Navajo Sandstone, which indicate that iron oxide nodules formed through simple mineral dissolution and precipitation20.

Figure 2. Effect of pore confinement on Ostwald ripening of iron oxide in fine-grained sandstone.

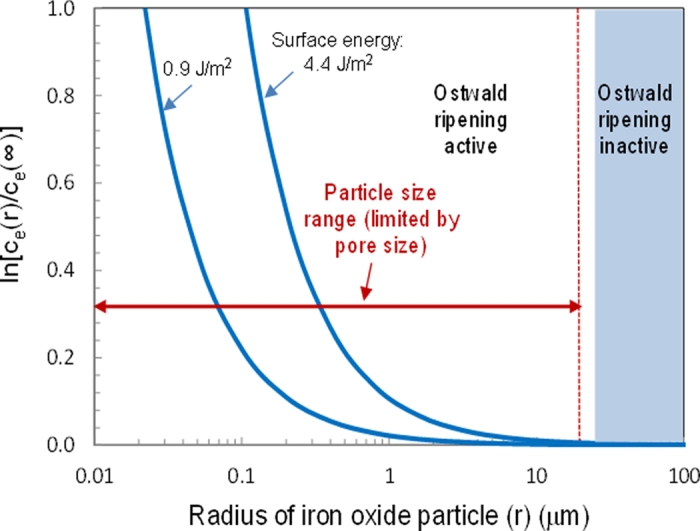
Figure 2

Open in a new tab

Ostwald ripening tends to occur in a particle size range where the solubility of a solid phase highly depends on the size of solid particles. In fine-grained sandstone, the particle size of iron oxide cement is limited by the pore size of the rock, rendering this type of rock to be an ideal system for Ostwald ripening. The boundary between the active and inactive regions is drawn at the particle size (~50 micrometers in diameter) corresponding to the solubility of the particle being ~0.1% of that of the bulk phase. The range of surface energy for iron oxide, 0.9–4.4 J/m2, is taken from reference 60. The typical pore size range for Navajo Sandstone is ~40 micrometers in diameter18.

The dependence of iron oxide solubility on particle size in sandstone is more complicated. Experiments suggest that porous host media could significantly affect precipitation pattern formation21. Iron oxide precipitates form coating films on sand grain surfaces22,23. Based on the Ostwald ripening principle, a thicker film [equivalent to larger particles in Equation (1)] has a lower solubility than a thinner film and therefore tends to grow even thicker at expense of the latter. However, this tendency is countered by other factors. In a coating film, a precipitate can interact strongly with their neighbors, depending on the coverage of the coating or the thickness of the film24. As new iron oxide crystallites are added, a sharp variation film thickness in the neighborhood would result in additional stress in the film or even create a new interface, thus adding energy to the film. This variation would also change the curvature of iron oxide-water interface, thus modifying the solubility of the solid. Furthermore, due to the pore confinement, the growth of a precipitate tends to push a neighboring particle away to make room for growth, which creates a crystallization force on its neighbors and also modify the solubility of the solid25,26. All these effects amount to smooth out a spatial discontinuity in film thickness or mineral content distribution. Therefore, it is reasonable to assume that the solubility of iron oxide at a given point 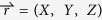Inline graphic depends not only on the local film thickness but also on its distribution within the neighborhood. 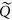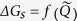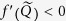To capture these effects, we assume that the excess Gibbs free energy (ΔGs) of an iron oxide film relative to the bulk phase at a given point is a monotonic decreasing function of the weighted iron oxide content within the neighborhood (Inline graphic): Inline graphic with Inline graphic. One reasonable choice for the function could be that 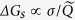Inline graphic, in analogue to Equation (1). The weighted iron oxide content 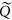Inline graphic can be related to the local iron oxide content in bulk rock Q by:

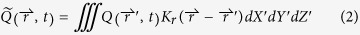graphic file with name srep10792-m8.jpg

where 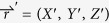Inline graphic is the coordinate vector for a point in the neighborhood; Kr is a kernel function with 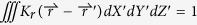Inline graphic, a weighting function that describes the textural dependence of the Gibbs free energy of iron oxide at a location 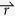Inline graphic on the iron oxide content distribution in the neighborhood. The kernel function Kr is assumed to be isotropic and independent of location, and it vanishes as 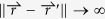Inline graphic as it is expected that the textural dependence diminishes as the two spatial points become further apart. Based on the Curie principle, by expanding the term Q in Equation (2), we can approximate Equation (2) by27,28:

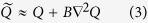graphic file with name srep10792-m13.jpg

where B is a constant characterizing the influence of mineral distribution in the neighborhood of a specific point on mineral solubility at that point. The weighted iron oxide content at a point is expected to increase with the mass in the neighborhood, and B must be positive. The solubility of iron oxide (Ce) at 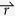Inline graphic can then be expressed as:

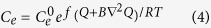graphic file with name srep10792-m15.jpg

where 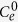Inline graphic is the solubility of the bulk phase. The precipitation rate (Rp) of iron oxide is assumed to follow the first order kinetics:

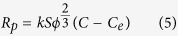graphic file with name srep10792-m17.jpg

where C is the dissolved iron concentration in pore water; k is the reaction rate constant; φ is the porosity; and the term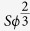Inline graphic represents the specific pore surface area available for iron oxide precipitation. Term 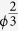Inline graphic converts the pore volume to the pore surface area with S as a geometric factor of the pores. We assume that iron oxide cementation proceeds through coating the pore surfaces22,23. Iron oxide cementation in sandstone can then be described by:

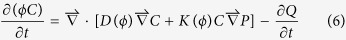graphic file with name srep10792-m20.jpg
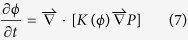graphic file with name srep10792-m21.jpg
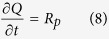graphic file with name srep10792-m22.jpg
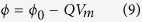graphic file with name srep10792-m23.jpg

where P is the hydraulic head; and φ0 is the porosity of sandstone without iron oxide cementation. The effective diffusion coefficient D(φ) and the hydraulic conductivity K(φ) are described by D(φ) = D0φm and 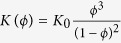Inline graphic, respectively29,30,31, where D0 is the diffusion coefficient of dissolved iron species in pore water and both m (≈2, ref. 30) and K0 are constants.

Pattern formation and symmetry breaking

We now want to show that an initially homogenous system can self-organize to form a repetitive pattern from infinitesimal fluctuations (or perturbations). We have performed a linear stability analysis of Equations (4), (5), (6), (7), (8) for a sandstone formation initially with a uniform distribution of iron oxide content (Q0) and porosity excluding iron oxide (φ0). Parameter φ0 remains constant during pattern formation. In the presence of an advective flow, water is assumed to percolate along x-axis. In the analysis, we first introduce a perturbation of wave number vector (ωx, ωy, ωz) around a uniformly distributed steady state and then determine the growth rate (ζ) of the perturbation as a function of the wave number vector (see Methods):

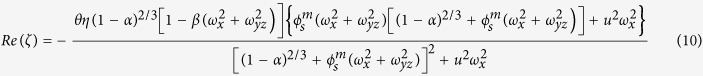graphic file with name srep10792-m25.jpg
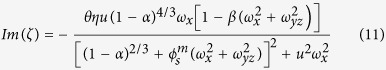graphic file with name srep10792-m26.jpg

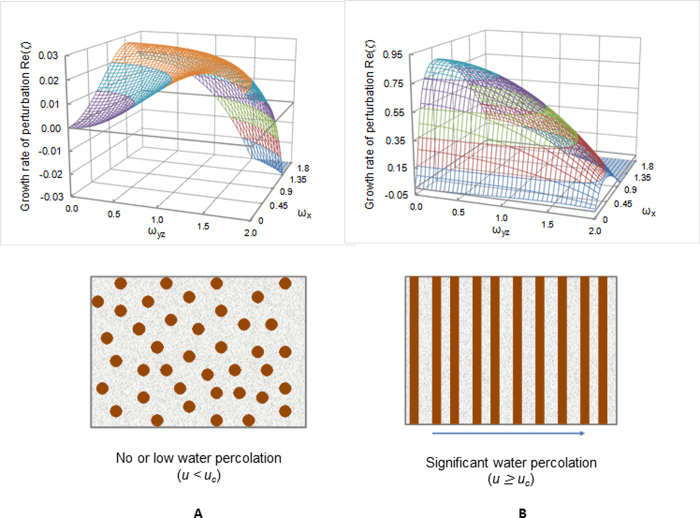
where θ = f(Q0)/RT; η = f′(Q0)Q0/f(Q0) < 0; α = Q0Vm/φ0; β = B/L2; φs = φ0(1–α); ωyz is the wave number along the direction perpendicular to the water flow 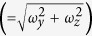Inline graphic; and u is a scaled flow velocity (see Methods). The real part of ζ, Re(ζ), represents the growth rate of the perturbation, while the imaginary part, Im(ζ), characterizes a temporal oscillatory behavior of the perturbation27,32. A positive Re(ζ) value indicates that the perturbation with the corresponding wave number tends to grow with time, leading to the emergence of a spatially repetitive pattern32. The wave number vector (ωmax,x, ωmax,y, ωmax,z) corresponding to the maximum growth rate determines the periodicity of the pattern actually formed. Note that this preferred wave number vector is independent of parameters θ and η, implying that the actual form of function f(Q0) has no effect on the periodicity of the pattern as long as f′(Q0) < 0. Figure 3 shows the general behavior of Re(ζ) as a function of the wave vectors.

Figure 3. Emergence of iron oxide cementation patterns predicted from a linear stability analysis.

Figure 3

Open in a new tab

The wave number with the maximum growth rate (ωmax) determines the geometry and scale of the emerging pattern. Groundwater is assumed to percolate along the x-direction. ωx is the wave number in the direction parallel to the groundwater flow and ωyz is the wave number in the direction perpendicular to the flow. In a case with no significant flow present, the growth rate of perturbation has equal maxima on both ωx and ωyz; therefore a precipitation pattern forms – i.e., spots or nodules – with no directional preference (A). But for significant or dominant water flow, the growth rate of perturbation displays a maximum only at ωyz = 0; consequently a pattern forms only along the flow path, while patterns along the direction normal to the flow direction are suppressed (B) since ωmax,yz = 0, as illustrated schematically in the lower panel. α = 0.013, φs = 0.15, θ = 1.0, η = − 1.0, β = 0.2, m = 2, and u = 0 (left) or 6 (>uc ≈ 1) (right).

The linear stability analysis shows that a spatially repetitive pattern can autonomously emerge from the pore-space-confined Ostwald ripening, as indicated by the existence of positive Re(ζ) values for certain wave numbers in Fig. 3. In a no or low groundwater flow case, the preferred wave number is identical in all directions, implying the formation of a spatially isotropic pattern (i.e., the formation of spots or nodules; Fig. 3A). Since Im(ζ) = 0, the pattern formed would be stationary. Whereas, in the presence of significant groundwater advection, ωmax,yz = 0, which implies an infinite wave length in the direction perpendicular to the flow, implying that the periodic iron oxide precipitation is suppressed in that direction and repetitive banding can form only along the flow path. Since Im(ζ) ≠ 0, the iron oxide content at a given spatial point would oscillate with time. The only way to have this situation is that the pattern formed would slowly move downstream, forming a chemical wave (Fig. 3B). Because of this chemical wave, iron oxides in fine-grained sandstone may be much more mobile than we thought before. As discussed below, with increasing the flow rate, the spacing of the banding increases and eventually become so large (i.e., ωmax,x → 0) that the bands disappear from our observational domain. The system then enters a svegliabile (dormant) state33, in which iron oxide cementation become relatively homogeneous within the observational domain. Large red and bleached patches observed in some sandstone34 may represent a svegliabile state33. This state can be “awaken” (i.e. become patterned) as the flow rate decreases at a later stage of a water flow regime, leading to an overprint of repetitive patterns on a previously uniformly cemented domain (Fig. 1D). The behaviors in pattern transition are summarized in Fig. 4. Given a typical range of D0 (5 × 10−5 – 5 × 10−4 cm2/s), the critical flow rate for the symmetry-breaking transition from nodules to repetitive bands is estimated to be very low, <0.2 cm/year (Fig. 4), implying that the occurrence of iron oxide nodules may indicate a practically stagnant hydrologic condition, consistent with the field observation at Lake Brown, Western Australia, where hematite nodules precipitated in a shallow sediment and groundwater was static35,36. At much higher flow velocities, around 10 meters/year, another symmetry-breaking transition takes place (Fig. 4), from banding behavior to a so-called svegliabile (or dormant) state noted above (top box in Fig. 4).

Figure 4. Symmetry breaking and pattern transitions of iron oxide cementation.

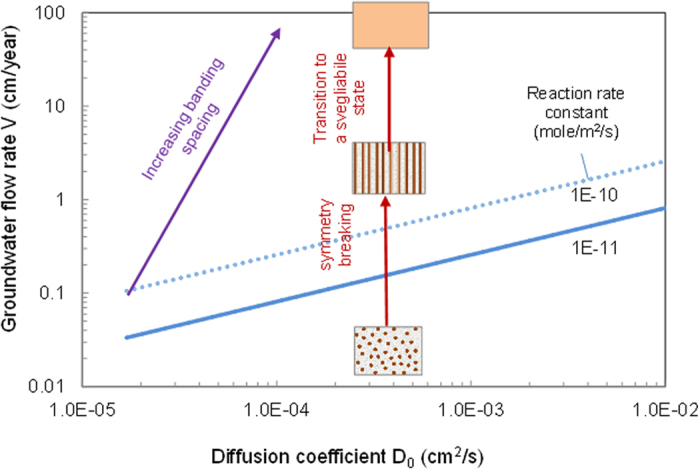
Figure 4

Open in a new tab

As the groundwater flow rate increases from zero, the cementation pattern “breaks” in symmetry from nodule formation to banding when crossing the boundary shown for two values of the reaction rate constant, 10−10 and 10−11 mole/m2/s. With further increase of the flow rate, the banding spacing becomes so large that the banding patterns disappear from our observational domain, entering a svegliabile33 state where iron oxide precipitation becomes relatively uniform. φs = 0.15, 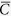Inline graphic = 5 × 10−10 mole/cm3 solution, 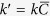Inline graphic = 10−11 - 10−10 mole/m2/s, Q0 = 10−3 mole/cm3 bulk sediment, 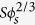Inline graphic = 0.2 m2/cm3 bulk sediment, and uc ≈ 1.

Reconstruction of paleo-flow fields

A sensible model must be able to predict the scale of patterns formed. The wave length of a cementation pattern can be estimated by (see Methods):

graphic file with name srep10792-m28.jpg
graphic file with name srep10792-m29.jpg

where uc is the critical scaled flow rate for a transition from nodule formation to banding. Note that parameter β characterizes the influence range of neighboring iron oxide precipitates, estimated to be on the order of a few sediment grains to the size of an individual iron oxide concretion or band (β = ∼ 0.1–1.0). For a stagnant flow case, taking the typical parameter values: φ = 0.1–0.3 (ref. 23), 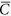Inline graphic = 10−10–10−9 mole/cm3 solution23,37, D0 = 5 × 10−5 – 5 × 10−4 cm2/s (accounting for the potential effect of mechanical dispersion)38, 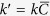Inline graphic = 10−11 – 10−10 mole/m2/s (ref. 39), 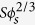Inline graphic = 0.02–0.2 m2/cm3 bulk sediment40, we estimate the wave length of a pattern to be 0.1 to 30 cm, consistent with field observations (Fig. 1)3,4,13,23,41. In an advective flow-dominant case, according to Equation (13), the spacing of the banding can vary greatly from millimeters to sub-meters, depending on the actual flow rate involved. Therefore, according to the theory presented here, the geometry of iron oxide cementation patterns provides rich information about paleo-diagenetic environments. The chemical wave concept introduced here provides a logical explanation for the observed positive correlation between the size and the spacing of concretions3, because both parameters are supposed to be proportional to the wave length.

Since 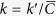Inline graphic (where k’ is in unit mole/m2/s), from Equations (12) and (13), we have: 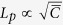Inline graphic. The scale of a pattern thus increases with the dissolved iron concentration. In general, a high dissolved iron concentration would enhance pattern formation, because mass transfer from one location to another is an important step for the proposed Ostwald ripening mechanism. The solubility of bulk iron oxides is known to be extremely low (~nanomolar)23. The dissolution of iron oxide precipitates in fine-grained sandstone can be enhanced by several factors, including the small size of the precipitates due to pore confinement (Fig. 2), the presence of Fe3+-complexing ligands37, and low pH conditions37. Sulfate (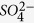Inline graphic) seems to play an important role in Fe3+ mobilization, due to its ability to complex with ferric iron42, and also because sulfate-rich waters in nature are usually acidic43. At Lake Brown in Western Australia, hematite nodules were found to precipitate in shallow subsurface sediments36. The size of nodules ranges from 2 mm to 4 cm. The waters involved in nodule formation are Na-Cl-Mg-SO4-rich acid saline waters with a 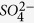Inline graphic concentration ranging from 1,600 to 3,300 ppm and a pH ranging from 3.5 to 4.3. Similarly, hematite spherules ~10–100 μm in diameter were found to precipitate in sulfate-rich rocks formed by aqueous, acid-sulfate alteration of basaltic tephra on Mauna Kea Volcano, Hawaii44. Note that sulfate-rich acidic waters can be formed from chemical divides driven by water evaporation43. This may explain why red beds and the associated repetitive iron oxide precipitation patterns seem likely to occur in hot and arid regions12.

Interestingly, the model developed above may allow us to reconstruct key paleo-environmental parameters from the geometry of cementation patterns. For illustration, let’s focus on two important parameters: chemical reaction rate constant and groundwater flow rate. We can first constrain the reaction rate constant from the size of nodules. If the spacing of nodules is 1 cm, from Equation (12), we estimate the reaction rate constant for hematite dissolution to be ~3 × 10−12 – 3 × 10−11 mole/m2/s (Fig. 5A), comparable with laboratory measurements (~10−11 mole/m2/s, ref. 39). With the estimated value, Equation (13) can then be used to constrain the groundwater flow rate for the formation of repetitive iron oxide precipitation bands (Fig. 5B). For example, a banding spacing of 10 cm may indicate a flow rate of 0.3 – 2.5 cm/year. The absolute estimated value of flow rate may be subject to large uncertainties, because it depends on the values chosen for a number of other parameters, especially for a typical dissolved iron concentration (Inline graphic), which could vary significantly as discussed above. Nevertheless, the concept developed here can allow us to reconstruct relative flow rates fairly accurately. This is because, for a given sandstone formation, all parameters, except scaled flow rate (u), in the right hand side of Equation (13) are expected to remain relatively constant. The relative flow rate is then directly proportional to Inline graphic. Note that cementation bands form normal to the flow direction (see the discussion above). A careful mapping of cementation patterns and banding spacing over rock outcrops can potentially allow us to reconstruct a past water flow field for a sandstone aquifer.

Figure 5. Estimation of key chemical and hydrologic parameters from iron oxide cementation patterns.

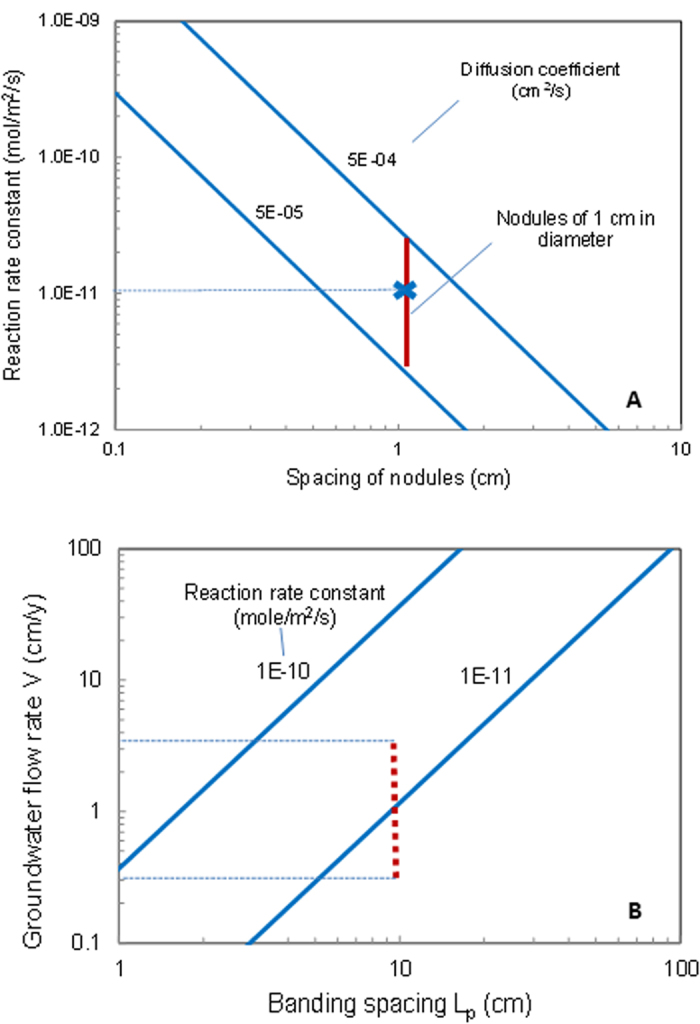
Figure 5

Open in a new tab

The rate constant for iron oxide precipitation can be estimated from the spacing of nodules using Equation (12) (A). Symbol x is the laboratory measurement of hematite dissolution rate39. For a given reaction rate constant, the groundwater flow rate can be estimated from the spacing of iron oxide bands using Equation (13) (B). Note that Equation (13) is valid only for relatively large flow rates. Vertical bars indicate the ranges of reaction rate constant and groundwater flow rate estimated from pattern sizes. 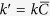φs = 0.15, Inline graphic = 5 × 10−10 mole/cm3 solution, Inline graphic = 10−11 mole/m2/s, Q0 = 10−3 mole/cm3 bulk sediment, 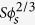Inline graphic = 0.2 m2/cm3 bulk sediment, β = 0.2, and D0 = 510−5 cm2/s (B).

The model presented here predicts other salient features of iron oxide cementation patterns in sandstone as well. The iron oxide cementation patterns studied here occur in two symmetries, bands and nodules, that are able to grade into each other in the field (Fig. 1C), and that are – according to our model – linked genetically to the velocity of groundwater flow, as shown in Figs. 3 and 4. The ability of the linear instability analysis to predict the two symmetries is one of the strengths of the model. From the model, it is expected that the banding spacing resulting from the proposed mechanism would remain more or less constant for a given flow regime, which is consistent with field observations (Fig. 1B) but cannot be explained by the classic Liesegang banding theories9. For the first time, we demonstrate that Ostwald ripening in an advective flow field is able to generate chemical waves along the flow pathway. Since they are induced by water advection, such bandings can develop pervasively in a large portion of geologic formations, as observed1,2. In contrast, the classic diffusion-based Liesegang banding is generally limited in space. Because of pore confinement (Fig. 2), iron oxide precipitates in fine-grained sandstone may be subjected to continual Ostwald ripening as flow regimes change, leading to a complex set and/or sequence of pattern formation (Fig. 1A and D).

Discussion

Using representative parameter value ranges constrained above, the typical time scale for iron oxide pattern formation (Tt) can be estimated by 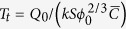Inline graphic (see Methods). It is estimated to range from tens of years to a few thousands of years, a perhaps surprising short geologic time, yet in good agreement with observations. For example, at Lake Brown in Western Australia, the diagenetic nodules were found to form within <3,000 years, based on dating of stratigraphically higher and lower beds36. Such a short time scale, combined with the dynamic nature of confined Ostwald ripening (Fig. 2), means that iron oxide cements and their patterns may be continually reworked over time. This evolutionary nature of iron oxide cementation is consistent with paleomagnetic measurements in Jurassic Navajo Sandstone which indicate that the Navajo has only recently acquired a new, stable secondary magnetic moment45. A (U-Th)/He geochronological study of iron oxide cements in sandstone of Colorado Plateau indicates that young waters (ca. 2-3 m.y.) passed through the system46. Similarly, the remnant magnetization in several Triassic and earliest Jurassic sediment units from the Colorado Plateau was found to be acquired over an extended time period (~35 m.y.) and not coeval with the stratigraphic age of the units47. The proposed concept also sheds light on a recently discovered dilemma between the latitudinal position of supercontinent Pangea reconstructed from paleomagnetic measurements and that deduced from wind directions recorded in dunes in eolian sandstones in the southwestern United States48. The atmospheric circulation constructed from the sand dunes shows a broad sweep of northeasterly winds over the northernmost part of the region and then curving to become northwesterly in the south part, indicating that the Jurassic sandstones were deposited close to the equator. This observation is at odds with the paleomagnetic measurements, which indicate that those sandstones were formed around the latitude of 20 oN (ref. 37). Given the dynamics of continual iron oxide dissolution-precipitation in cementation as discussed above, this inconsistency can possibly be attributed to multiple diagenetic episodes with more recent ones overprinting earlier ones on rock magnetization.

The model presented above assumes an initial condition of sand grains coated with iron oxide films. Such films form by oxidation and precipitation of ferrous iron released by early alteration of detrital grains of biotite and pyroxene and/or by precipitation of dissolved Fe3+ species carried in by acidic (and perhaps sulfate-rich) fluids. Iron oxide patterns may immediately start to form behind either an oxidation or a precipitation front13. Patterning suggested above may begin with repetitive banding and then switch to nodule formation as the fluid advection abates. The same physical domain may experience multiple hydrologic regimes, leading to complex pattern formations (Fig. 1)34,49. Early formed nodules may be subjected to further differentiation inside, resulting in internal concentric banding. This differentiation can be induced by a classic counter-diffusion Ostwald ripening process. Thus, internal concentric banding may indicate the maturity of nodule evolution, as it does also in the case of mature pisolites developed in lateritic weathering profiles50. Note that the linear analysis presented here in general applies only to an internal region of an aquifer, which is far from a water recharge boundary so that any boundary influence becomes negligible. At the boundary, an iron oxide dissolution front may be developed, and reactive infiltration instability may then be induced51. The proposed confined Ostwald ripening mechanism is expected to reinforce the infiltration instability, because it tends to induce more mineral precipitation in a lower porosity (iron oxide rich) domain and more mineral dissolution in a higher porosity domain. This coupling might be responsible for the formation of scalloped (Fig. 1D) or fingered precipitates (fig. 2 in ref. 51) and pipe-like concretions52, and in this case concretions would tend to orient along the flow direction.

As mentioned earlier, iron oxide concretions found in Navajo Sandstone have been used as a terrestrial analogue to hematite nodules detected on Mars. The work presented in this paper may provide additional insight into extraterrestrial biosignature detection and data interpretation for Mars explorations. Small (<0.5 cm) spherical hematite nodules were found in the Eagle Crater at Meridiani Planum on Mars3,53. Sediments at this site are composed of fined-grained clastic materials derived from weathering of basaltic rocks and contain high percentages of sulfate minerals, notably jarosite [KFe3+3(OH)6(SO4)2] (ref. 53). Jarosite is thought to form under oxidizing acidic environments and persist under arid conditions54. According to our model, such chemical environments would be conducive to Fe3+ mobilization and therefore iron oxide pattern formation. The occurrence of nodules may indicate a stagnant hydrologic environment involved in iron oxide diagenesis (Fig. 4)55. New NASA Mars Science Laboratory explorations of Curiosity rover in Gale Crater indicate more diagenetic spherules and nodules56. Since a persistent water circulation is generally required for a sustainable subsurface life, a site with iron oxide bands, if one were found, may offer a better chance for detecting biosignatures on Mars.

Finally, many repetitive cementation patterns of various scales and mineral compositions in sedimentary deposits may also have self-organizational origins. However, each case likely has its own unique underlying mechanisms, which can only be identified by careful field and laboratory observations and by testing model predictions against observations57. In this sense, we caution any attempt to grossly apply the mechanism proposed in this paper to the cementation pattern formation of other mineralogies and other geological environments. For example, elongate carbonate concretions occur in fluvial sediments and their orientation has been used as a proxy to the flow field of paleoaquifers58. Such carbonate concretions might have formed from localized microbial reactions59 coupled with infiltration instability. Despite their appearance resemblance to pipe-like iron oxide nodules as discussed above, elongate carbonate nodules are likely to form from a different mechanism. It should also be recognized that the mechanism proposed here doesn’t preclude the banding formation by a classic counter-diffusion mechanism, which may occur in some circumstances where waters are stagnant, isolated redox domains may exist, and counter-diffusion of oxidant (O2) and reductant (Fe2+) could be induced. However, such bandings would generally be localized in space (not pervasive as in advection-induced bandings) and concentric in geometry with no systematic spatial orientations. Given general oxidizing conditions in red-bed formations12, the occurrence of these bandings in such environments is expected to be limited. We believe that pervasive iron oxide diagenetic bandings in eolian sandstone described here were predominantly formed by the proposed advection-dominated confined Ostwald ripening mechanism. Our model combines both field observations and theoretical modeling to show the complexities of the interplay among pore geometries, fluid chemistry, and flow fields in mineral dissolution and precipitation at multiple scales.

Methods

Scaling and asymptotic analysis

For the system of interest, the relevant time and length scales emerge from the internal dynamics of the system, and they can be determined by scaling variables in Equations (4), (5), (6), (7), (8), (9). This scaling process also allows us to lump model parameters into minimum set of dimensionless parameters. Let’s first choose a typical dissolved iron concentration (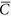Inline graphic) to be the solubility of iron oxide for Q = Q0: 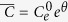Inline graphic. We then choose a time scale (Tt) from Equations (5) and (8) such that a significant iron oxide dissolution and precipitation can occur over the chosen time scale: 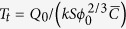Inline graphic. 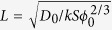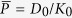The emerging length scale (L) and the typical hydraulic head (Inline graphic) can be obtained as: Inline graphic and Inline graphic, respectively, by making both the diffusion term and the advective term in equation (6) vary comparably with the chemical reaction term so that they can interact with each other, since field evidence indicates that the formation of iron oxide patterns is collectively controlled by diffusion, fluid flow and chemical reactions1,2. 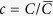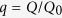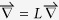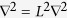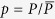Accordingly, the other variables and the related mathematical operators can be scaled as follows: Inline graphic, Inline graphic, τ = t/Tt, x = X/L, u = VTt/L, y=Y/L, Inline graphic, Inline graphic, and Inline graphic. Equations (4, 5, 6, 7, 8, 9) can then be cast into a set of dimensionless scaled equations:

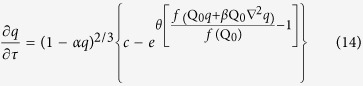graphic file with name srep10792-m51.jpg
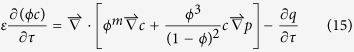graphic file with name srep10792-m52.jpg
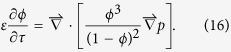graphic file with name srep10792-m53.jpg
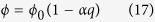graphic file with name srep10792-m54.jpg

where 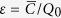Inline graphic. Given a typical value of 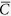Inline graphic (~5 × 10−10 mol/cm3 solution, ref.39) and Q0 (~10−3 mol/cm3 sediment23), ε < 10−6, indicating that, because of the natural difference between aqueous solutions and crystalline matter, aqueous concentrations of ions (here, iron) are always orders of magnitude smaller than their concentration in minerals, i.e., the density. Therefore, the left-hand side terms in Equations (15) and (16) are negligible, and the two equations can be treated to be pseudo-steady state on the time scale of pattern formation33.

Linear stability analysis

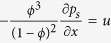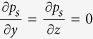Let ε → 0 in equations (14) through (17). A uniform steady state solution to the equations can be found: qs = 1, cs = 1, φs = φ0(1–α), Inline graphic, and Inline graphic. Linearizing the equations around the steady state solution with respect to perturbations δq, δc, δp, and δφ, we obtain:

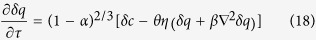graphic file with name srep10792-m59.jpg
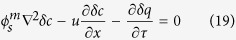graphic file with name srep10792-m60.jpg
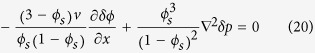graphic file with name srep10792-m61.jpg
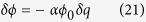graphic file with name srep10792-m62.jpg

Assuming that the perturbations have the form:

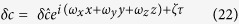graphic file with name srep10792-m63.jpg
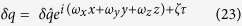graphic file with name srep10792-m64.jpg
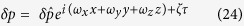graphic file with name srep10792-m65.jpg
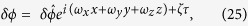graphic file with name srep10792-m66.jpg

we obtain the following homogeneous algebraic equations:

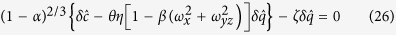graphic file with name srep10792-m67.jpg
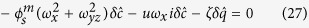graphic file with name srep10792-m68.jpg
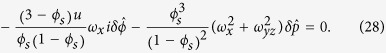graphic file with name srep10792-m69.jpg
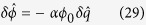graphic file with name srep10792-m70.jpg

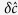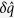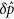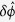The condition for a nontrivial solution of Inline graphic, Inline graphic, Inline graphic and Inline graphic is:

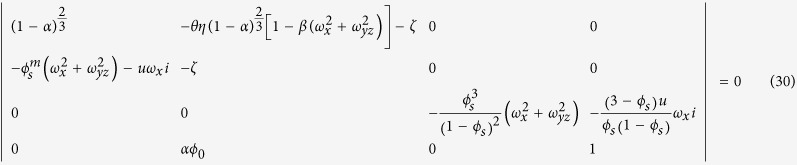graphic file with name srep10792-m75.jpg

Solving the equation for ζ, we obtain the dispersion equations (10) and (11).

Estimation of pattern scale

For a no-flow case (u = 0), from equation (10), we have

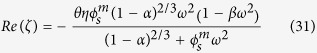graphic file with name srep10792-m76.jpg

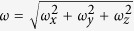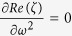where Inline graphic. The preferred wave number ωmax can be found by taking Inline graphic:

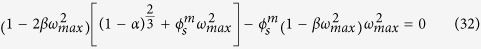graphic file with name srep10792-m79.jpg

We then have:

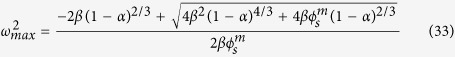graphic file with name srep10792-m80.jpg

Since 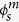Inline graphic << (1 – α) ≈ 1 and β is on the order of unity, we obtain:

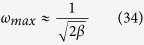graphic file with name srep10792-m82.jpg

or

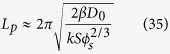graphic file with name srep10792-m83.jpg

Adding the term φs in the nominator to convert the unit of cm3 bulk sediment to the unit of cm3 solution, we obtain Equation (12).

For a flow case with a large u, since ωmax,2 = 0 (Fig. 3), from equation (10), we have

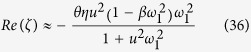graphic file with name srep10792-m84.jpg

Similarly, the preferred wave number ωmax,1 can be found by taking 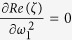Inline graphic:

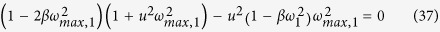graphic file with name srep10792-m86.jpg

Solving for 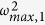Inline graphic, we obtain:

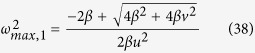graphic file with name srep10792-m88.jpg

We then have:

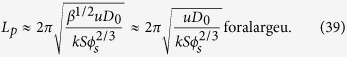graphic file with name srep10792-m89.jpg

Adding the factor φs to convert the unit of cm3 bulk sediment to the unit of cm3 solution, we obtain Equation (13).

Symbols

B – Constant characterizing the influence of mineral distribution mineral solubility

C – Dissolved iron concentration in pore water

Ce – Solubility of iron oxide particles

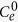Inline graphic – Solubility of the bulk phase

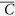Inline graphic – Typical dissolved iron concentration

c – Scaled dissolved iron concentration

cs – Scaled dissolved iron concentration at a steady state

D – Effective diffusion coefficient

D0 – Diffusion coefficient of dissolved iron species

f – Functional dependence of Gibbs free energy on weighted iron oxide content

K – Hydraulic conductivity

k – Reaction rate constant

Kr – Kernel function describing the textural dependence of Gibbs free energy of iron oxide

L – Typical length

Lp – Wave length of cementation pattern

P – Hydraulic head

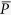Inline graphic – Typical hydraulic head

p – Scaled hydraulic head

ps – Scaled hydraulic head at a steady state

Q – Local iron oxide content in bulk rock

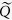Inline graphic – Weighted iron oxide content within the neighborhood

Q0 – Initial iron oxide content

q – Scaled iron oxide content

qs – Scaled iron oxide content at a steady state

R – Gas constant

Rp – Precipitation rate of iron oxide

rp – Radius of iron oxide particles

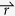Inline graphic – Spatial coordinate

S – Geometric factor of pores

T – Absolute temperature

Tt – Typical time

V – Groundwater velocity

Vm – Molar volume of the solid

u – Scaled groundwater velocity

uc – Scaled critical groundwater velocity for pattern transition

X, Y, Z – Spatial coordinate

x, y, z – Scaled spatial coordinate

α − Q0Vm/φ0

β − B/L2

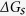Inline graphic – Excess Gibbs free energy of iron oxide film

δq, δc, δp, δφ – Perturbations of q, c, p, and φ respectively

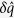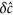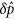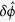Inline graphic, Inline graphic, Inline graphic, Inline graphic – Perturbation amplitudes of q, c, p, and φ respectively

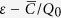
Inline graphic

ζ – Growth rate of a perturbation

η − f′(Q0)Q0/f(Q0)

θ − f(Q0)/RT

σ – Surface energy between iron oxide and water

τ – Scaled time

ωx, ωy, ωz – Wave number vector of a perturbation

ωmax,x, ωmax,y, ωmax,z – Wave number vector corresponding to the maximum perturbation growth rate

φ – Porosity

φ0 – Porosity of sandstone without iron oxide cementation

φs − φ0(1 − α)

Additional Information

How to cite this article: Wang, Y. et al. Self-organized iron-oxide cementation geometry as an indicator of paleo-flows. Sci. Rep. 5, 10792; doi: 10.1038/srep10792 (2015).

Supplementary Material

Supplementary Information
srep10792-s1.pdf (347.1KB, pdf)

Acknowledgments

Sandia National Laboratories is a multi-program laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-AC04-94AL85000. This work was partly supported by DOE Sandia LDRD Program. The work was also partly supported by an Energy Frontier Research Center (EFRC) funded by the U.S Department of Energy (DOE), Office of Sciences (BES). Chan’s effort was an outgrowth of work supported by the National Aeronautics and Space Administration under grant NNG06GI10G (to Chan) issued through the Mars Fundamental Research Program.

Footnotes

Author Contributions Y.W. developed the conceptual model and performed the mathematical analysis. M.A.C. performed field observations. Y.W. wrote the first draft of the manuscript. E.M. reviewed the mathematical model and made extensive editing of the manuscript. All three authors discussed the results and commented on the manuscript.

References

  1. Potter S. Diagenetic iron oxide precipitation: A proxy for supercritical CO2 spatiotemporal flow. Geol. Soc. Amer. Abs. Pro. 42, 211 (2010). [Google Scholar]
  2. Nielsen G. B. & Chan M. A. Mapping and correlation of diagenetic coloration facies, Jurassic Navajo sandstone, Snow Canyon State Park, Southwestern Utah. Geol. Geol. Res. Issues Western Utah 2009, 97–124 (2009). [Google Scholar]
  3. Chan M. A., Beitler B., Parry W. T., Ormo J. & Komatsu G. A possible terrestrial analogue for haematite concretions on Mars. Nature 429, 731–734 (2004). [DOI] [PubMed] [Google Scholar]
  4. Chan M. A., Beitler Bowen B., Parry W. T., Ormö J. & Komatsu G. Red rock and red planet diagenesis: Comparisons of Earth and Mars concretions. GSA Today 15, 4–10 (2005). [Google Scholar]
  5. Ostwald W. Lehrbuch des Allgemeineim Chemie (Engelman, Leipzig, 1897). [Google Scholar]
  6. Smith. D. A. On Ostwald’s supersaturation theory of rymthmic precipitation (Liesegang’s rings). J. Chem. Phys. 81, 3102–3115 (1984). [Google Scholar]
  7. Lifshitz I. M. & Slyozov V. V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 19, 35–50 (1961). [Google Scholar]
  8. Sultan R. & Ortoleva P. Periodic and aperiodic macroscopic patterning in two precipitate post-nucleation systems. Physica D: Nonlinear Phenomena 63, 202–212 (1993). [Google Scholar]
  9. Dee G. T. Pattern produced by precipitation at a moving reaction front. Phys. Rev. Letters 57, 275–278 (1986). [DOI] [PubMed] [Google Scholar]
  10. Spanbauer T. L., Kettler R. M., Loope D. B. & Weber K. A. Biosignatures in spheroidal iron oxide-rich concretions from the Navajo sandstone. Amer. Geophys. Union Fall Meeting Abs. 90, B23D–0404 (2009). [Google Scholar]
  11. Chan M. A., Johnson C. M., Beard B. L., Bowman J. R. & Parry W. T. Iron isotopes constrain the pathways and formation mechanisms of terrestrial oxide concentrations: A tool for tracing iron cycling on Mars? Geosphere 2, 324–332 (2006). [Google Scholar]
  12. Chukhrov F. V. On mineralogical and geochemical criteria in the genesis of red beds. Chem. Geol. 12, 67–75 (1973). [Google Scholar]
  13. Chan M. A. et al. Characteristics of terrestrial ferric oxide concretions and implications for Mars. Sed. Geol. Mars, SEPM Special Pub. 102, 253–269 (2012). [Google Scholar]
  14. Merino E. Textures of low temperature self-organization. Geochemistry of the Earth’s Surface Rodríguez Clemente R. & Tardy Y., (ed.), 597–610, (Consejo Superior Investigaciones Científicas and Centre Natl. Recherche Scientifique, Madrid, 1987). [Google Scholar]
  15. Nicolis G. & Prigogine I. Self-organization in Non-Equilibrium Systems (Wiley, New York, 1977). [Google Scholar]
  16. Nielsen A. E. Kinetics of Precipitation (MacMillan, New York, 1964). [Google Scholar]
  17. Fischer S. Zemke K., Liebscher A., Wandrey M. & the CO2SINK Group. Petrophysical and petrochemical effects of long-term CO2-exposure experiments on brine-saturated reservoir sandstone. Energy Procedia 4, 4487–4494 (2011). [Google Scholar]
  18. Danielson T. W. & Hood J. W. Infiltration to the Navajo Sandstone in the Lower Dirty Devil River Basin, Utah, with Emphasis on Techniques Used in its Determination, WRI Report 84–4154 (U. S. Geological Survey, Salt Lake City, 1984). [Google Scholar]
  19. Steefel C. I. & Van Cappellen P. A new kinetic approach to modeling water-rock interaction: The role of nucleation, precursors, and Ostwald ripening. Geochim. Cosmochim. Acta 54, 2657–2677 (1990). [Google Scholar]
  20. Busigny V. & Dauphas N. Tracing paleofluid circulations using iron isotopes: A study of hematite and goethite concretions from the Navajo Sandstone (Utah, USA). Earth Planetary Sci. Letters 254, 272–287 (2007). [Google Scholar]
  21. Barge L. M. et al. Precipitation Patterns Formed by Self-Organizing Processes in Porous Media. Geofluids 11, 124–133 (2011). [Google Scholar]
  22. Beitler B., Parry W. T. & Chan M. A. Fingerprints of fluid flow: chemical diagenetic history of the Jurassic Navajo Sandstone, southern Utah, USA. J. Sed. Res. 75, 545–549 (2005). [Google Scholar]
  23. Parry W. T. Composition, nucleation, and growth of iron oxide concretions. Sed. Geol. 233, 53–68 (2011). [Google Scholar]
  24. Spaepen F. Interfaces and stresses in thin films. Acta Mater. 48, 31–42 (2000). [Google Scholar]
  25. Maliva R. G. & Siever R. Diagenetic replacement controlled by force of crystallization. Geology 16, 688–691 (1988). [Google Scholar]
  26. Merino E. & Dewers T. Implications of replacement for reaction-transport modeling. J. Hydrology, 209, 137–146 (1998). [Google Scholar]
  27. Wang Y. & Budd D. A. Stress-induced chemical waves in sediment burial diagenesis. Nature Comm. 3, 685; 10.1038/ncomms1684 (2012). [DOI] [PubMed] [Google Scholar]
  28. Ortoleva P., Merino E. & Strickholm P. Kinetics of metamorphic layering in anisotropically stressed rocks. Amer. J. Science, 282, 6l7–643 (1982). [Google Scholar]
  29. Boudreau B. P. Diagenetic Models and Their Implementation: Modeling Transport and Reactions in Aquatic Sediments (Springer, Berlin, 1997).
  30. Oelkers E. H. Physical and chemical properties of rocks and fluids for chemical mass transport calculations. Rev. Mineral. 34, 131–191 (1996). [Google Scholar]
  31. Dullien F. A. L. Porous Media: Fluid Transport and Pore Structure (Academic Press, San Diego, 1992). [Google Scholar]
  32. Strogatz S. H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (Westview, Cambridge, 2001).
  33. Ortoleva P., Merino E., Moore C. & Chadam J. Geochemical self-organization, I. Feedbacks and quantitative modeling. Amer. J. Sci. 287, 979–1007 (1987). [Google Scholar]
  34. Potter S. & Chan M. A. Joint controlled fluid flow patterns and iron mass transfer in Jurassic Navajo Sandstone, Southern Utah, USA. Geofluids 11, 184–198 (2011). [Google Scholar]
  35. Gray D. J. Hydrogeochemistry in the Yilgarn Craton. Geochem. Explor. Environ. Anal. 1, 253–264 (2001). [Google Scholar]
  36. Bowen B. B., Benison K. C., Oboh-Ikuenobe F. E., Story S. & Mormile M. R. Active hematite concretion formation in modern acid saline lake sediments, Lake Brown, Western Australia. Earth Planetary Sci. Letters 268, 52–63 (2008). [Google Scholar]
  37. Duckworth O. W. & Martin S. T. Relationship between rates of ligand-promoted dissolution of hematite and the iron-ligand surface structures of C1 to C2 dicarboxylic acids. Paper presented at Chemical Speciation and reactivity in Water Chemistry and Water Technology, Washington DC, American Chemical Society (Aug. 20-24. 2000).
  38. Oelkers E. H., Helgeson H. C. Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: aqueous tracer diffusion coefficients of ions to 1000 oC and 5 kb. Geochem. Cosmochim. Acta 52, 63–85 (1988). [Google Scholar]
  39. Stumm W. Chemistry of the Solid-Water Interface: Processes at the Mineral-Water and Particle-Water Interface in Natural Systems (Willey, New York, 1992).
  40. Zhu C. In situ feldspar dissolution rates in an aquifer. Geochim. Cosmochim. Acta 69, 1435–1453 (2005). [Google Scholar]
  41. Chan M. A., Ormo J., Park A. J., Stich M., Souza-Egips V. & Komatsu G. Models of iron oxide concentration formation: field, numerical, and laboratory comparisons. Geofluids 7, 1–13 (2007). [Google Scholar]
  42. Casas J. M., Crisόstomo G. & Cifuentes L. Speciation of the Fe(II)-Fe(III)-H2SO4-H2O system at 25 and 50 oC. Hydrometallurgy 80, 254–264 (2005). [Google Scholar]
  43. Drever J. I. The Geochemistry of Natural Waters (Prentice-Hall, Englewood Cliffs, 1982). [Google Scholar]
  44. Morris R. V. et al. Hematite sperules in basaltic tephra altered under aqueous, acid-sulfate conditions on Mauna Kea volcano, Hawaii: Possible clues for the occurrence of hematite-rich spherules in the Burns formation at Meridiani Planum, Mars. Earth Planet. Sci. Letters 240, 168–178 (2005). [Google Scholar]
  45. Johnson A. H. Palaeomagnetism of the Jurassic Navajo Sandstone from Southwestern Utah. Geophys. J. R. Astr. Soc. 44, 161–175 (1976). [Google Scholar]
  46. Reiners P. W., Chan M. A., Evenson N. S. (U-Th)/He geochronology and chemical compositions of diagenetic cement, concretions, and fracture-filling oxide minerals in Mesozoic sandstones of the Colorado Plateau. Geol. Soc. Amer. Bullet. 126, 1363–1383 (2014). [Google Scholar]
  47. Beck M. E. Jr., Burmester R. F. & Housen B. A. The red bed controversy revisited: shape analysis of Colorado Plateau units suggests long magnetization times. Tectonophysics 362, 335–344 (2003). [Google Scholar]
  48. Rowe C. M., Loope D. B., Oglesby R. J., Van der Voo R. & Broadwater C. E. Inconsistencies between Pangea reconstructions and basic climate controls. Science 318, 1284–1286 (2007). [DOI] [PubMed] [Google Scholar]
  49. Potter S., Chan M. A., Peterson E. U., Dyar M. D. & Sklute E. Characterization of Navajo Sandstone concretions: Mars comparison and criteria for distinguishing diagenetic origins. Earth Planet. Sci. Letters 301, 444–456 (2011). [Google Scholar]
  50. Nahon D, Introduction to the petrology of soils and chemical weathering (Wiley, New York, 1991).
  51. Ortoleva P., Chadam J., Merino E. & Sen A. Geochemical self-organization, II. The reactive-infiltration instability in water-rock systems. Amer. J. Sci. 287, 1008–1040 (1987). [Google Scholar]
  52. Loope D. B., Kettler R. M. & Weber K. A. Morphologic clues to the origins of iron oxide-cemented spheroids, boxworks, and pipelike concretions, Navajo Sandstone of southern-central Utah, USA. J. Geology 119, 505–520 (2011). [Google Scholar]
  53. Squyres S. W. et al. In situ evidence for ancient aqueous environment at Meridiani Planum, Mars. Science, 306, 1709–1714 (2004). [DOI] [PubMed] [Google Scholar]
  54. Madden M. E. E., Bodnar R. J. & Rimstidt J. D. Jarosite as an indicator of water-limited chemical weathering on Mars. Nature 431, 821–823 (2004). [DOI] [PubMed] [Google Scholar]
  55. Squyres S. W & Knoll A. H. Sedimentary rocks at Meridiani Planum: Origin, diagenesis and implications for life on Mars. Earth Planet. Sci. 240, 1–10 (2005). [Google Scholar]
  56. Stack K. M. et al. Diagenetic origin of nodules in the Sheepbed member, Yellowknife Bay formation, Gale crater, Mars. J. Geophys. Res.: Planets, 119, 1637–1664 (2014). [Google Scholar]
  57. Merino E. & Wang Y. Geochemical self-organization in rocks: Occurrences, observations, modeling testing – with emphasis on agate genesis. Non-Equilibrium Processes and Dissipative Structures in Geoscience, Krug H.-J. & Kruhl J. H. (ed.), 13–45 (Duncker & Humblot, Berlin, 2001). [Google Scholar]
  58. Davis J. M. Oriented carbon concretions in a paleoaquifer: Insight into geologic controls on fluid flow. Water Res. Res. 35, 1705–1711 (1999). [Google Scholar]
  59. Mozley P. S. & Davis J. M. Internal structure and mode of growth of elongate calcite concretions: Evidence for small-scale, microbially induced, chemical heterogeneity in groundwater. Geol. Soc. Amer. Bullet. 117, 1400–1412 (2005). [Google Scholar]
  60. Bulgakov N. N. & Sadykov V. A. Surface energies of hematite faces and heats of oxygen adsorption: Calculations by modified semiempirical interacting bonds method. React. Kinet. Catal. Letters 58, 397–402 (1996). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep10792-s1.pdf (347.1KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES