Particle Segregation and Dynamics in Confined Flows

Abstract

Nonlinearity in finite-Reynolds-number flow results in particle migration transverse to fluid streamlines, producing the well-known “tubular pinch effect” in cylindrical pipes. Here we investigate these nonlinear effects in highly confined systems where the particle size approaches the channel dimensions. Experimental and numerical results reveal distinctive dynamics, including complex scaling of lift forces with channel and particle geometry. The unique behavior described in this Letter has broad implications for confined particulate flows.

Lateral migration of rigid spherical particles (radius a) across streamlines to specific equilibrium positions has been observed in macroscale pipe flows [1,2], with much recent interest in understanding these nonintuitive results theoretically and numerically [3–8]. Symmetry arguments based on the form of the linearized equations associated with viscosity-dominated low-Reynolds-number, i.e., Stokes, flow preclude cross-streamline migration. Thus inertial contributions to the Navier-Stokes equations must be significant in these flows for lateral migration to occur [9]. As this effect introduces significant complexity into analytical calculations, theoretical investigations have focused mainly on simplified model systems (e.g., parallel plates and circular tubes) of typical cross-sectional dimension H with minimal particle confinement (a/H ≪ 1). This restriction allowed theoretical developments based on “point-particle” or “point-force” approximations [3– 5] but could not account for the finite size of the suspended particles, which is shown to be significant here.

Recently, we described inertially driven lateral migration of particles in microfluidic systems, where fluid inertia is not usually significant [10,11]. We demonstrated practical applications for size-based particle filtration and focusing that exploited this nonlinear effect. The influence of fluid inertia on particle-laden flows in confined systems may also be of importance in exploring limits of operation for chromatographic separations [12] and particle-laden jets [13]. Numerical and theoretical results directly applicable to complex confined systems are few [6] but may yield new insights into particle dynamics when basic point-particle assumptions become invalid. Here we take steps towards uncovering basic rules for these systems by reporting equilibrium states for confined particles in finite-inertia flows through rectangular cross-section microchannels. We compare these observations with numerical results for the same systems and find good agreement. This then allows us to use the numerical model for further generalizations and understanding concerning particle behavior in confined systems.

The systems we studied used square or nearly square cross-section channels populated by particles with diameters approaching that of the channel width. The experimental system was fabricated using soft-lithography processes [10,11] and consisted of microchannels with a length of 5 cm and widths and heights between 20 and 50 µm. Polystyrene particles (ρ = 1.05 g/cm³, a = 5–20 µm) introduced into the channels were at dilutions of 0.1%–0.5% w/v such that particle-particle interactions were minimized. Particles, suspended in water, with 0.01% Tween 20 to prevent aggregation, were flowed at controlled rates using a syringe pump. In a subset of experiments to determine the rotation rate of particles, we used emulsion polymerized polydimethylsiloxane (PDMS) particles [10] with small internal air defects.

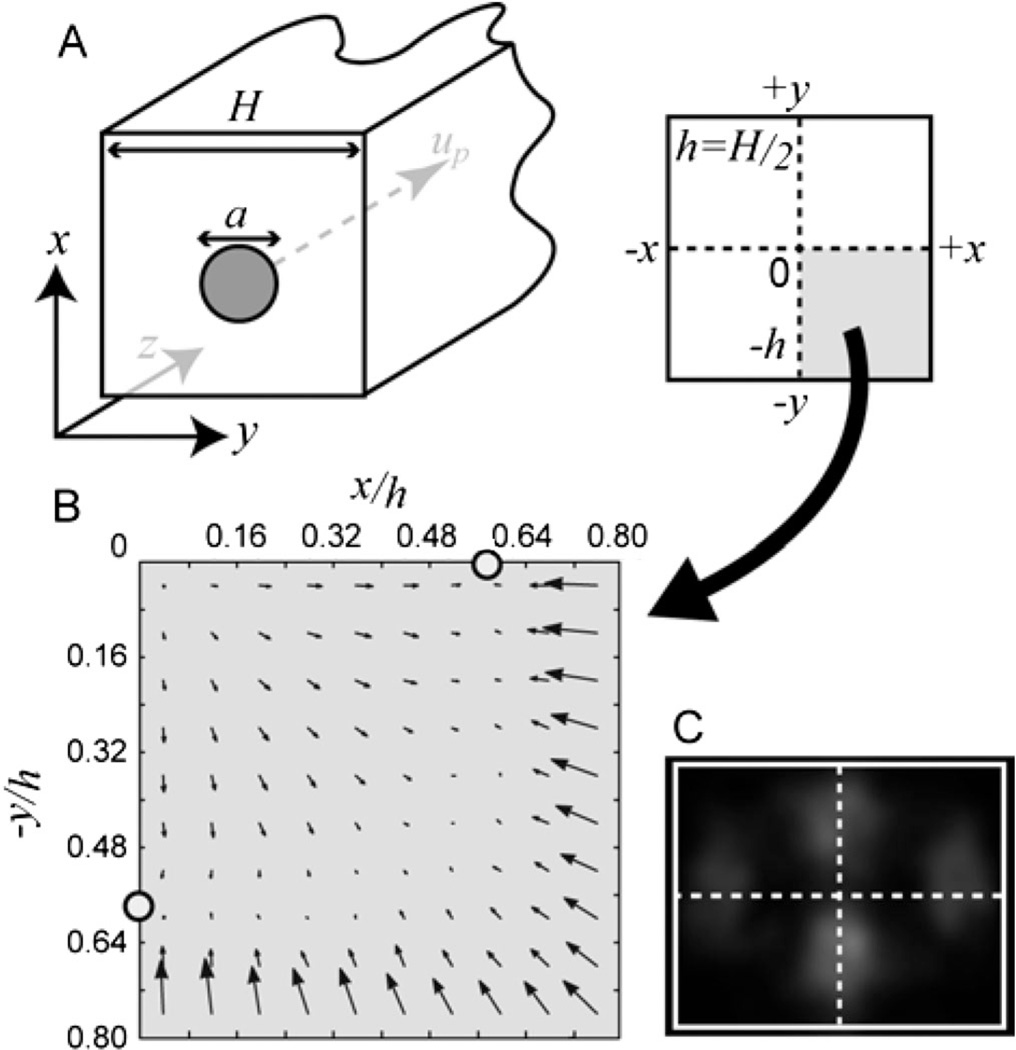
For computational ease, the numerical model took the reference frame where the sphere, of diameter a, was stationary in a square duct, of height H = 2h, with sidewalls moving backwards at the presumptive particle velocity u_p [Fig. 1(a)]. Volumetric flow rate q was specified by setting inlet or outlet boundary conditions to fully developed laminar inflow or outflow in software (comsol Multiphysics). This ensured that the flow at the position of the sphere corresponded to that for one isolated particle (no periodic boundary conditions). Rotation was modeled by modifying the slip velocity at the surface of the sphere according to its rigid rotation. With these boundary conditions, and the fluid density ρ and viscosity μ, corresponding to that of water, we conducted three-dimensional, finite-element simulations solving the steady-state Navier-Stokes equations. Beginning with the initial condition of a stationary sphere (particle and walls at rest), we determined forces and torques by integrating force per area (F″) and torque density (r × F″) across the particle surface in software. We then iteratively updated the wall velocity (−u_p) and particle rotation until the sphere translated force-free in the axial (z) direction and rotated with zero net torque in all directions, to the limit in numerical precision. We then determined the smaller transverse lift forces on the sphere that would yield lateral migration. Varying the sphere position yielded the steady-state forces and rotations for a particle held to a particular x-y position in the channel cross section [Fig. 1(b)]. These results were plotted for a channel Reynolds number (R_c = ρU_mH/μ) of 80, where U_m is the maximum channel velocity. The resulting vector force field reveals four point attractors centered at the faces of the fourfold symmetric channel that agree with experimental results [Fig. 1(c)] [11] and that are similar to four of the eight focusing points identified in simulations reported by Chun and Ladd [6] using the lattice-Boltzmann method.

FIG. 1.

Inertial lift forces in a square cross-section channel. (a) Schematic of the channel and particle geometry used in this work. (b) Inertial lift forces are simulated for a quarter of the channel cross section and shown in this vector plot for a/H = 0.22 and R_c = 80. Equilibrium positions are marked with circles. (c) Averaged confocal cross section for 10 µm particles flowing in a 50 × 40 µm channel reveals similar attractors at the channel faces.

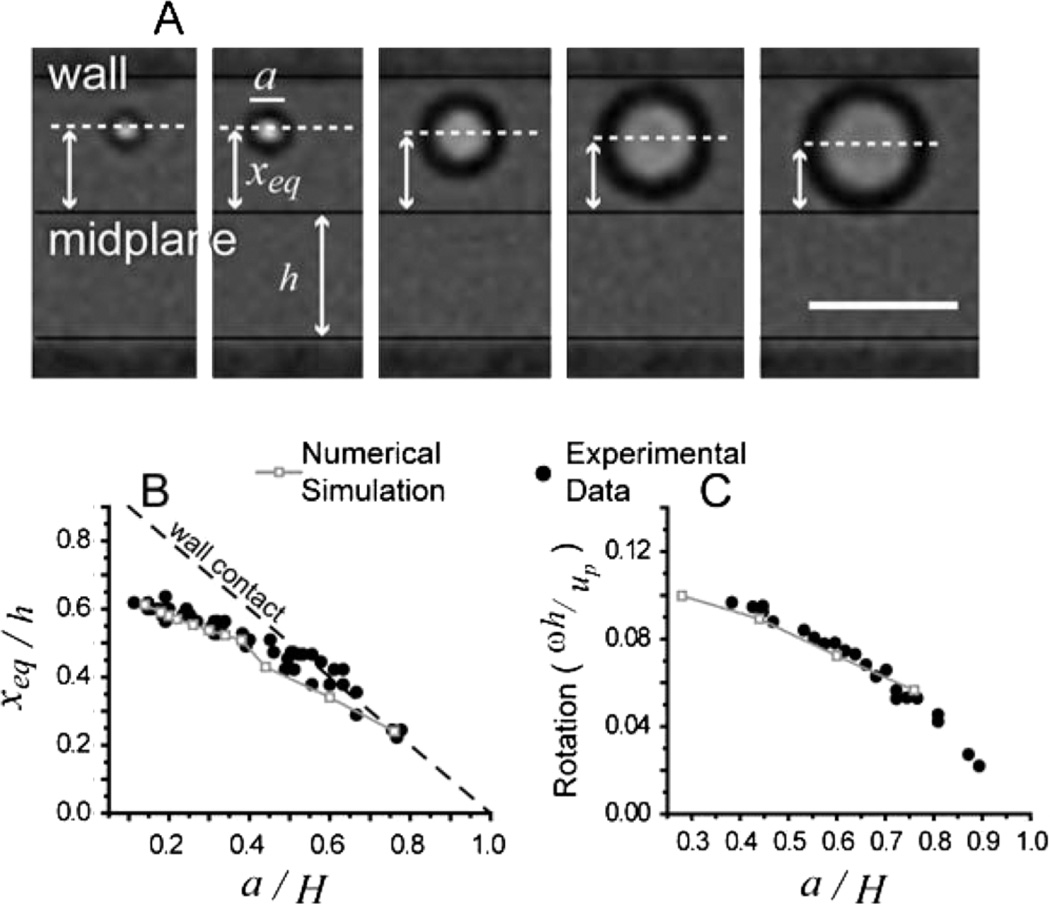
Both experimental and numerical results indicated that the locations of the attractors within the cross section of the channel are strongly dependent on the ratio of particle to channel dimensions a/H. Results for particle equilibrium positions as a function of a/H are plotted in Figs. 2(a) and 2(b). Experimentally and numerically, we observed a shift of the equilibrium position of the particle (x_eq) towards the channel center as a/H increases. For a/H ≪ 1 we also observed that x_eq/h approaches ~0.6 as in the original studies of Segre and Silberberg (for a circular pipe) [1]. Particles were observed off-center but displaced from the wall for the whole range of observed sizes (a/H = 0.1–0.9) even as the particle size approached the full width of the channel.

FIG. 2.

Numerical and experimental equilibrium positions and rotations. (a) The equilibrium positions are shown for different a/H. The scale bar is 10 µm. (b) Normalized equilibrium positions as a function of a/H are plotted at R_c = 20. The dashed line denotes positions where particles would be in contact with the wall. (c) The nondimensional rotation rate is plotted for particles focused to equilibrium positions at R_c = 20.

Particles confined to one of four cross-sectional-plane attractors translated at downstream velocities (u_p) which were observed to be largely independent of particle size. Experimentally measured velocities of particles (N = 20) at equilibrium for a/H in the range 0.4–0.9 varied only slightly (1.6%) for a constant channel Reynolds number (R_c = 20). There was also no significant correlation of u_p with particle size (r² = 0.03, linear regression). Numerical results reproduced this behavior and yielded a similar 1% deviation in particle velocity with no significant correlation between particle size and velocity (r² = 0.16) for a/H between 0.1 and 0.9. For simulations with U_m equal to 1.6 m/s, the ratio u_p/U_m averaged 0.67 ± 0.008.

However, particles at equilibrium positions were found to rotate at rates dependent on particle size. High-speed images allowed for the determination of particle rotation rates by observing the frequency with which air defects orbited about the center of each PDMS particle. As confinement increased, the nondimensional rotation rate ωh/u_p was observed to decrease experimentally and numerically [Fig. 2(c)]. It is interesting to note the consistency in measured rotation rates. For particles of the same size, the standard deviation (N = 6) for experimentally measured rotation rates was only 2%.

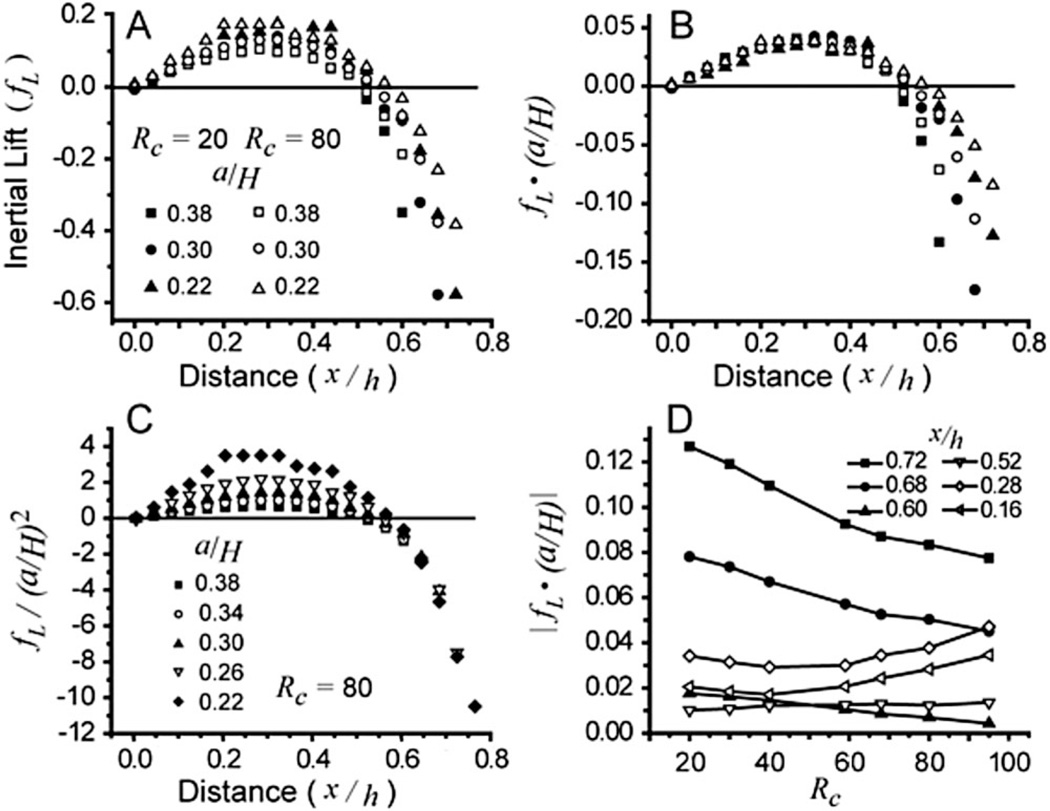
With good agreement between the experimental data and the numerical results for particle translation, rotation, and equilibrium position, we used the model to explore the more general behavior of particles in confined systems. Using our model, we inferred that lift forces follow a complex functional form that varies less strongly with a/H near the channel center line than in the near-boundary regions. To investigate this functional dependence, we computed the lateral forces along the midline of the channel cross section as a function of the dimensionless parameters x/h, a/H, and R_c (Fig. 3). Previous calculations using matched asymptotic expansions that assume particles do not cause a disturbance to the main channel flow have resulted in an inertial scaling for lift force $F_L=f_L\rho U_m^2{a}^4/H^2$, where f_L is a nondimensional lift coefficient that is dependent on x/h and R_c [3–5]. However, when our data are normalized using this analytical scaling [Fig. 3(a)], a more complicated dependence on a/H can be observed. The force as a function of normalized distance (x/h) appears to collapse to a single curve far from the wall (x/h < 0.5) when the lift force F_L is instead normalized as $F_L/(\rho U_m^2{a}^3/H)=f_L(a/H)$ [Fig. 3(b)]. A similar scaling was observed in circular cross-section channels (best fit of a^3.28).

FIG. 3.

Parameters affecting the nondimensional inertial lift force. (a) The nondimensional force [f_L = F_L/(ρU_m²a⁴/H²)] is plotted as a function of the fractional distance from the channel center line for the controlling dimensionless parameters. (b) The dimensionless lift force is plotted using a new functional dependence on a/H that better collapses the data near the channel center line [f_L • (a/H)]. (c) Normalization of the lift is modified such that one can observe collapse to a single curve in the nearwall region. (d) The lift force in the near-wall region (x/h > 0.52) appears to decrease with increasing R_c, but f_L is seen to increase near the channel center line (x/h > 0.52) for R_c greater than 60.

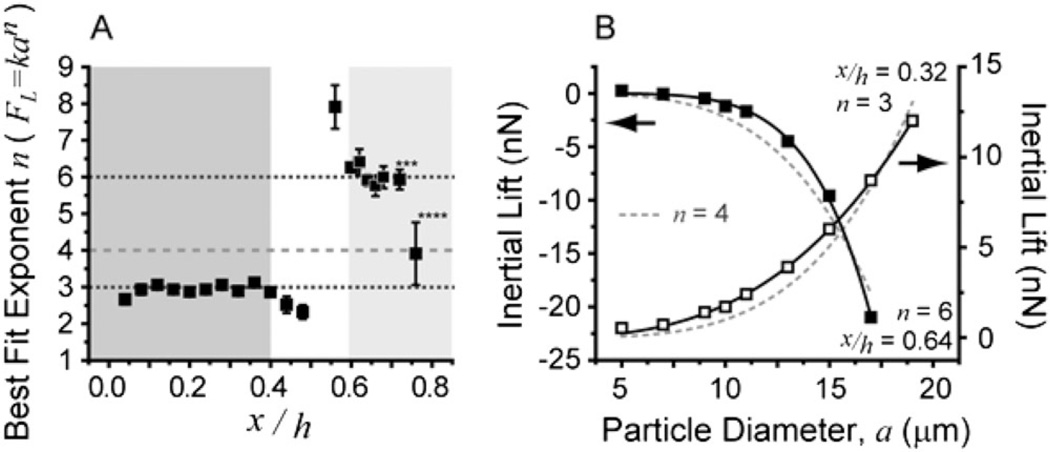
Furthermore, in the near-wall region, the dimensionless force appears to collapse to a single curve with $F_L/(\rho U_m^2{a}^6/H^4)$ [Fig. 3(c)]. This divergent scaling across the channel cross section is clearly shown by plotting the best fit exponent (n) for F_L = kaⁿ [Figs. 4(a) and 4(b)]. This behavior contrasts with that predicted using point-particle assumptions, where the lift force was found to scale identically throughout the channel [3–5]. The distinct scaling in our confined system was found to be valid at least to a/H = 0.1. Below a/H = 0.1, noise in the computed force leads to unreliable results. Although the physical basis for the difference in scaling compared to previous asymptotic theory is not known, future investigation is warranted to relax a key assumption of previous theory [3–5], that the particle motion does not disturb the main channel flow, as this assumption is not valid in our system.

FIG. 4.

Scaling of inertial lift with particle diameter. (a) Best fit exponents are plotted for fits of lift values at nine separate particle diameters from 5 to 19 µm. At large values of x/h, fewer points were used. (***) 6 and (****) 5 points. The near-wall region (light gray) and center region (dark gray) show stable fits at n = 3 and 6, respectively, while a transition region (white) where both effects contribute has divergent scaling. Error bars correspond to error in the fit. (b) Plots of best fits for n = 3 and 6 (solid black line) and fits based on previous asymptotic inertial lift theory of n = 4 (dotted gray line) at two cross-sectional positions.

Lift also varies with the channel Reynolds number in a complex fashion. Data in Figs. 3(a) and 3(d) show that near the wall, f_L decreases in magnitude with increasing R_c while increasing in magnitude near the channel center line. This response is in sharp contrast to previous predictions when a/H ≪ 1, where f_L is observed to decrease with increasing R_c over the whole domain [3,4]. Our results indicating opposing dependences on the channel Reynolds number in the two regions suggest that the positions of the attractors should shift towards the walls with increasing R_c in agreement with previous experimental results [7,8]. This and previous scaling differences support the idea that two separate physical processes account for particle behavior in the near-wall region and channel center line [4,14].

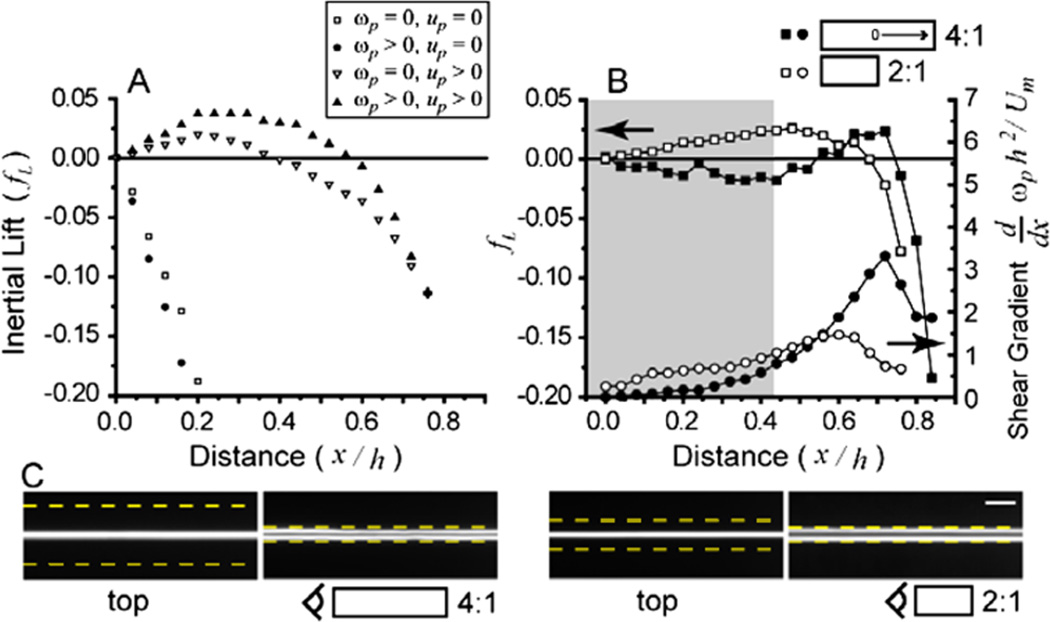
Numerical analysis allows for the decomposition of the flow into components to yield understanding of the underlying physical mechanisms. We found that a stationary sphere always experienced a force directed away from the wall [Fig. 5(a)]. However, when a sphere was allowed to translate force-free with the flow but was constrained from rotating, only small differences in lift force were observed when compared to a sphere allowed to both rotate and translate along with the flow. This suggests that rotational motion is not a key contributor to inertial lift. In separate simulations to decouple the shear gradient from wall-induced effects, we calculated forces for flows through high-aspect ratio channels where the shear gradient and shear rate both approach zero near the channel center line [Fig. 5(b)]. This geometry yielded results that are dramatically different when compared to the finite shear-gradient case, where an extra reversal of sign for lift force is observed near the channel center line. Presumably, as the shear gradient approaches zero, wall-directed shear-gradient-based lift is eliminated, which makes the small center-directed lift due to the wall effect observable. This may provide a partial explanation for the observed reduction from four focusing positions in square channels to two positions in high-aspect ratio channels [Fig. 5(c)] [15].

FIG. 5.

(color online). Deconstructing inertial lift. (a) The nondimensional force is plotted for a/H = 0.22 and R_c = 80. Filled triangles correspond to no constraints. Open triangles have a constraint that the sphere is not free to rotate. Squares show data when the sphere is constrained from translating and either constrained from rotation (open) or not (closed). (b) The nondimensional force is plotted along with a measure of the nondimensional shear gradient experienced by a particle for two different aspect ratio channels and a/H = 0.44 and R_c = 80. The gray region indicates a reversal of sign in lift for the 4.1 aspect ratio. (c) Images showing the top and side views of high-aspect ratio channels show two particle equilibrium positions. Dotted lines outline the channels. The scale bar is 50 µm.

The observed and predicted behaviors also have important implications for development of practical applications for inertial migration in confined flows [10,11,16,17]. Given the novel apparent scaling of inertial lift forces for highly confined systems, previous “inertial focusing” theory [10,11] based on analytical models assuming small a/H should be revisited. Additionally, we have shown that particle equilibrium position is dependent on particle size, suggesting another mechanism for continuous separation. Unexpectedly, even at different equilibrium positions within the flow, particle velocity in the direction of flow appears constant and independent of particle size to within experimental and numerical precision. As a result, the general assumption that the particle velocity will equal the unperturbed stream velocity at its center point should be reexamined when a/H is large [12,18,19].