Abstract
Oblique incident light fields are sometimes unavoidable for photodynamic therapy of skin cancers, e.g., for large fields on uneven surface. We have performed Monte-Carlo simulation for circular fields (R = 0.25, 0.35, 0.5, 1, 2, 3, and 8 cm) for reduced scattering coefficient μs’ = 10 cm−1 and attenuation coefficient μa = 0.1 – 1.0 cm−1. We used anisotropy g = 0.9 and the index of refraction n = 1.4 for all Monte-Carlo simulations. Compared to a broad beam of normal incidence, the peak fluence rate along the central-axis for a slanted beam is increased for otherwise the same geometrical conditions and optical properties. The effective attenuation coefficient is slightly decreased for a slanted beam compared to a normal incident beam. The beam profile for a slanted beam at a fixed depth is no longer symmetrical but is higher towards the lateral side of beam incidence. Since the broad beam with finite radius R can be considered as a convolution of a pencil beam, solution for a slanted pencil beam can be used to determine the light fluence distribution for circular beams with oblique beam incidence. An analytical solution can be obtained for the pencil beam obliquely incident on a semi-infinite medium. The solution can be approximated using the diffusion or P3 theory with one point source or two point sources located at appropriate depths with appropriate weights along the beam pathlength inside the phantom, with corresponding image sources to fulfill the extended boundary condition. The analytical solution agrees well with Monte-Carlo Simulation at depths z > 2cosθt/μ’t, θt is the incident angle after refraction at the interface. Measurements using an isotropic detector were made in a liquid phantom composed of intralipid and ink to verify the Monte-Carlo simulation results.
Keywords: Monte Carlo, Oblique incidence, in-vivo light dosimetry, tissue optical properties, diffusion theory, P3 theory
1. INTRODUCTION
Photodynamic therapy (PDT) is a cancer treatment that involves the use of a photosensitizer, oxygen, and light of a wavelength specific to the absorption characteristics of the photosensitizer1. Light dosimetry is important to ensure tumor kill and avoid damage to healthy tissue. Photofrin-mediated PDT is being used at University of Pennsylvania for patients with surface malignancies. When treating the surface lesions with PDT, it is often unavoidable to use oblique incident light. In many case, the lesion to be treated can also be a small circular field (as small as 2-cm in diameter).
For oblique incident and small circular field, the light fluence rate may reduce significantly from that for an infinite large field with normal incidence because of the reduced photon scattering by tissue and oblique incidence. The clinical questions to ask are (1) how does the light fluence rate change with field size and incident angle, given similar treatment conditions? (2) What lateral extent of the light field is sufficient to cover the tumor at depth in tissue? For the theoretical calculations, we used Monte-Carlo simulations as our gold standard. We then developed an analytical theory based on the 1st order (diffusion approximation) or 3rd order (P3) approximation of the light transport equation for pencil-beam incident on a semi-infinite surface. We also measured light fluence rate as a function of field size at tissue surface and at several depths in an optical phantom to confirm the theoretical calculation.
In a previous study, we determined the ratio between the light fluence rate and the irradiance ϕ/ϕair as a function of the tissue optical properties for normal incident circular fields on the surface, both inside and outside tissue2. The current work extends the relationship to a slanted circular beam. In this study, we concentrate on light dosimetry for the subcutaneous soft tissue, whereby tissue is treated as a homogeneous thick layer. The effect of multiple layers of tissue types3 are beyond the scope of the current study.
2. METHODS AND MATERIALS
1. Monte-Carlo Simulation
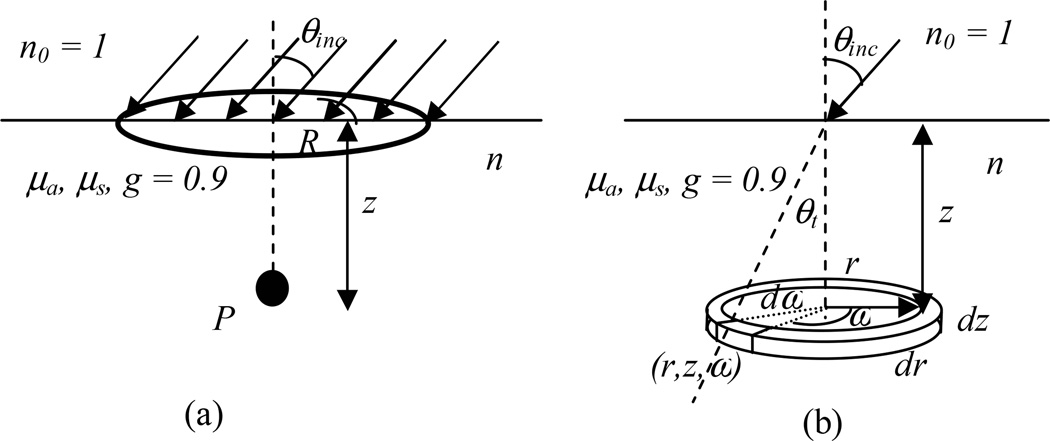
The experimental setup to be calculated by Monte-Carlo simulation for a semi-infinite medium with uniform optical properties, i.e. the absorption coefficient μa, the scattering coefficient μs, the scattering anisotropy g (= 0.9), and the index of refraction n is shown in Fig. 1a. The outside medium is air (n0 =1). The light field is parallel and uniform inside a circle with radius R and incident at an angle θinc toward the air-tissue interface. Inside tissue, the initial incident angle is θt, following sinθinc =n·sinθt (Fig. 1b). Most tissues have a preferantial scattering in the forward direction with a scattering anisotropy g = 0.90.4 In the diffusion approximation, the tissue scattering is converted to isotropic conditions (g = 0) and the tissue scattering property is described by a reduced scattering coefficient μs’ = μs (1−g).
Fig. 1.
(a) Experimental setup for a slanted circular field incident on a semi-infinite surface. The light fluence rate are calculated along the central-axis on the center of the field. (b) Pencil beam setup is actually used for the Monte Carlo simulation. The scoring voxel has radius width dr, angle increment, dω, and thickness dz at radius r, angle ω, and depth z in a cylindrical geometry.
To improve the scoring efficiency, Monte-Carlo simulation is performed for a pencil-beam incident on a semi-infinite tissue phantom (Fig. 1b). The photon density (ρn) is scored in a cylindrical geometric geometry using voxels at (r, z, ω) of 0.01 cm thickness (dz), 0.02 cm width (dr), and 1° angle increment (dω). The scoring voxel (rdrddω) along with a ring voxel (2πrdrdr) used to simplify calculation for broad beam on the central-axis are shown in Fig. 1b. The light fluence rate (ϕ) per unit incident light power of the pencil beam (in units of 1/cm2) is calculated as ρn/Ninc/μa, where ρn is the photon density (in units of 1/cm3), Ninc is the number of incident photons, and μa is the absorption coefficient (in units of 1/cm).
The ratio of light fluence rate ϕ to the light fluence rate in-air ϕair (or irradiance) for a circular field with radius R can be calculated using a convolution of the pencil-beam kernel p and the uniform unit incident light:
| (1) |
where I is 1 inside and 0 outside the light field radius. p is the pencil beam kernel calculated by MC simulation, ρn/Ninc/μa, and is a function of optical properties (μa, μs, g, and n), location (x, y, z), and the incident angle θinc. To calculate the light fluence rate on the central-axis (x = y = 0) of a circular field with radius R, Eq. 1 can be simplified as an area integral:
| (2) |
Here σn is the photon density scored in a ring voxel, i.e., σn =∫ρndω.
We also score the numer of photon per unit area ρexit (in units of 1/cm2) for photons escaping the air-tissue interface into the air through an area element (rdrdω) as a function of lateral radius r (with a resolution of 0.02 cm), angle ω (with a resolution of 1°), and emitting angle θ (with a resolution of 0.9°). The light fluence rate ϕ per unit incident power of the pencil-beam outside of tissue surface can be calculated as pexit(r, ω)=∫ρext/Ninc/cosθsinθdθ, where cosθ accounts for the reduced area (cosθrdrdω) for photons exiting the interface with an angle θ. We have shown before that the diffuse reflectance for the pencil-beam is .2 To calculate the light fluence rate ϕ for a circular beam outside tissue surface, one can use:
| (3) |
where I is 1 inside and 0 outside the light field. The additional term (1) in Eq. (3) accounts for the in-air incident fluence rate which is not accounted for by the diffuse reflected photons. We have described previously that Eq. (3) can be approximated as2,5–6
| (4) |
Here Rd is the diffuse reflectance for a circular beam with radius R. This approximation is valid under the assumption that the tissue surface is Lambertian, or the radiance7 emerging from the tissue surface is independent of the azimuth angle θ.8
The Monte-Carlo algorithm is similar to approaches used previously in the literature.9–12 The effect of reflection at the air-tissue interface, resulting from the refractive index mismatch, was modeled according to the Fresnel reflection coefficient for unpolarized light.9 Photons are propagated through the medium using a step size Δs = mfp·lnξ, where ξ is a uniform distributed random number and mft =1/(μs+μa) is the mean free path and a scattering angle selected from the phase function determined by the Henyey-Greenstein phase function10 with anisotropy g = 0.90. Each incident photon is followed until it is escaped from the turbid medium at the interface or when its weight is insignificant. Since the outcomes of MC are the same so long as the distances are scaled by mft and the albeto a = μs/(μs+μa) remains the same, one can determine the pencil-beam kernel for any optical properties (μa, μ's) using the pencil-beam kernel, p, for a fixed μ's0 provided the distances and μa are scaled by s=μs0/μs≔μ’s0/μ’s:
| (5) |
Here we have fixed μ's0 = μs0(1−g)= 10 cm−1. We followed 105 incident photons for each Monte-Carlo simulation. Each simulation takes about 4 hours on a 800 MHz Pentinum 4 PC, depending on the optical properties used. The code is written in matlab® language. The MC result for the broad circular beam has a typical statistical uncertainty of less than 0.1%. This small standard variation for only 105 incident photons is possible because a convolution of pencil-beam result is used to calculate the broad beam parameters.
2. Analytical Calculations
In the diffusion theory of light transport in turbid media, a normal incident pencil-beam is commonly represented by an isotropic point source of amplitude a’ = μ’s/(μ’s+μa) at a depth of 1/μ’t, μ’t=μ’s+μa.13 This model has been extended by Hull and Foster14 to the P3 approximation, which is significantly improved over the diffusion approximation for turbid medium with transport albeto a’ < 0.9, or high absorption coefficient μa. In the P3 approximation, two point sources of amplitude a’/2 at depths of 0 and 2/μ't are used to represent a pencil-beam.14
Following the formalism of Farrell et al13, a pencil-beam normally incident on a semi-infinite medium can be expressed as a source distribution of S0 = a’μ’t e−μ’tzδ(x)δ(y). For a slanted pencil-beam incident with an angle θt to the normal in the x-z plane, we express the source distribution as
| (6) |
In this expression, the distance along the beam is z/cosθt. In addition, the amount of light scattered out of the beam in a given depth interval dz is increased by a factor (1/cosθt). It is often desirable to represent incident beam in terms of simpler point source distributions. In this case, we use a distribution of n point sources as a sum of delta functions along the incident direction of the pencil-beam,
| (7) |
where zk and sk are the position and magnitude of the kth point source, respectively. The mth moment along the axis z’-axis (=z/cosθt), ∫S0z’mdz’, of the finite point sources (Eq. 7) should be the same as the corresponding moment of the pencil-beam source (Eq. 6), i.e.,
| (8) |
Equation 8 for m = 0 leads to the constraint that the total strength of all the isotropic sources must equal a’. If only one isotropic source is used, the first moment requires it to be placed at z’ = 1/μ’t.13 Thus, the ideal position for the point source representing a slanted beam is x0 = sinθt/μ’t and z0 =cosθt/μ’t. In the P3 approximation, two sources of equal strength a’/2 are used. The optimal placement of these sources is at z’1 = 0 and z’2 = 2/μ’t, or, x1=z1=0 and x2 = 2 sinθt/μ’t and z2 = 2cosθt/μ’t. This is obtained to ensure that the resulting distribution of sources matches the 1st and 2nd moments of the pencil-beam (m = 0, 1, 2).
For an isotropic point source at [x0= sinθt/μ’t, z0=cosθt/μ’t], the extended boundary condition12, 15 is satisfied by introducing a negative image source equidistant from the extrapolated boundary at [xim= sinθt/μ’t, zim=−(cosθt/μ’t + 2zb)], yielding14
| (9) |
where zb = 2AD, D = 1/3μ’t. The value of A depends on the refractive-index mismatch and is independent of the incident angle θt.14 For tissue and air interface (ndetector = 1, ntissue = 1.4), A = 2.949. This is the solution of the diffusion approximation using a single isotropic point source.
In the P3 approximation of a point source with unit source strength in an infinite medium, the fluence rate can be expressed as14
| (10) |
where
| (11) |
and
| (12) |
where
| (13) |
| (14) |
| (15) |
These values have been previously derived by Hull and Foster14, whose notation is reproduced here. When applying the extended boundary condition for a point source in a semi-infinte medium, similar image souce can be used as in Eq. 9 except for the extended boundary position is now at zb = 2Aμa/(ν−)2 and 2Aμa/(ν+)2 for the first and the second terms of Eq. (10), respectively. If one keeps the form of the diffusion approximation (Eq. 9) but replace μeff by ν− and D by μa/(ν−)2, the solution is called a P3-diffusion hybrid.14 P3-diffusion hybrid for pencil-beam with two point sources was found to be the best solution for the diffuse reflectance.14
Outside of tissue, the light fluence rate is obtained by determining the portion of the radiance that is transmitted across the boundary:14
| (16) |
Here cosθ = n·s. For diffuse approximation, L = ϕ + 3/2(−D∇ϕ)·(−ẑ) |z =0, thus pexit can be expressed as a sum of two terms14
| (17) |
where
| (18) |
and
| (19) |
where r1 and r2 are the corresponding distances in Eq. (18). The value of Cϕ and Cj is calculated using Eq. 16 and depends on the numerical aperture of the detector and the index mismatch. For an isotropic detector (NA = 1) and media with an index mismatch of 1.4, Cϕ = 0.1374 and Cj = 0.3533. Notice Eq. 17 for fluence rate has the same form as the formula for diffuse reflectance, but the value of Cϕ and Cj are slightly different (where Cϕ = 0.1178 and Cj = 0.3056).14
The closed form of pexit for P3 approximation is quite complicated and can be found in the paper by Hull and Foster for diffuse reflectance,14 except for the k values are different. For index mismatch of n = 1.4 and NA = 1, k1 = 1.7268, k2 = 1.4797, k3 = 1.2801, k4 = 0.5588, k5 = 0.3620, and k6 = 0.4923.
The convolution of the diffusion solution (Eq. 9) for a broad beam can be expressed in a closed form for infinite radius:
| (17) |
Here z0 = cosθt/μ’t. Notice that at deeper depths ϕ decreases exponentially with z, with the same effective attenuation coefficient μeff for any incident angle. ϕ/ϕair has a buildup for z < cosθt/μ’t. Although the analytical pencil-beam solution (Eq. 9) has a singularity at the location of the point sources, the convolution of the pencil-beam for broad circular fields does not have any singularity.
3. Phantom Experiments
Measurements were performed in a liquid phantom made of intralipid (0.65%) and ink to verify the Monte-Carlo results, as shown in Fig. 1. Series of circular fields (radius R = 0.25, 0.35, 0.5, 1, 1.5, 2, 3 cm), defined at the phantom surface, were produced by a circular block made of blackened aluminum sheets. The laser was connected to an optical fiber fitted with a microlens at the exit tip, producing a circular field on the phantom surface of 8 cm radius. A 15W diode laser (DioMed, Inc, Cambridge, UK) provided light source for 732 nm. The output of the laser was verified by a Coherent power meter with a calibration traceable to the National Institute of Standards and Technology. The phantom has known optical properties determined independently5. The phantom has a reduced scattering coefficients of (μs’ = 13 cm−1) and an absorption coefficient of μa = 0.041 cm−1. A 1 mm-diameter isotropic detector16 was used to measure the fluence rate on the phantom surface (0.2 cm above phantom) and inside the phantom at various depths (z = 0.2, 0.5, 1, 1.5 cm). The isotropic detector was manufactured by CardioFocus, Inc. (west Yarmouth, MA) with an anisotropy of less than 10% and should measure the fluence rate accurately. The isotropic detector was calibrated in a 15.2 cm diameter integrating sphere (Labsphere, North Sutton, NH) using the method previously described16.
Since the isotropic detector has different responses in air and in water due to the mismatch of the index of refraction8, we also made measurements of the isotropic detector response in pure water, without any scattering medium. The ratio of the isotropic detector response in liquid tissue-simulating phantom and pure water, under similar conditions, was used to determine the true light fluence rate in tissue. The measured fluence rate was then normalized to the incident light fluence rate for a broad beam in free air, at the same distance from the light source. An additional correction was made to correct for the under-response of the isotropic detector to scattered light due to a blind spot near the stem where light was not detectable.8 This effect was about 17% for the isotropic detector used in this study and was determined by measuring the ratio ϕ/ϕair of the isotropic detector with and without a perfectly diffused reflecting surface with a diffuse reflectance of Rd = 0.99.
3. RESULTS AND DISCUSSIONS
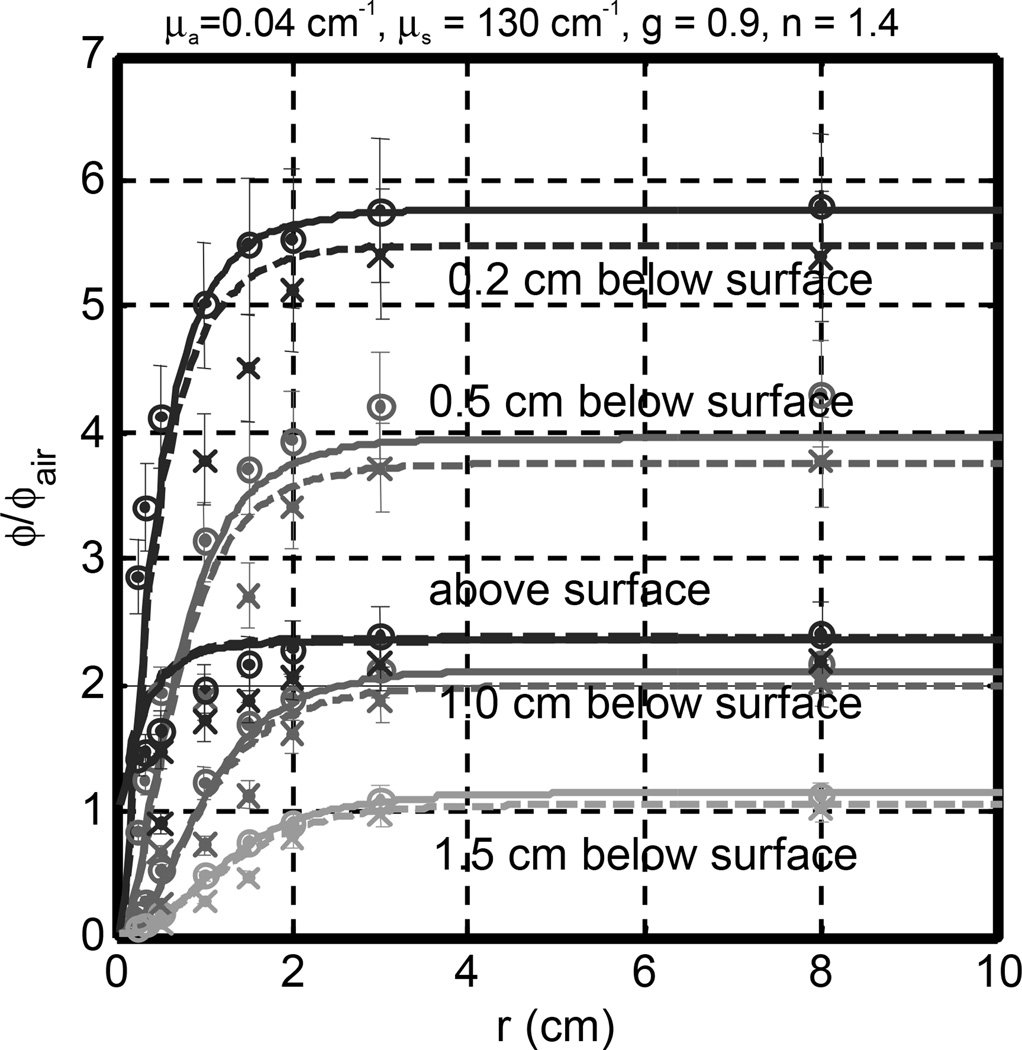
The comparison between measurements and Monte-Carlo simulations on a semi-infinite medium is shown in Figs. 2. The optical properties of the phantom are μa = 0.04 cm−1 and μ’s = 13 cm−1. The measured ϕ/ϕair agreed with Monte-Carlo (MC) simulation inside tissue to within 10% for normal incidence. The error bars in Fig. 2 are for 10% measurement error. The measured value tended to be larger than the MC calculation for small radii. On the tissue surface, the opposite became true, i.e. the measured ϕ/ϕair was smaller than that from the MC simulation. Significiant differences in ϕ/ϕair were observed on the phantom surface for circular radius smaller than 2 cm. This is attributed to detector angular collection deficiency due to obscuring by the fiber stem. The isotropic detector is estimated to underestimate light fluence rate by 10 % in a water-based turbid medium.17
Fig. 2.
Comparison of measured (symbols) and Monte Carlo calculated (lines) ϕ/ϕair in a semi-infinite turbid medium as a function of depth and circular field radius. The measured circular radius are R = 0.25, 0.35, 0.5, 1, 1.5, 2, 3, 8 cm. Symbols are measurement: o – 0°, x − 45°. The optical properties are μa = 0.04 cm−1, μs = 130 cm−1, g = 0.9, and n = 1.4.
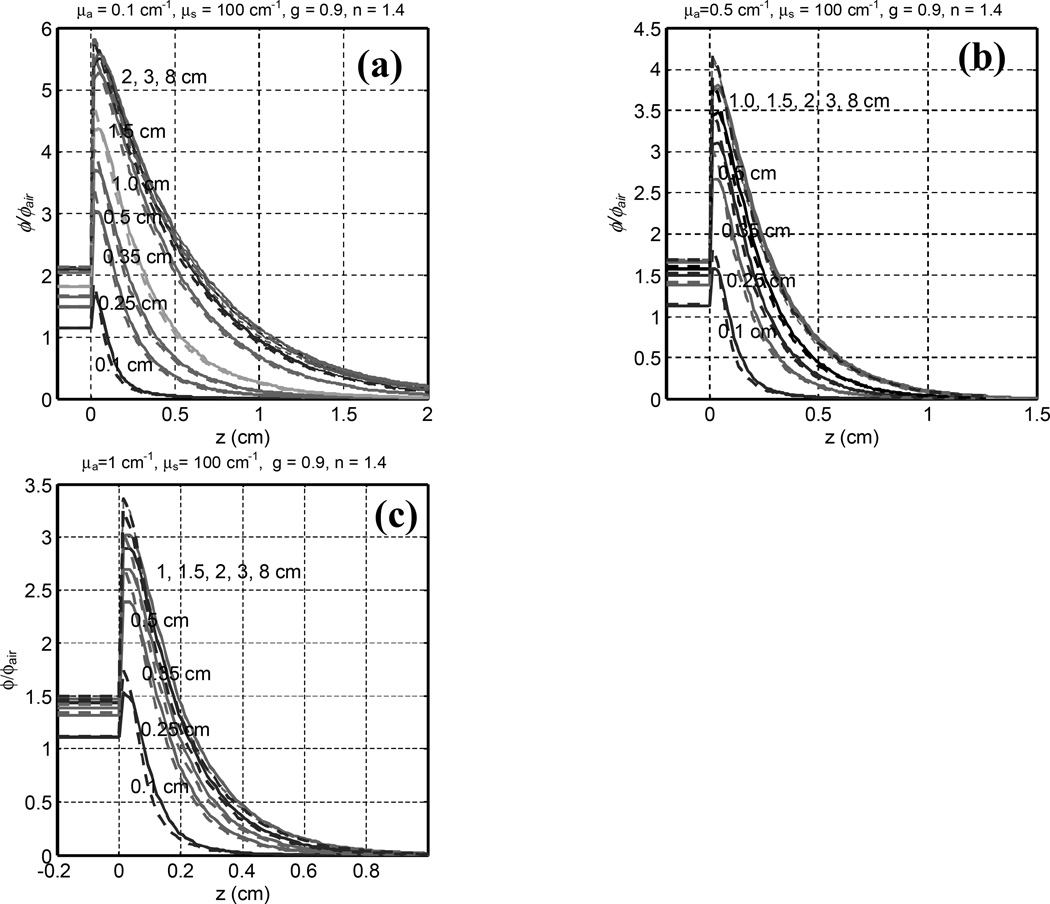
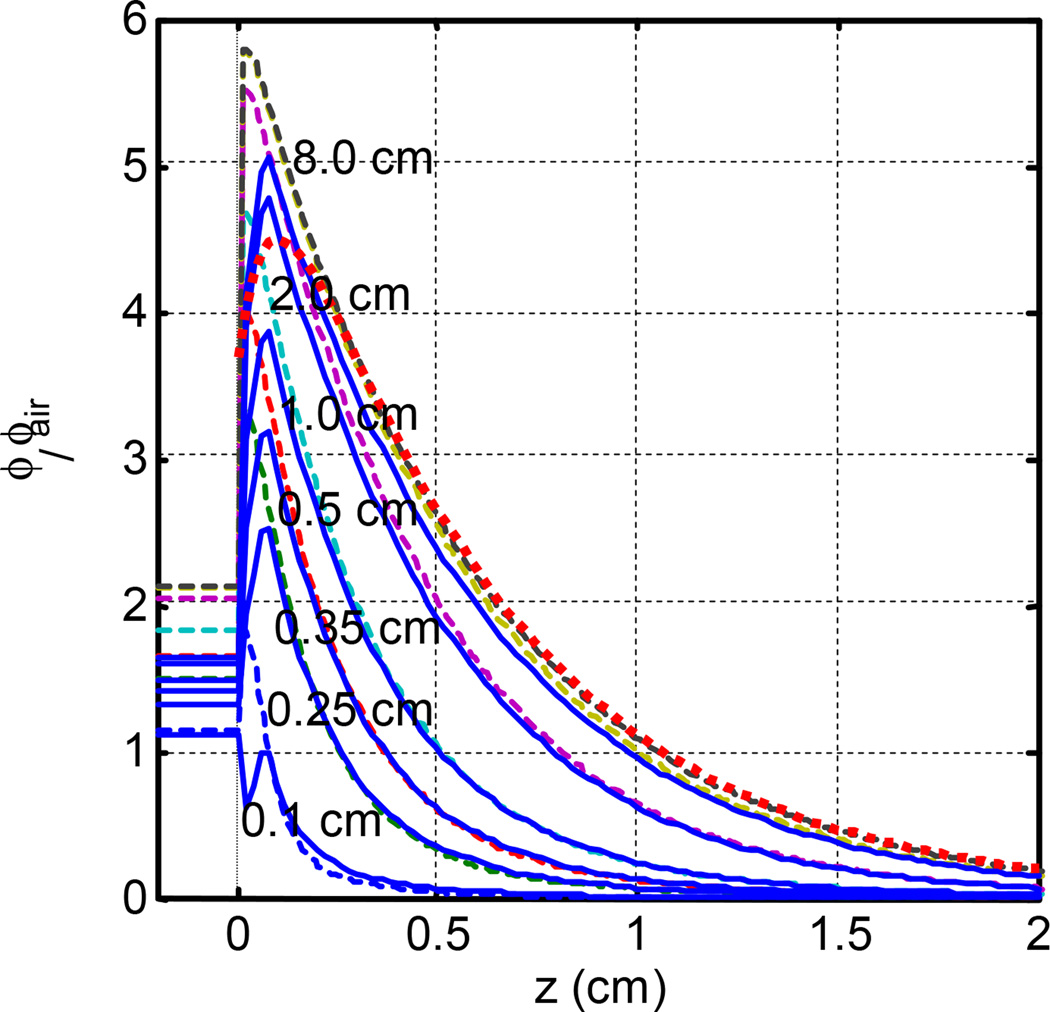
The depth dependence of ϕ/ϕair between normal and 45° incidences were compared (Fig. 3) for optical properties of μa = 0.1, 0.5, and 1.0 cm−1 and μs’ = 10 cm−1. For a fixed μ's, the peak light fluence rate decreases with decreasing μa (or μeff), as shown in Fig. 3. Just underneath the tissue surface, ϕ/ϕair increases significantly after an initial buildup. At depth of maximum fluence rate, ϕ/ϕair can be as high as 6. The ratio of peak fluence rate and incident irradiance for the broad beam is 5.7 and 3.4 for μeff = 1.7 and 5.5 cm−1, respectively, for 45° incidence. Comparing the fluence rate between 0° and 45° incidence for the same beam radius, the peak fluence rate for 45° beam is higher than that of 0° incidence by about 10% for all optical properties studied. At deeper depths (z > 1/μ’t), the fluence rate for 45° incidence is lower than that of 0° incidence by about 6%. Table 1 shows the range of the ratio of the peak fluence rate, relative to that of a broad beam (R = 8 cm), as a function of the radius R of the circular field in tissue. The ratio of the peak fluence rates between a circular beam and a broad beam under tissue is 0.78 – 1.0 or 0.89 – 1.00 for r between 0.5 – 2 cm and μeff = 1.7 or 5.5 cm−1, respectively.
Fig. 3.
Comparison of Monte Carlo calculated ϕ/ϕair in a semi-infinite trubid medium as a function of depth for normal (solid line) and 45° (dashed line) incidence for different tissue absorption coefficients μa = 0.1, 0.5, and 1 cm−1 and μs’ = 10 cm−1. Curves are for different field radius: from bottom to top, R = 0.1, 0.25, 0.35, 0.5, 1, 1.5, 2, 3, 8 cm.
Table 1.
Ratio of peak fluence rate in tissue between a circular beam and a broad beam (R = 8 cm). The absorption coefficient μa varied between 0.1 and 1 cm−1 and the reduced scattering coefficient μs’ is fixed at 10 cm−1.
| μeff (cm−1) \ R (cm) | θinc | 0.1 | 0.25 | 0.35 | 0.5 | 0.75 | 1.0 | 1.5 | 2 | 8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.7 | 0 | 0.295 | 0.543 | 0.661 | 0.782 | 0.941 | 0.982 | 0.994 | 0.999 | 1.000 |
| 45 | 0.332 | 0.596 | 0.718 | 0.837 | 0.987 | 1.022 | 1.033 | 1.037 | 1.037 | |
| 3.9 | 0 | 0.416 | 0.703 | 0.819 | 0.913 | 0.992 | 0.999 | 1.000 | 1.000 | 1.000 |
| 45 | 0.477 | 0.795 | 0.914 | 1.008 | 1.084 | 1.091 | 1.092 | 1.092 | 1.092 | |
| 5.5 | 0 | 0.507 | 0.793 | 0.891 | 0.959 | 0.998 | 1.000 | 1.000 | 1.000 | 1.000 |
| 45 | 0.579 | 0.900 | 1.003 | 1.074 | 1.114 | 1.115 | 1.116 | 1.116 | 1.116 | |
Table 2 shows that the penetration depth of light fluence rate (δ) decreases with decreasing radius due to the reduced scattering of photons for smaller fields. It is not sensitive to the incident angle. This value is obtained by an exponential fit to the depth dependence of ϕ/ϕair well within the tissue. For a larger field radius with sufficient photon scattering inside the irradiated area of the turbid phantom, the penetration depth becomes a constant (δ = 1/μeff), independent of the field radius. δ starts to reduce when the radius of circular field is less than 2 cm. The reduction of optical depth is less for smaller μeff than for larger μeff. The optical penetration depth δ varies from 0.46 – 0.56 cm for r between 0.5 and 2 cm, with the corresponding δ = 0.58 cm for the broad beam with 45° incidence.
Table 2.
Optical penetration depth δ (in unit of cm) as a function of the radius of circular beams, R. The absorption coefficient μa varied between 0.1 and 1cm−1 and the reduced scattering coefficient μs’ is fixed at 10 cm−1.
| μeff (cm−1) \ R (cm) | θinc | 0.1 | 0.25 | 0.35 | 0.5 | 0.75 | 1.0 | 1.5 | 2 | 8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.7 | 0 | 0.43 | 0.44 | 0.45 | 0.45 | 0.48 | 0.51 | 0.53 | 0.56 | 0.58 |
| 45 | 0.44 | 0.46 | 0.46 | 0.46 | 0.48 | 0.51 | 0.53 | 0.56 | 0.58 | |
| 3.9 | 0 | 0.21 | 0.21 | 0.21 | 0.22 | 0.24 | 0.25 | 0.25 | 0.25 | 0.25 |
| 45 | 0.21 | 0.21 | 0.22 | 0.22 | 0.24 | 0.25 | 0.25 | 0.25 | 0.25 | |
| 5.5 | 0 | 0.14 | 0.15 | 0.15 | 0.16 | 0.17 | 0.18 | 0.18 | 0.18 | 0.18 |
| 45 | 0.14 | 0.15 | 0.15 | 0.16 | 0.17 | 0.18 | 0.18 | 0.18 | 0.18 | |
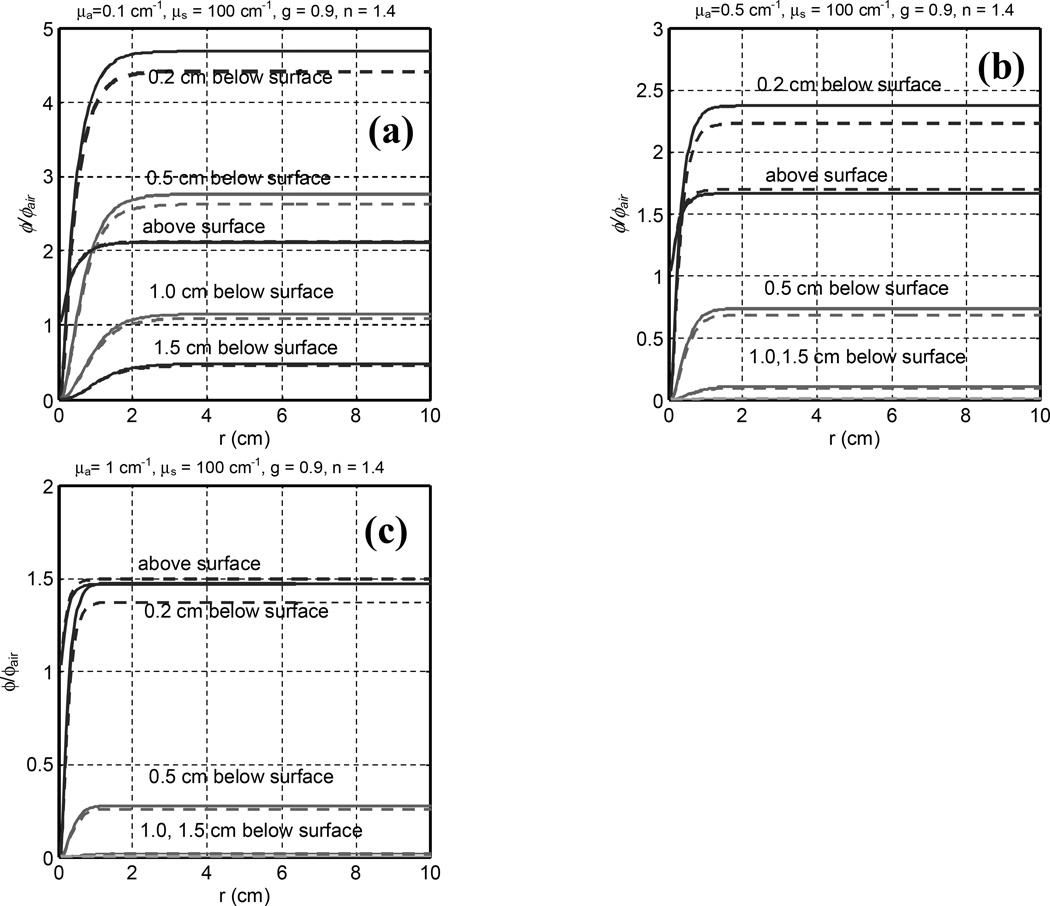
Figure 4 compares similar MC results between normal and 45° incidence as a function of radius for μa between 0.1 and 1.0 cm−1 and μs’ = 10 cm−1. Table 3 summarizes the values of ϕ/ϕair for different beam radii and depth in tissue for 45° incidence. ϕ/ϕair is always larger than 1 above the tissue surface, as predicted by Eq. (3). The ratio of fluence rate and incident irradiance above the tissue surface is 1.7 – 2.1 or 1.4 – 2.1 for R between 0.5 – 2 cm and μeff = 1.7 or 5.5 cm−1, respectively. Oblique incidence tends to reduce the light fluence rate for a fixed depth and beam radius for depths larger than 2 mm. Above the tissue surface, ϕ/ϕair for oblique incidence is higher than that for normal incidence.
Figure 4.
Radius dependence of light fluence rate under uniform (solid lines) and 45° oblique incident (dashed lines) irradiation of circular light beam at various depths in tissue. The curves are for different depths in the phantom. The tissue optical properties are (a) μa = 0.1, (b) 0.5, (c) 1.0 cm−1 and μ’s = 10 cm−1.
Table 3.
θ/θair at various depths for different optical properties (μa and μs’)
| μa, μs’ (cm−1) | Depth \ R (cm) | 0.1 | 0.3 | 0.5 | 0.7 | 1.1 | 1.5 | 2.1 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Above surface | 1.149 | 1.487 | 1.650 | 1.816 | 2.038 | 2.094 | 2.110 | 2.117 | |
| μa = 0.1 | 0.2 | 0.308 | 1.515 | 2.211 | 2.992 | 4.163 | 4.484 | 4.581 | 4.622 |
| μs’ = 10 | 0.5 | 0.047 | 0.362 | 0.657 | 1.117 | 2.143 | 2.532 | 2.664 | 2.726 |
| 1.0 | 0.008 | 0.067 | 0.133 | 0.259 | 0.687 | 0.948 | 1.067 | 1.136 | |
| 1.5 | 0.002 | 0.017 | 0.036 | 0.072 | 0.225 | 0.351 | 0.423 | 0.474 | |
| Above surface | 1.130 | 1.385 | 1.492 | 1.579 | 1.654 | 1.661 | 1.662 | 1.662 | |
| μa = 0.5 | 0.2 | 0.251 | 1.118 | 1.535 | 1.920 | 2.284 | 2.324 | 2.328 | 2.329 |
| μs’ = 10 | 0.5 | 0.020 | 0.161 | 0.283 | 0.443 | 0.682 | 0.720 | 0.726 | 0.726 |
| 1.0 | 0.001 | 0.011 | 0.021 | 0.039 | 0.085 | 0.099 | 0.102 | 0.102 | |
| 1.5 | 0.000 | 0.001 | 0.002 | 0.004 | 0.010 | 0.013 | 0.014 | 0.014 | |
| Above surface | 1.121 | 1.321 | 1.390 | 1.439 | 1.468 | 1.470 | 1.470 | 1.470 | |
| μa = 1.0 | 0.2 | 0.199 | 0.827 | 1.092 | 1.294 | 1.431 | 1.438 | 1.438 | 1.438 |
| μs’ = 10 | 0.5 | 0.011 | 0.078 | 0.132 | 0.194 | 0.263 | 0.269 | 0.269 | 0.269 |
| 1.0 | 0.000 | 0.002 | 0.004 | 0.008 | 0.015 | 0.016 | 0.016 | 0.016 | |
| 1.5 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.001 | 0.001 | 0.001 | |
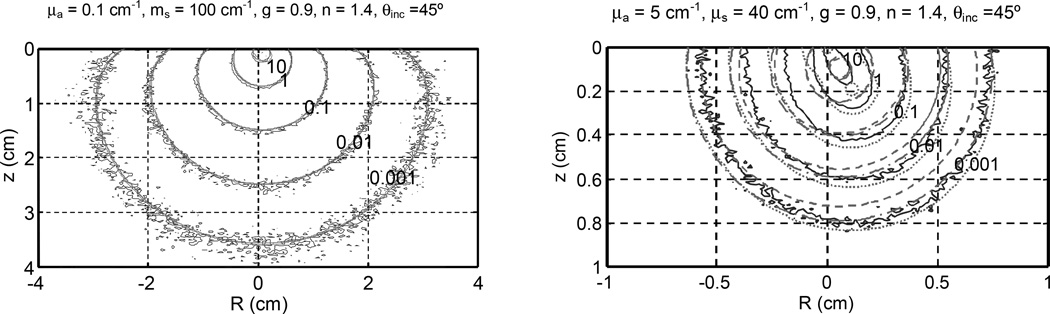
Figure 5 compares pencil-beam kernel results between analytical and MC calculations for different optical properties. In the range of optical properties common for PDT treatment (a' = μ's /(μa +μ's) ≥ 0.9), the agreement is excellent for fluence rate per source strength less than 1 cm−2, or z > 2z0. P3 hybrid agrees with diffusion theory. The net effect of oblique incidence is a shift of point off-axis from the entrance of the pencil-beam along the direction of beam incidence. For smaller transport albeto (a’ = 0.4), P3 hybrid (dotted lines) with two point sources gives better results than the diffusion approximation (dashed lines). It generally provides a good evaluation for fluence rates per source strength of less than 1 cm−2. However, neither theories work very well for z < z0, as expected.
Figure 5.
Comparison of pencil-beam kernels calculated by MC simulation and analytical calculation for 45° incidence. The analytical calculation uses diffusion approximation (dashed lines) with one source, P3 hybrid (dash-dotted lines) with one source, and P3 hybrid (dotted lines) with two sources. The optical properties are (a) μa = 0.1cm−1 and μs’ = 10 cm−1 and (b) μa = 5 cm−1 and μs’ = 4 cm−1.
Figure 6 compares fluence rate calculation results between analytical and MC calculations for different optical properties. The agreement is good for z > z0 (within about 10%) but the analytical calculation tends to underestimate ϕ in the buildup region (z < z0).
Figure 6.
Comparison of MC (dashed) and diffusion theory (solid) calculated light fluence rate for circular radius with 45° incidence on a semi-infinite media. μa = 0.1 cm−1 and μs’ = 10 cm−1. The dotted line is for broad beam of infinite radius calculated using the diffusion theory with infinite sources (theory not included in the paper).
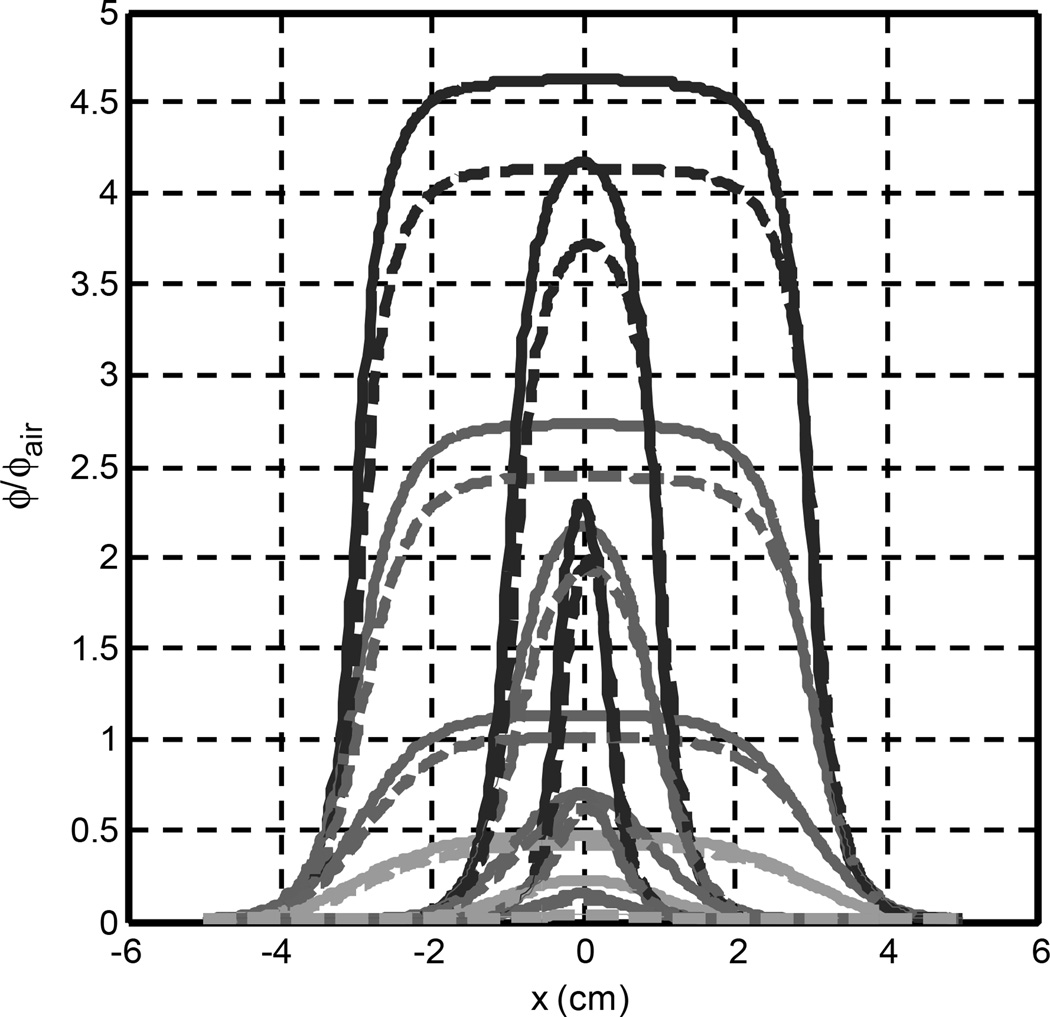
Figure 7 shows the lateral ϕ/ϕair distribution at different depths for three beam diameters (0.5, 2, 6 cm) for μa = 0.1 cm−1 and μs’ =10 cm−1. Calculations are made using the diffusion approximation. The beam penumbra width is approximately 2 cm regardless of the optical properties. If the beam radius is smaller than 1 cm, then it is possible for the penumbra of the light field to cut into each other, resulting in ϕ/ϕair on the central axis to decrease. Other than a reduction of fluence rate, oblique incidence does not change the beam profile significantly for beam diameter larger than 2 cm. The effect of oblique incidence can be expressed as a lateral shift of beam by sinθt/μ’t, which is typically in the order of 1 mm.
Figure 7.
The lateral distribution of light fluence rate for a 0.5, 2, and 6-cm diameter circular beam at various depths (from top to bottom, 0.2, 0.5, 1.0, 1.5 cm) for normal (solid) and 45° incident (dashed) beams. μa = 0.1cm−1 and μs’ = 10 cm−1
4. CONCLUSION
We have studied the ratio ϕ/ϕair between the light fluence rate and the incident irradiance using Monte Carlo calculations. An analytical solution is proposed to calculate the light fluence rate, both inside and outside of tissue. We have shown in this study the variation of ϕ/ϕair as a function of beam radius, incident angle, and depth.
ACKNOWLEDGEMENT
This work is supported by grants from DOD DAMD17-03-1-0132 and NCI P01 CA87971-01A1.
REFERENCES
- 1.Dougherty TJ, Gomer CJ, Henderson BW, Jori G, Kessel D, Korbelik M, Moan J, Peng Q. Photodynamic therapy. Journal of the National Cancer Institute. 1998;90:889–905. doi: 10.1093/jnci/90.12.889. [Review] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zhu TC, Dimofte A, Hahn SM, Lustig RA. Light Dosimetry at Tissue Surfaces for Small Circular Fields. Proc. SPIE. 2003:4952. doi: 10.1117/12.474144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shimada M, Yamada Y, Itoh M, Yatagai T. Melanin and blood concentration in a human skin model studied by multiple regression analysis: assessment by Monte Carlo simulation. Phys Med Biol. 2001;46:2397–2406. doi: 10.1088/0031-9155/46/9/309. [DOI] [PubMed] [Google Scholar]
- 4.Cheong WF, Prahl SA, Welch AJ. A review of the optical properties of biological tissues. IEEE J. Quant. Electron. 1990;26:2166–2185. [Google Scholar]
- 5.Dimofte A, Zhu TC, Hahn SM, Lustig RA. In Vivo Light Dosimetry for Motexafin Lutetium-mediated PDT of Recurrent Breast Cancer. Lasers Surg Med. 2002;31:305–312. doi: 10.1002/lsm.10115. [DOI] [PubMed] [Google Scholar]
- 6.Vulcan TG, Zhu TC, Rodriguez CE, His A, Fraker DL, Bass P, Murrer LHP, Star WM, Glatstein E, Yodh AG, Hahn SM. Comparison between Isotropic and Nonisotropic Dosimetry Systems During Intraperitoneal Photodynamic Therapy. Lasers Surg Med. 2000;26:292–301. doi: 10.1002/(sici)1096-9101(2000)26:3<292::aid-lsm7>3.0.co;2-t. [DOI] [PubMed] [Google Scholar]
- 7.Star WM. Light dosimetry in vivo. Phys Med Biol. 1997;42:763–787. doi: 10.1088/0031-9155/42/5/003. [DOI] [PubMed] [Google Scholar]
- 8.Marijnissen JPA, Star WM. Calibration of isotropic light dosimetry probes based on scattering bulbs in clear media. Phys Med Biol. 1996;41:1191–1208. doi: 10.1088/0031-9155/41/7/008. [DOI] [PubMed] [Google Scholar]
- 9.Wilson BC, Adam G. A Monte Carlo model for the absorption and flux distributions of light in tissue. Med Phys. 1983;10:824–830. doi: 10.1118/1.595361. [DOI] [PubMed] [Google Scholar]
- 10.Prahl SA, Keijzer M, Jacques SL, Welch AJ. A Monte Carlo model of light propagation in tissue. In: Miller GJ, Sliney DH, editors. Dosimetry of Laser Radiation in Medicine and Biology. IS5. Proc. SPIE Institute Ser.; 1989. pp. 102–111. [Google Scholar]
- 11.Jacques SL, Wang L. Monte Carlo modeling of light transport in tissues. In: Welch AJ, van Gemert MJC, editors. Optical-Thermal Response of Laser-irradiated Tissue. Plenum, New York: 1995. [Google Scholar]
- 12.Wang L, Jacques SL, Zheng L. MCML-Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995;47:131–146. doi: 10.1016/0169-2607(95)01640-f. [DOI] [PubMed] [Google Scholar]
- 13.Farrell TJ, Patterson MS, Wilson BC. A diffusion theory model of spatially resolved, steady-state diffuse reflectance for the noninvasive determination of tissue optical properties in vivo. med Phys. 1992;19:879–888. doi: 10.1118/1.596777. [DOI] [PubMed] [Google Scholar]
- 14.Hull EL, Foster TH. Steady-state reflectance spectroscopy in the P3 approximation. J Opt. Soc. Am. A. 2001;18:584–599. [Google Scholar]
- 15.Haskell RC, Svaasand LO, Tsay T, Feng T, McAdams MS, Tromberg BJ. Boundary conditions for the diffusion equation in radiative transfer. J Opt. Soc. Am. A. 1994;11:2727–2741. doi: 10.1364/josaa.11.002727. [DOI] [PubMed] [Google Scholar]
- 16.Van Staveren HJ, Marijnissen JPA, Aalders MCG, Star WM. Construction, quality assurance and calibration of spherical isotropic fibre optic light diffusers. Lasers Med Sci. 1995;10:137–147. [Google Scholar]
- 17.Marijnissen JPA, Star WM. Performance of isotropic light dosimetry probes based on scattering bulbs in turbid media. Phys Med Biol. 2002;47:2049–2058. doi: 10.1088/0031-9155/47/12/304. [DOI] [PubMed] [Google Scholar]
- 18.Martelli F, Sassaroli A, Zaccanti G, Yamada Y. Properties of the light emerging from a diffusive medium: angular dependence and flux at the external boundary. Phys Med Biol. 1999;44:1257–1275. doi: 10.1088/0031-9155/44/5/013. [DOI] [PubMed] [Google Scholar]