Estimating the lifetime risk of dementia in the Canadian elderly population using cross-sectional cohort survival data

Abstract

Dementia is one of the world’s major public health challenges. The lifetime risk of dementia is the proportion of individuals who ever develop dementia during their lifetime. Despite its importance to epidemiologists and policy-makers, this measure does not seem to have been estimated in the Canadian population. Data from a birth cohort study of dementia are not available. Instead, we must rely on data from the Canadian Study of Heath and Aging, a large cross-sectional study of dementia with follow-up for survival. These data present challenges because they include substantial loss to follow-up and are not representatively drawn from the target population because of structural sampling biases. A first bias is imparted by the cross-sectional sampling scheme, while a second bias is a result of stratified sampling. Estimation of the lifetime risk and related quantities in the presence of these biases has not been previously addressed in the literature. We develop and study nonparametric estimators of the lifetime risk, the remaining lifetime risk and cumulative risk at specific ages, accounting for these complexities. In particular, we reveal the fact that estimation of the lifetime risk is invariant to stratification by current age at sampling. We present simulation results validating our methodology, and provide novel facts about the epidemiology of dementia in Canada using data from the Canadian Study of Health and Aging.

1 Introduction

Dementia has been identified as one of the world’s major public health challenges, in particular in industrialized countries, in the 21st century (World Health Organization, 2006). With individuals living longer than ever, populations have been aging and the burden of dementia growing (Brookmeyer et al., 2007; Kawas and Brookmeyer, 2001). The toll of dementia on society is significant: because of its chronic and degenerative nature, this disease leads to considerable health care resource utilization and causes tremendous hardship for families. Medical researchers have been seeking to elucidate the pathogenesis of dementia and thereby unearth preventative and therapeutic strategies. Policy-makers need a better understanding of the dynamics of dementia in order to adequately allocate current and future health resources. To assist both, epidemiologists have investigated epidemiological parameters of dementia in populations. Measures including the prevalence (McDowell et al., 1994) and incidence of dementia (Addona et al., 2009; Carone et al., 2012) have been studied in the Canadian population and reported in the literature. However, despite its importance, the lifetime risk of dementia in Canada, defined as the proportion of Canadians developing dementia during their lifetime, does not seem to have been previously described. Estimation of lifetime risk has traditionally been difficult, ideally requiring data from a birth cohort study; such studies are particularly unfeasible in the investigation of diseases of the elderly. In this paper, we develop statistical tools to provide a first estimate of the lifetime risk of dementia in the Canadian elderly population using data from the Canadian Study of Health and Aging, a large cross-sectional study of dementia with follow-up.

The Canadian Study of Health and Aging was conducted in the following manner. A cross-sectional sample of the population was obtained in 1991, and recruited individuals were followed forward for survival only. At recruitment, every individual was assessed for dementia according to DSM-III-R criteria (American Psychiatric Association, 1987). Age at onset was retrospectively ascertained in prevalent cases using an algorithm based on the Cambridge Mental Disorders of the Elderly Examination (Rouah and Wolfson, 2001; Wolfson et al., 2001). Date of birth and other covariates were also recorded at recruitment. Because this type of design requires reduced follow-up periods and enrollment pool sizes in order to accrue sufficient case data, it is considered to be more feasible to conduct, both economically and logistically, than alternative designs. However, the data it generates suffer from systematic biases which, if ignored, can lead to incorrect conclusions; Wolfson et al. (2001) highlight an example of such. In particular, individuals with longer lifetimes are favored by the sampling process while individuals with longer disease durations are overrepresented in the collected case data. This bias in survival has been widely studied (Cox and Oakes, 1984; Tsai et al., 1987; Wang, 1998; Asgharian et al., 2002).

A first look at estimation of the lifetime risk in the setting of cross-sectional data dates back to Rhame and Sudderth (1981), which focused on equilibrium conditions. Narayan et al. (2003) studied the lifetime risk of diabetes mellitus using cross-sectional data by formulating a Markovian modeling framework. Recently, Mandel and Fluss (2009) derived and studied a methodology for estimating the probability of contracting a nosocomial infection before discharge from the intensive care unit using survival data obtained from a cross-sectional sample with follow-up. Their methodology necessitates weaker assumptions on the population structure than previously imposed. Nonetheless, their work requires simple random sampling as well as complete observation of the terminating event for each recruited individual. These requirements may fail to hold in practice, especially in the context of population-wide epidemiologic studies. For example, in the Canadian Study of Health and Aging, segments of the population were oversampled and the follow-up of nearly half of all recruited individuals ended before death was observed. Accounting for stratified sampling and loss to follow-up is therefore a necessity.

This paper is organized as follows. In Section 2, a probabilistic framework to study lifetime risk based on population point processes is established. Estimators of the lifetime risk, remaining lifetime risk and cumulative risk using cross-sectional survival data with right-censored follow-up are derived in Section 3. In Section 4, estimation of these risk measures in the context of stratified sampling is discussed; in particular, invariance results are established. In Section 5, results from a simulation study are presented. Data from the Canadian Study of Health and Aging are analyzed and insight into the lifetime risk of dementia in the Canadian elderly population is provided in Section 6. Concluding remarks are provided in Section 7.

2 Lifetime risk and population point processes

We begin by constructing a formal framework for studying lifetime risk using data from a cross-sectional survival study with follow-up. Suppose that a target population has been defined, and that birth dates of all individuals in the target population are contained in an interval (τ₀, τ₁). We denote by M = {M(t) : t > τ₀} the population birth point process, with M(t) the number of births that have occurred in the target population before calendar-time t, and assume that

$$M\mathrm{is\; a\; nonhomogeneous\; Poisson\; process}$$ (A1)

with cumulative rate function ${\mathrm{\Lambda }}_0(u)={\mathit{\int }}_{{\tau }_0}^u\mathrm{E}[M(w+\mathit{dw})-M(w)]$. For each individual in the population, we denote calendar time at birth and total lifetime by B* and Z*, respectively. We denote disease status at age u ≥ 0 by D*(u), taking value 1 to indicate onset of dementia prior to or at age u and 0 otherwise; {D*(u) : u ≥ 0} is therefore a counting process with absorbing state 1. We denote by D* the lifetime dementia status D*(∞) = D*(Z*). The lifetime risk of dementia, denoted by π, is defined as pr (D* = 1). Finally, in the case population, that is, those for whom D* = 1, we denote by X* the age at onset of dementia.

Suppose that sampling occurs at a fixed calendar-time t₀. To ensure the identifiability of relevant quantities, we require that the target population be such that

$${\tau }_1\le t_0\le \min ({\tau }_0+s_1,{\tau }_1+s_0),$$ (A2)

where s₀ and s₁ are the lower and upper endpoints, respectively, of the support of Z*. Provided birth rates in the target population are positive over (τ₀, τ₁), this requirement guarantees that all individuals in the target population have a positive probability of being sampled at t₀, and that the lifetime distribution is identified. If this requirement does not hold, the definition of the target population must be further restricted.

At recruitment time, a sample of n individuals was obtained from the cross-sectional population, the subset of the target population alive at t₀. For each sampled individual, date of birth B was recorded. Here, B denotes the counterpart of B* defined in the cross-sectional population. As such, the distribution of B is that of B* conditional upon the sampling criterion Z* ≥ t₀ − B*. A similar notation is adopted for other variables. We also define W* = t₀ − B* as the time elapsed from birth to recruitment, or the age at recruitment, with W the cross-sectional counterpart of W*. At time t₀, for each recruited individual, it was determined whether onset of dementia had already occurred: Δ₀ equals 1 if so and 0 otherwise. If Δ₀ = 1, age at onset X was retrospectively obtained and recorded. Each recruited individual was then followed in time until death or loss to follow-up (but not for future diagnosis of dementia); total follow-up time V and the death indicator Δ₁ were recorded. We denote by E the data collected on a given individual. A schematic depiction of the sampling scheme is provided in Figure 1, while the duration variables are illustrated in Figure 2. A summary listing of all defined random variables is provided in Table 1 as a reference. The data consist of n independent replicates E_i = (W_i, Δ_0i, X_i, V_i, Δ_1i), i = 1, 2, …, n. For all individuals with Δ_0i = 0, X_i is arbitrarily set as +∞. This emphasizes that, since there is no reassessment of disease status post-recruitment, information on disease status and onset is only obtained for individuals with disease at recruitment.

Figure 1.

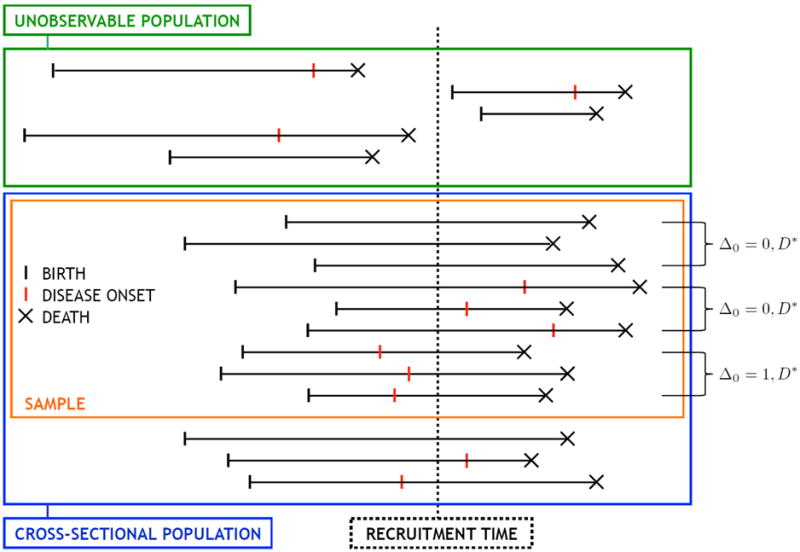
Schematic representation of cross-sectional sampling framework.

Figure 2.

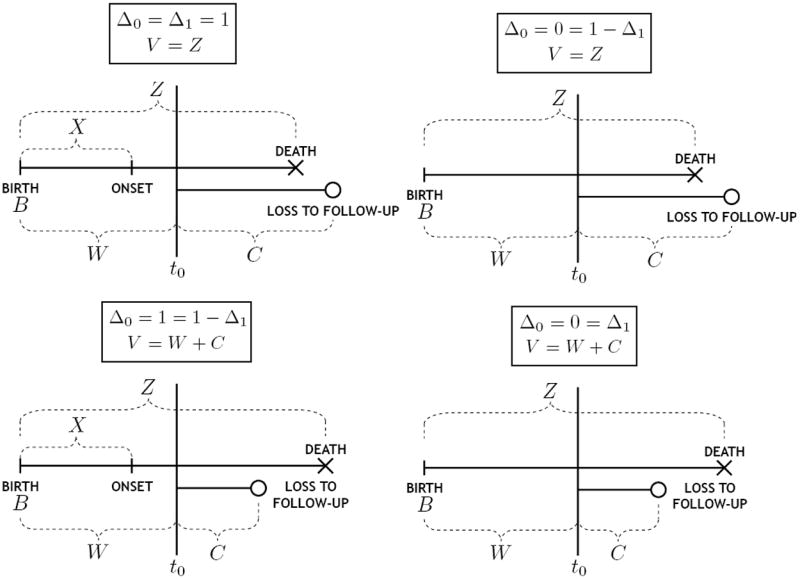
Illustration of duration variables for observed cases (Δ₀ = 1) and non-cases (Δ₀ = 0), either uncensored (Δ₁ = 1) or censored (Δ₁ = 0).

Table 1.

List of defined random variables.

DEFINITION	NOTATION IN
	TARGET	CROSS-SECTIONAL
	POPULATION
date of birth	B*	B
age at recruitment	W*	W
age at onset	X*	X
total lifetime	Z*	Z
disease status at age u	D*(u)	D(u)
lifetime disease status	D* = D*(∞)	D = D(∞)
censoring time	—	C
ind. of prevalence at time t0	—	Δ0 = 𝕀(0,W)(X)D
ind. of death	—	Δ1 = 𝕀(0,W+C)(Z)
total follow-up time	—	V = min(Z, W + C)

We define the population point processes N₁ = {N₁(t) : t > τ₀} and N₂ = {N₂(t) : t > τ₀}, where N₁(t) is the number of individuals in the target population born before calendar-time t, alive at calendar-time t₀, and diseased by calendar-time t₀, and N₂(t) the number of individuals in the target population born before calendar-time t, and alive at calendar-time t₀. Denote their respective cumulative rate functions by Λ₁ and Λ₂. Each of N₁ and N₂ are independent thinnings of M; they are thus nonhomogeneous Poisson processes themselves, and their cumulative rate functions are given by

$$\begin{array}{c}{\mathrm{\Lambda }}_1(t)={\mathit{\int }}_{{\tau }_0}^{\min (t,{\tau }_1)}\mathrm{pr}(Z^{\ast }\ge t_0-u,D^{\ast }(t_0-u)=1\mid B^{\ast }=u)d{\mathrm{\Lambda }}_0(u)\\ \mathrm{and}{\mathrm{\Lambda }}_2(t)={\mathit{\int }}_{{\tau }_0}^{\min (t,{\tau }_1)}\mathrm{pr}(Z^{\ast }\ge t_0-u\mid B^{\ast }=u)d{\mathrm{\Lambda }}_0(u).\end{array}$$

We can show, as in Carone et al. (2012), that dΛ₀(u) ∝ dG(t₀ − u), where G is the marginal distribution function of age at recruitment W*, and W* has support contained in (t₀ − τ₁, t₀ − τ₀). It follows then that

$$\begin{array}{lll}\frac{{\mathrm{\Lambda }}_1(t_0)}{{\mathrm{\Lambda }}_2(t_0)}& =& \frac{{\mathit{\int }}_{{\tau }_0}^{{\tau }_1}\mathrm{pr}(Z^{\ast }\ge t_0-u,D^{\ast }(t_0-u)=1\mid W^{\ast }=t_0-u)\mathit{dG}(t_0-u)}{{\mathit{\int }}_{{\tau }_0}^{{\tau }_1}\mathrm{pr}(Z^{\ast }\ge t_0-u\mid W^{\ast }=t_0-u)\mathit{dG}(t_0-u)}\\ & =& \frac{{\mathit{\int }}_{{\tau }_0}^{{\tau }_1}\mathrm{pr}(X^{\ast }\le t_0-u\le Z^{\ast },D^{\ast }=1\mid W^{\ast }=t_0-u)\mathit{dG}(t_0-u)}{{\mathit{\int }}_{{\tau }_0}^{{\tau }_1}\mathrm{pr}(Z^{\ast }\ge t_0-u\mid W^{\ast }=t_0-u)\mathit{dG}(t_0-u)}\\ & =& \frac{{\mathit{\int }}_{t_0-{\tau }_1}^{t_0-{\tau }_0}\mathrm{pr}(X^{\ast }\le w\le Z^{\ast }\mid W^{\ast }=w,D^{\ast }=1)\mathrm{pr}(D^{\ast }=1\mid W^{\ast }=w)\mathit{dG}(w)}{{\mathit{\int }}_{t_0-{\tau }_1}^{t_0-{\tau }_0}\mathrm{pr}(w\le Z^{\ast }\mid W^{\ast }=w)\mathit{dG}(w)}\\ & =& \frac{{\mathit{\int }}_{t_0-{\tau }_1}^{t_0-{\tau }_0}\mathrm{pr}(X^{\ast }\le w\le Z^{\ast }\mid W^{\ast }=w,D^{\ast }=1){\mathit{dG}}^{(1)}(w)\mathrm{pr}(D^{\ast }=1)}{{\mathit{\int }}_{t_0-{\tau }_1}^{t_0-{\tau }_0}\mathrm{pr}(Z^{\ast }\ge w\mid W^{\ast }=w)\mathit{dG}(w)}\\ & =& \frac{\mathrm{pr}(X^{\ast }\le W^{\ast }\le Z^{\ast }\mid D^{\ast }=1)\mathrm{pr}(D^{\ast }=1)}{\mathrm{pr}(W^{\ast }\le Z^{\ast })},\end{array}$$

where G⁽¹⁾ is the conditional distribution function of W* given D* = 1. We therefore obtain that

$$\pi =P(t_0)·\frac{\mathrm{pr}(W^{\ast }\le Z^{\ast })}{\mathrm{pr}(X^{\ast }\le W^{\ast }\le Z^{\ast }\mid D^{\ast }=1)},$$ (2.1)

where P(t₀) = Λ₁(t₀)/Λ₂(t₀) is the proportion of individuals alive at t₀ who are diseased by t₀, pr (W* ≤ Z*) is the proportion of individuals in the target population who are alive at t₀, and pr (X* ≤ W* ≤ Z* ∣ D* = 1) is the proportion of individuals in the subset of target population ever experiencing the disease who are alive and diseased at t₀. Equation (2.1) also appears in Mandel and Fluss (2009), albeit derived from a different perspective. If births emanate from a stationary Poisson process, then (2.1) reduces to

$$\pi =P(t_0)·\frac{\mathrm{E}(Z^{\ast })}{\mathrm{E}(Z^{\ast }-X^{\ast }\mid D^{\ast }=1)},$$

as first derived in Rhame and Sudderth (1981).

3 Estimation and inference

3.1 Lifetime risk

In the remainder, we assume that date of birth does not provide any information regarding longevity and the disease status process, or more succinctly, that birth cohort effects are absent. Specifically, we assume that

$$(Z^{\ast },D^{\ast }(·))\mathrm{is\; independent\; of}{B}^{\ast }.$$ (A3)

This independence assumption will often hold as long as there are no secular changes in life expectancy, in the incidence rate of disease, and in survival with the disease. In population-based studies, such changes can result from the introduction of novel diagnostic and therapeutic methods. If the time frame containing the birth dates of recruited individuals is sufficiently short, this assumption is generally plausible. This was the case in the Canadian Study of Health and Aging, of which a very large proportion of participants had a birth date contained in a 23-year interval. For nonparametric inference, this assumption or slightly weaker variants seem necessary. It is worthy to note, nonetheless, that a sensitivity analysis, described extensively in Part B of the Supplementary Material, suggests that the methods described below may be quite robust to realistic deviations from (A3).

In population-based studies, there may be substantial loss to follow-up. The censoring time C, the time elapsed between recruitment and loss to follow-up, is defined in the cross-sectional population alone; we denote its survival function by Q. We assume that

$$C\mathrm{is\; independent\; of}(Z,W)\mathrm{and\; of}(X,Z,W)\mathrm{given}{\mathrm{\Delta }}_0=1;$$ (A4)

this is an example of independent residual censoring. This assumption will be plausible if, for example, loss to follow-up is due to the end of the study or other administrative reasons; this was precisely the case for the vast majority of censored individuals in the Canadian Study of Health and Aging. We also assume that

$${\tau }_0+s_1\le t_0+c_1,$$ (A5)

where c₁ is the upper endpoint of the support of C, to ensure that censoring does not prohibit the observation of large values from the total lifetime distribution. The total observation time and death indicator are, respectively, V = min(Z, W + C) and Δ₁ = 𝕀_(0,W+C) (Z). Under the above assumptions, the key components of the right-hand side of (2.1) can be expressed in simpler terms and estimated consistently. Specifically, the conditional distribution function H of (X*, Z*) given D* = 1 can be expressed as

$$H(x,z)=\frac{\mathit{\int }\mathit{\int }{𝕀}_{[0,x]}(u){𝕀}_{[0,z]}(\upsilon ){\left[{\mathit{\int }}_{u\le w\le \upsilon }Q(\upsilon -w)G(\mathit{dw})\right]}^{-1}{H}^{\prime }(\mathit{du},\mathit{d\upsilon })}{\mathit{\int }\mathit{\int }{\left[{\mathit{\int }}_{u\le w\le \upsilon }Q(\upsilon -w)G(\mathit{dw})\right]}^{-1}{H}^{\prime }(\mathit{du},\mathit{d\upsilon })},$$

where H′ is the conditional distribution function of (X, V) given Δ₀ = 1 and Δ₁ = 1, and pr (X* ≤ W* ≤ Z* ∣ D* = 1) can be written as

$$\frac{\mathit{\int }\mathit{\int }[G(z)-G(x)]{\left[{\mathit{\int }}_{x\le w\le z}Q(z-w)G(\mathit{dw})\right]}^{-1}H\prime (\mathit{dx},\mathit{dz})}{\mathit{\int }\mathit{\int }{\left[{\mathit{\int }}_{u\le w\le \upsilon }Q(\upsilon -w)G(\mathit{dw})\right]}^{-1}H\prime (\mathit{du},\mathit{d\upsilon })}.$$

Further, we have that pr (W * ≤ Z*) = ∫ S(w)G(dw), where S is the survival function associated to the marginal distribution of the lifetime Z*. The distribution function H′ is estimated consistently by $H_n^{\prime }$, the empirical distribution function based on ${\{(X_i,V_i):{\mathrm{\Delta }}_{0i}={\mathrm{\Delta }}_{1i}=1\}}_{i=1}^n$. The truncation product-limit estimator based on ${\{(W_i,V_i,{\mathrm{\Delta }}_{1i})\}}_{i=1}^n$, given by

$$S_n(u)=\prod _{i=1}^n{\left[1-\frac{\mathrm{\Delta }{L}_{1n}(V_i)}{M_{1n}(V_i)}\right]}^{{𝕀}_{[V_i,\infty )}(u)},$$

where $L_{1n}(s)={\sum }_{i=1}^n{\mathrm{\Delta }}_{i1}{𝕀}_{[V_i,\infty )}(s)$ and $M_{1n}(s)={\sum }_{i=1}^n{𝕀}_{[W_i,V_i]}(s)$, is a consistent estimator of S (Kaplan and Meier, 1958; Tsai et al., 1987). The distribution function G is estimated consistently by the estimator G_n of Wang (1991) based on the full sample ${\{(W_i,V_i,{\mathrm{\Delta }}_{1i})\}}_{i=1}^n$, while the product-limit estimator Q_n based on ${\{(V_i^{\prime },{\mathrm{\Delta }}_{1i}^{\prime })\}}_{i=1}^n$, with $V_i^{\prime }=V_i-W_i$ and ${\mathrm{\Delta }}_{1i}^{\prime }=1-{\mathrm{\Delta }}_{1i}$, is a consistent estimator of Q. Specifically, we set

$$\begin{array}{c}{G}_n(u)={\left[\sum _{i=1}^n\frac{1}{S_n(W_i)}\right]}^{-1}\sum _{i=1}^n\frac{{𝕀}_{[W_i,\infty )}(u)}{S_n(W_i)}\mathrm{and}\\ Q_n(u)=\prod _{i=1}^n{\left[1-\frac{\mathrm{\Delta }{L}_{2n}(V_i^{\prime })}{M_{2n}(V_i^{\prime })}\right]}^{{𝕀}_{[V_i^{\prime },\infty )}(u)},\end{array}$$

where we define $L_{2n}(s)={\sum }_{i=1}^n{\mathrm{\Delta }}_{1i}^{\prime }{𝕀}_{[V_i^{\prime },\infty )}(s)$ and $M_{2n}(s)={\sum }_{i=1}^n{𝕀}_{[V_i^{\prime },\infty )}(s)$. Some calculations show that the substitution estimator for π obtained from (2.1) is then

$${\pi }_n=\sum _{i=1}^n{\mathrm{\Delta }}_{0i}{\left\{\sum _{i=1}^n{S}_n{(W_i)}^{-1}\sum _{i=1}^n[G_n(V_i)-G_n(X_i)]a_{n,i}\right\}}^{-1},$$ (3.1)

where we have defined ${\stackrel{\sim }{a}}_{i,n}={\mathrm{\Delta }}_{0i}{\mathrm{\Delta }}_{1i}/{\sum }_{j=1}^n{Q}_n(V_i-W_j)\mathrm{\Delta }{G}_n(W_j){𝕀}_{[X_i,V_i]}(W_j)$ and $a_{n,i}={\stackrel{\sim }{a}}_{n,i}/{{\sum }_{k=1}^n\stackrel{\sim }{a}}_{n,k}$. It is easy to verify that in the absence of censoring the proposed estimator reduces to that presented in Mandel and Fluss (2009).

It can be shown, under regularity conditions outlined in the Appendix and under simple random sampling from the cross-sectional population, that π_n is a consistent estimator of π and that n^1/2(π_n − π) converges in law to a normal variate. Nonetheless, the variance of this limiting distribution is intricate; as suggested by Mandel and Fluss (2009), the use of resampling techniques is, in practice, more expedient in constructing confidence intervals.

3.2 Remaining lifetime risk and cumulative risk

The lifetime risk of dementia provides a global measure of disease risk that does not incorporate knowledge of an individual’s current age. Because it represents the at-birth probability of ever developing dementia, it is often of greatest use for drawing population-wide epidemiological inference. Since, in practice, individuals are encountered with a history, its use in clinical settings may be limited. With this in mind, we consider the remaining lifetime risk at age z, π(z) = pr (D* = 1 ∣ D*(z) = 0, Z* > z), defined as the proportion of individuals in the target population who have reached age z disease-free and who go on to develop disease before death. Of course, π = π(0) and so, the family of remaining lifetime risks, over all z ≥ 0, provides a finer measure of disease occurrence than the lifetime risk.

Using Bayes’ Theorem, the definition of π(z) yields the relationship

$$\pi (z)=\frac{\mathrm{pr}(Z^{\ast }\ge z,D^{\ast }(z)=0\mid D^{\ast }=1)}{\mathrm{pr}(Z^{\ast }\ge z,D^{\ast }(z)=0)}·\pi .$$

Since pr (Z* ≥ z, D*(z) = 0 ∣ D* = 1) = pr (X* ≥ z ∣ D* = 1) and for each z > 0, {D*(z) = 1} ⊆ {D* = 1}, we have that

$$\begin{array}{lll}\mathrm{pr}(Z^{\ast }\ge z,D^{\ast }(z)=0)& =& \mathrm{pr}(Z^{\ast }\ge z)-\mathrm{pr}(Z^{\ast }\ge z,D^{\ast }(z)=1)\\ & & \mathrm{pr}(Z^{\ast }\ge z)-\mathrm{pr}(Z^{\ast }\ge z,D^{\ast }(z)=1\mid D^{\ast }=1)\mathrm{pr}(D^{\ast }=1)\\ & & \mathrm{pr}(Z^{\ast }\ge z)-\mathrm{pr}(X^{\ast }\le z\le Z^{\ast }\mid D^{\ast }=1)\mathrm{pr}(D^{\ast }=1),\end{array}$$

from which it follows that

$$\pi (z)=\frac{\mathrm{pr}(X^{\ast }\ge z\mid D^{\ast }=1)\pi }{\mathrm{pr}(Z^{\ast }\ge z)-\mathrm{pr}(X^{\ast }\le z\le Z^{\ast }\mid D^{\ast }=1)\pi }.$$ (3.2)

The above suggests the substitution estimator

$${\pi }_n(z)=\frac{{\pi }_n{\sum }_{i=1}^n{a}_{n,i}{𝕀}_{[0,X_i]}(z)}{S_n(z)-{\pi }_n{\sum }_{i=1}^n{a}_{n,i}{𝕀}_{[X_i,V_i]}(z)}.$$

Again, under the regularity conditions, the estimator π_n(·) is uniformly consistent and n^1/2[π_n(·) − π(·)] converges weakly to a mean-zero Gaussian process.

While all individuals in the study contribute to the estimation of the lifetime risk, it is not so for the remaining lifetime risk. Indeed, as z increases, a fewer number of study participants provide investigators any observation time during which they are at risk for experiencing onset of disease after age z. This is expected to translate into decreased precision. To visually depict this phenomenon in a given dataset, it may be useful to construct measures of data availability as a function of age z. Since in this study design prospective follow-up does not include reassessment of disease status, the age interval within which a participant contributes observation time for the sake of π(z), if at all, begins at age z and ends at the earliest of ages at onset X = x or recruitment W = w. If both x and w are smaller than z, then a participant makes no contribution. A generic measure of data availability at age z can thus be defined as $R_n(z)={\sum }_{i=1}^n{R}_{n,i}(z)/{\sum }_{i=1}^n{R}_{n,i}(0)$ with R_n,i(z) = max [K_z(min(X_i, W_i)) − K_z(z), 0] where $K_z:[0,\infty )\mapsto [0,\infty )$ is a non-decreasing function possibly indexed by z. Natural choices for K_z include:

1. K_z,0(u) = 𝕀_(z,∞)(u), so that R_n(z) is the proportion of study participants who contribute any observation time to estimation of π(z);

2. K_z,1(u) = u, so that R_n(z) is the proportion of total available time under observation available for estimating π(z) as opposed to π;

3. K_z,2(u) = H₀(u) with H₀ the distribution function of age at onset X* given D* = 1, so that R_n(z) is a relative measure of total available time under observation for estimating π(z) as opposed to π where each observation interval is weighed according to the age at onset distribution.

In practice, H₀ is usually unknown, and a consistent estimator of H₀ must be used as a substitute in choice 3. Treating all observation periods equally, as in choice 2, can yield misleading results unless disease onset occurs uniformly throughout decades of life. For example, in the case of dementia, an observation interval from ages 30 to 40 contains essentially no information whereas one from ages 80 to 90, despite having the same length, provides considerable information. To reflect this, in choice 3, observation periods in age intervals where onset is more likely are given greater weight than other periods. The measures introduced above allow practitioners to visualize the relative amount of relevant data available for estimating π(z) at any given z, and may help underscore the limitations of inferences at older ages.

An additional epidemiological measure of interest is the cumulative risk of dementia at age z, defined as the proportion of individuals in the target population who develop dementia by age z. This measure is sometimes alternatively referred to as the cumulative incidence. Estimation of the cumulative risk is easily accomplished using the framework above. Mathematically, the cumulative risk r(z) at age z is defined as pr (D*(z) = 1), which can be written as

$$\begin{array}{lll}r(z)& =& \mathrm{pr}(D^{\ast }(z)=1\mid D^{\ast }=1)·\pi \\ & =& \mathrm{pr}(X^{\ast }\le z\mid D^{\ast }=1)·\pi ,\end{array}$$ (3.3)

yielding the natural estimator $r_n(z)={\pi }_n{\sum }_{i=1}^n{a}_{n,i}{𝕀}_{[X_i,\infty )}(z)$ of r(z). As expected, we have that π_n = lim_z→∞ r_n(z), and r_n(·) exhibits usual asymptotic properties under the regularity conditions.

4 Adjustment for stratified sampling

The methodology above rests on the assumption that a cross-sectional sample is obtained via simple random sampling. In many settings however, including the Canadian Study of Health and Aging, the study design incorporates stratification in the sampling scheme. With appropriate knowledge of population characteristics, it is possible to recover correct population estimates from sample quantities via reweighting. We treat separately the case that stratification is performed relative to current age W at recruitment and that in which it is not; we refer to these cases as endogenous and exogenous sampling stratification, respectively. We present invariance results for endogenous stratification and propose two approaches for correcting exogenous stratification in the sampling scheme.

4.1 Invariance under endogenous stratification

The sampling scheme of certain studies incorporates stratification by current age W, with particular age subgroups of the cross-sectional population deliberately overrepresented. The adjustment then needed does not seem straightforward a priori, for current age is the truncation variable in the sampling scheme and cannot simply be conditioned upon. In reality however, this type of stratification does not warrant any adjustment because of a certain invariance property.

To study the impact of stratification by age on lifetime risk estimation, we first investigate its impact on the various quantities required in (2.1). Stratification by age in the sampling scheme does not have any impact on estimation of the distribution of Z* because the product-limit estimator S_n is derived from a likelihood conditional upon observed ages at recruitment W₁, W₂, …, W_n. Denote by A_s the event of being sampled, and let ζ(w) = pr (A_s ∣ W = w) be the sampling probability for an individual of age w at recruitment time. Define G′(w) = pr (W* ≤ w ∣ Z* ≥ W*) and $G_s^{\prime }(w)=\mathrm{pr}(W^{\ast }\le w\mid Z^{\ast }\ge W^{\ast },A_s)$, respectively. It is then easy to show that the distribution function G′ and the sampling distribution function $G_s^{\prime }$ of observable truncation times satisfy the relationship $G_s^{\prime }(\mathit{dw})=\zeta (w)G^{\prime }(\mathit{dw})/\mathit{\int }\zeta (u)G^{\prime }(\mathit{du})$. As a consequence, ignoring stratification by age, G_n converges to

$$G^{\mathrm{naive}}(w)={\mathit{\int }}_{u\le w}\frac{\zeta (u)G(\mathit{du})}{\mathit{\int }\zeta (\upsilon )G(\mathit{d\upsilon })}.$$

Furthermore, failing to account for stratification by age, the empirical prevalence proportion converges to

$$\begin{array}{lll}{P}^{\mathrm{naive}}(t_0)& =& \mathrm{pr}({\mathrm{\Delta }}_0=1\mid Z^{\ast }\ge W^{\ast },A_s)\\ & =& \frac{\mathrm{pr}(A_s\mid Z^{\ast }\ge W^{\ast },{\mathrm{\Delta }}_0=1)}{\mathrm{pr}(A_s\mid Z^{\ast }\ge W^{\ast })}·P(t_0).\end{array}$$ (4.1)

As such, both G and P(t₀) are in general inconsistently estimated if age-stratified sampling is ignored. However, this is not the case for H. Denoting by H^naive the limit (in probability) of H_n when stratification by age is ignored, the following result indicates that, under cross-sectional sampling, estimation of the bivariate distribution function of age at onset and total lifetime in the case population is invariant to stratification by age.

Property 1. Suppose assumptions (A1)-(A5) hold. Then, H^naive = H

This fact is useful in its own right, indicating that no adjustment is necessary to estimate consistently the joint distribution of age at onset and total lifetime in the presence of age-stratified sampling. It is also important because of its implication regarding the estimation of lifetime risk. Precisely, denoting by π^naive the limit (in probability) of π_n in the presence of stratification by age, the following result indicates that, under cross-sectional sampling, estimation of the lifetime risk is invariant to stratification by age.

Property 2. Suppose assumptions (A1)-(A5) hold. Then, π^naive = π

This property indicates that despite the fact that various components of π in (2.1) are estimated inconsistently in the absence of appropriate accounting for age-stratified sampling, their respective biases are such that the lifetime risk itself may be estimated consistently without any adjustment. In fact, it is not difficult to verify that this same phenomenon holds for the remaining lifetime risk and the cumulative risk as well. Practitioners may find these invariance properties to be particularly useful. A proof of these properties based on elementary calculations is provided in the Appendix. These properties can also be seen as a natural consequence of the cross-sectional sampling design. As discussed above, in such designs, the sampling distribution of observed duration variables is a biased version of the population distribution of these same variables. The involved bias function is determined by the truncation distribution. When stratification is implemented and depends only on age at recruitment (the truncation variable), this bias function is then determined by a composite truncation distribution, obtained as the product of the true truncation distribution and the stratification probability. In fact, when stratification is ignored, estimators of the true truncation distribution in fact estimate this composite truncation distribution. Consequently, usual adjustments for truncation based on naive estimators inadvertently adjust for the composite truncation process, thereby eliminating any additional bias resulting from stratification in the sampling scheme, and allowing unbiased estimation of both the marginal lifetime distribution and the joint distribution of age at onset and total lifetime in the case population. The argument may then be completed upon noting that, by thinning processes N₁ and N₂ by the stratification probabilities and repeating the derivations of Section 2 on these thinned processes, a version of equation (2.1) with P^naive(t₀) and G^naive in place of P(t₀) and G, respectively, emerges. Thus, the biased estimation of P(t₀) and G does not constitute a problem for the sake of the estimation of π.

4.2 Exogenous stratification: stratum-wise approach

Suppose that U* is a categorical stratifying covariate other than current age, defined for all individuals, either demented at recruitment or not. Suppose also that the marginal independence assumption stated in Section 3 holds conditionally upon U*, that is, within strata of U*. Total lifetime Z* has distribution function

$$\mathrm{pr}\left(Z^{\ast }\le y\right)=\sum _u\mathrm{pr}\left(Z^{\ast }\le y\mid U^{\ast }=u\right)\mathrm{pr}\left(U^{\ast }=u\right).$$

The subgroup-specific distribution function pr (Z* ≤ y ∣ U* = u) is directly estimable using the appropriate subset of the data; the same holds for pr (W* ≤ w ∣ U* = u) and pr (X* ≤ x, Z* ≤ z ∣ D* = 1, U* = u). The probability pr (U* = u) can sometimes be obtained externally. In many cases however, pr (U* = u ∣ Z* ≥ W*), the proportion of individuals from the cross-sectional population at calendar-time t₀ who are in the subgroup U* = u, is more readily available. In such cases, the fact that

$$\mathrm{pr}\left(U^{\ast }=u\right)=\frac{\mathrm{pr}\left(U^{\ast }=u\mid Z^{\ast }\ge W^{\ast }\right)/\mathrm{pr}\left(Z^{\ast }\ge W^{\ast }\mid U^{\ast }=u\right)}{{\sum }_{u\prime }\mathrm{pr}\left(U^{\ast }=u\prime \mid Z^{\ast }\ge W^{\ast }\right)/\mathrm{pr}\left(Z^{\ast }\ge W^{\ast }\mid U^{\ast }=u\prime \right)},$$

as implied by Bayes’ Theorem, is a particularly useful result given that the probability pr (Z* ≥ W* ∣ U* = u) can itself be estimated using estimators of pr (Z* ≤ z ∣ U* = u) and pr (W* ≤ w ∣ U* = u) along with the required conditional independence assumption. The lifetime risk may then be estimated by substituting these adjusted estimators of the various components required in (2.1).

4.3 Exogenous stratification: random exclusion approach

In practice, the above method can be unstable because of the use of inverse-weighting in determining correct stratum-specific weights and the much smaller sample sizes encountered within strata. An alternative approach to stratification adjustment, based on a random exclusion method, is much easier to implement and holds under the marginal independence assumption of Section 3. In terms of added stability, its use may be most advantageous when stratification causes only a slight distortion in population characteristics and at least one stratum includes relatively few observations. The general idea consists of discarding a number of individuals from the overrepresented stratum to restore sample representativeness. Suppose for simplicity that U* is a binary variable, and write p₁ = pr (U = 1). Denote by n₀ and n₁ the sizes of the strata corresponding, respectively, to U = 0 and U = 1; these are fixed by investigators. Suppose that individuals in stratum U = 1 have been oversampled, so that the observed proportion $p_1^{\prime }=n_1/(n_0+n_1)$ of recruited individuals in that stratum is greater than p₁ by design. The available sample is therefore not representatively drawn from the cross-sectional population. Setting

$${\widehat{n}}_1=\lfloor n_0\left(\frac{p_1}{1-p_1}\right)\rfloor ,$$

the dataset obtained by discarding completely at random n₁ − n̂₁ individuals from stratum U = 1 and preserving all other individuals can be perceived as an approximate simple random sample from the cross-sectional population. This can be justified by the following argument. Denoting by I the event of being included in the final dataset and by E any other generic data event, the sampling distribution pr (E ∣ I) of individuals in the fabricated dataset is

$$\mathrm{pr}\left(E\mid U=0,I\right)\mathrm{pr}\left(U=0\mid I\right)+\mathrm{pr}\left(E\mid U=1,I\right)\mathrm{pr}\left(U=1\mid I\right).$$

Because all individuals in stratum U = 0 are retained, and because excluded cases are chosen at random among individuals in stratum U = 1, we have the equalities pr (E ∣ U = 0, I) = pr (E ∣ U = 0) and pr (E ∣ U = 1, I) = pr (E ∣ U = 1). Additionally, some algebraic manipulations yield that pr (U = 1 ∣ I) = pr (U = 1) + ε_n0, where |ε_n0| < (1 − p₁)/n₀. It follows then that

$$|\mathrm{pr}\left(E\mid I\right)-\mathrm{pr}\left(E\right)|<\frac{2(1-p_1)}{n_0}.$$

In summary, a consistent estimator of the lifetime risk in the presence of exogenous sampling stratification can be obtained by applying the standard estimation procedure, as proposed in Section 3, on data incorporating random exclusion to recalibrate the sample. To minimize any variance inflation resulting from this exclusion process, the procedure can be repeated several times and results averaged out over the various runs to obtain a final estimate.

5 Simulation study

A simulation study was conducted to validate the methodology proposed above and evaluate its small-sample performance. In the remainder, we denote by F₀ the distribution function of Z* given D* = 0. Data were generated according to the following algorithm:

1. Set recruitment count N ← 0.

2. Generate age at recruitment w ~ G and lifetime disease status d ~ Bernoulli(π).

3. If d = 1, generate pair (x, z) ~ H. Else, generate lifetime z ~ F₀.

4. If w ≤ z, individual is recruited; set N ← N + 1.

5. If individual is recruited, generate residual censoring time c ~ Q. Consider the quadruple (x, υ = min(z, w + c), δ = 𝕀_(0,w+c)(z), w) as the observed data for prevalent cases (i.e., those for which d = 1 and x ≤ w), and the triple (υ = min(z, w + c), δ = 𝕀_(0,w+c)(z), w) for individuals healthy at recruitment (i.e., those for which d = 0, or d = 1 and x > w).

6. Repeat steps 2–5 until N equals the desired cohort size.

We considered four simulation settings, representing the different possible combinations of light and heavy truncation and censoring. Light and heavy truncation were characterized by truncation probabilities of about 10% and 50%, respectively. Similarly, light and heavy censoring were characterized by censoring probabilities of approximately 10% and 50%, respectively. All settings make the following distributional assumptions: D* is a Bernoulli variate with success probability π; Z* given D* = 0 is a Beta variate with parameters (α₀, β₀) scaled by z_max; Z* given D* = 1 is a Beta variate with parameters (α₁, β₁) scaled by z_max; W* is a Beta variate with parameters (α₂, β₂) scaled by z_max; X* given (Z* = z, D* = 1) is a uniform variate over (0, z); and C is an exponential variate with mean μ.

All simulation studies presented were conducted with true lifetime risk π = 0.3 and with (α₀, β₀) = (20, 5) and (α₁, β₁) = (14, 6), corresponding to unimodal distributions with mean 80 and 70 for the total lifetime in non-cases and cases, respectively. Light truncation was obtained by choosing the age at recruitment parameters to be (α₂, β₂) = (1, 1.7). At this level of truncation, light and heavy censoring was obtained by setting μ at values 0.0025 and 0.017, respectively. Heavy truncation was obtained by choosing (α₂, β₂) = (2.8, 1). At this level of truncation, light and heavy censoring was obtained by setting μ at values 0.0055 and 0.045, respectively. For each setting, more than 1,000 datasets were generated according to the algorithm described above. Median values of the number of cases observed, as well as empirical estimates of the relative bias, normalized standard error and root mean squared error of the lifetime risk estimator are provided in the tables below. Table 2 presents results for settings incorporating light truncation, and Table 3 reports findings for simulation studies with heavy truncation. The behavior of the remaining lifetime risk estimator was also evaluated using simulation studies based on the setup described above. In Part A of the Supplementary Material, relevant details about evaluating the remaining lifetime risk estimator are provided along with summary measures from the additional simulation studies, reported in Tables 3–10.

Table 2.

Median number of observed cases across simulated samples, and empirical relative bias, standardized standard error and root mean squared error of the lifetime risk estimator, under light truncation and both light (10%) and heavy (50%) censoring, using 1,000 simulated datasets.

% censoring:		~ 10%			~ 50%
# sampled	# cases	rel.bias	se(π̂)/π	$\sqrt{\mathrm{mse}}$	rel.bias	se(π̂)/π	$\sqrt{\mathrm{mse}}$
1,000	124	0.46%	17.0%	0.0511	-0.47%	22.9%	0.0686
2,000	246	-0.73%	15.4%	0.0462	0.52%	15.6%	0.0469
3,000	371	0.23%	15.2%	0.0456	-0.09%	11.1%	0.0332
4,000	494	-0.70%	13.7%	0.0413	-0.07%	10.2%	0.0307
5,000	615	-0.21%	8.8%	0.0263	-0.24%	9.9%	0.0297

Table 3.

Median number of observed cases across simulated samples, and empirical relative bias, standardized standard error and root mean squared error of the lifetime risk estimator, under heavy truncation and both light (10%) and heavy (50%) censoring, using 1,000 simulated datasets.

% censoring:		~ 10%			~ 50%
# sampled	# cases	rel.bias	se(π̂)/π	$\sqrt{\mathrm{mse}}$	rel.bias	se(π̂)/π	$\sqrt{\mathrm{mse}}$
1,000	171	0.28%	12.0%	0.0360	-0.27%	14.4%	0.0433
2,000	343	-0.01%	7.9%	0.0237	0.20%	8.8%	0.0264
3,000	515	-0.01%	6.4%	0.0192	0.38%	7.1%	0.0213
4,000	685	-0.29%	6.2%	0.0186	-0.03%	6.5%	0.0196
5,000	856	0.18%	5.0%	0.0150	0.15%	5.2%	0.0157

From the above tables, several patterns emerge. As sample size increases, both the standard error and mean squared error of π_n decrease monotonically. Regardless of sample size, π_n is essentially unbiased, with estimated mean value less than one percent away from the truth π = 0.3. From these simulation studies, both these observations seem to hold irrespective of the truncation and censoring levels. Increasing the level of censoring results in increasing variability of π_n, as evidenced by larger standard errors and mean squared errors. Bias does not exhibit any particular trend relative to the level of censoring. Furthermore, in the setup considered, settings including heavier truncation result in lesser variability, even after taking into account the larger proportion of cases sampled in those settings. Simulation results found in Part A of the Supplementary Material generally exhibit similar trends in the behavior of the remaining lifetime risk estimator, but also highlight the increasing variability and bias observed at older ages. Overall, these simulations lend much credence to both the asymptotic validity and good small-sample behavior of the proposed methods.

A sensitivity analysis was conducted to evaluate the robustness of π_n to deviations from (A3); technical and numerical details can be found in Part B of the Supplementary Material. For this purpose, we constructed a generalization of the simulation setting described above incorporating parameters controlling the degree of deviation from (A3). These deviations include (a) dependence of the lifetime risk on date of birth, and (b) dependence of the lifetime distribution on date of birth, as characterized by a shifted mean lifetime. Deviations as large as a change in the lifetime risk from 0.3 to 0.4 and a relative increase of 20% in mean lifetime over the range of observed dates of birth were considered. Our results indicate that our estimator of the lifetime risk enjoys significant robustness to deviations from (A3), with an asymptotic bias of no greater than 6%, even in the most extreme scenarios considered.

6 Results from the Canadian Study of Health and Aging

In 1989, researchers from the University of Ottawa, in conjunction with Health Canada, designed the Canadian Study of Health and Aging, a nationwide multi-center longitudinal study aiming to describe the epidemiology of dementia, including Alzheimer’s disease, in various subpopulations of Canada. The study design included three distinct stages. The first stage of the study took place in 1991 and served as primary recruitment phase. A cross-sectional sample of 10,263 individuals aged 65 or higher was drawn from more than 36 communities, both rural and urban, across Canada, with specific subsets drawn from both the community and institutions for the elderly. All ten provinces of Canada were represented in the sampling procedure. These individuals were assessed for various types of dementia by the staff of the 18 participating field centers and followed up according to certain guidelines. The second and third stages of the study took place five and ten years subsequent to the initial stage, and consisted primarily of follow-up on the individuals recruited as part of the first stage. Further details about the design of this study are provided in McDowell et al. (1994).

By utilizing the methods developed in this paper, we provide a first estimate of the lifetime risk π of dementia in the Canadian elderly population using data from the Canadian Study of Health and Aging. The available data consist of a total of 9,016 individuals, 808 of whom are prevalent cases. Though the follow-up on more than 47% of all participants was censored, less than 10% of prevalent cases were lost to follow-up. Because more than 90% of all participants were born during a 23-year interval, the absence of birth cohort effects is not an implausible assumption in this context. Institutionalized individuals were deliberately oversampled, representing 11.4% of our study sample versus 7.0% of the elderly Canadian population (McDowell et al., 2001). The random exclusion approach of Subsection 4.3 was employed with 20 repetitions to adjust for this. Figure 3 and 4 are plots of the estimated remaining lifetime risk of dementia at ages 65 to 95 and the estimated cumulative risk of dementia at ages 65 to 100, respectively, both with approximate pointwise 95% confidence intervals. All confidence intervals were obtained using the bootstrap with 500 replications. Since only individuals of age 65 and above were sampled, all estimands are interpreted as conditional upon survival to 65 years of age. Plots of the data availability measures of Subsection 3.2 based on K_z,0 (number of participants under observation) and K_z,2 (total weighted time under observation), provided in Figure 5, suggest that, at age 75, only slightly more than half of the available information in the sample (in both number of participants and weighted time under observation) is still available. By age 85, less than 10% of the information in the full dataset remains.

Figure 3.

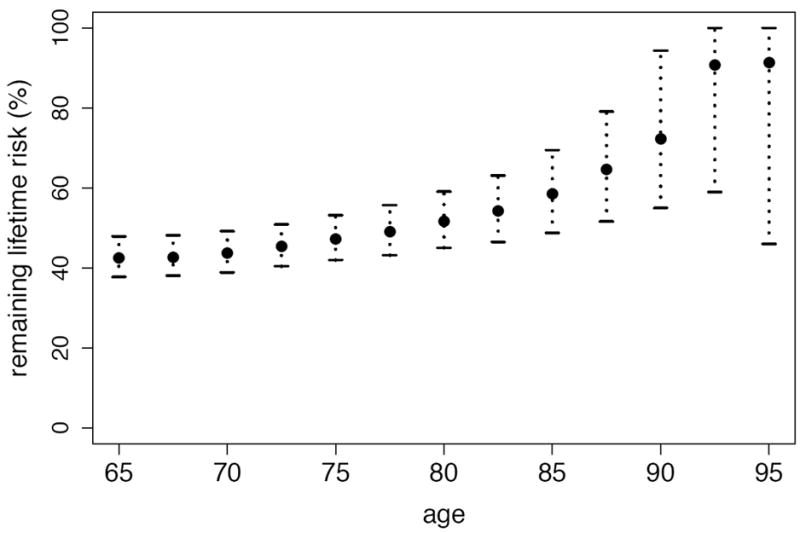
Estimated remaining lifetime risk of dementia in the Canadian elderly population.

Figure 4.

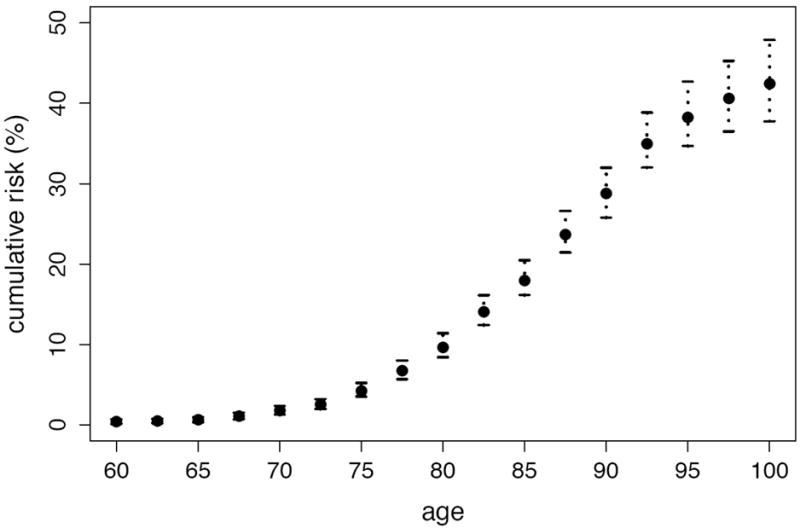
Estimated cumulative risk of dementia in the Canadian elderly population.

Figure 5.

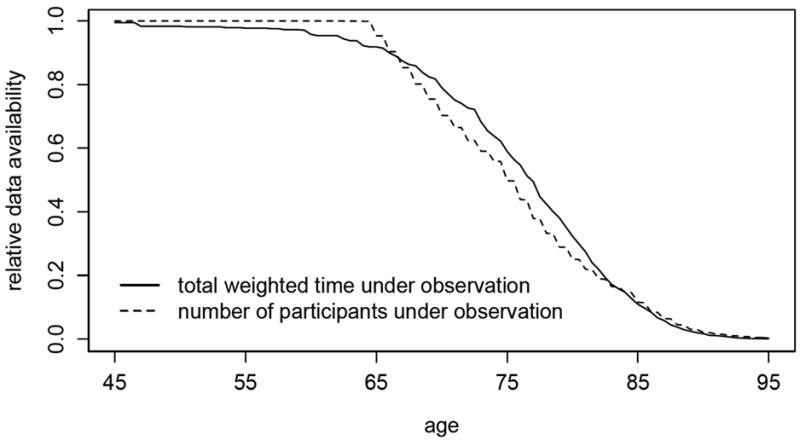
Relative measures of data availability as a function of age in the Canadian Study of Health and Aging sample, including total weighted time under observation and number of participants under observation. Weighting was performed according to a nonparametric estimate of the age-at-onset distribution.

Our findings suggest that more than two out of every five Canadians reaching the age of 65 develop dementia before death: precisely, the estimated lifetime risk of dementia in the Canadian elderly population is 42.6% (95% confidence interval: 38.1–48.4). We also find that the remaining lifetime risk exhibits a steady positive trend relative to age, with, for example, a risk of 42.4% (95% confidence interval: 37.7–47.9) at age 65, of 47.3% (95% confidence interval: 42.0–53.2) at age 75, and of 58.5% (95% confidence interval: 48.8–69.5) at age 85. These first estimates of lifetime risk and remaining lifetime risk in the Canadian elderly population may seem high. At least two reasons may explain this. First, as discussed by Erkinjuntti et al. (1997), prevalence estimates can vary dramatically depending upon the diagnostic criteria used, and DSM-III-R criteria have been found to yield prevalence estimates greater than most other classification systems, at least in the setting of the Canadian Study of Health and Aging. In view of (2.1), this fact directly translates to lifetime risk estimates as well. Second, the study setting likely allowed the identification, at recruitment, of many recently-demented individuals who may otherwise have died before ever being given a diagnosis of dementia. As such, the obtained estimates correspond to the number of elderly Canadians developing first symptoms of dementia before death, rather than ever formally receiving a clinical diagnosis. Our estimates of cumulative risk indicate that nearly 80% of all cases of dementia occur between ages 75 and 95. By age 80, 9.6% of the Canadian elderly population are estimated to develop dementia (95% confidence interval: 8.4–11.4), while by age 90, this same proportion is 28.7% (95% confidence interval: 25.8–32.0).

7 Concluding remarks

1. Inference on the lifetime risk in the setting of age-stratified sampling was studied in this paper. Age-stratified sampling usually results in the overrepresentation of certain age categories and underrepresentation of others. However, in many settings, including the Canadian Study of Health and Again, sampling may be restricted to an age range, leading to the complete absence of certain age groups in the sample. For simplicity, suppose that only individuals of age not smaller than m > 0 are recruited at time t₀. Then, the distributions of Z*, of (X*, Z*) given D* = 1, and of W*, each required in (2.1), are unidentifiable because no lifetime or age at recruitment below m may be observed. Instead, the conditional distributions of the first two of these variables given Z* ≥ m and of W* given W* ≥ m are identified by the data. From these, a conditional version of the lifetime risk, namely π_(m) = pr (D* = 1 ∣ Z* ≥ m), can be estimated using the fact that

$$P_{(m)}\left(t_0\right)={\pi }_{\left(m\right)}·\frac{\mathrm{pr}\left(X^{\ast }\le W^{\ast }\le Z^{\ast }\mid W^{\ast }\ge m,Z^{\ast }\ge m,D^{\ast }=1\right)}{\mathrm{pr}\left(W^{\ast }\le Z^{\ast }\mid W^{\ast }\ge m,Z^{\ast }\ge m\right)},$$ (7.1)

where P_(m)(t₀) is the prevalence proportion at t₀ among individuals of age at least m. Since estimators of the distributions required in the above are identical to those provided in Section 3, π_(m) can be directly estimated using (3.1).

It is possible to recover the unconditional lifetime risk π from data obtained via age-restricted sampling if certain population quantities are available externally. We note that

$$\pi ={\pi }_{(m)}·\frac{\mathrm{pr}\left(Z^{\ast }\ge m\right)}{\mathrm{pr}\left(Z^{\ast }\ge m\mid D^{\ast }=1\right)},$$

with π_(m) estimable from the data but pr (Z* ≥ m) and pr (Z* ≥ m ∣ D* = 1) required from alternate sources. The former is generally easily obtainable. It may be more challenging to obtain an estimate of the latter. Nonetheless, if most cases of disease occur beyond age m, then the approximation pr (Z* ≥ m ∣ D* = 1) ≈ 1 may be reasonable.

2. The study design described in this paper consists of a cross-sectional survey augmented with prospective follow-up for survival. Follow-up information allows the identification of the marginal distribution of Z* and the conditional distribution of (X*, Z*) given D* = 1: this is crucial for identifying π. It appears that, without additional knowledge regarding the birth process, these distributions cannot be identified from cross-sectional survey data alone. However, if such additional information is available, then identifiability can be established. For example, if the birth process is known to be stationary, then Keiding et al. (2002) describe estimation of S using cross-sectional survey data without follow-up, although the rate of estimation is then n^−1/3 rather than the regular n^−1/2 rate. Although estimation of H should be possible using such data, it has yet to be explicitly addressed in the literature.

8 Appendix

The asymptotic properties of π_n, π_n(·) and r_n(·) can be derived under the following regularity conditions:

1. the lifetime risk π lies in (0, 1);

2. H, S and Q are continuous, and τ = sup{t : S(t) > 0} < ∞;

3. G is absolutely continuous with strictly positive density;

4. there exists some δ > 0 such that pr (Z* > X* + δ ∣ D* = 1) = 1.

Condition 1 eliminates trivial situations. Condition 2 is a standard assumption to simplify derivations. Condition 3 is equivalent to assuming the population birth rate is never zero; it is almost certainly true in practice. Condition 4 implies that an individual cannot die within δ units of time of disease onset, with δ possibly very small. This should hold in many settings, particularly in the case of dementia. Setting

$$\mathrm{\Gamma }(u,\upsilon )={\mathit{\int }}_{u\le w\le \upsilon }Q(\upsilon -w)G(\mathit{dw}),$$

conditions 3 and 4 ensure that Γ is uniformly bounded away from zero on the support of H and thus negates the need for unnecessarily technical arguments to handle the singularities of Γ(u, υ) on u = υ. We conjecture that condition 4 may be weakened to requiring that some integral be finite, in the same spirit as the integral condition in Theorem 1 of Carone et al. (2012).

A bivariate integration by parts formula, shared by James A. Fill in a personal communication, is useful for studying these estimators. Let R be the triangle in R² delimited by points (0, 0), (0, τ) and (τ, τ), including its boundary minus its hypotenuse. Suppose ϕ : R → R⁺ is of bounded variation, then for each (x, y) ∈ R we have

$$\varphi (x,y)=\varphi (0,\tau )+{\mathit{\int }}_{(0,x]}\varphi (\mathit{du},\tau )-{\mathit{\int }}_{(y,\tau ]}\varphi (0,\mathit{d\upsilon })-\mathit{\int }{\mathit{\int }}_{(0,x]\times (y,\tau ]}\varphi (\mathit{du},\mathit{d\upsilon }).$$

Suppose Ψ is a bivariate distribution function with support contained in R. Then, by Fubini’s Theorem, we have

$$\begin{array}{lll}\mathit{\int }{\mathit{\int }}_R\varphi (u,\upsilon )\mathrm{\Psi }(\mathit{du},\mathit{d\upsilon })& =& \varphi (0,\tau )+{\mathit{\int }}_{(0,\tau ]}[1-\mathrm{\Psi }(u,\tau )]\varphi (\mathit{du},\tau )\\ & & -{\mathit{\int }}_{(0,\tau ]}\mathrm{\Psi }(\upsilon -,\upsilon -)\varphi (0,\mathit{d\upsilon })\\ & & -\mathit{\int }{\mathit{\int }}_R[\mathrm{\Psi }(\upsilon -,\upsilon -)-\mathrm{\Psi }(u-,\upsilon -)]\varphi (\mathit{du},\mathit{d\upsilon }).\end{array}$$

Uniform consistency of the proposed estimators at n^1/2-rate can be proved using the univariate integration-by-parts formula, its bivariate version derived above, the Continuous Mapping Theorem and the uniform consistency of G_n (Wang, 1991; Woodroofe, 1985; Carone et al., 2012), $H_n^{\prime }$ and Q_n (Wang, 1987). Weak convergence to a Gaussian limit can then be established using the functional delta method and the techniques in Chapter 12 of Kosorok (2008).

Proof of Property 1

It suffices to show that

$$H_s^{\prime }(\mathit{dx},\mathit{d\upsilon })\propto {\mathit{\int }}_{x\le w\le z}Q(\upsilon -w)G^{\mathrm{naive}}(\mathit{dw})·H(\mathit{dx},\mathit{d\upsilon })$$

as functions of x and υ, where $H_s^{\prime }$ denotes the sampling distribution of (X, V) given Δ₀ = 1 and Δ₁ = 1. Denote by J(dx, dz, dw) and J_s(dx, dz, dw) the differential quantities pr(X* ∈ [x, x + dx), Z* ∈ [z, z + dz), W* ∈ [w, w + dw) ∣ X* ≤ W* ≤ Z*, Δ₁ = 1, D* = 1) and pr(X* ∈ [x, x + dx), Z* ∈ [z, z + dz), W* ∈ [w, w + dw) ∣ X* ≤ W* ≤ Z*, Δ₁ = 1, D* = 1, A_s), respectively. Also, denote by s(x, z, w) the conditional sampling probability pr (A_s ∣ X* = x, Z* = z, W* = w, X* ≤ W* ≤ Z*, Δ₁ = 1, D* = 1).

We may then show that

$$\begin{array}{lll}{H}_s^{\prime }(\mathit{dx},\mathit{d\upsilon })& =& \mathrm{pr}(X\in [x,x+\mathit{dx}),V\in [\upsilon ,\upsilon +\mathit{d\upsilon })\mid {\mathrm{\Delta }}_0=1,{\mathrm{\Delta }}_1=1,A_s)\\ & =& {\mathit{\int }}_{x\le w\le \upsilon }{J}_s(\mathit{dx},\mathit{d\upsilon },\mathit{dw})\propto {\mathit{\int }}_{x\le w\le \upsilon )}s(x,\upsilon ,w)J(\mathit{dx},\mathit{d\upsilon },\mathit{dw}).\end{array}$$

The sampling scheme implies that s(x, z, w) = pr (A_s ∣ W* = w, W* ≤ Z*) = ζ(w). Then, in view of the fact that

$$\begin{array}{lll}J(\mathit{dx},\mathit{d\upsilon },\mathit{dw})& \propto & \mathrm{pr}({\mathrm{\Delta }}_1=1\mid X^{\ast }=x,Z^{\ast }=\upsilon ,W^{\ast }=w,X^{\ast }\le W^{\ast }\le Z^{\ast },D^{\ast }=1)\times \\ & & \mathrm{pr}(X^{\ast }=[x,x+\mathit{dx}),Z^{\ast }=[\upsilon ,\upsilon +\mathit{d\upsilon }),W^{\ast }\in [w,w+\mathit{dw})\mid D^{\ast }=1)\\ & =& Q(\upsilon -w)G(\mathit{dw})H(\mathit{dx},\mathit{d\upsilon }),\end{array}$$

the proof is complete using that G^naive(dw) ∝ ζ(w)G(dw).

Proof of Property 2

Denote by G″ the distribution function of W* given X* ≤ W* ≤ Z* and D* = 1. Then, we have that

$$\begin{array}{c}\mathrm{pr}(A_s\mid Z^{\ast }\ge W^{\ast },{\mathrm{\Delta }}_0=1)=\mathrm{pr}(A_s\mid X^{\ast }\le W^{\ast }\le Z^{\ast },D^{\ast }=1)\\ \begin{array}{lll}& =& \mathit{\int }\mathrm{pr}(A_s\mid X^{\ast }\le W^{\ast }\le Z^{\ast },D^{\ast }=1,W^{\ast }=w)G^{″}(\mathit{dw})\\ & =& \frac{\mathit{\int }\zeta (w)\mathrm{pr}(X^{\ast }\le w\le Z^{\ast }\mid D^{\ast }=1)G(\mathit{dw})}{\mathrm{pr}(X^{\ast }\le W^{\ast }\le Z^{\ast }\mid D^{\ast }=1)}\\ & =& \frac{\mathit{\int }\mathrm{pr}(X^{\ast }\le w\le Z^{\ast }\mid D^{\ast }=1)G^{\mathrm{naive}}(\mathit{dw})}{\mathrm{pr}(X^{\ast }\le W^{\ast }\le Z^{\ast }\mid D^{\ast }=1)}\mathit{\int }\zeta (w)G(\mathit{dw})\end{array}\end{array}$$

and similarly, that

$$\mathrm{pr}(A_s\mid Z^{\ast }\ge W^{\ast })=\frac{\mathit{\int }\mathrm{pr}(Z^{\ast }\ge w\mid D^{\ast }=1)G^{\mathrm{naive}}(\mathit{dw})}{\mathrm{pr}(Z^{\ast }\ge W^{\ast })}\mathit{\int }\zeta (w)G(\mathit{dw})$$

from which it follows, using (4.1), that

$$\pi =P^{\mathrm{naive}}(t_0)·\frac{\mathit{\int }\mathrm{pr}(Z^{\ast }\ge w)G^{\mathrm{naive}}(\mathit{dw})}{\mathit{\int }\mathrm{pr}(X^{\ast }\le w\le Z^{\ast }\mid D^{\ast }=1)G^{\mathrm{naive}}(\mathit{dw})}.$$

By Property 1, the distribution of (X*, Z*) given D* = 1 is estimated consistently by ignoring age-stratified sampling. As indicated above, the same holds for the distribution of Z*. The result then follows.