Genome-wide patterns and properties of de novo mutations in humans

Abstract

Mutations create variation in the population, fuel evolution, and cause genetic diseases. Current knowledge about de novo mutations is incomplete and mostly indirect ^1–10. Here, we analyze 11,020 de novo mutations from whole-genomes of 250 families. We show that de novo mutations in offspring of older fathers are not only more numerous ^11–13 but also occur more frequently in early-replicating, genic regions. Functional regions exhibit higher mutation rates due to CpG dinucleotides and reveal signatures of transcription-coupled repair, while mutation clusters with a unique signature point to a novel mutational mechanism. Mutation and recombination rates independently associate with nucleotide diversity, and regional variation in human-chimpanzee divergence is only partly explained by mutation rate heterogeneity. Finally, we provide a genome-wide mutation rate map for medical and population genetics applications. Our results reveal novel insights and refine long-standing hypotheses about human mutagenesis.

Understanding rates and patterns of human mutations is important for analyzing relationships among species and populations ^1,2 , for detecting natural selection ^3,4 and for mapping genes underlying complex traits ⁵ . The properties of mutations have traditionally been studied using model organisms ⁶ , fully penetrant dominant Mendelian diseases ^7,8 , and comparative genomics and population genetic approaches ^9,10 . However, these approaches are limited in scope, indirect, and influenced by other factors such as natural selection. Using high-throughput sequencing technologies, recent pedigree sequencing studies have provided whole-genome observations of germline de novo mutations and revealed that mutation rate increases with paternal age ^11–13 , varies along the genome in weak correlation with various epigenetic properties and is higher in conserved genomic regions including exons ¹¹ .

We identified de novo mutations in 250 Dutch parent-offspring families (231 trios, 11 families with monozygotic twins, 8 families with dizygotic twins) by whole-genome sequencing of blood-derived DNA to 13-fold coverage. We considered dizygotic twins as distinct and included one twin from each monozygotic twin pair, resulting in a total 258 offspring. We identified 11,020 de novo mutations, with an estimated sensitivity of 68.9% and specificity of 94.6% ¹³ . By comparing 350 validated mutations in monozygotic twins, we estimate that ~97% of the mutations in our data are germline and ~3% are somatic. To account for mutation calling biases inherent to sequencing data, we simulated de novo mutations taking into account the sequence coverage fluctuations (Methods) and used this simulated set as a “null” baseline against which we compared observed de novo mutations to characterize their patterns and properties. We also corrected for variation in the sequencing coverage of different family trios.

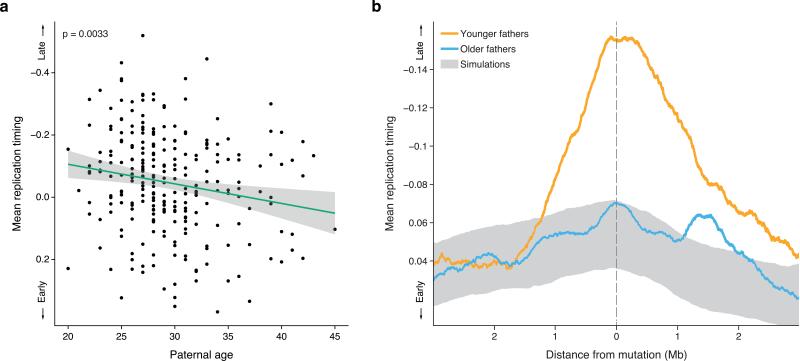
Paternal age explains about 95% of the variation in global mutation rate in the human population ¹² . Specifically, there is an increase of one to two mutations per year of paternal age ^11–13 , which is thought to stem from continuous cell divisions in the paternal germ line, beginning in the embryonic development of primordial germ cells and continuing in spermatogenesis throughout a man's life. A key question is whether changes in the global mutation rate are accompanied by a shift in the mechanisms of spontaneous mutagenesis. If so, this might be reflected by the genomic distribution of de novo mutations. Because previous studies suggested that the epigenetic landscape varies with age ¹⁴ , we investigated whether paternal age was associated with the location of de novo mutations with respect to various epigenetic variables (Methods). Using a linear regression model, we found that the replication timing of de novo mutations was significantly associated with paternal age (p = 0.0022, Fig. 1a), while chromatin accessibility, chromatin modifications and recombination rate were not (p > 0.098, Supplementary Fig. 1). Mutations in the offspring of younger fathers (< 28 years old) were strongly enriched in late-replicating genomic regions (p = 4.9 × 10⁻⁴; Fig. 1b), while there was no significant replication timing bias for mutations in the offspring of older fathers (≥28 years old; p = 0.68; Fig. 1b). The age groups were chosen to maximize the difference in replication timing between the mutations in offspring of younger and older fathers (p = 5.7 × 10⁻⁴, Supplementary Fig. 2). The age-dependent association between the distribution of mutations and DNA replication timing was not specific to the replication timing dataset nor the cell type in which it was measured (Supplementary Fig. 3, Supplementary Table 1).

Fig. 1. Mutations in offspring of younger fathers are biased towards later replicating regions.

a. Mean replication timing of de novo mutations in each of the 258 offspring as a function of their father's age. The green line shows the least-square regression line (p = 0.0033) and the grey area the 95% confidence interval. The downward slope of the regression line indicates a shift of mutations towards earlier replicating regions with advancing paternal age.

b. The mean replication timing profile around de novo mutations, stratified by paternal age (orange: under the age of 28, N = 3,697, blue: aged 28 or older, N = 7,323). The grey area shows the null expectation based on simulations (mean ±1 standard deviation). The age of the split between younger and older fathers was chosen to maximize the difference between the groups (p = 5.7 × 10^–4, 23 tests). Mutations in younger fathers tend to be located in large (~2Mb) regions of late-replicating DNA. In contrast, the replication timing distribution of mutations in older fathers is similar to that of simulated mutations. Together, this shows that de novo mutations in offspring of younger fathers are biased towards late-replicating regions, while those in offspring of older fathers are not.

To confirm that our results are due to paternal rather than maternal age (highly correlated with each other within families; r = 0.81), we restricted our analysis to mutations with unambiguous paternal or maternal origins (Methods). Consistent with the results above, paternal age was significantly associated with replication timing (N = 1,991, p = 0.032) but maternal age was not (N = 630, p = 0.26). The difference between paternal and maternal age was significant (p = 0.0019), controlling for the different numbers of mutations in the paternal and maternal lines (Supplementary Fig. 4).

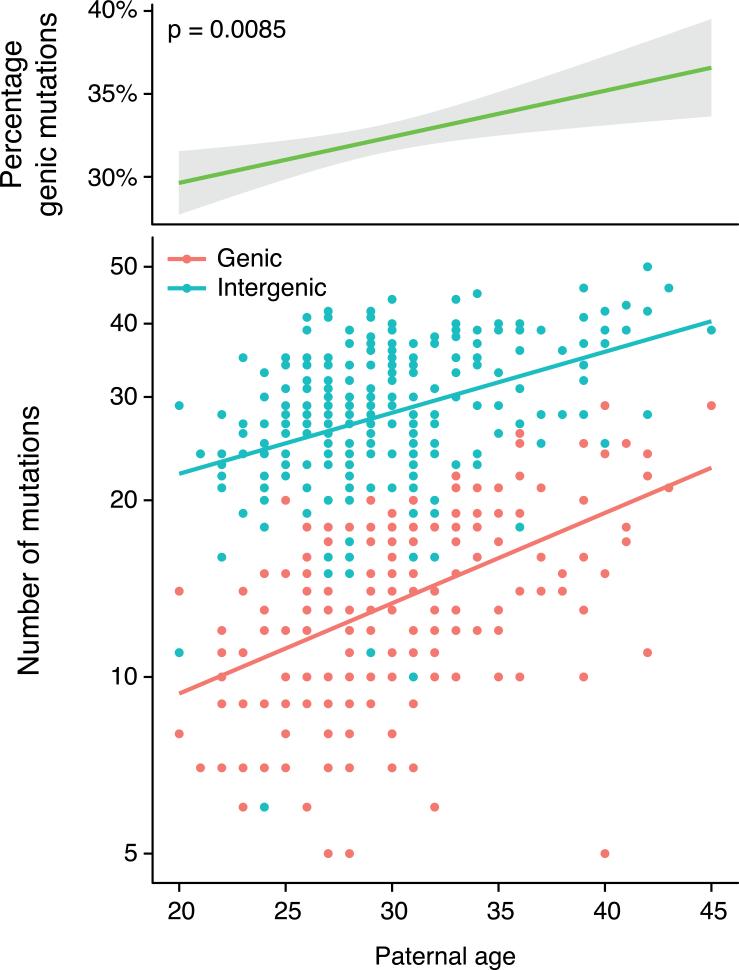
Replication timing itself correlates with chromatin structure and gene activity: early-replicating regions of the genome have a higher gene density and elevated gene expression levels compared to late-replicating genomic regions ¹⁵ . Therefore, the paternal age effects described above are likely to have functional consequences. Indeed, we found that the proportion of de novo mutations in genic regions increased by 0.26% with each additional year of paternal age (p = 0.0085; Fig. 2). On average, offspring born to 40 year-old fathers harbored twice as many genic mutations than offspring of 20 year-old fathers (19.06 vs 9.63 mutations), but only 55% more intergenic mutations (35.24 vs 22.68). An important implication of this result is that mutations in older fathers are not only more numerous, they are also individually more likely to be functional.

Fig. 2. Offspring of older fathers harbor a higher percentage of de novo mutations in genes.

Top panel: the percentage of de novo mutations within genic regions as a function of paternal age at conception (p = 0.0085, slope = 0.26% per year of paternal age).

Bottom panel: the number of genic (red) and intergenic (blue) de novo mutations in offspring (on a logarithmic scale) as a function of paternal age. The red line shows the least-square regression for genic mutations (p < 2 × 10⁻¹⁶), the blue line for intergenic mutations (p = 3.7 × 10⁻¹⁴). The steeper slope of the regression line for genic mutations indicates a faster relative increase in genic than intergenic mutations with paternal age.

Together, these observations suggest that the increase in the number of de novo mutations with paternal age is accompanied by a change in their mechanism of formation related to DNA replication timing, and consequently, their chromosomal distribution and functional impact. While the source of these differences is unclear, they could reflect variations in replication timing or mutagenesis between the symmetrical mitoses that occur during the generation of paternal germ cells, and the asymmetrical mitoses of the spermatogonia during spermatogenesis.

Irrespective of paternal age, mutation rates are higher in functional genomic regions ¹¹ . Indeed, 1.22% of de novo mutations were exonic, which represents a 28.7% enrichment compared to our simulated null baseline (p = 0.008). Similarly, mutation rates in regulatory regions marked by DNase I hypersensitive sites (DHS) were elevated (p = 0.005). The elevated mutation rate for both exons and DHS appeared to be driven by CpG dinucleotides, since after excluding CpGs we observed no significant difference from the null expectation. Methylated CpGs represent highly mutable sequences in humans. The increased mutation rates at CpG sites are thought to have evolved recently (around the time of mammalian radiation) ¹⁶ . Thus, while sequences of neutrally evolving regions of the genome have had sufficient time to equilibrate with respect to dinucleotide contexts, purifying selection has maintained hypermutable CpGs in functional regions ^17,18 .

Unlike observations in cancer somatic mutation ^19,20 and in comparative genomics studies⁹, we did not observe a reduction in mutation rates in transcribed and DHS regions after correcting for sequence context. However, we note that our study was only adequately powered to find a depletion of at least 17.4% in these regions (90% power, Supplementary Fig. 5).

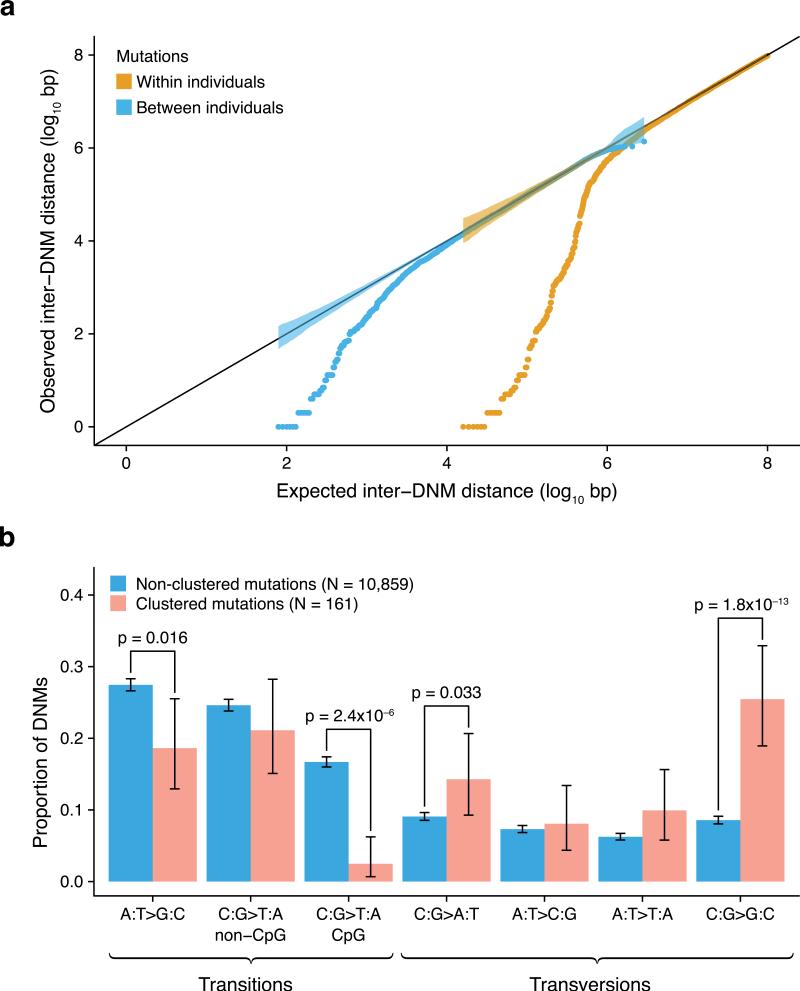
The distribution of de novo mutations along the genome was non-random, both within and across individuals (Fig. 3a) beyond correlations with epigenetic variables and functional elements. At the extreme, we observed clusters of nearby mutations in an individual. This clustering was particularly strong for distances of up to 20kb (p < 1 × 10⁻⁶), at which there were a total of 78 clusters of 2-3 mutations. These observations are consistent with, and expand on, previous studies based on more limited data ^11,21 . We did not find a significant difference between the 161 clustered mutations and the 10,859 non-clustered mutations with respect to recombination rates (p = 0.52) or replication timing (p = 0.059). Interestingly, mutations within clusters exhibit a unique spectrum (p = 9.7 × 10⁻¹⁶), with reduced transitions and strongly elevated C→G nucleotide changes (Fig. 3b), suggesting a specific underlying mechanism. Contexts of these clustered mutations are distinct from the previously observed same-strand TCW→TTW or TCW→TGW mutations (where W corresponds to either A or T) reminiscent of the activity of the APOBEC cytosine deaminases that leads to clustered mutations in cancer cells ^22,23 . Although not caused by APOBEC activity, C→G mutations may result from deaminated cytosines in single-stranded DNA that would be converted to apurinic sites by base-excision repair DNA glycosylases and subsequently subjected to error-prone translesion DNA synthesis ²⁴ .

Fig. 3. Mutation clusters exhibit a unique mutational spectrum.

a. The distances between adjacent de novo mutations (observed) compared to a uniform distribution of mutations across the genome (expected). Closely spaced mutations are enriched both across individuals (brown) and within individuals (blue). The strength of this effect is strongest within individuals, where 78 mutation clusters of up to 20kb in size are observed. In fact, 1.5% of all de novo mutations in our study are in such clusters. Shaded areas represent the 95% confidence intervals.

b. Comparison of mutation spectra between clustered (pink) and non-clustered (blue) de novo mutations (error bars indicate 95% CI). We defined mutation clusters as regions with two or more mutations within 20kb in the same individual. Mutations within clusters show a significantly reduced number of transitions (p = 1.2 × 10⁻¹² for all transitions, p = 4.1 × 10⁻⁶ when excluding C>T transitions at CpG sites) and a strongly elevated number of C→G transversions (p = 1.8 × 10⁻¹³), indicating a novel mutational mechanism.

Comparative genomics studies have predicted that mutation rate is variable at the megabase scale ^9,25 . However, the extent to which the mutation rates and patterns predicted from comparative genomic studies reflect the true underlying properties of germline mutations is unknown. Here, we sought to separate intrinsic properties of mutational processes from other population processes, such as background selection, hitchhiking, and biased gene conversion.

Previous studies have shown that nucleotide diversity within populations (π) is correlated with local recombination rate but it is unclear whether this is due to a mutagenic effect of recombination ²⁶ or to background selection and hitchhiking mechanisms ^27,28 . In our study, local recombination rates ²⁹ are significantly associated with de novo mutation rates (p = 0.0015), when controlling for CpG sites and GC content. Despite this association, we found that rates of both mutation (p < 2 × 10⁻¹⁶) and recombination (p < 2 × 10⁻¹⁶) independently contribute to nucleotide diversity. Thus, recombination appears to influence nucleotide diversity above and beyond any mutagenic effect.

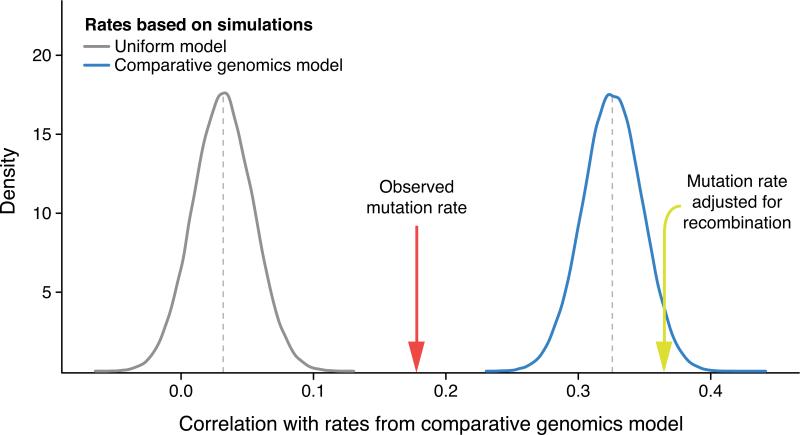
Next, we estimated the extent to which human-chimpanzee sequence divergence is influenced by mutation rates and recombination rates (Fig. 4). The correlation between substitution rates from a human-chimpanzee comparative genomics (HCCG) model ³⁰ and observed de novo mutations was significant (r = 0.18, p = 1.3 × 10⁻¹⁵). When compared to mutation rates based on sampling the HCCG itself for the same number of mutations (mean r = 0.33), we found that de novo mutation rates explained about a third of the human-chimpanzee sequence divergence along the genome (Methods). However, observed mutation rates adjusted for local recombination rates ³¹ are more strongly correlated with the HCCG model (r = 0.37) than observed mutation rates alone (Fig. 4). This illustrates that the comparative genomic model captures both variation in mutation rate and other, orthogonal evolutionary forces associated with recombination rate, as has been suggested by others ^27,32 .

Fig. 4. Influence of mutation and recombination rates on human-chimpanzee divergence.

The correlation to substitution rates computed from a human-chimpanzee comparative genomics (HCCG) model is plotted for mutation rates inferred from a uniform mutation rate model (grey distribution) and for mutation rates inferred from the HCCG model itself (blue distribution), both based on 100,000 simulations of N = 11,020 mutations and binned in 1Mb windows. By sampling the same number of mutations, comparisons between rate estimates are meaningful. The effect of sampling is illustrated by the mean correlation of the HCCG with itself at only 0.33, which would asymptotically reach unity with infinite sampling. The correlation is also given for observed de novo mutation rates (red arrow, N = 11,020) and observed de novo mutation rates adjusted for local recombination rates ³¹ (yellow arrow, N = 11,020). Correlation with observed de novo mutation rates (r = 0.18) is stronger than correlations with rates based on the uniform model (mean r = 0.032, p < 1 × 10⁻⁵), indicating that the HCCG model partly captures regional mutation rate variations. However, the correlation with observed de novo mutation rates is weaker than correlations with rates based on the HCCG model itself (mean r = 0.33, p < 1 × 10⁻⁵), suggesting other contributing factors. When adjusting observed de novo mutation rates for local recombination rates, the correlation is 0.37, illustrating that substitution rates computed from the HCCG model capture both mutation rates and orthogonal evolutionary forces associated with local recombination rates.

In contrast to the large-scale regional variation, we found that the influence of flanking nucleotides on de novo mutations was in excellent agreement with results based on comparative genomics ³³ (r² = 0.993; Supplementary Fig. 6), suggesting that the mutation spectrum has been relatively constant in recent evolution. We also observed a previously predicted^26–28 strand asymmetry for mutations in transcribed regions (Supplementary Fig. 7), especially for A→G mutations (p = 5.9 × 10⁻⁵). This is likely a byproduct of the action of transcription-coupled repair. We found a modest 2.8% depletion of mutations in transcribed regions relative to intergenic regions (p = 0.047). This is in sharp contrast with somatic cancer mutations where a similar strand asymmetry was accompanied by a strong reduction of mutations in transcribed regions ²⁰ .

Having a well-calibrated mutation model is essential for evaluating the significance of de novo mutation patterns observed in pedigree sequencing studies (especially in the absence of appropriate controls in disease studies) ³⁴ . Previous mutation models have been based on comparative genomics, but, as shown above, these models are not representative of germline mutation rates alone as they also incorporate other evolutionary forces. To bridge this gap, we used the empirical distribution of de novo mutations along the genome to refine a mutation model based on human-chimpanzee divergence rates, considering flanking sequence context, local recombination rates, mutation type and transcriptional strand in coding regions (Methods). In addition to the genome-wide rates, we also calculated gene-level mutation rates, separately estimating synonymous, missense and nonsense mutation rates. This mutation rate map can be used for evolutionary inferences based on human mutation rates and for the identification of disease genes with recurrent de novo mutations.

We described here the most extensive catalog to date of de novo germline mutations in healthy individuals, revealing several mechanisms influencing the distribution of mutations along the genome. In particular, clustered mutations suggest the existence of a novel mutagenic mechanism, and the effect of replication timing on germline mutations depends on paternal age. Mutation rate heterogeneity substantially influences genomic variation in the rate of sequence evolution, adding to the effects of evolutionary forces acting at the population level.

Online Methods

The Genome of the Netherlands data

This study uses de novo mutation data from the Genome of the Netherlands (GoNL) project, for which all data generation and processing steps were detailed in a previous publication ¹³ . A brief version is included here.

The Genome of the Netherlands project includes 250 Dutch parent-offspring families (231 trios, 8 quartets with dizygotic twins, 11 quartets with monozygotic twins) sampled throughout the Netherlands without phenotypic ascertainment. For this study, we used all 250 parents as well as 258 genetically unique offspring, removing one of the two twins (chosen randomly) in each of the monozygotic twin pairs.

Samples were sequenced using 91bp paired-end with 500 insert size libraries on Illumina HiSeq2000. The alignment and variant calling were devised based on the Genome Analysis Toolkit (GATK) best practices v2 ^35,36 : The sequence data were mapped to the human reference genome build 37 using bwa 0.5.9-r16 ³⁷ , duplicate reads were removed using Picard tools (http://picard.sourceforge.net), local indel realignment was performed around indels using GATK IndelRealigner and base qualities were recalibrated using GATK BaseQualityScoreRecalibration. Variants were called using GATK UnifiedGenotyper v1.4 on all samples simultaneously and filtered using GATK VariantQualityScoreRecalibration.

De novo mutation detection was performed using the trio-aware genotype caller GATK PhaseByTransmission which leverages familial, population and mutation rate, followed by filtering using a random forest machine-learning classifier (trained on 592 true positives and 1,630 false positive putative de novo mutations validated experimentally). We obtained a set of 11,020 high confidence mutations in the 269 children of the GoNL project with an estimated 92.2% accuracy ¹³ . All putative de novo mutations found in the 11 monozygotic twin quartets were subjected to validation in both twins. Out of the 680 mutations detected and validated in either twin, 660 were shared by both twins and 20 were unique to a single child. We therefore estimate that 97% of the mutations in our data are germline and 3% are somatic. Using GATK ReadBackedPhasing we assigned parental origin to 1,991 paternal and 630 maternal de novo mutations based on phase-informative reads.

Simulation of de novo mutations

We simulated de novo mutations at the read level to create a null distribution (uniform) while accounting for the effect of coverage fluctuation inherent to high-throughput sequencing. We generated 264k random positions throughout the GoNL accessible genome ¹³ (i.e. ~1/1000bp), excluding any position that was polymorphic in GoNL or outside the accessible genome. For each of these positions, we generated a random non-reference allele to be used as a decoy mutation. For each trio separately, we extracted children reads overlapping each of the positions to insert the decoy mutation. Since de novo mutations are always heterozygous, each read had a 50% probability to be selected to carry the mutation. For all reads selected to carry the mutation, we replaced the reference base with the decoy mutation base. Base and mapping qualities were kept intact under the assumption that altering a single base in 90 would not affect these significantly. We then applied our entire de novo mutation calling pipeline to each decoy mutation.

Using these simulations, our de novo mutation calling pipeline had an average sensitivity of 67.9. This was heavily influenced by the coverage across the entire trio (R = 0.87). One outlier sample showed abnormally low sensitivity (−5.8sd) but was kept in the study since there were no quality concerns based on earlier QC ¹³.

Based on these simulations, we estimated the power to call a de novo mutation as a function of coverage in each individual in the trio. We found that simulated mutations covered by at least 9 reads in each parents, 4 reads in the child and 30 reads across the entire trio were detected with 92.5% sensitivity. On average 68.8% of the genome was covered in each trio using these thresholds. We considered all bases covered by these thresholds as high confidence bases in our analyses.

To derive a null distribution for de novo mutations based on the simulations above, we randomly sampled a single child at each of the 264k sites at which we inserted decoy mutations. The sampling was done regardless of whether the simulated mutation was called in the child or not and lead to a total of 179,845 called mutations that we used to compare our de novo mutations against.

Paternal age influence on the genomic location of mutations

We annotated each de novo mutation with replication timing measured in lymphoblastoid cell lines (LCL) ³⁸ , expression levels in LCL ³⁹ , recombination rates ³¹ and DNAse I hypersensitivity sites and histone marks (H3K27ac, H3K4me1, H3K4me3) measured in lymphocytes (GM12878) from the ENCODE project ⁴⁰ . We then used a linear regression model to investigate possible relationships between paternal age and the localization of de novo mutations with respect to the epigenetic variables above (DNA replication timing, recombination rate, DNase I hypersensitivity, expression levels, and the histone marks H3K27ac, H3K4Me1 and H3K4Me3), while correcting for GC content, CpG sites and sequencing coverage. We used a stepwise AIC approach, starting with a saturated model including all variables and their interactions, to derive a parsimonious model. The resulting parsimonious model only contained DNA replication timing (p = 0.0022) and histone H3K4me3 levels (p = 0.35) due a weakly significant interaction between the two (p = 0.035). This interaction is possibly caused by the correlation between replication timing and histone H3K4me3 levels. We estimated the significance of the other epigenetic variables by adding each one by one into the model and comparing the resulting model against the parsimonious model using an ANOVA test (Supplementary Fig. 1).

We dichotomized our data based on the age of the father to contrast replication-timing profiles of younger and older fathers. We ran an exhaustive search for a threshold that maximizes the difference between the two groups. For each of the 23 possible age thresholds, we used a Kolmogorov-Smirnoff test to compare the replication timing profile of the younger and older fathers (Supplementary Fig. 2). We found a peak around 28 years of age (p = 5.7 × 10⁻⁴) and therefore used this as an age threshold. Hereafter, we will refer to fathers who were <28 years old at conception as “younger fathers”, and fathers who were ≥28 years old at conception as “older fathers”.

We compared the distribution of replication timing of mutations from younger and older fathers using a Mann-Whitney (MW) test and found that those of younger fathers were significantly shifted towards later replicating regions (p = 1.3 × 10⁻⁴). We also compared the distribution of the replication timing of simulated mutations against offspring of younger and older fathers and found these to be shifted towards later replication regions (p = 4.9 × 10⁻⁴) and similar (p = 0.68), respectively.

We repeated the same analyses using independent replication timing data ⁴¹ in four cell types (lymphoblastoid cells, neural precursor cells, embryonic stem cells (of four separate lines) and induced pluripotent stem cells (of two separate lines)) and observed consistent results across all cell types (Supplementary Fig. 3).

To delineate whether the effect we observed was paternal, maternal or both, we used mutations for which we could unambiguously determine parental origin and ran the linear regression model using the father's age on the 1,991 paternally inherited mutations (β = 0.0092, p = 0.038) and using the mother's age on the 630 maternally inherited mutations (β = −0.0096, p = 0.26) separately. Because of the difference in sample size between the mutation sets, we resampled 10,000 sets of 630 mutations from the paternally inherited mutations and ran the linear regression on these sets. We found that the expected paternal effect was significantly greater than the maternal one with the same number of mutations (p = 0.0023, Supplementary Fig. 4).

Next, we ran a robust linear regression model between the percentage of genic mutations in each of the 258 offspring and paternal age correcting for coverage and found a significant association (β = 0.0026, p = 0.0085). We used a robust linear regression model is to account for a single sample that showed an abnormally high percentage of genic mutations (>8sd away from the mean). This sample was no different from others in terms quality metrics such as coverage, SNP heterozygosity, proportion of known and novel SNPs and possible contamination.

We used linear regression models to compute the increase of mutations with paternal age for genic (β = 0.52, p < 2 × 10⁻¹⁶) and intergenic (β = 0.32, p = 3.7 × 10⁻¹⁴) mutations separately while correcting for coverage. Based on these, we estimated that an offspring born to a father aged 20 would receive on average 9.63 genic and 22.68 intergenic mutations whereas an offspring with a father aged 40 would receive on average 19.06 genic and 35.24 intergenic.

Mutations clusters

We tested whether the intra- and inter-individual distribution of de novo mutations deviated from a simulated uniform distribution across the genome correcting for detection power by assigning a probability equal to the average number of high confidence bases (see Simulations) across all trios at the kilobase scale. We used a Kolmogorov-Smirnoff test and found that both intra-individual (p = 3.3 × 10⁻⁴) and inter-individual p = 5.8 × 10⁻⁵) were enriched in more closely spaced mutations than expected (Fig. 3). The strongest enrichment was for intra-individual mutations up to ~20kbp and we therefore defined mutation clusters as regions of 20kbp or less containing two or more de novo mutations in the same sample. We observed 73 clusters of two and 5 clusters of three mutations. We ran 1mln permutations to test whether these clusters were due to generally hyper-mutated regions. In each permutation round, we permutated the samples to which each mutation belongs to and counted the number of clusters obtained. The maximum we found under this permutation scheme was 18 such clusters, far from the 78 we observe in total, indicating that clustered mutations are likely co-occurring rather than independent. We then looked at the substitution types for clustered de novo mutations and compared them against non-clustered de novo mutations using chi-square tests. We also looked for differences in larger context (multiple flanking nucleotides) but did not see any further signature.

Mutation rates in exonic regions

We annotated all observed and simulated de novo mutation with their coding status (exonic, intronic, intergenic) using UCSC CCDS track ⁴² . We used a chi-square test to investigate differences in the number of observed and simulated mutations between exonic and non-exonic and found a 28% enrichment of mutations in observed exonic regions (p = 0.008). When considering non-CpG sites only, there was no significant difference (p = 1.0). Using a bootstrapping approach (randomly removing mutations regardless of their coding status), we computed that we would have 83.5% power to detect the enrichment above when removing the exonic mutations if it was present.

Mutation rates in DNase I hypersensitivity sites

Using the ENCODE ⁴⁰ measurements of DNase I hypersensitivity sites (DHS), we defined a set of conserved peaks present in at least 2 cell types and annotated all observed and simulated mutations as within or outside a DHS peak (DHSstatus is 0 if outside a DHS peak, 1 if within). We used a logistic regression using a dummy variable DNMstatus (0 for simulated mutations and 1 for observed mutations) as the response variable and distance to DHS as the explanatory variables. Under this model, DHSstatus was significantly associated with DNMstatus (β = 0.11, p =0.0041). When adding a CpG covariate (0 for mutations outside CpGs, 1 for those at CpG sites) into the model, CpG was strongly associated with DNMstatus (β = 2.74, p < 2 × 10⁻¹⁶) and the distance to DHS was no longer significant (β = 0.038, p =0.34).

Influence of mutation and recombination rates on nucleotide diversity

We annotated all observed and simulated mutations with recombination rates from the DECODE recombination map ³¹ . We compared the distribution of recombination rates at mutation sites in observed and simulated mutation using a logistic regression model with a dummy variable DNMstatus (0 for observed, 1 for simulated mutation) as the response variable and recombination rate, correcting for CpGs and GC content (1kb up/downstream). We found a significant positive association between recombination rates and DNMstatus (β = 0.01, p = 0.0015).

We then computed nucleotide diversity (π) in regions of 10kb around each observed and simulated mutation using VCFTools ⁴³ . We ran a linear regression model with π as the response variable and DNMstatus and recombination rate as explanatory variables. We found that under this model both DNMstatus (β = 3.1 × 10⁻⁴, p < 2 × 10⁻¹⁶) and recombination rates (β = 7.64 × 10⁻⁶, p < 2 × 10⁻¹⁶) were independently associated with π. We repeated the analysis with π computed in 100kb regions around each mutation and found similar results. Correcting for local GC content (computed over the same region as π) and CpGs did not influence these associations either.

Influence of mutation and recombination rates on human-chimpanzee divergence

To estimate the influence of mutation rates on human-chimpanzee divergence, we studied the correlations between a human-chimpanzee comparative genomics (HCCG) model (described below) and mutation rates obtained using: (a) observed mutation rates based on 11,020 de novo mutations, (b) rates based on sampling 11,020 mutations based on the HCCG model, and (c) rates based on sampling 11,020 mutations based on a “null” context-dependent mutation rate model. All rate computations were done on 1Mb non-overlapping regions. Because our power to call de novo mutation varies along the genome, each of the regions was corrected for the average fraction of high confidence bases per trio in that region (based on simulations).

The HCCG substitution model was computed using genome-wide triple alignments using the Pecan 10 amniotes multiple alignments available at the Ensembl database version 56 ^44,45 (restricted to human, chimpanzee, and macaque) and excluding exons and CpG islands. We inferred substitution rates r_t,i for each substitution type t in {A→G , A→C, A→T, C→A, C→G, C→T ,CpG→TpG (to account for hypermutability of CpG sites)} in each region i using a maximum likelihood-based method as described elsewhere 30 . We assumed that the rates of complementary substitution processes to be equal, but did not assume that the substitution process is time-reversible.

We next computed the total substitution rate per window using the rate inferred above for all bases b in {A, C} using the following formula:

$$n_{b,i}{\sum }_{t_b}{r}_{t_b,i}+2n_{CpG,i}{r}_{CpG\to \mathrm{TpG},i}$$

where n_b,i is the number of high confidence bases b in window i, and t_b is the set of substitutions in t where the ancestral base is b (e.g. for b = A, t_b= {A→C, A→G, A→T}).

The genome-wide averaged model was computed assuming a uniform substitution rate matrix, defined as the mean of the substitution rate matrices over all 1Mb regions. We then applied the same procedure as above to obtain a uniform rate but context-dependent substitution model.

Using the above HCCG substitution-rate model and the genome-wide averaged model, we drew 100,000 genomic profiles of 11,020 mutations (same as the number of observed de novo mutations) using the Poisson random number generator in R ⁴⁶ . For each of these simulated substitution profiles, as well as the observed de novo mutation rates, we computed the correlation with the HCCG (Fig. 4).

To investigate the effect of local decode sex-averaged recombination rates on the HCCG model, we computed substitution rates s_i for each region i using the following Poisson regressing with both local recombination rates ρ_i and observed mutation counts n_i:

$$\log \left(s_i\right)={\beta }_0+{\beta }_{\rho }{\rho }_i+{\beta }_n{n}_i$$

We then computed the Pearson's correlation between the HCCG and the above Poisson regression.

Strand asymmetry in transcribed regions

Using the UCSC CCDS track, we annotated all genic de novo mutations with the direction of transcription. We annotated each de novo mutation with its corresponding strand-dependent substitution type (A→G, G→A, A→C, A→T, C→A, C→G). We used chi-square tests to evaluate strand differences for each substitution type in transcribed regions (Supplementary Fig. 6).

We used a chi-square test to compare observed and simulated mutation counts in intronic and intergenic regions and found a modest 2.8% depletion in observed intronic regions (p = 0.047).

Tri-nucleotide context dependency

We utilized the context-dependent substitution matrix from fixed differences in human, chimp and baboon (i.e. from multiple alignments of the three species) available on the UCSC genome browser ^42,47,48 to empirically calculate the “directed” 64×3 mutation matrix using the model implemented in SCONE ³³ . We accounted for multiple mutational events and restricted our analysis to non-exonic regions and removed CpG islands. We then computed the same mutation matrix based on de novo mutations and computed Pearson's correlation coefficient between the two matrices (r² = 0.993).

Mutation rate map

Although our set of de novo mutations is the largest available to date, it is still a relatively sparse sampling across the genome. For this reason, we set on using a human-chimpanzee-macaque primate substitution model ³⁰ and refine it using our observed mutations.

Local mutation rates derived from a human-chimpanzee-macaque primate substitution model ³⁰ were corrected for biases due to local recombination rate ³¹ , types of mutations, and the direction of transcription along the strand. This correction was applied for 2,339 1Mb non-overlapping windows across the autosomes after excluding windows where (1) the decode sex-averaged recombination rate is unavailable for more than 10% of the window, (2) the sex-averaged recombination rate across the window is 0 or greater than 3 cM/Mb, (3) the primate local substitution rate was estimated to be 0 or extremely high, or (4) more than 800 kb on average were below our high confidence calling threshold per trio (based on simulations). All mathematical details and computed correction factors are described in the Supplementary Note, Supplementary Table 2, Supplementary Table 3 and Supplementary Table 4.