Auditory spectral integration in the perception of static vowels

Abstract

Purpose

To evaluate potential contributions of broadband spectral integration in the perception of static vowels. Specifically, can the auditory system infer formant frequency information from changes in the intensity weighting across harmonics when the formant itself is missing? Does this type of integration produce the same results in the lower (F1) and higher (F2) regions? Does the spacing between the spectral components affect a listener’s ability to integrate the acoustic cues?

Method

Twenty young listeners with normal hearing identified synthesized vowel-like stimuli created for adjustments in the F1 (/ʌ/- /ɑ/, /ɪ/-/ɛ/) and in the F2 region (/ʌ/-/æ/). There were two types of stimuli: (1) two-formant tokens and (2) tokens in which one formant was removed and two pairs of sine waves were inserted below and above the missing formant; the intensities of these harmonics were modified to cause variations in their spectral center-of-gravity (COG). The COG effects were tested over a wide range of frequencies.

Results

Obtained patterns were consistent with calculated changes to the spectral COG, both in F1 and F2 regions. The spacing of the sine waves did not affect listeners’ responses.

Conclusion

The auditory system may perform broadband integration as a type of auditory wideband spectral analysis.

For more than fifty years, speech scientists and phoneticians have been examining the nature of the relevant acoustic cues that underlie vowel perception (see Delattre, Liberman, Cooper & Gerstman, 1952, and Fant, 1959, for first synthetic applications of spectrographic patterns). A standard approach in such experiments involves the creation and use of static signals (e.g., synthetic steady-state vowels) as the experimental stimuli and the systematic manipulation of specific parameters of the signal including formant (peak) frequencies, formant bandwidths, formant amplitudes, fundamental frequency, etc. Based on the evidence regarding the efficacy of these acoustic modifications to affect changes in vowel perception, several models of vowel perception were proposed which assigned different weights to the importance of primary and secondary acoustic cues.

The dominant view is that the frequencies of the first two or three lowest formants are primary determinants of vowel quality and the secondary acoustic cues such as formant bandwidth, formant amplitude, and global spectral tilt are relatively unimportant (Klatt, 1982; Peterson & Barney, 1952). This view, however, has been challenged by a number of findings which led to the development of alternative models of vowel perception known as spectral shape models (Bladon & Lindblom, 1981; Ito, Tsuchida, & Yano, 2001; Zahorian & Jagharghi, 1993). These models consider broadly defined global spectral characteristics rather than individual formants (which may be missing or unresolved in the vowel spectrum, for example) and propose that vowels can be identified on the basis of the (smoothed) spectral envelope (see Cheveigné & Kawahara, 1999, and Hillenbrand & Houde, 2003, for more recent developments of the spectral-shape family models and discussions).

In all of these studies, there is one recurring question which is also addressed in the present paper. In particular, what is the nature of the underlying auditory mechanisms and processes responsible for extracting and processing the relevant spectral information? It is by no means clear how the perceptual system extracts formant peaks from the raw acoustic signal which requires analysis of acoustic energy over a range of frequencies. Nor is it clear how these spectral details may be differentially weighted to form a vowel percept from the global spectral shape. A position intermediate between these two extremes admits the possibility of spectral integration, an auditory process which uses acoustic cues over a broader frequency range in the vowel spectrum. This view is pursued in the present study which seeks to characterize auditory spectral integration in vowel perception and its utilization of spectral amplitude cues to infer formant frequency information.

In psychoacoustic research, the term spectral integration applies to processes which explain improvement in detection and discrimination thresholds, or changes in stimulus attributes, as signal bandwidth is increased beyond the width of one critical band (Fletcher, 1940; Zwicker, Flottorp, & Stevens, 1957). The improvement in listener performance with widening bandwidth is thought to reflect the ability of the auditory system to sum or integrate information across a wide frequency range in a complex sound. For example, Feth and O’Malley (1977) used the discriminability of two-component complex tone pairs that had identical envelopes but differed in fine structure to investigate the spectral resolving power of the auditory system. They reported that P(C) in a 2IFC task increased from chance to close to 100% for moderate separations (1 to 3 Bark) of the two component frequencies. However, further separation of the components led to decreased discriminability, which occurred when the components were apparently resolved (i.e., perceived as two different individual components) by the auditory system. The frequency separation at which the two-component signals become indiscriminable was suggested as a psychophysical estimate of auditory spectral resolving power. For each center frequency tested, this estimate was approximately 3.5 Bark. More recently, Xu, Jacewicz, Feth and Krishnamurthy (2004) used two-component tone pairs and found that these two-tone complexes were resolved when their separation was sufficiently large, about 3.5 Bark. An integration process such as this implies spectral summation within a larger bandwidth, in which the listener has no access to the individual components.

A second type of spectral integration, of interest to this study, has been identified and pursued in vowel perception research. It pertains to the ability of the auditory system to combine acoustic cues such as formant frequency and formant amplitude into one unitary percept. However, in this type of integration, listeners still have access to both frequency and amplitude cues.

One early proposal that addressed the second type of spectral integration was the spectral center-of-gravity (COG) hypothesis advanced by Chistovich and her colleagues (e.g., Bedrov, Chistovich & Sheikin, 1978; Chistovich & Lublinskaja, 1979; Chistovich, Sheikin & Lublinskaja, 1979; Chistovich, 1985). This research proposed that, within the integration bandwidth of about 3.5 Bark, the changes in the relative amplitude ratios between two closely spaced formants modified their combined spectral COG. In a set of matching experiments, listeners demonstrated sensitivity to the variation in this spectral COG when making vowel quality decisions. In particular, when two formants differing in relative amplitude were close enough in frequency to allow spectral integration, the frequency of the resulting perceptual formant (F*) was closer to that of the stronger formant. When both formants were of equal strength, F* was located midway between them. This effect ceased when the frequency separation was larger than 3.5 Bark.

The COG hypothesis led to the development of the spectral centroid model (see Chistovich, 1985). Using the moment-of-inertia analogy from mechanics, Chistovich noted that the adjustable perceptual formant F* matched the COG of the vowel spectrum. The COG itself can be considered the first spectral moment (mean) of that portion of the auditory spectrum undergoing spectral integration at a higher level of auditory processing. A serial model of spectrum shape processing was proposed by Chistovich et al. (1979), with peak extraction at the peripheral levels as the first step, and auditory integration at the higher levels as the second. The occurrence of COG effects suggested that the auditory system may, to a certain degree, depend on the close relationship between formant frequencies and formant amplitude ratio in making phonetic quality decisions. Over the years, however, formant integration effects in vowel perception have not always been found (e.g., Assmann, 1991; Beddor & Hawkins, 1990; Fahey, Diehl & Traunmüller, 1996; Hoemeke & Diehl, 1994). Understandably, mixed results of experiments designed to replicate the COG effect reduced interest in considering this type of auditory spectral integration in speech perception theories and led to a practical cessation of any further investigation of this potentially significant auditory process.

A different view of auditory spectral integration in vowel perception was offered by Rosner and Pickering (1994) to whom broadband integration seems unnecessary for vowel catergorization. In proposing their loci-based integration model, Rosner and Pickering refer to earlier auditory-loci-based models (Miller, 1989; Sussman, 1986; Syrdal & Gopal, 1986; Traunmüller, 1987; 1988) which, in their view, did not attempt to identify a mechanism for the determination of auditory peaks and shoulders, but skipped “directly from the stage of an auditory transform to outputs of auditory locations” (p. 137). On the contrary, Rosner and Pickering’s model assumes a stage of weighted integration over a local spectral region which smoothes out peaks in the auditory loudness density pattern. A second integration then applies beyond the spectral smoothing (as a function of the auditory filterbank) which allows one to compute local effective vowel indicators or LEVIs. After this second integration, a peak-and-shoulder-picking mechanism determines the locations of the first two LEVIs, resulting in generating a peak and a shoulder for two closely spaced formants F1 and F2 in the lower part of the spectrum.

Reviewing the hypothesis of a broadband COG proposed by Chistovich and her colleagues, Rosner and Pickering pointed to the insufficient support in their data and concluded that their listeners may have performed a kind of psychophysical matching which tell us very little about the auditory processes involved. Today, it is still true that the underlying causes of the COG effect are not well understood, making it difficult to evaluate its potential contribution to vowel identification. In her review of the COG hypothesis, Chistovich (1985) underscored the functional role of the spectral COG rather than explaining the mechanism itself. She clarified that “the results argue against the hypothesis that the COG of the whole spectrum is the sole determinant of vowel quality of even a restricted class of vowels (back vowels) but that does not mean that this parameter is not used at all in vowel identification” (p. 796). She emphasized the importance of spectral details (or “small irregularities,” using her terminology) in the spectrum shape and the role of COG as that of a pointer to the spectral region where the pattern provides information about vowel discrimination.

The major difference between the spectral integration proposed by the COG hypothesis and that by the Rosner and Pickering model is in the frequency range. That is, the broadband COG was interpreted as an indication that the auditory system performs an additional spectral summation within a larger frequency bandwidth whereas the LEVIs arise from integration over more restricted regions in the auditory loudness density pattern. Because of their local application, LEVIs can also arise from a single harmonic and this is how Rosner and Pickering interpreted results from numerous experiments which used a restricted number of harmonics (or incomplete spectrum) to produce identifiable vowels (e.g., Assmann & Nearey, 1987; Kakusho, Hirato, Kato & Kobayashi, 1971).

The purpose of the present study is to evaluate whether and to what extent the type of spectral integration identified as broadband COG can indeed occur in vowel processing. The need to reevaluate this model arises from the inconclusive results in published studies which aimed to replicate the original results with Chistovich and her colleagues. If it can be demonstrated that the broadband spectral integration is involved in signal processing leading to vowel identification, we will have an argument for modification of the existing theories of vowel perception. At present, neither the formant-based nor the whole spectrum shape models can account for the processing of spectral detail which may supply an important cue in forming a vowel percept.

It is assumed that in the broadband spectral integration examined in the present study the listener has access to individual cues being combined. Therefore, a manipulation of one cue is expected to affect the perceptual response to another cue. As in the original COG model, modifications of amplitude cues are undertaken in order to evoke listener response to changes in the perceived formant frequency. However, unlike in the original COG model, it is not formant amplitude that determines the perceived formant frequency. Rather, it is intensities of the individual stimulus components —inserted sine wave pairs—that determine the perceived formant frequency. This point will be discussed in greater detail below. The current assumption is that if the COG effect can be manifested across a part of the spectrum where the actual formant is missing, listener’s response will serve as evidence that the auditory system does integrate spectral information over a broader frequency range and does not rely on the presence of formant frequency peaks in forming a percept of a vowel-like sound.

The present experiments are designed to answer the following questions:

1. Does the auditory system integrate spectral components over a relatively broad frequency range?

2. Does this type of spectral integration produce the same results in the lower (F1) and higher (F2) spectral regions where individual harmonics are resolved and unresolved, respectively?

3. Does the separation (i.e. spacing) of the spectral components affect listener’s ability to integrate the acoustic cues?

Creation of the testing signals for the current experiments—and specifically the methodology for modifying the spectral COG— was motivated by two separate considerations. First, we note that in the source-filter theory of speech production (Fant, 1960; Stevens, 1998) the formants represent the resonance frequencies of the vocal tract whose frequency are determined by the shape of the articulatory tract. The formants serve to filter (and selectively enhance or damp) the energy of the harmonics generated by the glottal pulse. Here, rather than modifying the amplitudes of the formants to change the spectral COG (the usual approach in the speech research literature on the COG effect; however, we note that manipulations of individual harmonics were done in testing the COG hypothesis by Assmann, 1991), we will be modifying the amplitudes of harmonic components individually.

Second, we adopt insights from research on sine wave speech (e.g., Remez, Rubin, Pisoni & Carell, 1981; Remez, Pardo, Piorkowski & Rubin, 2001). Sine wave speech is an acoustic (synthetic) signal which uses pure tones as replications of the frequency and amplitude pattern of the formant peaks. As it has been shown in a number of experiments and demonstrations, sine wave replications of a speech string are intelligible despite the fact that they discard the acoustic attributes of human speech which is an acoustic product of vocalization. Sine wave speech, using non-speech signals, can be viewed as the most distorted type of synthetic replication of individual phonemes, syllables or words. Yet, when one instructs listeners that such stimuli represent speech sounds (thus putting them into the speech mode of perception) even these distorted signals are able to evoke impressions of vowels and consonants so that listeners are able to recognize complete utterances synthesized by this method. Thus, although some portion of the signal (F1 or F2) will be removed and replaced with a smaller set of sine waves, we expect that listeners will be able to process these signals as speech-like sounds.

It should be noted that the term formant is sometimes used ambiguously in acoustic research. Although in the source-filter theory it represents an acoustic filter (described by a resonance curve), in spectrographic analysis one often refers to the dark bands as the formants (although they represent the acoustic energy present as a function of both the source harmonics and the formant filter). To clarify the present experimental approach, “removing a formant” in this study indicates removing the acoustic energy within a certain frequency range and replacing it with a set of sinusoidal components (whose amplitudes are being modified).

Experiment 1

Recall that in the matching experiments by Chistovich and her colleagues, the listener was asked to match the single-formant vowel with a two-formant vowel. What was manipulated was the amplitude of either of the two closely spaced formants in the latter signal. The single-formant signal was thus matched to a single perceptual formant (represented by the spectral COG) which was thought to arise from the spectral integration of the two-formant bundle. What needs to be emphasized here is that the perceptual formant (F*) or perceived frequency of the two-formant bundle was understood as a product of spectral integration and thus could not be measured directly in the spectrum. It is in this sense that Rosner and Pickering (1994, p. 142) referred to this matching procedure as a type of “psychophysical matches whose characteristics are unknown.”

Experiment 1 was designed to relate a perceived formant frequency to an actual (and measurable) formant in a vowel, which constitutes a departure from the original way of testing the spectral COG effect. In the first series of stimuli, two-formant vowels were presented for identification (and not matching) to establish the baseline performance, that is, how well listeners identified two-formant synthetic vowels. We will refer to this type of stimuli as actual formant (AF) vowels. In the other series, one of the formants (F1 in Experiment 1) was removed from the spectrum. In order to recreate the formant perceptually, two pairs of sine waves were inserted below and above the missing F1 and the intensities of these harmonics were modified to cause variation in the spectral COG of the experimental bundle. The question addressed in Experiment 1 was whether listeners could infer the frequency of the missing formant on the basis of intensities of the component sine waves. Thus, the actual measurable formant (in the AF series) was set as a model and the identification of stimuli with the missing F1 was taken as a measure of the degree of spectral integration. If listeners could infer the missing F1 from the intensity cues, their responses were understood as an evidence of broadband spectral integration. The stimuli in which the actual formant was missing are termed virtual formant or VF stimuli. A virtual formant is presumed to arise in listener’s perception of the signal. In this and subsequent experiments, the frequency of the VF is the calculated spectral COG of the pairs of sine waves.

Experiment 1 sought to answer all three research questions, pertaining to (1) the existence of the broadband spectral integration, (2) whether this type of integration takes place in the low spectral region (F1), and (3) whether listener’s response to the missing F1 stimuli is affected by the spacing between the sine wave pairs. If listeners can form the percept of F1 on the basis of intensity weighting across the pairs of sine waves (in the absence of a specific F1 peak), their responses to the changes in the spectral COG will support the existence of a spectral integration process.

Method

Participants

Twenty native speakers of American English whose age ranged from 20 to 40 years served as listeners. All were students at The Ohio State University and were paid for their efforts. The selected participants had normal hearing as determined by a pure-tone screening.

Stimuli

The American English /ʌ/-/ɑ/ vowel pair was selected as the most suitable for creating a step-wise synthetic continuum in the F1 region. Since most previous work that examined the COG effects used two-formant stimuli whose formants were closely spaced, the present experiment followed this approach. Consequently, the frequency separation between the measured F1 and F2 peaks for the /ʌ/-/ɑ/ pair ranged from 3.01 to 3.85 Bark.

Two types of stimuli were constructed for this vowel pair. First, a two-formant AF series was created using HLsyn (.kld option, parallel synthesis)¹. The F0 was set at 120 Hz and the duration of each token was 200 ms. F1 was increased in ten 12-Hz steps from 620 Hz (the /ʌ/ endpoint) to 730 Hz (the /ɑ/ endpoint) while F2 was held constant at 1220 Hz. The bandwidths of the two formants were 80 and 120 Hz, respectively. The parameter values of the formant amplitudes were set at 60 dB, using the default values as suggested by Klatt for this synthesis method.

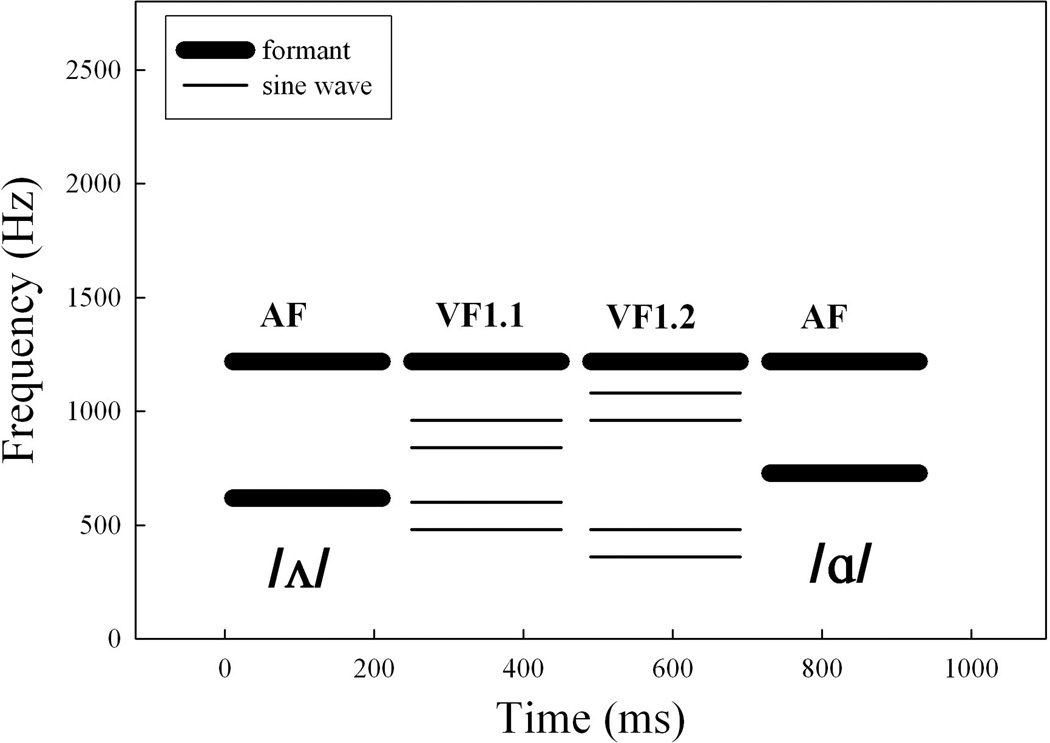
Next, from this original AF series two additional series were created in which F2 remained intact and F1 was removed from the signal by setting the amplitude of F1 to zero. This one-formant series (containing only a F2 peak) was used as the base for the creation of the second type of stimuli, which we call here virtual F1 (VF1) tokens. The VF1 was constructed by adding to the base two pairs of sine waves, the frequencies of which were multiples of the F0. Pairs of sine waves instead of a single sine wave were used in order to achieve a more natural sounding synthetic vowel. In the first VF1 series (VF1.1), the frequencies of the sine waves were 480 and 600 Hz for the lower pair and 840 and 960 Hz for the higher; in the second series (VF1.2) they were 360 and 480 Hz for the lower and 960 and 1080 Hz for the higher pair. In this way, the frequency separation between the two pairs of sine waves increased from 3.54 Bark (4.95 ERB) in VF1.1 and 5.36 Bark (7.61 ERB) in VF1.2. Bark values were calculated after Traunmüller (1990) and ERB after Moore and Glasberg (1983). Figure 1 shows a schematic representation of the tokens.

Figure 1.

Endpoints of the two-formant AF series and two virtual F1 series (VF1.1, VF1.2) used in Experiment 1 for the /ʌ/-/ɑ/ vowel pair. For each VF1 series, the frequencies of individual sine waves remained unchanged. The intensities of the sine waves pairs were varied systematically in ten steps.

For each VF series, the amplitudes of both individual sine waves within a given pair were identical. Within each 10-step series, relative amplitudes of the lower and the higher pair were varied for each step. These amplitude ratios (actually, the corresponding intensity ratios) for the endpoint stimuli were selected to match the spectral mean (or COG) of the composite. In all experiments described here, the COG of the composite (i.e., consisting of the four sine waves) was computed as an intensity-weighted average of the center frequencies of the pairs (which represents a reasonable estimate of the frequency of the VF after the composite is added to the base stimulus). Specifically, the COG of the added sinusoidal components was calculated as

$$\text{COG}={\sum }_{k=1}^4(I(k)*f(k))/{\sum }_{k=1}^{4}I(k)$$

where I(k) is the intensity of the k-th sinusoid and f(k) is the frequency of the k-th sinusoid. The constraint on intensity values is that the four intensities must sum to 2.0; also, I(1)=I(2), I(3)=I(4) and I(1)+I(3)=1.0. So, for the /ʌ/-endpoint using the added sinusoids with frequencies of 480, 600, 840 and 960 Hz, the intensities of the first two sine waves would be 0.778 and intensities of the second two sine waves would be 0.222.

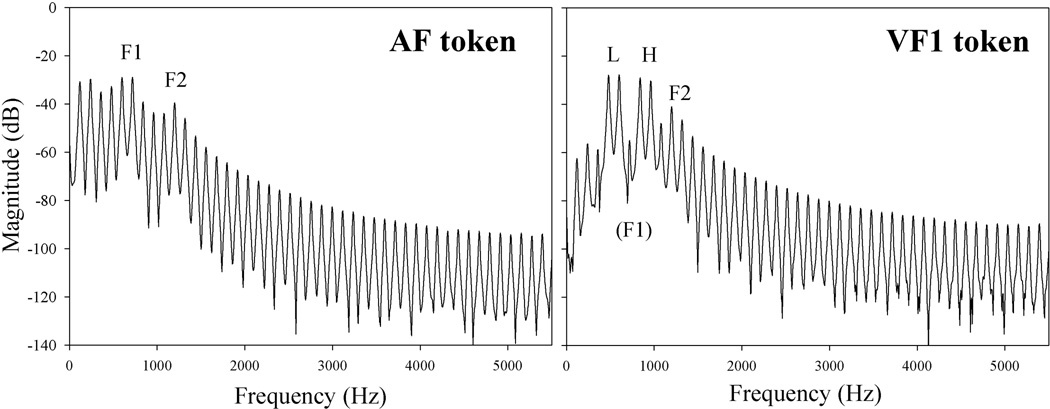
For each step in VF1.1 and VF1.2, the intensities of the added sine waves were set at values such that the calculated frequency value of COG (i.e., F1 target frequency) corresponded to the frequency value of the actual F1 in the original two-formant AF series. After each sine wave was created and its intensity adjusted, all four sine waves were added together and the overall intensity of this composite was scaled to that of the original F1. This sine wave composite was then added to the base. The overall rms amplitudes of each step of the AF series and its virtual counterpart were within 0.2 dB of one another. FFT spectra of a two-formant AF token and the corresponding VF1 token can be found in Figure 2. The intensity ratios used in the creation of the sine wave pairs for all VF tokens along with F1 target frequency for each step are listed in Table 1.

Figure 2.

FFT spectrum of the step 5 stimulus of the two-formant AF token (left) and of the virtual (VF) version of this token in VF1.1 series (right) used in Experiment 1. L=lower pair of sine waves, H=higher pair of sine waves, (F1)=missing F1.

Table 1.

F1 target frequency and intensity ratios used in each VF stimulus series in Experiment 1 for the /ʌ/-/ɑ/ vowel pair (/ʌ/= step 1; /ɑ/= step 10).

Virtual formant series	Series step	F1 target frequency (Hz)	Intensity ratio at each VF series step
			Lower pair	Higher pair
VF1.1			480/600 Hz	840/960 Hz
	1	620	0.778	0.222
	2	633	0.742	0.258
	3	645	0.708	0.292
	4	657	0.675	0.325
	5	669	0.642	0.358
	6	681	0.608	0.392
	7	693	0.575	0.425
	8	705	0.542	0.458
	9	717	0.508	0.492
	10	730	0.472	0.528
VF1.2			360/480 Hz	960/1080 Hz
	1	620	0.667	0.333
	2	633	0.645	0.355
	3	645	0.625	0.375
	4	657	0.605	0.395
	5	669	0.585	0.415
	6	681	0.565	0.435
	7	693	0.545	0.455
	8	705	0.525	0.475
	9	717	0.505	0.495
	10	730	0.483	0.517

Procedure

The stimuli were presented diotically via Sennheiser HD600 headphones to a listener seated in a sound-attenuating booth. In a two-alternative forced choice task, participants indicated their responses by using a mouse click on one of two response choices labeled “/ʌ/” and “/ɑ/” displayed on the computer monitor. Examples of these vowels in words were also shown (/ʌ/ as in “bud” and /ɑ/ as in “bod”). A short practice was given prior to the testing session to ensure that the listener can do the task. The presentation was blocked by series type. The stimuli were presented randomly in three blocks of 100 trials each (10 series steps × 10 repetitions) for a total number of 300 trials.

Results

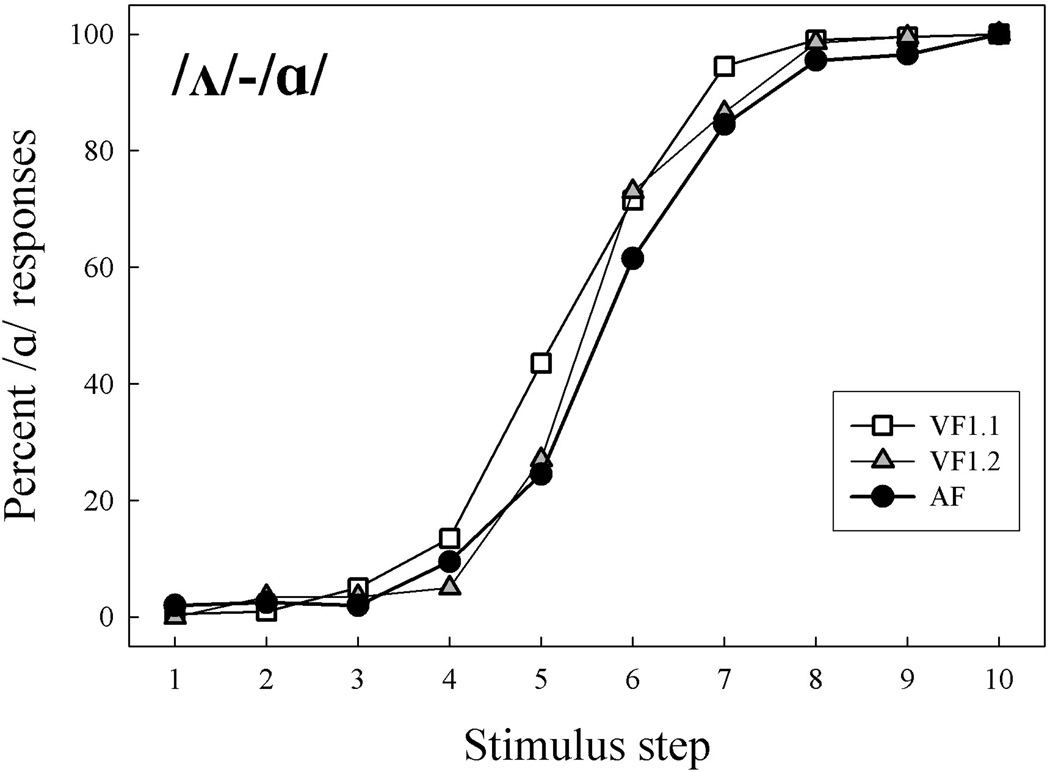
Listeners’ mean responses to the /ʌ/-/ɑ/ pair for AF and the two VF1 series are shown in Figure 3. For AF, the stimulus step with the lowest F1 frequency was usually identified as /ʌ/ while the token with the highest F1 was usually identified as /ɑ/. This tendency was also evident across both VF1 series, where the lowest spectral COG yielded mostly /ʌ/-responses and the highest spectral COG yielded mostly /ɑ/-responses. The consistency of responses across all series is noteworthy, especially in terms of the steepness of the identification functions between Steps 4 and 7.

Figure 3.

Experiment 1: Identification responses to /ʌ/-/ɑ/ across all stimulus series.

The results were initially analyzed using within-subject ANOVAs with the factors stimulus series and step. In these and all subsequent ANOVAs in this study, the degrees of freedom for the F-tests were Greenhouse-Geisser adjusted to avoid problems associated with violations of sphericity. The significance of the main effect of stimulus series is of particular interest here. The main effect of step is expected to be significant and is not reported unless it was non-significant.

The ANOVA of the identification responses revealed no significant effect of stimulus series (F(1.72,38)=2.73, p=0.088) or a stimulus series by stimulus step interaction (F(5.05, 95.89)=2.044, p=0.079). The identification results were then analyzed for category boundary (the 50%-crossover point) differences among the series using PROBIT analysis and were followed by a within-subject ANOVA with the within-subject factor stimulus series. As with the identification responses, there was no significant main effect of stimulus set (F(2,38)=2.688, p=0.081).

It is clear that the obtained identification functions are comparable across all three testing conditions. The patterns of responses did not differ as a function of stimulus series, indicating that vowel identification cues in the actual formants in the AF series and those in the two VF1 series were comparable. As for the AF stimuli, the argument can be made that listeners responded to the formant frequency cues. That is, the endpoint containing the lower F1 (620 Hz) was uniformly identified as /ʌ/ and the higher F1 (730 Hz) yielded the highest /ɑ/-identification. However, having only two phonetic categories available to label the signals, listeners must have reconstructed the missing formant frequency in the virtual F1 stimuli from intensity relations in the four sine waves which best corresponded to either /ʌ/ or /ɑ/. The identification pattern was as predicted if listeners were to respond to the spectral COG of the sine waves. It is noteworthy that spacing between the sine waves did not affect the identification results and the responses were comparable for smaller separations in VF1.1 series (3.54 Bark/4.95 ERB) and for larger in VF1.2 series (5.36 Bark/7.61 ERB). These results are difficult to explain without accepting the claim that a form of auditory spectral integration took place in combining and interpreting the intensity cues.

Experiment 2

The purpose of Experiment 2 was to determine whether the pattern of responses obtained in Experiment 1 can be replicated with front vowels. The operation of the COG effect was traditionally examined in back vowels whose first two formants are close in frequency (Assmann, 1991; Bedrov et al., 1978). This is because of the assumption that identity of back vowels can be determined by the gross maximum or COG of the spectrum (see Chistovich, 1985, for a discussion). The proximity of F1 and F2 in back vowels also inspired a number of earlier studies which investigated formant averaging or a perceptually grounded effective second formant, F2′ (e.g., Bladon & Fant, 1978; Carlson et al., 1970; Delattre, et al., 1952). However, if the auditory system integrates spectral information over a broad frequency range, we may expect integration effects to be manifested also in vowels with widely spaced formants such as in the /ɪ/-/ɛ/ pair selected in Experiment 2. Alternatively, if auditory spectral integration is not involved in the perception of signals with a “missing F1,” the VF1 stimuli with widely spaced sine waves would be expected to have a different phonetic quality than either endpoint of the two-formant AF series. Experiment 2 used the same participants and procedures as in Experiment 1.

Method

Stimuli

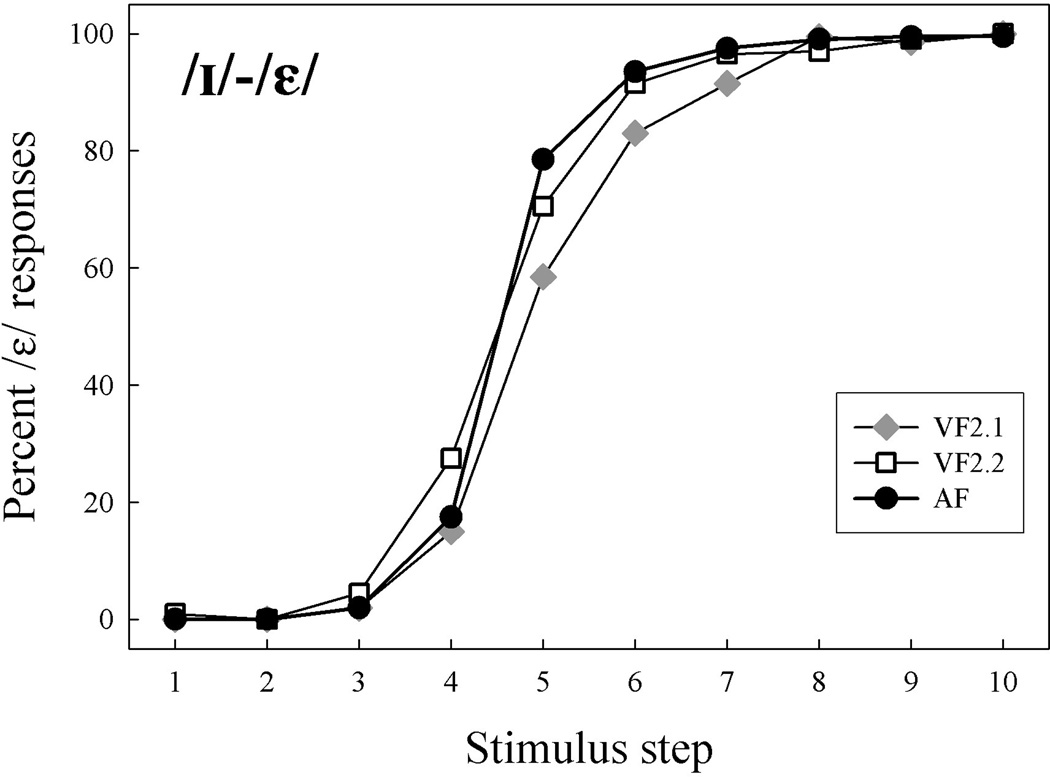
For the selected /ɪ/-/ɛ/ vowel pair, the frequency separation between the actual F1 and F2 was wide and ranged from 7.12 to 8.29 Bark. As in Experiment 1, two types of stimuli were constructed. For the two-formant AF series, F1 was increased in ten 14-Hz steps from 400 Hz (the /ɪ/ endpoint) to 530 Hz (the /ɛ/ endpoint) while F2 was held constant at 1800 Hz. The bandwidths of the two formants were 60 and 120 Hz, respectively. F0 was 120 Hz and the duration of each token was 200 ms.

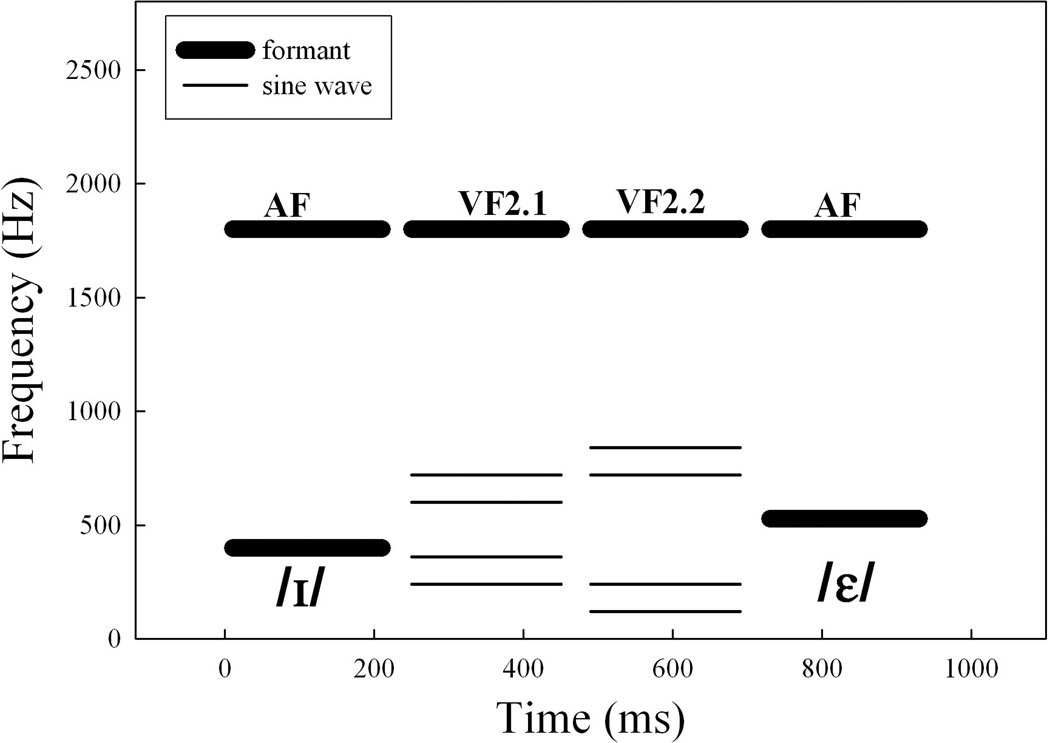
Next, two VF1 series were created in which the lower and the upper sine wave pairs were widely spaced. In the first series, VF1.1, the separation between the sine waves was 4.28 Bark/6.63 ERB and the frequencies of the lower pair were 240 and 360 Hz and the higher pair were 600 and 720 Hz, respectively. In the second series, VF1.2, the sine wave separation was 6.49 Bark/10.42 ERB and the frequencies of the lower pair were 120 and 240 Hz and the higher pair were 720 and 840 Hz, respectively. These VF stimuli were constructed exactly as described for the /ʌ/-/ɑ/ pair in Experiment 1. A schematic representation of the AF and VF1 tokens is shown in Figure 4. Table 2 provides further details about F1 target frequency and intensity ratio used in calculations of the spectral COG at each series step.

Figure 4.

Endpoints of the two-formant AF series and two virtual F1 series (VF1.1, VF1.2) used in Experiment 2 for the /ɪ/-/ɛ/ vowel pair.

Table 2.

F1 target frequency and intensity ratios used in each VF stimulus series in Experiment 2 for the /ɪ/-/ɛ/ vowel pair (/ɪ/= step 1; /ɛ/= step 10).

Virtual formant series	Series step	F1 target frequency (Hz)	Intensity ratio at each VF series step
			Lower pair	Higher pair
VF1.1			240/360 Hz	600/720Hz
	1	400	0.722	0.278
	2	414	0.683	0.317
	3	429	0.642	0.358
	4	443	0.603	0.397
	5	458	0.561	0.439
	6	472	0.522	0.478
	7	487	0.481	0.519
	8	501	0.442	0.558
	9	516	0.400	0.600
	10	530	0.361	0.639
VF1.2			120/240 Hz	720/840Hz
	1	400	0.633	0.367
	2	414	0.610	0.390
	3	429	0.585	0.415
	4	443	0.562	0.438
	5	458	0.537	0.463
	6	472	0.513	0.487
	7	487	0.488	0.512
	8	501	0.465	0.535
	9	516	0.440	0.560
	10	530	0.417	0.583

Results

As can be seen in Figure 5, the lowest F1 frequency for the two-formant AF series gave rise to the identifications as /ɪ/ and the highest F1 to the identifications as /ɛ/. The same was found for the two VF1 series. A within-subject ANOVA with the factors stimulus series and step showed no significant main effects of series (F(1.6, 29.8)=2.87, p=0.083). The analysis of category boundary differences using PROBIT means and a subsequent within-subject ANOVA showed no significant effect of stimulus series (F(1, 19)=2.61, p=0.123). These results clearly indicate that listeners’ identification responses were similar across all series.

Figure 5.

Experiment 2: Identification responses to /ɪ/-/ɛ/ across all stimulus series.

The results of Experiment 2 were similar to those in Experiment 1. The patterns of responses across stimulus steps did not differ as a function of stimulus series. If the sine wave components were not integrated perceptually, the responses across the stimulus steps in the virtual series might not have changed or at least would have given an indication of chance performance. This is clearly not the case, which shows that neither wide separation between the formants F1 and F2 nor wide separation between the sine wave pairs precluded integration. The fact that these effects (consistent with Experiment 1) occurred in the lower spectral region where individual harmonics are resolved (see Plomp, 1964; Plomp & Mimpen, 1968) suggests that the spectral information is combined above the level of peripheral interactions to produce the percept of F1.

Experiment 3

Experiment 3 examined whether similar effects could be found in the F2 region. In addition, since back vowels were used in Experiment 1 and front vowels in Experiment 2, the perceptual salience of a VF2 was assessed utilizing a vowel pair consisting of one back (/ʌ/) and one front (/æ/) vowel. For the selected vowel pair /ʌ/-/æ/, the frequency separation between F1 and F2 peaks ranged from 4.75 to 5.81 Bark, which was in between those used in Experiments 1 and 2. Experiment 3 used 18 of the same 20 participants and the procedures were as in Experiments 1 and 2.

Method

Stimuli

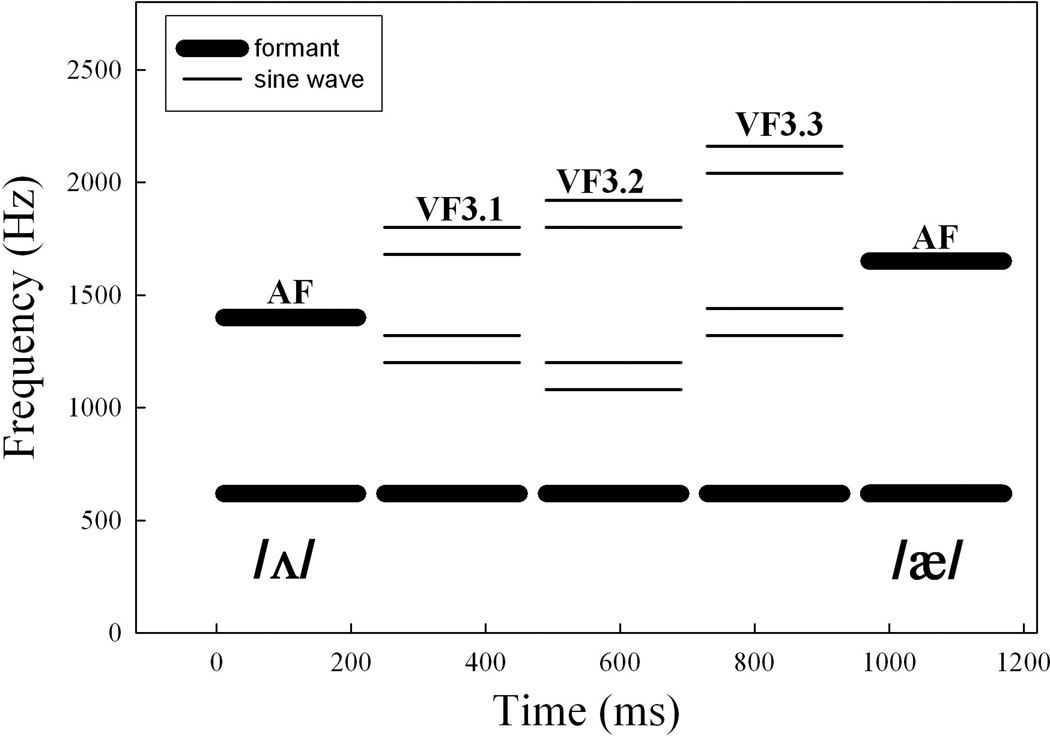
As before, two types of stimuli were constructed. For the two-formant AF series, F2 was increased in ten 28-Hz steps from 1400 Hz (the /ʌ/ endpoint) to 1650 Hz (the /æ/ endpoint). F1 was kept constant at 620 Hz. The bandwidths of the two formants were 80 and 120 Hz, respectively. F0 was 120 Hz and the duration of each token was 200 ms. Three VF series (VF2.1, VF2.2 and VF2.3) were then constructed in which F1 served as the base and a VF2 was created as it was done for the VF1 in Experiments 1 and 2, that is, by inserting two pairs of sine waves below and above the range of the spectral F2. The frequencies of the sine waves and amplitude ratios used in the calculation of the spectral COG are shown in Table 3. The frequency separations between the lower and the higher pair of sine waves were 2.65 Bark/3.31 ERB for series VF2.1, 3.75 Bark/4.69 Bark for VF2.2 and 3.27 Bark/4.07 ERB for VF2.3. Figure 6 provides a schematic overview of all four stimulus series used in Experiment 3.

Table 3.

F2 target frequency and intensity ratios used in each stimulus series in Experiment 3 for the /ʌ/-/æ/ vowel pair (/ʌ/= step 1; /æ/= step 10).

Virtual formant series	Series step	F1 target frequency (Hz)	Intensity ratio at each VF series step
			Lower pair	Higher pair
VF2.1			1200/1320Hz	1680/1800Hz
	1	1400	0.708	0.292
	2	1428	0.650	0.350
	3	1455	0.594	0.406
	4	1483	0.535	0.465
	5	1511	0.477	0.523
	6	1539	0.419	0.581
	7	1567	0.360	0.640
	8	1594	0.304	0.696
	9	1622	0.246	0.754
	10	1650	0.188	0.813
VF2.2			1080/1200Hz	1800/1920Hz
	1	1400	0.639	0.361
	2	1428	0.600	0.400
	3	1455	0.563	0.438
	4	1483	0.524	0.476
	5	1511	0.485	0.515
	6	1539	0.446	0.554
	7	1567	0.407	0.593
	8	1594	0.369	0.631
	9	1622	0.331	0.669
	10	1650	0.292	0.708
VF2.3			1320/1440Hz	2040/2160Hz
	1	1400	0.972	0.028
	2	1428	0.933	0.067
	3	1455	0.896	0.104
	4	1483	0.857	0.143
	5	1511	0.818	0.182
	6	1539	0.779	0.221
	7	1567	0.740	0.260
	8	1594	0.703	0.297
	9	1622	0.664	0.336
	10	1650	0.625	0.375

Figure 6.

Endpoints of the two-formant AF series and three virtual F2 series (VF2.1, VF2.2, VF2.3) used in Experiment 3 for the /ʌ/-/æ/ vowel pair.

Results

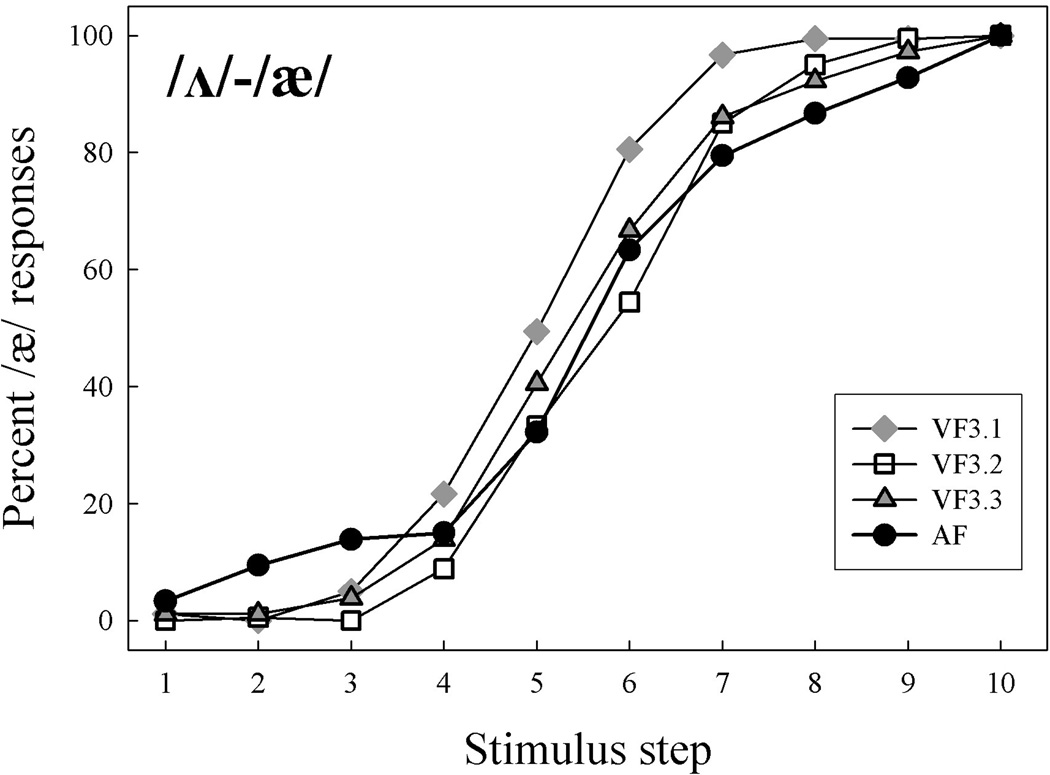
Listeners’ mean responses to the /ʌ/-/æ/ pair are shown in Figure 7. A consistent pattern was found across all stimulus series in that the lowest F2 frequency for AF tokens and the lowest COG value for all three VF series gave rise to the identifications as /ʌ/ while the highest F2 and the highest COG value gave rise to the identifications as /æ/. A within-subject ANOVA with the factors stimulus series and step indicated no significant main effect of series (F(2, 35.3)=2.45, p=0.099). A subsequent within-subject ANOVA analyzing category boundary differences using PROBIT means showed no significant effect of stimulus series (F(1.9, 32.4)=2.31, p=0.117). These patterns of responses show that listeners’ identifications are similar across all series (with comparable slopes and category boundaries), indicating that amplitudes of the added harmonics in the VF2 series was salient cue to vowel identity as was the formant frequency in the AF tokens. In short, the identification responses in the F2 region also produced a pattern consistent with changes to the spectral COG of the sine waves, providing further support for the suggested spectral integration effects.

Figure 7.

Experiment 3: Identification responses to /ʌ/-/æ/ across all stimulus series.

General Discussion

The results of the three experiments presented here suggest that a type of broadband integration may be involved in the perception of vowel spectra. As the study shows, this integration does not require the presence of formant peaks in the spectrum but can utilize spectral components other than formants. To better understand the nature of this integration, it will be helpful to briefly review the work which explored amplitude cues in vowel perception.

The reliance on and the success of the early speech synthesis studies (and their basic methodologies) reinforced the position that vowels are identified on the basis of formant peaks. Although formants are undeniably the primary determinants of (static) vowels (for a review, see Hillenbrand & Houde, 2003), this approach led to minimizing the role played by the underlying harmonic structure of vowels. That is, the primary focus in explorations of the large-scale integration effects including the COG hypothesis was on the integration of formants rather than on the integration of the underlying harmonics whose amplitudes are, in part, determined by the formants. However, the perception of formants in vowels is almost certainly a result of the spectral integration of the energy of underlying harmonics.

Exploration of the harmonic structure and examination of contribution of individual harmonics to vowel identification was undertaken primarily in the 1980s, following the psychoacoustic work on estimating the shape of the auditory filter and the introduction of the ERB scale (see Moore & Glasberg, 1983, for a review). Most of the relevant experimental work at that point concentrated on the low frequency region based on the fact that, given the resolving power of the auditory periphery, F1 can always be resolved into harmonics (see Berstein & Oxenham, 2003, for a more recent work). For example, Darwin and Gardner (1986) showed that a mistuned harmonic did not contribute to the percept of a vowel (because the auditory system was able to detect the lack of relationship between the mistuned harmonics and the remaining harmonics). In another study, Darwin and Gardner’s (1985) results indicated that a boosted individual harmonic remote from the F1 peak also contributed to the estimation of F1, which could only be due to its resolvability. The boosting of a remote harmonic significantly shifted the phoneme boundary, although its contribution to the perceptual estimate of a formant was less than that of the most intense harmonic near the formant peak. Assmann and Nearey (1987) conducted several experiments showing that only the two most prominent harmonics near the F1 peak are the primary determinants of vowel height. These studies established the importance of intensity cues of individual harmonics in the low frequency region to vowel perception.

However, there is also a substantial body of work showing that amplitude cues available in individual formant peaks also contribute to vowel identification (or at least demonstrate that listeners are sensitive to them) and these contributions take place apart from any formant integration effects (e.g., Aaltonen, 1985; Ainsworth & Millar, 1972, Jacewicz, 2005; Kiefte, Enright & Marshall, 2010; Lindqvist & Pauli, 1968; Schwartz & Escudier, 1989). Because these formant amplitude manipulations affect changes in spectral tilt, Kiefte and Kluender (2005) examined specifically the importance of this gross spectral tilt cue (i.e., relative spectral balance between low- and high-frequency energy) in vowel identification. The study found that listeners’ reliance on the spectral tilt cue was somewhat exaggerated in the perception of static synthetic vowels and it was attenuated in the perception of diphthongs. On the other hand, acoustic analyses show that considerable variations in formant amplitude do exist in naturally produced coarticulated vowels (Jacewicz & Fox, 2008). This indicates that amplitude cues, which undergo additional variations as a function of consonantal environment in vowel production, are always present in the vowel spectrum and the listener is exposed to these natural variations through language experience.

Given that both formant amplitudes and the amplitudes of individual harmonics can make significant contributions to vowel identification, the present study explored yet another possibility of broadband integration. What if there is no formant in the vowel spectrum and the intensities of sine waves placed in the positions remote from the missing formant peak are varied systematically as it was done in testing the COG effect? That is, given the evidence that listeners can use the amplitude cues in the closely spaced formants to build a percept of a formant (known as the “perceptual” formant frequency, F*), can they also use this ability to infer the missing formant frequency from the intensity relations among the sine waves? In testing this possibility, the study sought to answer the three questions posed at the outset.

Addressing the first question, whether the auditory system integrates spectral components over a relatively broad frequency range, the current results provide evidence that this type of integration does, in fact, take place and listeners are able to combine the available intensity cues in constructing the percept of a missing formant. The data demonstrate that listeners’ identification decisions in response to VF stimuli are comparable to the patterns obtained for AF stimuli, in which formant frequency information was available to them. Although we fully acknowledge the perceptual importance of formants in the perception of vowels, from the theoretical point of view, formants need not be expected to always carry the primary information about vowel identity. As has been shown in a number of studies, the precise location of spectral peaks is not needed for vowel identification (e.g., Bladon, 1982; Zahorian & Jagharghi, 1993). The present experiments are in line with this view, showing that listeners are able to effectively cope with a missing formant peak when forced to use other spectral cues.

The second inquiry of the study was whether this type of spectral integration produces the same results in the lower (F1) spectral region where individual harmonics are resolved and in the higher (F2) region where the harmonics are less likely to be resolved. No significant difference was found between the two testing conditions. The patterns of identification responses to the manipulations in the F1 region (Experiments 1 and 2) were basically the same as in the F2 region (Experiment 3), indicating that the resolution of the lower frequency region into harmonics does not exclude the possibility of an integrated intermediate representation which may be used in phonetic processing. This conclusion is consistent with the findings of Micheyl and Oxenham (2004) who, in a different context, suggested that harmonic resolvability differences do not interfere with across-frequency comparisons of F0. Therefore, the type of integration examined here is most likely to occur above the level of the auditory periphery, which was also the assumption underlying the occurrence of the COG effects in integrating spectral information in formant peaks.

Finally, this study examined whether the spacing of the spectral components affected a listener’s ability to integrate the acoustic cues. Two types of spacing were controlled for, spacing between the formants in the AF stimuli and spacing between the pairs of sine waves in the VF signals. Recall that the 3.5-Bark integration bandwidth was proposed by Chistovich and Lublinskaja (1979) as an indication of a possible limit for integrating spectral information in formants. After this limit has been reached, listeners’ performance changed. In particular, at the separation of about 3.5 Bark, one subject matched the frequency of F* to either F1 or F2 while the second subject showed chance performance. In both cases, this behavior was interpreted as a cessation of the COG effect. However, subsequent studies which explored this effect have failed to demonstrate the existence of a definitive 3.5-Bark limit for large-scale spectral integration, perhaps with the exception of Xu et al. (2004). Using the methodology by Chistovich and Lublinskaja (1979), Xu et al. (2004) were able to replicate the finding that variability in listeners’ responses increases when the separation between the two formants reached or exceeded the 3.5-Bark band. The variable patterns obtained for 3.5- and 4.0-Bark separations indicated change in listeners’ performance, which was interpreted as a gradual cessation of the COG effect.

The spacing between the two formants in the present AF stimuli was 3.01 to 3.85 Bark in Experiment 1, 7.12 to 8.29 Bark in Experiment 2 and 4.75 to 5.81 Bark in Experiment 3. Although the study did not examine COG effects in the AF stimuli, these frequency separations were selected to observe whether differences in formant spacing could produce some confounding effects on integration of cues in the pairs of sine waves. The second type of spacing, that in VF signals, was of immediate interest to the study and the COG effects were examined across a range of separations between the sine wave pairs: 3.54 and 5.36 Bark in Experiment 1, 4.28 and 6.49 Bark in Experiment 2 and 2.65, 3.27 and 3.75 Bark in Experiment 3. Thus, a variety of frequency separations between the sine waves was used, ranging from 2.65 to 5.36 Bark. No evidence emerged for a 3- to 3.5- Bark integration band. Neither the spacing between the component sine waves nor spacing between the actual formants seemed to have a differential effect on the pattern of listeners’ identification responses. Furthermore, the largest separation between the sine waves used here did not indicate a limit of broadband integration.

It is plausible that the putative 3.5-Bark integration band did not indicate any limit on auditory spectral integration in a first place. Chistovich herself was not firm as to its exact role in vowel perception (1985, p. 802): ”It is not clear at the moment whether this critical distance reflects the integration range or, for instance, the criterion applied in phoneme identification. The same 3.5-Bark distance between adjacent formants could serve as a criterion to differentiate among different groups of vowels.” Evidence accumulated over the years is in favor of the latter possibility. Syrdal and Gopal (1986) transformed the formant frequencies of American English vowels from values in Hz to Bark and observed that formant distance measures between F1-F0, F2-F1, F3-F2, F4-F3 and F4-F2 conform to the 3-Bark criterion. That is, based on whether the Bark-difference is within or exceeds the 3-Bark distance, F1-F0 measure corresponds to vowel height and F3-F2 to the front-back dimension. Hermansky (1990) proposed a computational PLP model that included the broadband processing of spectra, which effectively smeared narrowly spaced (about 3.5 Bark) spectral peaks. Extending this proposal, Xu et al. (2004) introduced a modified version of Hermansky’s PLP model which included a peak detection stage. Furthermore, the 3.5-Bark distance measure was used as a stability factor in the Dispersion-Focalization Theory of vowel systems proposed by Schwartz, Boë, Vallée and Abry (1997), which reduced variations around the formant convergence zone (within 3.5 Bark). This model is based on the general principle of perceptual contrast which is believed to be an independent motivation for shaping vowel inventories of human languages.

Based on these findings, it is rather unlikely that the 3.5-Bark formant integration range constitutes a limit of auditory spectral integration. Rather, this apparent limit appeared in testing the formant integration effects which used vowels as stimuli, in which, by necessity, the spacing of formants is predetermined by systemic properties of vowels and general constraints on vowel production. It is therefore not surprising that the 3.5-Bark limit was not operative in the present study which took more freedom in constructing the stimuli and did not examine the COG effects as a function of spacing between the actual formants.

We understand the integration effects found here to be the result of auditory wideband spectral analysis. Wideband integration effects are not uncommon in speech perception, in general. For example, Healy and Warren (2003) obtained 1% and 0% intelligibility for narrow bands of speech when presented separately at lower and higher frequency, respectively. However, a type of synergistic interaction occurred when these two bands were combined and the intelligibility increased to 81%. Also, Healy and Bacon (2007) suggested that integration of speech information across frequency may be accomplished through dual mechanisms such as those proposed for gap detection. If so, across-frequency integration can occur via between-channel processes while a within-channel mechanism would detect information in closely spaced components. The spectral (and temporal) integration processes point to the fact that the auditory system is a highly flexible system, capable of using a variety of cues when the critical information is unavailable.

In the present VF stimuli, the critical information about the (missing) formant frequency was unavailable. Yet, given the intensity cues in the sine waves and a specific relation between the intensities of the lower and higher sine wave pairs, listeners were able to combine this information and use it in forming a vowel percept. The intermediate position in the debate on the most effective cues (and representations) in vowel perception which is assumed in this study admits the importance of formants as well as the importance of spectral details. These details come into play when the expected frequency information in the vowel spectrum cannot be accessed. It needs to be pointed out that the broadband integration effects were examined here using a restricted type of stimuli. More evidence is needed and more experimental work remains to be done to confirm or reject the conclusions reached here.

It might also be argued that such broadband integration effects will disappear in the processing of dynamically changing spectra such as in diphthongal vowels, which primarily occur in natural speech. For example, Kiefte and Kluender (2005) showed that the importance of the global spectral tilt was mitigated in diphthongs. However, if the wideband spectral analysis is a real phenomenon which is used in vowel (and speech) processing in a variety of contexts, we should not expect it to cease in the processing of consonant-vowel transitions or diphthongal changes in vowels. Evidence exists that listeners use the amplitude cues (or moving COG cues) in the perception of /da/-/ga/ and /ta/-/ka/ transitions (Fox, Jacewicz & Feth, 2008). The dynamically changing COG cues were also shown to be utilized in the perception of diphthongal changes such as in the words we and you (Fox, Jacewicz & Chang, 2010). These effects are attributed to the operation of the common processing mechanism which is able to integrate spectral information over wide frequency bands regardless of whether the signals are static or dynamic in nature.

As a final point, we wish to address the question of whether such integration effects are specific to speech perception or may reflect a general property of auditory processing. This question dates back to the 1970s when an early psychoacoustic work on complex signals found an evidence of a broader integration bandwidth in a series of pitch matching experiments. Independently (and in ignorance) of the development of the COG concept by Chistovich and colleagues, Feth (1974) and Feth and O’Malley (1977) studied spectral integration in two-component, complex tones. This work suggested that the two-tone resolution bandwidth could play a similar role in auditory signal processing as the integration interval (3.5 Bark) observed by Chistovich in vowel matching tasks. Feth proposed the envelope-weighted average of instantaneous frequency (EWAIF) model to predict listener perception of the pitch of two-component, complex tones (to account for an earlier report by Helmholtz (1877) who found that the pitch of a two-component complex tone was shifted toward the frequency of the “stronger” component). In a subsequent work, Anantharaman, Krishnamurthy, and Feth (1993) proposed a revision of this model as the intensity-weighted average of instantaneous frequency (IWAIF), which differed primarily in the choice of a weighting function. This revised version showed that the IWAIF could be calculated in the frequency domain. The frequency domain equivalent has the intuitive interpretation as the COG of the positive frequency portion of the energy density spectrum of the signal. The IWAIF (thus, the COG) model was shown to outperform the EWAIF in pitch-matching experiments (Dai et al., 1996). A natural step in seeking further explanation of these results was to compare responses of the same listeners to the two types of signals (synthetic speech-like vowels and two-component complexes). This was done years later in Xu et al. (2004), suggesting that the integration interval in a vowel matching task and the complex-tone discriminability estimates might be linked to a common mechanism, i.e. to auditory spectral resolving power. When applied to synthetic vowels, the IWAIF model predictions agreed with Chistovich’s spectral centroid model. Although much work remains to be done, we suggest that the COG effect, in particular, and spectral integration, in general, is probably not restricted to speech processing. Rather, in either type of signals, information carried by neural activity in the auditory system is accumulated to improve detection or discrimination performance when the signal and/or masker are broadband in nature.