Impact of precision of Bayesian networks parameters on accuracy of medical diagnostic systems

Abstract

Objective

One of the hardest technical tasks in employing Bayesian network models in practice is obtaining their numerical parameters. In the light of this difficulty, a pressing question, one that has immediate implications on the knowledge engineering effort, is whether precision of these parameters is important. In this paper, we address experimentally the question whether medical diagnostic systems based on Bayesian networks are sensitive to precision of their parameters.

Methods and Materials

The test networks include Hepar II, a sizeable Bayesian network model for diagnosis of liver disorders and six other medical diagnostic networks constructed from medical data sets available through the Irvine Machine Learning Repository. Assuming that the original model parameters are perfectly accurate, we lower systematically their precision by rounding them to progressively courser scales and check the impact of this rounding on the models' accuracy.

Results

Our main result, consistent across all tested networks, is that imprecision in numerical parameters has minimal impact on the diagnostic accuracy of models, as long as we avoid zeroes among parameters.

Conclusion

The experiments' results provide evidence that as long as we avoid zeroes among model parameters, diagnostic accuracy of Bayesian network models does not suffer from decreased precision of their parameters.

1. Introduction

Decision-analytic methods provide a coherent framework for modeling and solving decision problems in decision support systems [1]. A popular modeling tool for complex uncertain domains, such as those encountered in medical applications, is a Bayesian network [2], an acyclic directed graph quantified by numerical parameters and modeling the structure of a domain and the joint probability distribution over its variables. There exist algorithms for reasoning in Bayesian networks that compute the posterior probability distribution over variables of interest given a set of observations. As these algorithms are mathematically correct, the ultimate quality of their results depends directly on the quality of the underlying models and their parameters. These parameters are rarely precise, as they are often based on rough subjective estimates or data that do not reflect precisely the target population. The question of sensitivity of Bayesian networks to precision of their parameters is of much interest to builders of intelligent systems. If precision does not matter, rough estimates or even qualitative “order of magnitude” estimates that are typically obtained in the early phases of model building, should be sufficient without the need for their painstaking refinement. Conversely, if network results are sensitive to the precise values of probabilities, a lot of effort has to be devoted to obtaining precise estimates. The question whether precision matters has, thus, important practical implications on knowledge engineering for Bayesian networks.

There is a popular belief, supported by some anecdotal evidence, that Bayesian network models are tolerant to imprecision in their numerical parameters. There are two lines of research that attempt to address this question systematically. The first line of work focuses on studying whether introducing noise in the parameters affects the models' accuracy. The experiments conducted introduce noise into the parameters and tests the impact of that noise on the network's diagnostic accuracy. The results of these experiments are mixed: Pradhan et al. [3] argue that Bayesian networks are not sensitive to noise over a wide range of noise while Onisko and Druzdzel [4, 5] suggest more caution, agreeing at the same time that small amount of noise has minimal impact on accuracy. The second line of work, called collectively sensitivity analysis, focuses on identifying parameters that are crucial for models' accuracy. Sensitivity analysis studies how much a model output changes as various model parameters vary through the range of their plausible values. It allows to get insight into the nature of the problem and its formalization, helps in refining the model so that it is simple and elegant, containing only those factors that matter, and checks the need for precision in refining the numbers [6]. It is theoretically possible that small variations in a numerical parameter cause large variations in the posterior probability of interest. Van der Gaag and Renooij [7] found that real networks may indeed contain such critical parameters. Chan and Darwiche [8] provide a theoretical explanation of their findings. Coupé et al. [9] showed empirically in one-way sensitivity analysis that a satisfactory network can be quantified by obtaining well-informed estimates for these parameters that are highly influential while other parameters can receive only rough estimates.

This paper probes the question whether Bayesian network models as a whole are sensitive to precision of their parameters. We manipulate the precision of Bayesian network parameters, starting with their original values and rounding them systematically to progressively rougher scales. This models a varying degree of precision of the parameters. Our results show that the diagnostic accuracy of Bayesian network models is very sensitive to imprecision in probabilities, if these are plainly rounded. However, the main source of this sensitivity appears to be in rounding small probabilities to zero. When zeroes introduced by rounding are replaced by very small non-zero values, imprecision resulting from rounding has almost no impact on models' diagnostic accuracy.

The remainder of this paper is structured as follows. Section 2 reviews existing work on the application of Bayesian networks in medical diagnosis. Section 3 provides a brief review of relevant literature on the topic of rounding probabilities. Sections 4 and 5 introduce the models and describe the results of our experiments, respectively. Finally, Section 6 summarizes the main insights obtained from our results.

2. Bayesian network models in medical diagnosis

The earliest work on medical expert systems was based on Bayesian approach [10, 11]. Pioneer medical systems based on Bayesian networks included the Nestor system [12] for diagnosis of endocrinology disorders, Munin [13], a medical system for diagnosing neuromuscular disorders, and Alarm [14], a system monitoring patients in intensive care units. Other notable systems were Pathfinder IV [15], a medical system for diagnosis of the lymph system diseases, and the decision-theoretic version of Qmr, a system for diagnosis in internal medicine based on the Cpcs model (Computer based Patient Case Simulation system) [16]. Other medical applications include Diaval [17], a diagnostic expert system for echocardiography or a Bayesian network model for oesophageal cancer [18]. Bayesian networks were also applied to management of infectious diseases in intensive care units [19]. A special issue of the journal Artificial Intelligence in Medicine [20] was devoted to applications of Bayesian networks in biomedicine and health-care. In the last decade, also dynamic Bayesian networks (DBNs), a temporal extension of Bayesian networks, found their applications in medicine. Early work in this direction was done by Leong and colleagues e.g., [21, 22]. Selected applications of DBNs in medicine included also a DBN for management of patients suffering from a carcinoid tumor [23], or NasoNet, a system for diagnosis and prognosis of nasopharyngeal cancer [24]. DBNs were also used in cellular systems [25] or for modeling dynamics of organ failure in patients in intensive care units [26].

Bayesian network models produce posterior probability distributions over hypotheses. In case of a diagnostic network, the output of a model can be viewed as an assignment of posterior probabilities to various disorders. In order to make a diagnostic decision, one needs to know the probabilities of rival hypotheses (in the idealized case, the joint probability distribution over all disorders). This allows for weighting the utility of correct against the disutility of incorrect diagnosis. If the focus of reasoning is differential diagnosis, it is of importance to observe how the posterior in question compares to the posteriors of competing disorders.

3. Rounding of probability distributions

Approximating a number amounts to rounding it to a value that is less precise than the original value. For example, according to the U.S. Census Bureau,¹ the estimated population of the World on 2 December 2011 at 6:07 UTC was 6,978,614,924. This number can be rounded to 6,978,615 thousand, 6,979 million, or 7 billion respectively, each successive rounding leading to some loss of precision. While several rounding rules exist, the most common, applied to the example above, rounds the fractional part to the nearest integer.

Rounding probabilities and, in general, proportions can be approached similarly, although there is an additional complication. If we round a set of proportions using a standard rounding method, the sum of rounded numbers will not necessarily equal to 1.0. In fact, as the number of categories approaches infinity, the probability that the sum of their rounded weights is equal to 1.0 approaches zero [27]. This problem has been studied for over two centuries with basic analysis conducted around the time of the design of the United States constitution, where the motivation for the research was the desire to develop rules for fair political representation. A moderately rich literature on the topic exists that studies various algorithms for ensuring that the sum of rounded proportions does add to 1.0. Balinski and Young [28], in their excellent monograph, demonstrate that among all rounding procedures only quotient methods (also called multipler methods) are free from irritating paradoxes.

For our experiments, we selected a generic stationary rounding algorithm for proportions based on a multiplier method, described in Heinrich et al. [29], and summarized below. The algorithm has three parameters: (1) stationarity parameter q (most common value used in rounding is q = 0.5), (2) accuracy n (this is the number of intervals that the proportions are to be expressed in, so n = 10 gives us the accuracy of 0.1), and (3) a global multiplier ν (the value of ν is typically chosen to be ν = n).

Let (w₁, w₂, …, w_c) be a vector of c weights. The algorithm focuses on finding a vector of integer numerators (N_q,1, N_q,2, …, N_q,c), such that ${\sum }_{i=1}^c{N}_{q,i}=n$, that uniquely determines the rounded weights. To derive a rounded weight w_q,i, it is sufficient to divide N_q,i by n. To obtain the numerators N_q,i, i = 1, …, c, we first compute the discrepancy D,

$$D=\left(\sum _{j\le c}{[\nu w_j]}_q\right)-n,$$

which is a random variable with integer values in the interval (ν − n − cq, ν −n + c(1 − q)). Then, for j = 1, …, c, we adjust the initial assignment [νw_j]_q to obtain the final numerators

$$N_{q,j}={[\nu w_j]}_q-sgn(D)m_{j,n}(D),$$

where m_j,n(D) is the count of how often index j appears among the |D| smallest quotients

$$\{\begin{array}{ccc}\frac{k-\nu w_i+{[\nu w_i]}_q+q-1}{w_i}& \text{for}i=1,\dots ,c\text{and}k=1,\dots ,-D;& \text{when}D<0;\\ \frac{k+\nu w_i+{[\nu w_i]}_q-q}{w_i}& \text{for}i=1,\dots ,c\text{and}k=1,\dots ,D;& \text{when}D>0\text{.}\end{array}$$

Example 1

Let (0.04, 0.14, 0.46, 0.36) be a vector of 4 weights and the desired accuracy be n = 10. We conveniently set ν = n = 10 and use the standard value of the rounding parameter q = 0.5. This yields the initial values of numerators νw = (0, 1, 5, 4) and the value of discrepancy D = 0. No adjustment to the numerators is needed and we obtain the vector of rounded weights of (0.0, 0.1, 0.5, 0.4) by dividing each of the numerators by n = 10.

Example 2

However, an initial vector of weights (0.04, 0.14, 0.48, 0.34) yields the initial values of numerators νw = (0, 1, 5, 3) and the value of discrepancy D = −1. Using the formula for D < 0, we compute the quotients of (2.5, 0.71, 1.08, 0.29) and adjust w₄ (the smallest of the quotients was for i = 4) by 1, yielding D = 0, the final vector of numerators (0, 1, 5, 4) and the resulting rounded weights of (0.0, 0.1, 0.5, 0.4).

4. Models studied

Our desire was to investigate the sensitivity of accuracy of diagnostic Bayesian network models to precision of their parameters in a context that is as close to reality as possible. We had a thorough understanding of one diagnostic Bayesian network model, the Hepar II model. In addition to Hepar II, we created diagnostic Bayesian network models from six real medical data sets from the Irvine Machine Learning Repository. This section describes these models.

We owe the reader an explanation of the metric that we used in testing the diagnostic accuracy of models. We define diagnostic accuracy as the percentage of correct diagnoses on real patient cases. This is obviously a simplification, as one might want to know the sensitivity and specificity data for each of the disorders or look at the global quality of the model in terms of ROC (Receiver Operating Characteristics) curve or AUC (Area Under the ROC Curve). This, however, is complicated in case of models focusing on more than one disorder — there is no single measure of performance but rather a measure of performance for every single disorder. We decided thus to focus on the percentage of correct diagnoses. Furthermore, because Bayesian network models operate only on probabilities, we assume that each model indicates as correct the diagnosis that is most likely given patient data.

4.1. The Hepar II model

The Hepar II model [30] is one of the largest practical medical Bayesian network models available to the community, carefully developed in collaboration with medical experts and parametrized using clinical data. The model consists of 70 variables modeling 11 different liver diseases and 61 medical findings, such as patient self-reported data, signs, symptoms, and laboratory tests results. The structure of the model, (i.e., the nodes of the graph along with arcs among them) is based on medical literature and conversations with domain experts, a hepatologist Dr. Hanna Wasyluk, a pathologist, Dr. Daniel Schwartz, and a specialist in infectious diseases, Dr. John N. Dowling. The elicitation of the structure took approximately 50 hours of interviews with the experts, of which roughly 40 hours were spent with Dr. Wasyluk and roughly 10 hours spent with Drs. Schwartz and Dowling. This includes model refinement sessions, where previously elicited structure was reevaluated in a group setting. The numerical parameters of Hepar II (there are 2,139 of these in the most recent version), i.e., the prior and conditional probability distributions, were learned from Hepar data. The Hepar database was created in 1990 and has been thoroughly maintained since then by Dr. Wasyluk at the Gastroentorogical Clinic of the Institute of Food and Feeding in Warsaw, Poland. Each hepatological case in the database is described by over 160 different medical findings, such as patient self-reported data, results of physical examination, laboratory tests, and finally a histopathologically verified diagnosis. The version of the Hepar data set that was available to us consisted of 699 patient records.

All our tests of diagnostic accuracy of Hepar II relied on its ability to discern among the 11 modeled liver disorders given the observations contained in each of the patient records. The most likely disorder became by definition Hepar II's diagnosis. Because we used the same, fairly small database to learn the model parameters, we applied the method of “leave-one-out” [31], which involved repeated learning from 698 records out of the 699 records available and subsequently testing it on the remaining 699th record. With diagnostic accuracy defined as above, the Hepar II model reaches the diagnostic accuracy of 57%. The correct diagnosis was among Hepar II's first two most likely disorders in 69% of the cases, among the three most likely disorders 75% of the cases, and among the first four most likely disorders 79% of the cases [32]. The problem of diagnosing a liver disorder without liver biopsy is hard and the model compared very favorably against general practitioners on a randomly selected set of 10 patient cases [33]. More details about Hepar II and its performance can be found in [30, 34]. Readers interested in the Hepar II model can download it from Decision Systems Laboratory's model repository at http://genie.sis.pitt.edu/ (Accessed: 26 June 2012).

4.2. The Irvine Machine Learning Repository models

In addition to Hepar II, we selected six data sets from the Irvine Machine Learning Repository: Acute inflammation [35], SPECT Heart [36], Cardiotocography [37], Hepatitis [38], Lymphography [39], and Primary Tumor [39]. In our selection, we were guided by the following two criteria: (1) Because we wanted to test the diagnostic accuracy of a model, the data set had to have at least one disorder variable, (2) In order to avoid confounding our study with additional modeling issues, we tried to avoid data sets with many missing values and many continuous variables.

Table 1 presents basic characteristics of the selected data sets, including Hepar data. Detailed description of each of the data sets can be found at the Irvine Machine Learning repository, in http://archive.ics.uci.edu/ml/ (Accessed: 26 June 2012).

Table 1. Medical data used in our experiments.

data set	#instances	#variables	variable types	#classes	mva
Acute Inflammation	120	8	categorial, integer	4	no
SPECT Heart	267	23	categorial	2	no
Cardiotocography	2,126	22	categorical, real	3	no
Hepatitis	155	20	categorial, real	2	yes
Lymphography	148	19	categorial, integer	4	no
Primary Tumor	339	18	categorial, integer	20	yes
Hepar	699	70	categorial, real	11	yes

^amv stands for missing values

We learned a Bayesian network model from each of the data sets in the following way. We first learned three different networks, using (1) a basic Bayesian search algorithm, (2) a Tree Augmented Network (TAN) learning algorithm, and (3) Naive Bayes algorithm, as implemented in GeNIe [40]. We subsequently tested these three networks for their accuracy using the leave-one-out method. Finally, of the three networks we selected the one that performed best (in terms of its diagnostic accuracy) on the original data set. All models that made it through this cut were those learned by the Bayesian search algorithm, except for Lymphography, created by the TAN learning algorithm, and Hepar II, constructed based on expert knowledge. Because each of the learning algorithms that we used accepts only discrete data, prior to learning we discretized those variables that were continuous. We used expert-based discretization, relying on domain-specific thresholds (e.g., in case of total bilirubin test, we divided the range into three intervals: normal, moderately high, and high). Because none of the learning algorithms was able to handle missing data, for the purpose of structure learning, we temporarily replaced all missing values with the “normal” state of the corresponding variable. This, as we demonstrated earlier [32] leads typically to best performance in medical systems. Table 2 presents the basic statistics of the Bayesian network models that resulted from this procedure, including the Hepar II model.

Table 2. Bayesian network models used in our experiments.

model	typea	#nodes	μ #states	μ in-degree	#arcs	#pars
Acute Inflammation	BSA	8	2.13	1.88	15	97
SPECT Heart	BSA	23	2.00	2.26	52	290
Cardiotocography	BSA	22	2.91	2.86	63	13,347
Hepatitis	BSA	20	2.50	1.90	38	465
Lymphography	TAN	19	3.00	1.84	35	940
Primary Tumor	BSA	18	3.17	1.83	33	877
Hepar II	Expert	70	2.24	1.73	121	2,139

^atype stands for structure type (BSA: Bayesian Search Algorithm network; TAN: Tree Augmented Network; Expert: structure elicited from experts);

#nodes: number of nodes; μ #states: average number of states per node; μ in-degree: average number of parents per node; #arcs: number of arcs; #pars: number of numerical parameters

We assumed that the models obtained this way were perfect in the sense of containing parameters as precise as the data would allow. The accuracy measure that we applied was identical to that described in the previous section for Hepar II, i.e., we deemed the most likely disorder to be the model's diagnosis.

5. The experiments

We performed three experiments to investigate how progressive rounding of models' probabilities affects their diagnostic accuracy. To that effect, we have successively created various versions of the models with different precision of parameters and tested the diagnostic accuracy of these versions. The following two sections describe the rounding process and the observed results respectively. Because each of the data sets was moderately sized, to maximize the training set and to avoid bias, we also used the leave-one-out procedure in testing the networks, i.e., for a data set of size n, we trained the corresponding network structures by means of the expectation-maximization (EM) algorithm using n − 1 records, rounded the parameters learned, and then tested the network on the remaining nth record, repeating the procedure n times, each time for a different test record. For this procedure we used the original data sets with missing values.

5.1. Progressive rounding of model parameters

For the purpose of our experiment, we used the accuracy values of n = 100, 10, 5, 4, 3, 2, and 1. As the reader may recall from Section 3, these correspond to the number of intervals in which the probabilities fall. And so, for n = 10, we divided the probability space into 10 intervals and each probability took one of 11 values, i.e., 0.0, 0.1, 0.2, …, 0.9, and 1.0. For n = 5, each probability took one of six values, i.e., 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0. For n = 2, each probability took one of only three values, i.e., 0.0, 0.5, and 1.0. Finally, for n = 1, the smallest possible value of n, each probability was either 0.0 or 1.0.

Figure 1 shows scatter plots of all 2,139 Hepar II's parameters (horizontal axis) against their rounded values (vertical axis) for n equal to 10, 5, 2, and 1. Please note the drastic reduction in precision of the rounded probabilities, as pictured by the vertical axis. When n = 1, all rounded probabilities are either 0 or 1. Also, note that the horizontal bars in the scatter plot overlap. For example, in the upper-right plot (n = 5), we can see that an original probability p = 0.5 in Hepar II was rounded sometimes to 0.4 and sometimes to 0.6. This is a simple consequence of the surrounding probabilities in the same distribution and the rounding algorithm making adjustments that ensured that the sum of rounded probabilities is 1.0.

Figure 1.

Rounded vs. original probabilities for various levels of rounding precision.

Figure 2 shows another view of the effect that progressive rounding has on the histogram of all Hepar II's parameters. The upper-left plot is the histogram of all 2,139 original model parameters. The subsequent plots show the histograms of parameters after rounding to 100, 10, and 5 intervals respectively. Please note that rounding preserves the basic shape of the original histogram, although this shape is progressively malformed.

Figure 2.

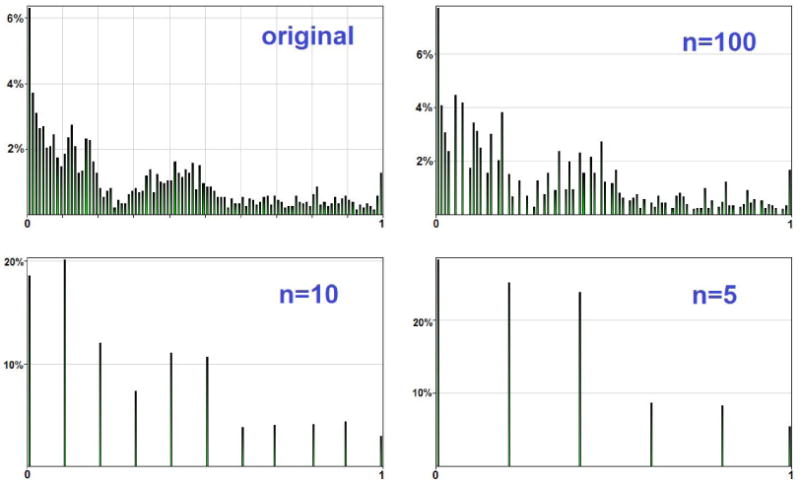
Histogram of the original and rounded parameters of the Hepar II model.

5.2. Effect of imprecision on accuracy of medical diagnostic systems

For the purpose of our experiments, we assumed that the model parameters were perfect and, effectively, the diagnostic accuracy achieved was the best possible. In the experiments, we studied how this baseline accuracy degrades with the reduction in parameter precision. Of course, in reality the parameters of the model may be imperfect and the original accuracy of the model can be improved upon.

5.2.1. Experiment 1

In our first experiment, we computed the diagnostic accuracy of various versions of our models, as produced by the straightforward rounding procedure. Figure 3 shows a summary of the main results for Hepar II in both graphical and tabular format. The horizontal axis in the plot corresponds to the number of intervals n in logarithmic scale, i.e., value 2.0 corresponds to the rounding n = 100, and value 0 to the rounding n = 1. Intermediate points, for the other roundings can be identified in-between these extremes.

Figure 3.

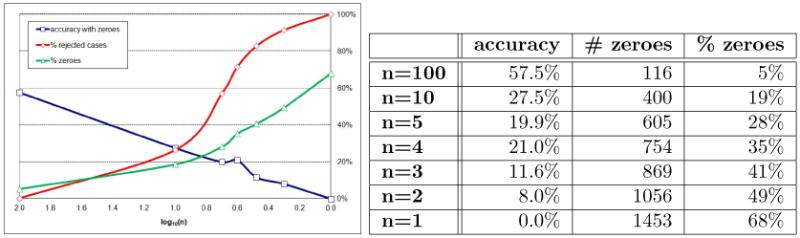
Diagnostic accuracy of Hepar II, % of rejected cases, and % of zeroes, as a function of the logarithm of parameter precision.

The three curves on the plot (Figure 3) show: diagnostic accuracy, the percentage of rejected cases, and the percentage of zeroes. A system rejects cases that the model judges as impossible. This happens when we try to enter an observation that is impossible given other observations. A vivid example of such an observation would be pregnancy in a male patient. Because each of the records in the Hepar and the Irvine data sets are real patient cases, the problem lies in all such cases with the model and we counted a record rejected by the system as a record diagnosed incorrectly.

The plot in Figure 3 shows that the diagnostic accuracy of the system decreases exponentially (we observe almost a straight line in logarithmic scale). We examined this further and came to the following conclusion. The algorithm presented in Section 3 rounds proportions on a linear scale. A small absolute difference between two proportions is treated in the same way, regardless of whether it is part of a large fraction or it is close to zero. In Example 2, the algorithm rounded 0.14 to 0.1, 0.34 to 0.3, and at the same time 0.04 to 0.0. While the first two rounding make perfect sense, the last one, i.e., rounding 0.04 to zero is quite a drastic step as the changes for 0.04 to 0.0 is infinite in relative terms. Zero is a special probability denoting an impossible event. A quick examination of Bayes theorem will show that once an event is found to be of zero probability, its probability remains zero, no matter how strong the evidence in its favor materializes later. This has serious practical consequences for a modeling formalism based essentially on Bayes theorem.

It can be shown that the rounding algorithm will turn most probabilities that are smaller than 1/(2n) into zero. As the right-most column in Figure 3 shows, there is an increasing proportion of zeroes among the model parameters as precision decreases. Please note that it is clearly the zeroes that cause that models reject patient cases. It is impossible to enter an observation that has zero probability. With an increased percentage of zero parameters, there is an associated increase in the percentage of posteriors that are zero.

Figure 4 shows the diagnostic accuracy of Hepar II as the function of the percentage of zeroes in the model — there is a clear, almost linear dependence between the two.

Figure 4.

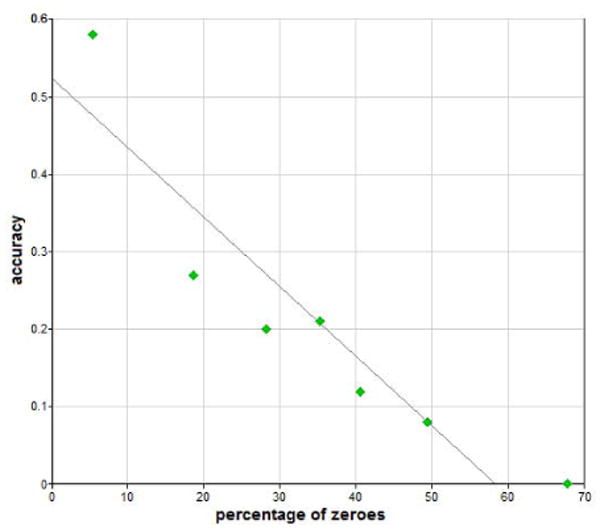
Diagnostic accuracy as a function of the percentage of zeroes for the Hepar II model.

We repeated the experiment for the six networks built from the Irvine repository data. Figure 5 shows the diagnostic accuracy of the six models as a function of the logarithm of parameter precision on the same plot. The results were qualitatively identical to those involving Hepar II.

Figure 5.

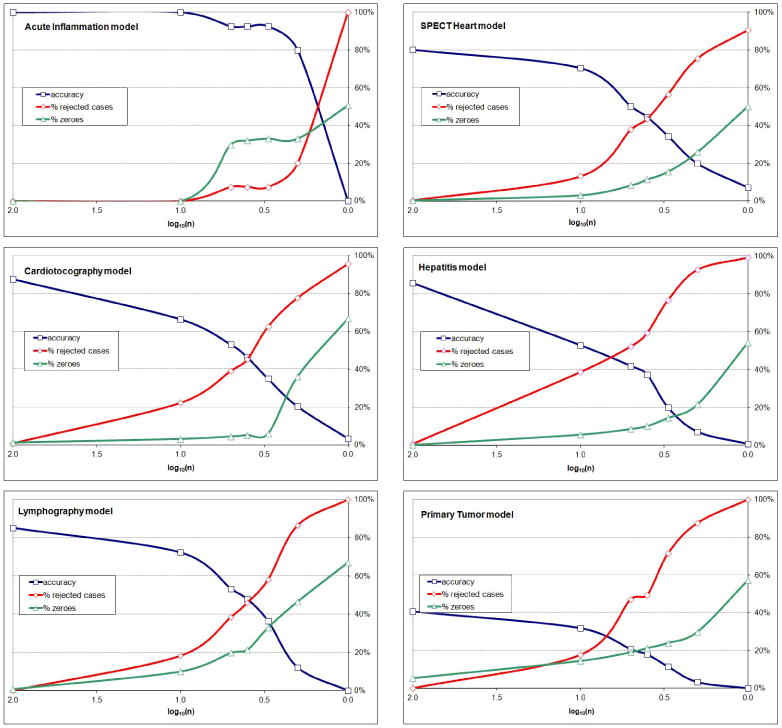
The diagnostic accuracy, % of rejected cases, and % of zeroes of the six Irvine models as a function of the logarithm of parameter precision.

5.2.2. Experiment 2

Our next experiment focused on the question whether zeroes are to blame for the exponential decrease in model's diagnostic accuracy. In this experiment, we replaced all zeroes introduced by the rounding algorithm by small ε probabilities and subtracted the introduced εs from the probabilities of the most likely outcomes in order to preserve the constraint that the sum of probabilities should be equal to 1.0. While this caused a small distortion in the probability distributions (e.g., a value of 0.997 instead of 1.0 when ε = 0.001 and three zeroes were transformed into ε), it did not introduce sufficient difference to invalidate the effect of rounding on the parameters. To give the reader an idea of what introducing the εs entailed in practice, we will reveal the so far withheld information that the plots in Figure 1 were obtained for data with ε = 0.001.

The effect of this modification on Hepar II's diagnostic accuracy was dramatic. We show it in Figure 6, each line for a different value of ε (we preserved the result of Experiment 1 in the plot). The meaning of the horizontal and vertical axes is the same as in Figure 3. As we can see, the actual value of ε did not matter much (we tried three values: 0.0001, 0.001, and 0.01). In each case, Hepar II's performance was barely affected by rounding, even when n = 1, i.e., when all probabilities were either ε or 1 − ε.

Figure 6.

Diagnostic accuracy of Hepar II as a function of the logarithm of parameter precision and ε.

We repeated the experiment for the six networks based on the Irvine repository data. Figure 7 shows the diagnostic accuracy of the six models as a function of the logarithm of parameter precision on the same plot. We used ε = 0.001 in all cases. The results were qualitatively identical to those involving Hepar II.

Figure 7.

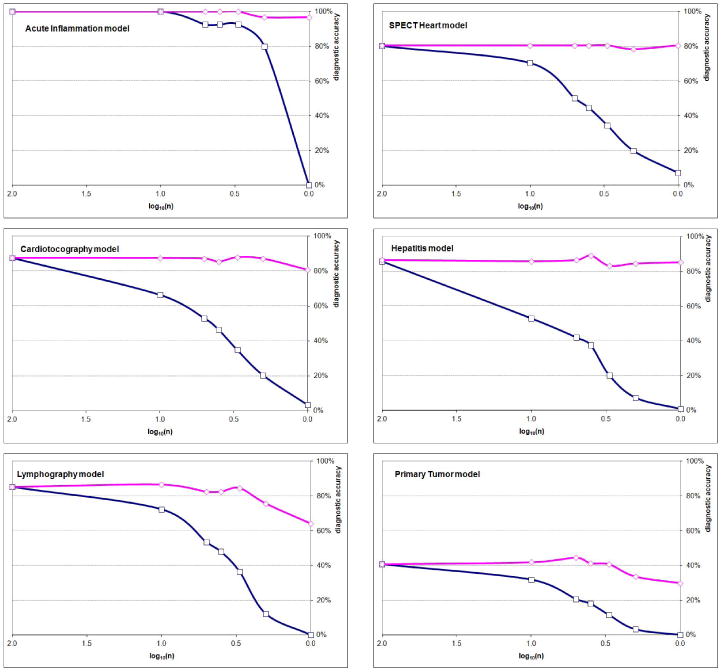
The diagnostic accuracy of the six Irvine models as a function of the logarithm of parameter precision with zeroes replaced by a small ε (upper curve of a plot) and with zeroes (bottom curve of a plot).

5.2.3. Experiment 3

When testing the diagnostic accuracy of models, we may be interested in both (1) whether the most probable diagnosis indicated by the model is indeed the correct diagnosis, and (2) whether the set of w most probable diagnoses contains the correct diagnosis for small values of w. The latter focus is of interest in diagnostic settings, where a decision support system only suggests possible diagnoses to a physician. The physician, who is the ultimate decision maker, may want to see several top alternative diagnoses before choosing one.

Our next experiment focused on the influence of precision in probabilities on Hepar II's accuracy for “windows” of size 1, 2, 3, and 4. Figure 8 shows a summary of the results in both graphical and tabular format. We can see that the stability of Hepar II's accuracy is similar for all window sizes. This suggests that decreasing precision of parameters does not have much impact on the order of diagnoses (i.e., the order among the possible disorders imposed by their posterior probability).

Figure 8.

Diagnostic accuracy of Hepar II as a function of the logarithm of parameter precision and various window sizes (w=1, 2, 3, 4).

5.3. Summary of the results

The experiments' results provide evidence that as long as we avoid zeroes among model parameters, diagnostic accuracy of Bayesian network models does not suffer from decreased precision of their parameters. The plots of models' accuracy as a function of the number of intervals are almost horizontal, which means that even for as few as two or even one interval, models perform reasonably close to the idealized situation, when all parameters are perfectly precise.

6. Discussion

We described a series of experiments studying the influence of precision in parameters on model accuracy in the context of a practical medical diagnostic model, Hepar II, and six additional models based on real medical data from the Irvine Machine Learning Repository. We believe that the study was realistic in the sense of studying real models and focusing on a practical performance measure.

While our experiments offer merely a handful of data points that shed light on the question of the importance of parameter accuracy in Bayesian networks, we observed a clear pattern across all tested models. Our results indicate that the diagnostic accuracy of Bayesian network models is sensitive to imprecision in probabilities, if these are rounded. However, the main source of this sensitivity appears to be in rounding small probabilities to zero. When we replaced zeroes introduced by rounding by very small non-zero ε values, imprecision resulting from rounding had minimal impact on the models' diagnostic accuracy. Furthermore, the precise value of ε did not seem to matter – our networks performed similarly well for ε ranging between 0.01 and 0.0001.

Sensitivity of Bayesian networks to zero values is not surprising. An examination of Bayes theorem, the formula on which all reasoning in Bayesian networks rests, shows that once an event's probability becomes zero, it will never change, regardless of the strength of subsequent evidence supporting the event. We recommend that unless they are justified with high certainty by domain knowledge, zeroes should be avoided in models. In case of learning models and their parameters from data, we recommend methods that avoid zeroes, such as Laplace estimation or, currently most popular, Bayesian approach with Dirichlet priors. Avoiding zeroes in medical models is fairly natural. In fact, we have hardly seen any zeroes in existing practical models, which reflects a widely shared belief that few things are impossible when it comes to human health.

Our study of the influence of precision of parameters on the diagnostic accuracy of Bayesian networks is inspired by a study performed by Clancey and Cooper [41], who probed the sensitivity of the MYCIN expert system [42] to the accuracy of its numerical specifications of degrees of belief, certainty factors (CF). CFs are considered an ad-hoc measure of uncertainty that does not suffer from the problems encountered in probability, such as the need to add up to 1.0 or the importance of zeroes. Similarly to our result, Clancey and Cooper noticed minimal effect of precision on the performance of MYCIN. However, they attributed it partly to a broad coverage of microorganisms that a possibly incorrectly recommended antibiotic would cover, resulting in a reasonably correct therapy.

In case of Bayesian networks we believe that a critical factor may be presentation of ordinal relationships among the parameters. Diagnosis, as interpreted typically in probabilistic context, amounts to finding the most probable hypothesis, which also rests on ordinal relationships among disorders.

The results of our experiments touch the foundations of qualitative modeling techniques. As qualitative schemes base their results on approximate or abstracted measures, one might ask whether their performance will match that of quantitative schemes, either in terms of their strength or the correctness of their results. Because our models performed reasonably well, even when every parameter in the model was equal either to ε or 1 − ε, it seems that approximate order of magnitude schemes might offer acceptable recommendations, at least if they conform to the basic rules of probability calculus, which is what our models did.

Our results support another approach, suggested by an anonymous reviewer. One might focus probability elicitation on obtaining verbal probability estimates, such as those on the Likert scale [43], covering the categories “very unlikely”, “unlikely”, “50-50”, “likely” and “very likely.” This should, of course, be done with much caution, as the meaning of verbal phases typically varies from human to human and is sensitive to context [44].

We have also studied the influence of rounding selectively parameters in each of the four major classes of variables in Hepar II: (1) medical history, (2) physical examination, (3) laboratory tests, and (4) diseases, on the diagnostic accuracy. Hepar II was the only model among the models that we studied and that we understood sufficiently well to make this distinction. However, the observed differences in diagnostic accuracy for these four classes were minimal. Rounding of parameters of variables representing the results of laboratory tests had a slightly higher impact on the diagnostic accuracy than the parameters in the other three groups.

Prompted by a question from an anonymous reviewer, we tested the impact of the structure type (i.e., naive Bayes, TAN, and general networks) on the effect of rounding. To this effect, we generated the three types of structures for the same data sets of the Irvine Machine Learning repository. We have observed no qualitative difference between the three classes of networks and rather small and inconsistent quantitative effects.

The study designed in this paper is related to other studies that we performed [4, 5]. In those experiments, we introduced noise into parameters, similarly to Pradhan et al. [3]. When the amount of noise (which we controlled) was sufficiently large, it sometimes led to a change in the ordinal relations among the parameters. This noticeably impacted the diagnostic accuracy of Bayesian network models.

Few empirical studies are ever complete. Three questions related to our experiments are worth further probing: (1) Will replacing true zeroes among the parameters by non-zero values lead to deterioration of model accuracy? (2) To what degree does imprecision in model structure impact accuracy? (3) Will other performance criteria outside of the most likely disorder, such as Most Probable Explanation (MPE) or Maximum A-Posteriori assignment (MAP), also be impacted? One difficulty in addressing the first question is that there are few models that have genuine zeroes among their parameters and, effectively, experiments will have to be performed on artificial models. The experimental results presented in this paper do not seem to shed much light on the importance of model structure. However, we are currently focusing in our work on the influence of structure on accuracy.