Diffeomorphic Shape Trajectories for Improved Longitudinal Segmentation and Statistics

Abstract

Longitudinal imaging studies involve tracking changes in individuals by repeated image acquisition over time. The goal of these studies is to quantify biological shape variability within and across individuals, and also to distinguish between normal and disease populations. However, data variability is influenced by outside sources such as image acquisition, image calibration, human expert judgment, and limited robustness of segmentation and registration algorithms. In this paper, we propose a two-stage method for the statistical analysis of longitudinal shape. In the first stage, we estimate diffeomorphic shape trajectories for each individual that minimize inconsistencies in segmented shapes across time. This is followed by a longitudinal mixed-effects statistical model in the second stage for testing differences in shape trajectories between groups. We apply our method to a longitudinal database from PREDICT-HD and demonstrate our approach reduces unwanted variability for both shape and derived measures, such as volume. This leads to greater statistical power to distinguish differences in shape trajectory between healthy subjects and subjects with a genetic biomarker for Huntington’s disease (HD).

1 Introduction

Statistical shape modeling and analysis is of critical importance for better understanding of longitudinal imaging and shape data, especially in the context of dynamic processes like aging and disease progression. To model evolution of shape, many regression approaches for cross-sectional data have been proposed [1–4]. However, regression has limitations when applied to longitudinal analysis, since each individual could start at a different point and evolve in a different manner. Longitudinal studies therefore entail development of subject-specific spatiotemporal models, and also a way to compare these models across different subjects [5–8].

Longitudinal image data has several sources of variability. First, there is inherent biological variability, both within a subject changing over time and also between subjects in a population. The goal of longitudinal analysis is to quantify this variability and make inferences about changes over time in a population. However, longitudinal imaging data also include unwanted sources of variability, such as noise in image acquisition, segmentation and registration errors, and human expert judgment, among others. These extraneous errors tend to dampen statistical power, especially when trying to distinguish between trajectories of two different populations, e.g., healthy and diseased.

In this paper, we propose a framework that first seeks to reduce this extraneous variability, thus improving consistency of longitudinal segmentations in the first stage. We follow the procedure of [9] by estimating diffeomorphic geodesic trajectories of shape evolution for each individual. The estimated trajectories are smooth, resulting in temporally consistent and more biologically plausible shape evolution. We then employ a mixed effects model for shapes [10, 7] to conduct longitudinal statistical shape analysis on the consistent shape trajectories. We demonstrate the benefit of our two stage approach by a comparison of longitudinal mixed-effects analysis on cortical volumes obtained from raw observed data against consistent measurements obtained from personalized spatiotemporal shape models. We also show our method reduces unwanted variability for both shape and derived measures, such as volume. This leads to greater statistical power to distinguish shape evolution between healthy subjects and subjects with a genetic biomarker for Huntington’s disease (HD).

2 Methodology

We present here methodology for the statistical analysis of longitudinal shape complexes. This is based on spatiotemporal modeling of diffeomorphic shape trajectories (Section 2.1) to produce temporally consistent shape sequences. Estimated model trajectories represent more biologically plausible and smooth shape changes associated with anatomical evolution in time. Statistical measures and group hypothesis testing is then conducted on both scalar measurements extracted from shape as well as the shape complexes themselves. For measuring individual and group shape differences, we estimate a multivariate mixed-effects model (Section 2.2) for shapes, designed to take advantage of longitudinal shape data.

2.1 Spatiotemporal modeling for consistency in longitudinal segmentation

Anatomical change over time associated with neurodevelopment or aging is assumed to be a smooth process. That is, the trajectory of a particle on an anatomical surface should be differentiable, with no instantaneous change of direction. The presence of a disorder such as Huntington’s disease (HD) would not invalidate the smoothness assumption. Rather, the neurodegeneration process associated with HD has been observed as a temporally smooth process [11]. However, our anatomical measurements (medical images and extracted anatomical shapes) are often not representative of samples from a smooth process, due to the natural variability attributed to image acquisition, subject positioning, segmentation, etc. Without temporal consistency in our measurements, it becomes difficult to distinguish between anatomical change associated with disease from changes due to noise.

One emerging model of smooth anatomical change is to consider continuous transformations of the ambient space by differentiable and invertible deformations. We model anatomical trajectories by a geodesic flow of diffeomorphisms that continuously deforms a given anatomical configuration X₀ over time to closely match a set of observed anatomical shapes O_ti [9]. The initial anatomical configuration (baseline shape), as well the flow of diffeomorphisms ϕ_t, are estimated by minimizing the criterion

$$E({\mathbf{X}}_0,{\varphi }_t)=\sum _{i}D({\varphi }_{t_i}({\mathbf{X}}_0)-{\mathbf{O}}_{t_i})+\text{Reg}({\varphi }_t),$$

where D represents a distance metric on shapes and Reg(ϕ_t) is a measure of the regularity of the geodesic flow of diffeomorphisms ϕ_t. For choice of D, we favor the metric on currents, which is robust to topological differences and allows for comparison between shapes without the need for point correspondence. Also, being in an infinite-dimensional space of diffeomorphisms, geodesic trajectories have the flexibility to capture complex deformations.

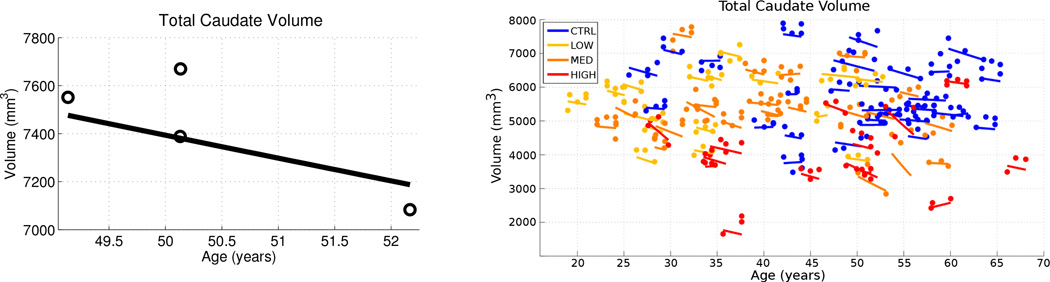
The continuous geodesic flow of diffemorphisms ϕ_t is applied to the estimated anatomical configuration to produce a continuous and temporally consistent sequence of shapes. The improved temporal consistency is illustrated on the left side of Fig. 1 by comparing the volume of observed caudates with the volume extracted continuously from the spatiotemporal model of caudate shape. Also note that we can now obtain shapes or measurements extracted from shapes at any time point of interest, not just those corresponding to observations.

Figure 1.

Left: For one subject, volume of observed caudates (open circles) and temporally consistent continuous volume extracted from diffeomorphic shape model (solid line). The difference in caudate volume extracted from scans obtained on the same day highlights the need for consistent segmentation. Right: Observed volume and volume extracted from diffeomorphic shape models for all 65 subjects. While the volume of the discrete shape observations show considerable variation, volume extracted from personalized models are continuous and temporally consistent.

2.2 Mixed effects model for shapes

We now have a diffeomorphic flow of anatomical shapes for each individual, from which we obtain shapes at time points corresponding to actual observations. These estimated shapes no longer represent independent (and potentially noisy) measurements, but instead take into account correlation between repeated scans of the same individual.

Statistical interpretation of longitudinal shape data is extremely useful in ascertaining differences in repeated image scans of an individual and also between individuals within and across populations. A compact statistical representation of shape was proposed by [10], wherein the surface of a shape is represented by a collection of points, also referred to as a particle system. Particle positions are optimized to be in correspondence across an ensemble of shape configurations. A faithful shape representation is achieved by minimizing a cost function, that balances a low residual error of model to data, also seeking configurations of uniformly-distributed correspondence positions on shape surfaces.

To analyze longitudinal data, [7] generalize the methods in [10] to incorporate a linear mixed-effects model in the optimization framework. Let Y_i be the longitudinal response variable for the ith individual (a shape configuration), and X_i denote the explanatory variable, typically time. The mixed-effects model for longitudinal correspondences is given as

$$Y_i=X_i(\alpha +b_i)+{\epsilon }_i,$$

where α are the fixed-effects parameters (group intercept, group slope), while b_i are random-effects parameters with ε_i being the error in correspondences for the ith individual. For details on model parameter estimation, see [7].

Hypothesis testing

In order to test the statistical significance of group-parameter differences between two groups of longitudinal data, [7] also outline a statistical hypothesis permutation test based on the Hotelling’s T² statistic.

Given two groups of data, {p₁, …, p_m} and {q₁, …, q_n}, with sample means p̄, q̄, recall that Hotelling’s T² statistic is a test statistic to test for significant differences between sample means, relative to the pooled sample covariance W:

$$W=\frac{{\sum }_i(p_i-\overline{p}){(p_i-\overline{p})}^T+{\sum }_i(q_i-\overline{q}){(q_i-\overline{q})}^T}{m+n-2}.$$

The T² statistic can be thought of as a squared Mahalanobis distance between the means, using the pooled covariance W. The sample T² statistic is given by

$$t^2=\frac{mn}{m+n}{(\overline{p}-\overline{q})}^T{W}^{-1}(\overline{p}-\overline{q}).$$

The permutation test procedure is as follows: (1) compute the t² statistic, (2) randomly permute (swap) data points between the p and q groups, computing a $t_k^2$ statistic for the permuted groups, (3) repeat step 2 for k = 1, …, P, (4) compute the p-value: p = B/(P + 1), where B is the number of $t_k^2<t^2$. The final p-value can be interpreted as the probability of finding a larger group difference by random chance under the null hypothesis (that there is no difference between the means). The underlying assumption of any permutation test is that the data should be exchangeable under the null distribution. Our null hypothesis is that the groups (e.g., healthy and diseased) are from the same distribution. We permute individuals (keeping their timepoints all intact), which under this null assumption is exchangeable.

To test for differences in anatomical trajectories between a healthy and disease group, also note that it is important to distinguish if the shape differences are present at baseline (intercept) or if they develop over time (slope). To make this distinction, we also separate the above Hotelling’s T² test into these two components.

3 Experimental Validation

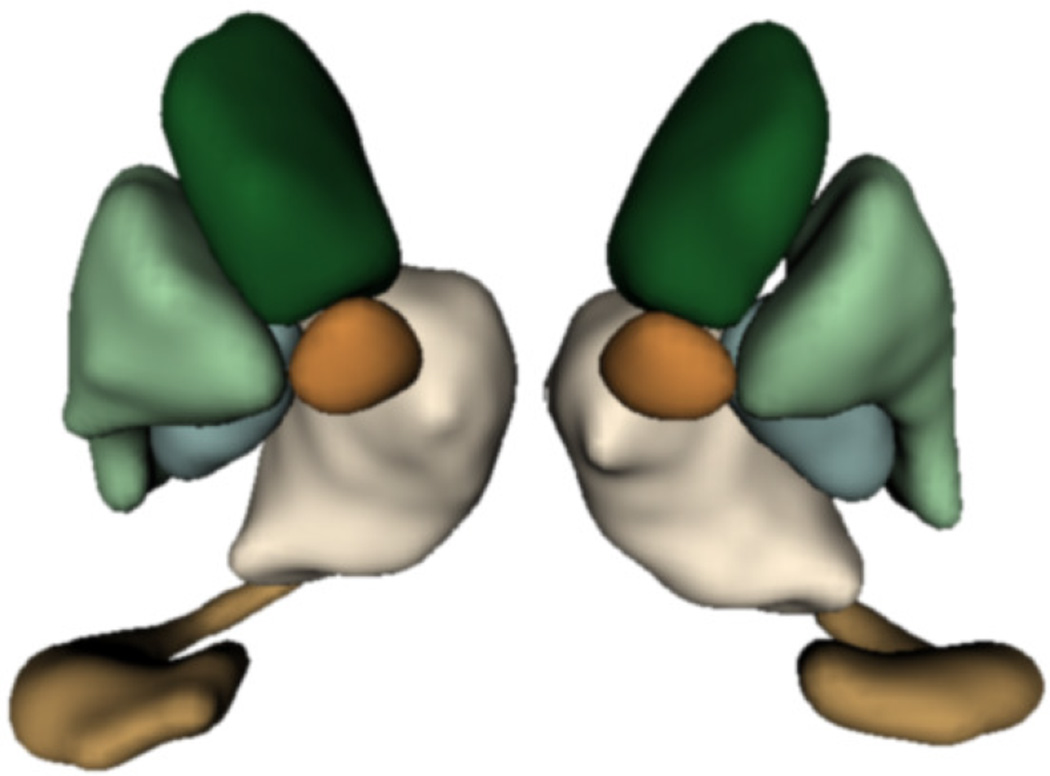
We study subcortical change associated with Huntington’s disease (HD), leveraging the longitudinal study PREDICT-HD. The longitudinal database consists of 65 female subjects: 23 controls (CTRL), 14 (LOW), 15 (MED), and 13 (HIGH). The LOW / MED / HIGH categories represent probability of onset of manifesting signs of HD. All subjects have had at least 3 MR images acquired approximately one year apart, with many subjects undergoing multiple scans per visit. Six subcortical pairs (caudate, putamen, hippocampus, thalamus, acumben, and pallidus) were segmented from each image (Fig. 2) and manually verified and cleaned [12].

Figure 2.

Example of six subcortical pairs extracted for each subject and timepoint.

The quality of each segmentation varies considerably for each time point, even when scans are obtained on the same day from the same scanner, as individual single-subject segmentation is prone to errors related to variability of imaging, image calibration, human expert judgment, and limited robustness of segmentation algorithms. While the segmentation quality is not easily assessed by viewing the 3D anatomical surfaces, the temporal inconsistency becomes clear by investigating volume extracted from the shapes. The right side of Fig. 1 shows the variability in segmentation, illustrated by the temporal inconsistency of observed caudate volume, motivating the need for temporally consistent segmentations which properly account for correlated longitudinal data.

Personalized spatiotemporal models of subcortical change

Continuous models of shape trajectory are estimated for each subject using the methodology outlined in 2.1, resulting in personalized and temporally consistent anatomical evolution. Model estimation does not require point correspondence, facilitating the inclusion of all subcortical shapes simultaneously without imposing any topological constraints. Each subject’s personalized model allows us to generate shapes at any instant in time, from which desired shape properties, such as volume, can be extracted. We can therefore obtain a continuous evolution of volume for all subcortical structures without any explicit modeling of volume. Fig. 1 shows caudate volume extracted from each subject’s continuous shape model, demonstrating the flexibility of the shape model to capture both linear and non-linear volume trends with no prior assumption or constraint on linearity. Though we only display caudate volume here, recall that each model is estimated by leveraging all shape data simultaneously (Fig. 2), which respects shape boundaries and locations, incorporating important geometric relationships between shapes.

Longitudinal analysis of striatal volume

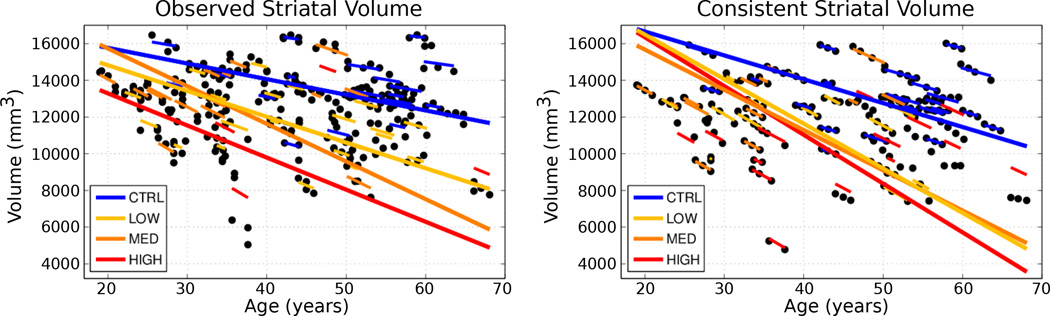
Here we conduct a univariate analysis of volume extracted from shape, as striatal volume loss has been shown to be associated with the progression of HD [11]. We aim to evaluate the benefit of spatiotemporal shape modeling, by comparing striatal volume extracted from the temporally consistent shapes with volume extracted from the raw shape observations. Figure 3 shows the results of linear mixed-effects analysis on striatal volumes for observed (left) and temporally consistent shapes (right), testing for the interaction between age and group membership. The estimated fixed-effects parameters for the temporally consistent (smoothed) category were found to be significant, as shown in Table 1. This demonstrates the benefit of spatiotemporal shape modeling, as striatal volumes extracted from the temporally consistent shapes provide better separation between the control and LOW groups, and also between the control and HIGH groups.

Figure 3.

Longitudinal mixed-effects analysis of striatal volumes obtained from observed shapes (Left) and temporally consistent shapes (Right). Volume data are shown as filled black circles with corresponding individual trends. Note the improvement of the model fit in the consistent striatal volume over the observed striatal volume, which results in lower standard error of estimated mixed-effects parameters. (See Table 1)

Table 1.

Comparison of the standard error and significance values of fixed-effects parameters of longitudinal volumes obtained from observed and temporally consistent shapes

Parameter	Std. error (obs.)	Std. error (smoothed)	p-value (obs.)	p-value (smoothed)
Fixed-effects (slope)	26.23	14.10	0.002	< 0.001
Slope (high)	66.56	23.73	0.182	< 0.001
Slope (med)	36.43	22.14	0.003	< 0.001
Slope (low)	38.73	26.60	0.143	< 0.001

Another benefit of spatiotemporal shape modeling is seen in the standard error of estimated parameters (Table 1). The standard error is consistently lower for temporally consistent shapes, which implies a reduction in unwanted variability present in the original segmentations. Further note in Fig. 3, the mixed-effects model fits the temporally consistent data better than the observed striatal volume. We also performed separate longitudinal mixed-effects analysis on the caudate and the putamen, and found a similar story in both cases.

Longitudinal analysis of striatal shape

We next perform a multivariate Hotelling’s T² hypothesis test (Section 2.2) of the baseline shape (intercept) and trend (slope) between controls and the combined HD groups. We compare the results for analyses using the original observed segmentations versus those obtained from spatiotemporal modeling as described in (Section 2.1). We represent these shapes in the particle optimization framework to estimate longitudinal fixed and random effects. Note that we do not normalize for size in these experiments, which means that we test for differences between control and combined HD groups based on both shape and size.

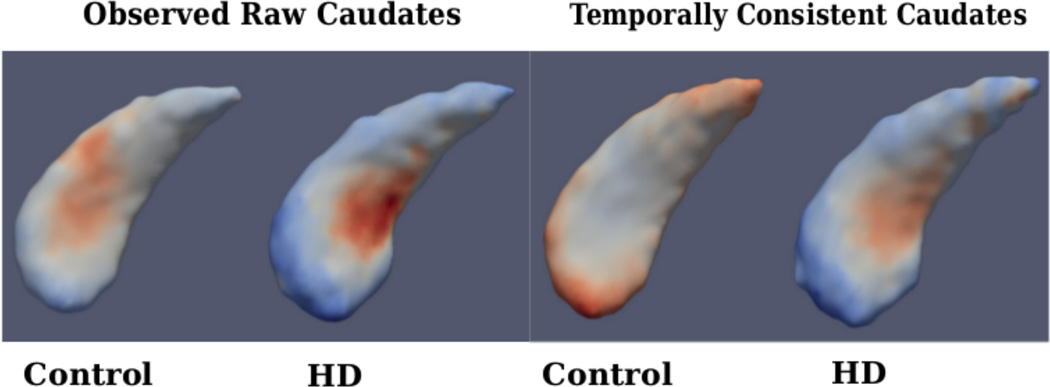
Figure 4 shows the estimated fixed-effects parameters for both groups, i.e., the baseline (intercept) shape with trajectory (slope) displayed as a color map. When comparing baseline shapes, we don’t find significant difference between controls and HD in either analysis. This is expected, as the onset of degeneration in HD is expected at a later age. But when comparing shape trends, we find significant differences between controls and HD for the temporally consistent shapes, but not in the case of raw shape observations.

Figure 4.

Left: Fixed-effects parameters for observed caudate shapes (Far Left-Control, Mid Left-HD), Right: Fixed-effects parameters for temporally consistent caudate shapes (Mid Right-Control, Far Right-HD); Fixed effects slope: Blue-Red indicates Local Contraction - Expansion

Table 2 provides the p-values from the statistical hypothesis test between the control and combined HD groups. In both the left and right caudate, the temporally consistent shapes result in lower p-values. Specifically, the left caudate is statistically significant at the 5% level. Similar to the volume analysis, this demonstrates that temporally consistent shape trajectories result in greater ability to distinguish differences in longitudinal trends between controls and HD groups.

Table 2.

p-values: Hypothesis test for differences in shape change (“slope”), between controls and HD groups, for observed caudates (Left) and temporally consistent caudate shapes (right)

Structure	Observed	Temporally consistent
Left caudate	0.15	0.005
Right caudate	0.23	0.06

4 Conclusion

Diffeomorphic trajectories are good at capturing smooth anatomical shape changes, while the particle optimization framework excels at finding compact statistical shape representations with increased statistical power. The novelty of our work is to leverage the strengths of both approaches, to provide an integrated solution, characterized by improved statistical performance in the analysis of both scalar and shape trajectory data derived from noisy segmentations. We demonstrate the advantages of our method through improved statistics on temporally consistent shape and volume measures in the analysis of the PREDICT-HD dataset.