Solving ptychography with a convex relaxation

Abstract

Ptychography is a powerful computational imaging technique that transforms a collection of low-resolution images into a high-resolution sample reconstruction. Unfortunately, algorithms that currently solve this reconstruction problem lack stability, robustness, and theoretical guarantees. Recently, convex optimization algorithms have improved the accuracy and reliability of several related reconstruction efforts. This paper proposes a convex formulation of the ptychography problem. This formulation has no local minima, it can be solved using a wide range of algorithms, it can incorporate appropriate noise models, and it can include multiple a priori constraints. The paper considers a specific algorithm, based on low-rank factorization, whose runtime and memory usage are near-linear in the size of the output image. Experiments demonstrate that this approach offers a 25% lower background variance on average than alternating projections, the ptychographic reconstruction algorithm that is currently in widespread use.

1. Introduction

Over the past two decades, ptychography [1, 2] has surpassed all other imaging techniques in its ability to produce high-resolution, wide field-of-view measurements of microscopic and nanoscopic phenomena. Whether in the X-ray regime at third-generation synchrotron sources [3–6], in the electron microscope for atomic scale phenomena [7], or in the optical regime for biological specimens [8], ptychography has shown an unparalleled ability to acquire hundreds of megapixels of sample information near the diffraction limit. The standard ptychography principle is simple: a series of diffraction patterns are recorded from a sample as it is scanned through a focused beam. These intensity-only measurements are then computationally converted into a reconstruction of the complex sample (i.e., its amplitude and phase), which contains more pixels than a single recorded diffraction pattern.

A recently introduced imaging procedure, termed Fourier ptychography (FP), uses a similar principle to create gigapixel optical images with a conventional microscope [9]. The only required hardware modification is an LED array, which illuminates a stationary sample from different directions as the microscope captures a sequence of images. As in standard ptychography, FP must also recover the sample's phase as it merges together the captured image sequence into a high-resolution output. Standard and Fourier ptychographic data are connected via a linear transformation [10], which allows both setups to use nearly identical image reconstruction algorithms.

Standard and Fourier ptychography both avoid the need for a large, well-corrected lens to image at the diffraction-limit. Instead, they shift the majority of resolution-limiting factors into the computational realm. Unfortunately, an accurate and reliable solver does not yet exist. As a coherent diffractive imaging technique [11], ptychography must reconstruct the phase of the scattered field from measured intensities, which is an ill-posed problem. To date, most ptychography algorithms solve the phase retrieval problem by applying known constraints in an iterative manner. We categorize this class of algorithm as an “alternating projection” (AP) strategy. The simplest example of an AP strategy is the Gerchburg-Saxton (i.e., error reduction) algorithm [12]. Our AP category also includes the iterative projection and gradient search techniques reviewed by Fienup [13] and Marchesini [14], which map to analogous procedures in ptychography [15]. All AP strategies, including several related variants [16–18], often converge to incorrect local minima or can stagnate [19]. Few guarantees exist regarding convergence, let alone convergence to a reasonable solution. Despite these shortcomings, many authors have pushed beyond the basic algorithms [20] to account for unknown system parameters [21, 22], improve outcomes by careful initialization [23], perform multiplexed acquisition [24], and attempt three-dimensional imaging [25, 26].

In this article, we formulate a convex program for the ptychography problem, which allows us to use efficient computational methods to obtain a reliable image reconstruction. Convex optimization has recently matured into a powerful computational tool that now solves a variety of challenging problems [27]. However, many sub-disciplines of imaging, especially those involving phase retrieval, have been slow to reap its transformative benefits. Several prior works [28–32] have connected convex optimization with abstract phase retrieval problems, but this is the first work that applies convex optimization to the quickly growing field of high-resolution ptychography.

While it is possible in some experiments to improve reconstruction performance using prior sample knowledge or an appropriate heuristic, we consider here the general case of unaided recovery, which is especially relevant in biological imaging. Under these circumstances, we will show that our convex optimization approach to ptychographic reconstruction has many advantages over AP. Our formulation has no local minima, so we can always obtain a solution with minimum cost. The methodology is significantly more noise-tolerant than AP, and the results are more reproducible. There are also opportunities to establish theoretical guarantees using machinery from convex analysis.

Furthermore, there are many efficient algorithms for our convex formulation of the ptychography problem. To obtain solutions at scale, we apply a factorization method due to Burer and Monteiro [33,34]. This method avoids the limitations of earlier convex algorithms for abstract phase retrieval, whose storage and complexity scale cubically in the number of reconstructed pixels [32]. Moreover, recent results establish that this factorization technique converges globally under certain conditions [35], offering a promising theoretical guarantee. The end result is a new, noise-tolerant algorithm for ptychographic reconstruction that is efficient enough to process the multi-gigapixel images that future applications will demand.

Here is an outline for the paper. First, we develop a linear algebraic framework to illustrate the ptychographic image formation process. Second, we manipulate this framework to pose its sample recovery problem as a convex program. This initial algorithm, termed “convex lifted ptychography” (CLP), supports a-priori knowledge of noise statistics to significantly increase the accuracy of image reconstruction in the presence of noise. Third, we build upon research in low-rank semidefinite programming [33, 34] to develop a second non-convex algorithm, called “low-rank ptychography” (LRP), which improves on the computational profile of CLP. Finally, we explore the performance of LRP in both simulation and experiment to demonstrate how it may be of great use in reducing the image capture time of Fourier ptychography.

2. Fundamentals

In this section, we outline the data capture process of Fourier ptychography (FP, see figure 1). At the end of this section, we discuss how a simple exchange of variables yields a nearly equivalent mathematical description of “standard” (i.e., diffraction imaging-based) ptychography data, which our proposed algorithm may also process. Since this exchange is straightforward, we choose to focus our attention on the FP problem for the majority of the manuscript. We encourage the interested reader to re-derive our algorithm for the standard ptychography arrangement. In addition, while the following analysis considers a two-dimensional experimental geometry for simplicity, extension to three dimensions is direct.

Figure 1.

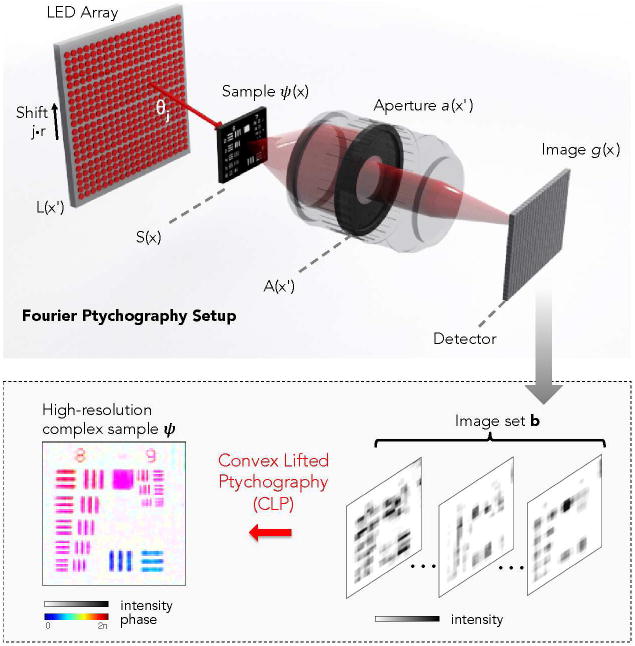
Diagram of the Fourier ptychography setup (top), where we use an LED array to illuminate a sample from different directions and acquire an image set b (bottom). This paper introduces a convex phase retrieval algorithm to transform this image set into a high-resolution complex sample estimate ψ. Included image set and reconstructed resolution target are experimental results.

We assume that a distant plane L(x′) contains q different quasi-monochromatic optical sources (central wavelength λ) evenly distributed along x′ with a spacing r. We assume each optical source acts as an effective point emitter that illuminates a sample ψ(x) at a plane S(x) a large distance l away from L(x′). Under this assumption, the jth source illuminates the sample with a spatially coherent plane wave at angle θ_j = tan⁻¹ (jr/l), where −q/2 ≤ j ≤ q/2. Additionally assuming the sample ψ(x) is thin, we may express the optical field exiting the thin sample as the product,

$$s(x,j)=\psi (x)e^{ikx{p}_j},$$ (1)

where the wavenumber k = 2π/λ and p_j = sinθ_j describes the off-axis angle of the jth optical source. The jth illuminated sample field s(x, j) then enters an imaging system with a low numerical aperture (NA). Neglecting scaling factors and a quadratic phase factor for simplicity, Fourier optics gives the field at the imaging system pupil plane, A(x′), as ℱ[s(x, j)] = ψ̂(x′ – p_j). Here, ℱ represents the Fourier transform between conjugate variables x and x′, ψ̂ is the Fourier transform of ψ, and we have applied the Fourier shift property. The shifted spectrum field ψ̂(x′ – p_j) is then modulated by the imaging system's aperture function a(x′), which acts as a low-pass filter. It is now useful to consider the spectrum ψ̂ discretized into n pixels with a maximum spatial frequency k. We denote the bandpass cutoff of the aperture function a as k · m/n, where m is an integer less than n. The modulation of ψ̂ by a results in a field characterized by m discrete samples, which propagates to the camera imaging plane and is critically sampled by an m-pixel digital detector. This forms a reduced-resolution image, g:

$$g(x,j)={|ℱ[a(x^{\text{'}})\widehat{\psi }(x^{\text{'}}-p_j)]|}^2.$$ (2)

g(x, j) is an (m × q) Fourier ptychography data matrix. Its jth column contains a low-resolution image of the sample intensity while it is under illumination from the jth optical source.

The goal of Fourier ptychographic post-processing is to reconstruct a high-resolution (n-pixel) complex spectrum ψ̂(x′), from the multiple low-resolution (m-pixel) intensity measurements contained within the data matrix g. Once ψ̂ is found, an inverse-Fourier transform will yield the desired complex sample reconstruction, ψ. As noted above, most current ptychography setups solve this inverse problem using alternating projections (AP): after initializing a complex sample estimate, ψ₀, iterative constraints help force ψ₀ to obey all known physical conditions. First, its amplitude is forced to obey the measured intensity set from the detector plane (i.e., the values in g). Second, its spectrum ψ̂₀ is forced to lie within a known support in the plane that is Fourier conjugate to the detector. Different projection operators and update rules are available, but are closely related [13–15]. While these projection strategies are known to converge when each constraint set is convex, the intensity constraint applied at the detector plane is not convex [36], leading to erroneous solutions [37] and possible stagnation [19].

The Fourier ptychography setup in figure 1 may be converted into a standard ptychography experiment by interchanging the sample plane S and the aperture plane A. This results in a standard ptychographic data matrix taking the form of equation 2 but now with a sample spectrum described in real space as ψ, which is filtered by the Fourier transform of the aperture function, â. This corresponds to illuminating a thin sample ψ (centered at position p) with an illumination probe field, â. These two simple functional transformations lead to a linear relationship between standard and Fourier ptychographic data [10]. To apply the algorithmic tools outlined next to standard ptychography, simply adhere to the following protocol wherever either variable appears: 1) replace the sample spectrum ψ̂ with the sample function ψ, and 2) replace the aperture function a with the shape of the focused probe field that illuminates the sample, â, in standard ptychography setups.

3. Results: Convex Lifted Ptychography (CLP)

3.1. The CLP solver

We begin the process of solving equation 2 as a convex program by expressing it in matrix form. First, we represent the unknown sample spectrum ψ̂ as an(n × 1) vector. Again, n is the known sample resolution before it is reduced by the finite bandpass of the lens aperture. Second, the jth detected image becomes an (m × 1) vector g_j, where again m is the number of pixels in each low-resolution image. The ratio n/m defines the ptychographic resolution improvement factor. It is equivalent to the largest angle of incidence from an off-axis optical source, divided by the acceptance angle of the imaging lens. Third, we express each lens aperture function a(x + p_j) as an (n × 1) discrete aperture vector a_j, which modulates the unknown sample spectrum ψ̂.

To rewrite equation 2 as a matrix product, we define ${\{{\mathbf{A}}_j\}}_{j=1}^q$ to be the sequence of (m × n) rectangular matrices that contain a deterministic aperture function a_j along a diagonal. For an aberration-free rectangular aperture, each matrix A_j has a diagonal of ones originating at (0, $p_j^{\text{'}}$) and terminating at (m, $p_j^{\text{'}}+m-1$), where $p_j^{\text{'}}$ is now a discretized version of our shift variable p_j. Finally, we introduce an m × m discrete Fourier transform matrix F^(m) to express the transformation of the low-pass filtered sample spectrum through our fixed imaging system for each low-resolution image g_j:

$${\mathbf{g}}_j={\left|{\mathbf{F}}^{(m)}{\mathbf{A}}_j\widehat{\psi }\right|}^2,1\le j\le q.$$ (3)

Ptychography acquires a series of q images, ${\{{\mathbf{g}}_j\}}_{j=1}^q$. We combine this image set into a single vector by “stacking” all images in equation 3:

$$\mathbf{b}={|\mathbf{F}\mathbf{A}\widehat{\psi }|}^2={|\mathbf{D}\widehat{\psi }|}^2.$$ (4)

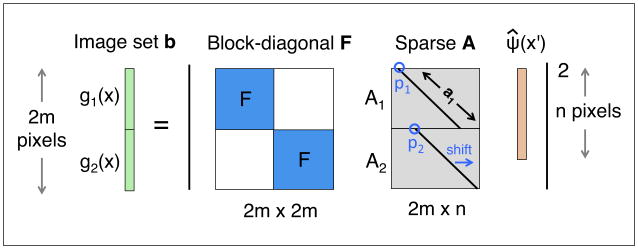
Here, b is {g} expressed asa(q · m × 1) stacked image vector (see figure 2). In addition, we define D = FA, where F is a (q · m × q · m) block diagonal matrix containing q copies of the low-resolution DFT matrices F^(m) in its diagonal blocks, and A has size (q · m × n) and is formed by vertically stacking each aperture matrix A_j:

Figure 2.

A set of images captured by Fourier ptychography stack together into a long data vector, b. Each associated matrix transform is similarly stacked and combined to form our final measurement matrix, D = FA. Here, we show stacking of just two images for simplicity. Typically, over 200 images are stacked.

$$\mathbf{F}=\left(\begin{array}{ccc}{\mathbf{F}}^{(m)}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathbf{F}}^{(m)}\end{array}\right),A=\left(\begin{array}{c}{A}_1\\ ⋮\\ A_q\end{array}\right).$$ (5)

We denote the transpose of the ith row of D as d_i, which is a column vector. The set {d_i} forms our measurement vectors. The measured intensity in the ith pixel is the square of the inner product between d_i and the spectrum ψ̂: b_i = | 〈d_i, ψ̂〉|². Next, we “lift” the solution ψ̂ out of the quadratic relationship in equation 4. As suggested in [30], we may instead express it in the space of (n × n) positive-semidefinite matrices:

$$b_i=\text{Tr}({\widehat{\psi }}^{\ast }{\mathbf{d}}_i{\mathbf{d}}_i^{\ast }\widehat{\psi })=\text{Tr}({\mathbf{d}}_i{\mathbf{d}}_i^{\ast }\widehat{\psi }{\widehat{\psi }}^{\ast })=\text{Tr}({\mathbf{D}}_i\mathbf{X}),$$ (6)

where ${\mathbf{D}}_i={\mathbf{d}}_i{\mathbf{d}}_i^{\ast }$ is a rank-1 measurement matrix constructed from the ith measurement vector d_i, X = ψ̂ψ̂* is an (n × n) rank-1 outer product, and 1 ≤ i ≤ q · m. Equation 6 states that our quadratic image measurements ${\{b_i\}}_{i=1}^{q\cdot m}$ are linear transforms of ψ̂ in a higher dimensional space. We may combine these q · m linear transforms into a single linear operator 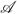to summarize the relationship between the stacked image vector b and the matrix X as, 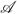(X) = b.

One can now pose the phase retrieval problem in ptychography as a rank minimization procedure:

$$\begin{array}{c}\text{minimize}\text{rank}(\mathbf{X})\\ \text{subject to}\mathcal{A}(\mathbf{X})=\mathbf{b},\mathbf{X}\ge 0,\end{array}$$ (7)

where X ≥ 0 denotes X is positive-semidefinite. This rank minimization problem is not convex and is a computational challenge. Instead, adapting ideas from [29], we form a convex relaxation of equation 7 by replacing the rank of matrix X with its trace. This creates a convex semidefinite program:

$$\begin{array}{c}\text{minimize}\text{Tr}(\mathbf{X})\\ \text{subject to}\mathcal{A}(\mathbf{X})=\mathbf{b},\mathbf{X}\ge 0.\end{array}$$ (8)

Several recent results establish that the relaxation in equation 8 is equivalent to equation 7 under certain conditions on the operator [38,39]. Although not necessarily equivalent in general, this relaxation consistently offers us highly accurate experimental performance. To account for the presence of noise, we may reform equation 8 such that the measured intensities in b are no longer strictly enforced constraints, but instead appear in the objective function:

$$\begin{array}{c}\text{minimize}\alpha \text{Tr}(\mathbf{X})+\frac{1}{2}\Vert \mathcal{A}(\mathbf{X})-\mathbf{b}\Vert \\ \text{subject to}\mathbf{X}\ge 0.\end{array}$$ (9)

Here, α is a scalar regularization variable that directly trades off goodness for complexity of fit. Its optimal value depends upon the assumed noise level. Equation 9 forms our final convex problem to recover a resolution-improved complex sample ψ from a set of obliquely illuminated images in b. Many standard tools are available to solve this semidefinite program (see Appendix A). Its solution defines our Convex Lifted Ptychography (CLP) approach.

In practice, CLP returns a low-rank matrix X, with a rapidly decaying spectrum, as the optimal solution of equation 9. The trace term in the CLP objective function is primarily responsible for enforcing the low-rank structure of X. While this trace term also appears like an alternative method to minimize the unknown signal energy, we caution that a fair interpretation must consider its effect in a lifted (n × n) solution space. We obtain our final complex image estimate ψ by first performing a singular value decomposition of X. Given low-noise imaging conditions and spatially coherent illumination, we set ψ to the Fourier transform of the largest resulting singular vector. Viewed as an autocorrelation matrix, we may also find useful statistical measurements within the remaining smaller singular vectors of X. We note that one may also identify X as the discrete mutual intensity matrix of a partially coherent optical field: X = 〈ψ̂ψ̂*〉, where 〈〉 denotes an ensemble average [40]. Under this interpretation, equation 9 becomes an alternative solver for the stationary mixed states of a ptychography setup [41].

Without any further modification, three points distinguish equation 9 from existing AP-based ptychography solvers. First, the convex solver has a larger search space. If AP is used to iteratively update an n-pixel estimate, equation 9 must solve for an n × n positive-semidefinite matrix. Second, this boost in the solution space dimension guarantees the convex program may find its global optimum with tractable computation. This allows CLP to avoid AP's frequent convergence to local minima (i.e., failure to approach the true image). Unlike prior solvers for the ptychography problem, no local minima exist in the CLP approach. However, CLP cannot yet claim a single global minimum, since it is not necessarily a strictly convex program. Finally, equation 9 implicitly considers the presence of noise by offering a parameter (α) to tune with an assumed noise level. AP-based solvers lack this parameter and can be easily led into incorrect local minima by even low noise levels, which we demonstrate next.

3.2. CLP simulations and noise performance

We simulate Fourier ptychography following the setup in figure 1. We capture multiple two-dimensional images in (x, y) from a three-dimensional optical geometry. The simulated FP setup contains a detector with m = 12² pixels that are each 4 μm wide, a 0.1 numerical aperture (NA) lens at plane A(x′, y′) (6° collection angle, unity magnification), and an array of spatially coherent optical sources at plane L(x′, y′) (632 nm center wavelength, 10 nm spectral bandwidth). The array is designed to offer an illumination NA of 0.2 (θ_max = 11.5° maximum illumination angle). Together, the lens and illumination NAs define the reconstructed resolution of our complex sample as n = 36² pixels, increasing the pixel count of one raw image by a factor n/m = 9.

Figure 3(b) shows example simulated raw images from a sample of absorptive microspheres modulated by a quadratic phase envelope. Within each raw image, the set of microspheres is not clearly resolved. Here, we simulate the capture of q = 8² low resolution images, each uniquely illuminated from one of q = 8² optical sources in the square array. We then input this image set into both the standard AP algorithm (i.e., the PIE strategy) [20], as well as CLP in equation 9, to recover a high resolution (36 × 36 pixel) complex sample. Here, we select the PIE strategy as our comparison benchmark for two reasons. First, it is one of the most widely used ptychography algorithms. Second, similar to CLP, its structure implicitly assumes a Gaussian noise model [15]. Even in the noiseless case, 5 iterations of nonlinear AP introduces unpredictable artifacts to both the recovered amplitude and phase (figure 3(d)), while CLP offers near perfect recovery (figure 3(c)). A constant phase offset is subtracted from both reconstructions for fair comparison, and we selected α = .001.

Figure 3.

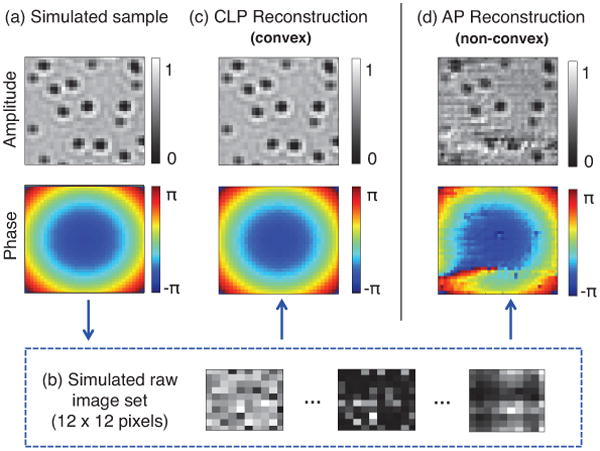
Simulation of the CLP algorithm. (a) An n = 36 × 36 pixel complex sample (simulated) consisting of absorptive microspheres modulated with an independent quadratic phase envelope. (b) Sequence of low-resolution simulated intensity measurements (m = 12 × 12 pixels each), serving as algorithm input. (c)-(d) Example CLP and AP reconstructions, where CLP is successful but AP converges to an incorrect local minimum. Here we use q = 8² images to achieve a resolution gain of 3 along each spatial dimension and simultaneously acquire phase.

Next, we quantify AP and CLP performance. We repeat the reconstructions in figure 3, again setting α = .001 in equation 9 while varying two relevant parameters: the number of captured images q, and their signal-to-noise ratio (SNR). We define the SNR as, SNR = 10log₁₀(〈|ψ|²〉/〈|N²|〉), where 〈|ψ|²〉 is the mean sample intensity and 〈|N²|〉 is the mean intensity of uniform Gaussian noise added to each simulated raw image. To account for the unknown constant phase offset in all phase retrieval reconstructions, we follow [21] and define our reconstruction mean-squared error as MSE = Σ_x |ψ(x) – ρs(x)|²/Σ_x |ψ(x)|², where ρ = Σ_x ψ(x)s*(x)/Σ_x |s(x)|² is a constant phase factor shifting our reconstructed phase to optimally match the known phase of the ground truth sample.

Figure 4 plots MSE as a function of SNR for this large set of CLP and AP reconstructions. Each of the algorithms' 3 independent curves simulates reconstruction using a different number of captured images, q. We summarize q by defining a Fourier spectrum overlap percentage: ol = 1 − (n − m)/qm. Each of the 6 points within one curve simulates a different level of additive measurement noise. Each point is an average over 5 independent trials. Since AP tends not to converge in the presence of noise, we represent each AP trial with the reconstruction that offers the lowest MSE across all iteration steps (up to 20 iterations). All CLP reconstructions improve linearly as SNR increases, while AP performance fluctuates unpredictably. For both algorithms, performance improves with increased spectrum overlap ol, and reconstruction fidelity quickly deteriorates and then effectively fails when ol drops below ∼60%.

Figure 4.

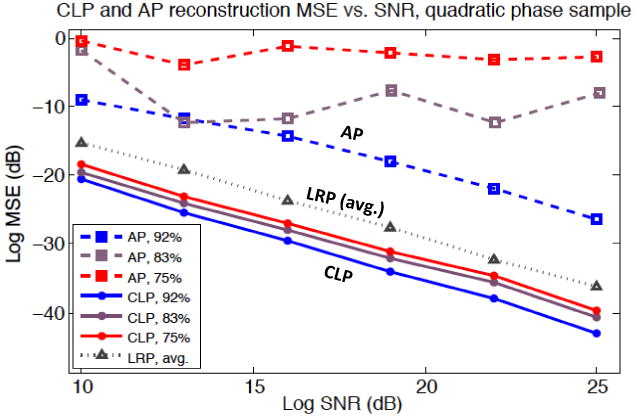
Reconstruction MSE versus signal to noise ratio (SNR) of CLP and AP (log scale, dB). Each curve represents reconstruction with a different number of captured images, q, corresponding to a different percentage of spectrum overlap (ol, noted in legend). Each point is an average over 5 independent algorithm runs with unique additive noise. Also included is the average performance of our LRP algorithm over the same 3 spectrum overlap settings (see Section 4).

4. Results: Factorization for Low-Rank Ptychography (LRP)

Posing the inverse problem of ptychography as a semidefinite program (equation 9) is a good first step towards a more tractable solver. However, the constraint that X remain positive-semidefinite is computationally demanding: each iteration typically requires a full eigenvalue decomposition of X. As the size of X scales with n², processable image sizes are limited to an order of 10⁴ pixels on current desktop machines. This scaling limit does not prevent large-scale CLP processing of ptychography data. It is common practice to segment each detected image into as few as 10³ pixels, process each segment separately, and then “tile” the resulting reconstructions back together into a final full-resolution solution [9]. CLP may also parallelize its computation with this strategy.

4.1. The LRP solver

While such tiling parallelization offers significant speedup, a simple observation helps avoid the poor scaling of CLP altogether: the desired solution of the ptychography problem in equation 7 is low-rank. Instead of solving for an n × n matrix X, it is thus natural to adopt a low-rank ansatz and factorize the matrix X as X = RR^T, where our decision variable R is now an n × r rectangular matrix containing complex entries, with r < n [33, 34]. Inserting this factorization into our optimization problem in equation 8 and writing the constraints in terms of the measurement matrix ${\mathbf{D}}_i={\mathbf{d}}_i{\mathbf{d}}_i^T$ creates the non-convex program,

$$\begin{array}{c}\text{minimize}\text{Tr}(\mathbf{R}{\mathbf{R}}^T)\\ \text{subject to}\text{Tr}({\mathbf{D}}_i\mathbf{R}{\mathbf{R}}^T)=b_i\text{for all}i.\end{array}$$ (10)

Besides removing the positive semidefinite constraint in equation 8, the factored form of equation 10 presents two more key adjustments to our original convex formulation. First, using the relationship $\text{Tr}(\mathbf{R}{\mathbf{R}}^T)={\Vert \mathbf{R}\Vert }_{\mathbf{F}}^2$, where F denotes a Frobenius norm, it is direct to rewrite the objective function and each constraint in equation 10 with just one n × r decision matrix, R. Now instead of storing an n × n matrix like CLP, LRP must only store an n × r matrix. Since most practical applications of ptychography require coherent optics, the desired solution rank r will typically be close to 1, thus significantly relaxing storage requirements (i.e., coherent light satisfies X = ψ̂ψ̂*, so we expect R as a column vector and RR^T a rank-1 outer product). Fixing r at a small value, LRP memory usage now scales linearly instead of quadratically with the number of reconstructed pixels, n.

Second, the feasible set of equation 10 is no longer convex. We thus must shift our solution strategy away from a simple semidefinite program. Prior work in [33, 34] suggests that an efficient and practically successful method of solving equation 10 is to minimize the following augmented Lagrangian function:

$$L(\mathbf{R},\mathbf{y},\sigma )=\text{Tr}(\mathbf{R}{\mathbf{R}}^T)-{\sum }_i{y}_i\cdot (\text{Tr}({\mathbf{D}}_i\mathbf{R}{\mathbf{R}}^T)-b_i)+\frac{\sigma }{2}\cdot {\sum }_i{(\text{Tr}({\mathbf{D}}_i\mathbf{R}{\mathbf{R}}^T)-b_i)}^2$$ (11)

where R ∈ ℂ^{n × r} is the unknown decision variable and the two variables y ∈ ℝ^q·m and σ ∈ ℝ⁺ are new parameters to help guide our algorithm to its final reconstruction. The first term in equation 11 is the objective function from equation 10, indirectly encouraging a low-rank factorized product. This tracks our original assumption of a rank-1 solution within a “lifted” solution space. The second term contains the known equality constraints in equation 10 (i.e., the measured intensities), each assigned a weight y_i. The third term is a penalized fitting error that we abbreviate with label v. It is weighted by one penalty parameter σ, mimicking the role of a Lagrangian multiplier.

With an appropriate fixed selection of y_i's and σ, the minimization of L(R, y, σ) with respect to R identifies our desired optimum of equation 10. Specifically, if a local minimum of L is identified each iteration (which is nearly always the case in practice), then the minimization sequence accumulation point is a guaranteed solution [34]. As an unconstrained function, the minimum of L is quickly found via standard tools (e.g., a quasi-Newton approach such as the LBFGS algorithm [42]), as previously demonstrated across a wide range of applications and experiments [33].

The goal of our low-rank ptychography (LRP) algorithm thus reduces to the following task: determine a suitable set of (y_i, σ) such that we may minimize equation 11 with respect to R, which leads to our desired solution. We use the iterative algorithm suggested in [33] to sequentially minimize L with respect to R^k at iteration k, and then update a new parameter set (y^k+1, σ^k+1) at iteration k + 1. We update parameters (y^k+1, σ^k+1) to ensure their associated term's contribution to the summation forming L is relatively small. This suggests R^k+1 is proceeding to a more feasible solution. The relative permissible size of the second and third terms in L are controlled by two important parameters, η < 1 and γ > 1: if the third term v sufficiently decreases such that v^k+1 ≤ ηv^k, then we hold its multiplier σ fixed and update the equality constraint multipliers, y_i. Otherwise, we increase σ by a factor γ such that σ^k+1 = γσ^k. A detailed discussion of these algorithmic steps is in [33,34].

We initialize the LRP algorithm with an estimate of the unknown high-resolution complex sample function ψ_o, contained within a low-rank matrix R⁰. We terminate the algorithm either if it reaches a sufficient number of iterations, or if the minimizer fulfills some convergence criterion. We form R⁰ using a spectral method, which can help increase solver accuracy and decrease computation time [43]. Specifically, we select the r columns of R⁰ as the leading r eigenvectors of D*diag[b]D, where D is the measurement matrix in equation 4. While this spectral approach works quite well in practice, a random initialization of R⁰ also often produces an accurate reconstruction.

4.2. LRP simulations and noise performance

Following the same procedure used to simulate the CLP algorithm, we test the MSE performance of the LRP algorithm as a function of SNR in figure 5. We again add different amounts of uncorrelated Gaussian noise to each simulated raw image set and compare the LRP reconstruction with ground truth. This simulated sample is the experimentally obtained amplitude and phase of a human blood smear. It is qualitatively similar to the sample used in figure 3. Unlike with the simulations in figures 3–4, the AP algorithm no longer malfunctions at lower spectrum overlap percentages (i.e., lower values of ol). Despite this apparent success, the MSE of the LRP minimizer is still ∼5–10 dB better than the MSE of the AP minimizer, across all levels of SNR. This reduced LRP reconstruction error follows without any parameter optimization or explicit noise modeling.

Figure 5.

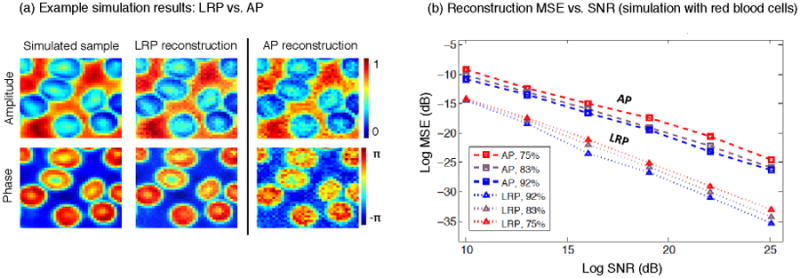
Simulation of the LRP and AP algorithms using the same parameters as for figures 3–4, but now with a different “red blood cell” sample, (a) Using 8² simulated intensity measurements as input (SNR=19, 12² pixels each), both algorithms successfully recover each cell's phase, but AP is less accurate, (b) MSE versus SNR plot with varying amounts of noise added to the same data set. The MSE for LRP is ∼5-10 dB lower than for AP across all noise levels and aperture overlap settings (each point from 5 independent trials).

In these simulations, we somewhat arbitrarily fix η and γ at 0.5 and 1.5, respectively, and set the desired rank of the solution, r, to 1. In practice, these free variables offer significant freedom to tune the response of LRP to noise. For example, similar to the noise parameter α in equation 9, the multiplier σ (controlled via γ) in equation 11 helps trade off complexity for goodness of fit by re-weighting the quadratic fitting error term.

In addition to reducing required memory, the LRP algorithm also improves upon the computational cost of CLP. For an n-pixel sample reconstruction, the per iteration cost of the CLP algorithm is currently O(n³), using big-O notation. The positive-semidefinite constraint in equation 9, which requires a full eigenvalue decomposition, defines this behavior limit. The per-iteration cost of the LRP algorithm, on the other hand, is O(n logn). This large per-iteration cost reduction is the primary source of LRP speedup. For example, LRP required ∼21 seconds to complete an average simulation of the example in figure 3, while CLP required ∼170 minutes and AP required 1 second on the same desktop machine.

5. Results: Experiment

We experimentally verify how LRP improves the accuracy and noise stability of ptychographic reconstruction using a Fourier ptychographic (FP) microscope. Our experimental procedure closely follows the protocol in [9]. While we demonstrate at optical wavelengths, it is straightforward to acquire a Fourier ptychographic data set in an X-ray or electron microscope (e.g., with a tilting source [44]). Alternatively, two trivial changes within equation 10 directly prepares standard ptychographic data for LRP processing (see end of section 2). Given its removal of local minima and improved treatment of noise, we expect our strategy will benefit both experimental arrangements.

In this section, we first quantitatively verify that LRP accurately measures high resolution and sample phase. Compared with AP reconstructions, our LRP algorithm generates fewer undesirable artifacts in experiment. Second, we will compare the AP and LRP reconstructions of a biological sample, which establishes the improved noise stability of our new algorithm.

5.1. Quantitative performance

Our FP microscope consists of a 15×15 array of surface-mounted LEDs (model SMD 3528, center wavelength λ=632 nm, 4 mm LED pitch, 150 μm active area diameter), which serve as our quasi-coherent optical sources. The array is placed l=80 mm beneath the sample plane, and each LED has an approximate 20 nm spectral bandwidth. Prior work establishes that the impact of non-ideal source coherence is gradual [10]. While negligible in these experiments, we may eventually account for source statistics in the multi-rank structure of the LRP optimizer R.

To quantitatively verify resolution improvement, we turn on each of the 15 × 15 LEDs beneath a U.S. Air Force (USAF) resolution calibration target. A 2X Olympus microscope objective (apochromatic Plan APO 0.08 NA) transfers each resulting optical field to a CCD detector (Kodak KAI-29050, 5.5 μm pixels), creating 225 low resolution images. Using this 0.08 NA microscope objective (5° collection angle) and a 0.35 illumination NA (θ_max = 20° illumination angle), our FP microscope offers a total complex field resolution gain of n/m = 25. Each image spectrum overlaps by ol ≈ 70% in area with each neighboring image spectrum.

For reconstruction, we select n = 25 · m and use the same aperture parameters with AP and LRP to create the high-resolution images in figure 6. For computational efficiency, we segment each low-resolution image into 3×3 tiles (n=480² per tile) and process the tiles in parallel, as performed in [9]. We determine the optimal number of AP and LRP algorithm iterations as 6 and 15, respectively, and fixed this for each tile (and all subsequent reconstructions). We typically initialize LRP with the following parameters: γ=1.5, η=0.3, y⁰=10 and σ⁰=10. We determine the microscope aperture function with an iterative procedure [46] before each experiment and fix it for each algorithm trial.

Figure 6.

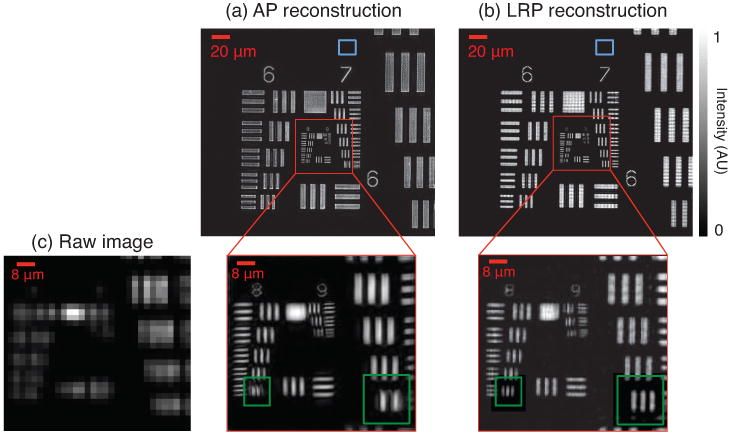
Experimental reconstruction of a USAF target, where the number of resolved pixels is increased by a factor of 25. We test two different ptychography algorithms: (a) AP and (b) LRP. Here we only show reconstructed intensity. LRP avoids artifacts (e.g., boxed in green) commonly encountered in the AP approach. Cited variances are measured in blue boxes (top). (c) Same cropped region of one low-resolution raw image, for comparison.

Both ∼1 megapixel reconstructions achieve their maximum expected resolving power (Group 9, Element 3: 1.56 μm line pair spacing). This is approximately 5 times sharper than the smallest resolved feature in one raw image (Group 7, Element 2 in Fig 6(c)). Our new LRP algorithm avoids certain artifacts that are commonly observed during the nonlinear descent of AP (boxed in green). Both reconstructions slowly fluctuate in background areas that we expect to be uniformly bright or dark. These fluctuations are caused in part by experimental noise, an imperfect aperture function estimate, and possible misalignments in the LED shift values, p_j. In a representative background area marked by a 40² pixel blue box in figure 6, AP and LRP exhibit normalized background amplitude variances of ${\sigma }_A^2=5.4\times {10}^{-4}$ and ${\sigma }_L^2=5.0\times {10}^{-4}$, respectively. Accounting for experimental uncertainty in the aperture function a and shifts p_j (e.g., following [45, 46]) may reduce this error in both algorithms.

To verify that our LRP solver reconstructs quantitatively accurate phase, we next image a monolayer of polystyrene microspheres (index of refraction n_m = 1.587) immersed in oil (n_o = 1.515, both indexes for λ = 632 nm light). To demonstrate the LRP algorithm easily generalizes to any ptychographic arrangement, we perform this experiment on a new “high-NA” FP microscope. The high-NA setup uses a larger 0.5 NA microscope objective lens with a 30° collection angle (20X Olympus 0.5 NA UPLFLN). For sample illumination, we now arrange 28 LEDs into 3 concentric rings of 8, 8 and 12 evenly spaced light sources (ring radii=16, 32 and 40 mm, respectively). We place this new light source array 40 mm beneath the sample to create a 0.7 illumination NA with a θ_max = 45° illumination angle. The synthesized numerical aperture of this new FP microscope, computed as the sum of the illumination NA and objective lens NA, is NA_s = 1.2. With a greater-than-unity synthetic NA, our reconstructions can offer oil-immersion quality resolution (∼385 nm smallest resolvable feature spacing [47]), without requiring any immersion medium between the sample and objective lens.

Using the same data and parameters for AP and LRP input, we obtain the high-resolution phase reconstructions of two adjacent microspheres in figure 7 (3 μm and 6 μm diameters). For this reconstruction, we set m=160² and n=320². We have subtracted a constant phase offset from the LRP solution in (b) to allow for direct comparison to the AP solution in (a). The two reconstructions appear qualitatively similar except at the center of the 6 μm sphere, where the AP phase profile unexpectedly flattens. We highlight this flattening by selecting phase values along each marked dashed line to plot the resulting sample thickness in figure 7(c). Phase ϕ and sample thickness t are related via t = kΔϕ(n_m – n₀)⁻¹, where k is the average wavenumber and Δϕ = ϕ – ϕ₀ is the reconstructed phase minus a constant offset. LRP closely matches the optical thickness of a ground-truth sphere (GT, black curve): the length of the vertical chord connecting the top and bottom arcs of a 6 μm diameter circle. The normalized amplitude variances from a 40²-pixel background area are ${\sigma }_A^2=9.2\times {10}^{-4}$ and ${\sigma }_L^2=5.8\times {10}^{-4}$, respectively. This again supports our observation that the high resolution reconstructions formed by LRP are more accurate than those formed by AP.

Figure 7.

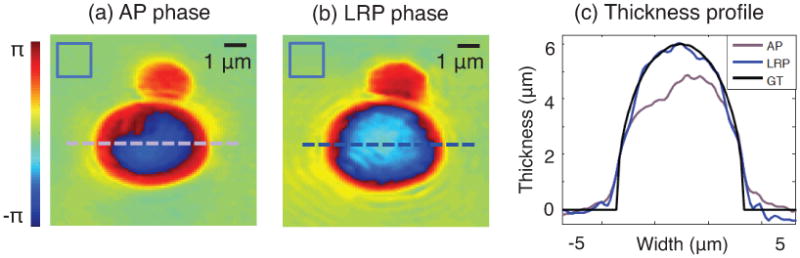
Experimental measurement of the quantitative optical phase emerging from two polystyrene microspheres. Both (a) AP and (b) LRP reconstruct phase maps that appear qualitatively similar, although the AP phase map flattens at the sphere's center. Variances measured in blue boxes. (c) Plot of microsphere thickness from a trace through the center of the large sphere (dashed line) demonstrates close agreement between LRP and ground truth (GT).

5.2. Biological sample reconstruction

Our third imaging example uses the same high-NA FP configuration (collection angle= 30°, θ_max = 45°) to resolve a biological phenomenon: the infectious spread of malaria in human blood. The early stages of a Plasmodium falciparum infection in erythrocytes (i.e., red blood cells) includes the formation of small parasitic “rings”. It is challenging to resolve these parasites under a microscope without using an immersion medium, even after appropriate staining. Oil-immersion is required for an accurate diagnosis of infection [48].

We use FP to resolve Plasmodium falciparum-infected cells with a 0.5 NA objective lens and using no oil in figure 8. We first prepare an infected blood sample following the protocol in [49]: we maintain erythrocyte asexual stage cultures of the P. falciparum strain 3D7 in culture medium, then we smear, fix with methanol and apply a Hema 3 stain. An example sample region containing two infected cells, imaged with a conventional high-NA oil-immersion microscope (NA =1.25) under Kohler illumination, is in figure 8(a).

Figure 8.

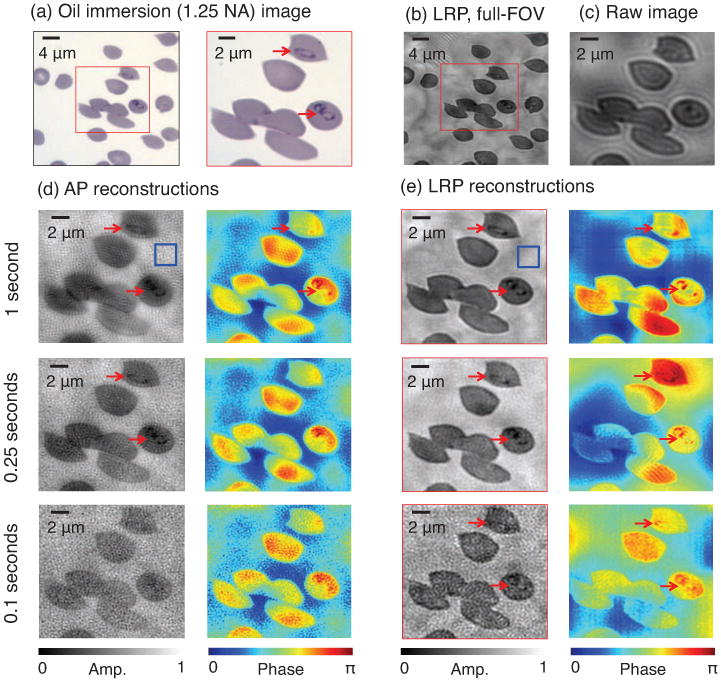
Experimental reconstruction of malaria-infected human red blood cells. (a) Oil immersion microscope image (1.25 NA) identifies two infected cells of interest (marked with arrows). (b) Example LRP reconstruction (area of interest in red box). (c) One example raw image used for AP and LRP algorithm input. (d) AP-reconstructed amplitude and phase from three different 29-image data sets, using 1 sec (top), 0.25 sec (middle) and 0.1 sec (bottom) exposure times for all images in each set. Variances measured within blue boxes. Increased noise within short-exposure images deteriorates reconstruction quality until both parasites are not resolved. (e) LRP reconstructions using the same three data sets. Both parasites are clearly resolved in the reconstructed phase for all three exposure levels.

Next, we capture 28 uniquely illuminated images of these two infected cells using our high-NA FP microscope. Figure 8(c) contains an example normally illuminated raw image, which does not clearly resolve the parasite infection. Figure 8(d) presents phase retrieval reconstructions using the standard AP algorithm, where we set m=120², n=240², run 6 iterations, and again subtract a constant phase offset. We include reconstructions from three data sets: images captured with a 1 second exposure (top), a 0.25 second exposure (middle), and 0.1 second exposure (bottom). A shorter exposure time implies increased noise within each raw image. While the 1 sec exposure-based AP reconstruction resolves each parasite, blurred cell boundaries and non-uniform fluctuations in amplitude suggest an inaccurate AP convergence. However, both parasite infections remain visible within the reconstructed phase. The parasites become challenging to resolve within the phase from 0.25 sec exposure data, and are not resolved within the phase from the 0.1 sec exposure data, due to increased image noise. The normalized background variance of each AP amplitude reconstruction, from a representative 40²-pixel window (marked blue square), is ${\sigma }_A^2=.0020$, .0027, and .0059 for the 1 sec, 0.25 sec, and 0.1 sec exposure reconstructions, respectively.

For comparison, reconstructions using our LRP algorithm are shown in figure 8(e) (sharpest solutions after 15 iterations). For each reconstructed amplitude, we set the desired solution rank to r = 3. We add the 3 modes of the resulting reconstruction in an intensity basis to create the displayed amplitude images. For each reconstructed phase, we set the desired solution matrix rank to r = 1 and leave all other parameters unchanged. For all three exposure levels, the amplitude of the cell boundaries remains sharper than in the AP images. Both parasite infections are resolvable in either the reconstructed amplitude or phase, or both, for all three exposure levels. The normalized amplitude variances from the same background window are now ${\sigma }_L^2=.0016(1sec)$, .0022 (0.25 sec), and .0035 (0.1 sec), an average reduction (i.e., improvement) of 26% with respect to the AP results. While not observed within our previous simulations or experiments, the AP reconstructions here offer a generally flatter background phase profile than LRP (i.e., less variation at low spatial frequencies). Without additional filtering or post-processing, the AP algorithm here might offer superior quantitative analysis during e.g. tomographic cell reconstruction, where low-order phase variations must remain accurate. However, it is clear within figure 8 that LRP better resolves the fine structure of each infection, which is critical during malaria diagnosis. A shorter image exposure time (i.e., up to 10 times shorter) may still enable accurate infection diagnosis when using LRP, as opposed to the standard AP approach.

6. Discussion and Conclusion

Through the relaxation in equation 8, we first transform the traditionally nonlinear phase retrieval process for ptychography into a convex program. We may now use well-established optimization tools to find the ptychography problem's global minimum. Then, we suggest a practically efficient algorithm to solve the resulting semidefinite program with an appropriate factorization. The result is a new ptychographic image recovery algorithm that is robust to noise. We demonstrate its successful performance in three unique experiments, concluding with a practical biological imaging scenario: the identification of malaria infection without using an oil immersion medium and under short-exposure imaging conditions.

Much future work remains to fully explore the specific benefits of our problem reformulation. Besides removing local minima from the recovery process, perhaps the most significant departure from prior phase retrieval solvers is a tunable solution rank, r. As noted earlier, r connects to statistical features of the ptychographic experiment, typically arising from the partial coherence of the illuminating field. Coherence effects are significant at third-generation X-ray synchrotron sources and within electron microscopes. An appropriately selected r may eventually help LRP measure the partial coherence of such sources, as outlined in [41]. The solution rank may also help identify setup vibrations, sample auto-fluorescence, or even 3D sample structure. As in prior work with low-rank matrix optimization, we may also artificially enlarge our solution rank to encourage the transfer of experimental noise into its smaller singular vectors.

Other extensions of LRP include simultaneously solving for unknown aberrations (i.e., the shape of the probe in standard ptychography), systematic setup errors, and inserting additional sample priors such as sparsity. These refinements are currently a critical component of ptychographic recovery in the fields of X-ray and electron microscopy, and will also improve our optical results. Along with algorithm refinement, a detailed comparison between LRP and various other recovery methods, especially under different sources of noise and error, will help identify the experimental conditions under which our strategy is of greatest benefit. What's more, as a particular solution to the general problem of phaseless measurement, our findings can also inform a wide variety of coherent diffractive imaging techniques. Regardless of the specific experimental application, convex analysis will continue to provide useful theoretical guarantees regarding phase retrieval algorithm performance, a crucial feature missing from current nonlinear solvers.

Appendix A. Computational specifics

We performed all processing on a high-end desktop containing two Intel Xeon 2.0 GHz CPUs and two 3GB GeForce GTX GPUs. Code was written in Matlab with built-in GPU acceleration. We solved our CLP semidefinite program using the TFOCS code package [50]. Our LRP algorithm borrows concepts from the LBFGS solver in [42] for one specific minimization step. LRP's total recovery time for the 1 megapixel example in Fig. 6 was approximately 130 seconds, while AP completed in approximately 15 seconds on the same desktop.