PRECISE:PRivacy-prEserving Cloud-assisted quality Improvement Service in hEalthcare

Abstract

Quality improvement (QI) requires systematic and continuous efforts to enhance healthcare services. A healthcare provider might wish to compare local statistics with those from other institutions in order to identify problems and develop intervention to improve the quality of care. However, the sharing of institution information may be deterred by institutional privacy as publicizing such statistics could lead to embarrassment and even financial damage. In this article, we propose a PRivacy-prEserving Cloud-assisted quality Improvement Service in hEalthcare (PRECISE), which aims at enabling cross-institution comparison of healthcare statistics while protecting privacy. The proposed framework relies on a set of state-of-the-art cryptographic protocols including homomorphic encryption and Yao’s garbled circuit schemes. By securely pooling data from different institutions, PRECISE can rank the encrypted statistics to facilitate QI among participating institutes. We conducted experiments using MIMIC II database and demonstrated the feasibility of the proposed PRECISE framework.

I. Introduction

Hospital quality is important to the reputation and financial sustainability of a hospital. Metrics such as infection rate and readmission rate reflect the quality of care. In order to improve the quality, it is necessary to compare local statistics with those from other hospitals to know what intervention needs to be prioritized. However, sharing of such statistics can be embarrassing and financially disadvantageous, which deters hospitals to exchange “sensitive” statistics. It would be beneficial if a mechanism allows hospital administrators compare these statistics to obtain a ranking without disclosing the underlying statistics.

This is closely related to the famous Yao’s millionaire problem, where two millionaires want to know who is richer without disclosing their total asset to the other [1], [2]. The problem for comparing measurements related to hospital quality is challenging as we need to consider a multi-institution comparison scenario to protect intermediary information exchange.

A. Motivating Example

Imagine several hospitals, which are located at different locations, want to study morbidity related to the bloodstream infection (BSI) in Emergency Room (ER) and improve the quality of care. They would like to know the morbidity ranking in terms of BSI morbidity stratified by age, gender, staff training, vascular access care audits, etc. Such ranking can help hospitals gain insights to identify necessary intervention for improvement but it should not disclose sensitive information from individual hospitals. For example, Hospital A might find that the less frequent vascular access care leads to higher ranked BSI morbidity in the elder population, for which intervention can be developed to improve the quality. Our framework can support such comparison in a privacy-preserving manner. Before we elaborate the details, let us review related methodology.

B. Related Techniques

Secure Multiparty Computation (SMC) [3] is one of the cryptographic techniques for securely aggregating information among different parties. However, SMC is not always practical as it requires inter-party (peer to peer) communication.

Alternatively, data perturbation based methods [4]–[8] have been proposed, which try to generalize or add noise to the raw data in order to hide the sensitive information. Among existing strategies, differential privacy based methods [4], [6], [9] have received a lot of attention as the privacy definition provides the strongest privacy protection (without making any assumption on attackers’ background knowledge). However, the main drawback of perturbation based methods is that added noise may destroy the utility of the outcome (i.e., in our case, the ranking orders). Order-preserving encryption [10] provides yet another workaround to conduct ranking operation on encrypted data, but it cannot support secure aggregation among distributed datasets, which is necessary for comparing local statistics with the global ones.

To address the limitations of existing techniques, we propose a privacy-preserving cloud-assisted framework for securely aggregating information from distributed data sources as well as performing global ranking in ciphertext.

II. Methodology

A. System Framework

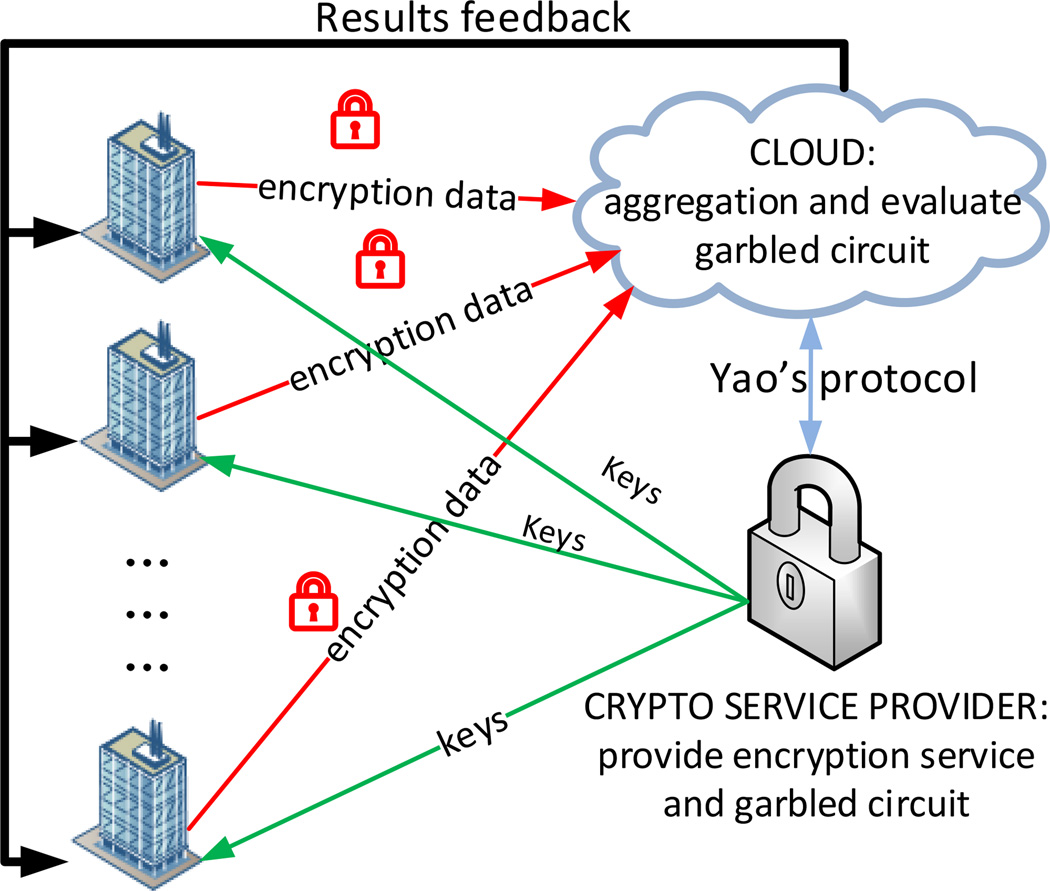
Fig. 1 illustrates the framework of the proposed method, which includes M hospitals, a cloud service, and a crypto service provider (CSP). The cloud service analyzes encrypted data from M different hospitals in a privacy-preserving manner, and answers aggregate queries. The CSP manages the public key (data encryption) and private key (data decryption), and it is the only entity capable of decrypting a ciphertext. All parties in this study are assumed to be semi-honest, which means they follow the protocol honestly but may try to deduce additional information from the received messages during the protocol execution. To minimize privacy risk, the cloud service is restricted to only answer the rank information (e.g., which hospital has the largest morbidity for a given cohort) rather than providing the actual counts.

Fig. 1.

System overview of the proposed PRECISE framework, which includes M hospitals, a cloud service and a Crypto Service Provider (CSP). In the proposed framework, neither the cloud nor the CSP can eavesdrop sensitive information from any of the M hospitals.

The workflow of the proposed framework is summarized as follows: first, the cloud gathers encrypted counts of different query criteria from each hospital using the homomorphic encryption algorithm and adds random masks to the encrypted count of each query so that the real counts cannot be revealed by the CSP. Next, a garbled circuit is designed based on the Yao’s protocol [1], by which the cloud (together with the CSP) can answer the ranking information using encrypted data.

The remaining of this section is organized as follows: we briefly present the relevant cryptographic tools used in our proposed protocol. Then, we will elaborate on the implementation details of the proposed protocol.

B. Homomorphic Encryption

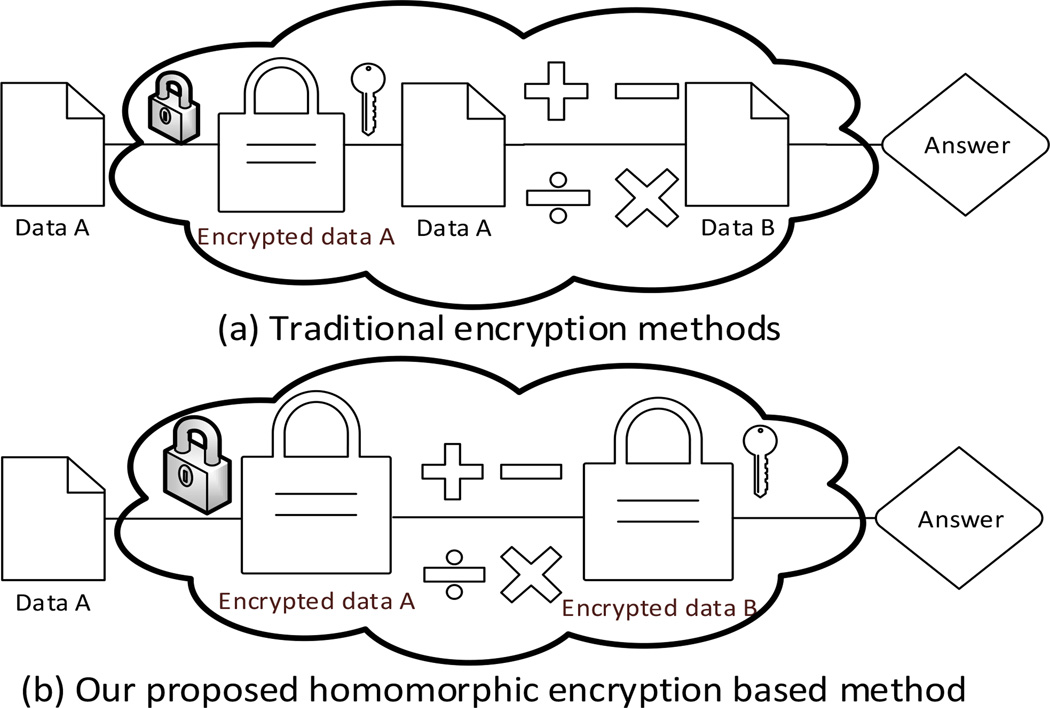
Homomorphic encryption [11], [12] is a form of encryption where a specific algebraic operation performed on the plaintext is equivalent to another algebraic operation performed on the ciphertext, and when decrypted, matches the results of the same operation performed on the plaintext. Fig. 2 illustrates the difference between homomorphic encryption and traditional encryption methods. In specific, there are three types of homomorphic encryption techniques [13]: (1) partially homomorphic encryption that is generally specialized in a single type of operations (e.g., either addition or multiplication) [14]–[16], (2) leveled homomorphic encryption that operates on both operations for a limited number of iterations and an increased computational complexity [17]. (3) fully homomorphic encryption that operations on both operations without limiting the number of iteration but it also results in the highest complexity [18]–[21]. For a given task, it is important to select a proper homomorphic encryption scheme to strike the right tradeoff between arithmetical flexibility and computational complexity. The addition operation is the basic primitive of our framework. We resort to the Paillier’s scheme [16], which is a partially homomorphic encryption techniques with homomorphic addition property, to conduct this operation. Let us denote by E(x₁) and E(x₂) the encrypted ciphertexts of two plaintexts x₁ and x₂. In Paillier’s homomorphic scheme, the product of two ciphertexts results in the encrypted version of the summation of both plaintexts (i.e., E(x₁) · E(x₂) mod n² = E(x₁ + x₂) mod n, where ‘mod’ denotes the modular operation and n = pq is the product of two large prime numbers p and q.)

Fig. 2.

Comparison between traditional encryption and homomorphic encryption methods.

C. 1–2 oblivious transfer (OT) protocol

Oblivious transfer (short for 1–2 OT) protocol is a constant round communication protocol, which guarantees that Party A can obtain one of the two messages from Party B without letting Party B knows which message is actually selected. We will not go through the details of the OT protocol in this paper, But, readers can find more implementation details in [22]. The OT protocol is one of the steps necessary to implement the following Yao’s protocol.

D. Yao’s Protocol [1]

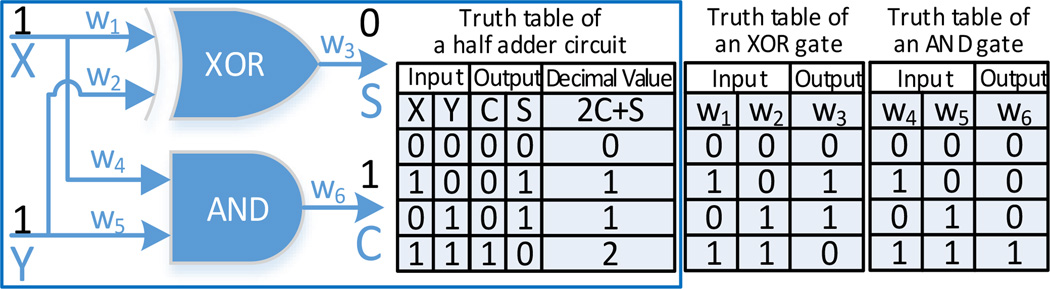
The original Yao’s protocol supposes two parties, for example, Alice and Bob, plan to compute a function f(x, y), where x is owned by Alice, and y is owned by Bob. However, none of these parties would like to expose its input to the other party in evaluating the function f(x, y). To satisfy this requirement, Alice will first convert the function f(x, y) into a Boolean circuit, in which several logic gates will be specifically combined together to realize the given function. Here, each logic gate can perform a logical operation on one or more binary inputs and produces a single binary output. Fig. 3 depicts an example of a half adder circuit to implement the function f_ha(x, y) = x + y with x, y ∈ {0, 1}, where the half adder circuit includes an XOR (i.e., eXclusive OR) gate and an AND gate with two inputs and two outputs. Moreover, each logic gate has three wires corresponding to two binary inputs and one binary output, where each wire will be assigned a unique index w_i with i = {1, 2, …, W} and W is the total number of wires in the Boolean circuit (e.g., W = 6 in Fig. 3).

Fig. 3.

An example of a half adder circuit in implementing function f_ha(x, y) = x + y with x, y ∈ {0, 1}, which includes an XOR gate and an AND gate. The half adder has two single binary inputs x and y and two outputs, i.e., sum (S) and carry (C), where the decimal output can be represented as f_ha(x, y) = 2C + S. Each logic gate (e.g., XOR or AND gate) has three wires, which correspond to two binary inputs (e.g., W₁ and W₂ in the XOR gate) and one binary output (e.g., W₃ in the XOR gate). The truth tables of the half adder circuit, XOR and AND gates have been shown as references.

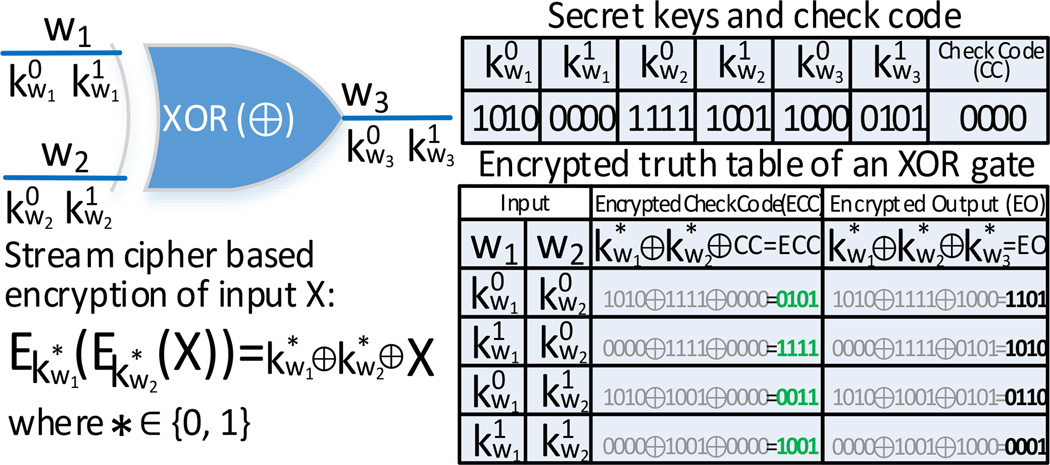
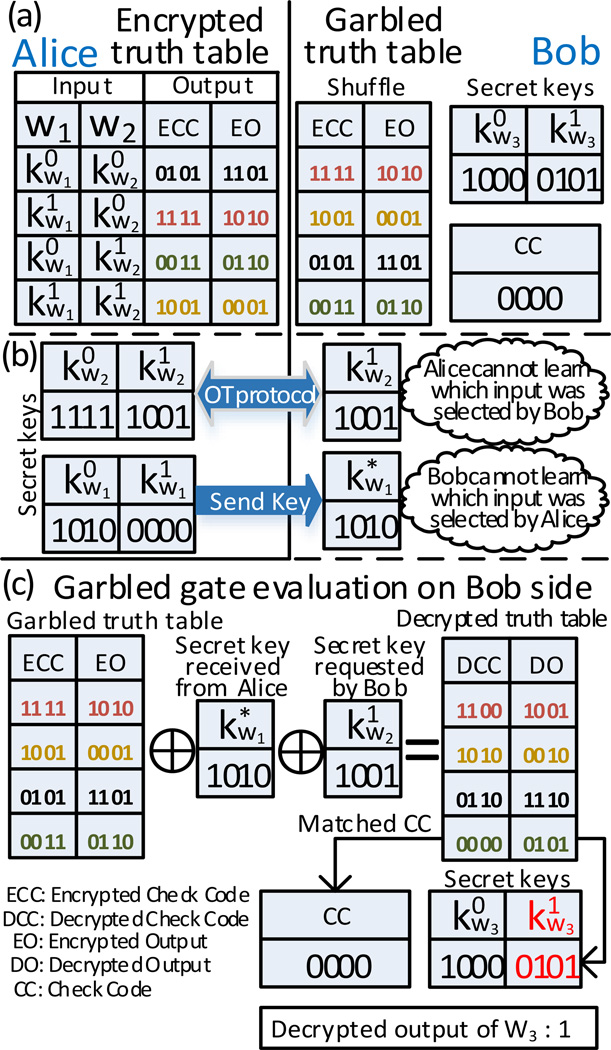
Next, Alice will randomly generate two secret keys (a.k.a., garbled values) $k_{w_i}^0$ and $k_{w_i}^1$ to represent 0 and 1, respectively, for each wire w_i with i = {1, 2, …, W}. For example, Alice needs to generate 6 keys for the XOR gate, where the input keys can be used to encrypt the output keys as shown in the encrypted truth table in Fig. 4. A stream cipher based scheme is applied to encrypt the output keys as well as a check code. The check code can be used to validate the output keys, which will be explained later. Besides, other encryption methods (e.g., AES [24]) can also be employed to enhance the security in practice. Then, Alice randomly permutes the encrypted truth table and sends the garbled table as well as the check code to Bob as shown in Fig. 5 (a). Besides, Alice will also send the output keys to Bob.

Fig. 4.

An example of an encrypted XOR gate, where w₁ and w₂ are the input wires and w₃ is the output wire. For each wire w_i i = {1, 2, 3}, two secret keys ${\mathrm{k}}_{{\mathrm{w}}_{\mathrm{i}}}^0$ and ${\mathrm{k}}_{{\mathrm{w}}_{\mathrm{i}}}^1$ will be selected to represent the 0 and 1, respectively. Then, a stream cipher based encryption scheme [23] is used to generate an encrypted truth table of the XOR gate with encrypted output and check code. Here, the check code can be utilized to validate the garbled output, which will be explained later.

Fig. 5.

An example of Yao's protocol using an XOR gate. This example is provided for illustrative purposes only, where the security protection cannot be achieved with this circuit. But, it can serve as the basic building block of a more complicated circuit. See Remark I for more discussions.

Let’s suppose the actual inputs from Alice and Bob are 0 and 1, respectively. As shown in Fig. 5 (b), Bob will obtain his garbled input $k_{w_2}^1$ from Alice using the OT protocol [22], by which Alice cannot learn what is the input from Bob. Furthermore, Alice will also send her garbled input (i.e., $GI(0)=k_{w_1}^0=1010$ in Fig. 5 (b)) to Bob, where Bob only learns $k_{w_1}^{*}=1010$ but cannot figure out if the ‘*’ corresponds to 0 or 1. Once Bob obtains both garbled inputs $k_{w_1}^{*}$ and $k_{w_2}^1$, he can decrypt the garbled truth table and match the check code provided by Alice to obtain a uniquely valid output of the gate, where the output is still a garbled value. Therefore, Bob cannot find out what the true value of the output is. As gates in a circuit are connected through wires, Bob can continue evaluating all gates in the circuit one by one, where the garbled output from previous gate can be used as the garbled input for the current gate. In case of reaching the end of the circuit, Bob can decrypt the output based on the secret keys obtained from Alice. Fig. 5 (c) shows an example of evaluating a circuit with a single XOR gate using Yao’s protocol.

Remark I

When evaluating the circuit, Bob needs to keep the encrypted intermediate outputs of each gate as secrets, so that Alice cannot infer Bob’s true inputs. Moreover, the security of a circuit is based on the assumption that neither Alice nor Bob cannot derive the other’s input based on the final output of a function and his/her own input. It is clear that many functions may be unable to satisfy the above assumption. For example, given the output of a single XOR gate and one input as depicted in Fig. 5 (c), one can easily infer the other input. It is worth mentioning that the example in Fig. 5 is provided for illustrative purposes only, which can serve as a basic building block for building a large garbled circuit. But users cannot achieve security protection with a single garbled XOR gate as shown in Fig. 5. In this study, we will focus on the design of a function for comparing the ranks of numerical inputs, where one cannot easily infer the original input based on the output.

E. Method Details

The general procedures of the proposed algorithm are summarized in Algorithm 1.

Lines 1–3

Each hospital H_i with i = 1,2, …, M, where M is total number of hospitals, will evaluate the same local function f(D_Hi) on its local private data D_Hi. Since none of the hospitals would like to expose their local sensitive results to others, each hospital H_i first encrypt its local output f(D_Hi) as Enc_HME(f(D_Hi)) by using a public homomorphic encryption key k_pub obtained from the CSP. Then, these encrypted inputs will be sent to the cloud for global function evaluation.

Lines 4–5

The cloud will evaluate the global function g_fun (Enc_HME (f (D_H1)), Enc_HME (f (D_H2)), …, Enc_HME (f (D_HM))) over encrypted inputs. In the proposed framework, the basic cryptographic primitives that allow certain operations to be evaluated over encrypted data, include Paillier’s homomorphic encryption [16], 1–2 OT [22] and Yao’s garbled circuit [1].

Algorithm 1.

Proposed procedures

1:	Local private data evaluation at M different Hospitals
2:	Each hospital Hi evaluates the same local function f (DHi) over its local private data DHi, where i = 1, 2, …, M
3:	Each hospital Hi encrypts the result as EncHME (f (DHi)) based on Paillier’s homomorphic encryption [16]. Then, the encrypted results will be sent to cloud service provider as inputs for further computation.
4:	Secure data aggregation:
5:	The cloud securely aggregates the inputs from each hospital based on the homomorphic addition property as depicted in (1) with the output ${\mathit{\text{Enc}}}_{HME}({\sum }_{i=1}^{M}f(D_{H_i}))$. Then, the cloud can perform secure multiplication between a constant and the encrypted aggregation output as shown in (2)
6:	Secure conversion between homomorphic encrypted data and Garbled data
7:	The cloud adds random masks on each homomorphic encrypted value based on (3), (4) and (5), such as ${\mathit{\text{Enc}}}_{HME}(f(D_{H_i})+{\mu }_{H_i}^1),{\mathit{\text{Enc}}}_{HME}(Cf(D_{H_i})+{\mu }_{H_i}^2)$, and ${\mathit{\text{Enc}}}_{HME}({\sum }_{i=1}^{M}f(D_{H_i})+{\mu }_{\mathit{\text{sum}}})$. Then, the cloud sends the masked data to the CSP.
8:	The CSP decrypts these masked values with its private key and converts the masked values into garbled masked values as illustrated in the Yao’s protocol, such as $GV(f(D_{H_i})+{\mu }_{H_i}^1),GV(Cf(D_{H_i})+{\mu }_{H_i}^2)$, and $GV({\sum }_{i=1}^{M}f(D_{H_i})+{\mu }_{\mathit{\text{sum}}})$.
9:	The cloud requests the garbled random mask values from CSP through OT protocol, such as $GV({\mu }_{H_i}^1),GV({\mu }_{H_i}^2)$, and GV(μsum).
10:	Garbled circuit evaluation:
11:	The cloud subtracts the garbled random mask values from the corresponding garbled masked values within the garbled circuit, by which the cloud can recover the garbled values of the original values as GV (f (DHi)), GV (Cf (DHi)) and $GV({\sum }_{i=1}^{M}f(D_{H_i}))$.
12:	The cloud continues evaluating a ranking garbled circuit with inputs GV (f (DHi)), i = 1, 2, …, M, where the outputs are the ranking information of the underlying value f (DHi).
13:	The cloud will also evaluate a comparison garbled circuit with pair wise inputs GV (Mf (DHi)) and $GV({\sum }_{i=1}^{M}f(D_{H_i}))$, where the output is whether $GV(Mf(D_{H_i}))>GV({\sum }_{i=1}^{M}f(D_{H_i}))$. This comparison is equivalent to assess whether an input from a hospital is larger than the mean of these from all hospitals.
14:	Results feedback
15:	The cloud will match the garbled output with garbled truth table provided by the CSP to identify a valid output (see Fig. 5 (c) as an example). Finally, the decrypted results (e.g., ranking information) will be sent back to each hospital.

In this step, the Paillier’s homomorphic encryption scheme is used to achieve secure addition and multiplication operations over encrypted data.

• Secure addition among homomorphic encrypted results using Paillier’s homomorphic addition property.

  $$g_{\mathit{\text{sum}}}\left({\mathit{\text{Enc}}}_{HME}\right(f(D_{H_1})),{\mathit{\text{Enc}}}_{HME}(f(D_{H_2})),\dots ,{\mathit{\text{Enc}}}_{HME}(f(D_{H_M})\left)\right)={\mathit{\text{Enc}}}_{HME}({\sum }_{i=1}^{M}f(D_{H_i}))$$ (1)
• Secure multiplication between a constant and encrypted value using Paillier’s homomorphic multiplication property.

  $$g_{\mathit{\text{mul}}}\left({\mathit{\text{Enc}}}_{HME}\right(f(D_{H_i})),C)={\mathit{\text{Enc}}}_{HME}(Cf(D_{H_i}))$$ (2)

Lines 6–9

The cloud adds random masks on encrypted values based on the homomorphic addition property as follows

$${\mathit{\text{Enc}}}_{HME}(f(D_{H_i}))+{\mathit{\text{Enc}}}_{HME}({\mu }_{H_i}^1)={\mathit{\text{Enc}}}_{HME}(f(D_{H_i})+{\mu }_{H_i}^1),$$ (3)

$${\mathit{\text{Enc}}}_{HME}(Cf(D_{H_i}))+{\mathit{\text{Enc}}}_{HME}({\mu }_{H_i}^2)={\mathit{\text{Enc}}}_{HME}(Cf(D_{H_i})+{\mu }_{H_i}^2),$$ (4)

$${\mathit{\text{Enc}}}_{HME}(\sum _{i=1}^{M}f(D_{H_i}))+{\mathit{\text{Enc}}}_{HME}({\mu }_{\mathit{\text{sum}}})={\mathit{\text{Enc}}}_{HME}({\sum }_{i=1}^{M}f(D_{H_i})+{\mu }_{\mathit{\text{sum}}}),$$ (5)

where C is a constant, ${\mu }_{H_i}^1,{\mu }_{H_i}^2$ and μ_sum are random masks generated by the cloud, H_i is the index of each hospital with i = 1,2, …, M for total M hospitals. Then, the cloud sends the encrypted masked data to the CSP, where these masked values will be decrypted using the CSP’s private key. The CSP converts the decrypted masked values into garbled values as illustrated in the Yao’s protocol, which can be denoted as $GV(f(D_{H_i})+{\mu }_{H_i}^1),GV(Cf(D_{H_i})+{\mu }_{H_i}^2)$, and $GV({\sum }_{i=1}^{M}f(D_{H_i})+{\mu }_{\mathit{\text{sum}}})$. The garbled values will be used as inputs to evaluate the garbled circuit in the next few steps. Moreover, the cloud needs to request the garbled value of each random mask from CSP through OT protocol, such as $GV({\mu }_{H_i}^1),GV({\mu }_{H_i}^2)$, and GV(μ_sum). The OT protocol ensures that the CSP cannot learn the underlying random mask generated by the cloud. Thus, the CSP cannot infer the masked values even after the decryption in line 8.

Lines 10–13

The cloud subtracts the garbled random mask values from the corresponding garbled masked values within the garbled circuit, by which the cloud can recover the garbled values of the original values as $GV(f(D_{H_i}))=GV(f(D_{H_i})+{\mu }_{H_i}^1)-GV({\mu }_{H_i}^1),GV(Cf(D_{H_i}))=GV(Cf(D_{H_i})+{\mu }_{H_i}^2)-GV({\mu }_{H_i}^2)$, and $GV({\sum }_{i=1}^{M}f(D_{H_i}))=GV({\sum }_{i=1}^{M}f(D_{H_i})+{\mu }_{\mathit{\text{sum}}})-GV({\mu }_{\mathit{\text{sum}}})$. The use of garbled circuit protect the original value from being disclosed to the cloud during the above evaluation. Then, the cloud continues evaluating a ranking garbled circuit with inputs GV(f(D_Hi)), i = 1,2, …, M, where the outputs are the ranking information of the underlying value f(D_Hi). In addition, the cloud will also evaluate a comparison garbled circuit with pair wise inputs GV(Mf(D_Hi)) and $GV({\sum }_{i=1}^{M}f(D_{H_i}))$, where the output is $GV(Mf(D_{H_i})>{\sum }_{i=1}^{M}f(D_{H_i}))$. This comparison is equivalent to assess whether an input from a hospital is larger than the mean of these from all hospitals.

Lines 14–15

The cloud will match the garbled output with garbled truth table provided by the CSP to identify a valid output (see Fig. 5 (c) as an example). Finally, the decrypted results (e.g., ranking information) will be sent back to each hospital.

Remark II

The cloud should keep all the intermediate garbled values as secrets, so that the CSP cannot infer any input.

In summary, both the cloud and the CSP will be involved in the secure computation on, but none of them knows these underlying values under the proposed framework. In the next section, we will evaluate the proposed framework based on a real clinical dataset.

III. Experiment

In this section, we evaluate the proposed framework with MIMIC II Clinical Dataset [25]. The goal of the proposed framework is to perform secure data aggregation and data comparison among different hospitals in a cloud assisted environment, by which each hospital is able to retrieve its relative ranking under certain criteria in a privacy-preserving manner.

We have extracted a dataset with 924 death records in intensive care unit (ICU) from the MIMIC II Clinical Database, where all the attributes used in the dataset have been listed in TABLE I. The dataset includes 6 categorical attributes and 1 numerical attributes.

TABLE I.

MIMIC II CLINICAL DATASET

Attribute	Data Type
Sex	1: Female; 2: Male
Age of Death	Range from 21 to 101
Marital Status	1: Divorced; 2: Married; 3:Separated; 4: Single; 5: Unknown; 6:Widowed
Ethnicity	1:Asian; 2:Black/African American; 3:Hispanic or Latino; 4:Hispanci/ Latino-Puerto Rican; 5:Multi Race Ethnicity; 6:Other; 7:Partient Declined to Answer; 8:Unable to obtain; 9:Unknown; 10:White; 11:White-Brazilian;
Overall Payer Group	1:Auto Liability; 2:Free Care; 3: Medicaid; 4:Medicare; 5:Medicare private; 6:Other; 7:Private; 8:Self-pay;
Religion	1:7th Day Adventist; 2:Baptist; 3:Buddhist; 4:Catholtc; 5:Christian Scientist; 6:Episcopalian; 7:Greek Orthodox; 8:Jehovah’s Witness; 9:Jewish; 10:Methodist; 11:Muslim; 12:Not Specified; 13:Other; 14:Protestant Quaker; 15:Romanian East; 16:Unobtainable;
Admission Type	1:Elective; 2:Emergency; 3:Urgent;

For our experiments, we suppose there are M = 4 hospitals such as H₁, H₂, H₃, H₄. Then, we equally split the dataset into four sub datasets for the 4 hospitals. For our experiment, each plaintext has 32 bits. For homomorphic encryption, a 128-bit encryption key is used in our experiment. For the garbled circuit, each key is 64 bits.

Suppose each hospital would like to compare its ICU mortality against other 3 hospitals under different age groups. In addition, each hospital may be interested in whether or not its ICU mortality is above the average level among all 4 hospitals. Each hospital first computed its local mortality under different age groups, and encrypted these local mortalities with homomorphic encryption, which was sent later to the cloud for secure global comparison. The cloud and the CSP will cooperate together to rank each age group’s mortality in each hospital under the proposed framework. As aforementioned, each hospital also wants to know whether or not its mortality is above the average level. To compute the average value, a division circuit under Yao’s protocol needs to be implemented, which may significantly increase the circuit complexity. As each hospital is only interested in the comparison, we can reformate the comparison as follows

$$\mathit{\text{if}}M\times f_{\mathit{\text{mor}}}(D_{H_i})\ge {\sum }_{j=1}^M{f}_{\mathit{\text{mor}}}(D_{H_i}),$$ (6)

where M = 4 is the number of hospitals, D_i is the dataset at hospital H_i and f_mor (D_Hi) is the local function for calculate the local motility. The multiplication and aggregation can be achieved by homomorphic addition and multiplication operations. The results from the garbled circuit are listed in TABLE II. In TABLE II, the rank of each age group corresponds to the ascend order of mortality, where ‘1’ and ‘4’ refer to the lowest and the highest mortalities, respectively. The mortality of each hospital that is above the average among all hospitals, is shaded in gray in TABLE II.

TABLE II.

RANKING OUTPUTS USING THE PROPOSED FRAMEWORK, WHERE ‘1’ AND ‘4’ REFERS TO THE LOWEST AND THE HIGHEST MORTALITIES, RESPECTIVELY, WHERE THE MORTALITY THAT IS HIGHER THE AVERAGE AMONG ALL HOSPITALS, IS HIGHLIGHTED IN GRAY.

Age	H1	H2	H3	H4
20~29	4	1	3	2
30~39	3	4	1	2
40~49	1	2	4	3
50~59	1	4	2	3
60~69	1	2	4	3
70~79	4	1	3	2
>80	3	4	1	2

TABLE II depicts that the hospitals can obtain useful information for improving their service quality. For example, H₁ finds out that the mortality of its young population (age between 20 and 39) is the highest among all hospitals, thus they may need to pay more attention about its young population. This experiment demonstrates a practical use case of the proposed method. In practice, hospitals can conduct more advanced inquiries using the proposed framework. For example, they are able to compare the mortalities of a sub-population. The sub-population can be defined by a criterion like “age is between 50 and 59, sex is male and marriage status is widowed”, which can be achieved by modifying the local function in each hospital, whereas the cloud and CSP can follow the same protocols unchanged. Therefore, the proposed framework is flexible to handle more complicated real-world scenarios.

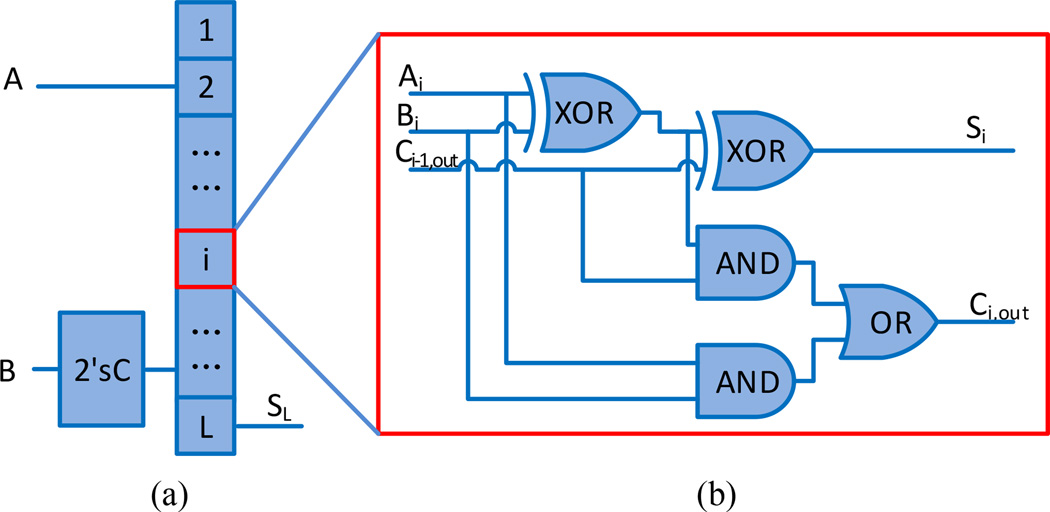
Remark III

For this experiment, we need to design a comparison garbled circuit for ranking operation. We designed the comparison circuit as shown in Fig. 6 (a), which consists of several full adder circuits (Fig. 6 (b)) and one two’s complement circuit (Fig. 6 (a)). In Fig. 6 (a), inputs are A and B with L bits, which can represent an integer ranging from 0 to 2^L − 1, and the output denoted by S_L is the most significant bit of A − B, as

$${\mathrm{S}}_{\mathrm{L}}=\{\begin{array}{c}0,\mathit{\text{if}}A\ge B\hfill \\ 1,\mathit{\text{otherwise}}\hfill \end{array}.$$ (7)

Fig. 6.

(a) A comparison circuit, where the comparison is achieved through a full adder circuit as shown in (b) with C_0,out = 0.

The comparison circuit can be used to rank the count of records in a query (e.g., a specific combination of attributes).

In this section, we used the secure aggregation and comparison operations as examples to illustrate the proposed framework. In practice, the cloud and CSP can securely compute many different functions by combining both homomorphic encryption and garbled circuits. We measured the execution time of some key cryptographic operations in a workstation with an Intel 3.2 GHz CPU, where all the results are averaged over 1000 single operations. The execution time of each basic cryptographic primitive has been profiled and shown in TABLE III.

TABLE III.

THE EXECUTION TIME OF EACH BASIC CRYPTOGRAPHIC PRIMITIVE USED IN THE PROPOSED FRAMEWORK

Operation	Time (milliseconds)
Homomorphic Encryption	3.1
Homomorphic Decryption	4.7
Homomorphic Add	1.7
Homomorphic Multiplication	0.5
OT Protocol	575.0
Comparison Garbled Circuit Evaluation	15.0

IV. Limitations and Discussion

The proposed system has several limitations that need the further investigation. One limitation is that the current framework only supports secure aggregation operations followed by secure rank operations. However, the proposed framework demonstrated the feasibility of combining homomorphic encryption and garbled circuit based crypto techniques for supporting QI studies. In theory, garbled circuit based protocol [1] can be used to securely evaluated arbitrary functions with the cost of specific circuit design. We will leave the circuit design of more advanced functions in our future work.

V. Conclusion

We introduced the PRECISE framework to facilitate privacy-preserving distributed quality metric comparison. The proposed framework supports secure ranking operation on aggregated data from distributed data sources in a cloud-assisted environment. We plan to develop more advanced system such as linear regression system using the garbled circuit protocol and homomorphic encryption primitives in order to expand the usability of the proposed framework.