White matter tract oriented deformation predicts traumatic axonal brain injury and reveals rotational direction-specific vulnerabilities

Abstract

A systematic correlation between finite element models (FEMs) and histopathology is needed to define deformation thresholds associated with traumatic brain injury (TBI). In this study, a FEM of a transected piglet brain was used to reverse engineer the range of optimal shear moduli for infant (5-day-old, 553-658 Pa) and 4-week old toddler piglet brain, (692-811 Pa) from comparisons with measured in situ tissue strains. The more mature brain modulus was found to have significant strain and strain rate dependencies not observed with the infant brain.

Age-appropriate FEMs were then used to simulate experimental TBI in infant (n=36) and pre-adolescent (n=17) piglets undergoing a range of rotational head loads. The experimental animals were evaluated for the presence of clinically significant traumatic axonal injury (TAI), which was then correlated with FEM-calculated measures of overall and white matter tract-oriented tissue deformations, and used to identify the metric with the highest sensitivity and specificity for detecting TAI. The best predictors of TAI were the tract-oriented strain (6–7%), strain rate (38–40 s⁻¹), and strain times strain rate (1.3–1.8 s⁻¹) values exceeded by 90% of the brain. These tract-oriented strain and strain rate thresholds for TAI were comparable to those found in isolated axonal stretch studies. Furthermore, we proposed that the higher degree of agreement between tissue distortion aligned with white matter tracts and TAI may be the underlying mechanism responsible for more severe TAI after horizontal and sagittal head rotations in our porcine model of nonimpact TAI than coronal plane rotations.

1. Introduction

Traumatic brain injury (TBI), including the spectrum from mild TBI (such as concussion) to severe TBI, contributes to a third of all injury-related deaths in the United States, and children aged 0 to 14 years account for almost half a million (473,947) emergency department visits annually due to TBI. (Faul et al. 2010; Langlois et al. 2004) TBI may have a focal or diffuse pattern, with diffuse traumatic axonal injury (TAI) being an important pathological correlate associated impaired neurological function; although lesser degrees of axonal injury, such as focal TAI involving the corpus callosum, are associated with mild TBI (Meaney and Smith 2011). The developing brain has different material properties than the adult brain and a distinct response to TBI. (Duhaime et al. 2003; Giza et al. 2007; Ommaya et al. 2002; Prange and Margulies 2002) Thus, it is imperative to utilize experimental and finite element models of the immature brain when investigating pediatric TBI. Despite the prevalence of pediatric TBI, there is still considerable uncertainty about the tolerance of the young brain to mechanical loading and whether the child is more or less vulnerable to TBI than the adult. A systematic correlation of finite element model simulations with histopathological responses to known applied loads is needed to define the tissue deformation thresholds for pediatric TBI. (Meaney et al. 2014)

Previous attempts to correlate head injury with kinematics-based criteria, such as the head injury criterion (HIC), and the rotational injury criterion (RIC) (Broglio et al. 2010; Guskiewicz et al. 2007; Kimpara and Iwamoto 2012; Pellman et al. 2003b; Takhounts et al. 2013) have been shown to be less accurate predictors than criteria based on tissue-level deformations as calculated by finite element modeling (FEM). (Deck 2008; Kimpara and Iwamoto 2012; Marjoux et al. 2008) Consequently, a range of FEM-based tissue injury prediction metrics have been studied by other investigators, including maximum principal strain, von Mises stress, the cumulative strain damage measure (CSDM), and the product of strain and strain rate. (Kimpara and Iwamoto 2012; Kleiven 2007; Lamy et al. 2013; Patton et al. 2013; Sahoo et al. 2013; Takhounts et al. 2003; Zhang et al. 2001) Furthermore, the results of in vitro axonal injury studies suggest that traumatic axonal injury (TAI) is the result of the specific strain components oriented along the longitudinal axis of the axons. (Cullen and LaPlaca 2006; LaPlaca et al. 2005)

Diffusion tensor imaging (DTI) makes it possible to non-invasively determine the three-dimensional orientation of axonal tracts within the brain. (Le Bihan et al. 2001) As a result, several groups have sought to use DTI in conjunction with FEM to explore not only the tissue-level strain, but also the tensile strain on the axons themselves. (Chatelin et al. 2011; Cloots et al. 2013; Colgan et al. 2010; Wright and Ramesh 2012) While these studies have calculated axonal elongation under realistic head loading conditions, they are limited by a lack of corresponding histopathological data that would enable verification of TAI as a result of these deformation parameters. This paucity is mainly due to the limited amount of human data with precise information on both the mechanical head loads and the resulting brain injuries.

Additionally, it has been frequently observed that the severity of head injury is dependent on the direction of head rotation. (Broglio et al. 2010; Eucker et al. 2011; Pellman et al. 2003a; Sullivan et al. 2013). However, no mechanical explanation has been established for why certain head rotational directions produce more TAI than other rotational directions. In this study, we hypothesized that rotational directions associated with greater TAI have larger strains along the white matter tracts than rotational directions associated with less TAI. WE further hypothesized that the infant brain has a lower strain threshold for TAI than the pre-adolescent brain.

To test these hypotheses, we used a piglet model of TBI in which we precisely controlled head loading conditions and quantified resulting axonal injury. We then developed a corresponding piglet brain FEM, used reverse engineering to optimize brain moduli such that the model mimicked the direct measurements of tissue strain, and used the FEM to compare estimates of deformation aligned with the white matter tracts to actual tissue deformation. The FEM deformations were correlated with histopathological measurements of injury to identify the strain metric with the highest sensitivity and specificity for detecting TAI in infant and pre-adolescent brains. The best performing parameters were used to define tissue-level thresholds for TAI and were compared across ages and head rotation directions.

2. Methods

2.1. Finite Element Model Development

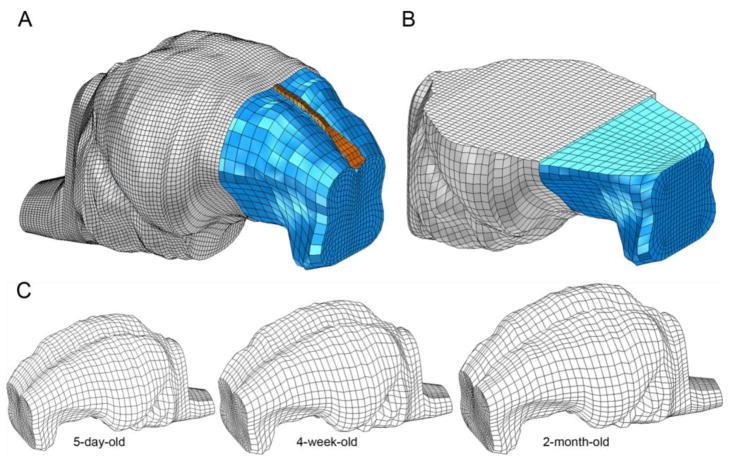
This study uses finite element models (FEM) of infant 5-day-old, toddler 4-week-old, and pre-adolescent 2-month-old piglet brains adapted from a previously reported piglet brain model. (Coats et al. 2012) Briefly, 4-week-old piglet brain coronal CT images were analyzed in MIMICS 9.0 (Materialise, MI) to determine brain geometry and scaled to the approximate dimensions of the 5-day-old and 2-month-old piglet brains. Previously, using measurements of ex vivo brains from each age group were made to determine scale factors (Eucker 2009; Maltese 2012a), we confirmed that there was no marked difference in shape between the 5-day-old and 4-week-old porcine brain, and therefore the 4-week-old model was scaled uniformly to create the infant (5-day-old) piglet FEM. However, we observed a shape change between the 4-week and 2-month old, and appropriate scale factors were used for each dimension to create the pre-adolescent (2-month-old) FEM. The skull was created by extending the cortical surface of the brain outward. Falx geometry was added based on ex vivo measurements of the falx in the 5-day-old piglet and scaled up for the toddler and pre-adolescent. The sulci and tentorium are not represented in the FE models. The brain, falx, and skull (Figure 1A) were meshed in MSC Patran (MSC Software, Santa Ana, CA) to form the completed FEM, and a convergence analysis was performed to ensure performance stability for each piglet age. Specifically, for each age group, at least 6 progressively finer mesh densities representing at least a 3-fold increase in mesh density were simulated with typical rotational velocity traces recorded from piglet studies in each rotational direction. The maximum principal strain in each element was calculated to establish strain distributions for that mesh density. As density increased, the resulting strain distributions rapidly reached an asymptote. The coarsest mesh density that produced stable strain distributions as compared to all progressively finer meshes was selected as the converged mesh for each age. The converged models consist of 13,018; 13,302; and 18,496 linear hexahedral brain elements for the 5-day, 4-week, and 2-month old models respectively, with 1,890 linear wedge elements in the falx and 17,722 rigid shell elements in the skull for each age (Figure 1C).

Figure 1.

(A) Whole brain FEM and (B) transection of the FEM for the 5-day-old piglet. Brain (blue), falx (orange), and skull (gray, A) or skull-PMMA- Plexiglas plate complex (gray, B). A portion of the frontal skull in each figure is cut away for illustration. (C) Isolated brain FEM for 5-day, 4-week, and 2-month-old piglets.

The brain tissue was modeled as homogeneous isotropic hyperelastic material using the first order Ogden strain energy density function, W, as shown in Equation 1, and a viscoelastic material using the two-term Prony series function in Equation 2. (Ogden 1984)

$$W=\frac{2\mu }{{\alpha }^2}\left({\lambda }_1^{\alpha }+{\lambda }_2^{\alpha }+{\lambda }_3^{\alpha }-3\right)$$ [Eq. 1]

$$\mu (t)={\mu }_0\left(1-\sum _{i=1}^2{C}_i\left(1-e^{-t/{\tau }_i}\right)\right)$$ [Eq. 2]

In Equation 1, λ_i^α represent the principal stretch ratios, and α is a previously derived tissue-specific parameter representing the brain tissue strain-sensitive nonlinear characteristics. (Prange and Margulies 2002) The brain tissue shear modulus, μ₀, was determined as a range of values for each age as derived from reverse engineering such that the validated model reproduced measured strains (Section 2.2.). The relaxation moduli, C_i, and time constants, τ_i, in the Prony series (Table 1) were derived from published shear experiments of gray and white matter from 5-day-old and 4-week-old piglets. (Prange and Margulies 2002) These shear ex vivo experiments showed that the modulus and viscoelastic properties of adult and 4-week-old porcine brain were not significantly different, so the same range of brain material properties was used for the 2-month-old and 4-week-old piglet FEMs.

Table 1.

Model material properties.

		5-day-old	4-week-old and 2-month-old
Brain
		μ0=553–658 Pa	μ0=692–811 Pa
	Ogden Model Coefficientsa	α=0.01	α=0.01
		C1 =0.3322	C1 =0.316
		C2=0.3890	C2=0.428
		τ1=2.96 s	τ1=3.0 s
	Prony Series Coefficients5	τ2=0.181 s	τ2=0.19 s
	Density	ρ=1.04 g/cm3
	Poisson’s Ratio	ν=0.49999
Falx
	Density33, 34	ρ=1.13 g/cm3
	Modulus33, 34	E=15 MPa
	Poisson’s Ratio33, 34	ν=0.45
Connectors
	Stiffness35	3460 N/mm

^aThis optimal range of moduli was determined during the model validation process (Section 2.2).

The falx was modeled as an isotropic, linear elastic material, with modulus determined by scaling the modulus of adult human dura according to the methods presented in Coats et al. (Coats et al. 2012) The skull was modeled as a rigid material.

Based on our previously published boundary condition validation (Coats et al. 2012), in which FEM predictions were validated against both measured displacements between brain and skull and calculated brain tissue strain during rapid head rotations, two-dimensional linear elastic spring connectors were used to link every surface node of the brain to the nearest node on the skull to approximate the combined response of the pia-arachnoid connective tissue, cerebral spinal fluid (CSF), and vasculature located between the brain and skull. The elastic modulus, cross-sectional area and length of cortical veins taken at autopsy (Monson et al. 2005) were used to define the stiffness of these connectors (Table 1). The 5-day-old and 2-month-old piglet models employed 2682 and 3012 connector elements, respectively.

2. Reverse Engineering Optimization of Finite Element Model Brain Material Properties

Brain material properties measured ex vivo vary dramatically based on the level of strain and strain rate (Chatelin et al. 2010; Prabhu et al. 2011; Prange and Margulies 2002; Rashid et al. 2012; Rashid et al. 2013; Thibault and Margulies 1998) underscoring the importance of matching properties to the loading conditions for accurate FEM-derived predictions. Previous ex vivo shear testing determined properties for pediatric porcine brain tissue at up to 80% principal strain and 19.38 s⁻¹ principal strain rate. (Prange and Margulies 2002) However, preliminary simulations using these material properties to simulate the more severe animal injuries obtained for this study demonstrated higher strains (peak maximum principal strain exceeding 100%) and much higher strain rates (peak maximum principal strain rate exceeding 300 s⁻¹). Thus, we determined the need to further optimize these measured brain tissue properties by comparing brain strain in FEM simulations with experimental brain strains measured in high strain and strain rate conditions. We used a previously developed methodology to measure in situ brain tissue deformation in six new horizontally transected infant 5-day-old and toddler 4-week-old piglet heads during a rapid rotational event of similar magnitude to our animal injuries. (Ibrahim et al. 2010a) The material properties derived for the 4-week-old piglet were then also used for the 2-month-old piglet FEM, as we have previously reported that there are no significant differences in ex vivo brain material properties between the 4-week-old piglet and adult pig. (Prange and Margulies 2002)

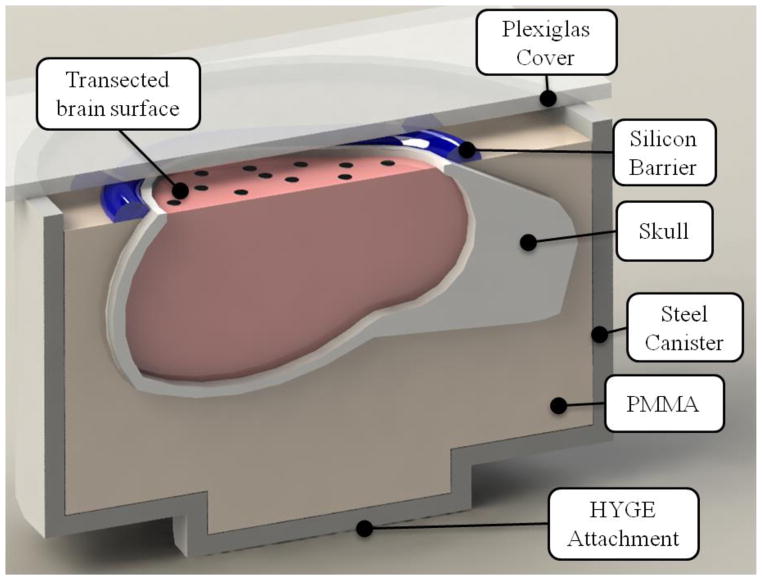
In these new in situ experiments, intact heads of 5-day-old (n=3) and 4-week-old (n=3) piglets obtained immediately after sacrifice were transected in a horizontal plane just above the supraorbital margin. The transected brains were potted into a cylindrical canister and marker dots placed across the transected surface to track brain strain. A clear plexiglass plate was placed on top of the canister to enclose the contents, and a layer of transparent lubricant provided a quasi-frictionless interaction between the brain surface and the plexiglass plate (Figure 2), as described in detail by Ibrahim et al. (Ibrahim et al. 2010a)

Figure 2.

Cut-away schematic view of the canister preparation with transected piglet head potted in polymethylmethacrylate (PMMA) resin.

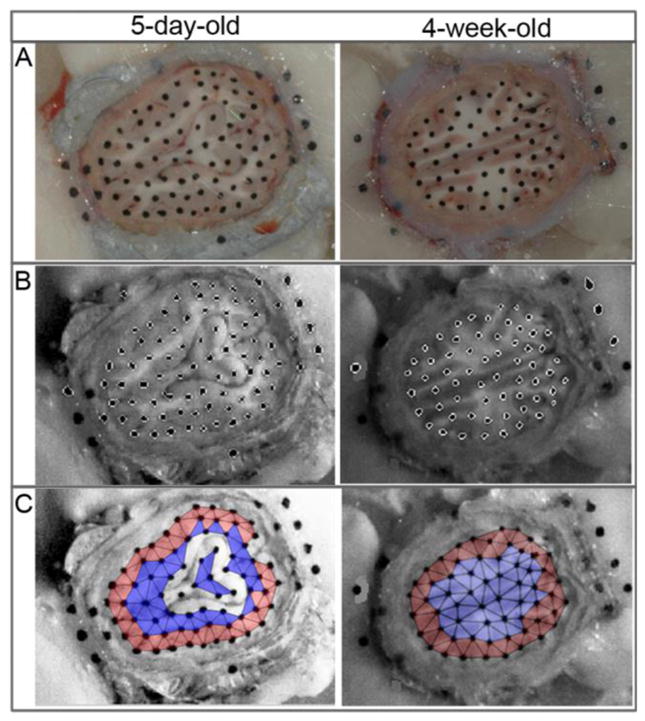
Canisters were rotated 65° at 121 ± 3.22 rad/s via a HYGE pneumatic actuator system (Bendix Corporation) (Raghupathi and Margulies 2002) while being filmed at 2500 fps with a high speed digital camera (HG TH, Redlake Tallahassee, FL; resolution of 0.4 mm/pixel). Two angular velocity transducers (Model ARS-06, ATA Inc., Albuquerque, NM) were attached to the actuator side arm and measured the angular velocities at 10,000 Hz. The velocity traces were filtered using a low pass 2^nd order Butterworth filter with a 1 kHz cutoff frequency. An in-house analysis program in MATLAB (MathWorks, Natick, MA) isolated the marker dots and tracked their position throughout the canister motion (Figure 3B). Only marker dots that could be tracked successfully through every video frame were included in subsequent analysis.

Figure 3.

(A) Representative images of the surface of a transected head for 5-day-old (left) and 4-week-old (right) piglets, demonstrating marker dots on brain tissue, skull and PMMA. (B) Single frame from high speed video demonstrating marker dots isolated by the MATLAB tracking program. (C) Non-overlapping triads covering the cut surface of the brain. Central triads (blue) were used for strain calculations, while peripheral triads (red) and triads encompassing portions of the lateral ventricles (no color) were not included for analysis.

All brain surface marker dots were placed into groups of three to form the maximum possible number of non-overlapping triads covering the surface of the exposed brain, but excluding any triad containing a portion of transected lateral ventricles (Figure 3C). Slip along the ventricles was not replicated in the continuous FEM and was not considered representative of actual brain tissue deformation, thus the ventricle area was not analyzed for strain. Each triad was defined as peripheral or central based on location. A triad was considered peripheral if its centroid was located within distance d from the skull-brain interface, where d was defined as 20% of the measured anterior-posterior length of the brain for each study. Peripheral triads covered primarily cortical gray matter, while central triads covered deeper gray matter and white matter tracts. The two-dimensional Lagrangian finite strain tensor was calculated for each triad. (Fung 1994) Although displacement may be a more direct, first-order measurement, we wanted to optimize material properties to yield accurate assessments of strain and strain rate, because the purpose of our study was to develop strain tolerances for axonal injury. Therefore, the reverse engineering process was conducted to optimize strain and strain rate values, and utilized only computed experimental strain data obtained from the central triads, which primarily encompassed the white matter tracts. To assess error in the tracking program, strain was also calculated for a triad consisting of 3 marker dots all on the PMMA. As the PMMA represents a rigid body, any deviation from zero strain represents measurement error in the tracking system.

The FEMs used to simulate the head transection experiments were created by making a corresponding horizontal brain transection in the three-dimensional geometries of the 5-day-old and 4-week-old FEMs. A rigid plate, representing the plexiglass cover, was placed 1 mm above the cut surface and meshed as part of the skull rigid body (Figure 1B). The brain geometry was meshed with the same mesh seed spacing as the corresponding full brain model for each age to maintain the converged mesh density in the transected FEM, and brain-skull connector elements from the full brain FEM that were remaining in the transection FEM (2,069 connectors in 5-day-old and 1988 connectors in 4-week-old). To replicate the frictionless boundary condition between the transected brain surface and the plexiglass plate in the experiment, a kinematic coupling constraint was prescribed for the nodes on the FEM’s cut brain surface, such that the nodes were free to translate in the two dimensions of the cut plane without friction but were restricted from out-of-plane displacements. All other model parameters were consistent with the full brain model for each age. The filtered velocity time history measured in each head transection experiment was used as the load input for each corresponding simulation. All simulations were run in ABAQUS Explicit version 6.9-EF (Simulia, Providence, RI) with double precision. Distortion and enhanced hourglass control were used to mitigate excessive mesh deformation.

The triad centroids on the brain surface of the six head transection studies were spatially matched to the closest corresponding nodes in the FEM for comparison. If a triad centroid did not correspond to the exact location of a node, up to four surrounding nodes were selected, and the FEM strain at the triad centroid location was interpolated. Each of the six head transection studies was thus compared to a unique subset of FEM nodes. The deformation metrics extracted from both experiments and FEM simulations for comparison were the peak values over all time of: the maximum principal strain (S), the maximum principal strain rate (SR), and the product of maximum principal strain and strain rate (SxSR).

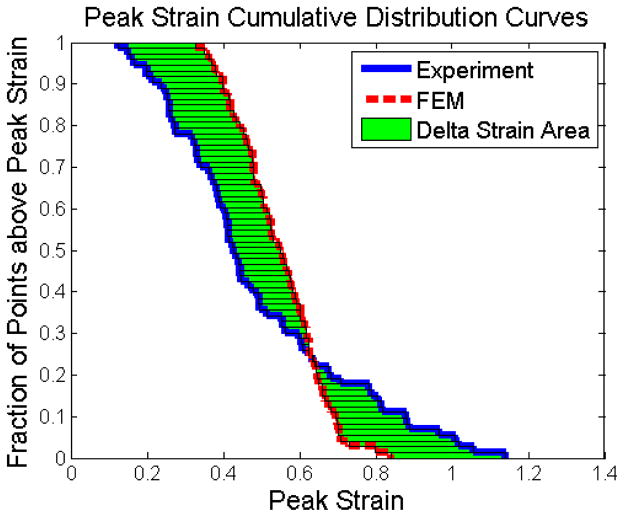
The transected FEM simulations were performed for at least 32 shear modulus values between 200Pa–1000Pa. The resultant metrics were compared to those of the actual transection experiments in order to identify the brain shear modulus that yielded the best agreement between FEM and experimental tissue strain data. The empirical cumulative distributions of each peak deformation metric for both FEM and experimental data were calculated over the entire simulation or corresponding experiment, respectively, and plotted in the manner shown in Figure 4. The area between the FEM and experimental data distributions could then be used as a metric for how well the FEM fit the experimental data, such that a smaller area indicated a better fit.

Figure 4.

Empirical cumulative distributions for experimentally-derived (solid blue) and FEM-predicted (dashed red) tissue strains, and the area between the curves (green) for one animal at one particular FEM shear modulus.

An optimization process was developed to establish the brain shear modulus for each age (5-day-old or 4-week-old). Using the area between the FEM and experimental cumulative distributions, a model error function was created that gave equal weighting to all three deformation metrics (S, SR, and SxSR) over all three experimental transection studies for each age. The areas (|x_EXPi − x_FEMi|) between the cumulative distribution curves for each metric (x) were summed across the three experimental studies, and normalized by dividing by the mean area to the left of the experimental cumulative distribution curve for that metric over all three studies ( $\overline{x_{\mathit{EXP}}}$). The resulting error terms for each metric (S, SR, and SxSR) were then summed to yield the final total model error compared to the experimental data (Equation 3). The brain shear modulus resulting in the lowest model error was defined as the optimized modulus for that age group.

$$\text{Model}\text{Error}=\frac{{\sum }_{i=1}^3\mid S_{\mathit{EXPi}}-S_{\mathit{FEMi}}\mid }{\overline{S_{\mathit{EXP}}}}+\frac{{\sum }_{i=1}^3\mid {SR}_{\mathit{EXPi}}-{SR}_{\mathit{FEMi}}\mid }{\overline{{SR}_{\mathit{EXP}}}}+\frac{{\sum }_{i=1}^3\mid {\mathit{SxSR}}_{\mathit{EXPi}}-{\mathit{SxSR}}_{\mathit{FEMi}}\mid }{\overline{{\mathit{SxSR}}_{\mathit{EXP}}}}$$ [Eq 3]

The model error plotted as a function of modulus demonstrated a range of moduli that all had similar performance, i.e. all moduli had an error term within 1.5% of the lowest calculated error for that age. Therefore, two simulations for each animal experiment in Section 2.3 using the full brain FEM were conducted using the low and high end of the modulus range, to establish a range of potential FEM responses for each piglet age.

To determine whether there was good statistical fit between the FEM-derived cumulative distribution curves (Figure 4) generated from these optimized moduli and those distributions derived experimentally, the Kolmogorov-Smirnov (KS) goodness of fit test for continuous distributions was performed to evaluate the statistical correlation between FEM and experimentally-derived S, SR, and SxSR distributions for each experimental study. A p-value of >0.05 was used to indicate that the distributions were not statistically different and, therefore, that the FEM was a good fit to the experimental data. We determined that moduli greater than ±1.5% from the calculated minimum error value had a statistically significant impact on the KS goodness of fit test against the experimental data. Therefore all brain moduli with error values less than 1.5% of the lowest calculated error were considered equivalent optimal brain moduli values. As such, the lowest and highest moduli of the optimal range were used in separate simulations of the animal studies.

2.3. Animal Studies

All protocols from the collected studies were approved by the Institutional Animal Care and Use Committee of the University of Pennsylvania. Previously conducted animal experiments with rapid head rotation in the sagittal, horizontal, or coronal plane in infant 5-day (n=36) (Eucker et al. 2011), and pre-adolescent 2-month (n=17) (Maltese 2012b) old female piglets were simulated with the age-appropriate FEM to establish which deformation metric and associated threshold was most predictive of axonal injury in these two ages. The animal studies resulted in a broad spectrum of TBI ranging from no neuropathology to severe traumatic axonal injury (TAI). Insufficient animal data was available in the toddler 4-week-old piglet for this analysis, so no deformation thresholds were derived for this age group.

In these animal studies, prior to injury 5-day-old piglets were anesthetized with 4% isoflurane, and the 2-month-old piglets received an intramuscular injection of ketamine (20 mg/kg) and xylazine (2 mg/kg) followed by 4% isoflurane. Piglets from both ages underwent a single, rapid non-impact head rotation in the coronal, horizontal, or sagittal plane using the same HYGE pneumatic actuator system as in the head transection experiments. During coronal and horizontal plane rotations the head rotated 90°, but sagittal plane rotations spanned only 60° due to the limited flexibility of the piglet cervical spine in this direction. To mimic the animal studies, the center of rotation for horizontal and sagittal rotations was the mid-cervical spine, while the brain rotated about the spine in the coronal rotations, with the majority of brain mass sitting above the axis of rotation. One or two angular velocity transducers (Model ARS-06, ATA Inc., Albuquerque, NM) were attached to the actuator side arm and measured the angular velocities at 10,000 Hz. The power spectral density of each velocity trace was plotted and used to obtain an appropriate cutoff frequency for low pass filtering of the trace. The number of animals for each age group and rotational plane, along with the average peak angular velocities and accelerations, are presented in Table 2.

Table 2.

Summary of animal studies simulated with FEM. Values listed are mean (range).

		5-day-old	2-month-old
Horizontal	N	25a	9
	Peak Angular Velocity (rad/s)	177 (115–214)	143 (115–166)
	Peak Angular Acceleration (rad/s2)	46,168 (19,794–80,174)	74,675 (22,388–168,682)
Sagittal	N	5a	5
	Peak Angular Velocity (rad/s)	159 (156–161)	126 (97–155)
	Peak Angular Acceleration (rad/s2)	49,926 (45,641–57,498)	44,489 (24,054–81,129)
Coronal	N	6a	3
	Peak Angular Velocity (rad/s)	200 (170–218)	170 (160–184)
	Peak Angular Acceleration (rad/s2)	53,715 (33,434–70,218)	45,491 (42,412–51,573)

^aPreviously published in Eucker et al⁸ except for N=12 horizontal.

At 6 hours post-injury, piglets were sacrificed via pentobarbital overdose. The brains were perfusion-fixed and carefully removed from the cranium for subsequent histological analysis. The fixed brains were cut into 3mm thick coronal sections and photographed. For 5-day-old piglets, half of the coronal sections were reserved for histological assessment (6 sections per brain), while all coronal brain sections were evaluated for the 2-month-old (12–18 sections per brain). 6 μm slices were cut from each coronal section, immunostained with β-amyloid precursor protein (β-APP, Chemicon 22C11, used at dilution of 1:5000), and lightly counterstained with Mayer’s hematoxylin. A single blinded neuropathologist examined the slices microscopically and marked regions of traumatic axonal injury (TAI) on photographs of the coronal sections. Each coronal section was analyzed using Adobe Photoshop CS4, and the total area of the forebrain—all of the sections excluding the midbrain, brainstem, and cerebellum—was measured. Each marked region of TAI within the forebrain was also traced and measured. The percentage of TAI in the forebrain was calculated as the area of TAI divided by the total area of the forebrain.

2.4. Strain Analysis

Previous computational studies in adults have found strain (S), strain rate (SR), and the product of strain and strain rate (SxSR) to correlate with predictions of TBI. (Kimpara and Iwamoto 2012; Kleiven 2007; Takhounts et al. 2003; Zhang et al. 2001) Furthermore, increasing strain and strain rate along the axonal fibers has been shown to produce injury in the CNS (Bain and Meaney 2000; Shi and Whitebone 2006; Singh et al. 2009). Given this information, our model evaluated the capability of S, SR, and SxSR to predict TAI in the piglet using three methods. The first method assumed that tensile strain in both the white and grey matter can be a predictor of TAI. For this method, the deformation metrics were calculated for all nodes in the entire forebrain of the model. The second method acknowledged that TAI is most likely to occur in the descending white matter tracts (WMT) of the brain and restricted the analysis to nodes that geometrically corresponded to the locations of the WMTs. The final method assumed not only that TAI occurs in the WMT, but that the tensile component of strain oriented along the WMT is the most important component in predicting TAI in the piglet. We hypothesized that this final method, which utilizes the components of the three deformation metrics oriented in the direction of the WMT, would be an improved predictor of TAI in the piglet.

Simulations were run for each animal injury study by uniformly scaling the piglet whole brain FEM developed in Section 2.1 to match the animal brain mass and by using that animal’s rotational velocity trace as the input loading condition. The center of rotation for the FEM was placed in the same location as the center of rotation in the animal injury studies. When two velocity transducers were employed in the animal study, the average reading from both was used as the input loading for the simulation. Simulations were performed in ABAQUS Explicit, version 11.2 with additional analysis in MATLAB. The strain rate (SR) was calculated as the discrete derivative of maximum principal or tract-oriented strains between time points. The strain times strain rate (SxSR) was calculated as the maximum principal or tract-orient strain at a node multiplied by its strain rate for each time point.

2.5. White Matter Tract (WMT) Analysis

DTI and high-resolution T2-weighted MRI scans were completed of uninjured perfusion fixed ex vivo piglet brains to determine the locations and orientations of WMTs in each piglet age group. A DTI scan was performed for each piglet age on a 7T Siemens magnet with a 32 channel human head coil (FOV: 64 × 40 × 58 mm³, resolution: 0.4 × 0.4 × 1 mm³, TR = 400 ms, TE = 60 ms, 6 diffusion directions, 1 baseline scan, and diffusion b-value = 1300 s/mm²) using a spin-echo sequence with a 3D DTI acquisition modified to acquire a single k-space line per TR. Boundaries between gray and white matter were imaged via high-resolution T2-weighted MRI scans conducted on a 9.4 T 31 cm horizontal bore MR system (5d FOV: 115 × 58 × 38 mm³, 2m FOV: 110 × 55 × 48 mm³, resolution: 0.15mm³). Diffusion matrices for each voxel were evaluated for eigenvectors, defining the local principal tissue orientation.

Coronal slices of the FEM sized to each simulated piglet brain were registered to corresponding coronal images from the MRI and DTI scans for that piglet age based on the slice spacing. For example, if there was 1.8mm between each FEM slice and 0.15mm between each DTI slice, then each FEM slice would be registered to every 12^th DTI slice. In situations where the spacing between the FEM and scans were not whole number increments and/or the FEM brain geometry did not properly match that of the numerically-selected MRI or DTI slice, adjacent MRI or DTI slices were evaluated to identify the one with the best match to the FEM brain shape. After manually overlaying the registered FEM, MRI, and DTI coronal images (Figure 5), the FEM nodes corresponding to the descending WMT voxel locations were identified. The DTI image eigenvectors at corresponding voxels were then used to obtain the unit direction vector (û′) of the WMT at each of these locations. To maintain symmetry within the FEM, the WMT nodes and associated direction vectors were determined for the right hemisphere of the brain and mirrored across the longitudinal fissure to generate the left hemisphere WMTs.

Figure 5.

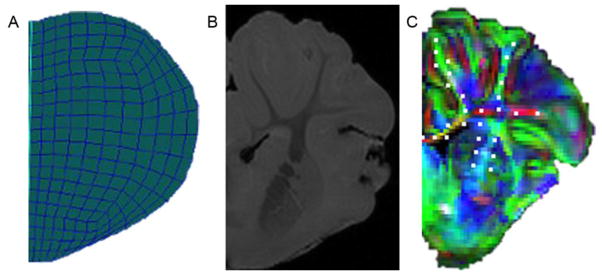
(A) Right half coronal slice of FEM. (B) Right half coronal slice of high-resolution MRI scan. (C) Right half coronal slice of diffuse tensor image with overlaid RGB color map representing tissue tract orientation (red: x-direction, green: y-direction, blue: z-direction). Mesh node locations corresponding to WMTs are marked with white dots.

For each head rotation simulation, the 6 components of the Lagrangian strain tensor (E_global) were obtained for each node (Equation 4), where ε₁₁, ε₂₂, ε₃₃ are the nominal strain components and γ₁₂, γ₁₃, γ₂₃ are the shear components.

$$E_{\mathit{global}}(t)=\left[\begin{array}{ccc}{\epsilon }_{11}(t)& {\gamma }_{12}(t)& {\gamma }_{13}(t)\\ {\gamma }_{12}(t)& {\epsilon }_{22}(t)& {\gamma }_{23}(t)\\ {\gamma }_{13}(t)& {\gamma }_{23}(t)& {\epsilon }_{33}(t)\end{array}\right]$$ [Eq. 4]

The peak maximum principal strain (S) was defined as the maximum eigenvalue of E_global across all time points for a given node.

The magnitude of tensile strain oriented in the direction of the WMT was calculated from the strain tensor E_global as follows. First, E_global was transformed out of the stationary global coordinate system into a coordinate system relative to the skull using the rotational matrix R(θ(t)) corresponding to the simulated direction of head rotation (Equation 5).

$$E_{\mathit{skull}}(t)=[R(\theta (t))][E_{\mathit{lab}}(t)]{[R(\theta (t))]}^T$$ [Eq. 5]

The rotational matrices used for the three injury directions were:

$$\begin{array}{lll}\text{Sagittal}\hfill & \text{Horizontal}\hfill & \text{Coronal}\hfill \\ R(\theta (t))=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos(\theta (t))& -sin(\theta (t))\\ 0& sin(\theta (t))& cos(\theta (t))\end{array}\right]\hfill & R(\theta (t))=\left[\begin{array}{ccc}cos(\theta (t))& 0& sin(\theta (t))\\ 0& 1& 0\\ -sin(\theta (t))& 0& cos(\theta (t))\end{array}\right]\hfill & R(\theta (t))=\left[\begin{array}{ccc}cos(\theta (t))& -sin(\theta (t))& 0\\ sin(\theta (t))& cos(\theta (t))& 0\\ 0& 0& 1\end{array}\right]\hfill \end{array}$$

At each time-point, the tract-oriented strain (TOS) was then calculated from the projection of the rotated tensor matrix (E_skull) onto the time-invariant unit direction vector (û′) of the WMT for each node at each time point (Equation 6). The peak tensile TOS was calculated as the maximum TOS across all time points for each WMT node.

$$\mathit{TOS}(t)={\widehat{u}}^{\prime }·[E_{\mathit{skull}}(t)]({\widehat{u}}^{\prime })$$ [Eq. 6]

2.6. Tissue Strain Predictions for Brain Injury

Threshold development requires a clear definition of the outcome measure, in this case traumatic axonal injury. While presence of any axonal injury could represent one definition of brain injury, evidence suggests that the degree of axonal injury must be above a certain level to manifest clinically significant injury. (Naim et al. 2010) A recent study involving mild TBI in 5-day-old piglets demonstrated no significant behavioral or cognitive deficits in animals with up to 0.18% TAI by tissue area on histopathology. (Naim et al. 2010) Therefore, for our analysis, levels of TAI at or below 0.18% of total forebrain area were defined as not clinically detectable. Animals with these low levels of TAI were considered uninjured for the purposes of threshold development, while animals with TAI levels >0.18% were considered injured.

Threshold development also requires independent validation to support the assertion that the threshold is universally applicable. (Anderson et al. 2007) The 5-day-old piglet simulations were randomly split into two groups for analysis. The first group included two-thirds of the total number of animals (n=24); this group was used to determine the measure(s) that best predicted brain injury and to develop the injury threshold value(s) for the predictive measure(s). The second group included the remaining one-third of animals (n=12) and was used as an independent validation group for the derived threshold value(s). Animals with and without clinically significant TAI were represented with approximately the same frequency in the development and validation groups.

The 2-month-old group had a much smaller dataset size (n=17) and there was an insufficient number of animals with and without axonal injury to employ an independent validation group. Therefore, all 2-month-old simulations were used for threshold development only.

The empirical cumulative distribution functions were calculated for S, SR, and SxSR using each of the three analysis methods described in Section 2.4. The values for each metric exceeded by 90% (Pop90), 50% (Pop50), and 10% (Pop10) of the nodes were extracted from these distributions as cumulative measures of the deformation experienced by the brain tissue (Figure 6).

Figure 6.

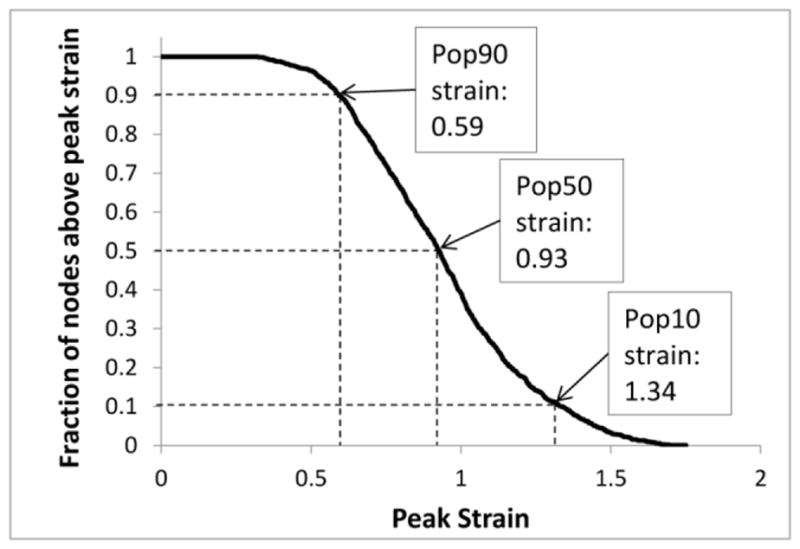
Example of a population distribution graph for strain derived from FEM data, with its corresponding population values (Pop90, Pop50, and Pop10) indicated by arrows.

Parameters were generated from the 3 population levels (Pop10, Pop50, and Pop90) of the 3 deformation metrics (S, SR, and SxSR) using the 3 analysis methods (peak metric values over the entire forebrain, peak metric values restricted to the WMTs, and peak tract-oriented metric values). These 27 parameters were evaluated using receiver operating characteristic (ROC) analysis to determine their ability to predict the presence or absence of TAI, with larger areas under the ROC curve (AUC) indicating better predictive capability. The predictive quality of these ROC-generated optimal parameter(s) were further evaluated using the Pearson correlation coefficient to determine how well each parameter correlated with TAI percentage.

From the ROC analysis of the optimal parameter(s) in each age group, two potential thresholds were extracted for each parameter: (1) Youden’s index, which maximizes additive sensitivity and specificity thus giving equal weight to sensitivity and specificity, and (2) the threshold with greatest specificity resulting in 100% sensitivity. These potential thresholds were then compared across developmental age. For the 5-day-old animals, these thresholds were also tested using the independent validation group to determine the working sensitivity, specificity, negative predictive value (NPV), and positive predictive value (PPV) for this group.

Finally, previous studies using this 5-day-old piglet dataset have shown that coronal plane rotations at similar levels of rotational velocity and acceleration as horizontal and sagittal plane rotations result in significantly less TAI. (Eucker et al. 2011) This has been hypothesized to be due to differences in brain tissue deformation metrics among the three injury directions. We further evaluated the relationships for each of the three injury directions (coronal, horizontal, sagittal), to identify whether the deformation parameters correlated with observed directional TAI differences.

3. Results

3.1. Reverse Engineering Optimization of Finite Element Model Brain Material Properties

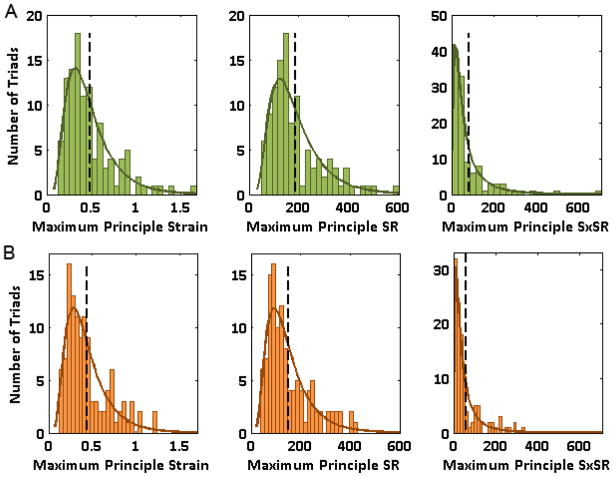
Six brain transection experiments were conducted at an average angular velocity of 121 rad/s for each age to compare with the piglet brain FEM (n=3/age) and optimize appropriate brain moduli. During each of these transection experiments, the largest deformations experienced by any of the central triads corresponded to values near or exceeding 100% peak maximum principal strain (S) and 300 s⁻¹ strain rate (SR), thus reaching expected deformation levels based on our previous studies. The S, SR, and SxSR distributions of all three experiments pooled for each of the two age groups were each found to fit log-normal distributions (Figure 7) based on Kolmogorov-Smirnov (KS) goodness of fit tests. The mean strain for the 5-day-old and 4-week-old groups was 0.48 and 0.44, the mean SR was 189 s⁻¹ and 150 s⁻¹, and the mean SxSR was 83 s⁻¹ and 60 s⁻¹, respectively.

Figure 7.

Distributions of S, SR, and SxSR for (A) 5-day-old and (B) 4-week-old transection experiments fitted with a log-normal continuous distribution. Vertical dashed lines correspond to the mean value for each distribution.

The tracking program uncertainty range, defined by non-zero strains measured in the rigid PMMA triads, was 0.0046 ± 0.0066 (mean ± standard deviation). While this uncertainty was statistically significant (Wilcoxon signed rank test, p<0.001), the magnitude of this error was well below the lowest measured brain tissue peak maximum principal strain (0.12), and therefore did not appreciably affect our strain measurements.

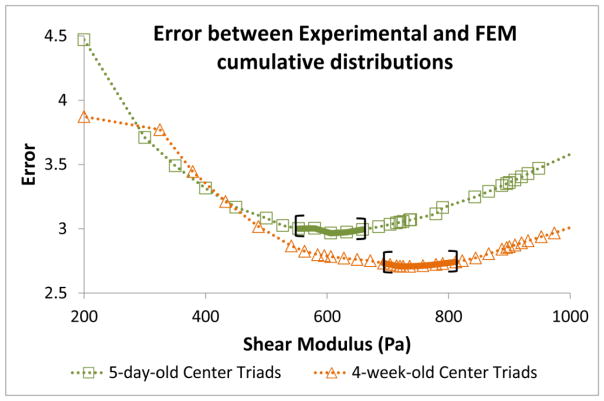
We simulated each infant 5-day-old and toddler 4-week-old transection experiment with over 30 different brain shear modulus values to empirically determine the 5-day-old and 4-week-old brain modulus at high strain and strain rates. The modulus for each age group was identified as the value that corresponded to the lowest model error (Equation 3) calculated from the deformation metrics computed by the transected FEM and compared to those measured in the experimental transection studies (Figure 4). However, our analysis revealed that for each of these minimum error values, there was a range of moduli (brackets, Figure 8) that performed with similar KS goodness of fit. Therefore, we determined a range of optimized moduli, defined as having error terms within 1.5% of the minimum calculated error, which were 553-658 Pa for the 5-day-old and 692-811 Pa for the 4-week-old (used subsequently for the 2-month-old FEM).

Figure 8.

Model error, as defined by Equation 3, calculated from the experimental and FEM cumulative distributions as a function of brain tissue shear modulus. The range of moduli resulting in the lowest model error, within 1.5% of the minimum error value, is bracketed for each age.

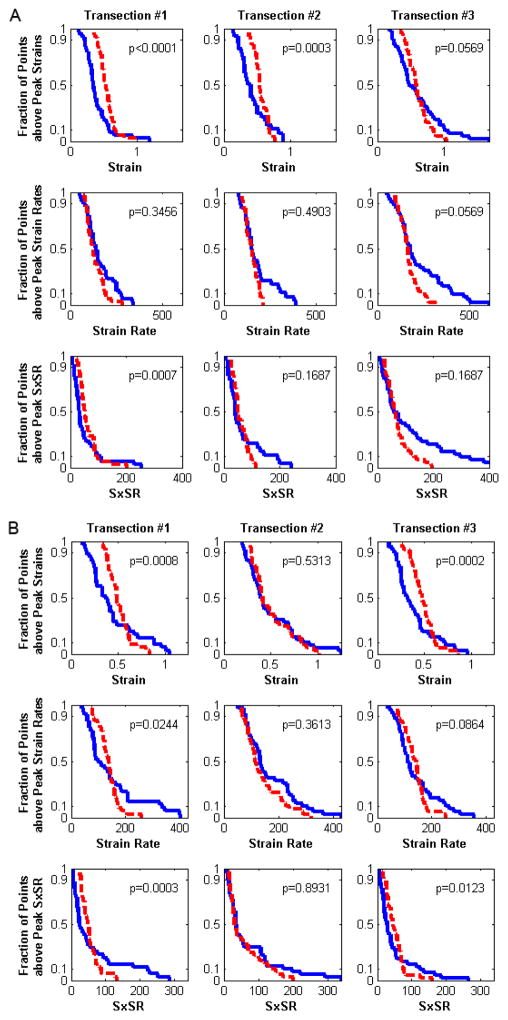
We observed relatively good statistical correlation between FEM-predicted and experimentally-derived deformation metric distributions within the optimized range of moduli for each age group (Figure 9). The number of well-matched distributions remained the same throughout the optimized range of moduli, but decreased for moduli outside this range in each age group. For the 9 distributions examined (3 experiments × 3 outcome metrics) 6 out of 9 for the 5-day-old and 4 out of 9 for the 4-week-old had well-matched FEM and experimental data. In general, SR were better fit by the FEM predictions than S, with at least 2 of 3 transection studies having statistically indistinguishable experimental and FEM distributions by the KS test for SR, but only 1 of 3 transection studies for S. Overall, the FEM-predicted strain magnitudes were similar to experimentally measured strains, with an absolute mean error of ±0.15 between measured and modeled peak strains.

Figure 9.

(A) 5-day-old and (B) 4-week-old experimentally-derived (blue solid lines) and FEM-predicted (red dashed lines) cumulative distributions for the lowest optimized modulus values (553Pa and 692Pa, respectively). A KS test p-value for each distribution comparison of greater than 0.05 indicates that the two populations are a good-fit.

The range of moduli for the 5-day-old is similar to the modulus (526.9 Pa) measured previously in ex vivo shear tests performed at large strains but much lower strain rates. However, the range of moduli for the 4-week-old is more than 2 times higher than previously measured values from 4-week-old and 2-month-old brain tissue (216.5–295.7 Pa). (Prange and Margulies 2002) This difference suggests greater strain and strain rate dependencies in the shear modulus of the older brain than in the younger brain.

3.2. Tissue Strain Brain Injury Prediction Results

The full brain FEM for each age was used to predict tissue strain (S), strain rate (SR), and SxSR metrics during rotational loading conditions from actual animal experiments. Each simulation was run twice, using either the lowest or highest value in the optimized modulus range derived during the reverse engineering optimization process (Section 3.1). The values for each metric exceeded by 10% (Pop10), 50% (Pop50), and 90% (Pop90) of the nodes were extracted from each metric distribution as cumulative measures of the deformation experienced by the brain tissue (Figure 6). Parameters were generated from the 3 population levels (Pop10, Pop50, and Pop90) of the 3 deformation metrics (S, SR, and SxSR) using the 3 analysis methods (peak metric values over the entire forebrain, peak metric values restricted to the white matter tracts (WMT), and peak tract-oriented metric values) (Tables 3 and 4).

Table 3.

5-day-old model ROC AUC values for the 27 tested parameters. For each parameter, the first value listed used a brain shear modulus of 553Pa, and the second value used a shear modulus of 658Pa. AUC values closer to 1.0 have better sensitivity and specificity.

5-day-old	AUC
	Pop 10	Pop 50	Pop 90
Forebrain S	0.78-0.77	0.84-0.84	0.80-0.80
Forebrain SR	0.69-0.69	0.73-0.73	0.83-0.88
Forebrain SxSR	0.72-0.70	0.8-0.79	0.82-0.85
WMT S	0.84-0.84	0.83-0.83	0.85-0.86
WMT SR	0.73-0.70	0.69-0.70	0.69-0.74
WMT SxSR	0.86-0.79	0.77-0.75	0.81-0.81
Tract-oriented S	0.56-0.55	0.93-0.92	0.98-0.98
Tract-oriented SR	0.59-0.59	0.91-0.94	1-1
Tract-oriented SxSR	0.59-0.58	0.97-0.97	1-1

Bold values indicate the best predictors across both ages.

Table 4.

2-month-old model ROC AUC values for the 27 tested parameters. For each parameter, the first value listed used a brain shear modulus of 692Pa, and the second value used a shear modulus of 811Pa. AUC values closer to 1.0 have better sensitivity and specificity.

2-month-old	AUC
	Pop 10	Pop 50	Pop 90
Forebrain S	0.68-0.70	0.77-0.80	0.85-0.89
Forebrain SR	0.92-0.92	0.88-0.89	0.97-0.98
Forebrain SxSR	0.82-0.83	0.83-0.85	0.92-0.95
WMT S	0.67-0.67	0.70-0.71	0.92-0.97
WMT SR	0.89-0.89	0.77-0.82	0.91-0.97
WMT SxSR	0.71-0.74	0.73-0.74	0.95-0.97
Tract-oriented S	0.56-0.56	0.92-0.91	1-1
Tract-oriented SR	0.74-0.74	0.95-0.95	1-1
Tract-oriented SxSR	0.62-0.65	0.94-0.98	1-1

Bold values indicate the best predictors across both ages.

The distributions of traumatic axonal injury (TAI) quantified from the corresponding animal experiments were compared with each of the 27 parameters to determine the parameter(s) most predictive of injury and the corresponding threshold(s) using receiver operating characteristic (ROC) area under the curve (AUC) (Metz 1978) analysis. Animals with TAI levels >0.18% total tissue area were considered injured, whereas animals with lower levels of TAI had clinically undetectable injury (Naim et al. 2010) and were considered uninjured, for the purposes of threshold development.

Most parameters performed well (Tables 3 and 4) with ROC AUC values >0.7, while some parameters performed very well with AUC values approaching 1. In general, the Pop90 parameters had higher AUC values than the Pop50 and Pop10 parameters in both age groups, indicating that the overall deformations experienced by the majority of brain tissue (Pop90) better predicted the presence of TAI than the median (Pop50) or most extreme (Pop10) deformations. In addition, the forebrain and WMT-only S, SR, and SxSR metrics performed similarly to each other in both age groups, but the tract-oriented metrics performed much better than these for Pop50 and Pop90. The overall best predictors of injury in both age groups were Pop90 tract-oriented S, SR and SxSR, with AUC values of 0.98–1 for each of these parameters.

The AUC values did not vary significantly with brain shear modulus within the optimized range (Tables 3 and 4). The largest differences when changing from the lower to higher modulus were a decrease in AUC from 0.86 to 0.79 for WM SxSR pop10 in the 5-day-old and an increase in AUC from 0.91 to 0.97 for WMT SR Pop90 in the 2-month-old. Furthermore, the brain injury thresholds developed from each of the deformation parameters also did not vary much with shear modulus (Tables 5 and 6).

Table 5.

5-day-old model threshold values for the 27 tested parameters. For each parameter, the first value listed used a brain shear modulus of 658Pa, and the second value used a shear modulus of 553Pa.

5-day		Pop10 Thresholds		Pop50 Thresholds		Pop90 Thresholds
		Youden’s Index	100% Sensitivity	Youden’s Index	100% Sensitivity	Youden’s Index	100% Sensitivity
Forebrain	S	0.834–0.884	0.624–0.679	0.529–0.586	0.321–0.349	0.198–0.228	0.182–0.194
	SR (s−1)	253–281	253–267	150–157	150–157	82.3–85.0	77.0–81.9
	SxSR (s−1)	117–140	117–140	58.9–68.0	33–37.5	10.1–11.8	10.1–11.8
WMT	S	0.803–0.849	0.487–0.526	0.574–0.609	0.305–0.327	0.330–0.365	0.212–0.227
	SR (s−1)	191–200	191–200	239–239	119–124	99.1–105	66.1–69.2
	SxSR (s−1)	117–136	58.7–69.0	59.3–63.5	25.6–29.2	22.7–23.4	10.1–11.4
Tract- oriented	S	0.513–0.553	0.284–0.303	0.168–0.182	0.147–0.158	0.060–0.065	0.060–0.065
	SR (s−1)	221–224	135–139	82.0–85.2	77.0–79.6	38.1–40.0	38.1–40.0
	SxSR (s−1)	68.6–76.6	22.9–26.7	8.16–9.33	6.78–7.59	1.39–1.62	1.39–1.62

Bold values indicate the thresholds associated with the best predictors across both ages.

Table 6.

2-month-old model threshold values for the 27 tested parameters. For each parameter, the first value listed used a brain shear modulus of 811Pa, and the second value used a shear modulus of 692Pa.

2-month		Pop10 Thresholds		Pop50 Thresholds		Pop90 Thresholds
		Youden’s Index	100% Sensitivity	Youden’s Index	100% Sensitivity	Youden’s Index	100% Sensitivity
Forebrain	S	0.887–0.944	0.629–0.682	0.482–0.625	0.356–0.379	0.170–0.184	0.170–0.184
	SR, s−1	299–315	299–315	181–182	154–155	79.9–87.6	78.7–79.9
	SxSR, s−1	248–274	108–120	46.8–59.4	34.1–38.1	11.0–11.8	11.0–11.8
WMT	S	0.846–0.892	0.526–0.564	0.504–0.634	0.341–0.363	0.260–0.314	0.236–0.247
	SR, s−1	249–278	201–213	167–171	121–125	75.3–77.8	73.2–75.3
	SxSR, s−1	139–146	65.3–74.4	47–53.1	25.5–28.3	11.7–20.0	11.7–12.0
Tract- oriented	S	0.357–0.382	0.310–0.333	0.185–0.200	0.158–0.172	0.065–0.071	0.065–0.071
	SR, s−1	136–141	136–141	87.9–89.3	71.0–73.7	38.3–38.7	38.3–38.7
	SxSR, s−1	23.7–27.5	23.7–27.5	8.15–9.57	6.92–8.15	1.56–1.83	1.56–1.83

Bold values indicate the thresholds associated with the best predictors across both ages.

The S, SR, and SxSR tissue thresholds for brain injury in each age group were similar between the entire forebrain and the WMTs only (Tables 5 and 6), suggesting all areas of the brain FEM experienced similar levels of deformation during rotation. In contrast, the corresponding tract-oriented S, SR, and SxSR threshold values were much lower, frequently 50–75% smaller, indicating that maximum principal strain in the FEM only rarely aligned with WMT fiber orientation. Thus, much higher overall tissue strains were required to achieve threshold-levels of WMT tensile strain. These results also suggest a greater risk of injury when the principal strains are oriented in the direction of the WMTs.

Brain injury thresholds for each parameter were similar between the infant 5-day-old and pre-adolescent 2-month-old piglet age groups, particularly with the most predictive parameters of Pop90 tract-oriented S, SR, and SxSR, for which the range of thresholds established by the range of FEM shear moduli overlap between the two age groups.

The thresholds associated with the best predictors of brain injury were tested using a randomly designated independent 5-day-old validation group (Table 7). The prediction performance with this validation group was the same across the entire range of thresholds tested. The overall predictive capability was high (≥89% for SR and SxSR), with similar sensitivity and somewhat lower specificity in the validation group than in the derivation group. Differences in predictive performance underscore the necessity of rigorous independent validation groups.

Table 7.

Threshold performance in the 5-day-old validation group of the optimal derived predictors of brain injury. For each threshold, the first value listed used a brain shear modulus of 553Pa, and the second value used a shear modulus of 658Pa.

5-day-old validation		Threshold Range	Sensitivity	Specificity	NPV	PPV
Tract-oriented	Pop90 S	0.065–0.060	100%–88%	0%–25%	n/a–50%	67%–70%
	Pop90 SR	40.0-38.1	100%	75%	100%	89%
	Pop90 SxSR	1.62-1.39	100%	75%	100%	89%

The correlation analysis revealed significant correlations between percentage of TAI and Pop90 tract-oriented S, SR, and SxSR in both age groups with correlation coefficients ranging from 0.69 to 0.78 (p<0.002 for all). Tract-oriented SR had the highest correlation coefficient for both ages (Table 8). A representative graph showing the correlation for tract-oriented SR is shown in Figure 10.

Table 8.

Correlation between TAI and tract-oriented S, SR, and SxSR for all 5-day-old and 2-month-old simulations.

Age	Pop90 Tract-oriented S	Pop90 Tract-oriented SR	Pop90 Tract-oriented SxSR
5d	ρ=0.69 p<0.0001.	ρ=0.76 p<0.0001.	ρ=0.75 p<0.0001
2m	ρ=0.71 p<0.0015	ρ=0.78 p<0.0002	ρ=0.71 p<0.0014

Figure 10.

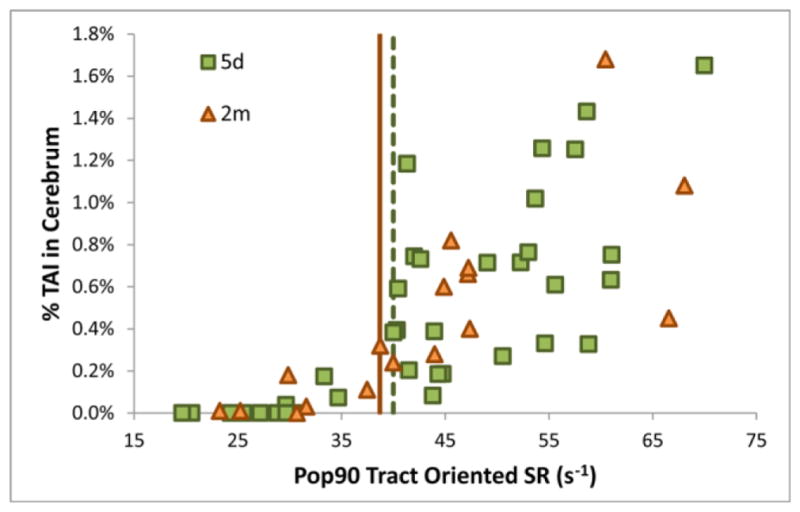
Correlation between %TAI in the forebrain and Pop90 for tract-oriented SR. The tract-oriented SR thresholds (using the lowest brain shear moduli) are shown for the 5-day-old (dashed green vertical line at 40s⁻¹) and 2-month-old (solid orange vertical line at 38.7s⁻¹).

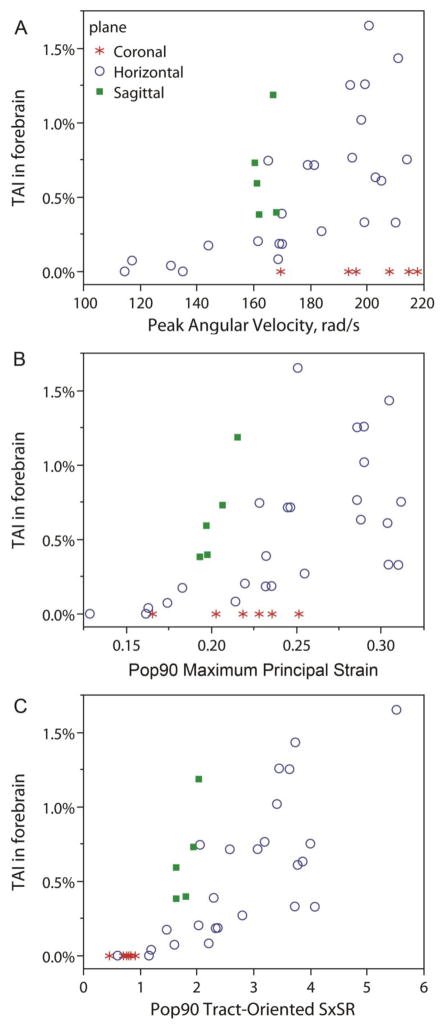
It has been previously observed in this 5-day-old and 2-month-old piglet dataset that coronal plane rotations result in significantly less TAI than horizontal or sagittal rotations at similar levels of rotational velocity and acceleration. (Eucker et al. 2011; Maltese 2012b) Consequently, the correlation between peak angular velocity and percent TAI is poor (ρ=0.35, p=0.0384), in part due to the lack of axonal injury from high velocity coronal rotations (Figure 11a). One hypothesis for this directional dependence is that coronal plane rotations produce lower overall levels of strain than the counterpart horizontal and sagittal plane rotations. The differences in strain are due to the geometrical asymmetry of the brain, such that the distance from the brain’s center of mass to the center of rotation using this injury device is shorter in coronal rotations than in horizontal and sagittal rotations. Indeed, percent TAI correlates better with Pop90 maximum principal strain (ρ=0.55 p=0.0005) than with peak angular velocity. However, these lower maximum principal strains seen with coronal rotations are still similar to strains observed in lower velocity horizontal and sagittal rotations where the animals sustain much higher levels of TAI (Figure 11b). These results suggest the decreases in forebrain tissue maximum principal strain are insufficient to explain the absence of TAI sustained during coronal rotations. The correlation between percent TAI and Pop90 tract-oriented SxSR is the strongest (ρ=0.75 p<0.0001), and the tract-oriented S, SR, and SxSR from coronal rotations are consistent with animals experiencing head rotations in other directions with no resulting axonal injury (Figure 11c). This result demonstrates that the maximum principal strains are not aligned with the fiber tracts during coronal rotations, and thus, TAI resulting from tensile deformation along the axon is minimal in this plane of rotation.

Figure 11.

Correlation between %TAI in the forebrain and (A) peak angular velocity, (B) Pop90 maximum principal strain, and (C) Pop90 tract-oriented SxSR by rotational plane.

4. Discussion

Brain shear modulus derived from in situ experiments

Brain tissue material properties are highly dependent on age, strain and strain rate. Therefore, we employed a novel method for optimizing the brain material properties at the large strains and strain rates associated with diffuse traumatic axonal injury. In situ tissue deformations were measured at appropriate ages, strains and strain rates, and the initial brain shear modulus was tuned to match the finite element and experimental deformations, yielding a range of appropriate shear moduli. The 5-day-old piglet, which developmentally corresponds to a human infant, had a modulus range of 553-658 Pa validated against in situ experiments with peak strains as high as 100–150% and mean tissue strains of ~50%, as well as peak strain rates as high as 400–600 s⁻¹ and mean strain rates of 150–200 s⁻¹. This range of moduli is very similar to ex vivo infant brain material properties published by others at shear strains of 0.5% to 50% and shear strain rates of 0.1s⁻¹ to 8.33s⁻¹. (Chatelin et al. 2012; Prange and Margulies 2002; Thibault and Margulies 1998) These studies demonstrated that shear testing across a range of strain magnitudes at constant strain rate produced little change in the infant shear modulus, suggesting that the infant shear modulus is insensitive to shear strain magnitude. (Prange and Margulies 2002; Thibault and Margulies 1998) Our study goes a step further to reveal that initial shear modulus values at high strain rates are very similar to those measured during ex vivo testing at substantially lower rates, demonstrating that the infant shear modulus is also relatively insensitive to strain rate.

Toddler aged human (22 month old) and porcine (4 week old) brain samples have both been shown to exhibit similar material properties to adult samples, (Chatelin et al. 2012; Prange and Margulies 2002) emphasizing that the primary change in brain material properties occurs during development from infant to toddler. However, previous studies have generated controversy regarding whether the more mature brain is softer or stiffer than the infant brain. Our results now shed light on this controversy by confirming strain and strain rate dependencies of mature brain tissue that are absent in the infant brain, and result in a reversal of relative brain stiffness between the two ages over the range of deformations producing TAI. The shear modulus of the mature brain has been shown to exhibit softening at higher strain magnitudes (Prange and Margulies 2002; Thibault and Margulies 1998) and stiffening at higher strain rates (Chatelin et al. 2010; Thibault and Margulies 1998) and our current results show the infant tissue displays neither characteristic. Consequently, under low shear strain (0.5% to 5%) and strain rate (0.1 to 20 s⁻¹) conditions the mature brain has been measured to be stiffer than the infant brain. (Chatelin et al. 2012; Thibault and Margulies 1998) But as the strain magnitude is increased (up to 50% shear strain) at low rates, the mature brain softens while the infant brain is insensitive to this change, and the modulus of the mature brain is measured to be lower than the infant brain under these conditions. (Prange and Margulies 2002) As the strain rate is increased (up to 300 s⁻¹), we now report that the toddler/mature brain stiffens to be slightly stiffer (692-811 Pa) than the infant brain (553-658 Pa). Future studies could explore the tissue-level conformational and compositional mechanisms responsible for age-dependent differences in the shear modulus strain and strain rate sensitivities. We conclude that because of the complex, non-linear interaction between strain, strain rate, and shear modulus for the mature brain, it is important to consider the anticipated strain and strain rate magnitudes when selecting appropriate material properties for future computational investigations.

Best predictors of clinical traumatic axonal injury (TAI)

We compared 27 different deformation metrics to identify the best predictor for the presence of clinical TAI in infant 5-day-old and pre-adolescent 2-month-old piglet models of TBI. Overall, we found that smaller peak deformations experienced by the vast majority of the tissue (Pop90) were better predictors of TAI than the median levels of deformation (Pop50), or the highest deformations experienced by only 10% of the brain (Pop10). The relative protection against small rapid fluctuations in deformation may be due to the limited area of tissue comprised of axons, CSF and/or blood volume shifts, or the viscous component of the brain tissue response. Alternatively, Pop90 may represent a better measure of the total energy delivered to the tissue than Pop10 and Pop50, with higher total energy producing a greater degree of injury.

Our population analysis of strain metrics is similar to another finite element based predictor, the cumulative strain damage measure (CSDM). (Takhounts et al. 2003; Takhounts et al. 2008) Our method of identifying the Pop90 strain level has an advantage over the CSDM in that it produces empirically-derived thresholds rather than requiring a pre-determined strain threshold in order to calculate an a priori measure such as CSDM. Whereas the Pop90 values in this work depict the strain level exceeded by 90% of the brain FEM, the cumulative strain damage measure presents the percent of the brain FEM that exceeded a particular pre-defined strain threshold. For example, the CSDM_0.1=80% means that 80% of the brain exceeds 0.1 maximum principal strain. Because our Pop90 values were better predictors of TAI than Pop50 or Pop10 overall, basing CSDM on lower strain thresholds (resulting in high CSDM values) should be better predictors of TAI. Consistent with this logic, the original CSDM development examined strain thresholds from 0.15 to 0.5 and concluded that the lowest cerebral tissue strain threshold of 0.15 with CSDM value of over 55% was the most predictive of severe diffuse structural axonal injury in the adult brain. Importantly, tissue strain was not as good a predictor as tract-oriented strain and strain rate suggesting potential improvement to the CSDM metric.

We hypothesized that the tensile component of strain oriented along the WMT is the most important factor in predicting TAI in the piglet. While Pop10 metrics were poor predictors of TAI across the board, for both Pop50 and Pop90, and both ages studied, the tract-oriented deformation metrics predicted the presence of TAI better than the maximum deformation metrics. Chatelin et al. similarly found a much better correlation between patterns of DAI documented historically in human patients and distribution of maximum axonal strains than with maximum overall tissue strain. (Chatelin et al. 2011) It is worth noting that we did not see incremental improvement in the prediction of TAI by looking only at the elements that comprised the WMT, but only saw improved predictions of TAI when the component of the deformation along the WMT was considered. This finding lends further support to our hypothesis that tensile strain along the axon is the mechanical insult which leads directly to traumatic axonal injury.

Comparison of TAI threshold by age

Differences in susceptibility to brain injury among the pediatric population have been noted by many studies. Comparing TAI 6 hours post-injury in infant 5-day-old⁵⁴ and toddler 4-week-old⁵⁵ piglets that experienced comparable head rotational kinematics scaled to account for age-related differences in brain mass, the 5-day-old had 1.2–1.8 times greater volume of TAI than the 4-week-old. The 5-day-old piglet tract-oriented S and SxSR thresholds for TAI in this study were 1.09–1.12 times lower than those of 2-month-old piglets, which is consistent with these previous findings that the infant brain is more vulnerable to TAI than older children. However, the SR thresholds were the same across both ages. Taken together, this suggests that infant 5-day-old piglets are slightly more vulnerable to strain-induced TAI than older pediatric piglets, but have a similar sensitivity to strain rate. In a detailed analysis of porcine brain development (Dickerson and Dobbing 1967), investigators noted rapid changes between 6 weeks before birth and 5 weeks after, with rapid increases in cellularity, followed by rapid increases in lipid deposition accompanied by myelination, and decreases in water content. Future studies may address whether these changes in composition may be associated with alterations in tissue deformation responsible for axonal injury.

Comparison of TAI threshold with published data

Unlike principal strain, which was much higher than tract-oriented strain thresholds, the tract-oriented strain thresholds for injury (6% to 7.1%) are similar to, but slightly lower than injury thresholds derived from in vivo and in vitro stretch of isolated axons. The most comparable axonal stretch study, an in vivo study of guinea pig optic nerve stretch by Bain and Meaney, found an optimal strain threshold of 21% for structural white matter damage as measured by the evidence of axonal swelling or retraction bulbs with NF68 and SMI 32 staining. (Bain and Meaney 2000) Because our tract-oriented strain threshold derived in this study was based on β-APP associated the white matter damage, it is not surprising that the threshold is considerably lower than a structural damage threshold. These data support previous side-by-side comparisons between damage assessments with β-APP and NF68. (Ibrahim et al. 2010b) Other in vitro idealized experimental preparations have shown evidence of injury at less than 10% strain, supporting our tract-oriented strain threshold of 6–7%. Specifically, Morrison et al. used stretched hippocampal slice cultures to develop a model of cell death as a function of strain and found that Lagrangian strains of 5% predicted 13–21% cell death in the hippocampus at 4 days post injury. (Cater et al. 2006) An in vivo study of stretched spinal nerve roots showed that 9% strain was needed for a 50% probability of complete conduction block in the nerve root under the highest strain rate tested (15 mm/s). (Singh et al. 2009)

The tract-oriented strain rate thresholds for TAI were even better predictors of injury and performed better in the validation group than tract-oriented strain alone. Many, but not all, axonal stretch experimental studies have found a strain rate dependency in the formation of injury. (Broglio et al. 2010; Shi and Whitebone 2006; Singh et al. 2009) The in vivo experiments with spinal nerve roots showed an increasing level of β-APP positive staining with increasing strain rate at each strain level tested. They further found that the strain threshold for injury decreased at higher testing rates, which supports the concept of including both strain and strain rate in a composite metric to predict axonal injury. (Singh et al. 2009) Studies involving micropatterned neuronal cell cultures with axons grown through microchannels on a stretchable membrane have also investigated axonal injury at different strain and strain rate magnitudes. (Broglio et al. 2010; Tang-Schomer et al. 2012) At low strain rates (0.01 s⁻¹), axons were able to stretch up to twice their original length and return back to their pre-stretched length without damage, while at higher strain rates (44 s⁻¹) they would display multiple regions of undulating distortions, which would evolve into regions of axonal swelling and accumulations of APP similar to pathology seen in acute severe TBI in humans. These areas of axonal swelling were also seen to be coincident with sites of microtubule breakages observed by transmission electron microscopy. A mathematical model of the axon which incorporated its viscoelastic microstructure derived a strain rate threshold for axonal injury between 22 and 44 s⁻¹, which agrees very closely with the tract-oriented strain rate threshold we found for TAI of 38 to 40 s⁻¹. (Pellman et al. 2003a) We conclude that tract-oriented deformation thresholds for injury derived through finite element modeling of the in vivo brain are comparable to axonal injury thresholds derived through in vitro and in vivo controlled axonal stretch studies.

TAI and tract-oriented strain by rotational plane

Many studies have noted that the rotational direction of the head during injury plays an important role in the development and severity of head injury. (Broglio et al. 2010; Eucker et al. 2011; Gennarelli et al. 1982; Pellman et al. 2003a; Sullivan et al. 2013) Eucker et al. reported that sagittal and horizontal head rotations in immature piglets resulted in significantly more TAI than coronal rotations, which did not produce significant TAI, and postulated that this was due to differences in the tissue mechanical loading for each rotational direction. (Eucker et al. 2011) We used an immature piglet FEM to investigate the tissue deformations for all three rotational directions and found that maximum principal strains did not discriminate between head rotation directions, and did not correlate well with axonal injury at 6 hours post-TBI (Figure 11b). However, the component of the deformation oriented along the WMT had the best correlation with axonal injury (Figure 11C). The small tensile deformations experienced by the WMTs during coronal rotations explains why there is so little TAI present after injury in this direction in our piglet model.

In contrast to our piglet model, TBI studies in subhuman primates showed severe diffuse axonal injury after coronal plane rotations. (Gennarelli et al. 1982) We speculate that this difference in the directional sensitivity to TAI between upright baboons and quadruped pigs may be due to different orientations of the white matter tracts relative to anatomic planes of symmetry, such that in the piglet brain coronal rotations do not produce strains aligned with the WMTs whereas in the primate brain the orientation could be such that coronal rotations do produce strains aligned with the WMTs and thus result in significant TAI.

5. Limitations

Several limitations deserve mention. First, while we were able to compare the FEM predictions of maximum principal strain and strain rate to experimentally measured values, we could not measure the WMT orientation in the in situ experiments, and thus, could not compare the FEM values for tract-oriented deformation directly against experimental data. Instead we show that the tract-oriented thresholds are similar to those experimentally derived in axon stretch studies. Second, during the reverse engineering optimization of the brain moduli, the boundary condition between the plexiglass plate and brain in the transected FEM was assumed to be frictionless with no out-of-plane motion. It is possible that the interaction between the brain, lubricant, and plexiglass was not completely frictionless, thus, the model may have slightly overestimated the tissue strains. Third, although we accounted for the change in the white matter orientation as the skull moved within the global coordinate system, we did not adjust the WMT direction vector to account for changes in its orientation due to the tissue motion, which could result in either over or under estimations of the tract-oriented deformation. Future studies should implement a method to reorient the WMT directions to account for tissue movement, which should give improved estimates of the axonal deformation. Fourth, our model performance has been validated for brain distortion and axonal injury in the frontal, parietal and temporal lobes and the midbrain. Because no tentorium was included, caution should be exercised in other regions, including the occiput and cerebellum, where we rarely, if ever, observe traumatic axonal injury in our non-impact porcine model of TBI. (Eucker et al. 2011; Ibrahim et al. 2010b; Raghupathi and Margulies 2002)

Lastly, we approximate the brain as homogeneous and isotropic, despite empirical evidence that the brain is heterogeneous and anisotropic. (Chatelin et al. 2010; Ning et al. 2006; Prange and Margulies 2002) Although brainstem is highly oriented, with 10-fold larger stiffness along the fibers (Ning et al. 2006), the corona radiata, which is more representative of the white matter tracts in this report, is only 1.4-fold stiffer along the fiber direction than perpendicular to it (Prange and Margulies 2002). In our idealized FEM representation, the anatomical detail of the white matter tracts was incorporated into our analysis by computing the oriented axonal strain, rather than by using an anisotropic constitutive model. In support of this approach, several studies have demonstrated better approximation of axonal strain using an isotropic representation for white matter and fiber orientation obtained from DTI, than von Mises stress or maximum principal strain. (Horgan 2004; Mao et al. 2010; Wright and Ramesh 2012) Other studies did note a slight increase in axon tensile strains when gray and white matter property distinctions were included compared to global isotropy, (Cloots et al. 2012; Cloots et al. 2013; Colgan et al. 2010) however, these differences were small when compared with differences between maximum principal tissue strain and tract-oriented strain. (Giordano et al. 2014) Importantly, when we compare our oriented axonal strain injury thresholds to in vitro thresholds, we find very good concurrence, underscoring that the axon-oriented strain distribution is resolved reasonably well with the isotropic model.

Our objective was that the FE model development and confirmation approach presented here may be used by investigators to develop human FE brain models for use in motor vehicle, military and sport safety equipment design in a way that is computationally efficient and practicable in the industrial engineering setting. Thus, we developed a somewhat implified model that included a smoothed cortical surface, isotropic and homogeneous brain material, and rigid skull, to make a parsimonious FE brain model with a reasonably short computation time. As computational capability increases, additional complexity (e.g. higher resolution, inclusion of heterogeneity and anisotropy) can be implemented to achieve improved correlation with in vitro and in vivo injury outcomes. Taken together, we feel that the isotropic material model predicts injury with reasonable confidence and has important value as an initial investigation.

6. Conclusions

We have derived a range of brain moduli for the infant and older child/adult brain suitable for use in high strain and strain rate finite element simulations, that should be confirmed in future material testing studies. We found that the infant brain is relatively insensitive to changes in strain and strain rate, while the more mature brain exhibits softening at increased strains and stiffening at increased strain rates. Our results emphasize the importance of selecting age-, strain- and strain-rate appropriate brain material properties, and the value of confirming that FEM predictions mimic actual tissue deformation.

We have also derived and validated a highly sensitive and specific threshold for functional traumatic axonal injury in the infant and older child/adult. The tract-oriented SxSR was a much better predictor of TAI than maximum principal strain. This finding supports the premise that TAI is due to tensile strains along the axon. The tract-oriented strain thresholds for injury in the infant were slightly lower than in the older child suggesting an age-related vulnerability to TAI. Finally, our hypothesis that rotational directions resulting in greater TAI will have larger tract-oriented strains than rotational directions resulting in less TAI was confirmed. Combined, these data demonstrate the value and improved accuracy when using white matter tract-oriented deformation metrics in FEM studies of axonal injury.